Multiple Kernel Stein Spatial Patterns for the Multiclass Discrimination of Motor Imagery Tasks
Abstract
1. Introduction
2. Methods
2.1. EEG Decomposition
2.2. Time-Series Similarity through the Stein Kernel for PSD Matrices
2.3. Spatial Filter Optimization Using Centered Kernel Alignment
2.4. Assembling of Multiple Kernel Representations
3. Experimental Setup
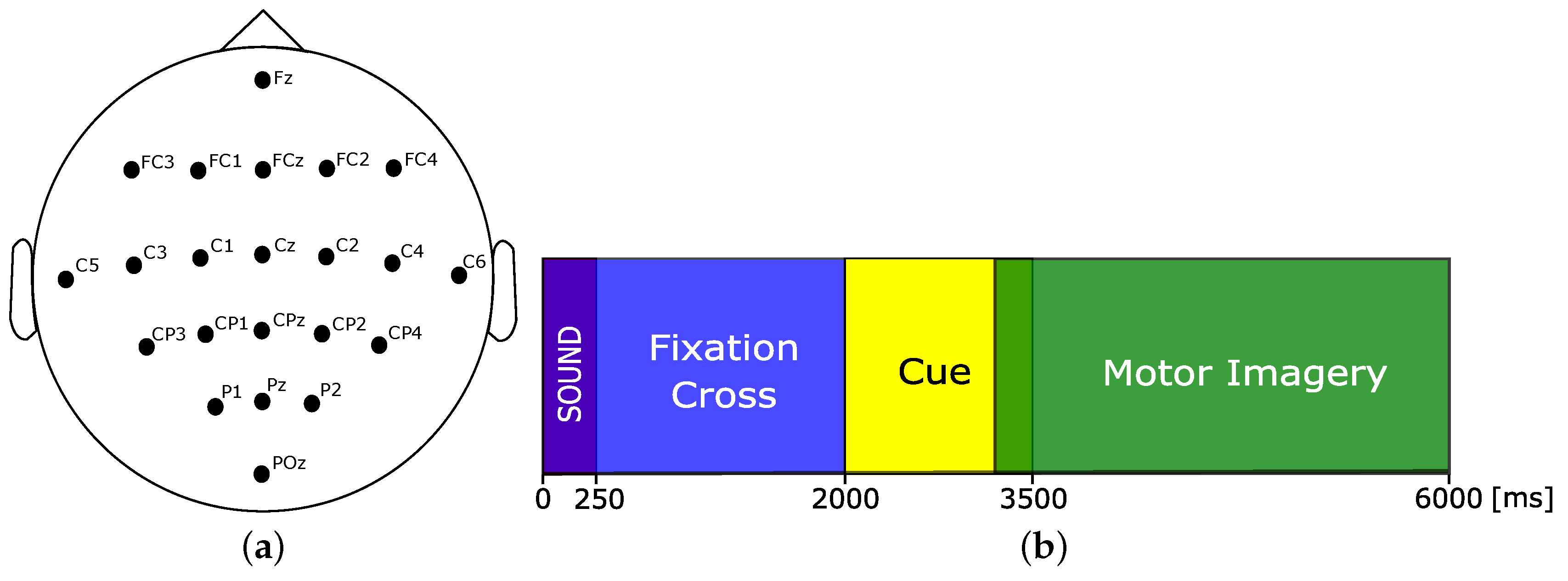
3.1. Dataset IIa from BCI Competition IV (BCICIV2a)
3.2. Proposed BCI Methodology
4. Results
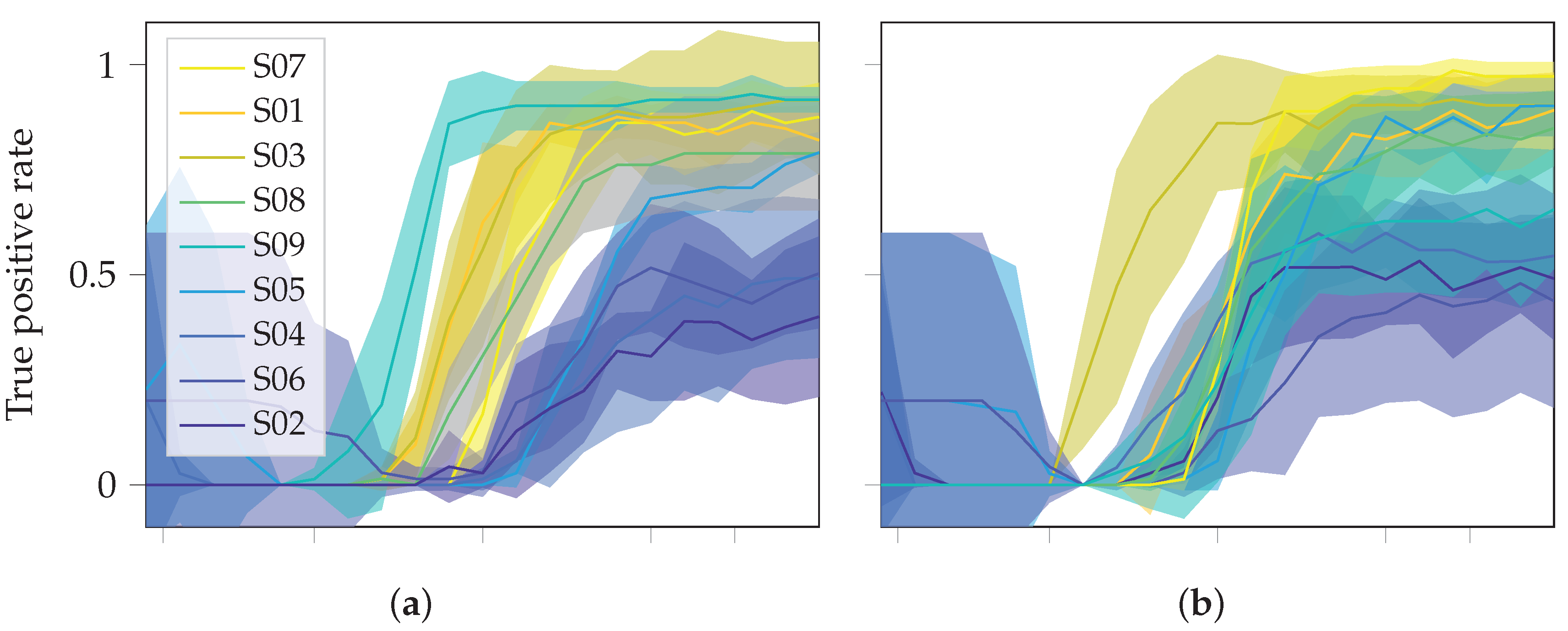
4.1. Performance Results
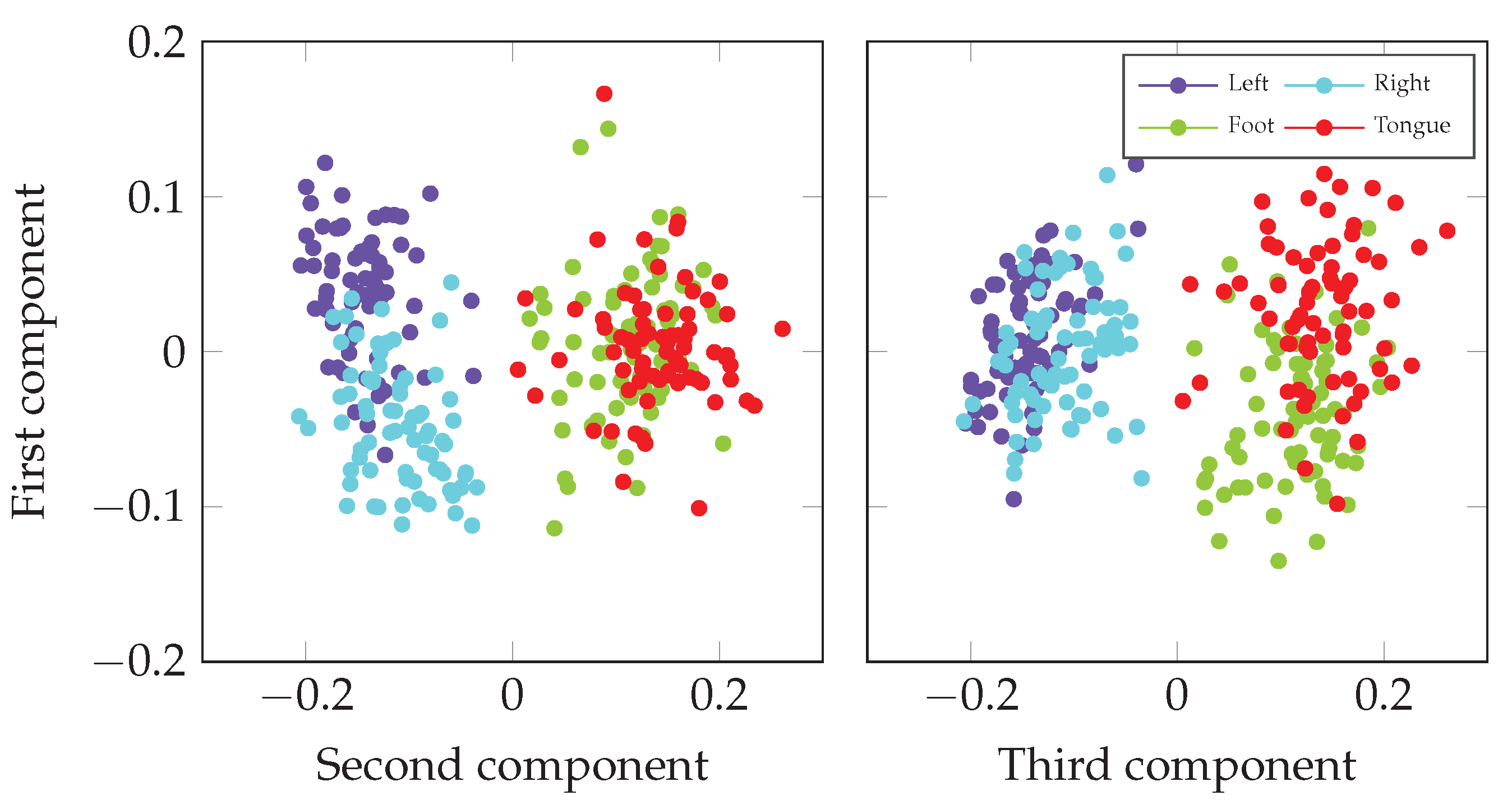
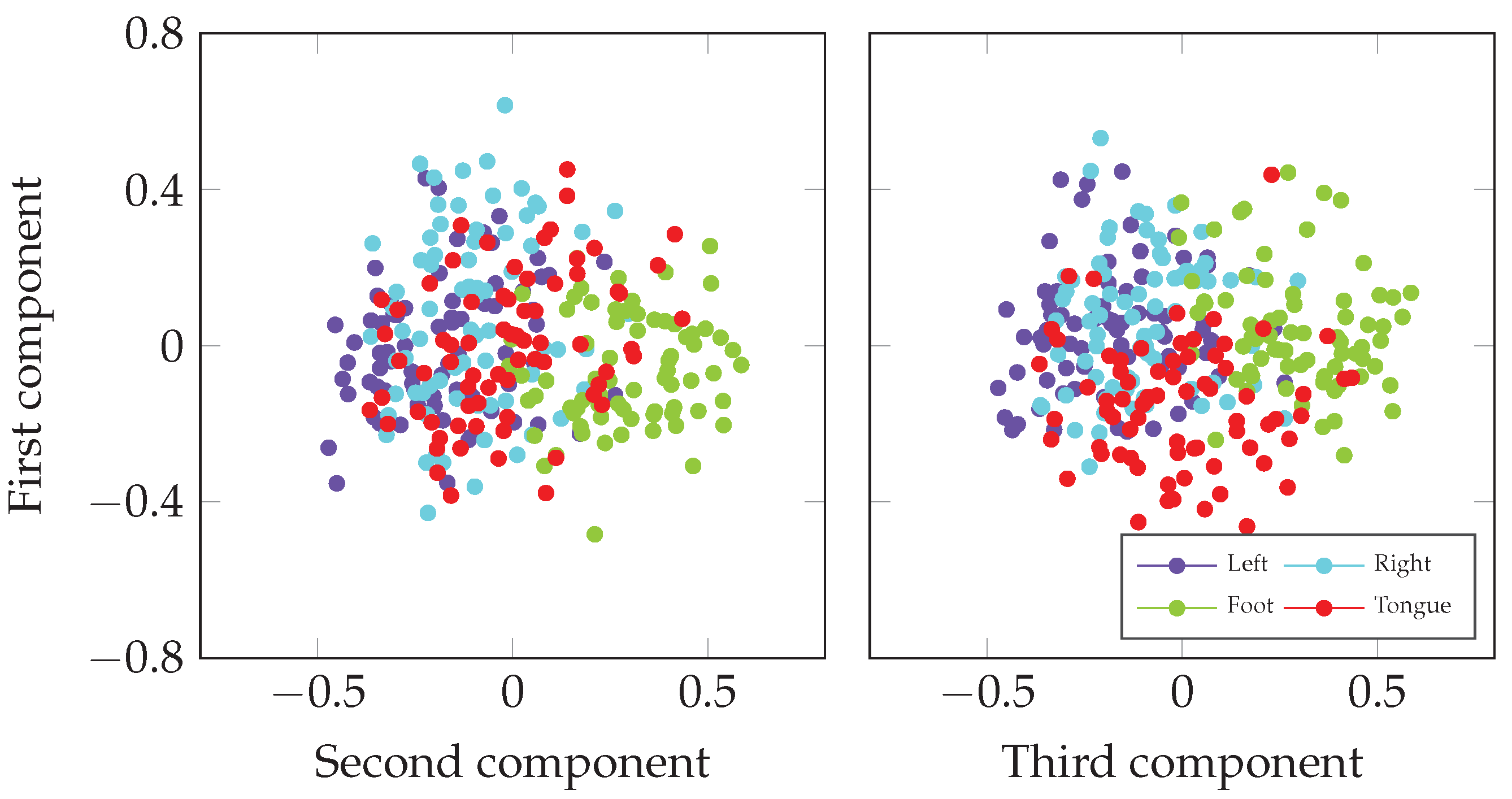
4.2. Model Interpretability
5. Discussion and Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BCI | Brain–Computer Interface |
| EEG | Electroencephalography |
| MI | Motor Imagery |
| CSP | Common Spatial Pattern |
| SPD | Symmetric Positive Definite |
| CKA | Centered Kernel Alignment |
| MKL | Multiple Kernel Learning |
| MKSSP | Multi-Kernel Stein Spatial Patterns |
References
- Chaudhary, U.; Birbaumer, N.; Ramos-Murguialday, A. Brain–computer interfaces for communication and rehabilitation. Nat. Rev. Neurol. 2016, 12, 513. [Google Scholar] [CrossRef] [PubMed]
- Ang, K.K.; Guan, C. Brain–computer interface for neurorehabilitation of upper limb after stroke. Proc. IEEE 2015, 103, 944–953. [Google Scholar] [CrossRef]
- Lazarou, I.; Nikolopoulos, S.; Petrantonakis, P.C.; Kompatsiaris, I.; Tsolaki, M. EEG-based brain–computer interfaces for communication and rehabilitation of people with motor impairment: A novel approach of the 21st century. Front. Hum. Neurosci. 2018, 12, 14. [Google Scholar] [CrossRef] [PubMed]
- Kilteni, K.; Andersson, B.J.; Houborg, C.; Ehrsson, H.H. Motor imagery involves predicting the sensory consequences of the imagined movement. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef]
- Krusienski, D.J.; Grosse-Wentrup, M.; Galán, F.; Coyle, D.; Miller, K.J.; Forney, E.; Anderson, C.W. Critical issues in state-of-the-art brain–computer interface signal processing. J. Neural Eng. 2011, 8, 025002. [Google Scholar] [CrossRef] [PubMed]
- Ang, K.K.; Guan, C. EEG-based strategies to detect motor imagery for control and rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 392–401. [Google Scholar] [CrossRef]
- Blankertz, B.; Tomioka, R.; Lemm, S.; Kawanabe, M.; Muller, K.R. Optimizing spatial filters for robust EEG single-trial analysis. IEEE Signal Process. Mag. 2007, 25, 41–56. [Google Scholar] [CrossRef]
- Ang, K.K.; Chin, Z.Y.; Wang, C.; Guan, C.; Zhang, H. Filter bank common spatial pattern algorithm on BCI competition IV datasets 2a and 2b. Front. Neurosci. 2012, 6, 39. [Google Scholar] [CrossRef]
- Lemm, S.; Blankertz, B.; Curio, G.; Muller, K.R. Spatio-spectral filters for improving the classification of single trial EEG. IEEE Trans. Biomed. Eng. 2005, 52, 1541–1548. [Google Scholar] [CrossRef]
- Dornhege, G.; Blankertz, B.; Krauledat, M.; Losch, F.; Curio, G.; Muller, K.R. Combined optimization of spatial and temporal filters for improving brain-computer interfacing. IEEE Trans. Biomed. Eng. 2006, 53, 2274–2281. [Google Scholar] [CrossRef]
- Novi, Q.; Guan, C.; Dat, T.H.; Xue, P. Sub-band common spatial pattern (SBCSP) for brain-computer interface. In Proceedings of the 2007 3rd International IEEE/EMBS Conference on Neural Engineering, Kohala Coast, HI, USA, 2–5 May 2007; pp. 204–207. [Google Scholar]
- Torres-Valencia, C.; Orozco, A.; Cárdenas-Peña, D.; Álvarez-Meza, A.; Álvarez, M. A Discriminative Multi-Output Gaussian Processes Scheme for Brain Electrical Activity Analysis. Appl. Sci. 2020, 10, 6765. [Google Scholar] [CrossRef]
- Chu, Y.; Zhao, X.; Zou, Y.; Xu, W.; Song, G.; Han, J.; Zhao, Y. Decoding multiclass motor imagery EEG from the same upper limb by combining Riemannian geometry features and partial least squares regression. J. Neural Eng. 2020, 17, 046029. [Google Scholar] [CrossRef] [PubMed]
- López-Montes, C.; Cárdenas-Peña, D.; Castellanos-Dominguez, G. Supervised Relevance Analysis for Multiple Stein Kernels for Spatio-Spectral Component Selection in BCI Discrimination Tasks. In Iberoamerican Congress on Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2019; pp. 620–628. [Google Scholar]
- Davoudi, A.; Ghidary, S.S.; Sadatnejad, K. Dimensionality reduction based on distance preservation to local mean for symmetric positive definite matrices and its application in brain–computer interfaces. J. Neural Eng. 2017, 14, 036019. [Google Scholar] [CrossRef] [PubMed]
- Goh, A.; Vidal, R. Clustering and dimensionality reduction on Riemannian manifolds. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–7. [Google Scholar]
- Harandi, M.T.; Salzmann, M.; Hartley, R. From manifold to manifold: Geometry-aware dimensionality reduction for SPD matrices. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014; pp. 17–32. [Google Scholar]
- Fletcher, P.T.; Lu, C.; Pizer, S.M.; Joshi, S. Principal geodesic analysis for the study of nonlinear statistics of shape. IEEE Trans. Med Imaging 2004, 23, 995–1005. [Google Scholar] [CrossRef] [PubMed]
- Barachant, A.; Bonnet, S.; Congedo, M.; Jutten, C. Classification of covariance matrices using a Riemannian-based kernel for BCI applications. Neurocomputing 2013, 112, 172–178. [Google Scholar] [CrossRef]
- Jayasumana, S.; Hartley, R.; Salzmann, M.; Li, H.; Harandi, M. Kernel methods on Riemannian manifolds with Gaussian RBF kernels. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 2464–2477. [Google Scholar] [CrossRef]
- Bhatia, R. Positive Definite Matrices, Princeton Ser. In Applied Mathematics; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Nielsen, F.; Boltz, S. The burbea-rao and bhattacharyya centroids. IEEE Trans. Inf. Theory 2011, 57, 5455–5466. [Google Scholar] [CrossRef]
- Cortes, C.; Mohri, M.; Rostamizadeh, A. Algorithms for learning kernels based on centered alignment. J. Mach. Learn. Res. 2012, 13, 795–828. [Google Scholar]
- Lu, Y.; Wang, L.; Lu, J.; Yang, J.; Shen, C. Multiple kernel clustering based on centered kernel alignment. Pattern Recognit. 2014, 47, 3656–3664. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, G.; Jin, J.; Wang, X.; Cichocki, A. Optimizing spatial patterns with sparse filter bands for motor-imagery based brain–computer interface. J. Neurosci. Methods 2015, 255, 85–91. [Google Scholar] [CrossRef]
- Chin, Z.Y.; Ang, K.K.; Wang, C.; Guan, C.; Zhang, H. Multi-class filter bank common spatial pattern for four-class motor imagery BCI. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 571–574. [Google Scholar]
- Nicolas-Alonso, L.F.; Corralejo, R.; Gomez-Pilar, J.; Álvarez, D.; Hornero, R. Adaptive semi-supervised classification to reduce intersession non-stationarity in multiclass motor imagery-based brain–computer interfaces. Neurocomputing 2015, 159, 186–196. [Google Scholar] [CrossRef]
- He, L.; Hu, D.; Wan, M.; Wen, Y.; Von Deneen, K.M.; Zhou, M. Common Bayesian network for classification of EEG-based multiclass motor imagery BCI. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 843–854. [Google Scholar] [CrossRef]
- Sadatnejad, K.; Ghidary, S.S. Kernel learning over the manifold of symmetric positive definite matrices for dimensionality reduction in a BCI application. Neurocomputing 2016, 179, 152–160. [Google Scholar] [CrossRef]
- Kumar, S.U.; Inbarani, H.H. PSO-based feature selection and neighborhood rough set-based classification for BCI multiclass motor imagery task. Neural Comput. Appl. 2017, 28, 3239–3258. [Google Scholar] [CrossRef]
- Nguyen, T.; Hettiarachchi, I.; Khosravi, A.; Salaken, S.M.; Bhatti, A.; Nahavandi, S. Multiclass EEG data classification using fuzzy systems. In Proceedings of the 2017 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Naples, Italy, 9–12 July 2017; pp. 1–6. [Google Scholar]
- Gaur, P.; Pachori, R.B.; Wang, H.; Prasad, G. A multi-class EEG-based BCI classification using multivariate empirical mode decomposition based filtering and Riemannian geometry. Expert Syst. Appl. 2018, 95, 201–211. [Google Scholar] [CrossRef]
- Selim, S.; Tantawi, M.M.; Shedeed, H.A.; Badr, A. A CSP∖AM-BA-SVM Approach for Motor Imagery BCI System. IEEE Access 2018, 6, 49192–49208. [Google Scholar] [CrossRef]
- Razi, S.; Mollaei, M.R.K.; Ghasemi, J. A novel method for classification of BCI multi-class motor imagery task based on Dempster–Shafer theory. Inf. Sci. 2019, 484, 14–26. [Google Scholar] [CrossRef]
- Ai, Q.; Chen, A.; Chen, K.; Liu, Q.; Zhou, T.; Xin, S.; Ji, Z. Feature extraction of four-class motor imagery EEG signals based on functional brain network. J. Neural Eng. 2019, 16, 026032. [Google Scholar] [CrossRef]
- Zhang, R.; Zong, Q.; Dou, L.; Zhao, X. A novel hybrid deep learning scheme for four-class motor imagery classification. J. Neural Eng. 2019, 16, 066004. [Google Scholar] [CrossRef]
- Ang, K.K.; Guan, C.; Chua, K.S.G.; Ang, B.T.; Kuah, C.; Wang, C.; Phua, K.S.; Chin, Z.Y.; Zhang, H. A clinical evaluation on the spatial patterns of non-invasive motor imagery-based brain-computer interface in stroke. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 4174–4177. [Google Scholar]
- Liu, T.; Huang, G.; Jiang, N.; Yao, L.; Zhang, Z. Reduce brain computer interface inefficiency by combining sensory motor rhythm and movement-related cortical potential features. J. Neural Eng. 2020, 17, 035003. [Google Scholar] [CrossRef]




| Approach | S06 | S05 | S02 | S04 | S01 | S09 | S03 | S08 | S07 | p-Value | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Challenge winner [26] | 0.27 | 0.40 | 0.42 | 0.48 | 0.68 | 0.61 | 0.75 | 0.75 | 0.77 | 0.57 ± 0.17 | 0.0002 |
| SUSS-SRKDA [27] | 0.35 | 0.56 | 0.51 | 0.68 | 0.83 | 0.75 | 0.88 | 0.84 | 0.90 | 0.70 ± 0.18 | 0.0179 |
| CBN [28] | 0.42 | 0.78 | 0.51 | 0.85 | 0.69 | 0.45 | 0.87 | 0.97 | 0.54 | 0.68 ± 0.19 | 0.0577 |
| KPCA with CILK [29] | 0.37 | 0.26 | 0.46 | 0.44 | 0.71 | 0.61 | 0.76 | 0.75 | 0.79 | 0.57 ± 0.18 | 0.0009 |
| PSO [30] | 0.53 | 0.62 | 0.62 | 0.77 | 0.87 | 0.76 | 0.90 | 0.82 | 0.80 | 0.74 ± 0.12 | 0.0282 |
| CSP-FLS [31] | 0.37 | 0.35 | 0.54 | 0.52 | 0.74 | 0.80 | 0.90 | 0.86 | 0.82 | 0.66 ± 0.20 | 0.0146 |
| EMD+Riemann [32] | 0.34 | 0.36 | 0.24 | 0.68 | 0.86 | 0.82 | 0.70 | 0.75 | 0.66 | 0.60 ± 0.21 | 0.0050 |
| CSP/AM-BA-SVM [33] | 0.41 | 0.58 | 0.55 | 0.60 | 0.87 | 0.80 | 0.89 | 0.84 | 0.88 | 0.71 ± 0.17 | 0.0147 |
| Dempster–Shafer [34] | 0.57 | 0.67 | 0.59 | 0.72 | 0.78 | 0.88 | 0.85 | 0.86 | 0.81 | 0.75 ± 0.11 | 0.0084 |
| Functional brain [35] | 0.61 | 0.63 | 0.54 | 0.70 | 0.77 | 0.86 | 0.84 | 0.84 | 0.77 | 0.73 ± 0.11 | 0.0036 |
| CNN-LSTM [36] | 0.66 | 0.77 | 0.54 | 0.78 | 0.85 | 0.90 | 0.87 | 0.83 | 0.95 | 0.80 ± 0.12 | 0.3313 |
| sDPLM [15] | 0.36 | 0.34 | 0.49 | 0.49 | 0.75 | 0.76 | 0.76 | 0.76 | 0.68 | 0.60 ± 0.17 | 0.0008 |
| uDPLM [15] | 0.36 | 0.30 | 0.49 | 0.47 | 0.76 | 0.76 | 0.76 | 0.76 | 0.69 | 0.59 ± 0.18 | 0.0012 |
| Proposed MKSSP | 0.68 | 0.83 | 0.66 | 0.72 | 0.90 | 0.87 | 0.89 | 0.89 | 0.90 | 0.82 ± 0.09 | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galindo-Noreña, S.; Cárdenas-Peña, D.; Orozco-Gutierrez, Á. Multiple Kernel Stein Spatial Patterns for the Multiclass Discrimination of Motor Imagery Tasks. Appl. Sci. 2020, 10, 8628. https://doi.org/10.3390/app10238628
Galindo-Noreña S, Cárdenas-Peña D, Orozco-Gutierrez Á. Multiple Kernel Stein Spatial Patterns for the Multiclass Discrimination of Motor Imagery Tasks. Applied Sciences. 2020; 10(23):8628. https://doi.org/10.3390/app10238628
Chicago/Turabian StyleGalindo-Noreña, Steven, David Cárdenas-Peña, and Álvaro Orozco-Gutierrez. 2020. "Multiple Kernel Stein Spatial Patterns for the Multiclass Discrimination of Motor Imagery Tasks" Applied Sciences 10, no. 23: 8628. https://doi.org/10.3390/app10238628
APA StyleGalindo-Noreña, S., Cárdenas-Peña, D., & Orozco-Gutierrez, Á. (2020). Multiple Kernel Stein Spatial Patterns for the Multiclass Discrimination of Motor Imagery Tasks. Applied Sciences, 10(23), 8628. https://doi.org/10.3390/app10238628






