Estimating Cycling Aerodynamic Performance Using Anthropometric Measures

Abstract

Aerodynamic drag force and projected frontal area (A) are commonly used indicators of aerodynamic cycling efficiency. This study investigated the accuracy of estimating these quantities using easy-to-acquire anthropometric and pose measures. In the first part, computational fluid dynamics (CFD) drag force calculations and A (m²) values from photogrammetry methods were compared using predicted 3D cycling models for 10 male amateur cyclists. The shape of the 3D models was predicted using anthropometric measures. Subsequently, the models were reposed from a standing to a cycling pose using joint angle data from an optical motion capture (mocap) system. In the second part, a linear regression analysis was performed to predict A using 26 anthropometric measures combined with joint angle data from two sources (optical and inertial mocap, separately). Drag calculations were strongly correlated with benchmark projected frontal area (coefficient of determination R² = 0.72). A can accurately be predicted using anthropometric data and joint angles from optical mocap (root mean square error (RMSE) = 0.037 m²) or inertial mocap (RMSE = 0.032 m²). This study showed that aerodynamic efficiency can be predicted using anthropometric and joint angle data from commercially available, inexpensive posture tracking methods. The practical relevance for cyclists is to quantify and train posture during cycling for improving aerodynamic efficiency and hence performance.

1. Introduction

In road cycling, aerodynamic drag force (or ‘drag’) contributes to 70–90% of the resistance to the cyclist on level ground [1]. Improving cycling performance is a priority for elite and amateur cyclists. A wind tunnel is the gold standard for measuring aerodynamic force, drag area, and studying air flow behavior. However, a wind tunnel is not easily accessible or affordable even for elite athletes. Several alternative methods for measuring aerodynamic performance in athletes in controlled environments are described in the literature including photogrammetry [2]; power meters [3]; and air pressure and speed sensors [4,5]. The approach of computational fluid dynamics (CFD) has been used on models of cyclists and bicycles under various conditions to determine the optimum cyclist pose and selection of equipment and accessories [6,7,8,9,10] as well as the influence of aerodynamics during professional cycling races [11,12,13].

To use CFD in the field of cycling aerodynamics, two-dimensional (2D) or three-dimensional (3D) models of the cyclist and equipment are required. A 3D scanning device provides accurate models, but state-of-the-art scanning equipment is difficult to access for most athletes. Indirect methods to predict the 3D shape of a given human using select anthropometric data have been described in the literature [14,15,16,17]. If the 3D model of a cyclist is available, directly or indirectly, but not in a desirable pose configuration, it is possible to re-pose the model using animation techniques [18,19]. In this study, we used 3D models obtained from an algorithm [16,17] and re-posed them to various pose configurations to investigate if the cyclist aerodynamic drag could be predicted by a combination of anthropometric data and CFD analyses.

Aerodynamic drag force F (N) on an object moving through a fluid is given by

F = 0.5 ∙ C_D ∙ ρ ∙ v² ∙ A,

(1)

where C_D is the drag coefficient, a dimensionless quantity that is a function of Reynold’s number, Mach number, the form drag and skin friction of the object (C_D is generally found from experiment); ρ is the air density at a given pressure and temperature (kg/m³); v is the velocity of air relative to the object (m/s); and A is the projected frontal area of object (m²).

Projected frontal area of the cyclist is the biggest factor influencing drag during cycling (up to 90%) [8] where the cyclist accounts for up to 70% and the rest is accounted for by the bicycle [20]. The importance of the projected frontal area as a key metric for cycling performance has been stressed in the literature, with several methods proposed for measurement and estimation including (digital) photogrammetry, planimetry, wind tunnel tests, and field tests [21,22,23,24,25].

The projected frontal area of a cyclist depends upon the shape and pose of the cyclist. The shape of a human can be estimated from anthropometric measures or features as described in [26]. The pose of a human can be uniquely described by a set of joint angles. In this study, we combined the shape and pose information to ultimately predict the projected frontal area of a cyclist. We did this by first predicting the 3D shape of 10 participants in a standardized (standing) pose using basic body measures. 3D shapes of the participants in the cycling pose will be produced using joint angle information using motion capture (mocap). From these final shapes, the projected frontal area can be calculated.

Anthropometric measures in this study were recorded manually by the researchers. Joint angles were recorded using two mocap techniques: optical and inertial. Optical mocap systems are considered the gold standard for human mocap [27], but it is typically restricted to indoor settings. Bike-fitting and aerodynamic analysis usually take place in indoor environments, where several outdoor conditions are neglected [28]. Analyzing cycling movements in realistic outdoor circumstances would be an added value. Therefore, mocap using inertial measurement units (IMUs), which have been shown as reliable for human mocap, can be used for this application [27]. The advantage of inertial mocap is that full body joint angles in multiple degrees of freedom can be provided continuously and analyzed directly in real-time or afterward.

The aim of this study was to investigate low-cost and easy-to-deploy methods to predict the drag and projected frontal area of cyclists using rudimentary anthropometric and joint angle data. Using information that is easy to acquire even by untrained personnel, we provide a proof of principle that aerodynamic analyses and pose-training can be done at home, indoors, potentially outdoors, and for various pose configurations at scale.

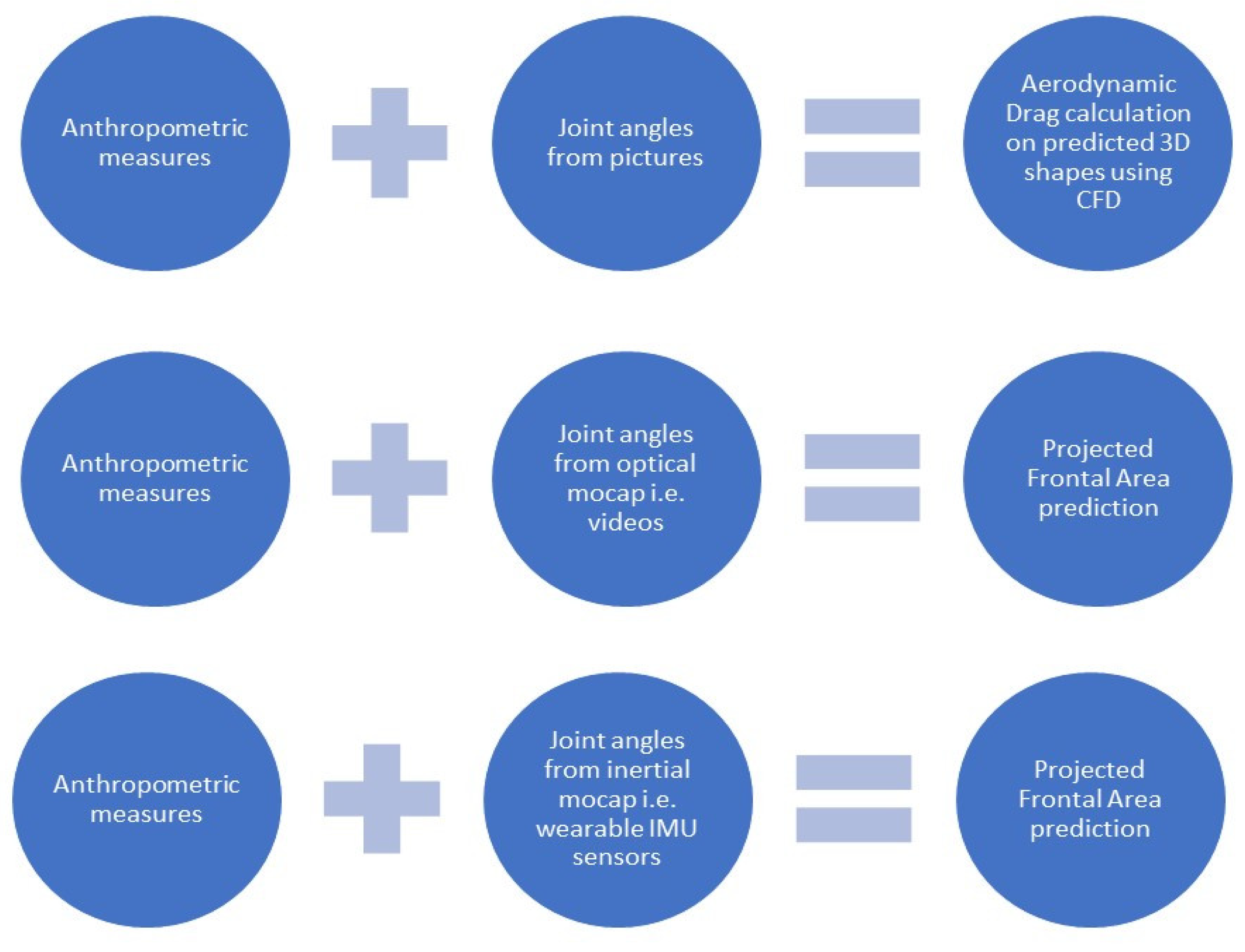
2. Materials and Methods

2.1. Participants

Ten male amateur cyclists were recruited in the study (n = 10, age = 32.5 ± 6.7 years, body height = 176.1 ± 5.8 cm and body mass = 74.6 ± 15.1 kg). Ethical approval and consent were obtained prior to the measurements (17/21/261, Ethics Committee, University of Antwerp, Antwerp, Belgium).

Table 1. List of participant data that was recorded from measurements and optical and inertial motion capture.

Anthropometric Data (cm)		2D Joint Angles Optical Mocap (°)	3D Joint Angles Inertial Mocap (°)
Body Height	Shoulder Breadth (acromion)	Left Knee	Left Knee
Chest Circumference	Hip Breadth (standing)	Left Elbow	Left Shoulder
Under-Bust Circumference	Chest Circumference (scye)	Left Hip	Left Elbow
Waist Circumference (minimum)	Hip Circumference	Back	Right Knee
Waist Circumference (trousers)	Arm Circumference (scye)	Head	Right Shoulder
Neck Circumference (shirt)	Shoulder Breadth (bideltoid)	Left Shoulder	Right Elbow
Neck Circumference (tight, hull)	Hip Breadth (sitting)		Neck (2D)
Lower Arm Circumference (mid, Hull)	Upper Arm Length		Left Hip
Biceps Circumference Hull	Lower Arm Length		Right Hip
Spine-Shoulder Length	Sternum to Femur Length		Pelvis
Arm Length	Upper Leg Length		Left Wrist
Back Length (shirt)	Lower Leg Length		Right Wrist
Torso Length (shirt)	Body Mass (kg)		Chest
Age (years)	Gender (m/f)

lists the anthropometric parameters collected from tape measures by one researcher corresponding with the ISAK guidelines as well as ISO 8559 guidelines.

2.2. Optical Mocap

The camera of a smartphone (Lenovo Group Limited, China) was used to record 2D angles of the participant. The camera, which could record pictures as well as videos (at 30 Hz), was positioned on the left-hand side of the participant at a fixed distance, with the lens parallel to the sagittal plane of the participant. The images and videos were analyzed for joint angles using an open-source image-processing algorithm (Detectron, Facebook AI Research, Facebook Inc., USA) to identify the human in frame, the major joints of the skeleton, and the lines between the joints. The joint centers were defined as (Figure 1a): ankle joint as the lateral malleolus, knee joint as the patella, hip joint as the greater trochanter, shoulder joint as the acromion, elbow joint as the lateral epicondyle, and wrist joint as the lunate bone. Based on the joint coordinates, flexion/extension angles were determined (Table 1). Joint angles of the right-hand side of the participants were provided by the algorithm, but were excluded from analyses to avoid unreliable data induced by parallax errors.

The projected frontal area of the participants was captured using an infrared depth-sensing camera (Intel^® RealSense™ Depth Camera D415, Intel Corporation, Mountain View, CA, USA) with a sampling frequency of 3 Hz placed in front of the cyclist (Figure 2). Furthermore, an average of ten iterations was calculated to eliminate the influence of noise and different pedal position [29].

2.3. Inertial Mocap

The inertial sensors comprised of a set of 11 wearable units (Figure 1b) (Notch Interfaces Inc., Brooklyn, NY, USA) strapped to various body segments of the participant (Figure 3). The units consisted of accelerometers, gyroscopes, and magnetometers. The accuracy of the IMUs was 2° for yaw, pitch, and roll rotations, whereas the accuracy of the whole system was optimized by considering several factors such as a correct steady pose, a tight fit of the sensors during the measurements, and avoiding magnetic interference from the environment. They were calibrated to continuously obtain 3D joint angle measurements of knees, hips, shoulders, elbows, wrists, neck, pelvis, and chest (full list in Table 1). Hip and pelvis joint angles were excluded from the analysis since the hip strap moves during cycling due to unavoidable contact with the upper legs and this induced errors in recording angles.

2.4. Protocol

Participants were asked to follow a series of instructions on a road bike (Btwin, Decathlon S.A., Lille, France) fixed on a stationary mount. All participants were provided with tight-fitting clothing. The experiment consisted of:

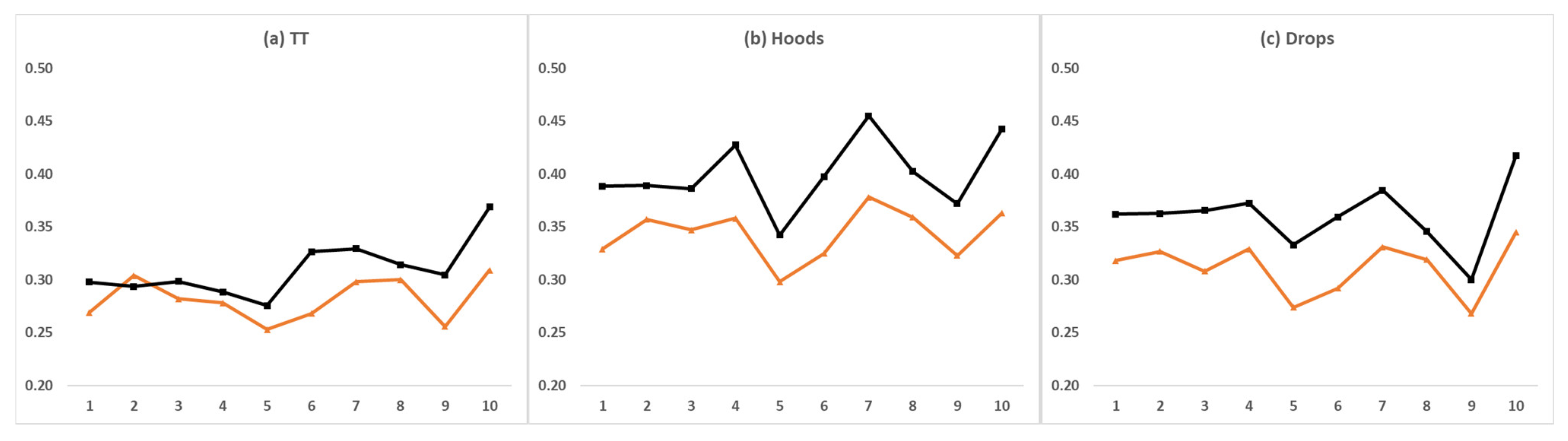
• Static protocol, where the instruction was to maintain three poses (Figure 3) for at least five seconds each, with the right leg extended to the bottom of the pedal stroke:
  • Time Trial (TT): race pose with arms resting horizontally on the clip-on handlebars;
  • Hoods: relaxed pose with hands on the hoods of the handlebar; and
  • Drops: race pose with hands on the dropped handlebars.

For each pose, a picture with the sagittal camera and a frontal camera were simultaneously recorded.

2.

Dynamic protocol, which lasted roughly two minutes per participant. The cyclists were instructed to pedal at a cadence of roughly 1 Hz and position their hands on the handlebar hoods and:

• bend their back from the highest possible to lowest possible inclination and back over 30 s;
• pronate knees from closest to farthest from top tube and back over 30 s;
• extend neck from lowest possible to highest possible angle and back over 30 s; and
• proceed to perform 30 s of comfortable cycling.

Along with a video recording at a rate of 30 frames per second from the sagittal camera, the projected area (3 Hz) and joint angles from IMUs were registered continuously (10 Hz).

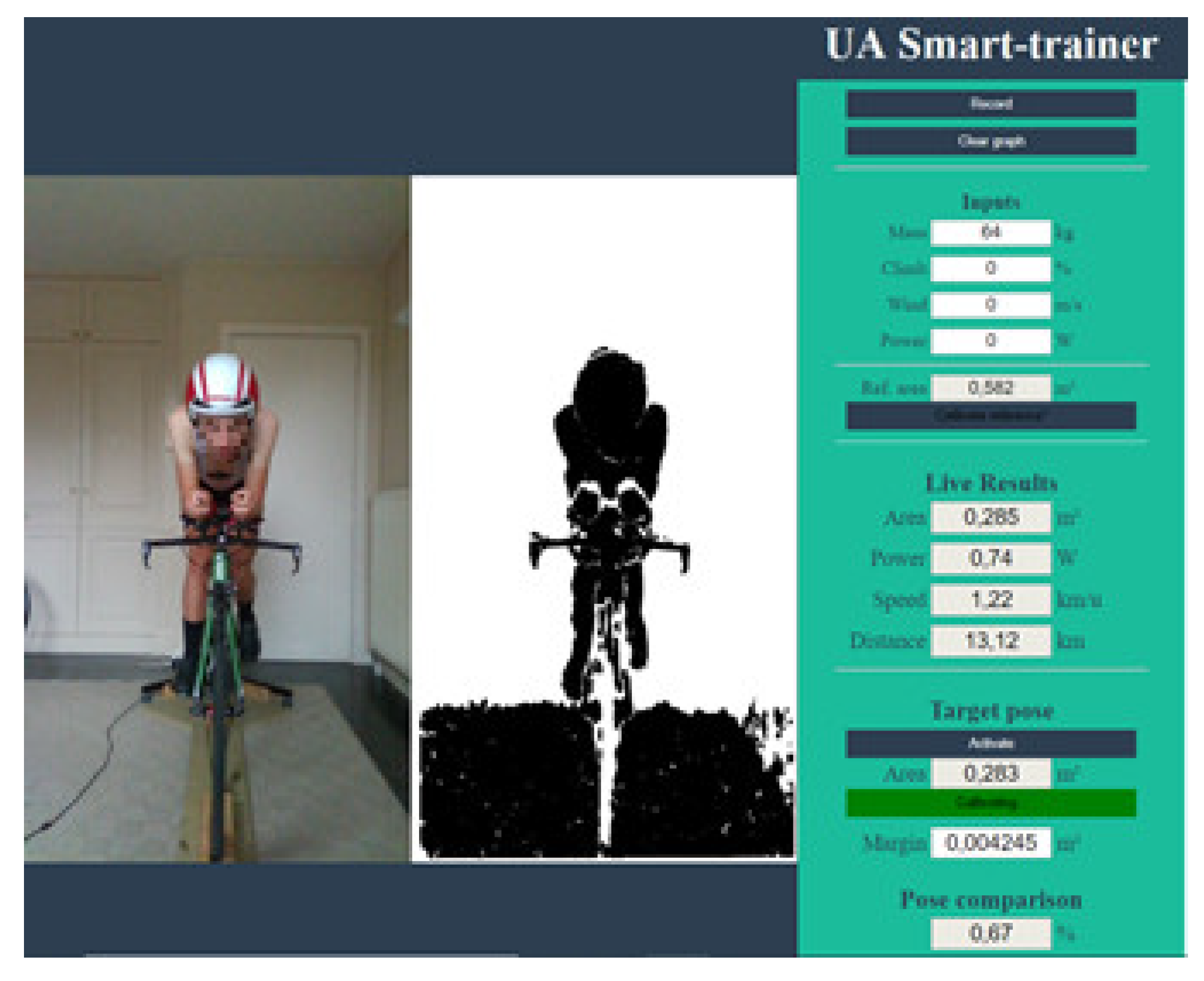
2.5. Procedure

The measurements from the static protocol were used to investigate the relation between CFD drag force and benchmark projected frontal area. Predicted 3D models of the participants in a standing pose were obtained using anthropometric measures. These models were re-posed to the cycling pose using the angles from the optical mocap and were used in CFD analysis to calculate drag force.

Second, the data from the dynamic protocol were used to perform a regression analysis with the aim to predict the projected frontal area based on anthropometric data and joint angles. Figure 4 shows an overview of the methods.

2.5.1. 3D Models

The models were generated using a statistical shape model using the methodology described in the literature [17]. The method utilizes a partial least square regression between body measurements and principal component analysis (PCA) components. Using this method, given a set of measurements (in this study: age, gender, body height, body mass, chest circumference, hip circumference maximum, and arm length), we can obtain PCA components that can be used to predict a 3D shape of a human body. The database and body measurements are described in [16]. Each model is a combination of 100 (PCA) components with a corresponding weight (or ‘score’) attached to each component. The model provides the best-fit human shape for the given inputs. The physical meaning of individual components is not readily apparent, but the relevant modes will be discussed in the Results section.

The 3D models were obtained in a standardized standing ‘A-pose’ (Figure 5). Since all models in the statistical shape model were registered to match certain body landmarks (i.e., joints), it was easy to rig a skeleton in the 3D models (Figure 6a). The skeleton was based on the models proposed by the International Society of Biomechanics and was optimized using large datasets of 3D human scans in different poses.

Using joint angles from the optical mocap, the standing models were re-posed to TT, Hoods, and Drops poses (Figure 6b,c) using animation software (Blender, Blender Foundation, Amsterdam, The Netherlands). The skeleton in the optical mocap method had fewer bones compared to the skeleton of the predicted 3D models. The angles from the optical mocap were accordingly adjusted to fit the 3D model skeleton (e.g., the back was modeled as one straight bone as a simplification). We assumed that the upper body of the 3D models were symmetric, as instructed to the participants. Hence, the left-hand side upper body angles were sufficient for re-posing these models to the unique pose of every participant. The pictures were used as a reference when required.

Projected frontal area of the 3D models was calculated using drawing software (PTC Creo, PTC Inc., Boston, MA, USA). This data will be compared to the benchmark projected frontal area obtained from the depth sensing camera.

2.5.2. Computational Fluid Dynamics (CFD) Analysis

CFD calculations on the 3D models were conducted (Star CCM+, Siemens Industry Software Inc., Plano, TX, USA) in a domain that consisted of a wind tunnel of 6.5 m × 2.5 m × 2.5 m (L × B × H), modeled after a wind tunnel facility [30]. Cyclist models were positioned at 2 m from the inlet of the test section, with the models ‘facing’ the opposite direction of the wind. The surface of the objects was assumed to be uniform and smooth. The bicycle was not included in the CFD domain. We adopted parameters based on previous literature [1], which are summarized in

Table 2. List of parameters for computational fluid dynamics (CFD) analysis.

Parameter	Value
Air Viscosity	1.81 × 10−5 Pa∙s
Inlet Velocity/ Air Speed U∞ (free stream)	16.7 m/s = 60 km/h
Outlet Pressure	0 Pa (static)
Temperature	295.3 K
Relative Humidity	39.9 %
Atmospheric Pressure	100,480 Pa
Saturation Vapor Pressure	269,225.2 Pa
Air Density	1.181 kg/m³
Turbulence Model	Shear Stress Transport (SST) k-ω
Meshers	Polyhedral
	Surface Remesher
	Prism Layer Mesher
Base Cell Size	0.15 m
Prism Layers	5
Reynolds number Re	1.33 × 106
L (dimension of object)	<1 m
C, f (skin friction coefficient)	3.46 × 10−3
Wall Shear Stress τ	2.84 × 10−1 m/s
U* (dimensionless velocity)	4.91 × 10−1 m/s
Y (first layer cell height)	0.00281304 m
Y+	90
δ (prism layer height)	0.039 m

.

The size of individual cells in the domain determines total cell count, accuracy, and computation time. For a given domain, a lower base cell size implies higher mesh resolution and accuracy, but implies longer computational time. To obtain the least base cell size for which reliable drag values can be calculated, a mesh convergence study was conducted. We investigated drag for one cyclist model in the domain over 700 iterations each with base cell sizes of 0.1500 m, 0.1000 m, 0.080 m, 0.060 m, 0.050 m, and 0.0039 m. The results of the mesh convergence study revealed that the average drag for the last 50 iterations for the model in each of these domains was 32.75 N, 33.53 N, 31.96 N, 32.23 N, 33.97 N, and 32.35 N. It was concluded that the drag force obtained from the calculations at a base cell size of 0.15 m (~200,000 cells) can provide reliable results for the sake of obtaining trends in drag area at a significantly lower computational time (an average duration of 90 min per simulation, which is roughly 70% faster than the same for the finest mesh). To obtain a high degree of absolute accuracy of modeling the air flow (e.g., a detailed visualization of the wake of the cyclist), we recommend a higher resolution in the domain. However, the aim of the present study was to estimate drag area and compare trends therein with values reported in the literature.

2.5.3. Regression Analyses

The regression between the drag force of the 3D models and the projected area from the frontal camera is a simple least squares method to fit the data.

For the second part, the projected frontal area and joint angles data were first synchronized using a hand raise at the beginning of the dynamic protocol. At this point, the projected frontal area reached a maximum, which was matched with a maximal back/chest and elbow flexion angle. Furthermore, the projected frontal area had a sample rate of 3 Hz, whereas it was 30 Hz for the optical mocap and 10 Hz for the inertial mocap. To align the data, average values of one-second intervals were used. One subject was excluded due to an error in projected frontal area calculation, resulting in a total of 914 data points in the final regression analyses.

Two linear regression models were generated to predict the projected frontal area based on different input data, consisting of

(1)

anthropometric data (Table 1), 2D joint angles from the optical mocap system (Table 1), and the weights of the first 20 principal components of body shape; and

(2)

anthropometric data and joint angles from the inertial mocap system (Table 1).

The stepwise linear regression method (SPSS Statistics 27, IBM, Armonk, NY, USA) was used to define the optimal model. From the optimal model, the importance of each included variable in the equation was analyzed using standardized beta coefficients.

To determine the accuracy of both regression models, the equation was cross-validated by subsequently leaving the data of one subject out to form a linear regression equation and applying these results to the excluded subject, repeating this procedure for each subject. The cross-validated prediction values were compared with the actual projected frontal area to determine the intraclass correlation coefficient (ICC) [31,32]. The two-way-random ICC-model, type absolute agreement, was calculated for the entire dataset. Furthermore, the root mean square error (RMSE) (m²) projected frontal area between the prediction and actual values was calculated as well as the relative error of the predicted value compared to the actual projected frontal area.

3. Results

3.1. Drag Force versus Projected Frontal Area

Aerodynamic drag force from the CFD simulations of the 3D models of all 10 participants is shown in

Table 3. Drag force of the 3D models from the Static protocol. C_D was obtained by using Equation (1) and the area from the projected frontal area camera.

	Participant	1	2	3	4	5	6	7	8	9	10
TT	Drag (N)	28.79	26.81	27.49	26.94	26.84	29.59	31.30	28.71	29.86	35.71
	CD	0.70	0.58	0.64	0.63	0.69	0.72	0.69	0.63	0.76	0.76
Hoods	Drag (N)	37.43	35.99	37.31	44.23	31.80	39.07	45.03	36.13	35.97	41.67
	CD	0.74	0.66	0.70	0.81	0.70	0.79	0.78	0.66	0.73	0.75
Drops	Drag (N)	32.29	33.15	32.40	32.56	30.07	33.99	35.08	31.32	25.99	40.01
	CD	0.66	0.66	0.69	0.65	0.72	0.76	0.69	0.64	0.63	0.76

. Using these and the corresponding projected frontal area, drag coefficients C_D can be obtained from Equation (1) as air density and wind velocity are known and are constant (Table 2). These C_D values are also listed in Table 3. Drag force is plotted with projected frontal area in Figure 7. This area was compared with area from the depth camera and the comparison per pose is shown in Figure 8. The regression analysis of drag and corresponding area for all poses (3 poses × 10 participants = 30 data points) yielded a coefficient of determination of R² of 0.72.

3.2. Projected Frontal Area Prediction Based on Anthropometrics and Joint Angles

The regression model to predict the projected frontal area (m²) using anthropometric data (cm), 2D joint angles (°) from the optical mocap, and the scores associated with the 20 principal components of the 3D body shape is shown in Equation (2). The regression model based on inertial joint angles is shown in Equation (3). The adjusted R² value corresponding to Equation (2) is 0.78 (p < 0.001) and 0.81 (p < 0.001) for Equation (3).

Projected Frontal Area (Optical) = 0.166678 + 0.000505 × Back Flexion + 0.000075 × Score 6 + 0.005565 × Upper Arm Length + 0.000326 × Left Elbow Flexion + 0.001023 × Neck Circumference (tight) − 0.000188 × Head Flexion − 0.00335 × Hip Breadth (sitting) + 0.000805 × Left Hip Flexion + 0.000393 × Left Knee Flexion − 0.002276 × Lower Arm Length + 0.000176 × Left Shoulder Flexion,

(2)

Projected Frontal Area (Inertial) = −0.322372 + 0.006888 × Neck Circumference (tight) − 0.000998 × Chest Anterior Tilt − 0.00027 × Neck Flexion + 0.002636 × Shoulder Breadth (Acromion) + 0.005635 × Lower Arm Length + 0.000704 × Chest Lateral Tilt + 0.012827 × Upper Leg Length + 0.000426 × Left Elbow Flexion − 0.00047 × Right Knee Flexion − 0.000388 × Left Knee Flexion − 0.005606 × Back Length + 0.000708 × Chest Rotation − 0.000349 × Right Shoulder Flexion + 0.000296 × Right Elbow Supination + 0.001107 × Neck Circumference (Shirt) + 0.000187 × Left Shoulder Internal Rotation + 0.000072 × Right Shoulder Internal Rotation,

(3)

Table 4. Standardized beta coefficients for the included variables in the regression model based on the optical and inertial mocap data.

Optical Regression		Inertial Regression
Variable	Beta coefficient	Variable	Beta coefficient
Back angle	0.19	Neck circumference (tight)	0.79
Score 6	0.49	Chest anterior tilt	−0.80
Upper arm length	0.31	Neck flexion	−0.31
Left elbow flexion	0.23	shoulder breadth (acromion)	0.18
Neck circumference (tight)	0.12	Lower arm length	0.31
Head flexion	−0.12	Chest lateral tilt	0.44
Hip Breadth (while sitting)	−0.31	Upper leg length	0.66
Left hip flexion	0.36	Left elbow flexion	0.32
Left knee flexion	0.17	Right knee flexion	−0.20
Lower arm length	−0.13	Left knee flexion	−0.30
Left shoulder flexion	0.09	Back length	−0.52
		Chest rotation	0.35
		Right shoulder flexion	−0.27
		Right elbow supination	0.34
		Neck circumference (shirt)	0.13
		Left shoulder internal rotation	0.16
		Right shoulder internal rotation	0.09

shows the beta coefficients for each included variable for both the optical and inertial regression model.

Table 5. The accuracy of both regression models in terms of ICC, RMSE, and relative error.

	Optical Regression	Inertial Regression
ICC	0.43 (p < 0.001)	0.51 (p < 0.001)
RMSE (m2)	0.037	0.032
Relative error (%)	−0.18 ± 9.98	1.70 ± 8.72

shows the accuracy of the regression models after cross validation in terms of ICC, RMSE, and relative error.

4. Discussion

The results show that the projected frontal area is an indicator of drag force and can be considered the benchmark for practical purposes in the analysis in this study. Furthermore, the linear regression analysis indicates that the projected frontal area can be predicted using anthropometric data combined with joint angle data, providing several practical applications in cycling.

4.1. Drag Force versus Projected Frontal Area

The instructed poses ranged from least aerodynamic to most aerodynamic (i.e., TT is more aerodynamically efficient than Drops, which is more efficient than Hoods) [33]. From Table 3, the drag values follow this order. The C_D values of the participants agree with those found in the literature [21]. Considering that drag force was predicted from the input parameters that contained very simple anthropometric data (i.e., age, gender, height, weight, chest girth, hip circumference maximum, and arm length), the R² value of 0.72 is promising. The angles were also obtained from a low-cost, basic smartphone camera using an open source algorithm. When compared to the cost of state-of-the-art wind tunnel measurements or 3D scanners, these results are affordable for the amateur cyclist. The predicted drag force can, for instance, be compared across poses for evaluating the relative ranking of these on-bike poses. In this way, the notion of a ‘virtual wind tunnel’ that enables aerodynamic bike fitting, pose evaluation, and on-bike posture training can be introduced to amateur cyclists.

The 3D models were not identical replicas of the shapes of the participants. The other anthropometric data (up to 15) of the participants in Table 1 were not always an exact match with those of the 3D models (for instance, forearm length was different for all participants). The models were generated considering the shape data of thousands of human shapes. Hence, individual differences are expected. For future research, we recommend evaluating the methods proposed in this study with 3D shapes obtained from other algorithms to predict human shape in motion [34,35,36,37]. For instance, these state-of-the-art algorithms can also accurately model the soft tissue deformation, especially around joints with extreme flexion.

The image-processing algorithm Detectron can capture 2D angles reliably. Hence, we considered the left-hand side angles in our methods and we assumed that the left and right upper body were symmetric. However, there is the chance of parallax error despite the best efforts from researchers and participants to align with the camera. Additionally, the method of modeling the head angle was not the same in the skeleton of the 3D model (Figure 6a). In cycling aerodynamics, the head (and helmet) is one of the most important factors of a cyclist’s aerodynamic posture. The sensitivity of the head is suspected to be a contributing factor for the discrepancies in the drag values in the TT pose, which did not have as good a correlation with the projected frontal area as the other poses. Whether the discrepancies in the drag of the models in the TT pose are due to the soft tissue deformations or due to the sensitivity of the various body segments in the extreme position are to be investigated.

The area obtained from the projection of 3D models did not include the bicycle, but the projected frontal area camera recorded total projected area of the bike and cyclist combination. The bicycle alone was found to be 0.15 m². Hence, the area from 3D models was expected to be lower than the camera values by around 0.15 m². However, the area from 3D models was consistently higher. However, the error seemed to be systematic, as observed in Figure 8. This leads us to believe that this could be due to an offset error in the camera calibration.

Area is a strong indicator of drag and can be considered the benchmark for practical purposes in the analysis in this study. For future research, we recommend comparison of CFD drag with gold standard wind tunnel drag to validate the methods described in this study. As mentioned in the Materials and Methods, the CFD predictions can become closer to ground truth drag with a more detailed mesh, longer domain, and accurate modeling of surface roughness (bike, clothes, helmets, accessories, etc.).

4.2. Projected Frontal Area Prediction Based on Anthropometrics and Joint Angles

Furthermore, this study investigated the opportunities to predict the projected frontal area as an indicator of aerodynamic drag using several body dimensions and joint angles. Previous research showed the correlation between projected frontal area and several joint angles [38], which indicates the opportunities to link aerodynamic efficiency and mocap. The optical regression method uses 2D joint angles from pictures, added with scores of the parametric 3D body shapes and anthropometric measurements. The inertial regression method provides the same anthropometric data, added with more extensive 3D joint angles data from IMUs.

The optical model uses 11 variables to predict the projected frontal area, where the inertial mocap model includes 17 variables. Regarding anthropometric data, the tight neck circumference and lower arm length are included in both regression models, whereas the upper arm length (optical model) and the neck circumference (inertial model) have the biggest influence on the projected frontal area. The change in body shape corresponding with principal component (or ‘mode’) #6 has the biggest influence on predicting projected frontal area (beta coefficient 0.49), where other components were not included in the regression model. From Figure 9, mode 6 appears to be linked with the upper body girth and the width of the upper legs.

Regarding joint angles, previous studies indicated that torso, shoulder, head, and elbow angle have the most considerable influence on aerodynamics [39,40], which were all included in our models. The hip flexion angle had the highest beta coefficient for the optical model. However, the hip angle was excluded in the inertial mocap analysis due to moving of the strap during cycling, which causes unreliable data. This issue can be solved by using double-sided tape to attach the inertial sensor directly on the hip-joint level or using the sensor at the rear rather than front of the participant. It could be an improvement to use a similar method for the legs as well, since the straps should be really tightened to prevent from coming loose, which can be impeding or annoying for the participant during cycling.

Including the back/chest angle, elbow flexion angle, and shoulder flexion angle in the regression models is obvious since these angles determine the position of the upper body. The higher these angles, the more upright the position and the higher the projected frontal area. In both regression models, joint angles are more used to predict the aerodynamics compared to anthropometric data, since they also consider the movement during cycling, where anthropometric data can only be used to predict the general influence on the projected frontal area independent of the cycling pose.

The inertial regression model includes 3D joint angles, but the added value in predicting the projected frontal area is limited, since only the lateral tilt and rotation of the chest and rotation of the elbow and shoulder are included. To improve the accuracy of both models, analyzing regression models using relative values compared to the pose with the minimal projected frontal area as a reference pose was considered, but did not result in improved accuracy. Furthermore, logarithmic and exponential models can be used in future studies to optimize accuracy. Finally, combined effects of anthropometric data can be worth considering (e.g., multiplication of body height and weight can be an approach of the shape of the body).

The accuracy of both models is equivalent, where the inertial mocap model has a slightly higher accuracy in general. The results of the cross-validation showed an RMSE of 0.037 m² for the optical model and 0.032 m² for the inertial mocap model. Each step in the process of predicting the projected frontal area induces possible errors. Anthropometric data are obtained by hand measurements by one researcher, which means that the error in this step is negligible. The accuracy of the pictures and videos from the side camera is dependent on the visibility of joints that are used to calculate 2D angles and can be neglected in this study design since the correctness of joint angles is checked by the researchers. The highest inaccuracy occurred for the IMUs, with a possible error of 1 to 2° for an individual sensor. The calibration, placing of sensors, and magnetic interference can cause even more considerable errors for full body 3D joint angles.

However, the accuracy of the regression models indicates that both models can have advantageous applications. The inertial mocap model can provide an estimation of the projected frontal area without the use of any software or postprocessing method, which means that it can be used for real-time outdoor estimating of the aerodynamic quality of a certain cycling pose.

5. Conclusions

Drag force and projected frontal area are two commonly used metrics in evaluating the aerodynamic efficiency of a cyclist. This study investigated low-cost methods to estimate these two quantities using easy to acquire anthropometric measures, CFD analyses, a smartphone camera in combination with open-source optical mocap, and inertial mocap from commercially available plug-and-play wearable sensors. Drag calculations were strongly correlated with benchmark projected frontal area measurements (R² = 0.72). Projected frontal area can accurately be predicted using anthropometric data and joint angles from optical motion capture (RMSE = 0.037 m²) and inertial measurement units (RMSE = 0.032 m²). These methods have practical relevance for amateur as well as elite cyclists: crucially, the training toward an optimized aerodynamic posture with the goal to improve performance. An individual cyclist can compare several poses to determine the relative aerodynamic efficiency of a given pose without accessing expensive wind tunnel facilities or expensive 3D scanners. The methods can be implemented in indoor cycling as an addition to indoor training platforms to provide real-life effects of posture and movement changes of the cyclist with the aim to enable real-time analysis of the biomechanical and aerodynamic effects and hence has added value over some current commercial offerings [41,42]. Furthermore, this method can potentially be employed in outdoor cycling settings given the portability of the inertial mocap system, where real-time estimations of the aerodynamic efficiency can be provided during training or for analysis afterward. This can be interesting for professional riders to observe how accurately they can retain their optimal aerodynamic pose for long durations or for amateurs to provide an indication of the effect of different cycling poses.