Long Term Soil Gas Monitoring as Tool to Understand Soil Processes
Abstract
:Featured Application
Abstract
1. Introduction
1.1. Why Soil Gases?
1.2. How to Measure Gas Fluxes?
1.3. The Gradient-Flux Method: Set-Ups, Approaches, Uncertainties
1.4. Soil Gas Monitoring at the Forest Research Institute Baden Wuerttemberg (FVA-BW)
2. Materials and Methods
2.1. Soil Gas Monitoring
2.1.1. Gas Sampling
2.1.2. Gas Analysis
2.2. Calculating Fluxes Using the Gradient Flux Method
2.2.1. Theoretical Background
2.2.2. Estimation of Soil Gas Diffusion Coefficients
2.2.3. Measurements and Modelling of Soil Water Content
2.2.4. Calculation Approaches for Soil Gas Fluxes
2.3. Monitoring Sites
3. Results and Discussion
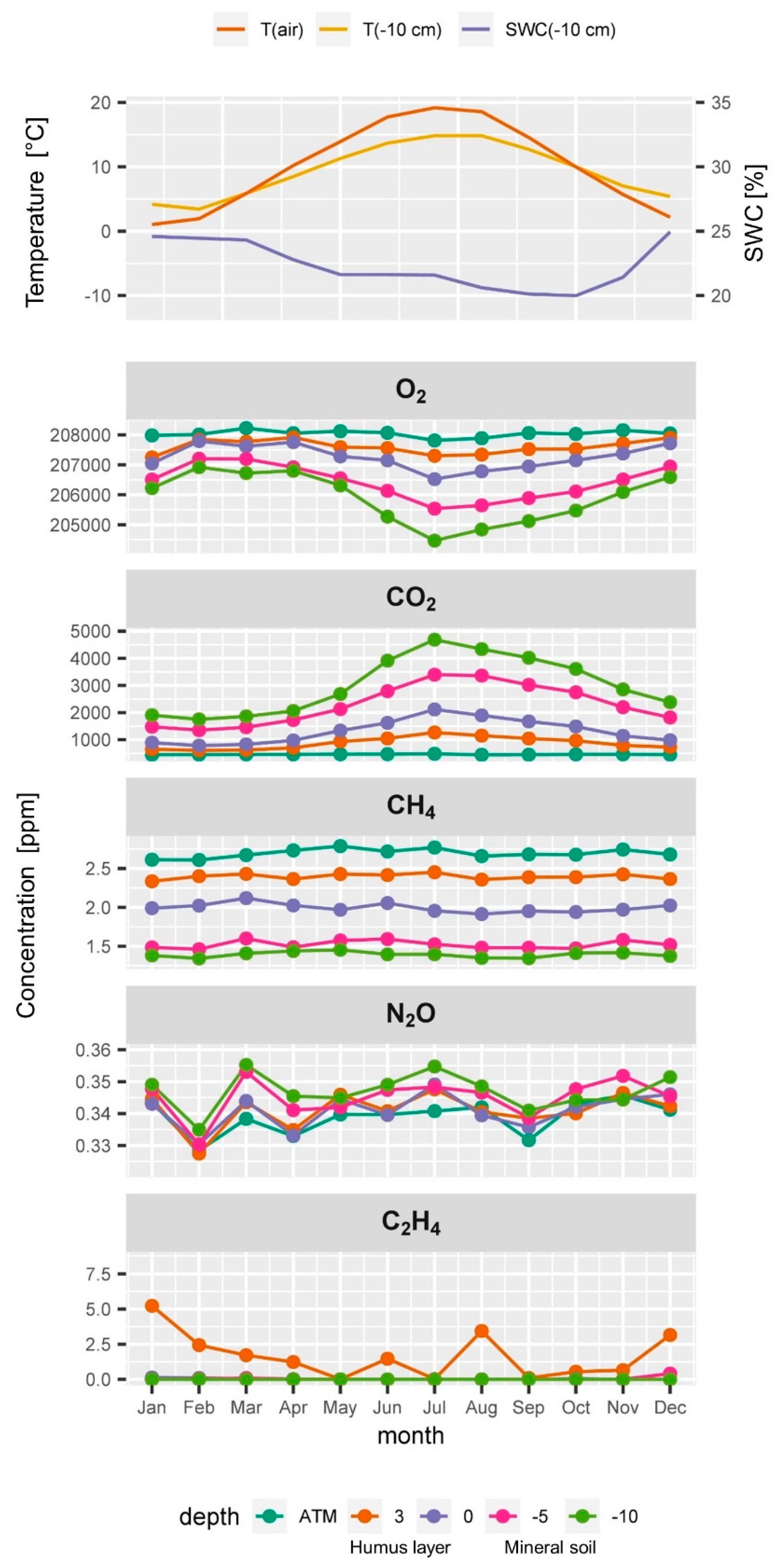
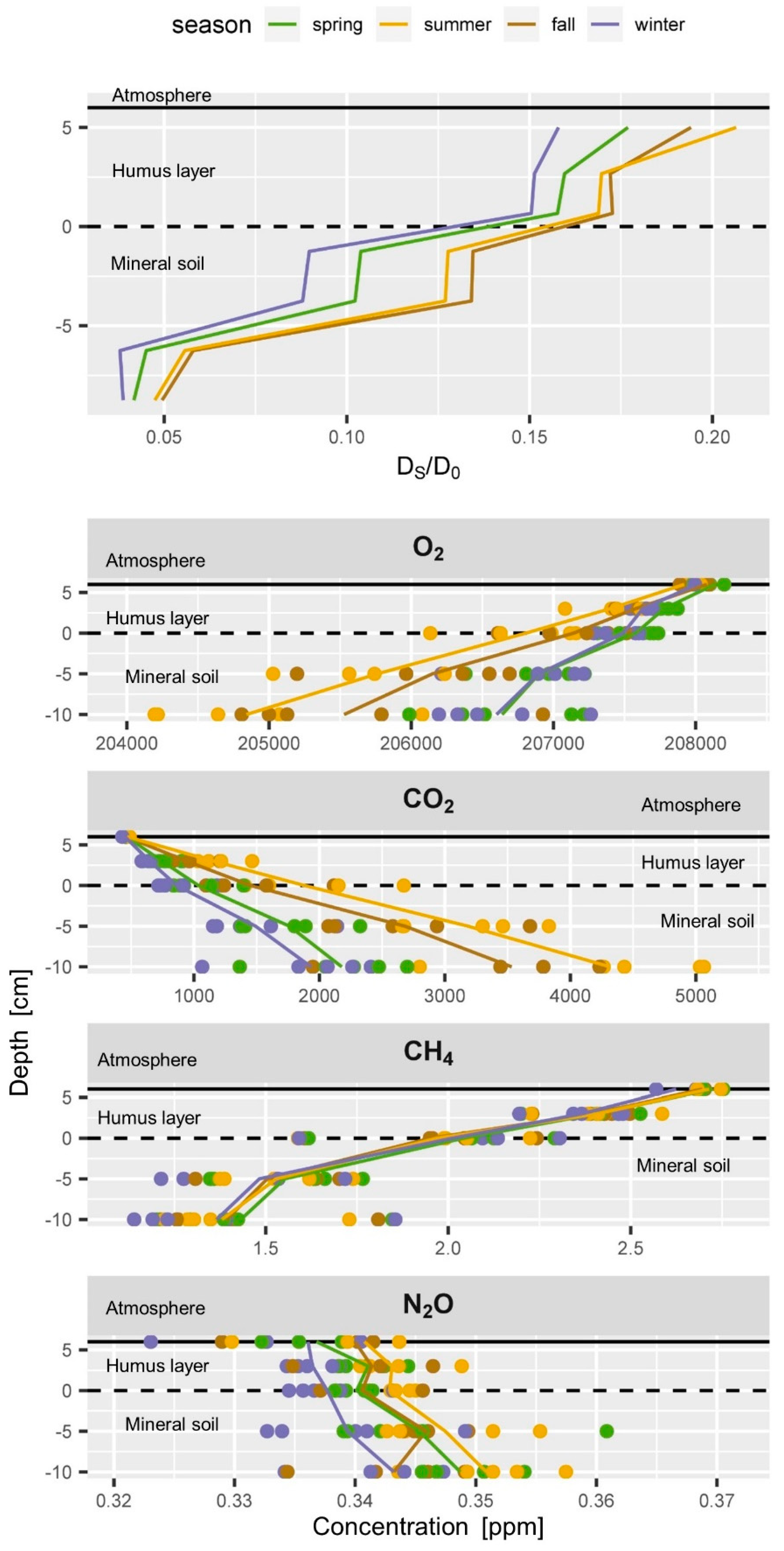
3.1. Time Series of O2, CO2, CH4, N2O and C2H4 and Typical Soil Gas Profiles
3.1.1. Time Series and Seasons
3.1.2. Typical Soil Gas Profiles
3.2. Effect of Different Calculation Approaches for Gas Flux Estimation
3.2.1. Comparison of Calculation Approaches
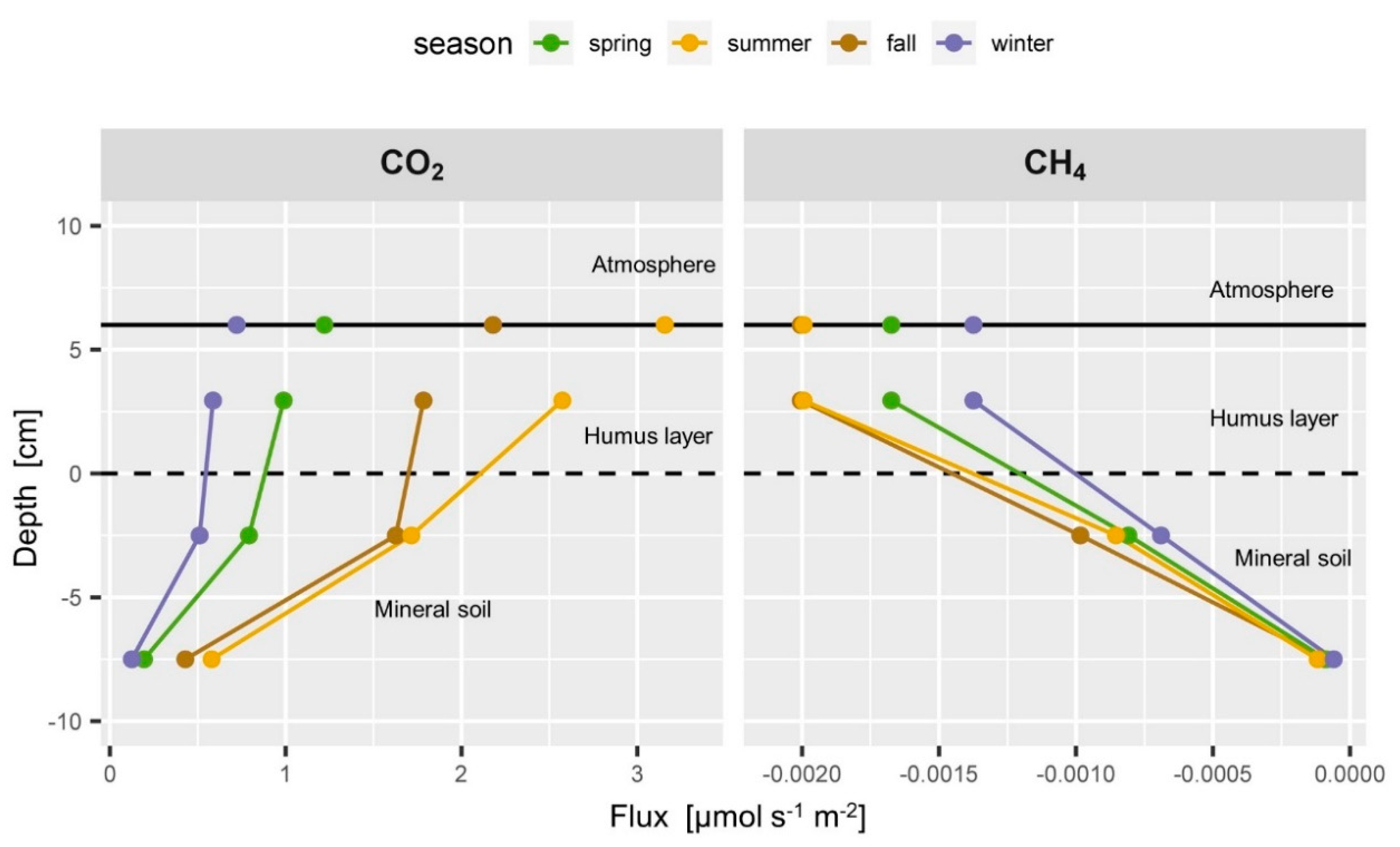
3.2.2. Vertical Partitioning of Soil Gas Fluxes
3.3. Time Series and Interaction of Soil-Atmosphere Fluxes of O2, CO2 and CH4
3.3.1. Time Series Soil-Atmosphere Fluxes
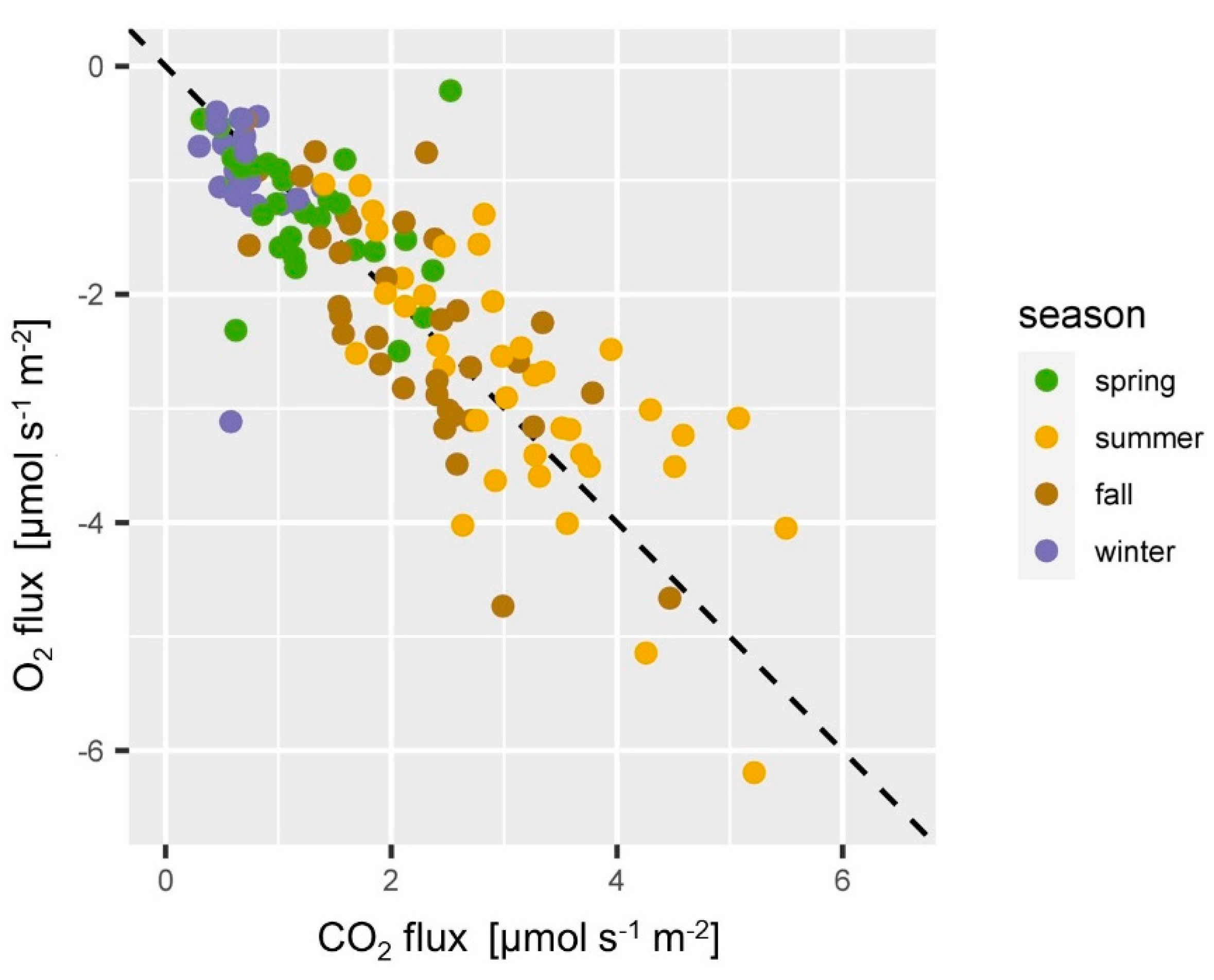
3.3.2. Relationship of O2 and CO2 Fluxes
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, B.; Brewer, P.E.; Shugart, H.H.; Lerdau, M.T.; Allison, S.D. Soil aggregates as biogeochemical reactors and implications for soil-atmosphere exchange of greenhouse gases—A concept. Glob. Chang. Biol. 2019, 25, 373–385. [Google Scholar] [CrossRef] [PubMed]
- Chesworth, W. Encyclopedia of Soil Science; Springer: Dorderecht, The Netherlands, 2009; p. 902. [Google Scholar]
- Smith, K.A.; Ball, T.; Conen, F.; Dobbie, K.E.; Rey, A. Exchange of greenhouse gases between soil and atmosphere: Interactions of soil physical factors and biological processes. Eur. J. Soil Sci. 2018, 69, 2–4. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Cambridge, UK; New York, NY, USA, 2013.
- Conrad, R. Soil microorganisms as controllers of atmospheric trace gases (H2, CO, CH4, OCS, N2O, and NO). Microbiol. Rev. 1996, 60, 609–640. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Cañete, E.P.; Kowalski, A.S.; Serrano-Ortiz, P.; Pérez-Priego, O.; Domingo, F. Deep CO2 soil inhalation/exhalation induced by synoptic pressure changes and atmospheric tides in a carbonated semiarid steppe. Biogeosciences 2013, 10, 6591–6600. [Google Scholar] [CrossRef] [Green Version]
- NOAA. Global Monitoring Laboratory Earth System Research Laboratories. Available online: https://www.esrl.noaa.gov/gmd/ccgg/trends/ (accessed on 22 November 2020).
- Ryan, M.G.; Law, B.E. Interpreting, measuring, and modeling soil respiration. Biogeochemistry 2005, 73, 3–27. [Google Scholar] [CrossRef]
- Maier, M.; Schack-Kirchner, H.; Hildebrand, E.E.; Schindler, D. Soil CO2 efflux vs. soil respiration: Implications for flux models. Agric. Meteorol. 2011, 151, 1723–1730. [Google Scholar] [CrossRef]
- Chen, L.; Liu, L.; Qin, S.; Yang, G.; Fang, K.; Zhu, B.; Kuzyakov, Y.; Chen, P.; Xu, Y.; Yang, Y. Regulation of priming effect by soil organic matter stability over a broad geographic scale. Nat. Commun. 2019, 10, 5112. [Google Scholar] [CrossRef] [Green Version]
- Goffin, S.; Aubinet, M.; Maier, M.; Plain, C.; Schack-Kirchner, H.; Longdoz, B. Characterization of the soil CO2 production and its carbon isotope composition in forest soil layers using the flux-gradient approach. Agr. Met. 2014, 188, 45–57. [Google Scholar] [CrossRef]
- Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 165–173. [Google Scholar] [CrossRef]
- Conrad, R. Soil microbial processes involved in production and consumption of atmospheric trace gases. Adv. Microb. Ecol. 1995, 14, 207–250. [Google Scholar]
- Smith, K.A.; Ball, T.; Conen, F.; Dobbie, K.E.; Massheder, J.; Rey, A. Exchange of greenhouse gases between soil and atmosphere: Interactions of soil physical factors and biological processes. Eur. J. Soil Sci. 2003, 54, 779–791. [Google Scholar] [CrossRef] [Green Version]
- Kuzyakov, Y.; Blagodatskaya, E. Microbial hotspots and hot moments in soil: Concept & review. Soil Biol. Biochem. 2015, 83, 184–199. [Google Scholar] [CrossRef]
- Maier, M.; Longdoz, B.; Laemmel, T.; Schack-Kirchner, H.; Lang, F. 2D profiles of CO2, CH4, N2O and gas diffusivity in a well aerated soil: Measurement and Finite Element Modeling. Agr. Met. 2017, 247, 21–33. [Google Scholar] [CrossRef]
- Von Fischer, J.C.; Hedin, L.O. Separating methane production and consumption with a field-based isotope pool dilution technique. Glob. Biogeochem. Cycles 2002, 16, 8-1–8-13. [Google Scholar] [CrossRef]
- Dutaur, L.; Verchot, L.V. A global inventory of the soil CH4 sink. Glob. Biogeochem. Cycles 2007, 21. [Google Scholar] [CrossRef]
- Chapuis-Lardy, L.; Wrage, N.; Metay, A.; Chotte, J.-L.; Bernoux, M. Soils, a sink for N2O? A review. Glob. Chang. Biol. 2007, 13, 1–17. [Google Scholar] [CrossRef]
- Davidson, E.A.; Verchot, L.V. Testing the Hole-in-the-Pipe Model of nitric and nitrous oxide emissions from soils using the TRAGNET Database. Glob. Biogeochem. Cycles 2000, 14, 1035–1043. [Google Scholar] [CrossRef]
- Ingwersen, J.; Butterbach-Bahl, K.; Gasche, R.; Richter, O.; Papen, H. Barometric Process Separation: New Method for Quantifying Nitrification, Denitrification, and Nitrous Oxide Sources in Soils. Soil Sci. Soc. Am. J. 1999, 63, 117–128. [Google Scholar] [CrossRef]
- Well, R.; Maier, M.; Lewicka-Szczebak, D.; Köster, J.-R.; Ruoss, N. Underestimation of denitrification rates from field application of the 15N gas flux method and its correction by gas diffusion modelling. Biogeosciences 2019, 16, 2233–2246. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.M. Ethylene in Soil Biology. Annu. Rev. Phytopathol. 1976, 14, 53–73. [Google Scholar] [CrossRef]
- Neljubow, D. Über die horizontale Nutation der Stengel von Pisum sativa und einiger Anderer Pflanzen. Beih. Bot. Cent. 1901, 10, 128–139. [Google Scholar]
- Arshad, M.; Frankenberger, W.T. Ethylene in Soil; Springer: Boston, MA, USA, 2002; pp. 139–193. [Google Scholar] [CrossRef]
- Jackson, M.B. Ethylene and Responses of Plants to Soil Waterlogging and Submergence. Annu. Rev. Plant Physiol. 1985, 36, 145–174. [Google Scholar] [CrossRef]
- Zechmeister-Boltenstern, S.; Smith, K.A. Ethylene production and decomposition in soils. Biol. Fertil. Soils 1998, 26, 354–361. [Google Scholar] [CrossRef]
- Davidson, E.A.; Belk, E.; Boone, R.D. Soil water content and temperature as independent or confounded factors controlling soil respiration in a temperate mixed hardwood forest. Glob. Chang. Biol. 1998, 4, 217–227. [Google Scholar] [CrossRef] [Green Version]
- Goffin, S.; Wylock, C.; Haut, B.; Maier, M.; Longdoz, B.; Aubinet, M. Modeling soil CO2 production and transport to investigate the intra-day variability of surface efflux and soil CO2 concentration measurements in a Scots Pine Forest (Pinus Sylvestris, L.). Plant Soil 2015, 390, 195–211. [Google Scholar] [CrossRef] [Green Version]
- Conant, R.T.; Dalla-Betta, P.; Klopatek, C.C.; Klopatek, J.M. Controls on soil respiration in semiarid soils. Soil Biol. Biochem. 2004, 36, 945–951. [Google Scholar] [CrossRef]
- Luo, G.J.; Kiese, R.; Wolf, B.; Butterbach-Bahl, K. Effects of soil temperature and moisture on methane uptake and nitrous oxide emissions across three different ecosystem types. Biogeosciences 2013, 10, 3205–3219. [Google Scholar] [CrossRef] [Green Version]
- Luo, G.; Brüggemann, N.; Wolf, B.; Gasche, R.; Grote, R.; Butterbach-Bahl, K. Decadal variability of soil CO2, NO, N2O, and CH4 fluxes at the Höglwald Forest, Germany. Biogeosciences 2012, 9, 1741–1763. [Google Scholar] [CrossRef] [Green Version]
- Subke, J.-A.; Moody, C.S.; Hill, T.C.; Voke, N.; Toet, S.; Ineson, P.; Teh, Y.A. Rhizosphere activity and atmospheric methane concentrations drive variations of methane fluxes in a temperate forest soil. Soil Biol. Biochem. 2018, 116, 323–332. [Google Scholar] [CrossRef]
- Keller, M.; Varner, R.; Dias, J.D.; Silva, H.; Crill, P.; de Oliveira, R.C.; Asner, G.P. Soil–Atmosphere Exchange of Nitrous Oxide, Nitric Oxide, Methane, and Carbon Dioxide in Logged and Undisturbed Forest in the Tapajos National Forest, Brazil. Earth Interact. 2005, 9, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Fest, B.; Wardlaw, T.; Livesley, S.J.; Duff, T.J.; Arndt, S.K. Changes in soil moisture drive soil methane uptake along a fire regeneration chronosequence in a eucalypt forest landscape. Glob. Chang. Biol. 2015, 21, 4250–4264. [Google Scholar] [CrossRef] [PubMed]
- Wolf, B.; Chen, W.; Brüggemann, N.; Zheng, X.; Pumpanen, J.; Butterbach-Bahl, K. Applicability of the soil gradient method for estimating soil-atmosphere CO2, CH4, and N2O fluxes for steppe soils in Inner Mongolia. J. Plant Nutr. Soil Sci. 2011, 174, 359–372. [Google Scholar] [CrossRef]
- Janssens, I.A.; Lankreijer, H.; Matteucci, G.; Kowalski, A.S.; Buchmann, N.; Epron, D.; Pilegaard, K.; Kutsch, W.; Longdoz, B.; Grunwald, T.; et al. Productivity overshadows temperature in determining soil and ecosystem respiration across European forests. Glob. Chang. Biol. 2001, 7, 269–278. [Google Scholar] [CrossRef]
- Smith, K.A.; Dobbie, K.E.; Ball, B.C.; Bakken, L.R.; Sitaula, B.K.; Hansen, S.; Brumme, R.; Borken, W.; Christensen, S.; Priemé, A.; et al. Oxidation of atmospheric methane in Northern European soils, comparison with other ecosystems, and uncertainties in the global terrestrial sink. Glob. Chang. Biol. 2000, 6, 791–803. [Google Scholar] [CrossRef]
- Dore, S.; Fry, D.L.; Stephens, S.L. Spatial heterogeneity of soil CO2 efflux after harvest and prescribed fire in a California mixed conifer forest. Ecol. Manag. 2014, 319, 150–160. [Google Scholar] [CrossRef]
- Darenova, E.; Pavelka, M.; Macalkova, L. Spatial heterogeneity of CO2 efflux and optimization of the number of measurement positions. Eur. J. Soil Biol. 2016, 75, 123–134. [Google Scholar] [CrossRef]
- Maier, M.; Cordes, M.; Osterholt, L. Soil respiration and CH4 consumption covary on the plot scale. Geoderma 2021, 382, 114702. [Google Scholar] [CrossRef]
- Maier, M.; Paulus, S.; Nicolai, C.; Stutz, K.; Nauer, P. Drivers of Plot-Scale Variability of CH4 Consumption in a Well-Aerated Pine Forest Soil. Forests 2017, 8, 193. [Google Scholar] [CrossRef] [Green Version]
- Sabrekov, A.F.; Glagolev, M.V.; Fastovets, I.A.; Smolentsev, B.A.; Il’yasov, D.V.; Maksyutov, S.S. Relationship of methane consumption with the respiration of soil and grass-moss layers in forest ecosystems of the southern taiga in Western Siberia. Eurasian Soil Sci. 2015, 48, 841–851. [Google Scholar] [CrossRef]
- Maier, M.; Schack-Kirchner, H. Using the gradient method to determine soil gas flux: A review. Agric. For. Meteorol. 2014, 192–193, 78–95. [Google Scholar] [CrossRef]
- Kühne, A.; Schack-Kirchner, H.; Hildebrand, E.E. Gas diffusivity in soils compared to ideal isotropic porous media. J. Plant Nutr. Soil Sci. 2012, 175, 34–45. [Google Scholar] [CrossRef]
- Lange, S.F.; Allaire, S.E.; Rolston, D.E. Soil-gas diffusivity in large soil monoliths. Eur. J. Soil Sci. 2009, 60, 1065–1077. [Google Scholar] [CrossRef]
- Pavelka, M.; Acosta, M.; Kiese, R.; Altimir, N.; Brümmer, C.; Crill, P.; Longdoz, B.; Ortiz, S. Standardisation of chamber technique for CO2, N2O and CH4 fluxes measurements from terrestrial ecosystems. Int. Agrophys. 2018, 32, 569–587. [Google Scholar] [CrossRef]
- Massman, W.J.; Lee, X. Eddy covariance flux corrections and uncertainties in long-term studies of carbon and energy exchanges. Agric. Meteorol. 2002, 113, 121–144. [Google Scholar] [CrossRef]
- Davidson, E.A.; Savage, K.; Verchot, L.V.; Navarro, R. Minimizing artifacts and biases in chamber-based measurements of soil respiration. Agric. Meteorol. 2002, 113, 21–37. [Google Scholar] [CrossRef]
- De Jong, E.; Schappert, H.J.V. Calculation of Soil Respiration and Activity From CO2 Profiles in the Soil. Soil Sci. 1972, 113, 328–333. [Google Scholar] [CrossRef]
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef] [Green Version]
- Lundegardh, H. Carbon dioxide evolution of soil and crop growth. Soil Sci. 1927, 23, 417–453. [Google Scholar] [CrossRef]
- Hutchinson, G.L.; Livingston, G.P. Vents and seals in non-steady-state chambers used for measuring gas exchange between soil and the atmosphere. Eur. J. Soil Sci. 2001, 52, 675–682. [Google Scholar] [CrossRef]
- Livingston, G.P.; Hutchinson, G.L.; Spartalian, K. Trace Gas Emission in Chambers. Soil Sci. Soc. Am. J. 2006, 70, 1459. [Google Scholar] [CrossRef] [Green Version]
- Pumpanen, J.; Kolari, P.; Ilvesniemi, H.; Minkkinen, K.; Vesala, T.; Niinistö, S.; Lohila, A.; Larmola, T.; Morero, M.; Pihlatie, M.; et al. Comparison of different chamber techniques for measuring soil CO2 efflux. Agric. Meteorol. 2004, 123, 159–176. [Google Scholar] [CrossRef]
- Pihlatie, M.K.; Christiansen, J.R.; Aaltonen, H.; Korhonen, J.F.J.; Nordbo, A.; Rasilo, T.; Benanti, G.; Giebels, M.; Helmy, M.; Sheehy, J.; et al. Comparison of static chambers to measure CH4 emissions from soils. Agric. Meteorol. 2013, 171–172, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Hogberg, P.; Nordgren, A.; Buchmann, N.; Taylor, A.F.; Ekblad, A.; Hogberg, M.N.; Nyberg, G.; Ottosson-Lofvenius, M.; Read, D.J. Large-scale forest girdling shows that current photosynthesis drives soil respiration. Nature 2001, 411, 789–792. [Google Scholar] [CrossRef] [PubMed]
- Maier, M.; Mayer, S.; Laemmel, T. Rain and wind affect chamber measurements. Agric. Meteorol. 2019, 279, 107754. [Google Scholar] [CrossRef]
- Hillel, D. Fundamentals of Soil Physics; Academic Press: New York, NY, USA, 1980; p. 413. [Google Scholar]
- Davidson, E.A.; Savage, K.E.; Trumbore, S.E.; Borken, W. Vertical partitioning of CO2 production within a temperate forest soi. Glob. Chang. Biol. 2006, 12, 944–956. [Google Scholar] [CrossRef] [Green Version]
- de Jong, E.; Redmann, R.E.; Ripley, E.A. A Comparison of Methods To Measure Soil Respiration. Soil Sci. 1979, 127, 300–306. [Google Scholar] [CrossRef]
- Pumpanen, J.; Ilvesniemi, H.; Kulmala, L.; Siivola, E.; Laakso, H.; Kolari, P.; Helenelund, C.; Laakso, M.; Uusimaa, M.; Hari, P. Respiration in boreal forest soil as determined from carbon dioxide concentration profile. Soil Sci. Soc. Am. J. 2007, 72, 1187–1196. [Google Scholar] [CrossRef]
- Vargas, R.; Allen, M.F. Dynamics of Fine Root, Fungal Rhizomorphs, and Soil Respiration in a Mixed Temperate Forest: Integrating Sensors and Observations. Vadose Zone J. 2008, 7, 1055–1064. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Baldocchi, D.D.; Qi, Y.; Xu, L. Assessing soil CO2 efflux using continuous measurements of CO2 profiles in soils with small solid-state sensors. Agric. Meteorol. 2003, 118, 207–220. [Google Scholar] [CrossRef]
- Maier, M.; Schack-Kirchner, H.; Hildebrand, E.E.; Holst, J. Pore-space CO2 dynamics in a deep, well-aerated soil. Eur. J. Soil Sci. 2010, 61, 877–887. [Google Scholar] [CrossRef]
- Seok, B.; Helmig, D.; Williams, M.W.; Liptzin, D.; Chowanski, K.; Hueber, J. An automated system for continuous measurements of trace gas fluxes through snow: An evaluation of the gas diffusion method at a subalpine forest site, Niwot Ridge, Colorado. Biogeochemistry 2009, 95, 95–113. [Google Scholar] [CrossRef] [Green Version]
- Pihlatie, M.; Pumpanen, J.; Rinne, J.; Ilvesniemi, H.; Simojoki, A.; Hari, P.; Vesala, T. Gas concentration driven fluxes of nitrous oxide and carbon dioxide in boreal forest soil. Tellus B Chem. Phys. Meteorol. 2007, 59, 458–469. [Google Scholar] [CrossRef]
- Goffin, S.; Longdoz, B.; Maier, M.; Schack-Kirchner, H.; Aubinet, M. Soil Respiration in forest Ecosystems: Combination of a multilayer Approach and an Isotopic Signal Analysis. Commun. Agric. Appl. Biol. Sci. 2012, 72, 139–144. [Google Scholar]
- Laemmel, T.; Maier, M.; Schack-Kirchner, H.; Lang, F. An in situ method for real-time measurement of gas transport in soil. Eur. J. Soil Sci. 2017, 68, 156–166. [Google Scholar] [CrossRef]
- Parent, F.; Plain, C.; Epron, D.; Maier, M.; Longdoz, B. A new method for continuously measuring the δ13C of soil CO2 concentrations at different depths by laser spectrometry. Eur. J. Soil Sci. 2013, 64, 516–525. [Google Scholar] [CrossRef]
- Kammann, C.; Grünhage, L.; Jäger, H.J. A new sampling technique to monitor concentrations of CH4, N2O and CO2 in air at well-defined depths in soils with varied water potential. Eur. J. Soil Sci. 2001, 52, 297–303. [Google Scholar] [CrossRef]
- Maier, M.; Machacova, K.; Lang, F.; Svobodova, K.; Urban, O. Combining soil and tree-stem flux measurements and soil gas profiles to understand CH4 pathways in Fagus sylvatica forests. J. Plant Nutr. Soil Sci. 2018, 181, 31–35. [Google Scholar] [CrossRef] [Green Version]
- Vicca, S.; Bahn, M.; Estiarte, M.; van Loon, E.E.; Vargas, R.; Alberti, G.; Ambus, P.; Arain, M.A.; Beier, C.; Bentley, L.P.; et al. Can current moisture responses predict soil CO2 efflux under altered precipitation regimes? A synthesis of manipulation experiments. Biogeosci. Discuss. 2014, 11, 853–899. [Google Scholar] [CrossRef]
- Vargas, R.; Allen, M.F. Environmental controls and the influence of vegetation type, fine roots and rhizomorphs on diel and seasonal variation in soil respiration. New Phytol. 2008, 179, 460–471. [Google Scholar] [CrossRef] [Green Version]
- Warlo, H.; Machacova, K.; Nordstrom, N.; Maier, M.; Laemmel, T.; Roos, A.; Schack-Kirchner, H. Comparison of portable devices for sub-ambient concentration measurements of methane (CH4) and nitrous oxide (N2O) in soil research. Int. J. Environ. Anal. Chem. 2018, 98, 1030–1037. [Google Scholar] [CrossRef]
- Schack-Kirchner, H.; Kublin, E.; Hildebrand, E.E. Finite-Element Regression to Estimate Production Profiles of Greenhouse Gases in Soils. Vadose Zone J. 2011, 10, 169–183. [Google Scholar] [CrossRef]
- Sánchez-Cañete, E.P.; Scott, R.L.; van Haren, J.; Barron-Gafford, G.A. Improving the accuracy of the gradient method for determining soil carbon dioxide efflux. J. Geophys. Res. Biogeosci. 2017, 122, 50–64. [Google Scholar] [CrossRef] [Green Version]
- Schack-Kirchner, H.; Hildebrand, E.E.; von Wilpert, K. Ein konvektionsfreies Sammelsystem für Bodenluft—Soil gas sampling avoiding mass-flow. Z. Für Pflanz. Und Bodenkd. 1993, 156, 307–310. [Google Scholar] [CrossRef]
- Levintal, E.; Dragila, M.I.; Kamai, T.; Weisbrod, N. Free and forced gas convection in highly permeable, dry porous media. Agric. Meteorol. 2017, 232, 469–478. [Google Scholar] [CrossRef] [Green Version]
- Maier, M.; Schack-Kirchner, H.; Aubinet, M.; Goffin, S.; Longdoz, B.; Parent, F. Turbulence Effect on Gas Transport in Three Contrasting Forest Soils. Soil Sci. Soc. Am. J. 2012, 76, 1518–1528. [Google Scholar] [CrossRef] [Green Version]
- Laemmel, T.; Mohr, M.; Longdoz, B.; Schack-Kirchner, H.; Lang, F.; Schindler, D.; Maier, M. From above the forest into the soil–How wind affects soil gas transport through air pressure fluctuations. Agric. Meteorol. 2019, 265, 424–434. [Google Scholar] [CrossRef]
- Sánchez-Cañete, E.P.; Kowalski, A.S. Comment on “Using the gradient method to determine soil gas flux: A review” by M. Maier and H. Schack-Kirchner. Agric. Meteorol. 2014, 197, 254–255. [Google Scholar] [CrossRef]
- Flechard, C.R.; Neftel, A.; Jocher, M.; Ammann, C.; Leifeld, J.; Fuhrer, J. Temporal changes in soil pore space CO2 concentration and storage under permanent grassland. Agric. Meteorol. 2007, 142, 66–84. [Google Scholar] [CrossRef]
- Jassal, R.; Black, A.; Novak, M.; Morgenstern, K.; Nesic, Z.; Gaumont-Guay, D. Relationship between soil CO2 concentrations and forest-floor CO2 effluxes. Agric. Meteorol. 2005, 130, 176–192. [Google Scholar] [CrossRef]
- Troeh, F.R.; Jabro, J.D.; Kirkham, D. Gaseous diffusion equations for porous materials. Geoderma 1982, 239–253. [Google Scholar] [CrossRef]
- Moldrup, P.; Olesen, T.; Gamst, J.; Schjønning, P.; Yamaguchi, T.; Rolston, D.E. Predicting the Gas Diffusion Coefficient in Repacked Soil: Water-Induced Linear Reduction Model. Soil Sci. Soc. Am. J. 2000, 64, 1588–1594. [Google Scholar] [CrossRef]
- Penman, H.L. Gas and vapour movements in the soil: I. The diffusion of vapours through porous solids. J. Agric. Sci. 1940, 30, 437. [Google Scholar] [CrossRef]
- Millington, R. Gas diffusion in porous media. Science 1959, 130, 100–102. [Google Scholar] [CrossRef] [PubMed]
- Deepagoda, T.; Moldrup, P.; Schjønning, P.; Jonge, L.W.d.; Kawamoto, K.; Komatsu, T. Density-corrected models for gas diffusivity and air permeability in unsaturated soil. Vadose Zone J. 2011, 10, 226–238. [Google Scholar] [CrossRef] [Green Version]
- Thorbjørn, A.; Moldrup, P.; Blendstrup, H.; Komatsu, T.; Rolston, D.E. A Gas Diffusivity Model Based on Air-, Solid-, and Water-Phase Resistance in Variably Saturated Soil. Vadose Zone J. 2008, 7, 1276. [Google Scholar] [CrossRef]
- Moldrup, P.; Olesen, T.; Yoshikawa, S.; Komatsu, T.; Rolston, D.E. Predictive-descriptive models for gas and solute diffusion coefficients in variably saturated porous media coupled to pore-size distribution: II. Gas diffusivity in undisturbed soil. Soil Sci. 2005, 170, 867–880. [Google Scholar] [CrossRef]
- Maier, M.; Lang, V. Gas Diffusivity in the Forest Humus Layer. Soil Sci. 2019, 184, 13–16. [Google Scholar] [CrossRef]
- Massman, W.J. A review of the molecular diffusivities of H2O, CO2, CH4, CO, O3, SO2, NH3, N2O, NO, and NO2 in air, O2 and N2 near STP. Atmos. Environ. 1998, 32, 1111–1127. [Google Scholar] [CrossRef]
- Hammel, K.; Kennel, M. Charakterisierung und Analyse der Wasserverfügbarkeit und des Wasserhaushalts von Waldstandorten in Bayern Mit Dem Simulationsmodell BROOK90; Heinrich Frank: München, Germany, 2001; Volume 185, p. 148. [Google Scholar]
- Shuttleworth, W.J.; Wallace, J. Evaporation from sparse crops-an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Federer, C.A.; Vörösmarty, C.; Fekete, B. Sensitivity of Annual Evaporation to Soil and Root Properties in Two Models of Contrasting Complexity. J. Hydrometeorol. 2003, 4, 1276–1290. [Google Scholar] [CrossRef]
- Federer, C. BROOK90: A Simulation Model for Evaporation, Soil Water, and Streamflow. 1995. Available online: http://www.ecoshift.net/brook/brook90.htm (accessed on 22 November 2020).
- Schmidt-Walter, P.; Ahrends, B.; Mette, T.; Puhlmann, H.; Meesenburg, H. NFIWADS: The water budget, soil moisture, and drought stress indicator database for the German National Forest Inventory (NFI). Ann. For. Sci. 2019, 76, 39. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Baldocchi, D.D.; Xu, L. Tree photosynthesis modulates soil respiration on a diurnal time scale. Glob. Chang. Biol. 2005, 11, 1298–1304. [Google Scholar] [CrossRef]
- Turcu, V.E.; Jones, S.B.; Or, D. Continuous Soil Carbon Dioxide and Oxygen Measurements and Estimation of Gradient-Based Gaseous Flux. Vadose Zone J. 2005, 4, 1161–1169. [Google Scholar] [CrossRef] [Green Version]
- Hirano, T. Long-term half-hourly measurement of soil CO2 concentration and soil respiration in a temperate deciduous forest. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Borken, W.; Davidson, E.A.; Savage, K.; Sundquist, E.T.; Steudler, P. Effect of summer throughfall exclusion, summer drought, and winter snow cover on methane fluxes in a temperate forest soil. Soil Biol. Biochem. 2006, 38, 1388–1395. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Gómez-Rubio, V. ggplot2—Elegant Graphics for Data Analysis (2nd Edition). J. Stat. Softw. 2017, 77. [Google Scholar] [CrossRef] [Green Version]
- Wickham, H.; François, R.; Henry, L.; Müller, K. dplyr: A Grammar of Data Manipulation. R package Version 1.0.2; 2020; Available online: https://github.com/tidyverse/dplyr/ (accessed on 22 November 2020).
- Bund-Länder-AG. Forstliches Umweltmonitoring in Deutschland; Bundesministerium für Ernährung und Landwirtschaft: Berlin, Germany, 2016; p. 39. [Google Scholar]
- The World Reference Base for Soil Resources (WRB). International Soil Classification System for Naming Soils and Creating Legends for Soil Maps. World Soil Resources Reports No. 106; FAO: Rome, Italy, 2015. [Google Scholar]
- Clough, T.J.; Rochette, P.; Thomas, S.M.; Pihlatie, M.; Christiansen, J.R.; Thorman, R.E. Global Research Alliance N2O chamber methodology guidelines: Design considerations. J. Env. Qual. 2020, 49, 1081–1091. [Google Scholar] [CrossRef]
- Schack-Kirchner, H. (Ed.) Struktur und Gashaushalt von Waldböden; Ber. Forschungszentrum Waldökosysteme: Göttingen, Germany, 1994; Volume 112, p. 145. [Google Scholar]
- Franco-Luesma, S.; Cavero, J.; Plaza-Bonilla, D.; Cantero-Martínez, C.; Tortosa, G.; Bedmar, E.J.; Álvaro-Fuentes, J. Irrigation and tillage effects on soil nitrous oxide emissions in maize monoculture. Agron. J. 2020, 112, 56–71. [Google Scholar] [CrossRef]
- Warlo, H.; von Wilpert, K.; Lang, F.; Schack-Kirchner, H. Black Alder (Alnus glutinosa (L.) Gaertn.) on Compacted Skid Trails: A Trade-off between Greenhouse Gas Fluxes and Soil Structure Recovery? Forests 2019, 10, 726. [Google Scholar] [CrossRef] [Green Version]
- Seibt, U.; Brand, W.A.; Heimann, M.; Lloyd, J.; Severinghaus, J.P.; Wingate, L. Observations of O2:CO2exchange ratios during ecosystem gas exchange. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Thomson, A. A global database of soil respiration data. Biogeosciences 2010, 7, 1915–1926. [Google Scholar] [CrossRef] [Green Version]
- Borken, W.; Xu, Y.-J.; Davidson, E.A.; Beese, F. Site and temporal variation of soil respiration in European beech, Norway spruce, and Scots pine forests. Glob. Chang. Biol. 2002, 8, 1205–1216. [Google Scholar] [CrossRef]
- Ni, X.; Groffman, P.M. Declines in methane uptake in forest soils. Proc. Natl. Acad. Sci. USA 2018, 115, 8587–8590. [Google Scholar] [CrossRef] [Green Version]
- Angert, A.; Yakir, D.; Rodeghiero, M.; Preisler, Y.; Davidson, E.A.; Weiner, T. Using O2 to study the relationships between soil CO2 efflux and soil respiration. Biogeosciences 2015, 12, 2089–2099. [Google Scholar] [CrossRef] [Green Version]
- Hodges, C.; Kim, H.; Brantley, S.L.; Kaye, J. Soil CO2 and O2 Concentrations Illuminate the Relative Importance of Weathering and Respiration to Seasonal Soil Gas Fluctuations. Soil Sci. Soc. Am. J. 2019, 83, 1167–1180. [Google Scholar] [CrossRef]
- Sanchez-Canete, E.P.; Barron-Gafford, G.A.; Chorover, J. A considerable fraction of soil-respired CO2 is not emitted directly to the atmosphere. Sci. Rep. 2018, 8, 13518. [Google Scholar] [CrossRef]
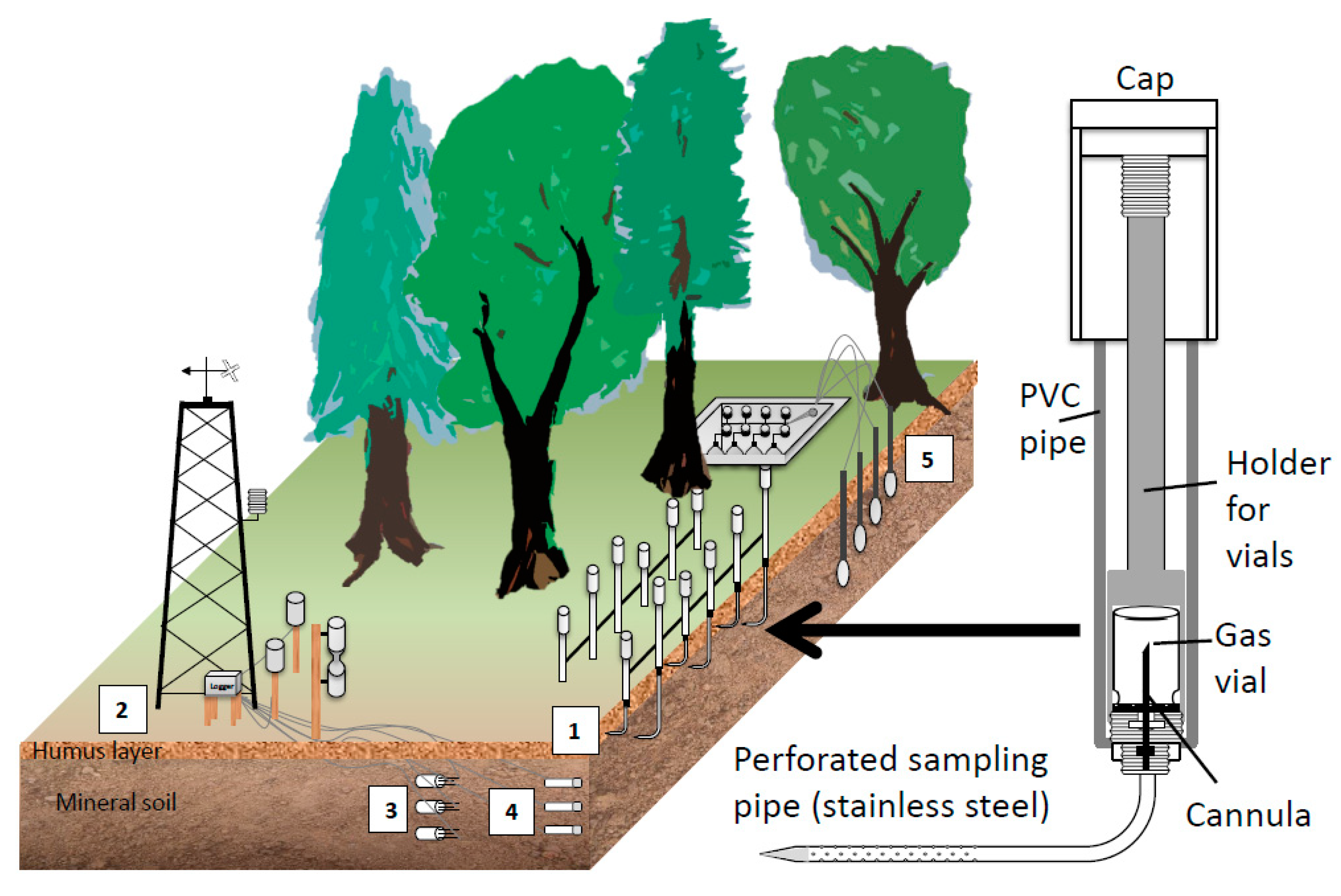
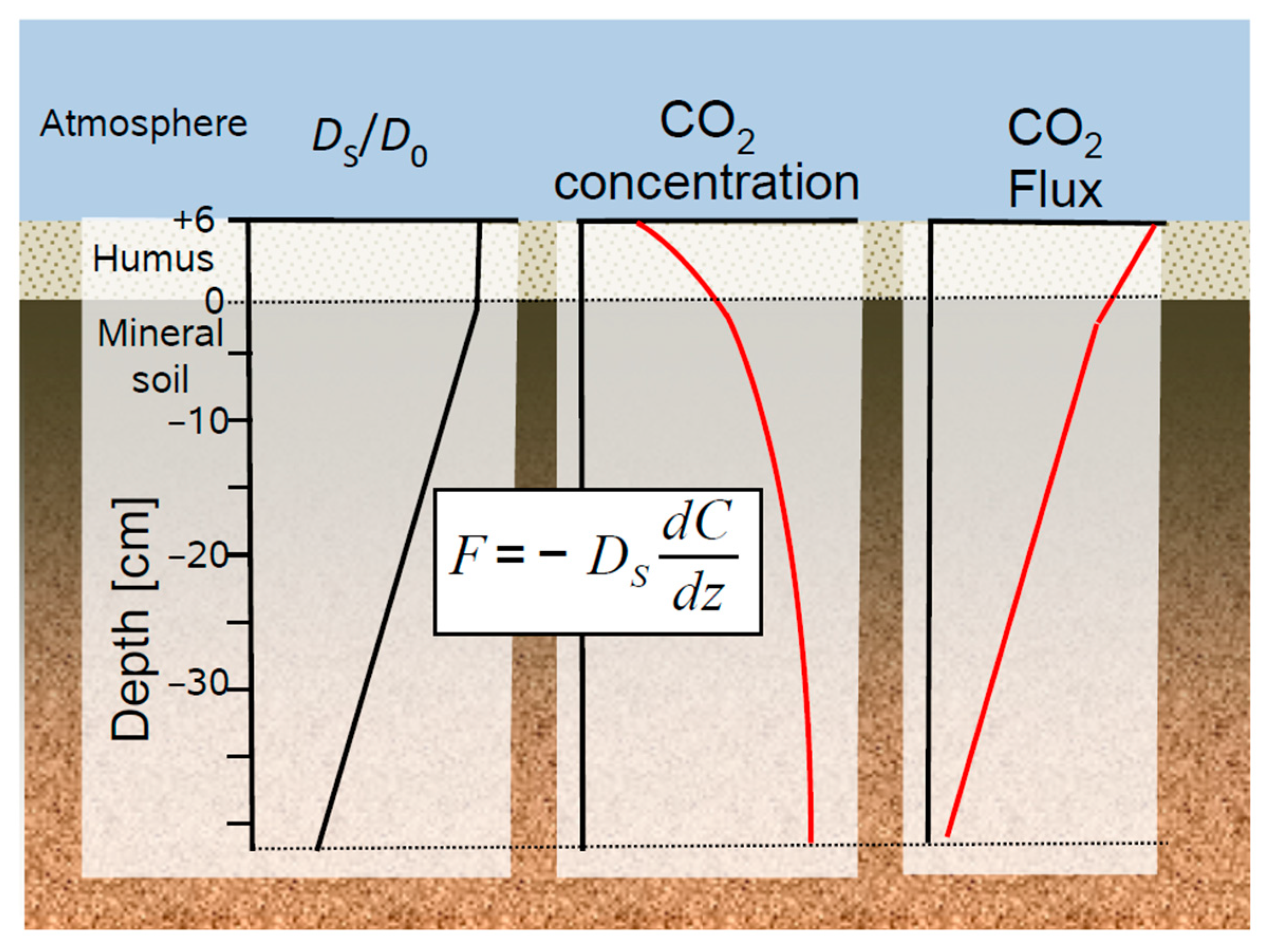
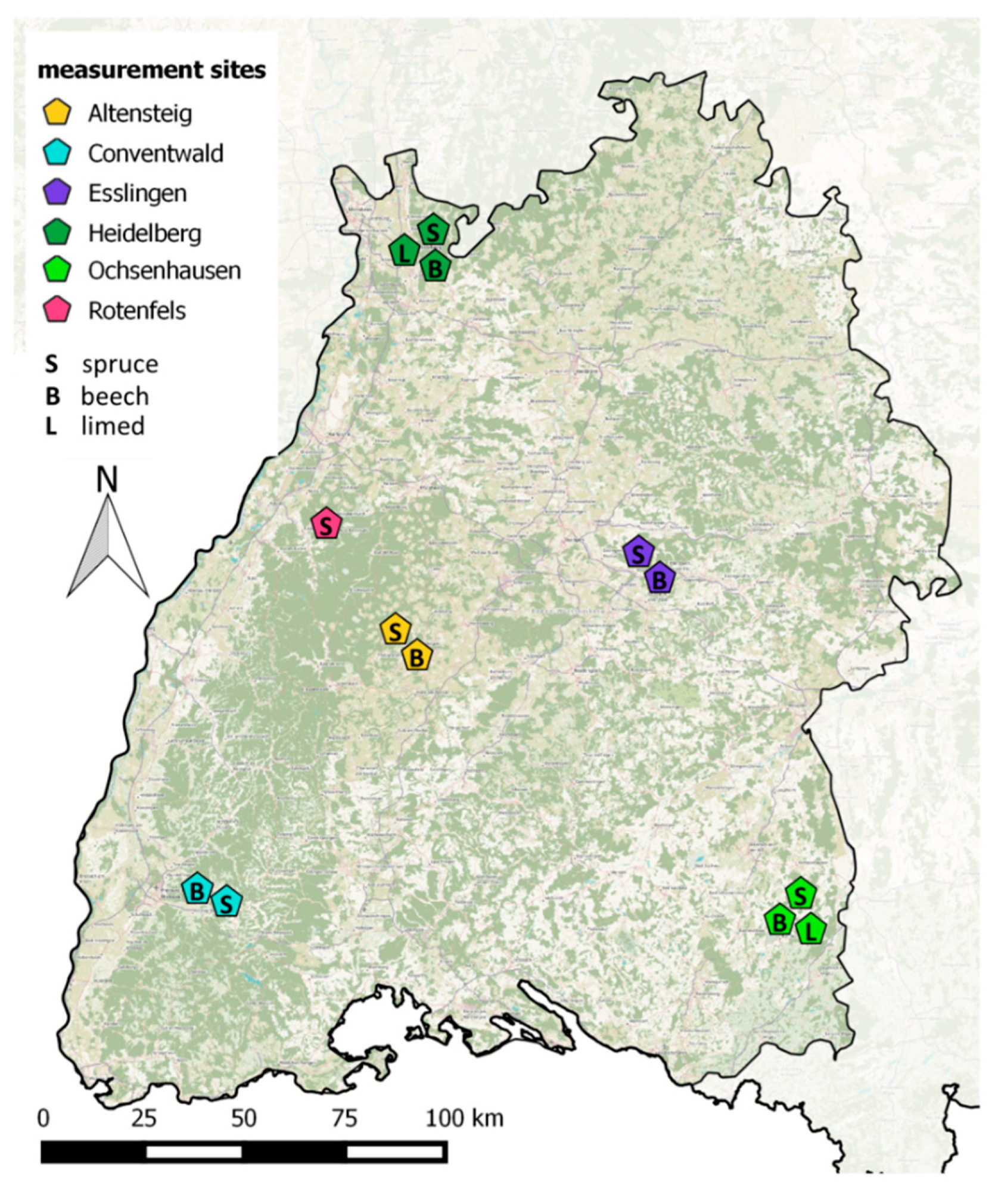
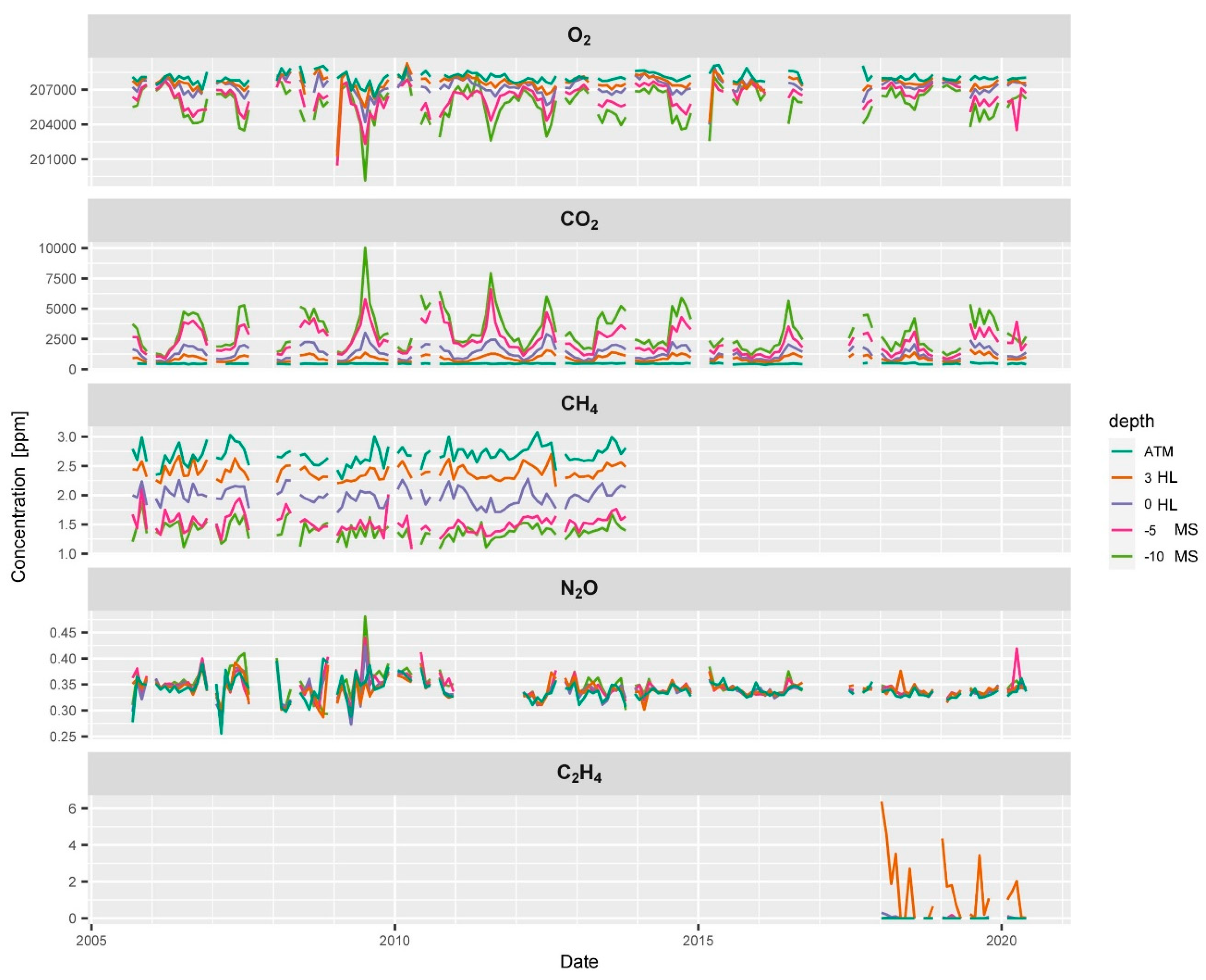


| Gas | GC | Column | Detector | Limit of Detection | Precision | Atmospheric Concentration | Typical Soil Air * |
|---|---|---|---|---|---|---|---|
| CO2 | Perkin Elmer Clarus 680 GC | CP-PoraBond Q | TCD | 30 ppm | 1.0% | ca. 400 ppm | 500–20,000 ppm |
| O2 | CP-Molsieve 5A | 0.5% | 0.6% | 20.95% | 0–20.95% | ||
| N2 | 1.7% | 0.6% | 78.08% | ca. 78.08% | |||
| Ar | 0.02% | 0.8% | 0.93% | ca. 0.93% | |||
| CH4 | CP-SilicaPlot | FID | 0.27 ppm | 1.6% | 1.95 ppm | <0.3 to >100 ppm | |
| C2H4 | 0.04 ppm | 2.3% at 0.5 ppm | 0 ppm | 0 to >5 ppm | |||
| N2O | Varian CP 3800 | CP-PoraBond Q | ECD | 0.02 ppm | 1.1% | 0.33 ppm | <0.2–10 ppm |
| Site | Acronym | Plot | Latitude | Longitude | Altitude (m) | Precipitation (mm) | Temperature (°C) |
|---|---|---|---|---|---|---|---|
| Rotenfels | RO | 1 | 48.82° | 8.40° | 600 | 1258 | 9.0 |
| Altensteig | AL | 2 | 48.59° | 8.63° | 512 | 821 | 8.5 |
| Conventwald | CO | 2 | 48.02° | 7.97° | 810 | 1385 | 8.3 |
| Esslingen | ES | 2 | 48.76° | 9.43° | 348 | 781 | 9.6 |
| Heidelberg | HD | 3 | 49.45° | 8.75° | 510 | 1113 | 7.4 |
| Ochsenhausen | OC | 3 | 48.01° | 9.96° | 680 | 1111 | 8.6 |
| Forest Stand | Soil | Humus | ||||||
|---|---|---|---|---|---|---|---|---|
| Plot | Age | Height (m) | Type | pH | Texture | Coarse Soil (%) | Type | Depth (cm) |
| RO spruce | 128 | 37.2 | Hyperalbic Podzol | 2.94 | Su3 | 25 | Rawhumus (ROR) | 15 |
| AL spruce | 110 | 37.1 | Haplic Cambisol | 3.26 | Sl3 | 5 | Mull (MUO) | 8 |
| AL beech | 138 | 28 | Stagnic Cambisol | 3.77 | Sl3 | 1 | Mull (MUO) | 6 |
| CO spruce | 98 | 34 | Haplic Cambisol | 3.43 | Sl4 | 80 | Moder (MOT) | 10 |
| CO beech | 138 | 31.5 | Skeletic Cambisol | 3.1 | Ls2 | 50 | Moder (MOT) | 3 |
| ES spruce | 110 | 41.9 | Vertic Stagnosol | 3.24 | Ls2 | 0 | Moder (MOT) | 6 |
| ES beech | 138 | 33.2 | Haplic Stagnosol | 3.61 | Sl4 | 2 | Mull (MUF) | 4 |
| HD spruce | 108 | 32.3 | Haplic Cambisol | 2.87 | Sl3 | 10 | Moder (MOT) | 7 |
| HD* spruce | 108 | 32.3 | Haplic Cambisol | 2.87 | Sl3 | 10 | Moder (MOT) | 7 |
| HD beech | 83 | 27.5 | Haplic Stagnosol | 3.52 | Ls2 | 1 | Mull (MUF) | 3 |
| OC spruce | 100 | 33.6 | Abruptic Luvisol | 3.15 | Lu | 2 | Moder (MOR) | 9 |
| OC * spruce | 100 | 33.6 | Abruptic Luvisol | 4.1 | Lu | 8 | Moder (MOR) | 10 |
| OC beech | 138 | 36.4 | Epidystric Luvisol | 3.25 | Ut3 | 2 | Moder (MOR) | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maier, M.; Gartiser, V.; Schengel, A.; Lang, V. Long Term Soil Gas Monitoring as Tool to Understand Soil Processes. Appl. Sci. 2020, 10, 8653. https://doi.org/10.3390/app10238653
Maier M, Gartiser V, Schengel A, Lang V. Long Term Soil Gas Monitoring as Tool to Understand Soil Processes. Applied Sciences. 2020; 10(23):8653. https://doi.org/10.3390/app10238653
Chicago/Turabian StyleMaier, Martin, Valentin Gartiser, Alexander Schengel, and Verena Lang. 2020. "Long Term Soil Gas Monitoring as Tool to Understand Soil Processes" Applied Sciences 10, no. 23: 8653. https://doi.org/10.3390/app10238653
APA StyleMaier, M., Gartiser, V., Schengel, A., & Lang, V. (2020). Long Term Soil Gas Monitoring as Tool to Understand Soil Processes. Applied Sciences, 10(23), 8653. https://doi.org/10.3390/app10238653






