Analysis of the Influence of Surface Roughness on Measurement of Ultrasonic Nonlinearity Parameter Using Contact-Type Transducer
Abstract
:1. Introduction
2. Ultrasonic Nonlinearity Parameter
3. Experiments
3.1. Specimen Preparation and Experimental Procedures
3.2. Absolute Nonlinearity Parameter Measurement
3.3. Relative Nonlinearity Parameter Measurement
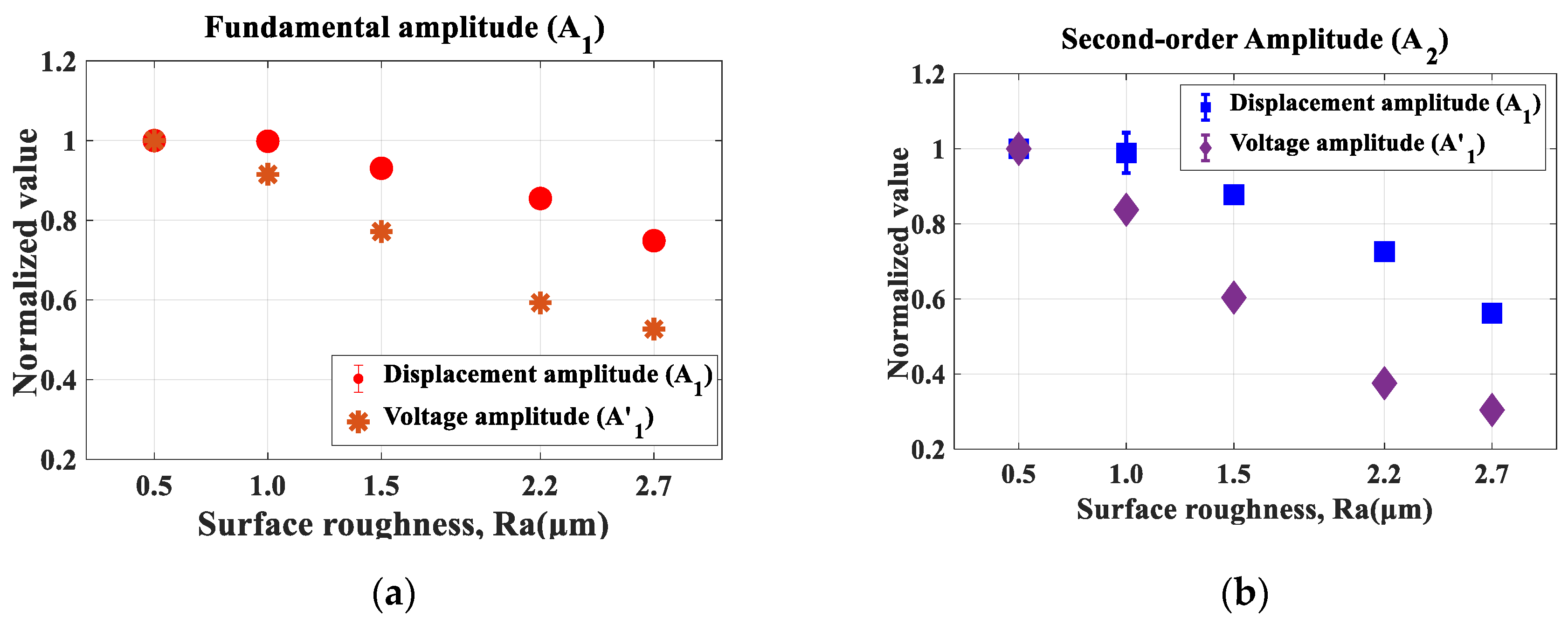
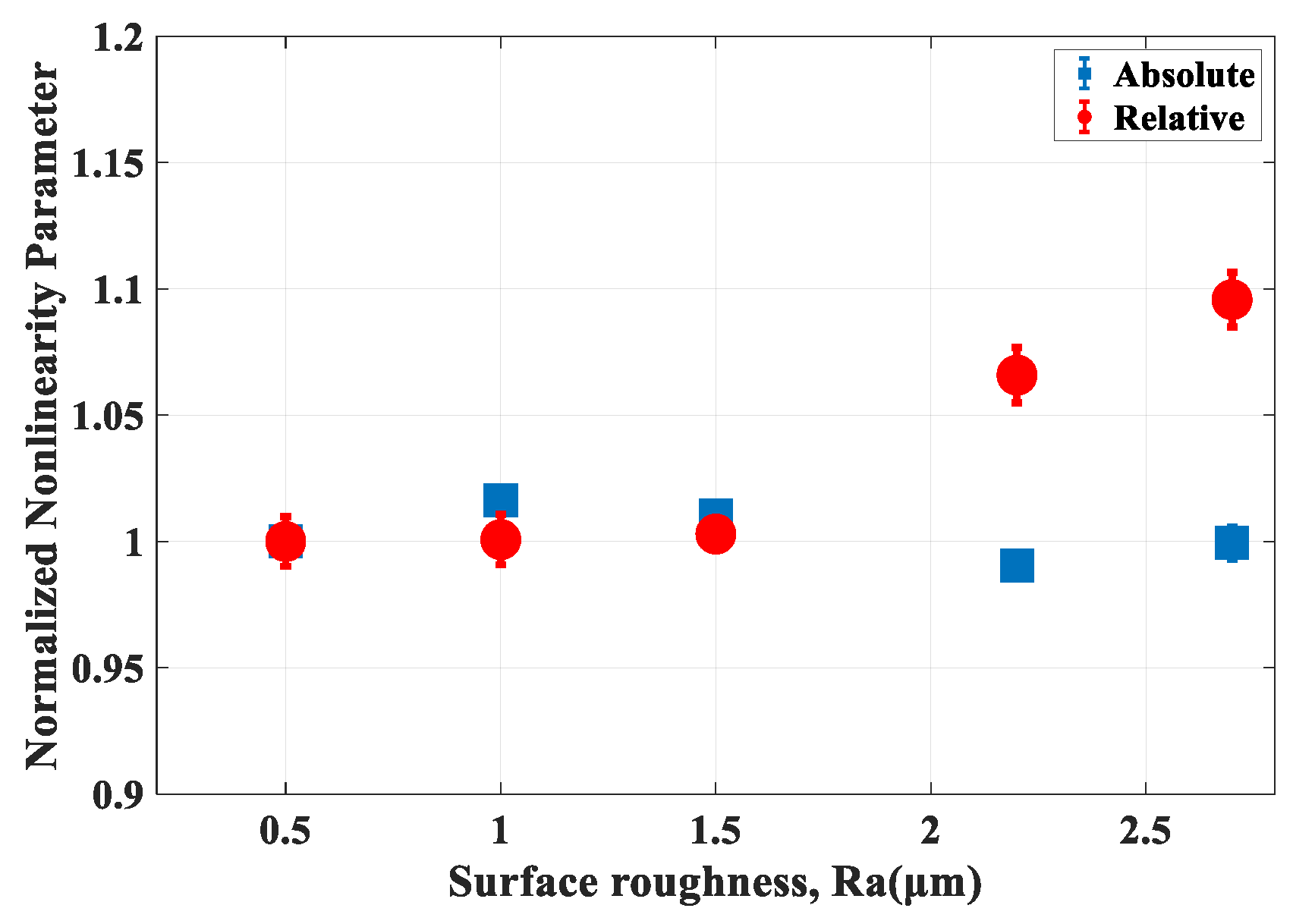
4. Experimental Results
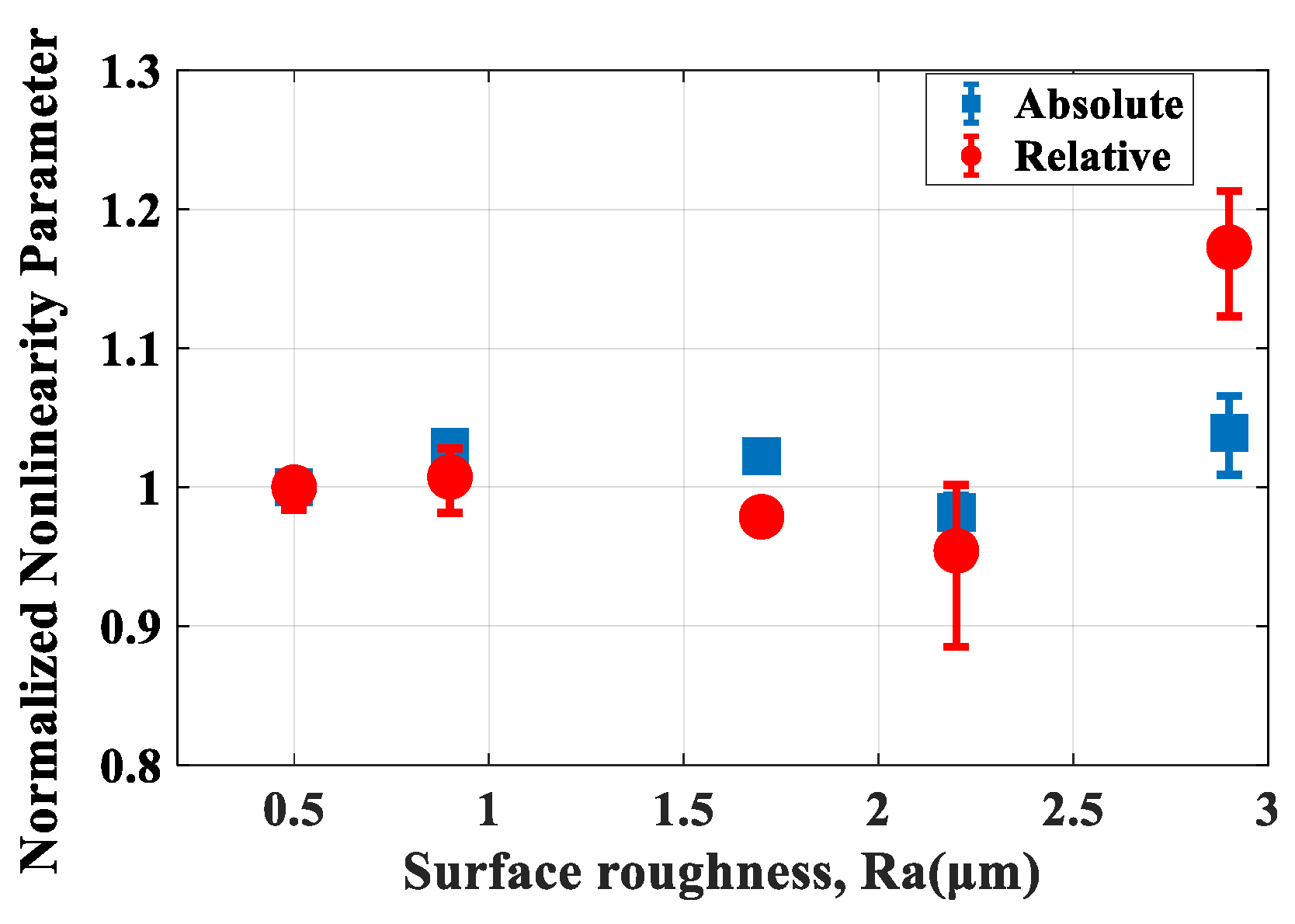
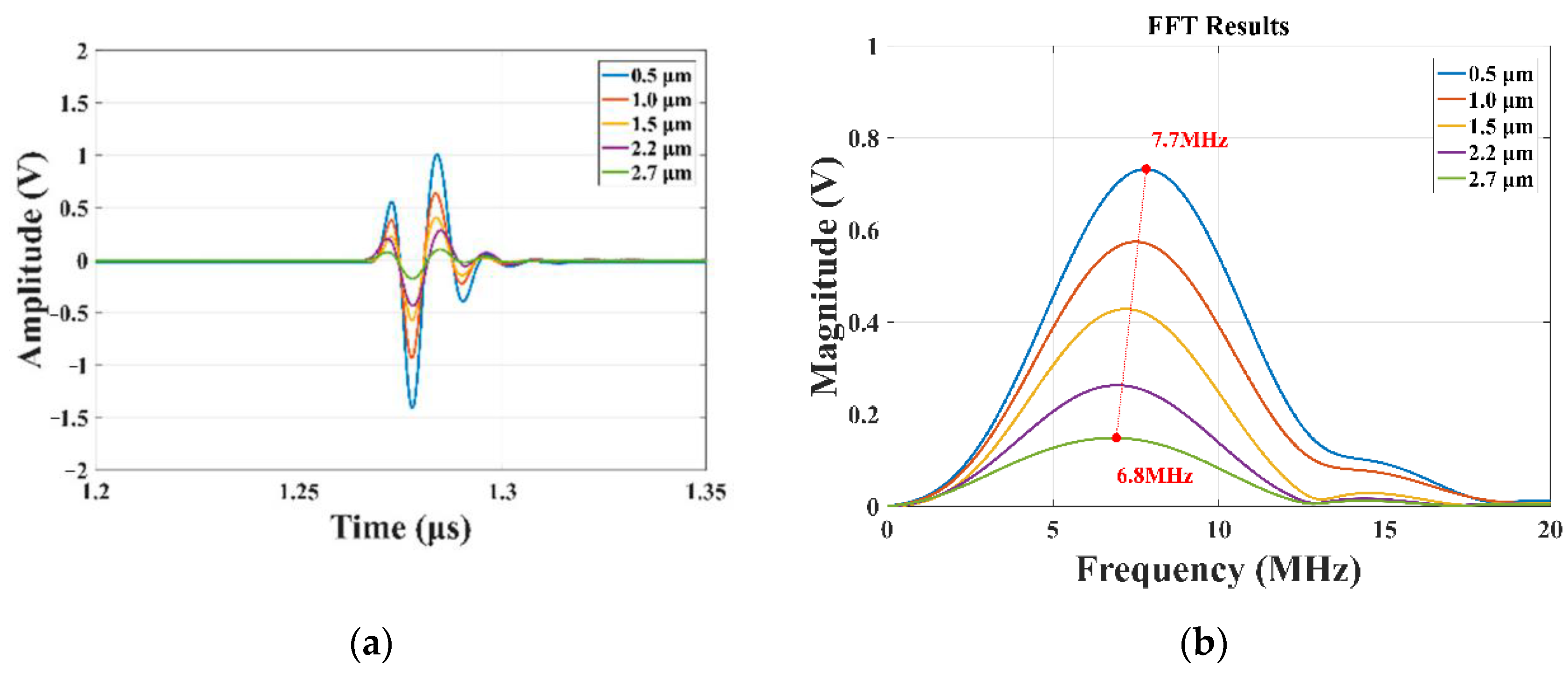
4.1. Rough Surfaces on both Sides
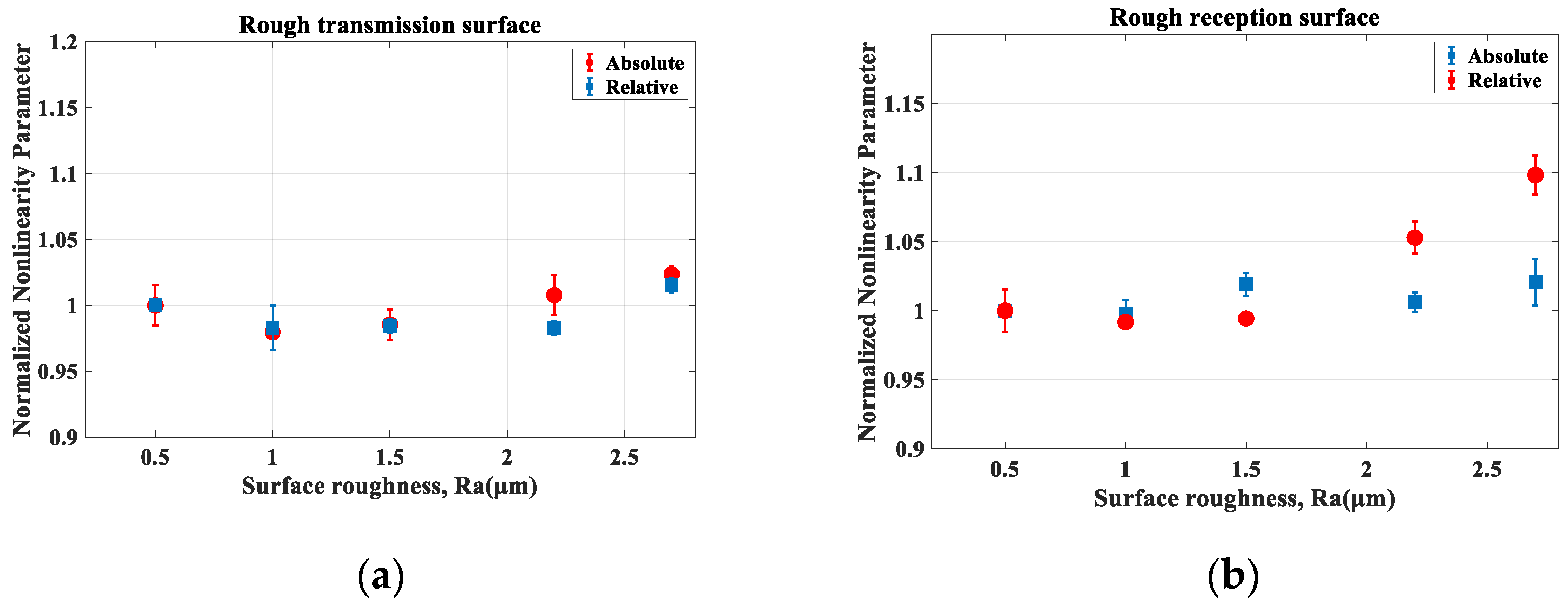
4.2. Al 6061-T6 with One Rough Surface and One Smooth Surface
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jhang, K.-Y. Nonlinear ultrasonic techniques for nondestructive assessment of micro damage in material: A review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135. [Google Scholar] [CrossRef]
- Jhang, K.-Y. Application of nonlinear ultrasonics to the NDE of material degradation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 540–548. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Effect of precipitate coherency strains on acoustic harmonic generation. J. Appl. Phys. 1997, 81, 2957–2962. [Google Scholar] [CrossRef]
- Hikata, A.; Chick, B.B.; Elbaum, C. Dislocation contribution to the second harmonic generation of ultrasonic waves. J. Appl. Phys. 1965, 36, 229–236. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Jacobs, L.J.; Qu, J.; Littles, J.W. Experimental characterization of fatigue damage in a nickel-base superalloy using nonlinear ultrasonic waves. J. Acoust. Soc. Am. 2006, 120, 1266–1273. [Google Scholar] [CrossRef]
- Cantrell, J.H. Quantitative assessment of fatigue damage accumulation in wavy slip metals from acoustic harmonic generation. Philos. Mag. 2006, 86, 1539–1554. [Google Scholar] [CrossRef] [Green Version]
- Hong, M.; Su, Z.; Wang, Q.; Cheng, L.; Qing, X. Modeling nonlinearities of ultrasonic waves for fatigue damage characterization: Theory, simulation, and experimental validation. Ultrasonics 2014, 54, 770–778. [Google Scholar] [CrossRef]
- Balasubramaniam, K.; Valluri, J.S.; Prakash, R.V. Creep damage characterization using a low amplitude nonlinear ultrasonic technique. Mater. Charact. 2011, 62, 275–286. [Google Scholar] [CrossRef]
- Kim, J.; Jhang, K.-Y. Evaluation of ultrasonic nonlinear characteristics in heat-treated aluminum alloy (Al-Mg-Si-Cu). Adv. Mater. Sci. Eng. 2013, 407846, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Jhang, K.-Y. Assessment of thermal degradation by cumulative variation of ultrasonic nonlinear parameter. Int. J. Precis. Eng. Manuf. 2017, 18, 23–29. [Google Scholar] [CrossRef]
- Xiang, Y.; Deng, M.; Xuan, F.-Z. Thermal degradation evaluation of HP40Nb alloy steel after long term service using a nonlinear ultrasonic technique. J. Nondestruct. Eval. 2014, 33, 279–287. [Google Scholar] [CrossRef]
- Kim, J.; Song, D.-G.; Jhang, K.-Y. Absolute measurement and relative measurement of ultrasonic nonlinear parameters. Res. Nondestruct. Eval. 2017, 28, 211–225. [Google Scholar] [CrossRef] [Green Version]
- Dace, G.E.; Thompson, R.B.; Buck, O. Measurement of the acoustic harmonic generation for materials characterization using contact transducers. Rev. Prog. Quant. Nondestruct. Eval. 1992, 11B, 2069–2076. [Google Scholar]
- Yost, W.T.; Cantrell, J.H. Absolute ultrasonic displacement amplitude measurements with a submersible electrostatic acoustic transducer. Rev. Sci. Instrum. 1992, 63, 4182–4188. [Google Scholar] [CrossRef]
- Hurley, D.C.; Fortunko, C.M. Determination of the nonlinear ultrasonic parameter using a Michelson interferometer. Meas. Sci. Technol. 1997, 8, 634–642. [Google Scholar] [CrossRef]
- Bilgen, M.; Rose, J.H. Rough-surface effects on incoherent scattering from random volumetric scatterers: Approximate analytic series solution. J. Acoust. Soc. Am. 1994, 96, 2856–2869. [Google Scholar] [CrossRef]
- Wilhjelm, J.E.; Pedersen, P.C.; Jacobsen, S.M. The influence of roughness, angle, range, and transducer type on the echo signal from planar interfaces. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 511–521. [Google Scholar] [CrossRef] [Green Version]
- Nagy, P.B.; Adler, L. Surface roughness induced attenuation of reflected and transmitted ultrasonic waves. J. Acoust. Soc. Am. 1987, 82, 193–197. [Google Scholar] [CrossRef]
- Sukmana, D.D.; Ihara, I. Application of air-coupled ultrasound to noncontact surface roughness evaluation. Jpn. J. Appl. Phys. 2005, 44, 4417–4420. [Google Scholar] [CrossRef]
- Na, J.K. Effects of surface roughness and nonparallelism on the measurement of the acoustic nonlinearity parameter in steam turbine blades. AIP Conf. Proceed. 2000, 509, 1417–1424. [Google Scholar]
- Chakrapani, S.K.; Howard, A.; Barnard, D. Influence of surface roughness on the measurement of acoustic nonlinearity parameter of solids using contact piezoelectric transducers. Ultrasonics 2018, 84, 112–118. [Google Scholar] [CrossRef]
- Lee, K.-J.; Kim, J.; Song, D.-G.; Jhang, K.-Y. Effect of window function for measurement of ultrasonic nonlinear parameter using fast fourier transform of tone-burst signal. J. Korean Soc. Nondestruct. Test. 2015, 35, 251–257. [Google Scholar] [CrossRef] [Green Version]
- Choi, I.-H.; Lee, J.-I.; Kwon, G.-D.; Jhang, K.-Y. Effect of system dependent harmonics in the measurement of ultrasonic nonlinear parameter by using contact transducers. J. Korean Soc. Nondestruct. Test. 2008, 28, 358–363. [Google Scholar]
- Zheng, Y.; Maev, R.G.; Solodov, I.Y. Review/Sythèse nonlinear acoustic applications for material characterization: A review. Can. J. Phys. 2000, 77, 927–967. [Google Scholar] [CrossRef]
- Kim, J.; Lee, K.-J.; Jhang, K.-Y. Comparison of ultrasonic nonlinear parameters measured by PZT and LiNbO3 transducers. In Proceedings of the 42nd Annual Review of Progress in Quantitative Nondestructive Evaluation, Minneapolis, MN, USA, 26–31 July 2016; Volume 1706, p. 060008. [Google Scholar]

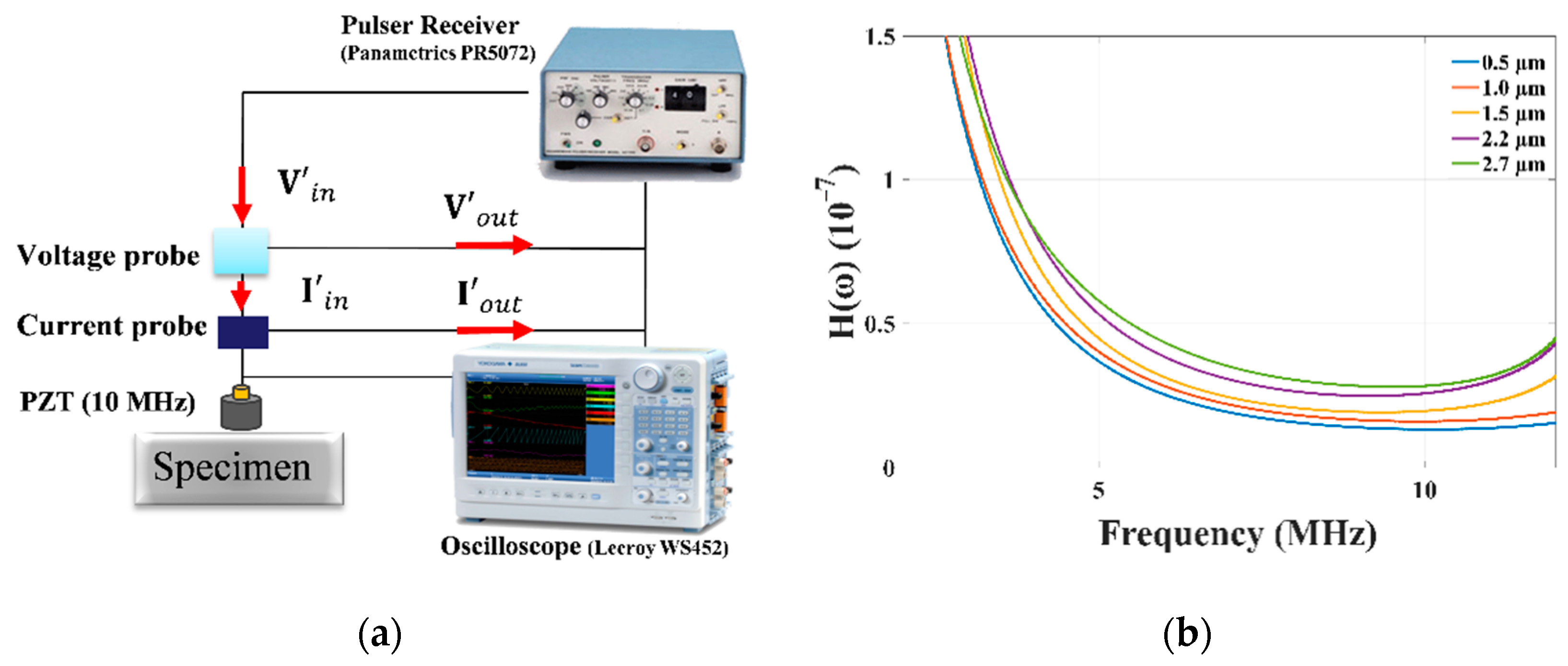

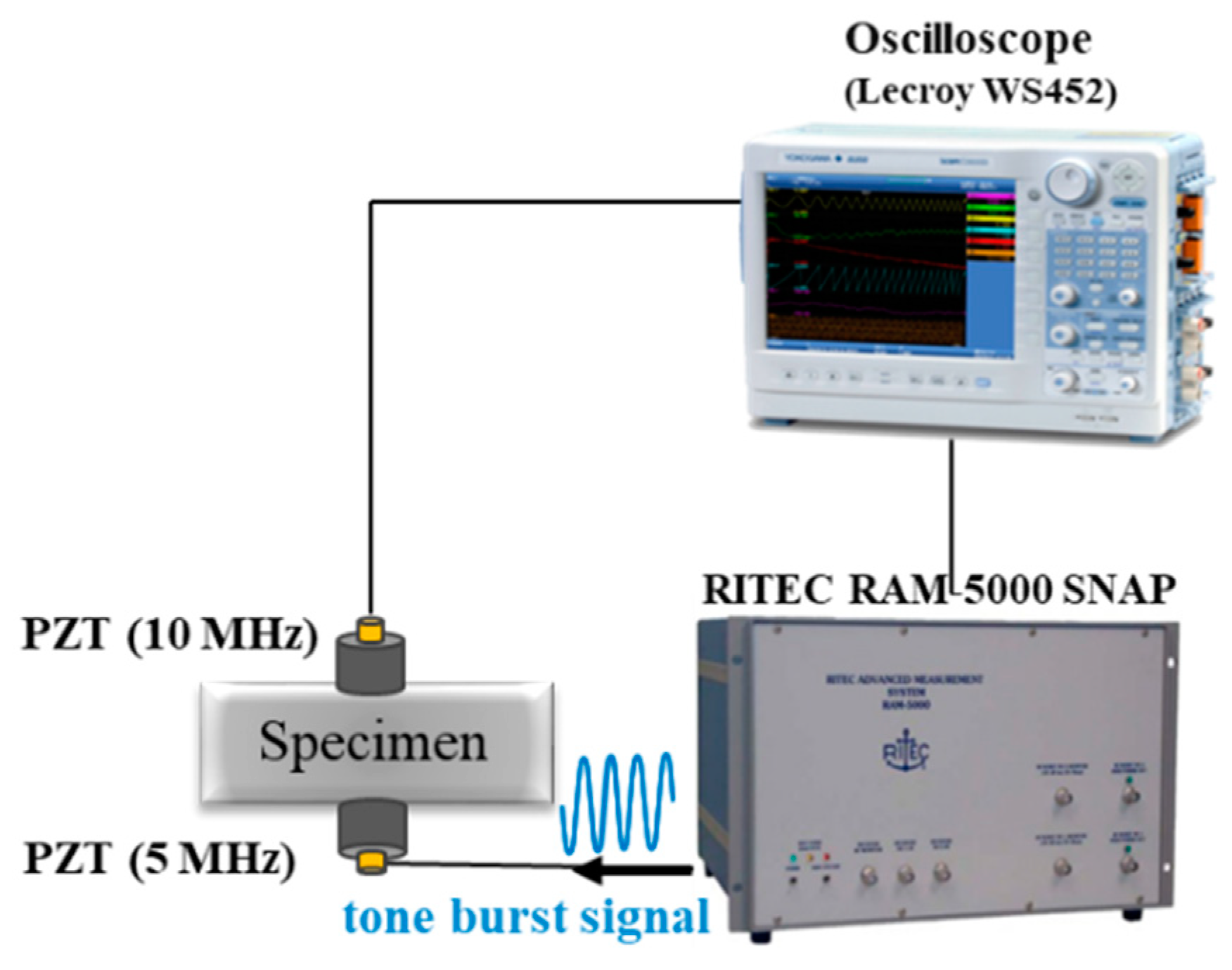
| 0.5 μm | 1.0 μm | 1.5 μm | 2.2 μm | 2.7 μm | |
|---|---|---|---|---|---|
| 5 MHz | 3.69 × 10−8 | 4.03 × 10−8 | 4.49 × 10−8 | 5.26 × 10−8 | 5.34 × 10−8 |
| 10 MHz | 1.33 × 10−8 | 1.61 × 10−8 | 1.97 × 10−8 | 2.49 × 10−8 | 2.84 × 10−8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Ha, H.-P.; Kim, K.-M.; Jhang, K.-Y. Analysis of the Influence of Surface Roughness on Measurement of Ultrasonic Nonlinearity Parameter Using Contact-Type Transducer. Appl. Sci. 2020, 10, 8661. https://doi.org/10.3390/app10238661
Kim J, Ha H-P, Kim K-M, Jhang K-Y. Analysis of the Influence of Surface Roughness on Measurement of Ultrasonic Nonlinearity Parameter Using Contact-Type Transducer. Applied Sciences. 2020; 10(23):8661. https://doi.org/10.3390/app10238661
Chicago/Turabian StyleKim, Jongbeom, Hong-Pil Ha, Kyung-Mo Kim, and Kyung-Young Jhang. 2020. "Analysis of the Influence of Surface Roughness on Measurement of Ultrasonic Nonlinearity Parameter Using Contact-Type Transducer" Applied Sciences 10, no. 23: 8661. https://doi.org/10.3390/app10238661
APA StyleKim, J., Ha, H.-P., Kim, K.-M., & Jhang, K.-Y. (2020). Analysis of the Influence of Surface Roughness on Measurement of Ultrasonic Nonlinearity Parameter Using Contact-Type Transducer. Applied Sciences, 10(23), 8661. https://doi.org/10.3390/app10238661






