Hardware in the Loop Platform for Testing Photovoltaic System Control
Abstract
1. Introduction
2. Structure of the Photovoltaic System
2.1. Photovoltaic Panel Emulator
2.2. DC-DC Boost Power Electronic Converter
2.3. Maximum Power Point Tracking Controller
2.4. Voltage Controller
3. Design and Implementation of Emulators in Hardware in the Loop
3.1. Photovoltaic Panel
3.2. Boost Converter
3.3. Photovoltaic System
3.4. P&O Controller
3.5. PI Controller
3.6. Experimental Platform
4. Results
4.1. Photovoltaic Panel Emulator
4.2. Boost Converter Emulator
4.3. Open Loop Photovoltaic System Emulator
4.4. Maximum Power Point Tracking Controller Emulator
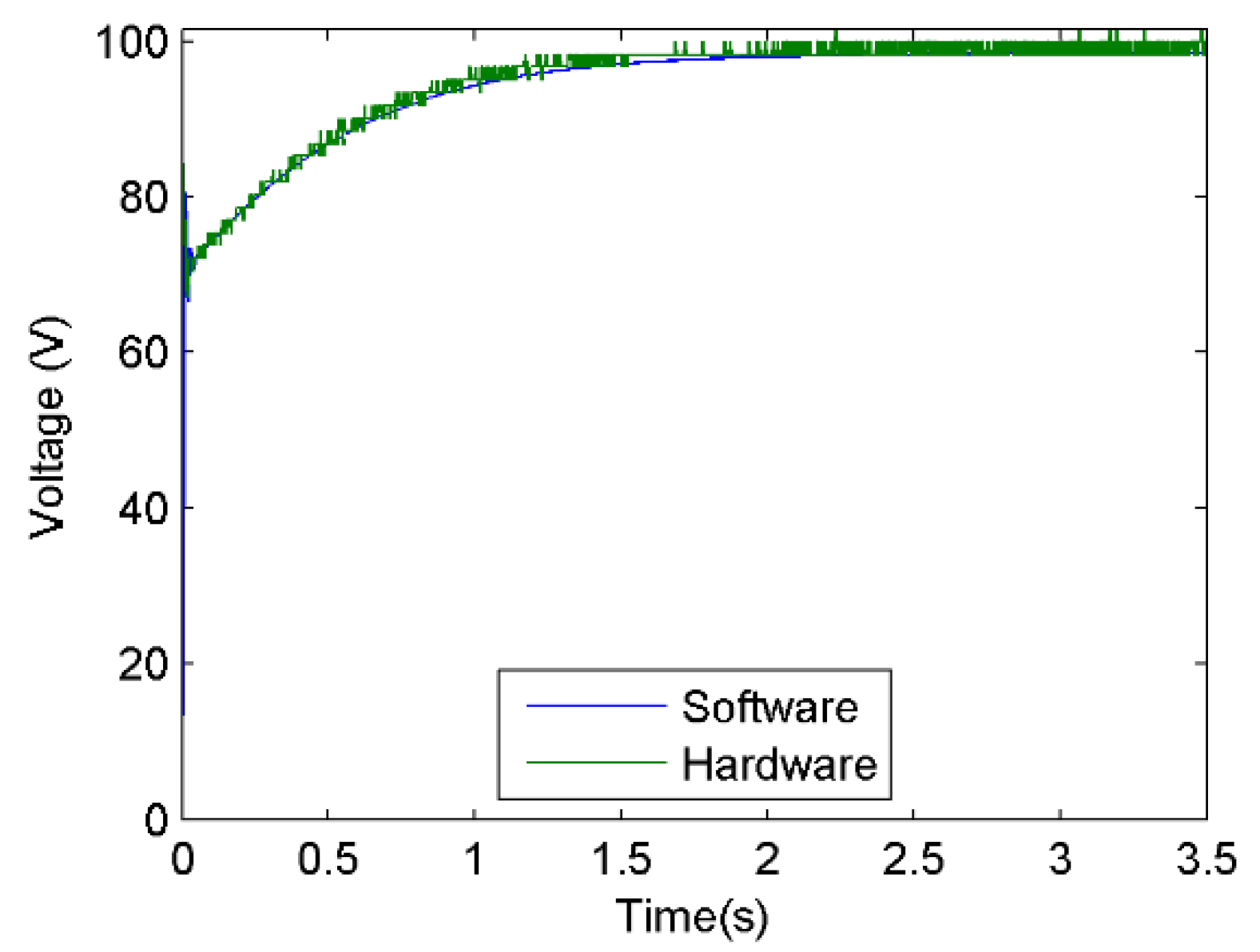
4.5. PI Classic Controller Emulator
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- UNFCCC. Adoption of the Paris Agreement, Conference of the Parties, Twenty-First Session FCCC/CP/2015/L.9; United Nations Framework Convention on Climate Change: Paris, France, 2015. [Google Scholar]
- IPCC. Global Warming of 1.5 °C. In Special Report of the Intergovernmental Panel on Climate Change; IPCC: Bangkok, Thailand, 2016. [Google Scholar]
- International Renewable Energy Agency. Global Energy Transformation: A Roadmap to 2050; International Renewable Energy Agency: Abu Dhabi, UAE, 2018; Available online: www.irena.org/publications (accessed on 19 September 2020).
- Kang, J.-N.; Wei, Y.; Liu, L.-C.; Han, R.; Yu, B.; Wang, J.-W. Energy systems for climate change mitigation: A systematic review. Appl. Energy 2020, 263, 114602. [Google Scholar] [CrossRef]
- Pilakkat, D.; Kanthalakshmi, S. An improved P&O algorithm integrated with artificial bee colony for photovoltaic systems under partial shading conditions. Sol. Energy 2019, 178, 37–47. [Google Scholar] [CrossRef]
- Loukriz, A.; Messalti, S.; Harrag, A. Design, simulation, and hardware implementation of novel optimum operating point tracker of PV system using adaptive step size. Int. J. Adv. Manuf. Technol. 2018, 101, 1671–1680. [Google Scholar] [CrossRef]
- Ram, J.P.; Pillai, D.S.; Ghias, A.M.; Rajasekar, N. Performance enhancement of solar PV systems applying P&O assisted Flower Pollination Algorithm (FPA). Sol. Energy 2020, 199, 214–229. [Google Scholar] [CrossRef]
- Takruri, M.; Farhat, M.; Barambones, O.; Ramos-Hernanz, J.A.; Turkieh, M.J.; Badawi, M.; Alzoubi, H.; Sakur, M.A. Maximum Power Point Tracking of PV System Based on Machine Learning. Energies 2020, 13, 692. [Google Scholar] [CrossRef]
- Tobón, A.; Peláez-Restrepo, J.; Montano, J.; Florez, M.D.; Herrera, J.; Ibeas, A. MPPT of a Photovoltaic Panels Array with Partial Shading Using the IPSM with Implementation Both in Simulation as in Hardware. Energies 2020, 13, 815. [Google Scholar] [CrossRef]
- Hadji, S.; Gaubert, J.-P.; Krim, F. Real-Time Genetic Algorithms-Based MPPT: Study and Comparison (Theoretical an Experimental) with Conventional Methods. Energies 2018, 11, 459. [Google Scholar] [CrossRef]
- Macaulay, J.; Zhou, Z. A Fuzzy Logical-Based Variable Step Size P&O MPPT Algorithm for Photovoltaic System. Energies 2018, 11, 1340. [Google Scholar] [CrossRef]
- Loukil, K.; Abbes, H.; Abid, H.; Abid, M.; Toumi, A. Design and implementation of reconfigurable MPPT fuzzy controller for photovoltaic systems. Ain Shams Eng. J. 2020, 11, 319–328. [Google Scholar] [CrossRef]
- Farajdadian, S.; Hosseini, S.M.H. Optimization of fuzzy-based MPPT controller via metaheuristic techniques for stand-alone PV systems. Int. J. Hydrogen Energy 2019, 44, 25457–25472. [Google Scholar] [CrossRef]
- Senthilvel, A.; Vijeyakumar, K.; Vinothkumar, B. FPGA based implementation of MPPT algorithms for photovoltaic system under partial shading conditions. Microprocess. Microsyst. 2020, 77, 103011. [Google Scholar] [CrossRef]
- Ram, J.P.; Manghani, H.; Pillai, D.S.; Babu, T.S.; Miyatake, M.; Rajasekar, N. Analysis on solar PV emulators: A review. Renew. Sustain. Energy Rev. 2018, 81, 149–160. [Google Scholar] [CrossRef]
- Ayop, R.; Tan, C.W. A comprehensive review on photovoltaic emulator. Renew. Sustain. Energy Rev. 2017, 80, 430–452. [Google Scholar] [CrossRef]
- Moussa, I.; Khedher, A.; Bouallegue, A. Design of a Low-Cost PV Emulator Applied for PVECS. Electronics 2019, 8, 232. [Google Scholar] [CrossRef]
- Ullah, N.; Nisar, F.; Al-Ahmadi, A.A. Closed Loop Control of Photo Voltaic Emulator Using Fractional Calculus. IEEE Access 2020, 8, 28880–28887. [Google Scholar] [CrossRef]
- Joshi, D.; Sharma, S. PV Emulator Modeling and Design Using Buck Converter. In En Applications of Computing, Automation and Wireless Systems in Electrical Engineering; Springer: Singapore, 2019; pp. 639–648. [Google Scholar] [CrossRef]
- Moussa, I.; Khedher, A. Photovoltaic emulator based on PV simulator RT implementation using XSG tools for an FPGA control: Theory and experimentation. Int. Trans. Electr. Energy Syst. 2019, 29, e12024. [Google Scholar] [CrossRef]
- Ayop, R.; Tan, C.W. A novel photovoltaic emulator based on current-resistor model using binary search computation. Sol. Energy 2018, 160, 186–199. [Google Scholar] [CrossRef]
- Ulaganathan, M.; Devaraj, D. Programmable DC Power Supply based Solar PV Module Emulator using LabVIEW and Multisim. Int. J. Renew. Energy Res. (IJRER) 2019, 9, 1892–1900. [Google Scholar]
- Ulaganathan, M.; Devaraj, D. Hardware and Software Co-emulation Technique based Solar Photovoltaic Sources Emulator. In Proceedings of the 2019 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS), Tamilnadu, India, 11–13 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Merenda, M.; Iero, D.; Carotenuto, R.; Della Corte, F.G. Simple and Low-Cost Photovoltaic Module Emulator. Electronics 2019, 8, 1445. [Google Scholar] [CrossRef]
- Ebe, F.; Idlbi, B.; Stakic, D.; Chen, S.; Kondzialka, C.; Casel, M.; Heilscher, G.; Seitl, C.; Bründlinger, R.; Strasser, T.I. Comparison of Power Hardware-in-the-Loop Approaches for the Testing of Smart Grid Controls. Energies 2018, 11, 3381. [Google Scholar] [CrossRef]
- De Farias, A.B.C.; Rodrigues, R.S.; Murilo, A.; Lopes, R.V.; Avila, S. Low-Cost Hardware-in-the-Loop Platform for Embedded Control Strategies Simulation. IEEE Access 2019, 7, 111499–111512. [Google Scholar] [CrossRef]
- Syed, M.H.; Guillo-Sansano, E.; Wang, Y.; Vogel, S.; Palensky, P.; Burt, G.M.; Xu, Y.; Monti, A.; Hovsapian, R. Real-Time Coupling of Geographically Distributed Research Infrastructures: Taxonomy, Overview and Real-World Smart Grid Applications. IEEE Trans. Smart Grid 2020, 1. [Google Scholar] [CrossRef]
- Salcedo, R.; Corbett, E.; Smith, C.; Limpaecher, E.; Rekha, R.; Nowocin, J.; Lauss, G.; Fonkwe, E.; Almeida, M.; Gartner, P.; et al. Banshee distribution network benchmark and prototyping platform for hardware-in-the-loop integration of microgrid and device controllers. J. Eng. 2019, 2019, 5365–5373. [Google Scholar] [CrossRef]
- Estrada, L.; Vázquez, N.; Vaquero, J.; De Castro, A.; Arau, J. Real-Time Hardware in the Loop Simulation Methodology for Power Converters Using LabVIEW FPGA. Energies 2020, 13, 373. [Google Scholar] [CrossRef]
- Raikwar, S.; Wani, L.J.; Kumar, S.A.; Rao, M.S. Hardware-in-the-Loop test automation of embedded systems for agricultural tractors. Measurement 2019, 133, 271–280. [Google Scholar] [CrossRef]
- Razzaghi, R.; Mitjans, M.; Rachidi, F.; Paolone, M. An automated FPGA real-time simulator for power electronics and power systems electromagnetic transient applications. Electr. Power Syst. Res. 2016, 141, 147–156. [Google Scholar] [CrossRef]
- Renaux, P.B.; Linhares, R.R.; Renaux, D.P.B. Douglas Paulo Bertrand. Hardware-in-the-Loop Simulation Low-Cost Platform. In Proceedings of the 2017 VII Brazilian Symposium on Computing Systems Engineering (SBESC), Curitiba, Brazil, 6–10 November 2017; pp. 173–180. [Google Scholar] [CrossRef]
- Shao, Y.; Zulkefli, M.A.M.; Sun, Z.; Huang, P. Evaluating connected and autonomous vehicles using a hardware-in-the-loop testbed and a living lab. Transp. Res. Part C Emerg. Technol. 2019, 102, 121–135. [Google Scholar] [CrossRef]
- Dang, D.; Gao, F.; Hu, Q. Motion Planning for Autonomous Vehicles Considering Longitudinal and Lateral Dynamics Coupling. Appl. Sci. 2020, 10, 3180. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, C.; Xiao, G.; Li, H.; Ye, J.; Liu, Y. Research for Nonlinear Model Predictive Controls to Laterally Control Unmanned Vehicle Trajectory Tracking. Appl. Sci. 2020, 10, 6034. [Google Scholar] [CrossRef]
- Amin, M.M.; Aziz, G.A.A. A Hardware-in-the-Loop Realization of a Robust Discrete-Time Current Control of PMa-SynRM for Aerospace Vehicle Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 936–945. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, P.; Yang, H. Hardware-in-the-Loop Real-time Simulation for Speed-Sensorless Vector Control of High-Power Induction Motor. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Hsieh, M.-F.; Weng, Y.-C. A Low Torque Ripple Direct Torque Control Method for Interior Permanent Magnet Motor. Appl. Sci. 2020, 10, 1723. [Google Scholar] [CrossRef]
- Garramiola, F.; Poza, J.; Del Olmo, J.; Nieva, T. Hardware-in-the-loop performance analysis of a railway traction system under sensor faults. J. Eng. 2019, 2019, 3797–3801. [Google Scholar] [CrossRef]
- Wang, Y.; Syed, M.H.; Guillo-Sansano, E.; Xu, Y.; Burt, G.M. Inverter-Based Voltage Control of Distribution Networks: A Three-Level Coordinated Method and Power Hardware-in-the-Loop Validation. IEEE Trans. Sustain. Energy 2019, 11, 2380–2391. [Google Scholar] [CrossRef]
- Wang, Y.; Nguyen, T.L.; Syed, M.H.; Xu, Y.; Guillo-Sansano, E.; Nguyen, V.-H.; Burt, G.M.; Tran, Q.-T.; Caire, R. A Distributed Control Scheme of Microgrids in Energy Internet Paradigm and Its Multisite Implementation. IEEE Trans. Ind. Inform. 2020, 17, 1141–1153. [Google Scholar] [CrossRef]
- Palahalli, H.; Huo, Y.; Gruosso, G. Real Time Simulation of Photovoltaic System Using Fpga. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 865–870. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, W.; Gan, J.; Yao, G. Hardware in Loop Simulation Test of Photovoltaic Virtual Synchronous Generator. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Iman-Eini, H.; Tennakoon, S.B. Investigation of a cascaded H-bridge photovoltaic inverter under non-uniform insolation conditions by hardware-in-the-loop test. Int. J. Electr. Power Energy Syst. 2019, 105, 330–340. [Google Scholar] [CrossRef]
- Doosthosseini, M.; Mishra, P.P.; Fathy, H.K. Hardware-in-the-Loop Testbed Development for Validating Novel Photovoltaic Battery Energy Storage System Concepts. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 1587–1592. [Google Scholar] [CrossRef]
- Palahalli, H.; Ragaini, E.; Gruosso, G. Smart Grid Simulation Including Communication Network: A Hardware in the Loop Approach. IEEE Access 2019, 7, 90171–90179. [Google Scholar] [CrossRef]
- Kumar, G.V.B.; Kaliannan, P.; Padmanaban, S.; Holm-Nielsen, J.B.; Blaabjerg, F. Effective Management System for Solar PV Using Real-Time Data with Hybrid Energy Storage System. Appl. Sci. 2020, 10, 1108. [Google Scholar] [CrossRef]
- User Guide and Specifications NI myRIO-1900. Available online: https://www.ni.com/pdf/manuals/376047c.pdf (accessed on 19 November 2020).
- Pan, Y.; Yang, Y.; Blaabjerg, F. Distributed Control of Islanded Series PV-Battery-Hybrid Systems with Low Communication Burden. In Proceedings of the 2020 IEEE 11th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Dubrovnik, Croatia, 28 September–1 October 2020; pp. 315–321. [Google Scholar] [CrossRef]
- Kanathipan, K.; Emamalipour, R.; Lam, J. A Single-Switch High-Gain PV Microconverter with Low-Switch-Voltage-to-High-Voltage-Bus Ratio. IEEE Trans. Power Electron. 2020, 35, 9530–9540. [Google Scholar] [CrossRef]
- Pan, Y.; Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. A Series Interharmonic Filter for Cascaded H-bridge PV Inverters. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 341–346. [Google Scholar] [CrossRef]
- Upadhyay, P.; Pulipaka, S.; Sharma, M.; Kumar, R. A proposed maximum power point operating strategy for photovoltaic applications using monthly irradiance estimates. Sol. Energy 2017, 141, 266–277. [Google Scholar] [CrossRef]
- Lin, Z.; Xie, W.; Dong, M.; Lan, J. Research of S 3 MPR Engineering Application on Space Power Sources. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; pp. 817–823. [Google Scholar] [CrossRef]
- Fernandes, D.; Almeida, R.; Guedes, T.; Filho, A.S.; Costa, F. State feedback control for DC-photovoltaic systems. Electr. Power Syst. Res. 2017, 143, 794–801. [Google Scholar] [CrossRef]
- Keysight Technologies, Inc. Keysight Technologies Series E4360 Modular Solar Array Simulator. 2018. Available online: http://literature.cdn.keysight.com/litweb/pdf/E4360-90001.pdf (accessed on 19 October 2020).
- Shen, Y.; Qin, Z.; Wang, H. Modeling and Control of DC-DC Converters. In En Control of Power Electronic Converters and Systems; Academic Press: Cambridge, MA, USA, 2018; pp. 69–92. [Google Scholar] [CrossRef]
- Bahari, M.I.; Tarassodi, P.; Naeini, Y.M.; Khalilabad, A.K.; Shirazi, P. Modeling and simulation of hill climbing MPPT algorithm for photovoltaic application. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, Italy, 22–24 June 2016; pp. 1041–1044. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Samanta, S. DC Link Voltage Control based Power Management Scheme for Standalone PV Systems. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- NI LabVIEW High-Performance FPGA Developer’s Guide. Available online: https://www.ni.com/es-mx/support/documentation/supplemental/13/the-ni-labview-high-performance-fpga-developer-s-guide.html (accessed on 25 April 2020).
- ENF Solar. Directorio de Productos, Mono 415–450W Topsun Co., Ltd. Available online: https://es.enfsolar.com/pv/panel-datasheet/crystalline/10499 (accessed on 15 May 2020).































| Parameter | Maximum Observed | Minimum Observed | Type of Data Selected | Maximum According to the Type of Data Selected | Resolution According to the Data |
|---|---|---|---|---|---|
| Voc | 61.97 V | 22.42 V | +9,6 | 63.875 V | 0.125 V |
| Vmpp | 49.67 V | 17.69 V | +9,6 | 63.875 V | 0.125 V |
| Isc | 9.35 A | 0.29 A | +7,4 | 15.875 A | 0.125 A |
| Impp | 8.86 A | 0.27 A | +7,4 | 15.875 A | 0.125 A |
| Variable | Data Type Selected | Maximum According to the Type of Data | Resolution According to the Type of Data |
|---|---|---|---|
| Rs | +10,2 | 3.996094 | 0.00390625 |
| a | +8,0 | 0.996094 | 0.00390625 |
| N | +15,7 | 63.996094 | 0.00390625 |
| Variable | Data Type Selected |
|---|---|
| Vin | 49.25 V |
| Vout | 98.5 V |
| RL | 25 Ω |
| f | 10 kHz |
| vr | 5% |
| r | 0.09375 Ω |
| C | 45.8 µF |
| L | 400.5 µH |
| Absolute Error (V) | Percent Error (%) | |
|---|---|---|
| Maximum Value | 4.6043 | 100 |
| Minimum Value | 0 | 0 |
| Mean Value | 1.0930 | 2.0478 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samano-Ortega, V.; Padilla-Medina, A.; Bravo-Sanchez, M.; Rodriguez-Segura, E.; Jimenez-Garibay, A.; Martinez-Nolasco, J. Hardware in the Loop Platform for Testing Photovoltaic System Control. Appl. Sci. 2020, 10, 8690. https://doi.org/10.3390/app10238690
Samano-Ortega V, Padilla-Medina A, Bravo-Sanchez M, Rodriguez-Segura E, Jimenez-Garibay A, Martinez-Nolasco J. Hardware in the Loop Platform for Testing Photovoltaic System Control. Applied Sciences. 2020; 10(23):8690. https://doi.org/10.3390/app10238690
Chicago/Turabian StyleSamano-Ortega, Víctor, Alfredo Padilla-Medina, Micael Bravo-Sanchez, Elías Rodriguez-Segura, Alonso Jimenez-Garibay, and Juan Martinez-Nolasco. 2020. "Hardware in the Loop Platform for Testing Photovoltaic System Control" Applied Sciences 10, no. 23: 8690. https://doi.org/10.3390/app10238690
APA StyleSamano-Ortega, V., Padilla-Medina, A., Bravo-Sanchez, M., Rodriguez-Segura, E., Jimenez-Garibay, A., & Martinez-Nolasco, J. (2020). Hardware in the Loop Platform for Testing Photovoltaic System Control. Applied Sciences, 10(23), 8690. https://doi.org/10.3390/app10238690







