A Novel VBSHM Strategy to Identify Geometrical Damage Properties Using Only Frequency Changes and Damage Library

Abstract

Vibration-based structural health monitoring is an efficient way to diagnose damage and structural integrity at the earliest stage. In this paper, a new strategy is developed for damage localization and estimation, as well as damage properties identification for a rectangular geometry damage using only eigenfrequencies of the healthy and damaged structure. This strategy is applied to a cantilever beam. In this framework, a damage library is built by correlating 2D and 3D finite element models. The correlation is done by minimizing a so-called frequency shift coefficient. The proposed strategy also uses the frequency shift coefficient to correlate a 2D damaged model with an unknown beam case. The 2D damage, represented by a bending stiffness reduction, is then associated to a 3D damage by employing the damage library. Numerical cases with single and double damage of varying position and severity are tested and used to validate the approach. Finally, experimental results are proposed that show the relevance of the strategy.

1. Introduction

In recent decades, significant research has been conducted on Structural Health Monitoring (SHM) by using many techniques which are applied in various fields such as aerospace, civil and mechanical engineering. SHM aims to provide maintenance services throughout the life of the structure. Vibration based structure health monitoring (VBSHM) is widely used as a structure diagnostic technique over the years because of its ability to monitor and detect damage from global testing of the structure [1,2]. Worden and Dulieu-Barton [3] gave an overview strategy for damage detection such as the definition based on a taxonomy of damage, operational evaluation with the use of a hierarchical damage identification scheme, an approach to sensor prescription and optimization and a data processing methodology. More recently, Kong et al. [4] reviewed the state of the art on the framework of vibration-based damage identification in different levels including the prediction of the remaining useful life of structures and the decision making for proper actions. Toh and Park [5] provided a summary of studies applying machine learning algorithms for health monitoring using vibration factors to categorize the studies.

The first step for damage identification using modal analysis relies on changes in the properties of the structure, mainly their eigenvalues. Salawu [6] proposed a review on methods using eigenfrequencies only for the localization and identification of damage in structure. Several works are described more precisely here, and more recent research works are added. Cawley and Adams [7] developed the first study for damage localization and estimation, using changes in natural frequencies for 1D and 2D structures and relying on a FE model of the structures. Messina [8] proposed Damage Location Assurance Criterion (DLAC) and after extended to the statistical correlation coefficient, which is called Multiple Damage Location Assurance Criterion (MDLAC) [9]. The two methods rely on changes in natural frequencies for estimating the position and size of defects in complex structures. Hassiotis and Jeong [10] developed a method for the estimation of damage using measured changes in the natural frequencies. They presented eigenvalues variation to localize damage using reductions in the stiffness by derived equations from the first-order perturbation. They have also introduced a criterion to solve these equations by minimizing the difference between eigenvalue problems for the undamaged and damaged structures. It was concluded that few frequencies allows the estimation and location of single or multiple defect in structures such as beams but that the results are sensitive to uncertainty on the natural frequencies. Meneghetti and Maggiore [11] made a sensitivity analysis on a cracked beam and used a local modal crack sensitivity in order to localize damage using natural frequency measurement only. According to Doebling [12], Silva and Gomes [13] proposed a technique to detect the crack size and position using a so-called Frequency Shift Coefficient.

Sinha et al. [1] use a model for stiffness reduction due to a crack and a minimization involving the sensitivity matrix from a Finite Element (FE) model and a set of five measured natural frequencies for finding crack depth and location on a cantilever beam. Khiem and Toan [14] examined natural frequencies from the Rayleigh quotient for a clamped beam with an arbitrary number of cracks. The cracks are represented as spring stiffnesses. Through an iterative procedure, three experimentally measured frequencies of a beam with fixed ends are sufficient to locate cracks and estimate their severity using the explicit expression of the Rayleigh quotient. Le et al. [15] introduced a method based on the first-order analytical estimation of the variation of natural frequencies due to structural modifications. It allows, with the help of a minimization procedure, to quantify and localize several structural modifications i.e., damage on a Euler–Bernoulli beam subject to axial constraint, using only modal shapes of the intact structure and natural frequencies of both intact and modified structures. Dahak and Benseddiq [16] used normalized frequencies method for a specifical damage location in the cantilever beam. The damaged zone is determined only by the classification of the normalized frequencies of the structure. The change in stiffness caused by the damage is reflected locally in the frequencies. Yang and Oyadiji [17] have presented a theoretical and experimental study of a frequency-based damage detection method. The method uses the modal frequency curve of a beam with moving point mass and discrete wavelet transform in order to build a damage index. Gillich et al. [18] used the link between natural frequency shift and modal curvature to localize and identify defects in a multispan beam. Sha et al. [19] presented a study of relative natural frequency change curves for characterization of damage in a fixed-fixed beam. They detail the relationship between these curves and mode shapes. They introduced a novel probabilistic damage indicator for localizing single and multiple damages and severity factor to quantify the damage. Serra and Lopez [20] proposed a new methodology based on combined modal wavelet transform strategy to cope with noisy signals, while at the same time, able to extract the relevant information from each mode shape. Pan et al. [21] presented a noise response rate to evaluate the sensitivity of each mode of the frequency shift to noise. The authors developed a novel method of mode selection for improving the accuracy of frequency-based damage detection.

In some experimental studies, Niemann et al. [22] presented an optimization approach for damage localization based on the correlation of a local stiffness loss and the change in experimental modal parameters. They applied this approach to a composite laminate beam. Masoumi and Ashory [23] proposed a method based on the flexibility matrix and the use of stationary wavelet transform to localize cracks in cantilever beams. Gautier et al. [24] use a 4SID technique combined with a FE model updating procedure coupled and an iterative domain partitioning procedure to localize damages. Altunişik et al. [25] considered multiple crack effects on a cantilever beam. In their work, Enhanced Frequency Domain Decomposition and Stochastic Subspace Identification were implemented to extract the dynamic characteristics; the Modal Assurance Criterion, the Coordinated Modal Assurance Criterion and the natural frequencies are used to update a FE model and the approach was validated by experiment.

From this literature overview, it can be concluded that for simple structures at least, natural frequencies may be sufficient for the localization and estimation of single or multiple damage. Several indicators exist and the use of modal shapes may provide more accuracy. Yet, few studies make the link between natural frequencies variation and the geometry of damage; this paper is going beyond a severity indicator by estimating the geometry of single or multiple damages. To achieve this goal, a novel VBSHM strategy is developed based only on frequency changes for the identification of geometrical damage properties, i.e., location, severity, and size. In this matter, the focus is made on the development of a damage library in order to estimate the geometry damage parameters. For the sake of simplicity, a cantilever beam is chosen. The proposed strategy uses the Frequency Shift Coefficient (FSC) as cost function to correlate position, element stiffness reduction and geometry of damage between different FE models of the structure, using a minimization algorithm. The correlation between 2D and 3D FE models allows us to build a numerical damage library for the beam. As the FSC only uses natural frequencies, it will also be used to update a 2D FE model using a small set of natural frequencies of a tested structure. We can thus solve the damage identification problem (single and multiple damages) as a function of damage position and severity. Rectangular geometry damage cases are tested, and their properties are identified based on obtained damage library. The proposed strategy is demonstrated on numerical cases. Finally, the experimental test is carried out by considering the geometry damage in a real beam in order to validate the efficiency of the strategy.

The rest of paper is organized as follows. In Section 2, the dynamics of the specific case of a cantilever beam in flexural vibration are recalled, and FE models (2D and 3D) are introduced to extract the dynamic parameters of a structure. In Section 3, the proposed strategy for damage identification is given, and an approach that involves minimizing the FSC as a function of position and severity is proposed. In Section 4, 2D and 3D FE models of beams are used to build a so called damage library. In addition, this section contains numerical examples that are used to validate FSC based approach. Different test cases are examined to localize and estimate the damages which concern (i) four numerical cases, consisting of 2D vs. 2D FE model correlation that contains single and multiple damages, and (ii) two numerical cases for rectangular geometry damage, consisting of 3D vs. 2D FE model correlation. Finally, in Section 5, an experimental beam is tested to identify damage properties.

2. Beam Bending Vibration and FE Models

2.1. General Context

The equation of motion for the flexural vibration of a cantilever Euler–Bernoulli beam can be written:

$$M\left(x\right)\frac{{\partial }^{2}w(x,t)}{\partial t^2}+C\left(x\right)\frac{\partial w(x,t)}{\partial t}+\frac{{\partial }^2}{\partial x^2}\left(EI\left(x\right)\frac{{\partial }^{2}w(x,t)}{\partial x^2}\right)=F(x,t),$$

(1)

where x is the coordinate along the main direction of the beam, t is the time, $w(x,t)$ is the transverse deflection, $M\left(x\right)$ is the mass per unit length, $C\left(x\right)$ is the viscous damping coefficient, $EI\left(x\right)$ is the bending stiffness and $F(x,t)$ is the external force per unit length of the beam. The solution of Equation (1) can be sought under the following form:

$$w(x,t)=X\left(t\right)u\left(x\right),$$

(2)

where $X\left(t\right)$ and $u\left(x\right)$ are time and displacement solution parts. Let us now consider a beam that is clamped in x = 0 and free in $x=L$ (cantilever beam); then the solution must satisfy $u^{″}\left(L\right)=u^{‴}\left(L\right)=0$ and $u^{\prime }\left(0\right)=u\left(0\right)=0$.

When discretized, for example using the finite element method, the equation of motion may take the following matrix form:

$$\left[M\right]\left\{\ddot{X}\right\}+\left[C\right]\left\{\dot{X}\right\}+\left[K\right]\left\{X\right\}=\left\{F\right\},$$

(3)

where $\left[M\right]$ is the mass matrix, $\left[C\right]$ is the damping matrix and $\left[K\right]$ is stiffness matrix for the system, $\left\{\ddot{X}\right\}$, $\left\{\dot{X}\right\}$, $\left\{X\right\}$ are vectors containing acceleration, velocity and displacement respectively in all degrees of freedom of the model; and $\left\{F\right\}$ contains external forces actuating in the system.

If we neglect damping and assume free motion, the eigenvalue problem for a healthy structure is written as:

$$(\left[K\right]-{\omega }_i^2\left[M\right])y_i=0,$$

(4)

where ${\omega }_i$ and $y_i$ are the ith natural frequency and modal shape of a healthy structure. Conversely, let us consider the case of a damaged structure. The associated eigenvalue problem can be written as:

$$(\left[K_d\right]-{\omega }_i^{*2}\left[M_d\right])y_i^{*}=0,$$

(5)

where $\left[M_d\right]$ and $\left[K_d\right]$ are the mass and stiffness matrix of a damaged structure (yet to be defined) while ${\omega }_i^{*}$ and $y_i^{*}$ are the ith natural frequency and modal shape of a damaged structure.

2.2. 2D FE Model of Healthy and Damaged Beam

Equation (1) is discretized using 2-nodes beam elements with 2 degrees of freedom (DOFs) per node, a vertical translation v and a bending rotation ${\theta }_z$. As can be seen in Figure 1, the beam is divided into N elements of equal size of and the model has N + 1 nodes. The damage is assumed to be placed within the beam elements of the FE model. Consider the damage at location $x_l$ within node i and $i+1$ of beam. It will be assumed that stiffness reduction falls within one or several elements.

Natural frequencies of healthy and damaged 2D beam are obtained from solving the eigenvalue formulation using MATLAB eig () function and their expression (in Hz) is $f_i=\frac{{\omega }_i}{2\pi }$.

In this 2D FE model, the damage is simulated by reducing the stiffness of selected element. Here, damage severity is represented by the reduction coefficient ${\alpha }_i$, which is the ratio of the stiffness reduction to the initial stiffness. The stiffness matrix of a damaged beam is defined as a sum of elemental matrices multiplied by coefficient by the following equation:

$$\left[K_d\right]=\sum _{i=1}^N(1-{\alpha }_i)\left[k_e\right],$$

(6)

where $\left[K_d\right]$ is the global stiffness matrix for damaged beam, $\left[k_e\right]$ is elemental stiffness matrix and ${\alpha }_i$ is a bending stiffness reduction coefficient, which varies from 0 to 1 for the damaged structure. A value of ${\alpha }_i$ = 0 indicates healthy element.

According to a convergence study, the beam is divided into 100 elements of equal size (10 mm). The 2D FE model has a total number of 202 DOFs.

2.3. 3D FE Model of Healthy and Damaged Beam

In this section, a 3D FE model of healthy and damaged beam with clamped-free boundary condition is proposed. The models are implemented in COMSOL Multiphysics. In this context, we emphasize that a damage has a physical geometry.

The beams are meshed with tetrahedral elements (6 DOFs per node). The mesh density is in fine controlled by COMSOL. Typically, converged models with damage have 22,000 DOFs. A high mesh density is applied close to the damage area. Figure 2a,b represent 3D healthy and damaged FE models, respectively. A zoomed view of the rectangular geometry damage is shown on Figure 2b.

Natural frequencies of 3D healthy and damaged models are obtained using COMSOL Multiphysics’ own solver.

2.4. 3D FE Frequency Convergence Test

A convergence test is performed to ensure that the 3D FE model is adequately meshed. It is here given for the damaged beam, with a damage at midposition with a width of 2 mm and a depth of 2.5 mm. The beam properties are given in

Table 1. Beam dimensions and steel properties.

Beam Properties	Value
Length (L)	1000 $\mathrm{mm}$
Width (W)	25 $\mathrm{mm}$
Thickness (T)	$5.3$$\mathrm{mm}$
Young’s modulus (E)	210 GPa
Mass density ($\rho$)	7850 $\mathrm{kg}/{\mathrm{m}}^3$
Poisson’s ratio (v)	0.33

. The convergence test is carried out by changing the mesh densities. Using the five mesh standard parameters proposed in COMSOL Multiphysics: Finer, Fine, Normal, Coarse, Coarser, the first seven bending natural frequencies are computed. Note that these standard mesh parameters correspond to a number of DOFs varying from 22,000 to 2300 respectively, using tetrahedral elements, and that we rely on COMSOL Multiphysics to adequately mesh the damage area, as shown in Figure 2b. In a convergence study shown in Figure 3, the relative error on the natural frequency (with respect to the “Finer” mesh configuration) is determined. It is shown that the relative error for the “Fine” mesh is below 0.5%. Therefore, it can be concluded that the results are converged for both “Fine” and “Finer” mesh parameters and the frequencies are independent on the mesh size. For this reason, the “Finer” mesh is used in the rest of the study to build a damage library and to estimate geometry damage parameters.

3. Strategy and Objective Function for Damage Identification

It is well known that the presence of damages modifies dynamic parameters and behavior of the structure. In the proposed strategy, numerical cases and experimental validation is performed with only using frequencies changes between healthy and damaged structure. In this work, the novelty consists in using an existing severity indicator building a damage library for estimating properties of rectangular damage.

3.1. Proposed Strategy

In this section, a methodology for damage properties identification is described in three main steps. Figure 4 represents a complete flowchart of the proposed strategy for geometry damage properties identification.

Step 1: A set of healthy state frequencies are identified from the experimental beam. 2D and 3D FE healthy model are built, and Young’s modulus of FE models are updated to closely match the frequencies with the healthy beam (the cost function is described later on). Then, in the 3D FE model, the damage is materialized as a rectangular discontinuity considering the position, width and depth of the damage. At the same time, the damage is materialized as a local reduction of bending stiffness in one element in the 2D FE model. Numerical correlation using FSC minimization between 2D and 3D FE models is performed, that is, for each set of physical parameter, a bending stiffness reduction is sought in the 2D model. At the end of this step, damage library is obtained, where 3D rectangular damage provides the width and depth, and 2D model gives bending stiffness reduction in percentage value of severity at particular damage position. More precisely, the damage library is a relation between physical parameters and bending stiffness reduction. Moreover, these parameters can be extracted in the form of one item from the damage library.

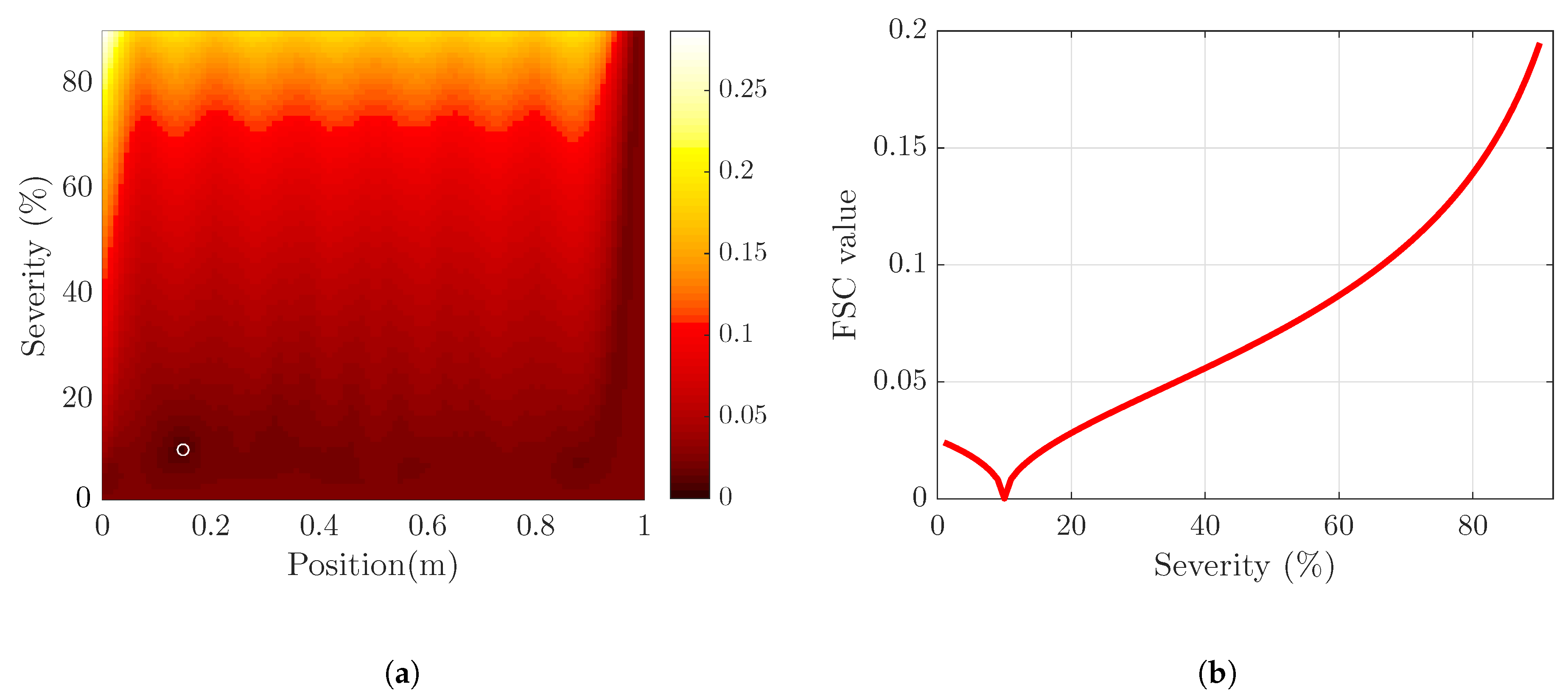
Step 2: An updating of the 2D FE model of damaged beam is performed using FSC to identify location and severity of single or multiple damage. Typically, the basis for the model update is a set of frequencies issued from a 2D model, a 3D model or an experimental measurement. For a given updating procedure, four beam models with the same characteristics (healthy beam case, damaged beam case, 2D healthy model and 2D stiffness updated damaged model) are used. The stiffness reduction coefficient (or severity) and the localization of the reduction are updated during this procedure. The minimum value of the FSC is sought during the updating process. The argument of the minimum yield wanted location and severity. Practically, the minimization is performed using particle swarm optimization (PSO) [26] in MATLAB global optimization toolbox. If the damage is identified, then we can proceed to the next step for geometry investigation.

Step 3: In this step, based on the results of Step 2 and Step 3, the identification of damage physical parameters can be done. The estimated damage severity from Step 2 is searched in the damage library. It corresponds to a (potentially nonunique) set of width and depth for a rectangular geometry. Note that curve fitting may be necessary if the library is not precise enough and that a tolerance can be introduced. The nonuniqueness of the solution and the way to go beyond will be discussed later on.

Remark: The interest of using a damage library instead of directly correlating the tested structure to a 3D model is indeed to reduce the computational time.

3.2. Initial Model Updating

According to Figure 4, an initial updating of the numerical models (2D and 3D) with respect to an experimental healthy beam is done first. Only the Young’s modulus is updated. A maximization problem is formulated which uses the inverse of the statistical error on the natural frequencies. The updated Young’s modulus is then given by:

$$E=argmax\left(\frac{1}{\sqrt{\frac{1}{m}\left|\right|{\sum }_{i=1}^m{\left(f_i^{2D/3D}-f_i^h\right)}^2\left|\right|}}\right),$$

(7)

where $f_i^{2D/3D}$ is the ith frequency of 2D/3D FE model of the beam, $f_i^h$ is the ith healthy beam frequency which is obtained from the experimental modal analysis.

3.3. Frequency Shift Coefficient (FSC)

The modal method for damage detection relies on changes in dynamic properties of the structure and particularly natural frequencies. Any changes in the structure, such as the reduction in stiffness, will cause changes in the natural frequencies. One of the important advantages of natural frequency is that it can be easily measured through vibration measurements. Classical measurements schemes can be used for the determination of experimental resonant frequencies. In this context, the Frequency Shift Coefficient is first presented by Silva and Gomes [13] for damage identification problems. This coefficient uses four sets of natural frequencies. We consider on the one hand so called experimental frequencies denoted X (issues from a numerical model or an experiment) and on the other hand frequencies from a model, denoted A. In each category, there can be frequencies from a healthy or reference structure, denoted h and frequencies from an unknown, or damaged structure, denoted d. To be clear, there is a set of experimental healthy frequencies $(h,X)$, a set of experimental unknown frequencies $(d,X)$, a set of frequencies obtained with a healthy model $(h,A)$ and a set obtained with a damaged model $(d,A)$. The frequency shift coefficient is defined as:

$$FSC=\sqrt{\frac{1}{m}\left|\right|\sum _{i=1}^m\left(\frac{{\left({\mathsf{\Gamma }}_i\right)}_X-{\left({\mathsf{\Gamma }}_i\right)}_A}{{\left({\mathsf{\Gamma }}_i\right)}_X}\right)\left|\right|}\mathrm{and}{\mathsf{\Gamma }}_i=\frac{f_i^d}{f_i^h},$$

(8)

where m is number of modes taken into account, X is the damaged case, A is the 2D beam model (reference), $f_i^d$ is the damaged beam frequencies, $f_i^h$ is healthy beam frequencies and i denotes modes’ indices.

The FSC is then used to qualify $(d,X)$ by updating $(d,A)$ using the shifts with respects to the sets $(h,A)$ and $(h,X)$. Remember that $(h,A)$ was first updated with respect to $(h,X)$. In other words, the location and severity of damage in $(d,X)$ are given by minimizing the value of FSC.

4. Numerical Assessment of the Strategy Using 3D and 2D Models

Following the methodology proposed in Section 3, numerical assessments are performed using 3D and 2D models. In the beginning, beam properties and Young’s modulus updating procedure are detailed. Complimenting the 2D model made in MATLAB, a 3D model built with COMSOL is going to be used to be simulated as well as correlated using FSC minimization in order to build a damage library using Step 1. Cases with Single and multiple damage are tested to validate the bending stiffness based identification using Step 2. Furthermore, rectangular damage cases modeled with 3D FE are investigated; Step 3 is used in order to distinguish the damage properties and size (width and depth) based on the obtained severity.

4.1. Material and Geometry

The numerical simulation test is performed to verify the efficiency of the proposed VBSHM method. A cantilever steel beam was taken into consideration for the numerical test and beam properties are given below in Table 1.

The updating procedure is done for 2D and 3D healthy FE models with respect to an experimental beam presented in Section 5. Young’s modulus is updated from an initial value of 210 GPa according to Section 3.2 by obtaining the maximum value of the function expressed in Equation (7). Seven bending frequencies are used in the procedure, which are indicated in

Table 2. Eigenfrequencies of healthy cantilever beam.

Mode	${\mathit{f}}_{\mathit{e}\mathit{x}\mathit{p}\mathit{e}\mathit{r}\mathit{i}\mathit{m}\mathit{e}\mathit{n}\mathit{t}\mathit{a}\mathit{l}}$ (Hz)	3D FE Updated $\mathit{E}=188.90$ GPa		2D FE Updated $\mathit{E}=189.26$ GPa
		${\mathit{f}}_{3\mathit{D}}$ (Hz)	Error $(\%)$	${\mathit{f}}_{2\mathit{D}}$ (Hz)	Error $(\%)$
1	4.23	4.21	0.48	4.20	0.71
2	26.33	26.36	0.11	26.35	0.08
3	73.26	73.81	0.75	73.77	0.69
4	142.34	144.63	1.58	144.56	1.54
5	240.12	239.04	0.46	238.96	0.49
6	355.67	357.03	0.38	356.97	0.36
7	499.66	498.56	0.22	498.57	0.22
			Mean = 0.569		Mean = 0.584

for the healthy experimental beam. In the 3D model, a procedure is first applied to filter the results and consider only the frequencies corresponding to bending modes. The updated results of Young’s modulus are found to be 189.26 GPa with 0.8635 maximized value for the 2D beam and 188.90 GPa with 0.8466 maximized value for the 3D beam. The frequencies of the updated 2D and 3D FE models of the beam structure are reported in Table 2. Note that the mean error values are 0.569% for 3D model and 0.584% for 2D model, respectively.

Note that, just as in the initial updating procedure, the seven lowest frequencies are assumed to be sensitive enough to find damage parameters with the help of FSC. Remember that Ref. [21] suggests that the modes can be selected in a smarter way, which is not done here for the sake of simplicity. Finally, in this study, the bending frequencies with two digits after the decimal are considered, which proves necessary to correctly correlate the FE models.

4.2. Damage Library Using 3D and 2D Model Correlation

In this section, 2D and 3D FE models are correlated using FSC minimization in order to obtain a damage library. The damage library is built for rectangular geometry damage. First, the library is built in midposition (0.5 m) of a cantilever beam. The process detailed in Step 1 (see Figure 4) is implemented. In order to build a damage library, a beam embedding a rectangular damage is simulated using 3D FE, while the correlation between the two FE models permits us to obtain the corresponding 2D bending stiffness reduction. The physical parameters of the rectangular geometry are then varied and the process is repeated. In the library, stiffness reduction is performed in a single element while the width and depth of the rectangular damage are varied from 0.01 mm to 10 mm and 0.01 mm to 4.0 mm, respectively. Each item from the damage library is a triplet: width and depth of the rectangular damage in the 3D model and bending stiffness reduction in the 2D model.

Figure 5 shows the surface view of the damage library built at midposition on the beam. The colorbar represents severity associated to the size of damage. The result of the simulation is, as expected, a smooth surface. Here, the library also illustrates a monotonic response to the size of damages. Interestingly, the width of damage contributes to the decrement of severity to a larger extent compared to its depth.

Notice that the damage severity here ranges from 1 to 99%. It is not in the scope of this paper to assess whether or not it is relevant to model a deep damage with linear assumptions and an important stiffness reduction. In the rest of the study, the damage dimensions will be kept small and severity will be kept less than 50%.

The effect of beam position for building a library is investigated. A library is built by choosing a different beam position, with a damage positioned at 0.3 m. Again, a range of sizes for the rectangular damage is computed and the stiffness is reduced in a selected element during 2D and 3D correlation. Figure 6a,b shows contour view of two different damage libraries which are built at 0.30 m and 0.50 m beam positions, respectively. Note that Figure 6b is simply another view of the results seen in Figure 5. The colorbar represents the percentage of severity corresponding to the depth and width of the damage. The evolution of severity with the geometry of damage is similar for the two positions. In fact, the maximum difference of severity between the two position is 1.8% on the entire domain. Moreover, Figure 6c shows the severity equivalent to a given damage for a range of positions along the beam. Two geometries are shown here: the blue curve is associated to a 1 mm × 1.5 mm damage, and the red curve to a 1 mm × 2.5 mm damage. The results show that the severity corresponding to a given damage geometry has a very small dependence to the position on the range displayed. Thus, it means that the library does not depend on the beam position. Indeed, it is possible to build a library at any position of the beam. Finally, note that it takes approximately 1.5 h on a Intel Core i7 (2.6 GHz) to build an entire map such as the one in Figure 5.

4.3. Localization and Quantification of Single Damage

In this section, the proposed methodology (see Figure 4) is tested by considering numerical damaged cases (see Figure 7), i.e., a 2D damaged FE model is used to generate a set of frequencies, and Step 2 is used to find position and severity based on this set. In given cases, the damage is introduced at different beam positions: (a) 0.15 m near the clamped end (b) and 0.80 m close to the free end of the beam with 10% and 5% stiffness reduction, respectively. The first seven frequencies for each case were used in the FSC computation. They are plotted in

Table 3. Numerically measured natural frequencies of single damaged cases (a) and (b) with parameters of position and severity.

Damaged Cases	Natural Frequencies (Hz)
	1	2	3	4	5	6	7
(a) 10% at position 0.15 m	4.20	26.34	73.77	144.50	238.76	356.62	498.23
(b)  4% at position 0.80 m	4.20	26.34	73.74	144.48	238.88	356.94	498.56

. Note that differences between the two cases are very small. The minimization of the FSC (see Equation (8)) is carried out to localize and estimate damage. The two parameters considered in the procedure are hence the position and severity of the stiffness reduction.

In Figure 8a, FSC is shown in color levels as a function of position and severity of the damage for case (a) schematized in Figure 7a. Note that this color map is only an illustration of the variation of FSC on the whole range of parameters, the definitive result being provided by the minimization algorithm. We notice several dark areas (low value of FSC) that correspond to frequency shifts between healthy and updated damaged model that, overall, are close to the actual frequency shifts. The dark area for positions close to the free end of the beam is especially interesting: it means that from the FSC point view, any stiffness reduction close to the free end is quite similar to the investigated case. The white circle indicates the set of parameters that minimized the FSC: location and severity values of damage are obtained at x abscissa 0.15 m with 10%, respectively. The zero value of FSC for this set of parameters indicates that the tried damaged case and the unknown case are similar from FSC point of view. The minimum value is likely to indicate the parameters of damaged case, especially if it is zero or close to zero. Figure 8b shows a slice view of the FSC as a function of severity only in the range [1, 90]% at absissa 0.15 m. On this view, it is more clear that the FSC reaches zero for a severity of 10%. Figure 9 also indicates results for another single damaged case (b) (see Figure 7b) where the minimum value of FSC is obtained with 4% estimated damage at x abscissa 0.80 m, respectively. Again, a slice view at absissa 0.8 m is shown in Figure 9b, which represents estimated severity for single damaged case (b). Thus, minimization of FSC provides accurate values for location and estimated severity of the damage. In terms of CPU times, the algorithm takes 5–10 s on a Intel Core i7 (2.6 GHz) using MATLAB’s particleswarm for a given case.

4.4. Localization and Quantification of Double Damage

For highlighting the potential of the method, it is applied to localize and estimate double damage based on the given strategy (Step 2) from Figure 4. Numerical cases with two damaged areas are proposed in Figure 10. Two damaged cases are investigated: (a) at 0.3 m and 0.7 m beam positions with 40% and 30% stiffness reduction (see Figure 10a), (b) and near the clamped area of the beam at 0.10 m and 0.20 m with 7% and 2% stiffness reduction (see Figure 10b), respectively.

The test was initiated by obtaining a set of frequencies from each numerical case. The natural frequencies are given in

Table 4. Numerically computed natural frequencies of double damage cases (a) and (b) with parameters of position and severity.

Damaged Cases	Natural Frequencies (Hz)
	1	2	3	4	5	6	7
(a) 40% at 0.50 m and 30% at 0.70 m	4.18	26.25	73.00	144.01	238.72	353.61	495.02
(b) 7% at 0.10 m and  2% at 0.20 m	4.20	26.33	73.76	144.53	238.90	356.84	498.32

for damaged cases. Damage identification is done by updating a model embedding two damages, thanks to the FSC. As with single damage, the first seven natural frequencies of the damaged structure were used as an input for the FSC. In double damage identification, there are four parameters (position 1, position 2, severity 1 and severity 2) to identify. Evolution of FSC with parameters for the two studied cases is plotted on Figure 11 and Figure 12. Because it is difficult to represent a variable of four parameters, the plot is split in two in these examples: First, in Figure 11a and Figure 12a, for the actual severities for the two damages (40 and 30% in Figure 11a, 7 and 2% in Figure 12a), the FSC is represented as a function of positions only. Second, in Figure 11b and Figure 12b, for the actual positions of the damages (0.30 and 0.70 m in Figure 11b, 0.45 and 0.55% in Figure 12b), the FSC is represented as a function of severities only. The minimization of FSC gives the following results (indicated as white circles in Figure 11 and Figure 12): for case (a), the severities are 30% and 40% and positions are 0.30 m and 0.70 m. For case (b), the severities are 7% and 2% for two damage localized at 0.10 m and 0.20 m). In the two cases, the estimation correspond to the values given in Figure 10. In other words, the algorithm is employed satisfactorily to identify both locations and severities of double damage.

Note that the same number of frequencies has been used in the single and the double damage cases. The numerical study that is described here demonstrates that seven frequencies are sufficient. Further work needs to be done to study the effect of adding more natural frequencies.

4.5. In the Case of Rectangular Geometry Damage

In this section, the strategy is carried out in order to investigate the rectangular geometry damage using all Steps. Figure 13a,b show a detailed 2D view of rectangular geometry cases. Here, the width $\left(W_d\right)$, depth $\left(D_d\right)$ and height $\left(H_d\right)$ are 2.5 mm, 0.75 mm and 25 mm for rectangular damaged case (a), while 0.9 mm, 1.34 mm and 25 mm dimensions for rectangular damaged case (b), respectively. The rectangular damaged case (a) and (b) are assumed at positions 200 mm and 700 mm on the beam. Numerical cases are meshed and computed in COMSOL Multiphysics in order to obtain the natural frequencies. These frequencies are tabulated in

Table 5. Numerically measured natural frequencies of rectangular damaged case (a) and (b) with parameters of position and geometry size.

Damaged Cases	Natural Frequencies (Hz)
	1	2	3	4	5	6	7
(a) 3D rectangular ($D_d=0.716$ mm, $W_d=2.50$ mm)	4.20	26.37	73.79	144.43	238.76	356.91	498.50
(b) 3D rectangular ($D_d=1.327$ mm, $W_d=0.90$ mm)	4.21	26.31	73.53	144.44	238.97	355.96	497.47

for the two rectangular damaged cases.

The rectangular geometry damaged case (a) is investigated to find damage properties. Based on the set of frequencies of Table 5, minimizing the FSC yields estimation of position and equivalent severity. Figure 14a shows identified position and severity for rectangular damaged case (a) where the white circle represent 14.37% damage extent at position 0.20 m with a minimum value of 0.011 for the FSC. After obtaining the severity of the damage, it is possible to examine physical damage parameters (width and depth). Figure 14b represents the different possibilities of extracted geometry parameters for 14.37% severity from the damage library (according to Section 4.2). Specifically, the blue dots represent the raw extraction from the library with a 1% tolerance. The red curve is a cubic fit of the raw result. Remember that one value of severity corresponds to two parameters, hence the line. In this section, it is assumed that the width of damage is the actual value, while the depth is a parameter to identify. It is a good way to check the method because if the damage library is reliable, the obtained depth should be the actual depth. In a more general case, it is also possible to assume the smallest detectable size as a width. This makes sense in an experimental context, where a visual inspection would be limited by this smallest detectable size, let us say a hairline thickness. For the rectangular damaged case (a), the assumed width is 2.5 mm. Hence, the result of estimated depth is 0.716 mm, as shown in Figure 14b (black cross). A difference between estimated and actual depth would lie in the tolerance in the library extraction and the curve fitting that is applied.

Similarly, the rectangular damaged case (b) is investigated to recover its physical properties. Figure 15a represents the identified position and severity using FSC algorithm. In this case, a 25.35% damage extent is obtained at 0.70 m beam position with 0.012 minimum value. The severity of 25.35% is searched in the damage library, as shown in Figure 15b. Hereafter, the width size is assumed based on the actual value, which is 0.9 mm for the geometry case (b). Based on width, the obtained depth is estimated 1.327 mm from the library. Based on these numerical investigations, the proposed strategy seems reliable to identify the physical geometry of damage.

Remark: Here, the number of element of the updated 2D beam is the same as for the model used in the damage library. Therefore, the elements have the same size and the bending stiffness reduction found in the updating process is employed to find the physical parameters in the damage library. Although it is not mandatory to use the same number of elements, this aspect has not yet been studied in detail.

5. Identification of Damage on an Experimental Beam

5.1. Experimental Setup

An experimental cantilever beam is studied in order to investigate the accuracy of the proposed strategy using FE based FSC approach. As with the numerical studies, the study is done for a rectangular damage. A steel beam (length L = 1 m, width W = 25 mm and thickness T = 5.3 mm) is instrumented with 2 accelerometers, as displayed in Figure 16. Material properties (E, $\rho$, v) of beams for the experiment are similar to those depicted in Section 4.1. Two experimental beams were measured and tested; the first is considered as healthy, and the second is a damaged beam. On damaged beam, a rectangular damage is done (saw cut) and measured with a depth of 1.55 mm and a width of 1.3 mm. It is placed at 710 mm from the clamped end. In order to extract the natural frequencies from the healthy and damaged beam, impact testing is chosen, and signals are recorded with a Siemens LMS multianalyser. The input excitation is produced through an impact hammer, while monoaxial accelerometers (Brüel et Kjær) record the output data. Two accelerometers are placed at 0.35 m and 0.75 m from the clamped end. Frequencies of a healthy and damaged structure are obtained from frequency response function by applying circle fit method using EasyMod package [27]. The first seven experimentally identified frequencies for each beam are listed in

Table 6. Experimentally identified natural frequencies of healthy and rectangular damaged beam.

Experimental Beam Case	Natural Frequencies (Hz)
	1	2	3	4	5	6	7
$f_{healthy}$	4.23	26.33	73.26	142.34	240.12	355.67	499.66
$f_{damaged}$ (rectangular)	4.24	26.21	72.82	141.73	239.38	354.36	498.00

. Slight differences in natural frequencies are noticeable.

5.2. Results

The measured natural frequencies are used to identify the damage properties. First, the 2D beam model based on the FE mesh (100 elements) depicted in Figure 1 is correlated to the experiment. The bending stiffness updating technique is employed in a 2D damaged model to obtain the updated model. It should be pointed out that the mass of accelerometers is not taken into account in the FE model as localized mass; however, the model is updated based on the natural frequencies of the experimental beam with accelerometers.

In this experimental case, the damage is first localized and quantified; After, based on the severity, its geometry is recovered. The FSC is computed as a function of position and severity using Step 2 and plotted as a color map on Figure 17a. As previously mentioned, the colorbar indicates FSC value and the white circle gives position and severity, according to the minimization. In this case, the damage severity is 34.93% at 0.72 m beam position, where the FSC minimum value is 0.039. Note that the estimation of localization (0.72 m) is very close to the real position (0.71 m). Again, it takes 5–10 s to solve the minimization problem.

The obtained severity (34.93%) is searched in the damage library in order to extract width and depth using Step 3. Again, several sizes of damage correspond to a single severity, as shown in Figure 17b. For the sake of the demonstration, we here assume the width to be the actual width (1.3 mm). It is found that the depth corresponding to 1.3 mm width is 1.62 mm (see Figure 17b). This estimation is close to the real value of depth (1.55 mm). It indicates that the physical parameters are correctly identified through the damage library. Hence, the proposed strategy constitutes an efficient identification tool for the estimation of geometry damage properties in an experimental context.

6. Conclusions

In this work, a strategy has been developed for physical damage properties (position, severity and size) identification based on bending stiffness reduction. The procedure makes use of natural frequencies only and of FE models of the structure. It is applied on a cantilever beam but nothing prevents its use with more complex structures. In this context, the minimization of the Frequency Shift Coefficient is used in two ways. First, we are able to build a damage library by correlating 2D and 3D model of damaged beam. The library was built for a rectangular damage and links depth and width in the 3D model with a bending stiffness reduction in the 2D model. The library does not depend on the beam position. Second, a simple model of the damaged beam is updated in order to identify position and severity of the damage. The damage library is then used to obtain more information about the geometry of the damage. The strategy has been tested numerically by recovering information about numerical damaged beam modeled in 2D or 3D. Single and double damage have been investigated. The lowest severity quantified in this numerical study was 2%. The strategy has also been successfully tested in an experimental cantilever beam embedding a saw-cut damage. In the future, this methodology will be tested with other types of structure, structural behavior and damage geometries (hole, oblique or triangular cut) in order to validate its efficiency.