Dynamic Modeling and Simulation of a Robotic Lander Based on Variable Radius Drums
Abstract
1. Introduction
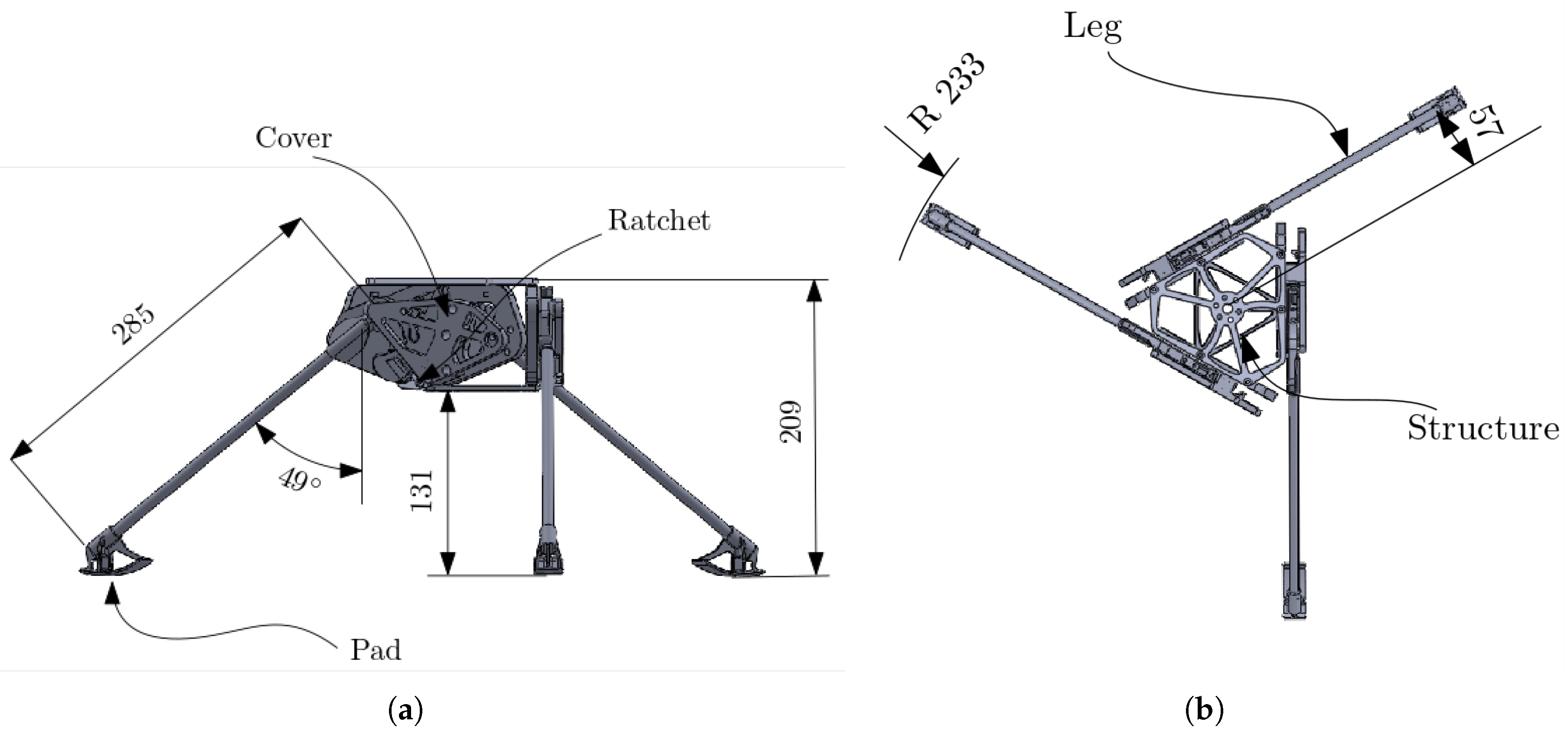
2. Dynamic Modeling of the Robotic Lander
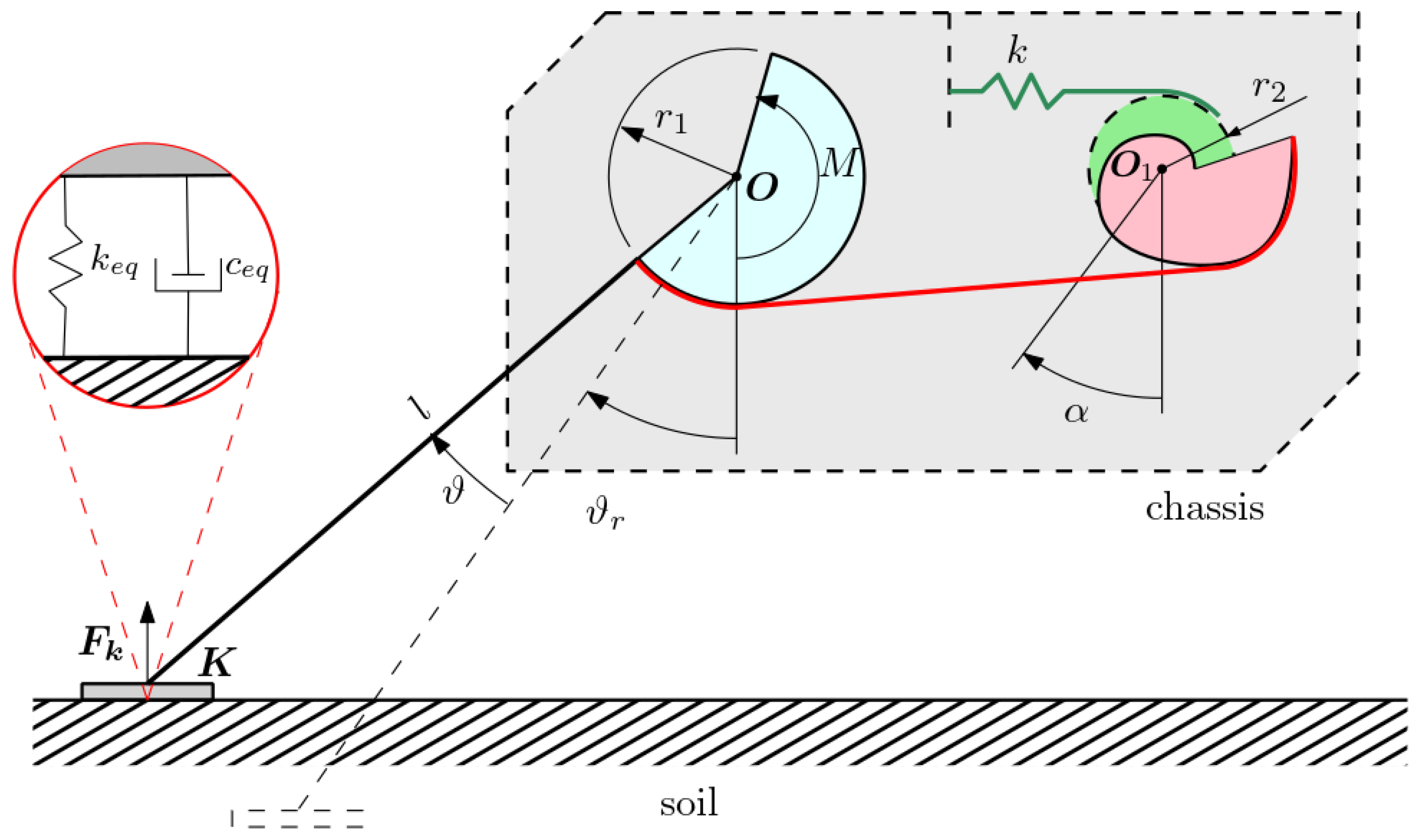
2.1. Variable Radius Drum Mechanism
2.2. Dynamic Model
2.3. Soil Characterization
3. Simulated Test Bed
4. Simulation Results
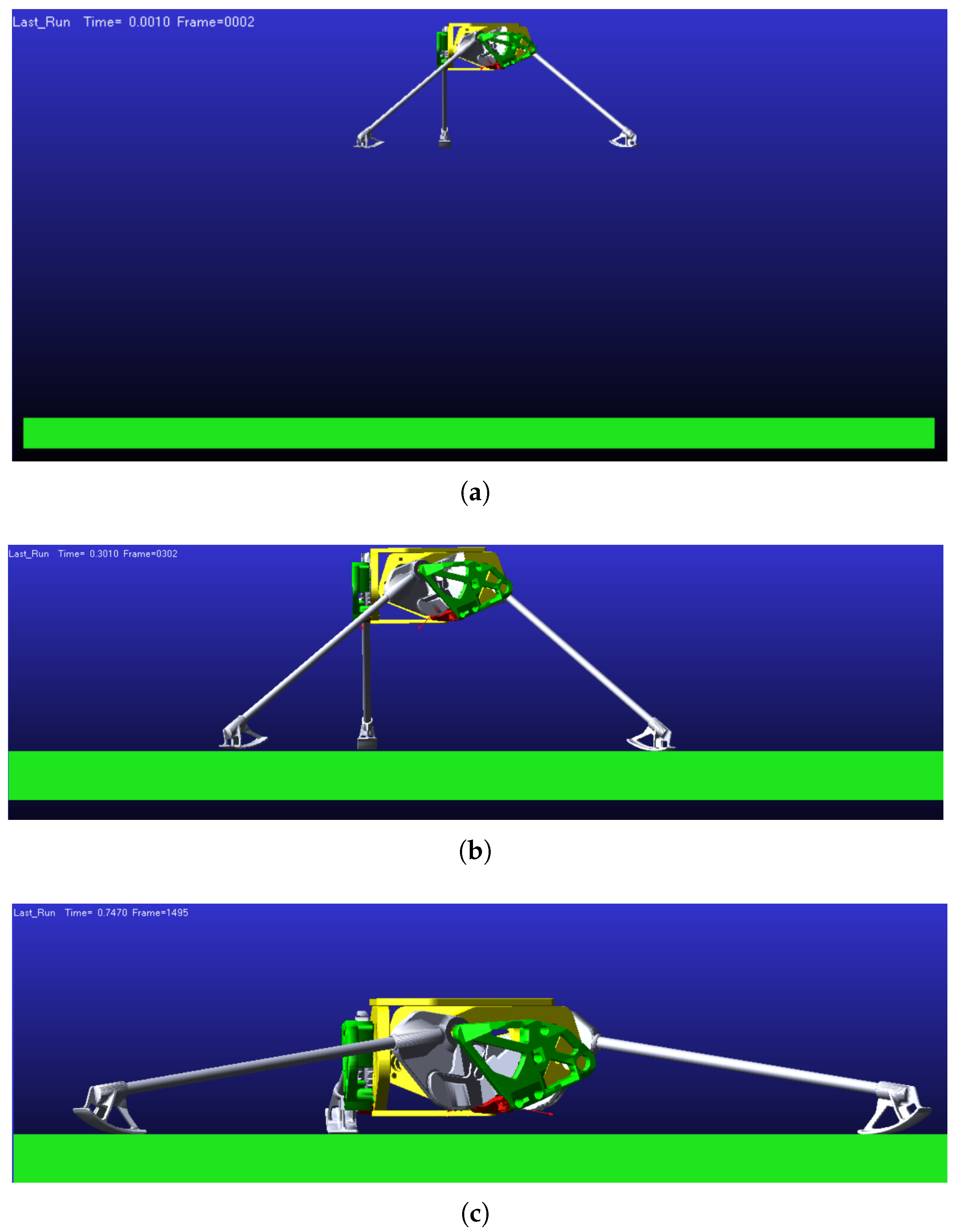
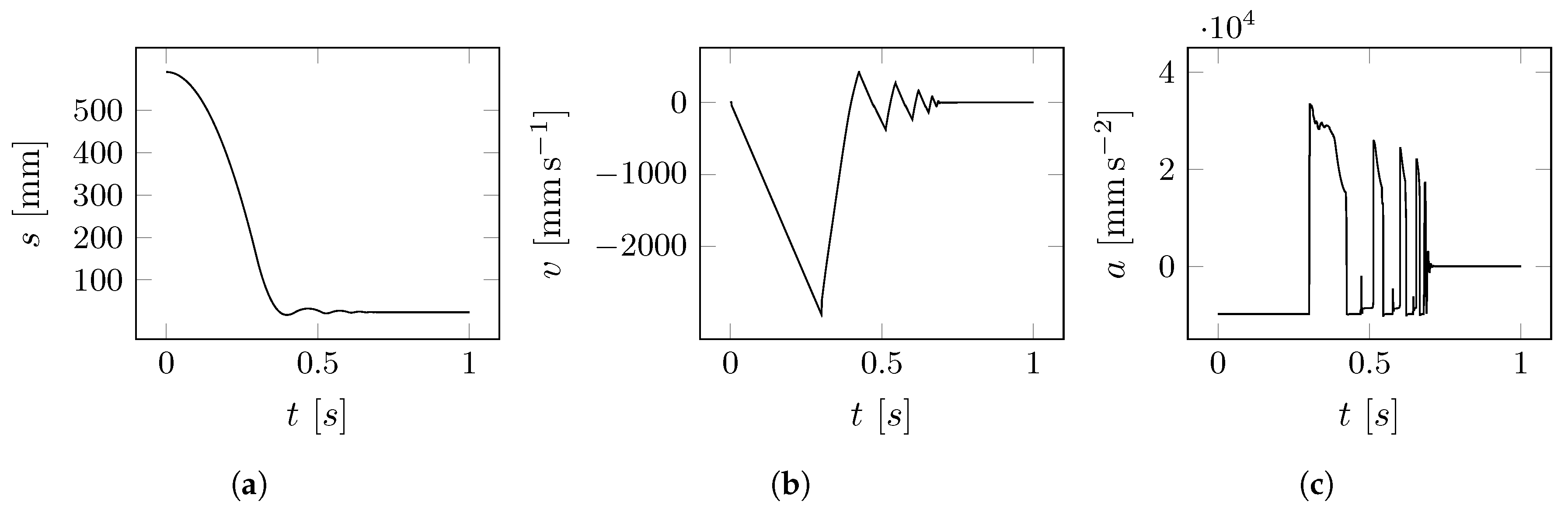
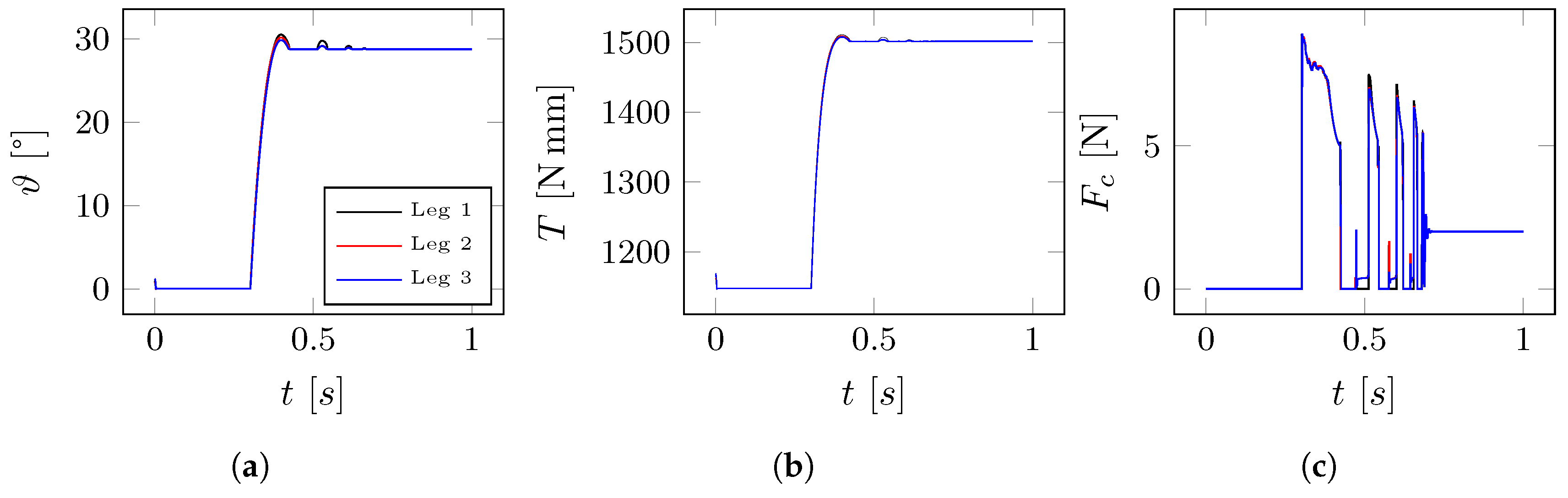
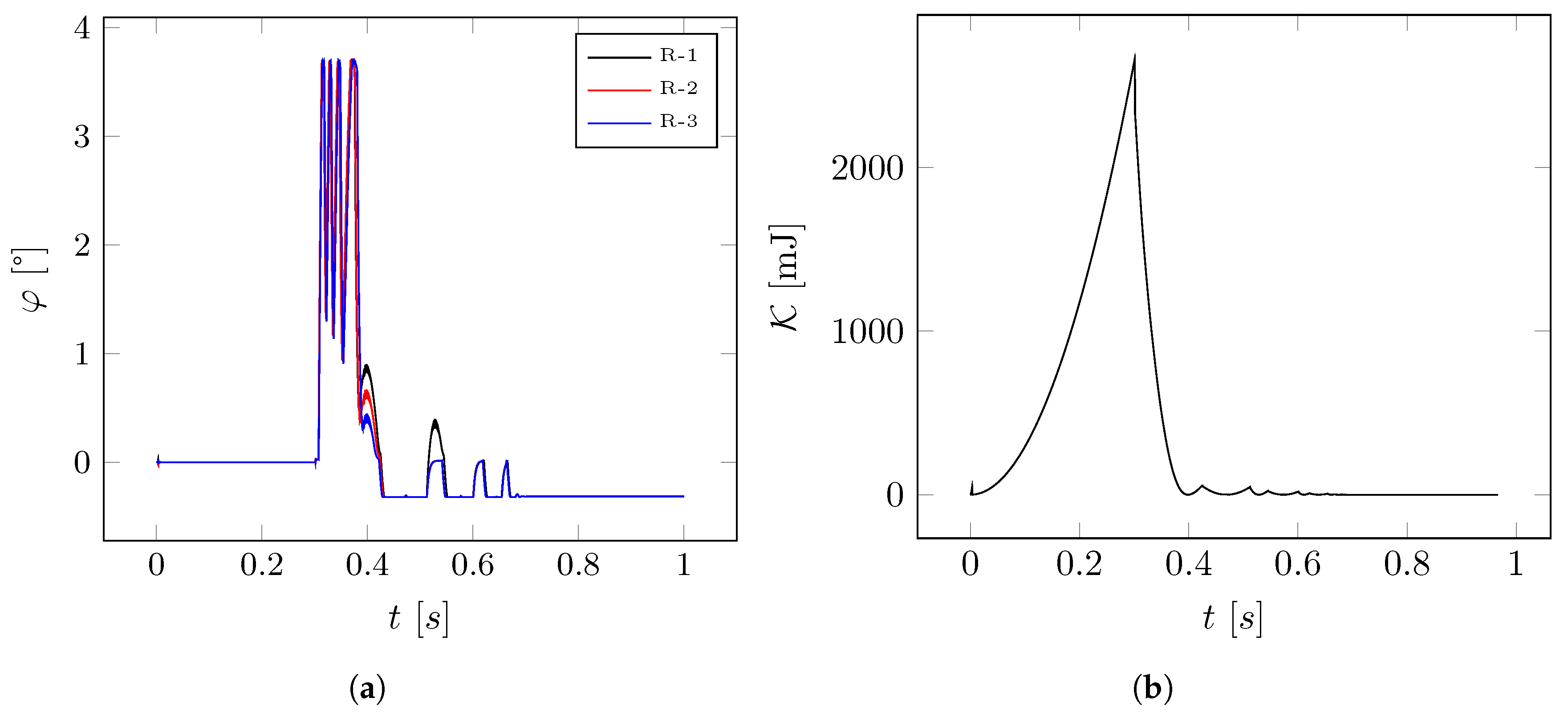
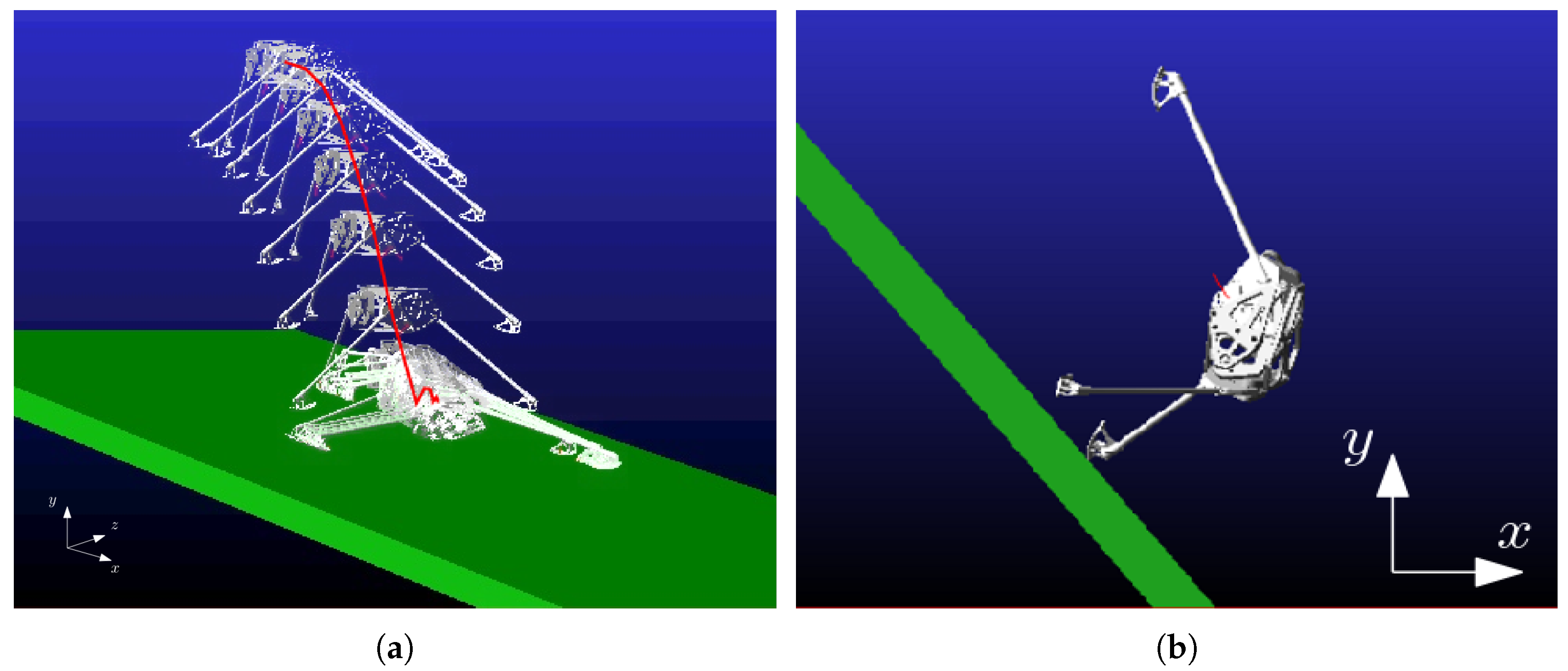
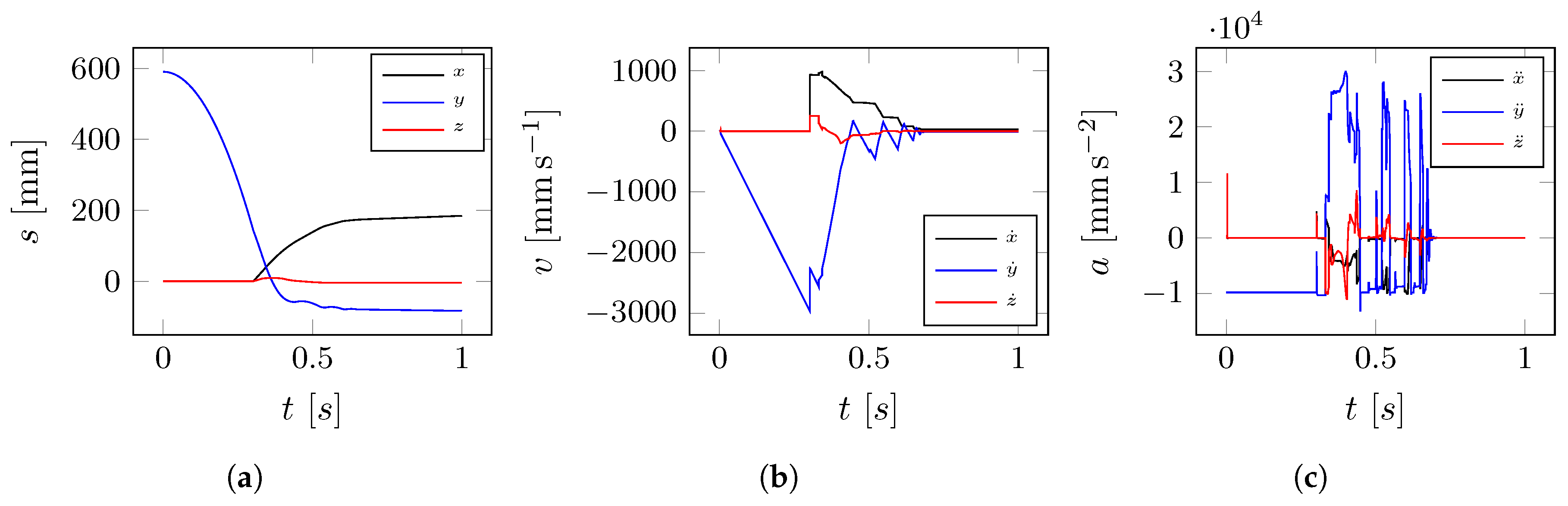
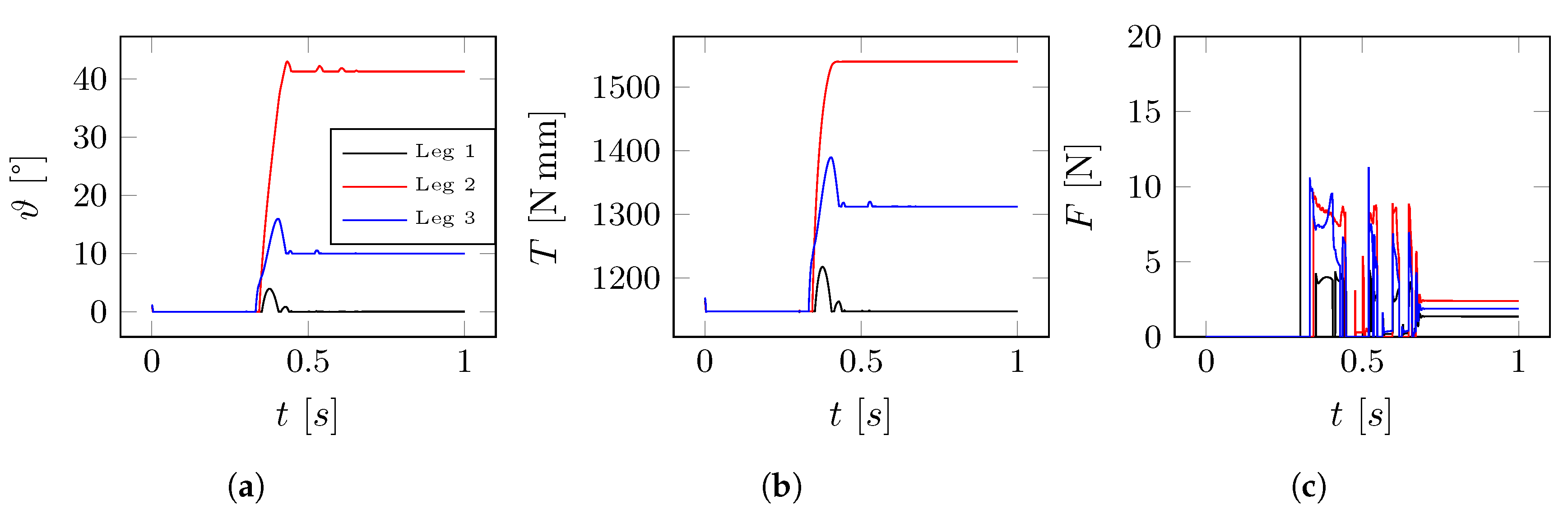
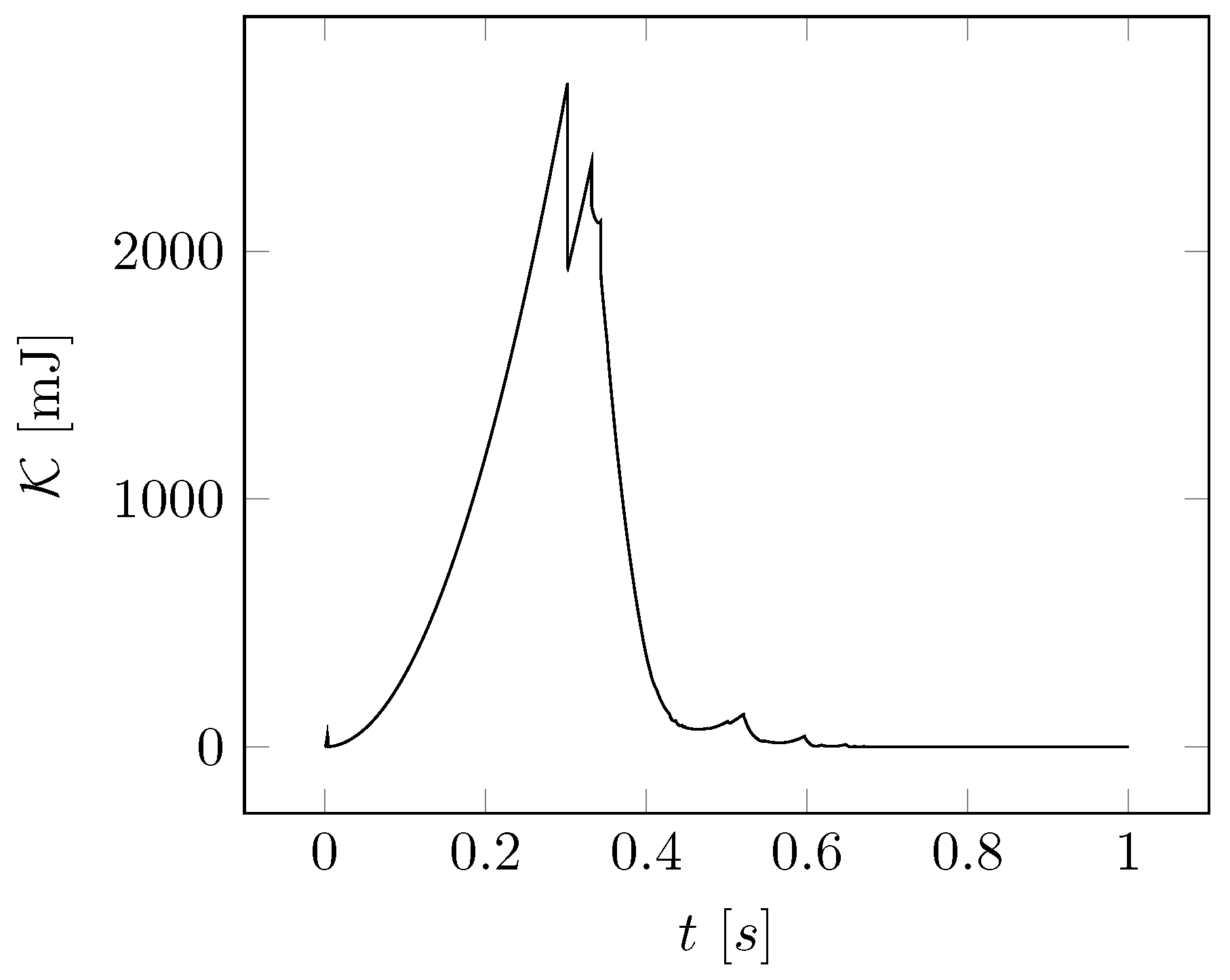
- Case (1): impact simulation on flat surface. In this simulation the behavior is investigated of the lander free-falling from a fixed height and impacting on a flat horizontal surface. In particular, we analyze the contact force distribution, the lander deceleration, the angular displacement of the leg, and the ratchet action.
- Case (2): topple simulation. In this simulation, the behavior is investigated of the lander impacting on an inclined surface, after a free-fall from a fixed height. Subsequently, the critical angle is found at which the lander topples.
4.1. Case (1): Impact Simulation on Flat Surface
4.2. Case (2): Topple Simulation
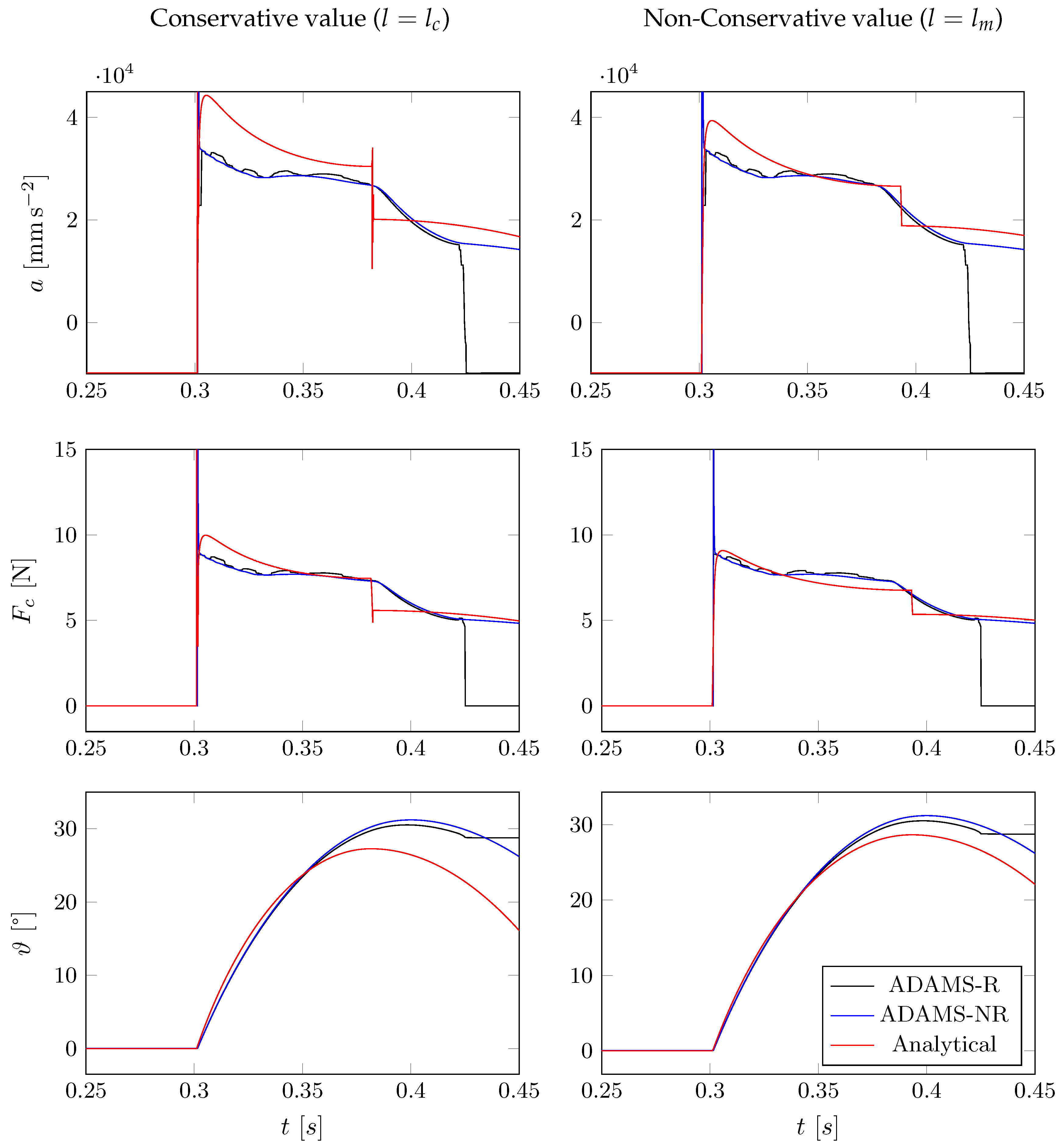
5. Discussion
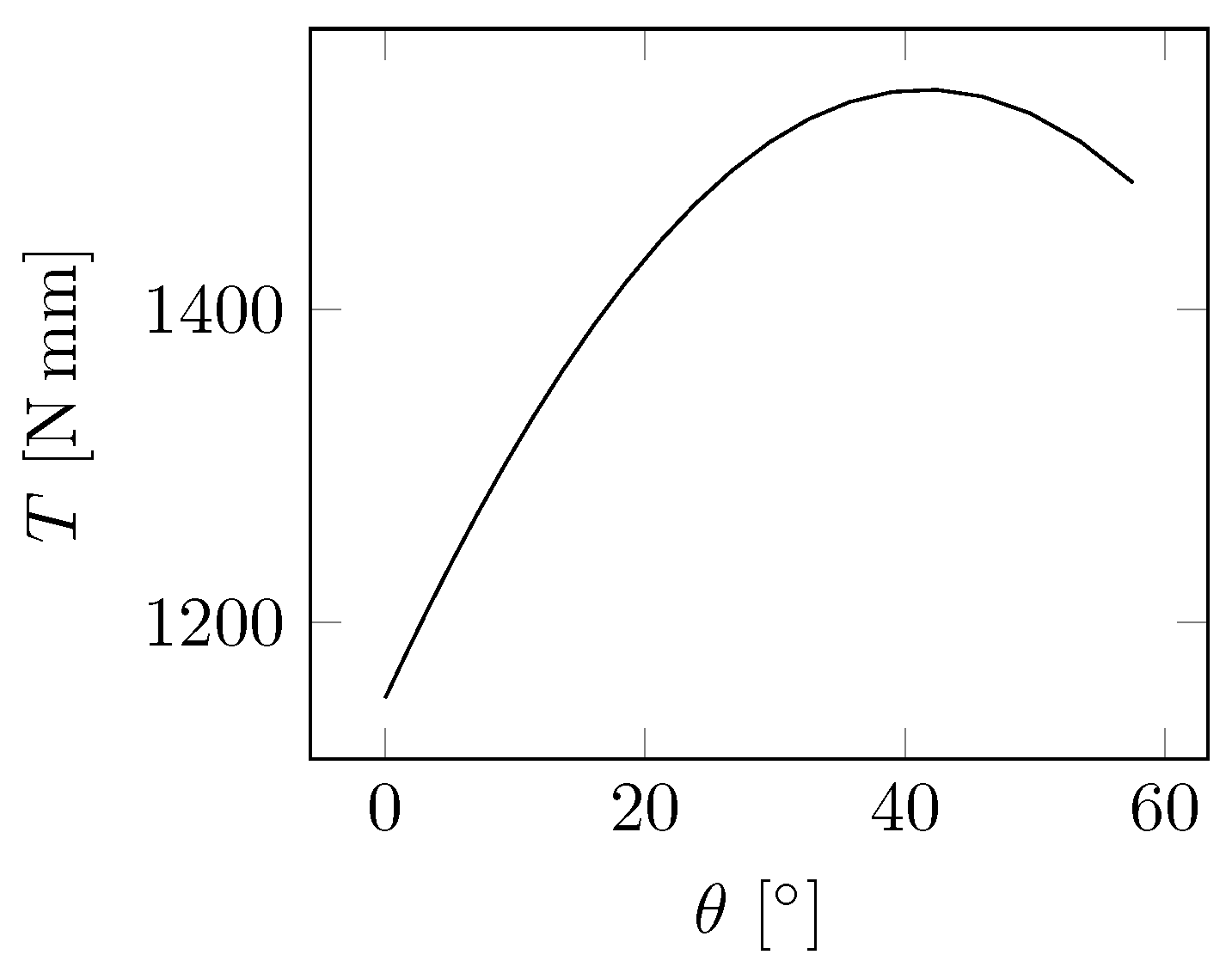
5.1. Comparison with the Theoretical Model
5.2. Case (1): Simulation on Horizontal Surface
5.3. Case (2): Topple Simulation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rogers, W. Apollo Experience Report: Lunar Module Landing Gear Subsystem; NASA: Washington, DC, USA, 1972.
- O’Neil, W.J.; Rudd, R.P.; Farless, D.L.; Hildebrand, C.E.; Mitchell, R.T.; Rourke, K.H.; Euler, E.A. Viking Navigation; Technical Report NASA-CR-162917, JPL-PUB-78-38, NASA, JPL; California Institute of Technology Pasadena: Pasadena, CA, USA, 1979. [Google Scholar]
- Behrends, R.; Dillon, L.K.; Fleming, S.D.; Stirewalt, R.E.K. Mars Pathfinder Airbag Impact Attenuation System; Technical Report AIAA-95-1552-CP; American Institute of Aeronautics and Astronautics: East Lansing, MI, USA, 2006. [Google Scholar]
- Cao, P.; Hou, X.; Xue, P.; Tang, T.; Deng, Z. Research for a modeling method of mars flexible airbag based on discrete element theory. In Proceedings of the 2017 2nd International Conference on Advanced Robotics and Mechatronics (ICARM), Hefei and Tai’an, China, 27–31 August 2017; pp. 351–356. [Google Scholar] [CrossRef]
- Accomazzo, A.; Lodiot, S.; Companys, V. Rosetta mission operations for landing. Acta Astronaut. 2016, 125, 30–40. [Google Scholar] [CrossRef]
- Woods, D. Review of the Soviet Lunar exploration programme. Spaceflight 1976, 18, 273–290. [Google Scholar]
- Efanov, V.; Dolgopolov, V. The Moon: From research to exploration (to the 50th anniversary of Luna-9 and Luna-10 Spacecraft). Sol. Syst. Res. 2017, 51, 573–578. [Google Scholar] [CrossRef]
- Malenkov, M. Self-propelled automatic chassis of Lunokhod-1: History of creation in episodes. Front. Mech. Eng. 2016, 11, 60–86. [Google Scholar] [CrossRef]
- Li, S.; Jiang, X.; Tao, T. Guidance summary and assessment of the Chang’e-3 powered descent and landing. J. Spacecr. Rocket. 2015, 53, 258–277. [Google Scholar] [CrossRef]
- Wu, W.; Yu, D.; Wang, C.; Liu, J.; Tang, Y.; Zhang, H.; Zhang, Z. Technological breakthroughs and scientific progress of the Chang’e 4 mission. Sci. China Inf. Sci. 2020, 63, 1–4. [Google Scholar] [CrossRef]
- Wang, C.; Nie, H.; Chen, J.; Lee, H.P. The design and dynamic analysis of a lunar lander with semi-active control. Acta Astronaut. 2019, 157, 145–156. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, S.; Qian, J.; Chen, M.; Chen, J. Improving the buffer energy absorption characteristics of movable lander-numerical and experimental studies. Materials 2020, 13, 3340. [Google Scholar] [CrossRef]
- Liu, Y.; Song, S.; Wang, C. Multi-objective optimization on the shock absorber design for the lunar probe using nondominated sorting genetic algorithm II. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417720467. [Google Scholar] [CrossRef]
- Lin, R.; Guo, W.; Li, M. Novel design of legged mobile landers With decoupled landing and walking functions containing a rhombus joint. J. Mech. Robot. 2018, 10, 061017. [Google Scholar] [CrossRef]
- Lin, R.; Guo, W. Creative design of legged mobile landers with multi-loop chains based on truss-mechanism transformation method. J. Mech. Robot. 2020, 13, 011013. [Google Scholar] [CrossRef]
- Xu, L.; Nie, H.; Wan, J.; Lin, Q.; Chen, J. Analysis of landing impact performance for lunar lander based on flexible body. In Proceedings of the 2011 IEEE International Conference on Computer Science and Automation Engineering, Shanghai, China, 10–12 June 2011; Volume 1, pp. 10–13. [Google Scholar]
- Wan, J.; Nie, H.; Chen, J.; Lin, Q. Modeling and simulation of Lunar lander soft-landing using transient dynamics approach. In Proceedings of the 2010 International Conference on Computational and Information Sciences, Chengdu, China, 17–19 December 2010; pp. 741–744. [Google Scholar]
- Zheng, G.; Nie, H.; Chen, J.; Chen, C.; Lee, H.P. Dynamic analysis of lunar lander during soft landing using explicit finite element method. Acta Astronaut. 2018, 148, 69–81. [Google Scholar] [CrossRef]
- Liang, D.; Chai, H.; Chen, T. Landing dynamic analysis for landing leg of lunar lander using Abaqus/Explicit. In Proceedings of the 2011 International Conference on Electronic & Mechanical Engineering and Information Technology, Harbin, China, 12–14 August 2011; Volume 8, pp. 4364–4367. [Google Scholar]
- Aravind, G.; Vishnu, S.; Amarnath, K.; Hithesh, U.; Harikrishnan, P.; Sreedharan, P.; Udupa, G. Design, analysis and stability testing of Lunar lander for soft-landing. Mater. Today Proc. 2020, 24, 1235–1243. [Google Scholar] [CrossRef]
- Udupa, G.; Sundaram, G.; Poduval, A.P.; Pillai, K.; Kumar, N.; Shaji, N.; Nikhil, P.C.; Ramacharan, P.; Rajan, S.S. Certain investigations on soft lander for Lunar exploration. Procedia Comput. Sci. 2018, 133, 393–400. [Google Scholar] [CrossRef]
- Pham, V.; Zhao, J.; Goo, N.; Lim, J.; Hwang, D.; Park, J. Landing stability simulation of a 1/6 Lunar module with aluminum honeycomb dampers. Int. J. Aeronaut. Space Sci. 2013, 14, 356–368. [Google Scholar] [CrossRef][Green Version]
- Sun, Y.; Hu, Y.; Liu, R.; Den, Z. Touchdown dynamic modeling and simulation of lunar lander. In Proceedings of the 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics, Harbin, China, 8–10 June 2010; pp. 1320–1324. [Google Scholar]
- Liu, Y.; Song, S.; Li, M.; Wang, C. Landing stability analysis for Lunar landers using computer simulation experiments. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417748441. [Google Scholar] [CrossRef]
- Seriani, S. A new mechanism for soft landing in robotic space exploration. Robotics 2019, 8, 103. [Google Scholar] [CrossRef]
- Seriani, S.; Gallina, P. Variable radius drum mechanisms. J. Mech. Robot. 2015, 8, 021016. [Google Scholar] [CrossRef]
- Endo, G.; Yamada, H.; Yajima, A.; Ogata, M.; Hirose, S. A passive weight compensation mechanism with a non-circular pulley and a spring. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 3843–3848. [Google Scholar]
- Scalera, L.; Gallina, P.; Seriani, S.; Gasparetto, A. Cable-Based Robotic Crane (CBRC): Design and implementation of overhead traveling cranes based on variable radius drums. IEEE Trans. Robot. 2018, 34, 474–485. [Google Scholar] [CrossRef]
- Fedorov, D.; Birglen, L. Differential noncircular pulleys for cable robots and static balancing. J. Mech. Robot. 2018, 10, 061001. [Google Scholar] [CrossRef]
- Suh, J.W.; Kim, K.Y. Harmonious cable actuation mechanism for soft robot joints using a pair of noncircular pulleys. J. Mech. Robot. 2018, 10, 061002. [Google Scholar] [CrossRef]
- Fedorov, D.; Birglen, L. Design of a compliant mechanical device for upper leg rehabilitation. IEEE Robot. Autom. Lett. 2019, 4, 870–877. [Google Scholar] [CrossRef]
- Scalera, L.; Palomba, I.; Wehrle, E.; Gasparetto, A.; Vidoni, R. Natural motion for energy saving in robotic and mechatronic systems. Appl. Sci. 2019, 9, 3516. [Google Scholar] [CrossRef]
- Li, M.; Cheng, W.; Xie, R. Design and experimental validation of two cam-based force regulation mechanisms. J. Mech. Robot. 2020, 12, 031003. [Google Scholar] [CrossRef]
- Grotzinger, J.; Crisp, J.; Vasavada, A.; Anderson, R.; Baker, C.; Barry, R.; Blake, D.; Conrad, P.; Edgett, K.; Ferdowski, B.; et al. Mars Science Laboratory mission and science investigation. Space Sci. Rev. 2012, 170, 5–56. [Google Scholar] [CrossRef]
- Yue, Z.; Di, K.; Liu, Z.; Michael, G.; Jia, M.; Xin, X.; Liu, B.; Peng, M.; Liu, J. Lunar regolith thickness deduced from concentric craters in the CE-5 landing area. Icarus 2019, 329, 46–54. [Google Scholar] [CrossRef]
- Donaldson Hanna, K.; Schrader, D.; Cloutis, E.; Cody, G.; King, A.; McCoy, T.; Applin, D.; Mann, J.; Bowles, N.; Brucato, J.; et al. Spectral characterization of analog samples in anticipation of OSIRIS-REx’s arrival at Bennu: A blind test study. Icarus 2019, 319, 701–723. [Google Scholar] [CrossRef]
- Slyuta, E. Physical and mechanical properties of the lunar soil (a review). Sol. Syst. Res. 2014, 48, 330–353. [Google Scholar] [CrossRef]
- Carrier, W.D. Lunar soil grain size distribution. Moon 1973, 6, 250–263. [Google Scholar] [CrossRef]
- Graf, J. Lunar Soils Grain Size Catalog; NASA Reference Publication; National Aeronautics and Space Administration, Office of Management, Scientific and Technical Information Program: Washington, DC, USA, 1993.
- Seriani, S.; Scalera, L.; Gasparetto, A.; Gallina, P. Preloaded structures for space exploration vehicles. In IFToMM Symposium on Mechanism Design for Robotics; Springer: Cham, Switzerland, 2018; pp. 129–137. [Google Scholar]
- Seriani, S.; Gallina, P.; Scalera, L.; Lughi, V. Development of n-DoF preloaded structures for impact mitigation in cobots. J. Mech. Robot. 2018, 10, 051009. [Google Scholar] [CrossRef]

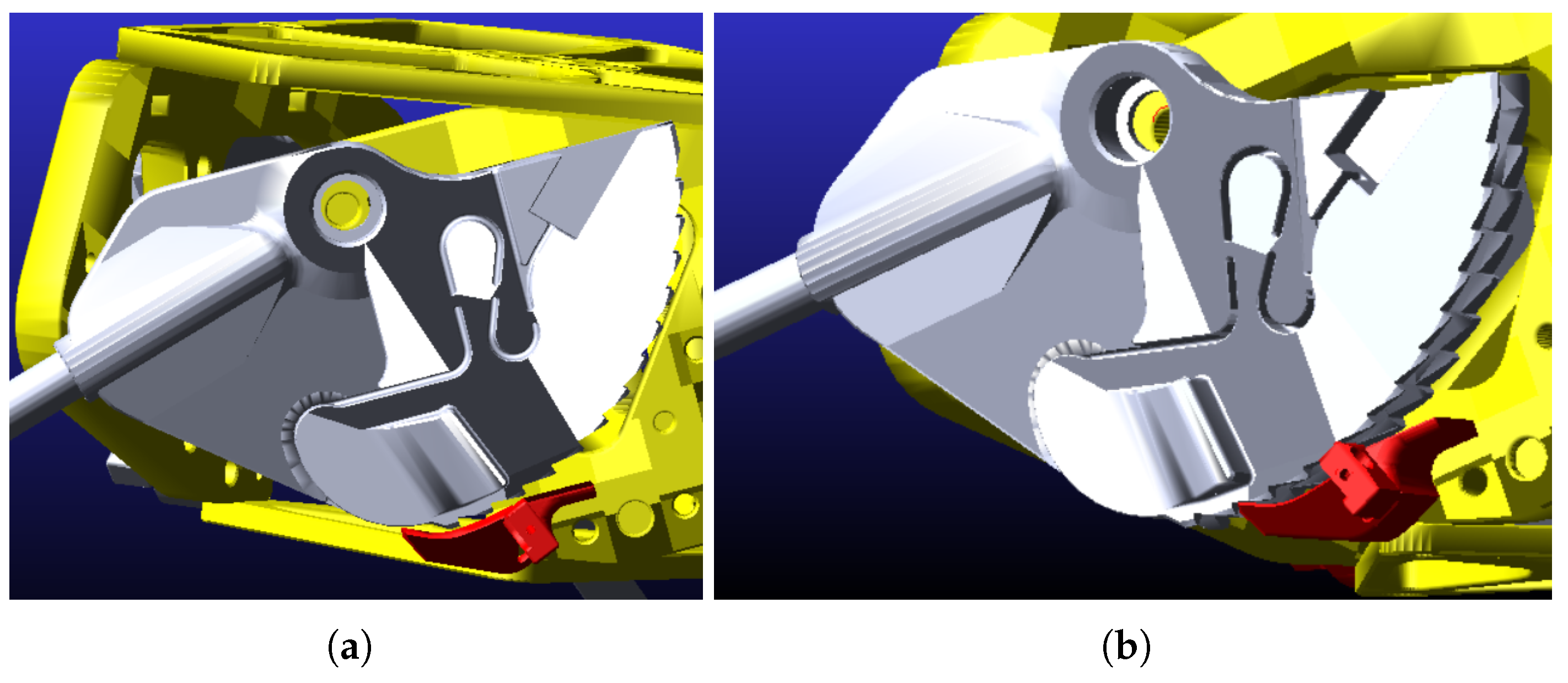

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| r | m | g | |
| H | |||
| m | f | ||
| 3.70 | |||
| Material | PLA |
| Bodies | Ixx | Iyy | Izz | |
|---|---|---|---|---|
| Structure | 0.5 | 430.14 | 684.78 | 430.14 |
| Leg | 3.7 | 374.29 | 10.67 | 364.37 |
| Ratchet | ||||
| Cover | 17.00 | 11.49 | 6.45 |
| First Body | Second Body | Joint Type |
|---|---|---|
| Structure | Leg | Revolute |
| Structure | Ratchet | Revolute |
| Structure | Cover | Fixed |
| Soil | Ground | Fixed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caruso, M.; Scalera, L.; Gallina, P.; Seriani, S. Dynamic Modeling and Simulation of a Robotic Lander Based on Variable Radius Drums. Appl. Sci. 2020, 10, 8862. https://doi.org/10.3390/app10248862
Caruso M, Scalera L, Gallina P, Seriani S. Dynamic Modeling and Simulation of a Robotic Lander Based on Variable Radius Drums. Applied Sciences. 2020; 10(24):8862. https://doi.org/10.3390/app10248862
Chicago/Turabian StyleCaruso, Matteo, Lorenzo Scalera, Paolo Gallina, and Stefano Seriani. 2020. "Dynamic Modeling and Simulation of a Robotic Lander Based on Variable Radius Drums" Applied Sciences 10, no. 24: 8862. https://doi.org/10.3390/app10248862
APA StyleCaruso, M., Scalera, L., Gallina, P., & Seriani, S. (2020). Dynamic Modeling and Simulation of a Robotic Lander Based on Variable Radius Drums. Applied Sciences, 10(24), 8862. https://doi.org/10.3390/app10248862







