Robust Adaptive Synchronization of a Class of Uncertain Chaotic Systems with Unknown Time-Delay
Abstract
:1. Introduction
2. Preliminaries and Problem Formulation
3. Adaptive Controller Design for Robust Synchronization of Fractional Order Chaotic Systems with Unknown Time Delay, Uncertainty and Disturbance
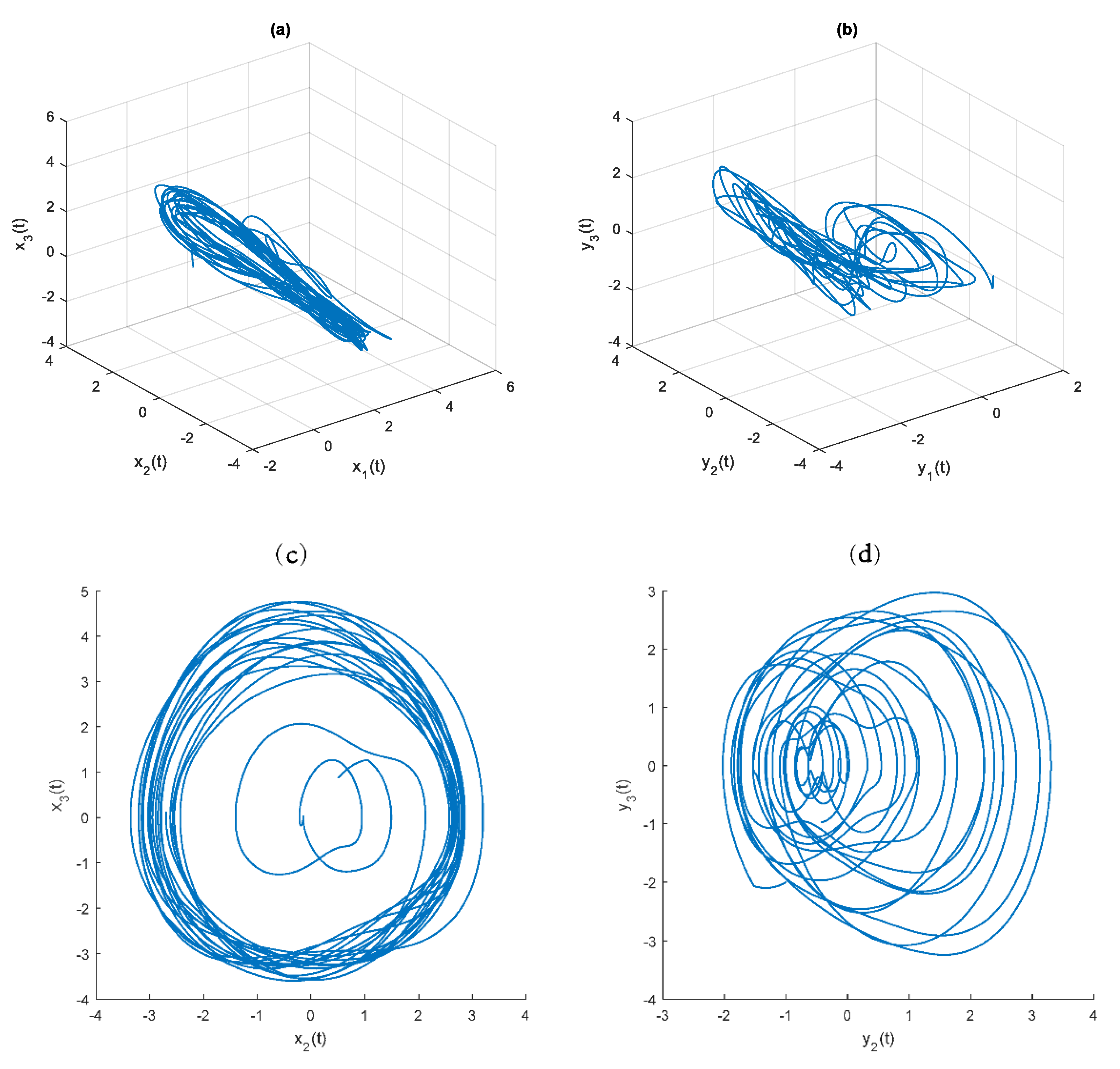
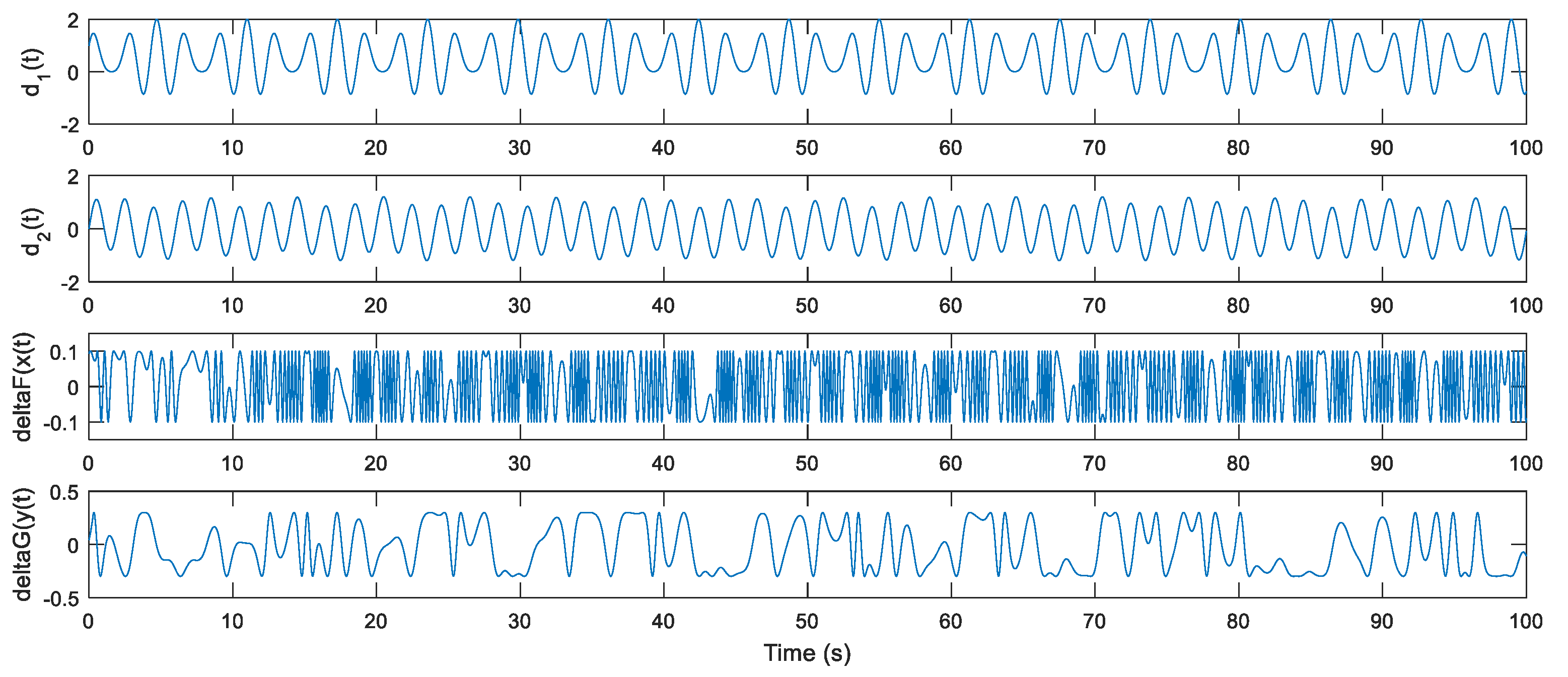
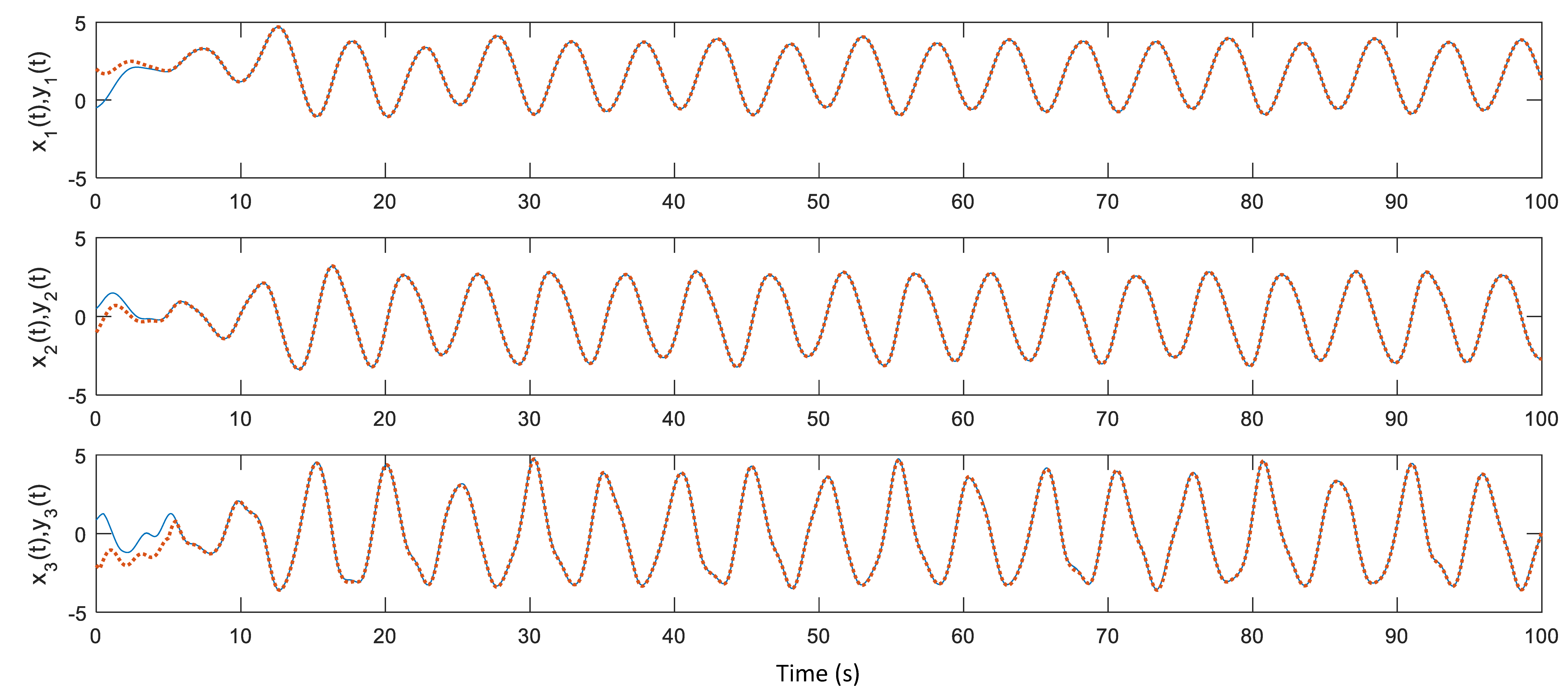
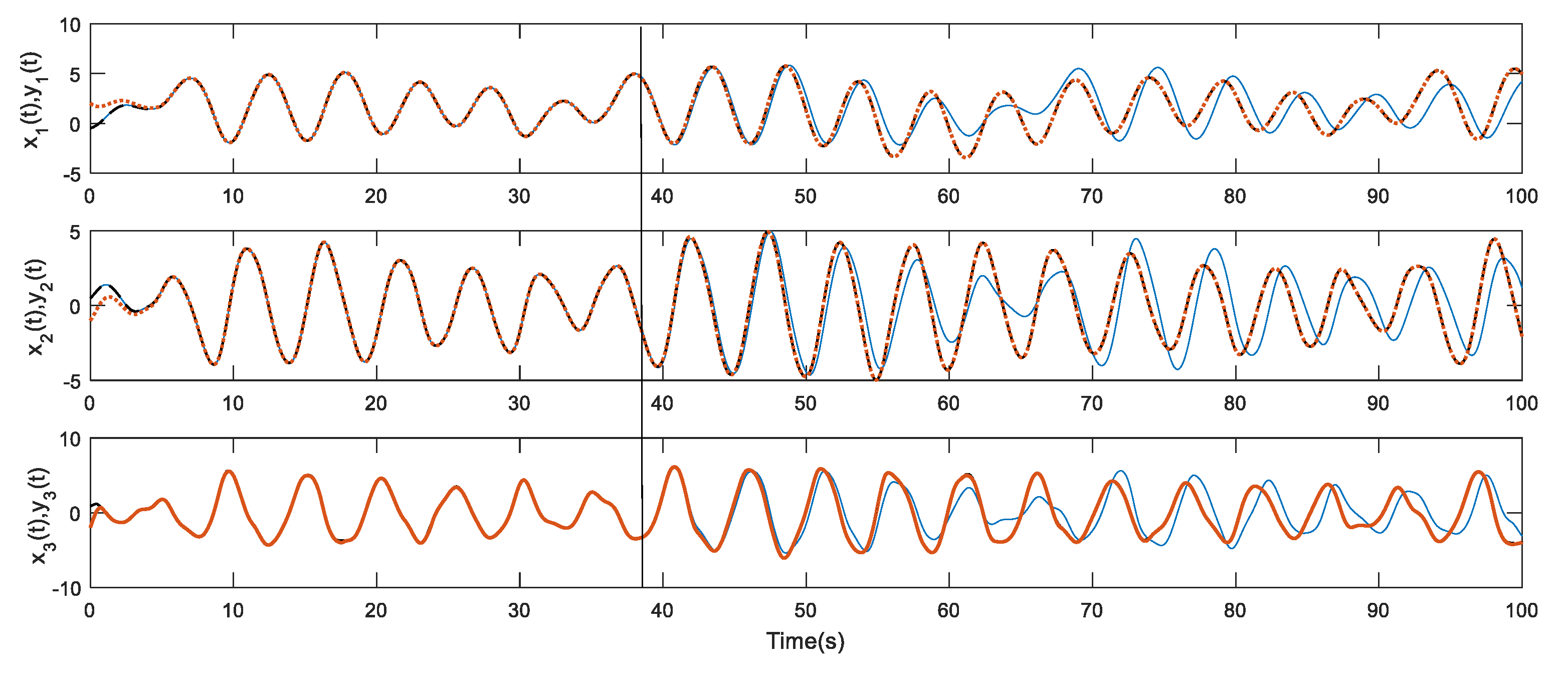
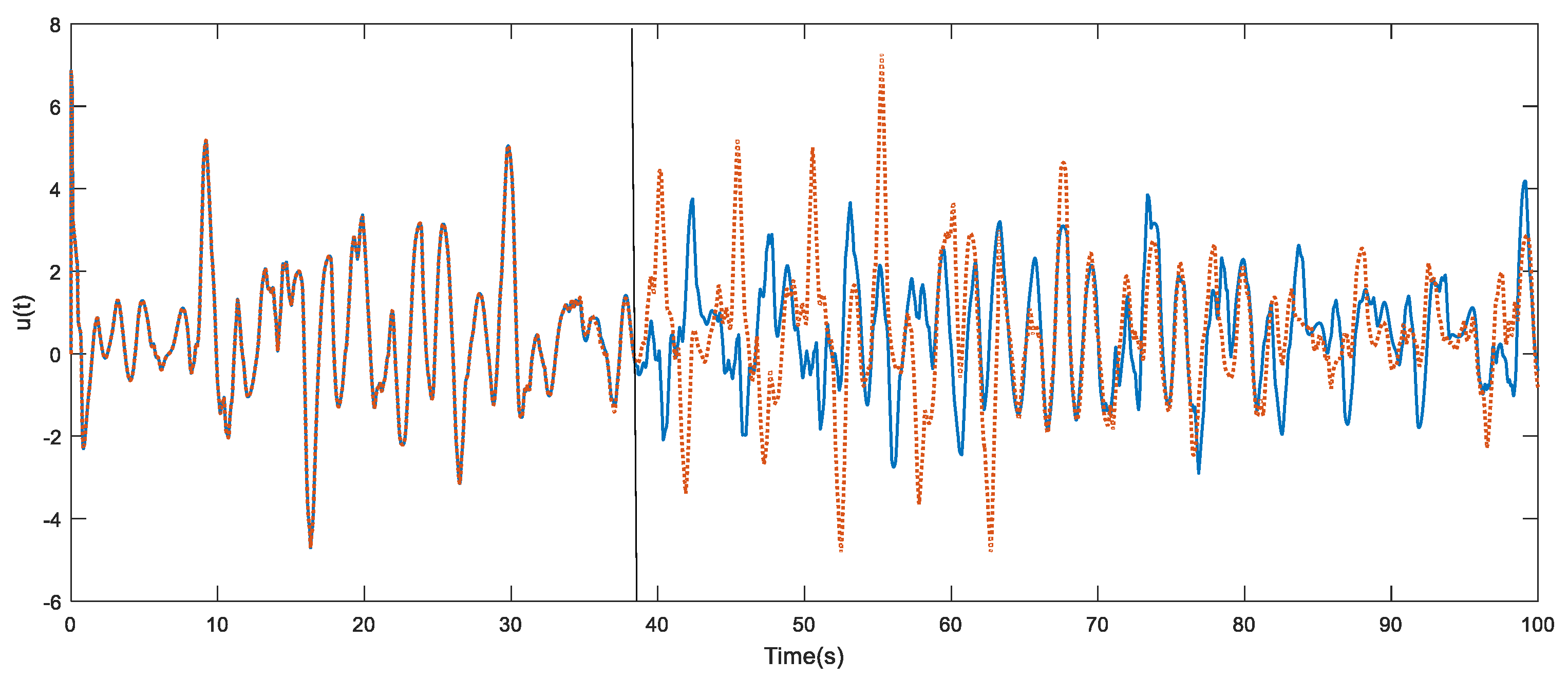
4. Simulation Example and Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, G. Controlling Chaos and Bifurcations in Engineering Systems; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- N’doye, I.; Laleg-Kirati, T.M.; Darouach, M.; Voos, H. Adaptive observer for nonlinear fractional-order systems. Int. J. Adapt. Control Signal Process. 2017, 31, 314–331. [Google Scholar] [CrossRef]
- Andrievskii, B.R. Control of Chaos: Methods and Applications. I. Methods. Autom. Remote Control 2003, 64, 673–713. [Google Scholar] [CrossRef]
- Liao, T.-L.; Lin, H.-R.; Wan, P.-Y.; Yan, J.-J. Improved Attribute-Based Encryption Using Chaos Synchronization and Its Application to MQTT Security. Appl. Sci. 2019, 9, 4454. [Google Scholar] [CrossRef] [Green Version]
- Ouannas, A.; Debbouche, N.; Wang, X.; Pham, V.-T.; Zehrour, O. Secure Multiple-Input Multiple-Output Communications Based on F–M Synchronization of Fractional-Order Chaotic Systems with Non-Identical Dimensions and Orders. Appl. Sci. 2018, 8, 1746. [Google Scholar] [CrossRef] [Green Version]
- Liao, T.-L.; Wan, P.-Y.; Yan, J.-J. Design of Synchronized Large-Scale Chaos Random Number Generators and Its Application to Secure Communication. Appl. Sci. 2019, 9, 185. [Google Scholar] [CrossRef] [Green Version]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef]
- Fradkov, A.L.; Pogromsky, A.Y. Introduction to Control of Oscillations and Chaos; World Scientific: Singapore, 1998; Volume 35. [Google Scholar]
- Tirandaz, H.; Hajipour, A. Adaptive synchronization and anti-synchronization of TSUCS and Lü unified chaotic systems with unknown parameters. Optick 2017, 130, 543–549. [Google Scholar] [CrossRef]
- Fradkov, A.L.; Nijmeijer, H.; Markov, A. Adaptive Observer-Based Synchronization for Communication. Int. J. Bifurc. Chaos 2000, 10, 2807–2813. [Google Scholar] [CrossRef]
- Chen, X.; Park, J.H.; Cao, J.; Qiu, J. Sliding mode synchronization of multiple chaotic systems with uncertainties and disturbances. Appl. Math. Comput. 2017, 308, 161–173. [Google Scholar] [CrossRef]
- Benchabane, I.; Boukabou, A. Predictive synchronization of chaotic and hyperchaotic energy resource systems. Optik 2016, 127, 9532–9537. [Google Scholar] [CrossRef]
- Tirandaz, H.; Aminabadi, S.S.; Tavakoli, H. Chaos synchronization and parameter identification of a finance chaotic system with unknown parameters, a linear feedback controller. Alex. Eng. J. 2018, 57, 1519–1524. [Google Scholar] [CrossRef]
- Yu, J.; Lei, J.; Wang, L. Backstepping synchronization of chaotic system based on equivalent transfer function method. Optik 2017, 130, 900–913. [Google Scholar] [CrossRef]
- Ahmed, H.; Ríos, H.; Salgado, I. Robust Synchronization of Master Slave Chaotic Systems: A Continuous Sliding-Mode Control Approach with Experimental Study. In Recent Advances in Chaotic Systems and Synchronization; Elsevier BV: Amsterdam, The Netherlands, 2019; pp. 261–275. [Google Scholar]
- Chen, C.-S.; Chen, H.-H. Robust adaptive neural-fuzzy-network control for the synchronization of uncertain chaotic systems. Nonlinear Anal. Real World Appl. 2009, 10, 1466–1479. [Google Scholar] [CrossRef]
- Zhao, X.; Shi, P.; Zheng, X. Fuzzy Adaptive Control Design and Discretization for a Class of Nonlinear Uncertain Systems. IEEE Trans. Cybern. 2015, 46, 1476–1483. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, X.; Zong, G.; Li, H. Fuzzy-Approximation-Based Adaptive Output-Feedback Control for Uncertain Nonsmooth Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2018, 26, 3847–3859. [Google Scholar] [CrossRef]
- Chen, M.; Xu, X. Robust adaptive neural network synchronization controller design for a class of time delay uncertain chaotic systems. Chaos Solitons Fractals 2009, 41, 2716–2724. [Google Scholar] [CrossRef]
- Cheng, C.-K.; Chao, P.C.-P. Chaotic Synchronizing Systems with Zero Time Delay and Free Couple via Iterative Learning Control. Appl. Sci. 2018, 8, 177. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Liu, P.X.; Shi, P. Observer-Based Fuzzy Adaptive Output-Feedback Control of Stochastic Nonlinear Multiple Time-Delay Systems. IEEE Trans. Cybern. 2017, 47, 2568–2578. [Google Scholar] [CrossRef]
- Wang, H.; Sun, W.; Liu, P.X. Adaptive Intelligent Control of Nonaffine Nonlinear Time-Delay Systems with Dynamic Uncertainties. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 1474–1485. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Li, D.; Yang, D. Adaptive Synchronization for a Class of Fractional Order Time-delay Uncertain Chaotic Systems via Fuzzy Fractional Order Neural Network. Int. J. Control Autom. Syst. 2019, 17, 1209–1220. [Google Scholar] [CrossRef]
- Shi, L.; Yang, X.; Li, Y.; Feng, Z. Finite-time synchronization of nonidentical chaotic systems with multiple time-varying delays and bounded perturbations. Nonlinear Dyn. 2015, 83, 75–87. [Google Scholar] [CrossRef]
- Shang-Guan, X.-C.; He, Y.; Lin, W.-J.; Wu, M. Improved synchronization of chaotic Lur’e systems with time delay using sampled-data control. J. Frankl. Inst. 2017, 354, 1618–1636. [Google Scholar] [CrossRef]
- Zhang, R.; Zeng, D.; Zhong, S. Novel master–slave synchronization criteria of chaotic Lur’e systems with time delays using sampled-data control. J. Frankl. Inst. 2017, 354, 4930–4954. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Zhang, B.; Zhao, Y. Regulation cooperative control for heterogeneous uncertain chaotic systems with time delay: A synchronization errors estimation framework. Automatica 2019, 108, 108486. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Duan, P. Observer-based sliding mode control for synchronization of delayed chaotic neural networks with unknown disturbance. Neural Netw. 2019, 117, 268–273. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Ahmad, W.M.; Sprott, J. Chaos in fractional-order autonomous nonlinear systems. Chaos Solitons Fractals 2003, 16, 339–351. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zare, A.; Mirrezapour, S.Z.; Hallaji, M.; Shoeibi, A.; Jafari, M.; Ghassemi, N.; Alizadehsani, R.; Mosavi, A. Robust Adaptive Synchronization of a Class of Uncertain Chaotic Systems with Unknown Time-Delay. Appl. Sci. 2020, 10, 8875. https://doi.org/10.3390/app10248875
Zare A, Mirrezapour SZ, Hallaji M, Shoeibi A, Jafari M, Ghassemi N, Alizadehsani R, Mosavi A. Robust Adaptive Synchronization of a Class of Uncertain Chaotic Systems with Unknown Time-Delay. Applied Sciences. 2020; 10(24):8875. https://doi.org/10.3390/app10248875
Chicago/Turabian StyleZare, Assef, Seyede Zeynab Mirrezapour, Majid Hallaji, Afshin Shoeibi, Mahboobeh Jafari, Navid Ghassemi, Roohallah Alizadehsani, and Amir Mosavi. 2020. "Robust Adaptive Synchronization of a Class of Uncertain Chaotic Systems with Unknown Time-Delay" Applied Sciences 10, no. 24: 8875. https://doi.org/10.3390/app10248875
APA StyleZare, A., Mirrezapour, S. Z., Hallaji, M., Shoeibi, A., Jafari, M., Ghassemi, N., Alizadehsani, R., & Mosavi, A. (2020). Robust Adaptive Synchronization of a Class of Uncertain Chaotic Systems with Unknown Time-Delay. Applied Sciences, 10(24), 8875. https://doi.org/10.3390/app10248875





