The Effects of Hydrogen Distribution on the Elastic Properties and Hydrogen-Induced Hardening and Softening of ?-Fe
Abstract
:1. Introduction
2. Calculation Methods
2.1. Elastic Constants
2.2. Hardening and Softening Due to Hydrogen Microscopic Distribution
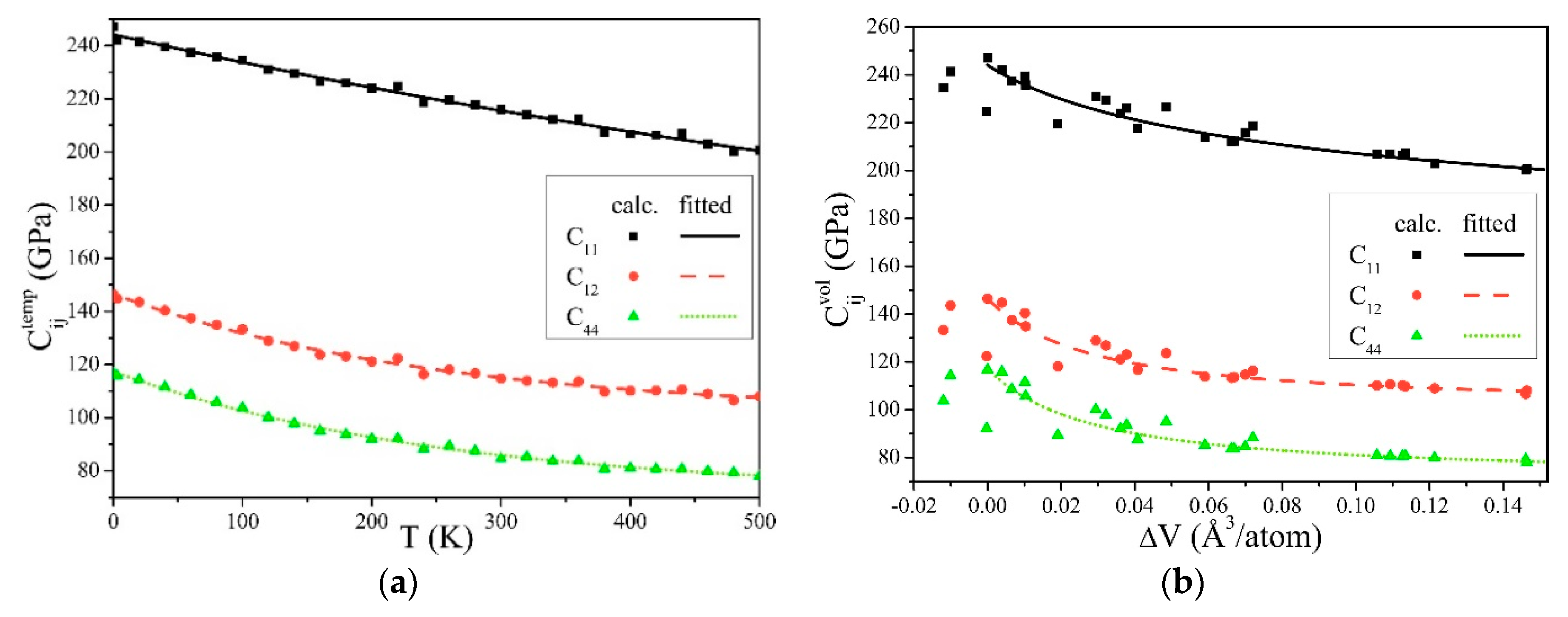
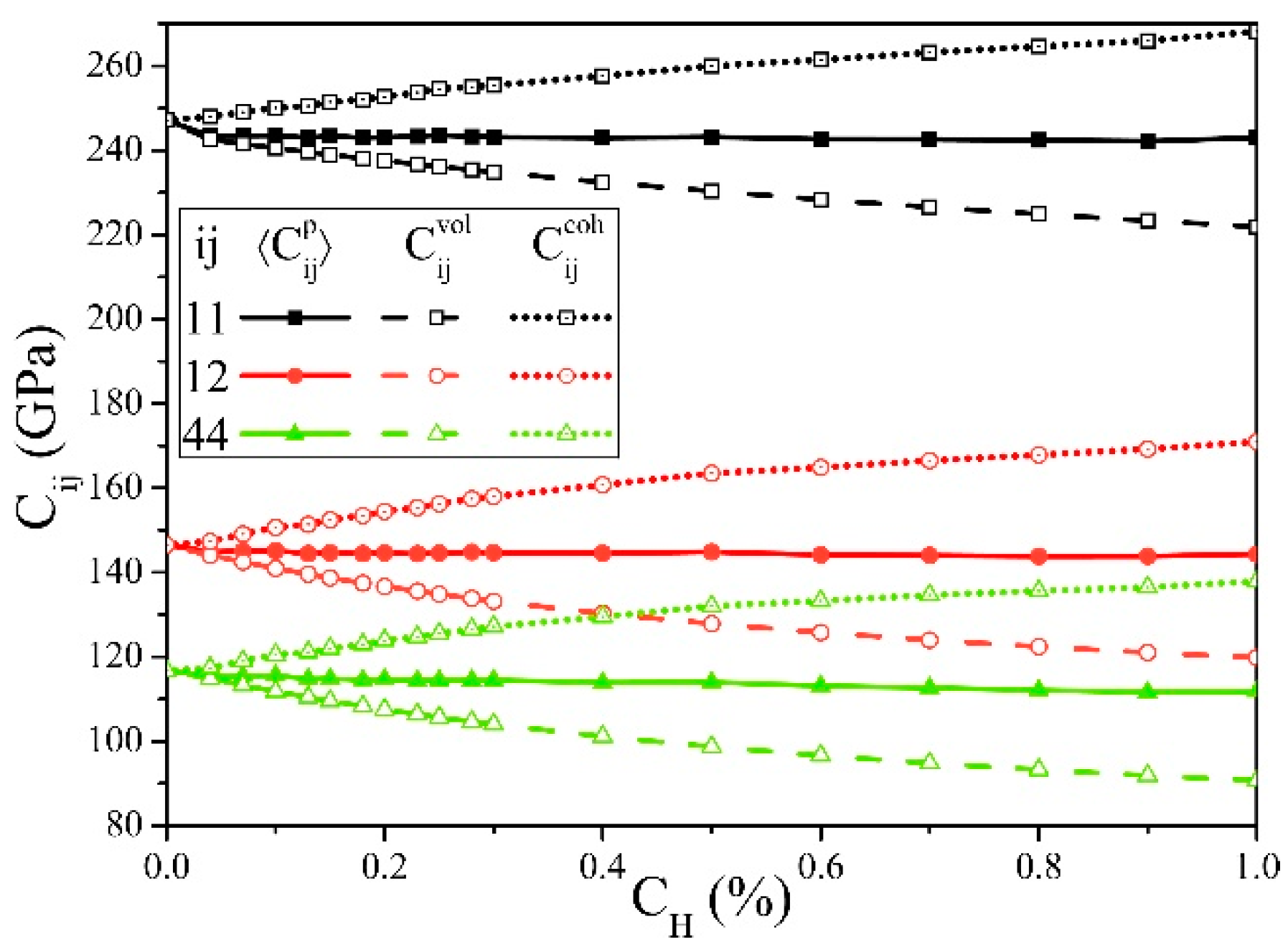
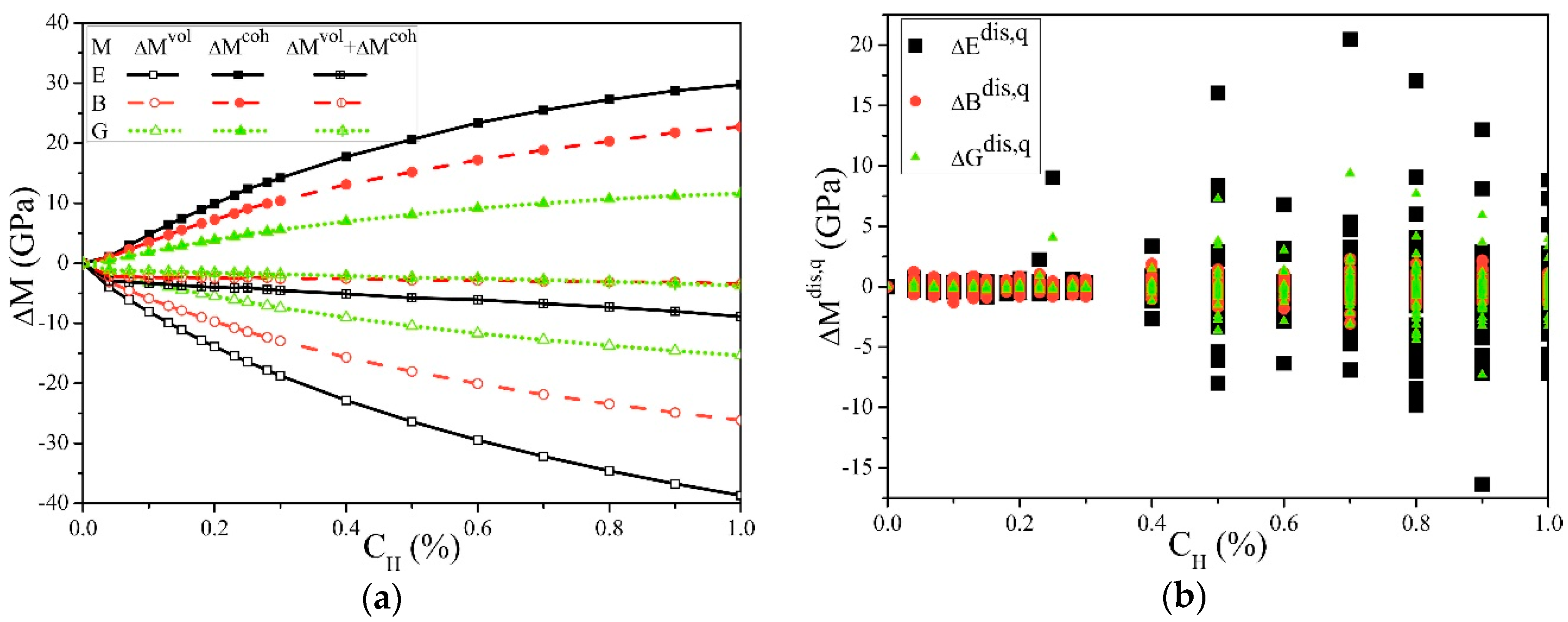
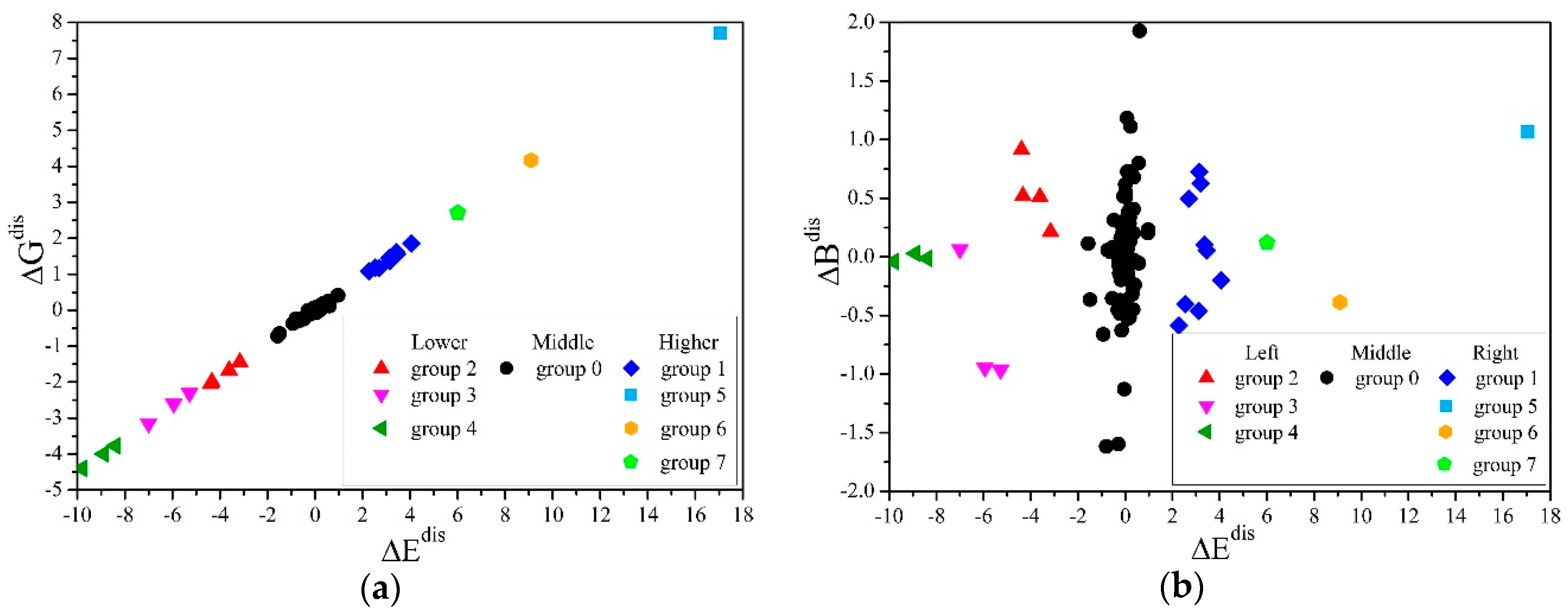
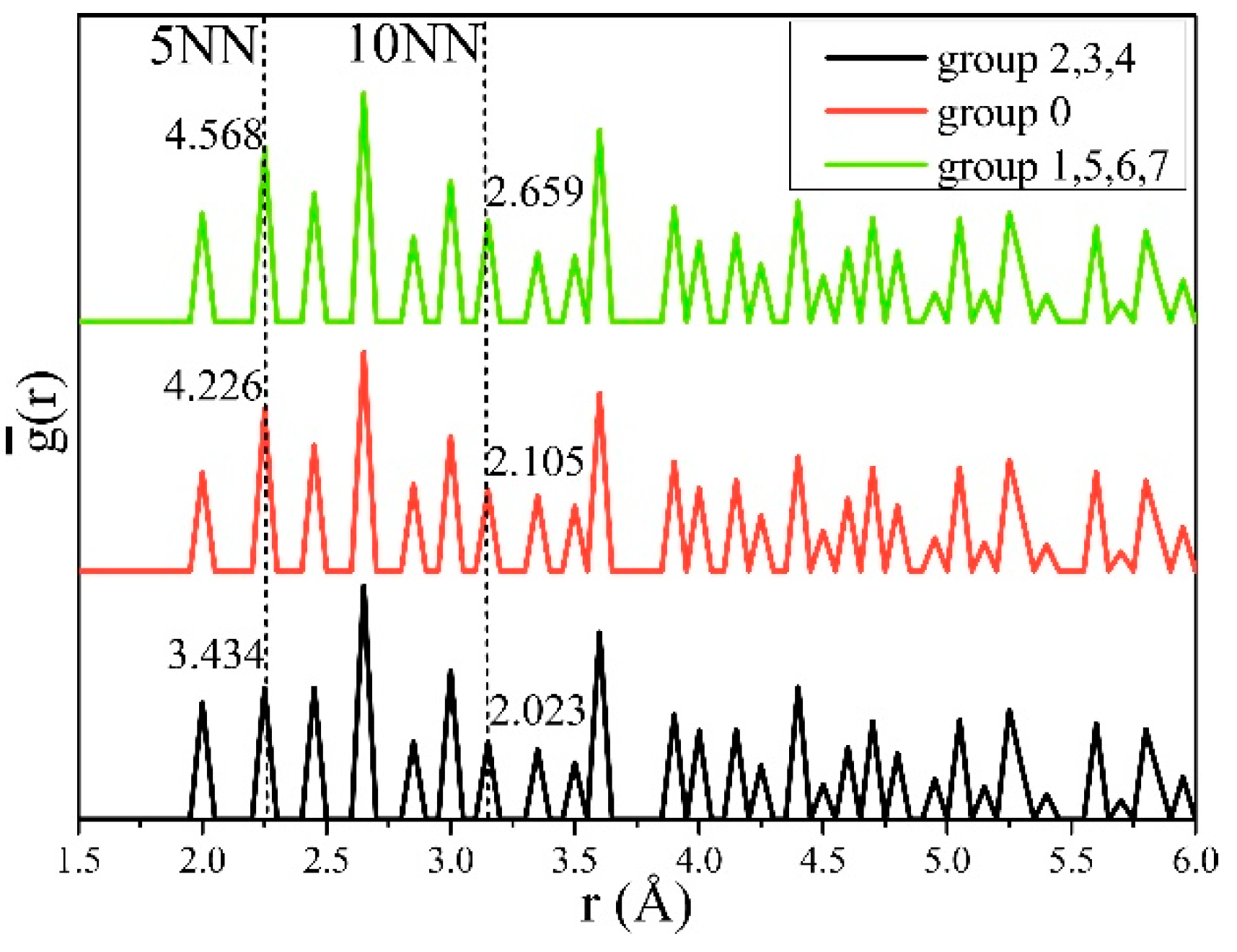
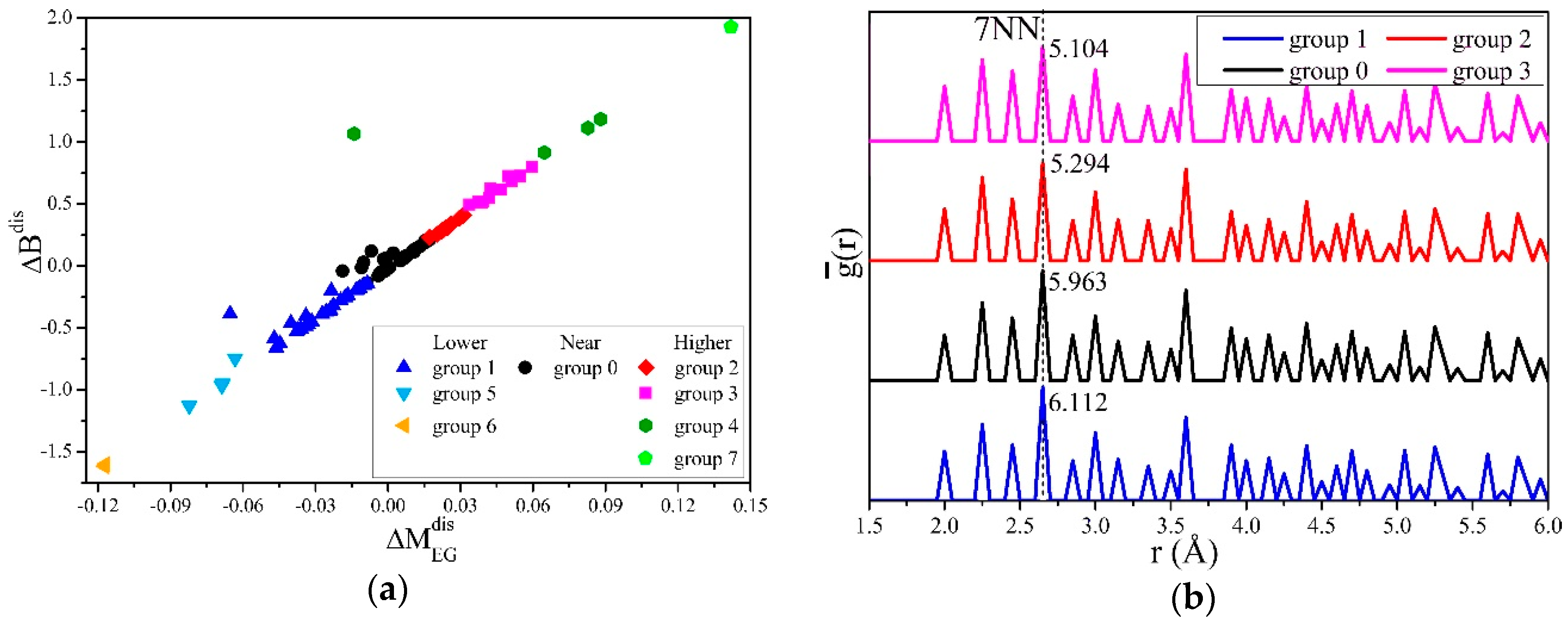
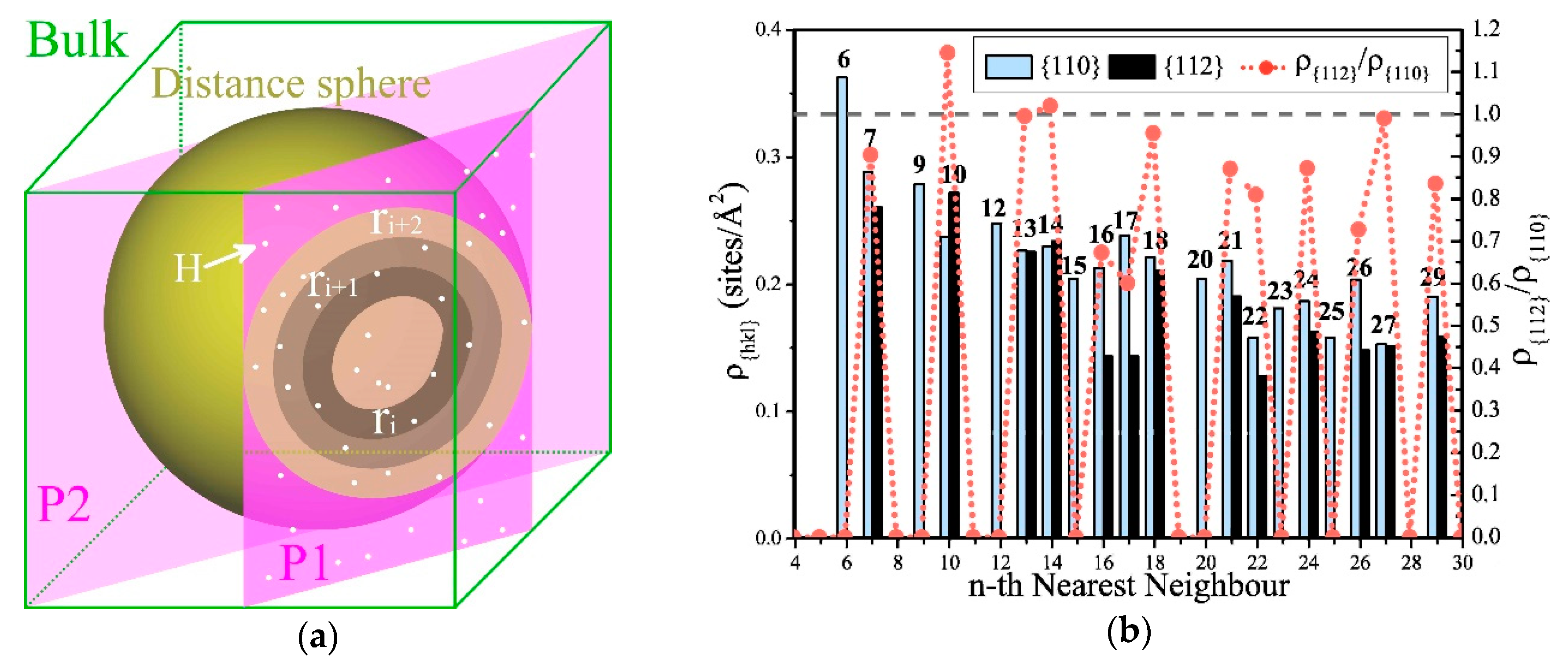
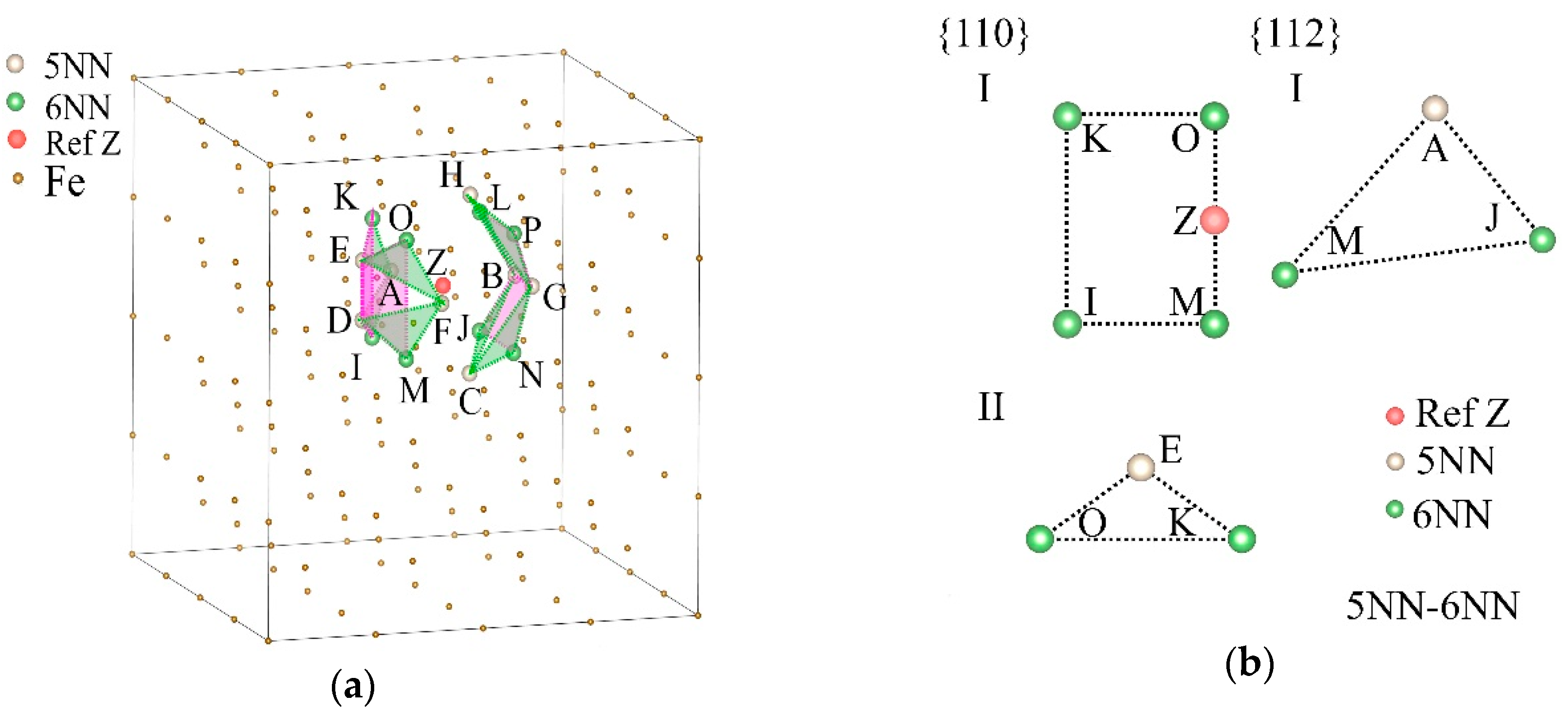
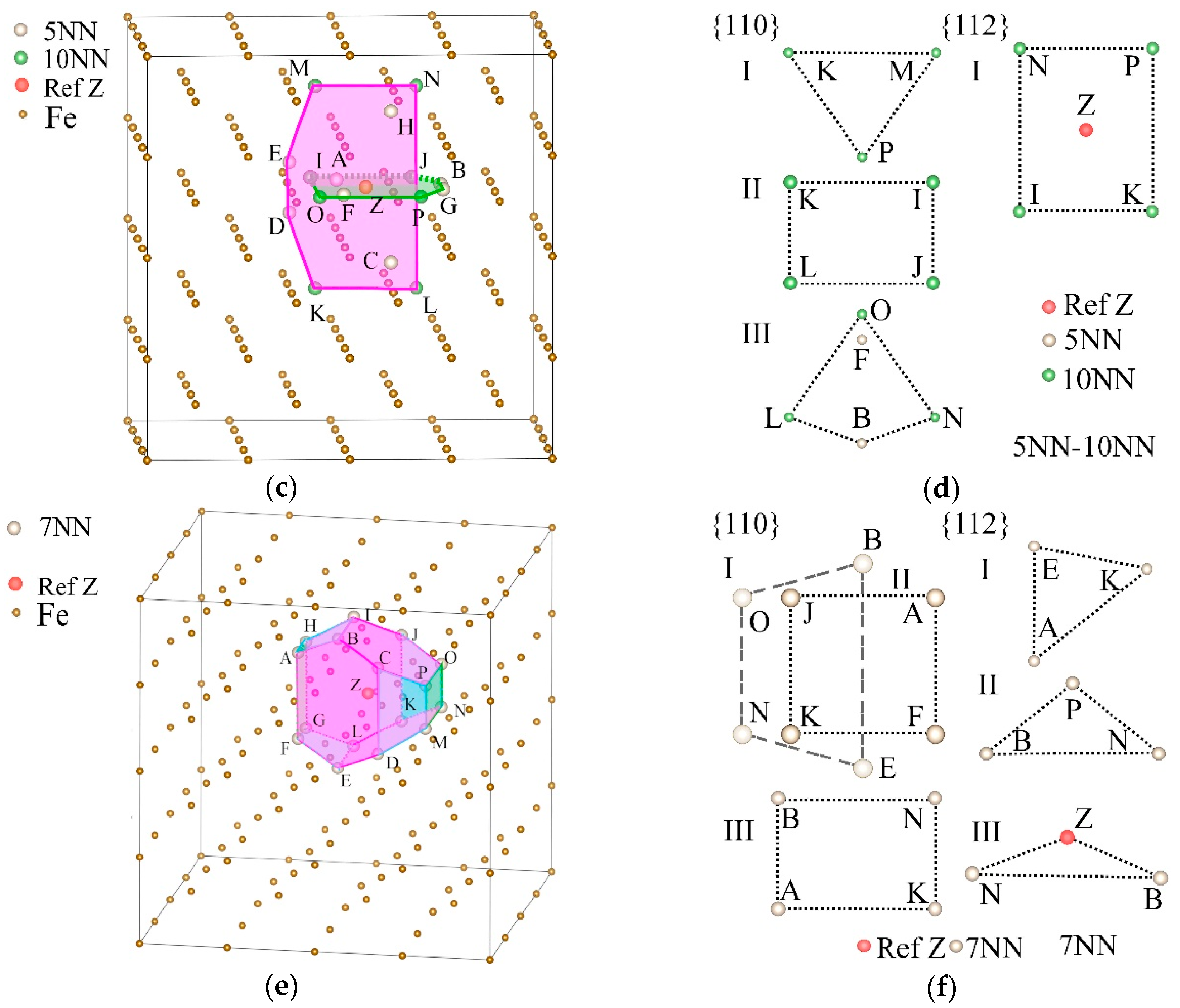
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nagumo, M. Fundamentals of Hydrogen Embrittlement; Springer: Singapore, 2016; ISBN 9789811001611. [Google Scholar]
- Robertson, I.M.; Sofronis, P.; Nagao, A.; Martin, M.L.; Wang, S.; Gross, D.W.; Nygren, K.E. Hydrogen Embrittlement Understood. Metall. Mater. Trans. A 2015, 46, 2323–2341. [Google Scholar] [CrossRef] [Green Version]
- Troiano, A.R. The Role of Hydrogen and Other Interstitials in the Mechanical Behavior of Metals. Metallogr. Microstruct. Anal. 2016, 5, 557–569. [Google Scholar] [CrossRef]
- Lynch, S. Hydrogen embrittlement phenomena and mechanisms. Corros. Rev. 2012, 30, 105–123. [Google Scholar] [CrossRef]
- Pfeil, L.B. The effect of occluded hydrogen on the tensile strength of iron. J. Franklin Inst. 1927, 203, 331–332. [Google Scholar] [CrossRef]
- Oriani, R.A. The Physical and Metallurgical Aspects of Hydrogen in Metals. In Proceedings of the Fourth International Conference on Cold Fusion, Lahaina, Maui, 6–9 December 1993. [Google Scholar]
- Beachem, C.D. A new model for hydrogen-assisted cracking (hydrogen “embrittlement”). Metall. Mater. Trans. B 1972, 3, 441–455. [Google Scholar] [CrossRef]
- Sofronis, P.; Robertson, I.M. Transmission electron microscopy observations and micromechanical/continuum models for the effect of hydrogen on the mechanical behaviour of metals. Philos. Mag. A Phys. Condens. Matter, Struct. Defects Mech. Prop. 2002, 82, 3405–3413. [Google Scholar] [CrossRef]
- Ferreira, P.J.; Robertson, I.M.; Birnbaum, H.K. Hydrogen effects on the interaction between dislocations. Acta Mater. 1998, 46, 1749–1757. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.H.; Lee, J.A.; Seok, M.Y.; Baek, U.B.; Nahm, S.H.; Jang, J. Il Stress-dependent hardening-to-softening transition of hydrogen effects in nanoindentation of a linepipe steel. Int. J. Hydrogen Energy 2014, 39, 1897–1902. [Google Scholar] [CrossRef]
- Kimura, H.; Matsui, H. Mechanism of hydrogen-induced softening and hardening in iron. Scr. Metall. 1987, 21, 319–324. [Google Scholar] [CrossRef]
- Kirchheim, R. Solid solution softening and hardening by mobile solute atoms with special focus on hydrogen. Scr. Mater. 2012, 67, 767–770. [Google Scholar] [CrossRef]
- Miresmaeili, R.; Liu, L.; Kanayama, H. A possible explanation for the contradictory results of hydrogen effects on macroscopic deformation. Int. J. Press. Vessel. Pip. 2012, 99–100, 34–43. [Google Scholar] [CrossRef]
- Katzarov, I.H.; Pashov, D.L.; Paxton, A.T. Hydrogen embrittlement I. Analysis of hydrogen-enhanced localized plasticity: Effect of hydrogen on the velocity of screw dislocations in α-Fe. Phys. Rev. Mater. 2017, 1, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Tomatsu, K.; Omura, T.; Nishiyama, Y.; Todaka, Y. Influence of hydrogen on local mechanical properties of pure Fe with different dislocation densities investigated by electrochemical nanoindentation. ISIJ Int. 2016, 56, 2298–2303. [Google Scholar] [CrossRef] [Green Version]
- Du, J.J.; Mao, O.; Wang, X. Softening and Hardening Due to Hydrogen in Iron and Iron Based Alloys. Mech. Behav. Mater. V 1988, 855–860. [Google Scholar] [CrossRef]
- Ogawa, T.; Koyama, M.; Noguchi, H. Suppression mechanism of strain-age hardening in carbon steel associated with hydrogen uptake. Tetsu Hagane J. Iron Steel Inst. Japan 2015, 101, 546–551. [Google Scholar] [CrossRef] [Green Version]
- Hirth, J.P. Effects of hydrogen on the properties of iron and steel. Metall. Trans. A 1980, 11, 861–890. [Google Scholar] [CrossRef]
- Kimura, A.; Kimura, H. Hydrogen embrittlement in high purity iron single crystals. Mater. Sci. Eng. 1986, 77, 75–83. [Google Scholar] [CrossRef]
- Taketomi, S.; Matsumoto, R.; Hagihara, S. Molecular statics simulation of the effect of hydrogen concentration on {112}<111> edge dislocation mobility in alpha iron. ISIJ Int. 2017, 57, 2058–2064. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Seok, M.Y.; Choi, I.C.; Lee, Y.H.; Park, S.J.; Ramamurty, U.; Suh, J.Y.; Jang, J. Il The role of hydrogen in hardening/softening steel: Influence of the charging process. Scr. Mater. 2015, 107, 46–49. [Google Scholar] [CrossRef]
- Matsui, H.; Kimura, H.; Moriya, S. The effect of hydrogen on the mechanical properties of high purity iron I. Softening and hardening of high purity iron by hydrogen charging during tensile deformation. Mater. Sci. Eng. 1979, 40, 207–216. [Google Scholar] [CrossRef]
- Oguri, K.; Takaki, S.; Kimura, H. Hydrogen-induced softening and hardening in high purity FeC alloys. Mater. Sci. Eng. 1982, 53, 223–232. [Google Scholar] [CrossRef]
- Hashimoto, M.; Latanision, R.M. The role of dislocations during transport of hydrogen in hydrogen embrittlement of iron. Metall. Trans. A 1988, 19, 2799–2803. [Google Scholar] [CrossRef]
- Wang, S.; Ohnuki, S.; Hashimoto, N.; Chiba, K. Hydrogen effects on tensile property of pure iron with deformed surface. Mater. Sci. Eng. A 2013, 560, 332–338. [Google Scholar] [CrossRef] [Green Version]
- Asano, S.; Otsuka, R. The lattice hardening due to dissolved hydrogen in iron and steel. Scr. Metall. 1976, 10, 1015–1020. [Google Scholar] [CrossRef]
- Psiachos, D.; Hammerschmidt, T.; Drautz, R. Ab initio study of the modification of elastic properties of α-iron by hydrostatic strain and by hydrogen interstitials. Acta Mater. 2011, 59, 4255–4263. [Google Scholar] [CrossRef] [Green Version]
- Xing, X.; Yu, M.; Chen, W.; Zhang, H. Atomistic simulation of hydrogen-assisted ductile-to-brittle transition in α-iron. Comput. Mater. Sci. 2017, 127, 211–221. [Google Scholar] [CrossRef]
- Song, J.; Curtin, W.A. Atomic mechanism and prediction of hydrogen embrittlement in iron. Nat. Mater. 2013, 12, 145–151. [Google Scholar] [CrossRef]
- Matsumoto, R.; Taketomi, S.; Matsumoto, S.; Miyazaki, N. Atomistic simulations of hydrogen embrittlement. Int. J. Hydrogen Energy 2009, 34, 9576–9584. [Google Scholar] [CrossRef]
- Nosengo, N. The material code. Nature 2016, 533, 22–25. [Google Scholar] [CrossRef] [Green Version]
- Schleder, G.R.; Padilha, A.C.M.; Acosta, C.M.; Costa, M.; Fazzio, A. From DFT to machine learning: Recent approaches to materials science—A review. J. Phys. Mater. 2019, 2, 032001. [Google Scholar] [CrossRef]
- Bedolla, E.; Padierna, L.C.; Castañeda-Priego, R. Machine Learning for Condensed Matter Physics. J. Phys. Condens. Matter 2020. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, X.; Yang, X.-S.; He, W.; Shi, S.-Q.; Ma, X. Atomistic simulation of the effect of the dissolution and adsorption of hydrogen atoms on the fracture of α-Fe single crystal under tensile load. Int. J. Hydrogen Energy 2020. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics for the United States Department of Energy under Contract DE.ACO4-76DPOO789. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Ramasubramaniam, A.; Itakura, M.; Carter, E.A. Interatomic potentials for hydrogen in alpha-iron based on density functional theory. Phys. Rev. B 2010, 81, 099902. [Google Scholar] [CrossRef] [Green Version]
- Thompson, A.P.; Plimpton, S.J.; Mattson, W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 2009, 131, 154107. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.Y.; Jiang, F.X.; Chu, W.Y.; Hsiao, C.M. Effect of hydrogen on the Young’s modulus of iron. Metall. Trans. A 1985, 16, 1655–1662. [Google Scholar] [CrossRef]
- Knuth, D.E. The Art of Computer Programming: Seminumerical Algorithms, 3rd ed.; Addison Wesley Longman: Reading, MA, USA, 1997. [Google Scholar]
- Shinoda, W.; Shiga, M.; Mikami, M. Rapid estimation of elastic constants by molecular dynamics simulation under constant stress. Phys. Rev. B 2004, 69, 1341031. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Strain fluctuations and elastic constants. J. Chem. Phys. 1982, 76, 2662–2666. [Google Scholar] [CrossRef]
- Gusev, A.A.; Zehnder, M.M.; Suter, U.W. Fluctuation formula for elastic constants. Phys. Rev. B 1996, 54, 1–4. [Google Scholar] [CrossRef]
- Ray, J.R. Ensembles and Computer Simulation Calculation of Response Functions BT—Handbook of Materials Modeling: Methods; Yip, S., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 729–743. ISBN 978-1-4020-3286-8. [Google Scholar]
- Switendick, A.C. Band Structure Calculations for Metal Hydrogen Systems. Zeitschrift Phys. Chem. 1979, 117, 89. [Google Scholar] [CrossRef] [Green Version]
- Newnham, R.E. Properties of Materials:Anisotropy, Symmetry, Structure, 1st ed.; Oxford University Press: Oxford, UK, 2005; ISBN 0-19-852075-1. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Ni, X.D.; Wang, Z.; Sun, X.; Shen, J.; Chen, N.X. Mechanism of Ag and Al on improving the glass forming ability of CuZr-based alloys. Int. J. Miner. Metall. Mater. 2011, 18, 424–429. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Yang, X.S.; Zhu, J.H.; Xing, F. Atomistic simulation study of the grain-size effect on hydrogen embrittlement of nanograined Fe. Int. J. Hydrogen Energy 2020, 45, 3294–3306. [Google Scholar] [CrossRef]
- Dragoni, D.; Ceresoli, D.; Marzari, N. Vibrational and thermoelastic properties of bcc iron from selected EAM potentials. Comput. Mater. Sci. 2018, 152, 99–106. [Google Scholar] [CrossRef] [Green Version]
- Adams, J.J.; Agosta, D.S.; Leisure, R.G.; Ledbetter, H. Elastic constants of monocrystal iron from 3 to 500 K. J. Appl. Phys. 2006, 100. [Google Scholar] [CrossRef]
- Shirkhorshidi, A.S.; Aghabozorgi, S.; Wah, T.Y.; Herawan, T. Big data clustering: A review. Lect. Notes Comput. Sci. 2014, 8583 LNCS, 707–720. [Google Scholar] [CrossRef]
- Parker, A.J.; Barnard, A.S. Selecting Appropriate Clustering Methods for Materials Science Applications of Machine Learning. Adv. Theory Simulations 2019, 2, 1–8. [Google Scholar] [CrossRef]
- Spitzig, W.A.; Keh, A.S. Orientation and temperature dependence of slip in iron single crystals. Metall. Trans. 1970, 1, 2751. [Google Scholar] [CrossRef]
| Data Source | Elastic Constants (GPa) | Elastic Moduli (GPa) | ||||
|---|---|---|---|---|---|---|
| C11 | C12 | C44 | E | B | G | |
| This work | 247.13 | 146.47 | 116.75 | 231.83 | 180.02 | 90.18 |
| Experiment [53] | 239.55 | 135.75 | 120.75 | 236.50 | 170.35 | 93.21 |
| Parameter | Result | Parameter | Result | Parameter | Result |
|---|---|---|---|---|---|
| (Å3/atom) | −0.03212 | (Å3/atom) | 0.03199 | (K) | −286.533 |
| (GPa) | −121.484 | (GPa) | 118.488 | (K) | 1085.129 |
| (GPa) | −45.014 | (GPa) | 45.113 | (K) | 250.363 |
| (GPa) | −44.799 | (GPa) | 45.431 | (K) | 253.642 |
| s5NN-6NN | s5NN-10NN | s7NN | ||||||
|---|---|---|---|---|---|---|---|---|
| Plane Family | Density (Sites/Å2) | Mark by Sites | Plane Family | Density (Sites/Å2) | Mark by Sites | Plane Family | Density (Sites/Å2) | Mark by Sites |
| {210} | 0.5122 | DEMO, BGJN, DEIK, BGLP | {100} | 0.5163 | IJBGPO, DEMNLK | {120} | 0.5122 | CDMP, JKON, EFGL, ABHI |
| {531} | 0.4845 | ADI, BCJ, CGN, DFM, GHP, AEK, BHL, EFO | {120} | 0.4704 | ABCDEF, BCIJOP, GHIJKL, DEKLMN | |||
| {100} | 0.4652 | AFGH, MNOP | ||||||
| Plane Family | s5NN-6NN | s5NN-10NN | s7NN | |||
|---|---|---|---|---|---|---|
| Type | Mark by Sites | Type | Mark by Sites | Type | Mark by Sites | |
| {110} | I | ILMPZ, IKNPZ, JLMOZ, JKNOZ | I | JKM, JKP, JMP, KMP | I | BENO, ILMP, ADHK, CFGJ |
| II | AIK, BJL, CJN, DIM, EKO, FMO, GNP, HLP | II | IJLK, IJMN, MNOP, KLOP | II | AFKJ, BIMN, ELOP, CDGH | |
| III | AGLNI, BFLNO, CEIOL, DHION | III | ABNK, CGLP, EFJO, DHIM | |||
| {112} | I | AJM, ALO, BIN, BKP, CIL, CMP, DJK, DNO, EIL, EMP, FIN, FKP, GJM, GLO, HJK, HNO | I | IKNPZ, ILMPZ, JKNOZ, IJMOZ | I | AEK, BFJ, CGI, BDN, CEO, DHL, IKM, JLP |
| II | BNP, EMO, IMO, LNP, ACG, AGK, DFH, FHJ | |||||
| III | BNZ, IMZ, EOZ, LPZ | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Shi, X.; Yang, X.-S.; Liu, Z.; Shi, S.-Q.; Ma, X. The Effects of Hydrogen Distribution on the Elastic Properties and Hydrogen-Induced Hardening and Softening of ?-Fe. Appl. Sci. 2020, 10, 8958. https://doi.org/10.3390/app10248958
Wang Z, Shi X, Yang X-S, Liu Z, Shi S-Q, Ma X. The Effects of Hydrogen Distribution on the Elastic Properties and Hydrogen-Induced Hardening and Softening of ?-Fe. Applied Sciences. 2020; 10(24):8958. https://doi.org/10.3390/app10248958
Chicago/Turabian StyleWang, Zheng, Xiaoming Shi, Xu-Sheng Yang, Zhuhong Liu, San-Qiang Shi, and Xingqiao Ma. 2020. "The Effects of Hydrogen Distribution on the Elastic Properties and Hydrogen-Induced Hardening and Softening of ?-Fe" Applied Sciences 10, no. 24: 8958. https://doi.org/10.3390/app10248958
APA StyleWang, Z., Shi, X., Yang, X.-S., Liu, Z., Shi, S.-Q., & Ma, X. (2020). The Effects of Hydrogen Distribution on the Elastic Properties and Hydrogen-Induced Hardening and Softening of ?-Fe. Applied Sciences, 10(24), 8958. https://doi.org/10.3390/app10248958






