Structure, Properties, and Reactivity of Porphyrins on Surfaces and Nanostructures with Periodic DFT Calculations
Abstract
:Featured Application
Abstract
1. Introduction
2. PDFT Simulations of Porphyrins in Nanostructures
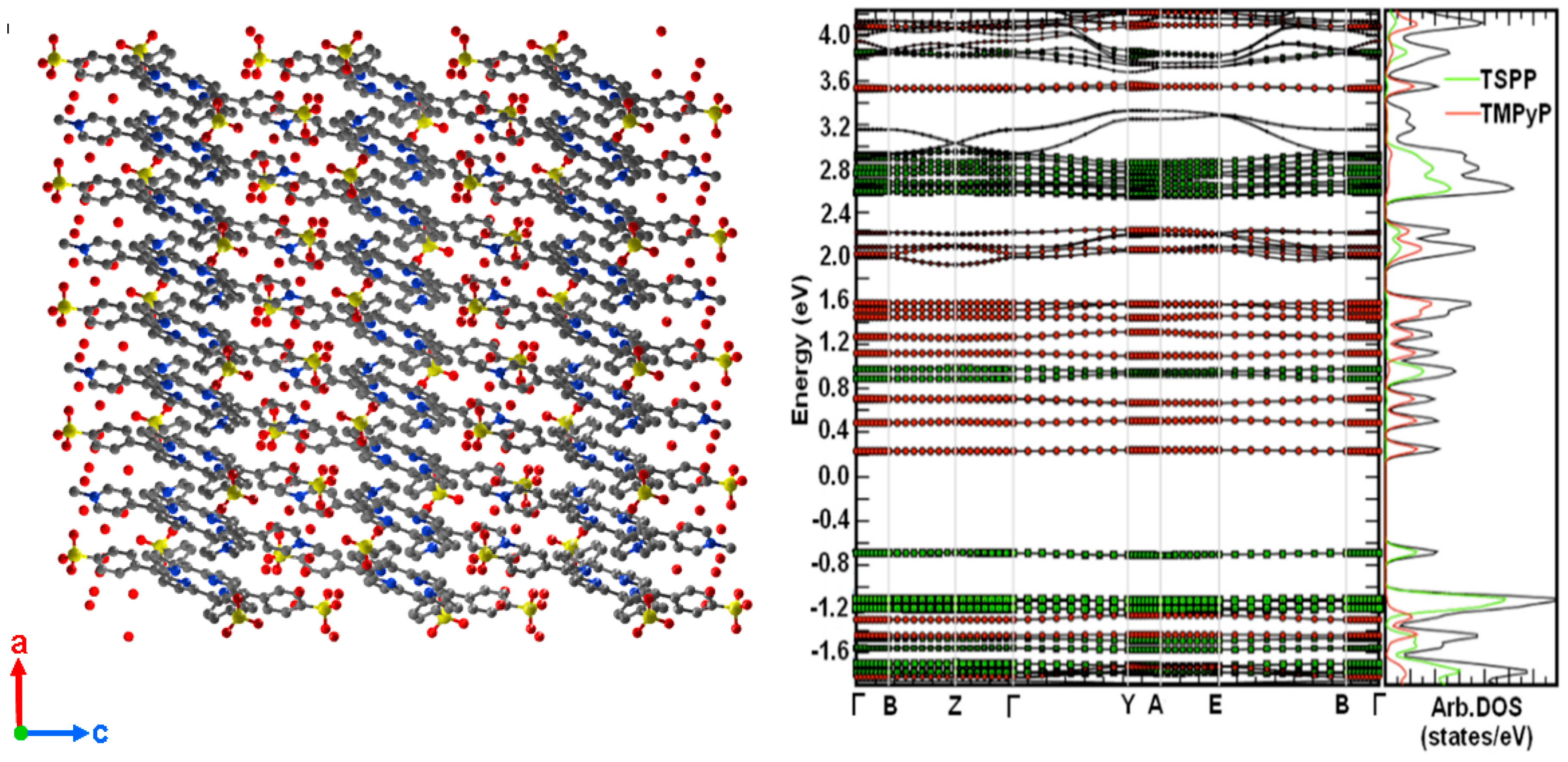
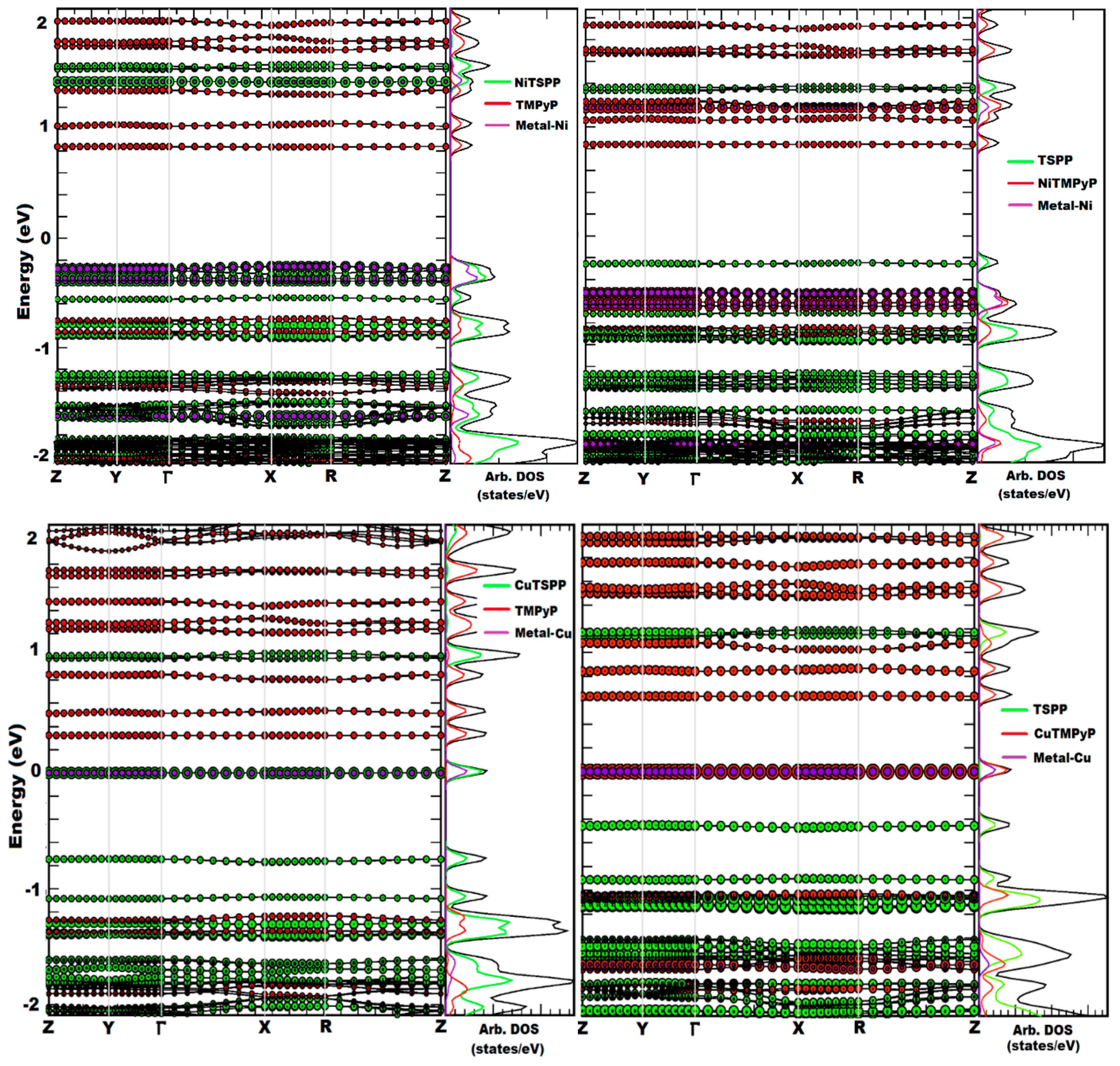
2.1. Porphyrin Nanostructures Using Crystal Geometries
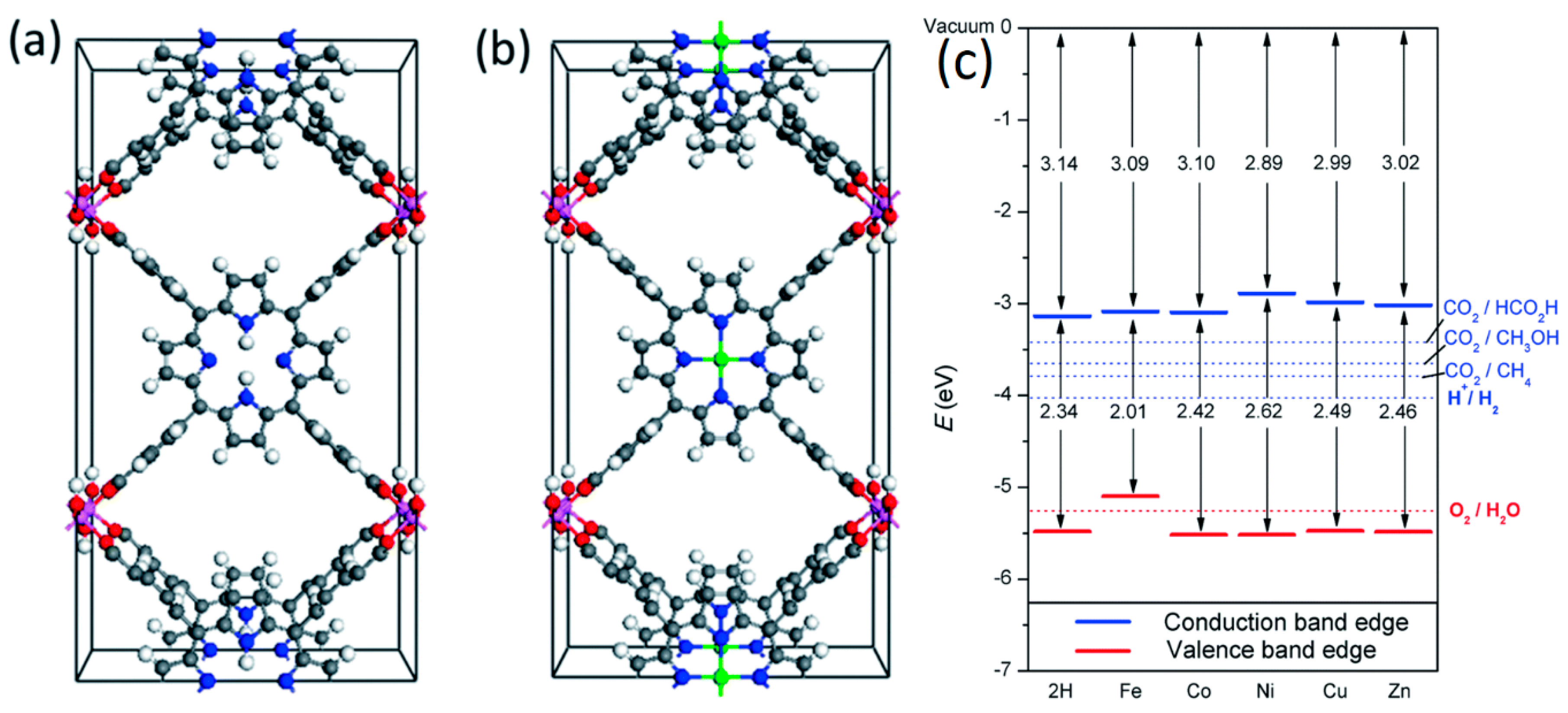
2.2. Porphyrins in Organic Frameworks
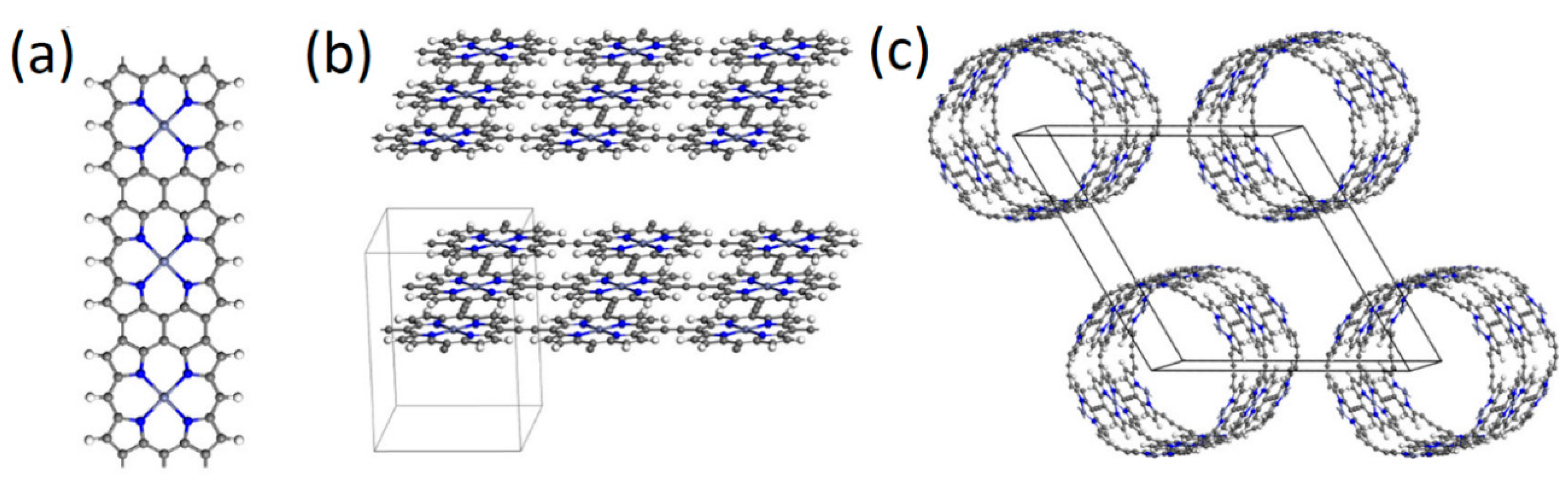
2.3. Porphyrins as Nano Wires, Sheets, Tubes, and Ladders
3. PDFT Simulations of Porphyrins on Surfaces
3.1. Conformational Studies of Meso-Substituted Porphyrins on Substrates
3.2. Conformational Studies of Non-Meso-Substituted Porphyrins on Substrates
3.3. Porphyrins on Single Layer Substrates
3.4. Porphyrins on Oxide Supports
3.5. PDFT Simulations of Substrate Bound Porphyrin Reactions and Catalysis
3.6. Magnetic Couplings in Substrate Bound Porphyrins
3.7. Porphyrin Molecular Junctions
3.8. Ligand-Porphyrin Reactions on Surfaces
4. Summary
Funding
Conflicts of Interest
References
- Huang, H.; Song, W.; Rieffel, J.; Lovell, J.F. Emerging applications of porphyrins in photomedicine. Front. Phys. 2015, 3, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Imran, M.; Ramzan, M.; Qureshi, A.K.; Khan, M.A.; Tariq, M. Emerging Applications of Porphyrins and Metalloporphyrins in Biomedicine and Diagnostic Magnetic Resonance Imaging. Biosensors 2018, 8, 95. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, W.; Aida, T. Dendrimer Porphyrins and Phthalocyanines. Chem. Rev. 2009, 109, 6047–6076. [Google Scholar] [CrossRef] [PubMed]
- Aziz, A.; Ruiz-Salvador, A.; Hernández, N.C.; Calero, S.; Hamad, S.; Grau-Crespo, R. Porphyrin-based metal-organic frameworks for solar fuel synthesis photocatalysis: Band gap tuning via iron substitutions. J. Mater. Chem. A 2017, 5, 11894–11904. [Google Scholar] [CrossRef] [Green Version]
- Maldotti, A.; Amadelli, R.; Bartocci, C.; Carassiti, V.; Polo, E.; Varani, G. Photochemistry of Iron-porphyrin complexes. Biomimetics and catalysis. Coord. Chem. Rev. 1993, 125, 143–154. [Google Scholar] [CrossRef]
- Barona-Castaño, J.C.; Carmona-Vargas, C.C.; Brocksom, T.J.; de Oliveira, K.T. Porphyrins as Catalysts in Scalable Organic Reactions. Molecules 2016, 21, 310. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Diau, E.W. Porphyrin-sensitized solar cells. Chem. Soc. Rev. 2012, 42, 291–304. [Google Scholar] [CrossRef]
- Paolesse, R.; Nardis, S.; Monti, D.; Stefanelli, M.; Di Natale, C. Porphyrinoids for Chemical Sensor Applications. Chem. Rev. 2017, 117, 2517–2583. [Google Scholar] [CrossRef] [Green Version]
- Jurow, M.; Schuckman, A.E.; Batteas, J.D.; Drain, C.M. Porphyrins as Molecular Electronic Components of Functional Devices. Coord. Chem. Rev. 2010, 254, 2297–2310. [Google Scholar] [CrossRef] [Green Version]
- Lopes, D.M.; Araújo-Chaves, J.C.; Menezes, L.R.; Nantes-Cardoso, I.L. Technological Applications of Porphyrins and Related Compounds: Spintronics and Micro-/Nanomotors. Solid State Phys. 2019. [Google Scholar] [CrossRef] [Green Version]
- Hoang, M.H.; Choi, D.H.; Lee, S.J. Organic field-effect transistors based on semiconducting porphyrin single crystals. Synth. Met. 2012, 162, 419–425. [Google Scholar] [CrossRef]
- Hoang, M.H.; Ngo, T.T.; Nguyen, D.N. Effect of molecular packing of zinc(II) porphyrins on the performance of field-effect transistors. Adv. Nat. Sci. Nanosci. Nanotechnol. 2014, 5, 045012. [Google Scholar] [CrossRef] [Green Version]
- Che, C.; Xiang, H.; Chui, S.S.; Xu, Z.; Roy, V.A.L.; Yan, J.J.; Fu, W.; Lai, P.T.; Williams, I.D. A High-Performance Organic Field-Effect Transistor Based on Platinum(II) Porphyrin: Peripheral Substituents on Porphyrin Ligand Significantly Affect Film Structure and Charge Mobility. Chem. Asian J. 2008, 3, 1092–1103. [Google Scholar] [CrossRef] [PubMed]
- Seol, M.; Choi, S.; Kim, C.; Moon, D.; Choi, Y. Porphyrin–Silicon Hybrid Field-Effect Transistor with Individually Addressable Top-gate Structure. ACS Nano 2012, 6, 183–189. [Google Scholar] [CrossRef] [PubMed]
- El Abbassi, M.; Zwick, P.; Rates, A.; Stefani, D.; Prescimone, A.; Mayor, M.; Van Der Zant, H.S.J.; Dulić, D. Unravelling the conductance path through single-porphyrin junctions. Chem. Sci. 2019, 10, 8299–8305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feixas, F.; Solà, M.; Swart, M. Chemical bonding and aromaticity in metalloporphyrins. Can. J. Chem. 2009, 87, 1063–1073. [Google Scholar] [CrossRef]
- Senge, M.O.; Fazekas, M.; Notaras, E.G.A.; Blau, W.J.; Zawadzka, M.; Locos, O.B.; Ni Mhuircheartaigh, E.M. Nonlinear Optical Properties of Porphyrins. Adv. Mater. 2007, 19, 2737–2774. [Google Scholar] [CrossRef]
- Tran-Thi, T. Assemblies of phthalocyanines with porphyrins and porphyrazines: Ground and excited state optical properties. Coord. Chem. Rev. 1997, 160, 53–91. [Google Scholar] [CrossRef]
- Saito, S.; Osuka, A. Expanded Porphyrins: Intriguing Structures, Electronic Properties, and Reactivities. Angew. Chem. Int. Ed. 2011, 50, 4342–4373. [Google Scholar] [CrossRef]
- Adinehnia, M.; Eskelsen, J.R.; Hipps, K.W.; Mazur, U. Mechanical behavior of crystalline ionic porphyrins. J. Porphyr. Phthalocyanines 2019, 23, 154–165. [Google Scholar] [CrossRef] [Green Version]
- Phillips, J.N. Chapter II—Physico-chemical Properties of Porphyrins. In Comprehensive Biochemistry; Florkin, M., Stotz, E.H., Eds.; Elsevier: Amsterdam, The Netherlands, 1963; Volume 9, pp. 34–72. [Google Scholar]
- Jensen, K.P.; Ryde, U. Comparison of the Chemical Properties of Iron and Cobalt Porphyrins and Corrins. ChemBioChem 2003, 4, 413–424. [Google Scholar] [CrossRef] [PubMed]
- Brothers, P.J.; Collman, J.P. The organometallic chemistry of transition-metal porphyrin complexes. Acc. Chem. Res. 1986, 19, 209–215. [Google Scholar] [CrossRef]
- Shubina, T.E. Computational Studies on Properties, Formation, and Complexation of M(II)-Porphyrins. In Advances in Inorganic Chemistry; van Eldik, R., Harvey, J., Eds.; Academic Press: New York, NY, USA, 2010; Volume 62, pp. 261–299. [Google Scholar]
- Baerends, E.; Ricciardi, G.; Rosa, A.; Van Gisbergen, S. A DFT/TDDFT interpretation of the ground and excited states of porphyrin and porphyrazine complexes. Coord. Chem. Rev. 2002, 230, 5–27. [Google Scholar] [CrossRef]
- Kepenekian, M.; Calborean, A.; Vetere, V.; Le Guennic, B.; Robert, V.; Maldivi, P. Toward Reliable DFT Investigations of Mn-Porphyrins through CASPT2/DFT Comparison. J. Chem. Theory Comput. 2011, 7, 3532–3539. [Google Scholar] [CrossRef] [PubMed]
- Aydin, M. Geometric and Electronic Properties of Porphyrin and its Derivatives. In Applications of Molecular Spectroscopy to Current Research in the Chemical and Biological Sciences; IntechOpen: Rijeka, Croatia, 2016; p. 10. [Google Scholar]
- Rappoport, D.; Crawford, N.R.M.; Furche, F.; Burke, K. Which functional should I choose? In Computational Inorganicand Bioinorganic Chemistry; Solomon, E.I., Scott, R.A., King, B.R., Eds.; Wiley John & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Liao, M.-S.; Lu, Y.; Scheiner, S. Performance assessment of density-functional methods for study of charge-transfer complexes. J. Comput. Chem. 2003, 24, 623–631. [Google Scholar] [CrossRef] [PubMed]
- De Visser, S.P.; Stillman, M.J. Challenging Density Functional Theory Calculations with Hemes and Porphyrins. Int. J. Mol. Sci. 2016, 17, 519. [Google Scholar] [CrossRef] [Green Version]
- Kratzer, P.; Neugebauer, J. The Basics of Electronic Structure Theory for Periodic Systems. Front. Chem. 2019, 7, 106. [Google Scholar] [CrossRef] [Green Version]
- Tosoni, S.; Tuma, C.; Sauer, J.; Civalleri, B.; Ugliengo, P. A comparison between plane wave and Gaussian-type orbital basis sets for hydrogen bonded systems: Formic acid as a test case. J. Chem. Phys. 2007, 127, 154102. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Physics: Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; Vande Vondele, J. cp2k: Atomistic simulations of condensed matter systems. Wires Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef] [Green Version]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Keith, R.; Payne, M.C. First principles methods using CASTEP. Z. Für Krist. Cryst. Mater. 2009, 220, 567. [Google Scholar] [CrossRef] [Green Version]
- Delley, B. DMol, a standard tool for density functional calculations: Review and advances. In Theoretical and Computational Chemistry; Seminario, J.M., Politzer, P., Eds.; Elsevier: Amsterdam, The Netherlands, 1995; Volume 2, pp. 221–254. [Google Scholar]
- Soler, J.M.; Artacho, E.; Gale, J.D.; Garcia, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order- N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef] [Green Version]
- Hutter, J.; Marcella, I. CPMD: Car-Parrinello molecular dynamics. Z. Für Krist. Cryst. Mater. 2009, 220, 549. [Google Scholar] [CrossRef]
- Adinehnia, M.; Borders, B.; Ruf, M.; Chilukuri, B.; Hipps, K.W.; Mazur, U. Comprehensive structure--function correlation of photoactive ionic π-conjugated supermolecular assemblies: An experimental and computational study. J. Mater. Chem. C 2016, 4, 10223–10239. [Google Scholar] [CrossRef]
- Klimes, J.; Bowler, D.R.; Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 2009, 22, 022201. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207. [Google Scholar] [CrossRef] [Green Version]
- Brothers, E.N.; Izmaylov, A.F.; Normand, J.O.; Barone, V.; Scuseria, G.E. Accurate solid-state band gaps via screened hybrid electronic structure calculations. J. Chem. Phys. 2008, 129, 11102. [Google Scholar] [CrossRef] [PubMed]
- Klimes, J.; Bowler, D.R.; Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef] [Green Version]
- Borders, B.; Adinehnia, M.; Chilukuri, B.; Ruf, M.; Hipps, K.W.; Mazur, U. Tuning the optoelectronic characteristics of ionic organic crystalline assemblies. J. Mater. Chem. C 2018, 6, 4041–4056. [Google Scholar] [CrossRef]
- Tian, X.; Lin, C.; Zhong, Z.; Li, X.; Xu, X.; Liu, J.; Kang, L.; Chai, G.; Yao, J. Effect of Axial Coordination of Iron Porphyrin on Their Nanostructures and Photocatalytic Performance. Cryst. Growth Des. 2019, 19, 3279–3287. [Google Scholar] [CrossRef]
- Krasnov, P.O.; Kuzubov, A.A.; Kholtobina, A.S.; Kovaleva, E.; Kuzubova, M.V. Optical charge transfer transitions in supramolecular fullerene and porphyrin compounds. J. Struct. Chem. 2016, 57, 642–648. [Google Scholar] [CrossRef]
- Boyd, P.D.W.; Hodgson, M.C.; Rickard, C.E.F.; Oliver, A.G.; Chaker, L.; Brothers, P.J.; Bolskar, R.D.; Tham, F.S.; Reed, C.A. Selective Supramolecular Porphyrin/Fullerene Interactions1. J. Am. Chem. Soc. 1999, 121, 10487–10495. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Gajdoš, M.; Hümmer, K.; Kresse, G.; Furthmüller, J.; Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 2006, 73, 045112. [Google Scholar] [CrossRef] [Green Version]
- Hamad, S.; Hernandez, N.C.; Aziz, A.; Ruiz-Salvador, A.; Calero, S.; Grau-Crespo, R. Electronic structure of porphyrin-based metal–organic frameworks and their suitability for solar fuel production photocatalysis. J. Mater. Chem A 2015, 3, 23458–23465. [Google Scholar] [CrossRef] [Green Version]
- Fateeva, A.; Chater, P.A.; Ireland, C.P.; Tahir, A.A.; Khimyak, Y.Z.; Wiper, P.V.; Darwent, J.R.; Rosseinsky, M.J. A Water-Stable Porphyrin-Based Metal-Organic Framework Active for Visible-Light Photocatalysis. Angew. Chem. Int. Ed. 2012, 51, 7440–7444. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhou, W.; Liu, J.; Howard, I.; Kilibarda, G.; Schlabach, S.; Coupry, D.; Addicoat, M.; Yoneda, S.; Tsutsui, Y.; et al. Photoinduced Charge-Carrier Generation in Epitaxial MOF Thin Films: High Efficiency as a Result of an Indirect Electronic Band Gap? Angew. Chem. Int. Ed. 2015, 54, 7441–7445. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhou, W.; Liu, J.; Fujimori, Y.; Higashino, T.; Imahori, H.; Jiang, X.; Zhao, J.; Sakurai, T.; Hattori, Y.; et al. A new class of epitaxial porphyrin metal-organic framework thin films with extremely high photocarrier generation efficiency: Promising materials for all-solid-state solar cells. J. Mater. Chem. A 2016, 4, 12739–12747. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef] [Green Version]
- Posligua, V.; Aziz, A.; Haver, R.; Peeks, M.D.; Anderson, H.L.; Grau-Crespo, R. Band Structures of Periodic Porphyrin Nanostructures. J. Phys. Chem. C 2018, 122, 23790–23798. [Google Scholar] [CrossRef] [Green Version]
- Allec, S.I.; Ilawe, N.V.; Wong, B.M. Unusual Bandgap Oscillations in Template-Directed Ï€-Conjugated Porphyrin Nanotubes. J. Phys. Chem. Lett. 2016, 7, 2362–2367. [Google Scholar] [CrossRef] [Green Version]
- Singh, H.K.; Kumar, P.; Waghmare, U.V. Theoretical Prediction of a Stable 2D Crystal of Vanadium Porphyrin: A Half-Metallic Ferromagnet. J. Phys. Chem. C 2015, 119, 25657–25662. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Zeng, B.; Li, M.; Long, M. First-principles predictions on charge mobility and half-metallicity in two dimensional metal coordination polyporphyrin sheets. Org. Electron. 2017, 49, 45. [Google Scholar] [CrossRef]
- Yamaguchi, Y. Theoretical study of two-dimensionally fused zinc porphyrins: DFT calculations. Int. J. Quantum Chem. 2009, 109, 1584–1597. [Google Scholar] [CrossRef]
- Kumar, S.; Choudhuri, I.; Pathak, B. An atomically thin ferromagnetic half-metallic pyrazine-fused Mn-porphyrin sheet: A slow spin relaxation system. J. Mater. Chem. C 2016, 4, 9069–9077. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Aryasetiawan, F.; Lichtenstein, A.I. First-principles calculations of the electronic structure and spectra of strongly correlated systems: Dynamical mean-field theory. J. Phys. Condens. Matter 1997, 9, 767–808. [Google Scholar] [CrossRef] [Green Version]
- Gao, G.; Kang, H.S. Engineering of the electronic structures of metal-porphyrin tapes and metal-hexaphyrin tapes: A first-principles study. Chem. Phys. 2010, 369, 66. [Google Scholar] [CrossRef]
- Medforth, C.J.; Senge, M.O.; Smith, K.M.; Sparks, L.D.; Shelnutt, J.A. Nonplanar distortion modes for highly substituted porphyrins. J. Am. Chem. Soc. 1992, 114, 9859–9869. [Google Scholar] [CrossRef]
- Otsuki, J. STM studies on porphyrins. Coord. Chem. Rev. 2010, 254, 2311–2341. [Google Scholar] [CrossRef]
- Zotti, L.A.; Teobaldi, G.; Hofer, W.A.; Auwärter, W.; Weber-Bargioni, A.; Barth, J.V. Ab-initio calculations and STM observations on tetrapyridyl and Fe(II)-tetrapyridyl-porphyrin molecules on Ag (1 1 1). Surf. Sci. 2007, 601, 2409–2414. [Google Scholar] [CrossRef]
- Chen, X.; Lei, S.; Lotze, C.; Czekelius, C.; Paulus, B.; Franke, K.J. Conformational adaptation and manipulation of manganese tetra(4-pyridyl)porphyrin molecules on Cu(111). J. Chem. Phys. 2017, 146, 092316. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Zheng, X.; Kuang, G.; Wang, W.; Zhu, L.; Pang, R.; Shi, X.; Shang, X.; Huang, X.; Liu, P.N.; et al. Single-Molecule Investigations of Conformation Adaptation of Porphyrins on Surfaces. J. Phys. Chem. Lett. 2017, 8, 1241–1247. [Google Scholar] [CrossRef]
- Rojas, G.; Chen, X.; Bravo, C.; Kim, J.-H.; Kim, J.-S.; Xiao, J.; Dowben, P.A.; Gao, Y.; Zeng, X.C.; Choe, W.; et al. Self-Assembly and Properties of Nonmetalated Tetraphenyl-Porphyrin on Metal Substrates. J. Phys. Chem. C 2010, 114, 9408–9415. [Google Scholar] [CrossRef] [Green Version]
- Hamprecht, F.A.; Cohen, A.J.; Tozer, D.J.; Handy, N.C. Development and assessment of new exchange-correlation functionals. J. Chem. Phys. 1998, 109, 6264–6271. [Google Scholar] [CrossRef]
- Boese, A.D.; Doltsinis, N.L.; Handy, N.C.; Sprik, M. New generalized gradient approximation functionals. J. Chem. Phys. 2000, 112, 1670–1678. [Google Scholar] [CrossRef]
- Lepper, M.; Köbl, J.; Schmitt, T.; Gurrath, M.; Siervo, A.d.; Schneider, M.A.; Steinrück, H.; Meyer, B.; Marbach, H.; Hieringer, W. “Inverted” porphyrins: A distorted adsorption geometry of free-base porphyrins on Cu (111). Chem. Commun. 2017, 53, 8207–8210. [Google Scholar] [CrossRef] [PubMed]
- Houwaart, T.; Le Bahers, T.; Sautet, P.; Auwarter, W.; Seufert, K.; Barth, J.V.; Bocquet, M. Scrutinizing individual CoTPP molecule adsorbed on coinage metal surfaces from the interplay of STM experiment and theory. Surf. Sci. 2015, 635, 108–114. [Google Scholar] [CrossRef]
- Weber-Bargioni, A.; Auwärter, W.; Klappenberger, F.; Reichert, J.; Lefrançois, S.; Strunskus, T.; Wöll, C.; Schiffrin, A.; Pennec, Y.; Barth, J.V. Visualizing the Frontier Orbitals of a Conformationally Adapted Metalloporphyrin. ChemPhysChem 2008, 9, 89–94. [Google Scholar] [CrossRef]
- Donovan, P.; Robin, A.; Dyer, M.S.; Persson, M.; Raval, R. Unexpected Deformations Induced by Surface Interaction and Chiral Self-Assembly of CoII-Tetraphenylporphyrin (Co-TPP) Adsorbed on Cu (110): A Combined STM and Periodic DFT Study. Chem. A Eur. J. 2010, 16, 11641–11652. [Google Scholar] [CrossRef]
- Auwärter, W.; Seufert, K.; Klappenberger, F.; Reichert, J.; Weber-Bargioni, A.; Verdini, A.; Cvetko, D.; Dell’Angela, M.; Floreano, L.; Cossaro, A.; et al. Site-specific electronic and geometric interface structure of Co-tetraphenyl-porphyrin layers on Ag(111). Phys. Rev. B 2010, 81, 245403. [Google Scholar] [CrossRef]
- Fatayer, S.; Veiga, R.G.A.; Prieto, M.J.; Perim, E.; Landers, R.; Miwa, R.H.; De Siervo, A. Self-assembly of NiTPP on Cu(111): A transition from disordered 1D wires to 2D chiral domains. Phys. Chem. Chem. Phys. 2015, 17, 18344–18352. [Google Scholar] [CrossRef] [Green Version]
- Hötger, D.; Abufager, P.F.; Morchutt, C.; Alexa, P.; Grumelli, D.E.; Dreiser, J.; Stepanow, S.; Gambardella, P.; Busnengo, H.F.; Etzkorn, M.; et al. On-surface transmetalation of metalloporphyrins. Nanoscale 2018, 10, 21116–21122. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Moreno-López, J.C.; Mowbray, D.J.; Paz, A.P.; Ferreira, R.C.D.C.; Dos Santos, A.C.; Ayala, P.; De Siervo, A. Roles of Precursor Conformation and Adatoms in Ullmann Coupling: An Inverted Porphyrin on Cu(111). Chem. Mater. 2019, 31, 3009–3017. [Google Scholar] [CrossRef]
- Mielke, J.; Hanke, F.; Peters, M.V.; Hecht, S.; Persson, M.; Grill, L. Adatoms underneath Single Porphyrin Molecules on Au(111). J. Am. Chem. Soc. 2015, 137, 1844–1849. [Google Scholar] [CrossRef] [PubMed]
- Bassiouk, M.; Alvarez-Zauco, E.; Basiuk, V.A. Theoretical analysis of the effect of surface defects on porphyrin adsorption and self-assembly on graphite. J. Comput. Nanosci. 2012, 9, 532–540. [Google Scholar] [CrossRef]
- Catellani, A.; Calzolari, A. Functionalization of SiC(110) Surfaces via Porphyrin Adsorption: Ab Initio Results. J. Phys. Chem. C 2012, 116, 886–892. [Google Scholar] [CrossRef]
- El Garah, M.; Makoudi, Y.; Palmino, F.; Duverger, E.; Sonnet, P.; Chaput, L.; Gourdon, A.; Cherioux, F. STM and DFT Investigations of Isolated Porphyrin on a Silicon-Based Semiconductor at Room Temperature. ChemPhysChem 2009, 10, 3190–3193. [Google Scholar] [CrossRef]
- Boukari, K.; Sonnet, P.; Duverger, E. DFT-D Studies of Single Porphyrin Molecule on Doped Boron Silicon Surfaces. ChemPhysChem 2012, 13, 3945–3951. [Google Scholar] [CrossRef]
- Chin, Y.; Panduwinata, D.; Sintic, M.; Sum, T.J.; Hush, N.S.; Crossley, M.J.; Reimers, J.R. Atomic-Resolution Kinked Structure of an Alkylporphyrin on Highly Ordered Pyrolytic Graphite. J. Phys. Chem. Lett. 2011, 2, 62–66. [Google Scholar] [CrossRef]
- Dapprich, S.; Komáromi, I.; Byun, K.S.; Morokuma, K.; Frisch, M.J. A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives1Dedicated to Professor Keiji Morokuma in celebration of his 65th birthday.1. J. Mol. Struct. 1999, 461, 1–21. [Google Scholar] [CrossRef]
- Reimers, J.R.; Panduwinata, D.; Visser, J.; Chin, Y.; Tang, C.; Goerigk, L.; Ford, M.J.; Baker, M.; Sum, T.J.; Coenen, M.J.J.; et al. From Chaos to Order: Chain-Length Dependence of the Free Energy of Formation of Meso-tetraalkylporphyrin Self-Assembled Monolayer Polymorphs. J. Phys. Chem. C 2016, 120, 1739–1748. [Google Scholar] [CrossRef] [Green Version]
- Fanetti, M.; Calzolari, A.; Vilmercati, P.; Castellarin-Cudia, C.; Borghetti, P.; Di Santo, G.; Floreano, L.; Verdini, A.; Cossaro, A.; Vobornik, I.; et al. Structure and Molecule–Substrate Interaction in a Co-octaethyl Porphyrin Monolayer on the Ag(110) Surface. J. Phys. Chem. C 2011, 115, 11560–11568. [Google Scholar] [CrossRef]
- Chilukuri, B.; Mazur, U.; Hipps, K.W. Effect of dispersion on surface interactions of cobalt(II) octaethylporphyrin monolayer on Au(111) and HOPG(0001) substrates: A comparative first principles study. Phys. Chem. Chem. Phys. 2014, 16, 14096–14107. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Tada, K.; Maeda, Y.; Ozaki, H.; Tanaka, S.; Yamazaki, S. Theoretical investigation on the interaction between RhIII octaethylporphyrin and a graphite basal surface: A comparison study of DFT, DFT-D, and AFM. Phys. Chem. Chem. Phys. 2018, 20, 20235–20246. [Google Scholar] [CrossRef] [PubMed]
- Sena, A.M.P.; Brazdova, V.; Bowler, D.R. Density functional theory study of the iron-based porphyrin haem(b) on the Si(111):H surface. Phys. Rev. B 2009, 79, 245404/1–245404/7. [Google Scholar] [CrossRef]
- Tersoff, J.; Hamann, D.R. Theory of the scanning tunneling microscope. Phys. Rev. B 1985, 31, 805–813. [Google Scholar] [CrossRef] [PubMed]
- Hanke, F.; Haq, S.; Raval, R.; Persson, M. Heat-to-connect: Surface commensurability directs organometallic one-dimensional self-assembly. ACS Nano 2011, 5, 9093–9103. [Google Scholar] [CrossRef]
- Dyer, M.S.; Robin, A.; Haq, S.; Raval, R.; Persson, M.; Klimeš, J. Understanding the Interaction of the Porphyrin Macrocycle to Reactive Metal Substrates: Structure, Bonding, and Adatom Capture. ACS Nano 2011, 5, 1831–1838. [Google Scholar] [CrossRef]
- Miller, D.P.; Hooper, J.; Simpson, S.; Costa, P.S.; Tyminska, N.; McDonnell, S.M.; Bennett, J.A.; Enders, A.; Zurek, E. Electronic Structure of Iron Porphyrin Adsorbed to the Pt(111) Surface. J. Phys. Chem. C 2016, 120, 29173–29181. [Google Scholar] [CrossRef]
- Leung, K.; Rempe, S.B.; Schultz, P.A.; Sproviero, E.M.; Batista, V.S.; Chandross, M.E.; Medforth, C.J. Density Functional Theory and DFT+U Study of Transition Metal Porphines Adsorbed on Au(111) Surfaces and Effects of Applied Electric Fields. J. Am. Chem. Soc. 2006, 128, 3659–3668. [Google Scholar] [CrossRef] [Green Version]
- Berland, K.; Hyldgaard, P. Exchange functional that tests the robustness of the plasmon description of the van der Waals density functional. Phys. Rev. B 2014, 89, 035412. [Google Scholar] [CrossRef] [Green Version]
- Nandi, G.; Chilukuri, B.; Hipps, K.W.; Mazur, U. Surface directed reversible imidazole ligation to nickel (II) octaethylporphyrin at the solution/solid interface: A single molecule level study. Phys. Chem. Chem. Phys. 2016, 18, 20819–20829. [Google Scholar] [CrossRef] [PubMed]
- Gurdal, Y.; Hutter, J.; Iannuzzi, M. Insight into (Co)Pyrphyrin Adsorption on Au(111): Effects of Herringbone Reconstruction and Dynamics of Metalation. J. Phys. Chem. C 2017, 121, 11416–11427. [Google Scholar] [CrossRef]
- Gurdal, Y. Theoretical investigation of metalated and unmetalated pyrphyrins immobilized on Ag(111) surface. J. Incl. Phenom. Macrocycl. Chem. 2019, 95, 273–283. [Google Scholar] [CrossRef]
- Jahanbekam, A.; Chilukuri, B.; Mazur, U.; Hipps, K.W. Kinetically Trapped Two-Component Self-Assembled Adlayer. J. Phys. Chem. C 2015, 119, 25364–25376. [Google Scholar] [CrossRef]
- Chilukuri, B.; Mazur, U.; Hipps, K.W. Cooperativity and coverage dependent molecular desorption in self-assembled monolayers: Computational case study with coronene on Au (111) and HOPG. Phys. Chem. Chem. Phys. 2019, 21, 10505–10513. [Google Scholar] [CrossRef]
- Touzeau, J.; Barbault, F.; Maurel, F.; Seydou, M. Insights on porphyrin-functionalized graphene: Theoretical study of substituent and metal-center effects on adsorption. Chem. Phys. Lett. 2018, 713, 172–179. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, K. A nearly perfect spin filter and a spin logic gate based on a porphyrin/graphene hybrid material. Phys. Chem. Chem. Phys. 2018, 20, 3997–4004. [Google Scholar] [CrossRef]
- Meir, Y.; Wingreen, N.S. Landauer formula for the current through an interacting electron region. Phys. Rev. Lett 1992, 68, 2512–2515. [Google Scholar] [CrossRef]
- Zhao, J.; Ding, Y. Functionalization of Single-Walled Carbon Nanotubes with Metalloporphyrin Complexes: A Theoretical Study. J. Phys. Chem. C 2008, 112, 11130–11134. [Google Scholar] [CrossRef]
- Correa, J.D.; Orellana, W. Optical response of carbon nanotubes functionalized with (free-base, Zn) porphyrins, and phthalocyanines: A DFT study. Phys. Rev. B 2012, 86, 125417. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Tagle, I.; Orellana, W. Iron porphyrin attached to single-walled carbon nanotubes: Electronic and dynamical properties from ab-initio calculations. Phys. Rev. B 2010, 82, 115406. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Ding, Y. Theoretical studies of chemical functionalization of the (8,0) boron nitride nanotube with various metalloporphyrin MP (M=Fe, Co, Ni, Cu, and Zn) complexes. Mater. Chem. Phys. 2009, 116, 21–27. [Google Scholar] [CrossRef]
- Gomez, T.; Zarate, X.; Schott, E.; Arratia-Perez, R. Role of the main adsorption modes in the interaction of the dye [COOH–TPP-Zn(II)] on a periodic TiO2 slab exposing a rutile (110) surface in a dye-sensitized solar cell. RSC Adv. 2014, 4, 9639–9646. [Google Scholar] [CrossRef]
- Lin, Y.; Zhu, C.; Jiang, Z.; Zhao, Y.; Wang, Q.; Zhang, R.; Lin, S.H. Enhanced photovoltaic performance of dye-sensitized solar cells by the adsorption of Zn-porphyrin dye molecule on TiO2 surfaces. J. Alloy. Compd. 2019, 794, 35–44. [Google Scholar] [CrossRef]
- Lovat, G.; Forrer, D.; Abadia, M.; Dominguez, M.; Casarin, M.; Rogero, C.; Vittadini, A.; Floreano, L. Hydrogen capture by porphyrins at the TiO2(110) surface. Phys. Chem. Chem. Phys. 2015, 17, 30119–30124. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Fan, Q.; Han, Y.; Martínez, J.I.; Martín-Gago, J.A.; Wang, W.; Ju, H.; Gottfried, J.M.; Zhu, J. Metalation of tetraphenylporphyrin with nickel on a TiO2(110)-1 × 2 surface. Nanoscale 2015, 8, 1123–1132. [Google Scholar] [CrossRef] [Green Version]
- Lewis, J.P.; Jelinek, P.; Ortega, J.; Demkov, A.A.; Trabada, D.G.; Haycock, B.; Wang, H.; Adams, G.; Tomfohr, J.K.; Abad, E.; et al. Advances and applications in the FIREBALL ab initio tight-binding molecular-dynamics formalism. Phys. Status Solidi 2011, 248, 1989–2007. [Google Scholar] [CrossRef]
- Spoerke, E.D.; Small, L.J.; Foster, M.E.; Wheeler, J.; Ullman, A.M.; Stavila, V.; Rodriguez, M.; Allendorf, M.D. MOF-Sensitized Solar Cells Enabled by a Pillared Porphyrin Framework. J. Phys. Chem. C 2017, 121, 4816–4824. [Google Scholar] [CrossRef]
- Xie, M.; Bai, F.; Wang, J.; Zheng, Y.; Lin, Z. Theoretical investigations on the unsymmetrical effect of β-link Zn-porphyrin sensitizers on the performance for dye-sensitized solar cells. Phys. Chem. Chem. Phys. 2018, 20, 3741–3751. [Google Scholar] [CrossRef]
- Niskanen, M.; Kuisma, M.; Cramariuc, O.; Golovanov, V.; Hukka, T.I.; Tkachenko, N.; Rantala, T.T. Porphyrin adsorbed on the (1010) surface of the wurtzite structure of ZnO—conformation induced effects on the electron transfer characteristics. Phys. Chem. Chem. Phys. 2013, 15, 17408–17418. [Google Scholar] [CrossRef]
- Torres, A.; Amaya Suarez, J.; Remesal, E.R.; Marquez, A.M.; Fernandez Sanz, J.; Rincon Canibano, C. Adsorption of Prototypical Asphaltenes on Silica: First-Principles DFT Simulations Including Dispersion Corrections. J. Phys. Chem. B 2017. Ahead of Print. [Google Scholar] [CrossRef] [PubMed]
- Quinn, T.; Choudhury, P. Direct oxidation of methane to methanol on single-site copper-oxo species of copper porphyrin functionalized graphene: A DFT study. Mol. Catal. 2017, 431, 9–14. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef] [Green Version]
- Sheppard, D.; Terrell, R.; Henkelman, G. Optimization methods for finding minimum energy paths. J. Chem. Phys. 2008, 128, 134106. [Google Scholar] [CrossRef] [Green Version]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Grill, L.; Dyer, M.; Lafferentz, L.; Persson, M.; Peters, M.V.; Hecht, S. Nano-architectures by covalent assembly of molecular building blocks. Nat. Nanotechnol. 2007, 2, 687–691. [Google Scholar] [CrossRef]
- Shi, K.; Shu, C.; Wang, C.; Wu, X.; Tian, H.; Liu, P. On-Surface Heck Reaction of Aryl Bromides with Alkene on Au(111) with Palladium as Catalyst. Org. Lett. 2017, 19, 2801–2804. [Google Scholar] [CrossRef]
- Shu, C.; Xie, Y.; Wang, A.; Shi, K.; Zhang, W.; Li, D.; Liu, P. On-surface reactions of aryl chloride and porphyrin macrocycles via merging two reactive sites into a single precursor. Chem. Commun. 2018, 54, 12626–12629. [Google Scholar] [CrossRef]
- Wende, H.; Bernien, M.; Luo, J.; Sorg, C.; Ponpandian, N.; Kurde, J.; Miguel, J.; Piantek, M.; Xu, X.; Eckhold, P.; et al. Substrate-induced magnetic ordering and switching of iron porphyrin molecules. Nat. Mater. 2007, 6, 516–520. [Google Scholar] [CrossRef]
- Oppeneer, P.M.; Panchmatia, P.M.; Sanyal, B.; Eriksson, O.; Ali, M.E. Nature of the magnetic interaction between Fe-porphyrin molecules and ferromagnetic surfaces. Prog. Surf. Sci. 2009, 84, 18–29. [Google Scholar] [CrossRef]
- Weber, A.P.; Caruso, A.N.; Vescovo, E.; Ali, M.E.; Tarafder, K.; Janjua, S.Z.; Sadowski, J.T.; Oppeneer, P.M. Magnetic coupling of Fe-porphyrin molecules adsorbed on clean and c (2 × 2) oxygen-reconstructed Co(100) investigated by spin-polarized photoemission spectroscopy. Phys. Rev. B 2013, 87, 184411. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.E.; Sanyal, B.; Oppeneer, P.M. Tuning the Magnetic Interaction between Manganese Porphyrins and Ferromagnetic Co Substrate through Dedicated Control of the Adsorption. J. Phys. Chem. C 2009, 113, 14381–14383. [Google Scholar] [CrossRef]
- Chylarecka, D.; Kim, T.K.; Tarafder, K.; Müller, K.; Gödel, K.; Czekaj, I.; Wäckerlin, C.; Cinchetti, M.; Ali, M.E.; Piamonteze, C.; et al. Indirect Magnetic Coupling of Manganese Porphyrin to a Ferromagnetic Cobalt Substrate. J. Phys. Chem. C 2011, 115, 1295–1301. [Google Scholar] [CrossRef]
- Waeckerlin, C.; Maldonado, P.; Arnold, L.; Shchyrba, A.; Girovsky, J.; Nowakowski, J.; Ali, M.E.; Haehlen, T.; Baljozovic, M.; Siewert, D.; et al. Magnetic exchange coupling of a synthetic Co(II)-complex to a ferromagnetic Ni substrate. Chem. Commun. 2013, 49, 10736–10738. [Google Scholar] [CrossRef] [Green Version]
- Hermanns, C.F.; Tarafder, K.; Bernien, M.; Kruger, A.; Chang, Y.; Oppeneer, P.M.; Kuch, W. Magnetic coupling of porphyrin molecules through graphene. Adv. Mater. 2013, 25, 3473–3477. [Google Scholar] [CrossRef]
- Lamoen, N.; Ballone, N.; Parrinello, N. Electronic structure, screening, and charging effects at a metal/organic tunneling junction: A first-principles study. Phys. Rev. B 1996, 54, 5097–5105. [Google Scholar] [CrossRef]
- Picozzi, S.; Pecchia, A.; Gheorghe, M.; Di Carlo, A.; Lugli, P.; Delley, B.; Elstner, M. Organic/metal interfaces: An ab initio study of their structural and electronic properties. Surf. Sci. 2004, 566, 628–632. [Google Scholar] [CrossRef]
- Long, M.; Chen, K.; Wang, L.; Qing, W.; Zou, B.S.; Shuai, Z. Negative differential resistance behaviors in porphyrin molecular junctions modulated with side groups. Appl. Phys. Lett. 2008, 92, 243303. [Google Scholar] [CrossRef] [Green Version]
- An, Y.; Yang, Z.; Ratner, M.A. High-efficiency switching effect in porphyrin-ethyne-benzene conjugates. J. Chem. Phys. 2011, 135, 044706. [Google Scholar] [CrossRef]
- Liu, Z.; Wei, S.; Yoon, H.; Adak, O.; Ponce, I.; Jiang, Y.; Jang, W.; Campos, L.M.; Venkataraman, L.; Neaton, J.B. Control of Single-Molecule Junction Conductance of Porphyrins via a Transition-Metal Center. Nano Lett. 2014, 14, 5365–5370. [Google Scholar] [CrossRef]
- Stein, T.; Eisenberg, H.; Kronik, L.; Baer, R. Fundamental Gaps in Finite Systems from Eigenvalues of a Generalized Kohn-Sham Method. Phys. Rev. Lett. 2010, 105, 266802. [Google Scholar] [CrossRef] [PubMed]
- Quek, S.Y.; Venkataraman, L.; Choi, H.J.; Louie, S.G.; Hybertsen, M.S.; Neaton, J.B. Amine−Gold Linked Single-Molecule Circuits: Experiment and Theory. Nano Lett. 2007, 7, 3477–3482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quek, S.Y.; Choi, H.J.; Louie, S.G.; Neaton, J.B. Length Dependence of Conductance in Aromatic Single-Molecule Junctions. Nano Lett. 2009, 9, 3949–3953. [Google Scholar] [CrossRef] [PubMed]
- Cho, W.J.; Cho, Y.; Min, S.K.; Kim, W.Y.; Kim, K.S. Chromium Porphyrin Arrays as Spintronic Devices. J. Am. Chem. Soc. 2011, 133, 9364–9369. [Google Scholar] [CrossRef]
- Sedghi, G.; García-Suárez, V.M.; Esdaile, L.J.; Anderson, H.L.; Lambert, C.J.; Martín, S.; Bethell, D.; Higgins, S.J.; Elliott, M.; Bennett, N.; et al. Long-range electron tunnelling in oligo-porphyrin molecular wires. Nat. Nanotechnol. 2011, 6, 517–523. [Google Scholar] [CrossRef]
- García-Suárez, V.M.; Ferradás, R.; Carrascal, D.; Ferrer, J. Universality in the low-voltage transport response of molecular wires physisorbed onto graphene electrodes. Phys. Rev. B 2013, 87. [Google Scholar] [CrossRef] [Green Version]
- Sanders, J.K.; Bampos, N.; Clyde-Watson, Z.; Darling, S.L.; Hawley, J.C.; Kim, H.J.; Webb, S.J. Axial Coordination Chemistry of Metalloporphyrins. In The Porphyrin Handbook; Kadish, K.M., Smith, K.M., Guilard, R., Eds.; Academic: San Diego, CA, USA, 2000; pp. 1–48. [Google Scholar]
- Gottfried, J.M. Surface chemistry of porphyrins and phthalocyanines. Surf. Sci. Rep. 2015, 70, 259–379. [Google Scholar] [CrossRef]
- Gottfried, J.M.; Marbach, H. Surface-Confined Coordination Chemistry with Porphyrins and Phthalocyanines: Aspects of Formation, Electronic Structure, and Reactivity. Zeitschrift Fur Physikalische Chemie-Int. J. Res. Phys. Chem. Chem. Phys. 2009, 223, 53–74. [Google Scholar] [CrossRef]
- Hieringer, W.; Flechtner, K.; Kretschmann, A.; Seufert, K.; Auwärter, W.; Barth, J.V.; Görling, A.; Steinrück, H.; Gottfried, J.M. The surface trans effect: Influence of axial ligands on the surface chemical bonds of adsorbed metalloporphyrins. J. Am. Chem. Soc. 2011, 133, 6206–6222. [Google Scholar] [CrossRef]
- Seufert, K.; Auwärter, W.; Barth, J.V. Discriminative Response of Surface-Confined Metalloporphyrin Molecules to Carbon and Nitrogen Monoxide. J. Am. Chem. Soc. 2010, 132, 18141–18146. [Google Scholar] [CrossRef]
- Friesen, B.A.; Bhattarai, A.; Mazur, U.; Hipps, K.W. Single Molecule Imaging of Oxygenation of Cobalt Octaethylporphyrin at the Solution/Solid Interface: Thermodynamics from Microscopy. J. Am. Chem. Soc. 2012, 134, 14897–14904. [Google Scholar] [CrossRef] [PubMed]
- Wäckerlin, C.; Tarafder, K.; Siewert, D.; Girovsky, J.; Hählen, T.; Iacovita, C.; Kleibert, A.; Nolting, F.; Jung, T.A.; Oppeneer, P.M.; et al. On-surface coordination chemistry of planar molecular spin systems: Novel magnetochemical effects induced by axial ligands. Chem. Sci. 2012, 3, 3154–3160. [Google Scholar] [CrossRef]
- Janet, J.P.; Zhao, Q.; Ioannidis, E.I.; Kulik, H.J. Density functional theory for modelling large molecular adsorbate–surface interactions: A mini-review and worked example. Mol. Simul. 2017, 43, 327–345. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, D.; Parida, P.; Pati, S.K. Spin-state switching of manganese porphyrin by conformational modification. J. Phys. Chem. C 2016, 120, 3625–3634. [Google Scholar] [CrossRef]
- Nguyen, T.Q.; Aspera, S.M.; Nakanishi, H.; Kasai, H. NO adsorption effects on various functional molecular nanowires. Comput. Mater. Sci. 2009, 47, 111–120. [Google Scholar] [CrossRef]
- Nguyen, T.Q.; Escaño, M.C.S.; Shimoji, N.; Nakanishi, H.; Kasai, H. Adsorption of diatomic molecules on iron tape-porphyrin: A comparative study. Phys. Rev. B 2008, 77, 195307. [Google Scholar] [CrossRef]
- Nguyen, T.Q.; Escaño, M.C.S.; Shimoji, N.; Nakanishi, H.; Kasai, H. DFT study on the adsorption of NO on iron tape-porphyrin. Surf. Interface Anal. 2008, 40, 1082–1084. [Google Scholar] [CrossRef]


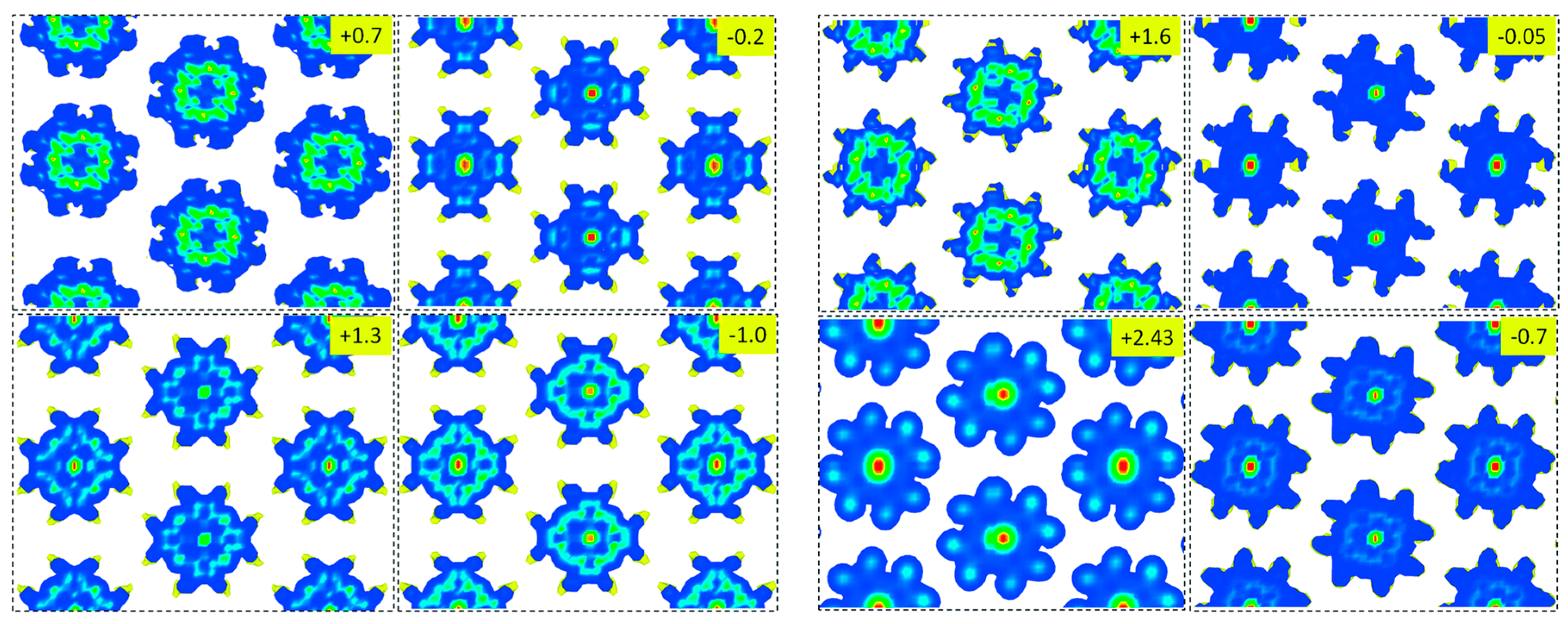

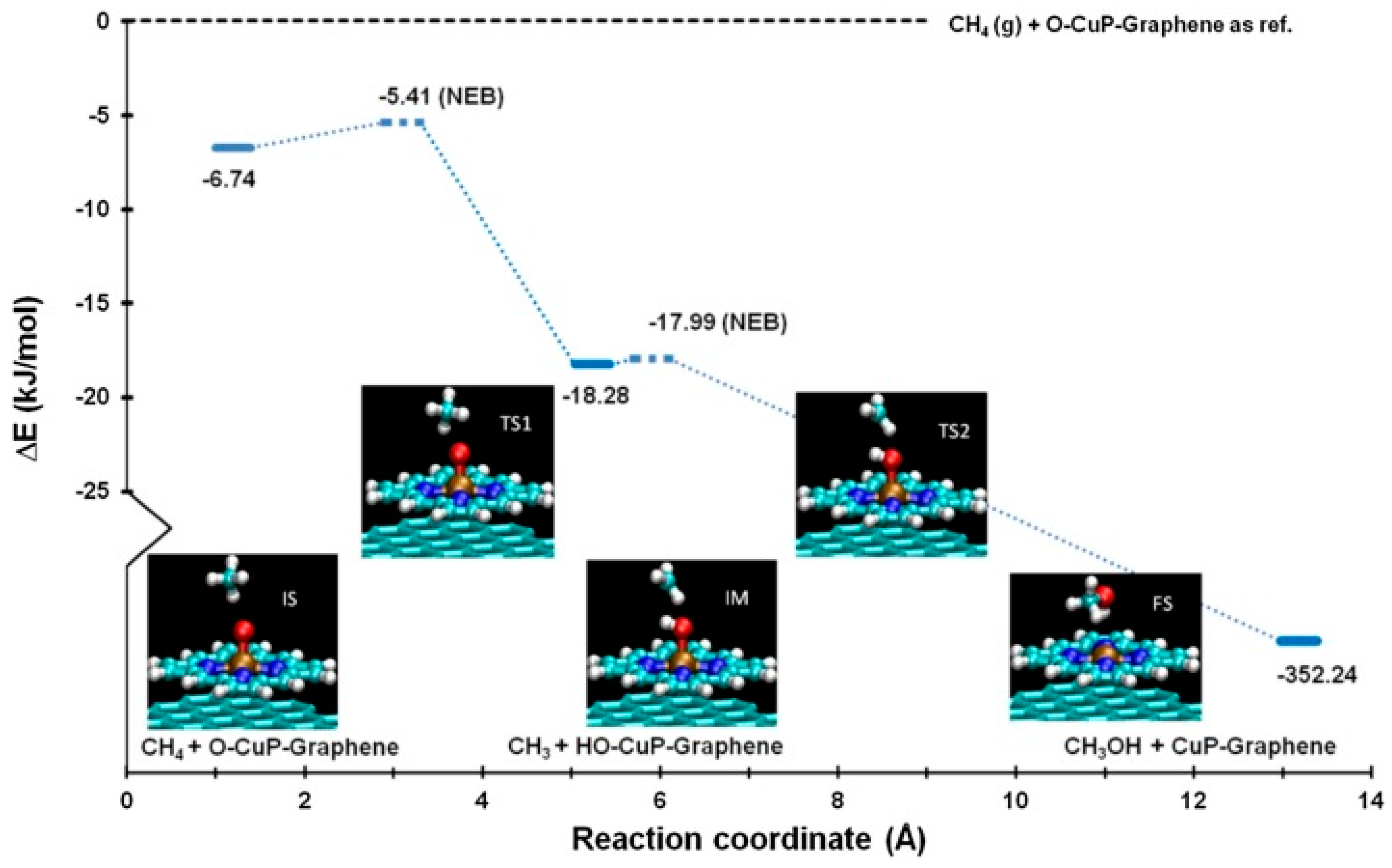
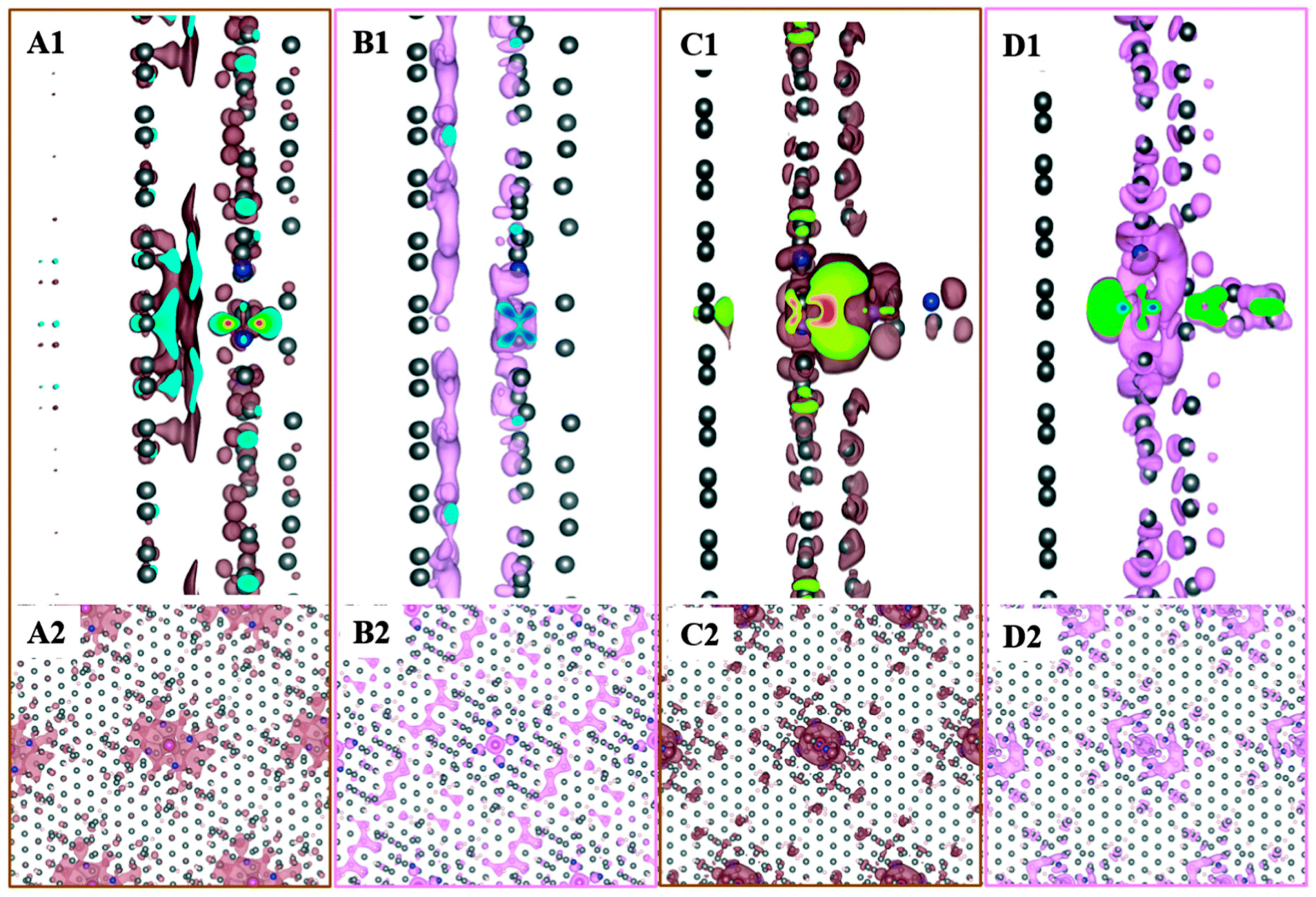
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chilukuri, B.; Mazur, U.; Hipps, K.W. Structure, Properties, and Reactivity of Porphyrins on Surfaces and Nanostructures with Periodic DFT Calculations. Appl. Sci. 2020, 10, 740. https://doi.org/10.3390/app10030740
Chilukuri B, Mazur U, Hipps KW. Structure, Properties, and Reactivity of Porphyrins on Surfaces and Nanostructures with Periodic DFT Calculations. Applied Sciences. 2020; 10(3):740. https://doi.org/10.3390/app10030740
Chicago/Turabian StyleChilukuri, Bhaskar, Ursula Mazur, and K. W. Hipps. 2020. "Structure, Properties, and Reactivity of Porphyrins on Surfaces and Nanostructures with Periodic DFT Calculations" Applied Sciences 10, no. 3: 740. https://doi.org/10.3390/app10030740
APA StyleChilukuri, B., Mazur, U., & Hipps, K. W. (2020). Structure, Properties, and Reactivity of Porphyrins on Surfaces and Nanostructures with Periodic DFT Calculations. Applied Sciences, 10(3), 740. https://doi.org/10.3390/app10030740




