Temperature Dependence of the Fracture Toughness JC of Random Fibrous Material
Abstract
:1. Introduction
2. Experiment Description
2.1. Material
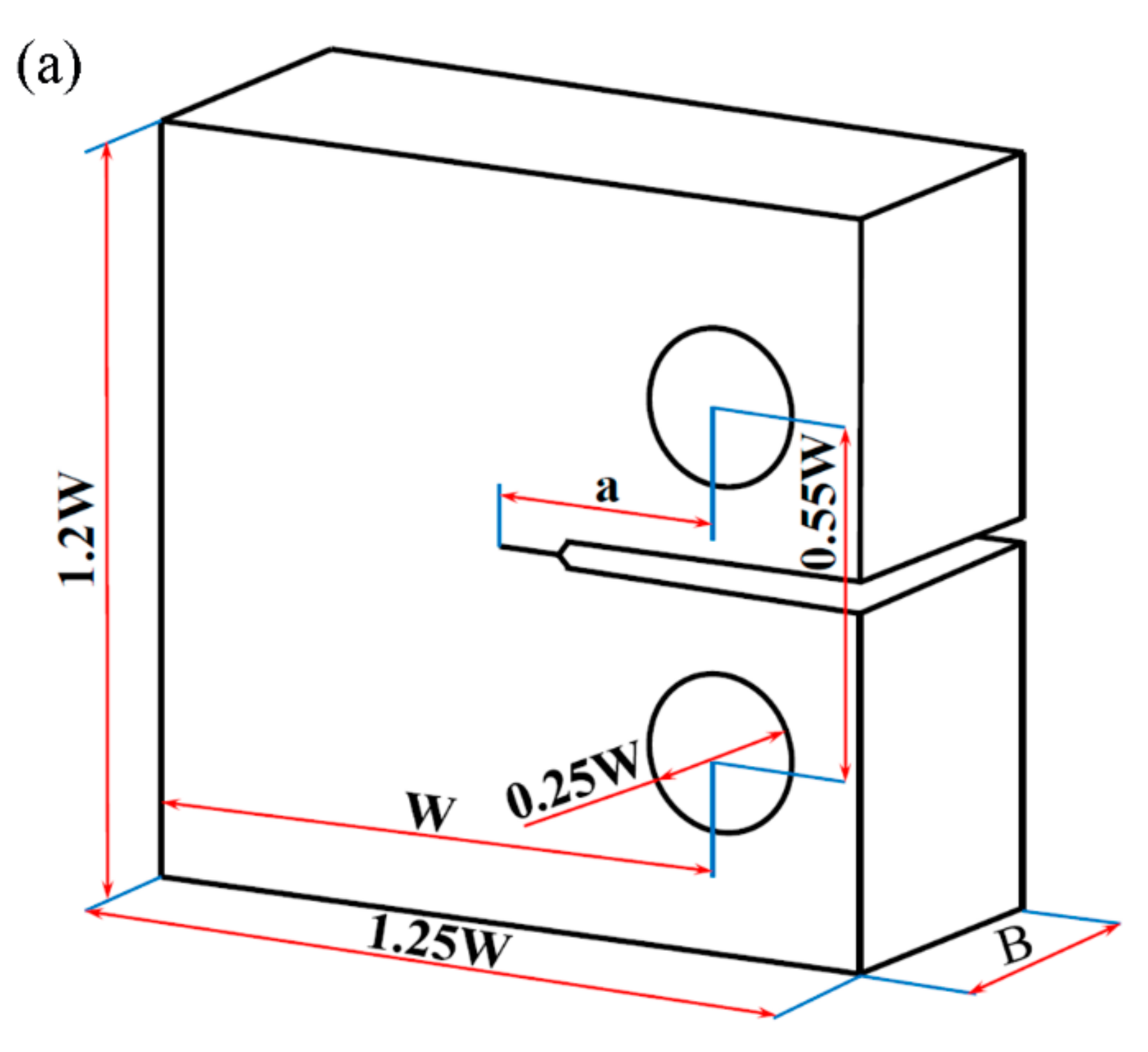
2.2. Compact Tension Specimen
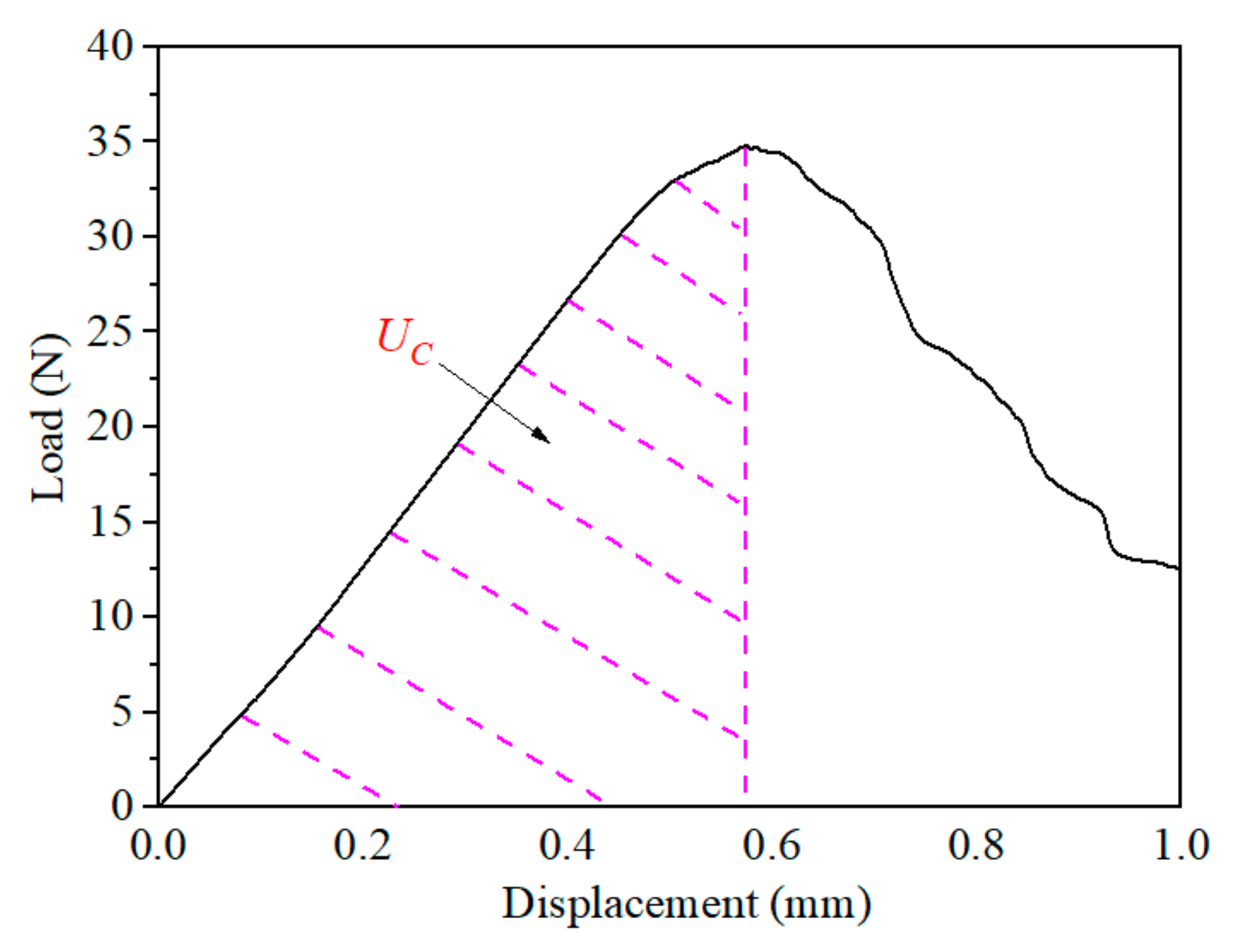
2.3. Experimental Results of the Fracture Toughness
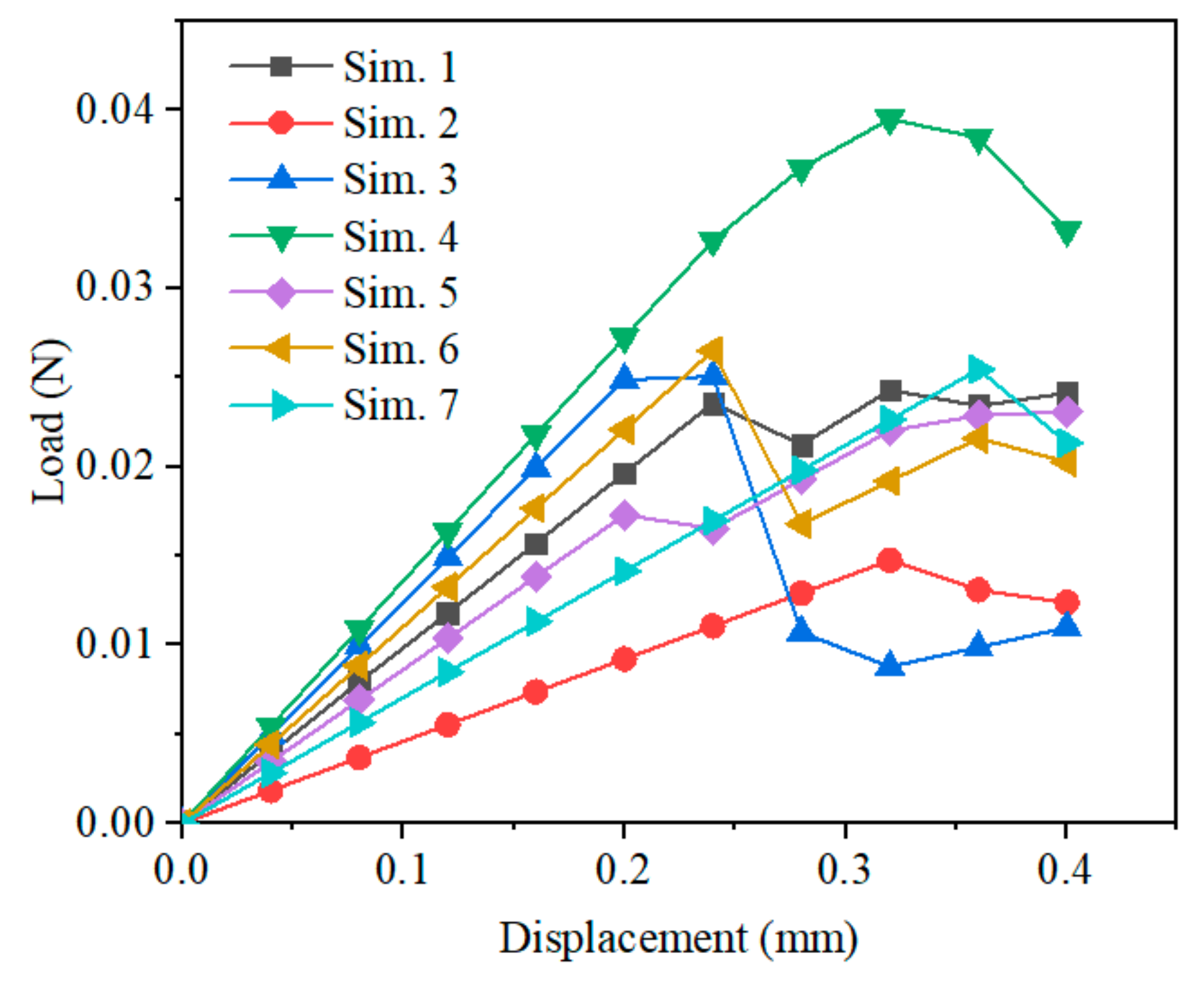
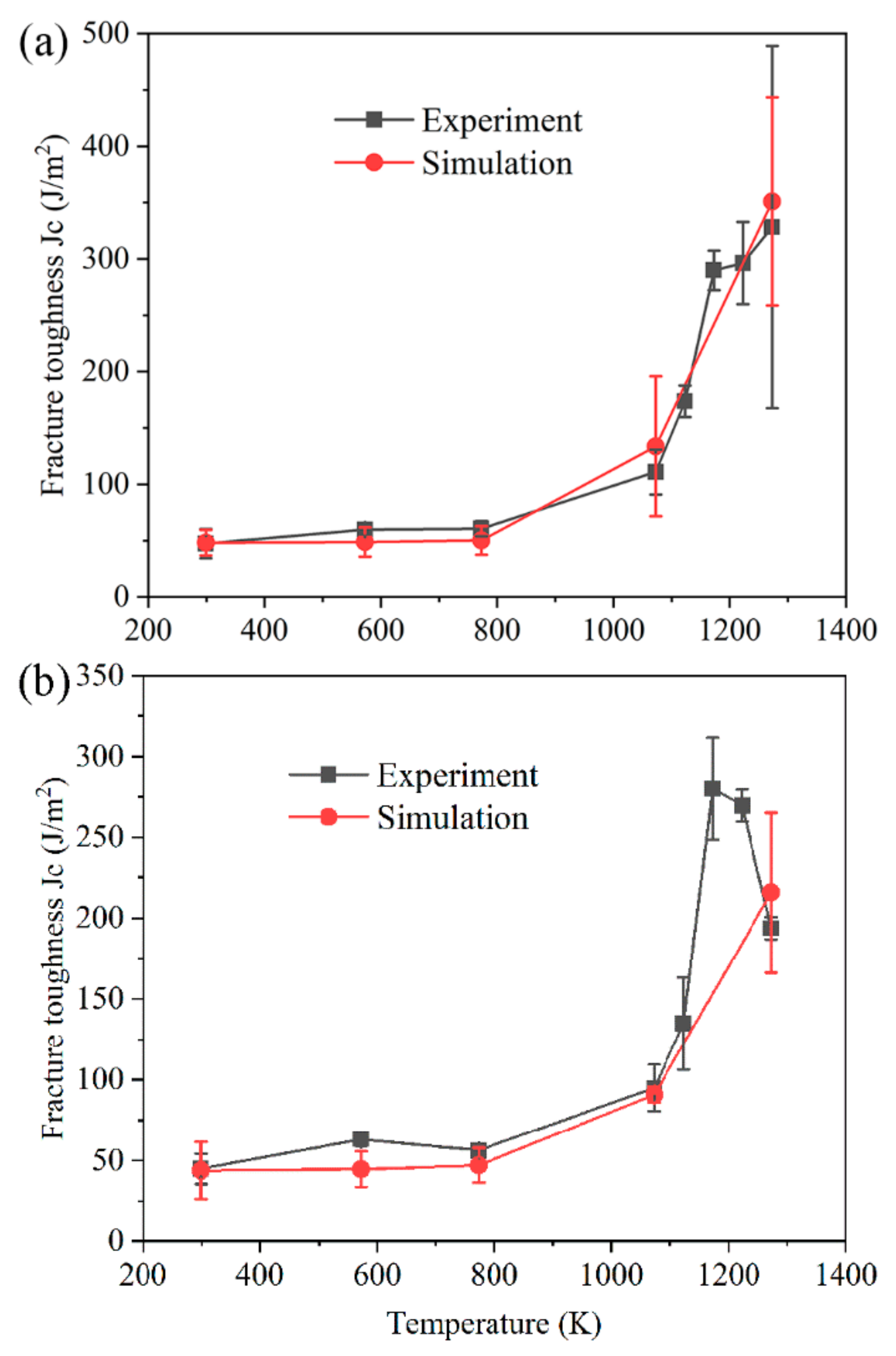
3. Simulation and Discussion
4. Conclusions
- (1)
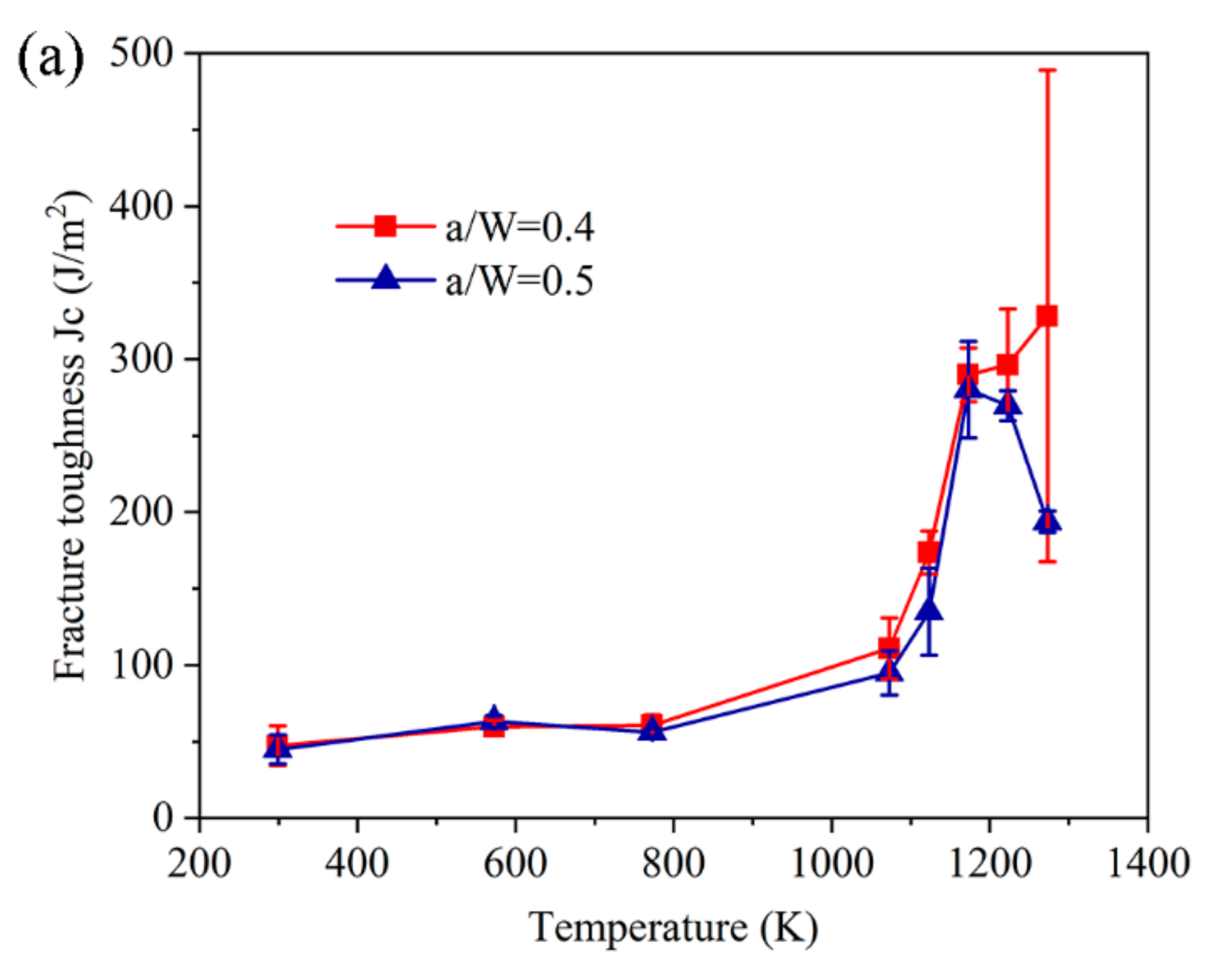
- The experimental observations revealed that the fracture toughness JC along the TTT direction of the 3D RF materials, with a crack length-to-width ratio of 0.4, increased by approximately 574% (from 47.32 to 328.28 J/m2) from 299 to 1273K and, when the ratio was 0.5, it increased from 44.92 to 280.09 J/m2 (by approximately 524%) from 299 to 1173 K;
- (2)
- We developed a scaled FE model with the CT specimen shape and considered the morphological characteristics of the material in this model. Using the material mechanical property of the silica fibers at room temperature, the effectiveness of the developed FE model was verified. The fracture strength of the fibers at elevated temperatures was predicted—it almost kept constant from 299 to 1073 K and sharply increased from 1073 to 1273K;
- (3)
- Based on the precited fracture strength of the fibers and the developed scaled FE model, the fracture toughness JC was well simulated, and it fit well with experimental observations.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hou, Z.; Du, H.; Liu, J.; Hao, R.; Dong, X.; Liu, M. Fabrication and properties of mullite fiber matrix porous ceramics by a TBA-based gel-casting process. J. Eur. Ceram. Soc. 2013, 33, 717–725. [Google Scholar] [CrossRef]
- Liu, Q.; Lu, Z.; Hu, Z.; Li, J. Finite element analysis on tensile behaviour of 3D random fibrous materials: Model description and meso-level approach. Mater. Sci. Eng. A 2013, 587, 36–45. [Google Scholar] [CrossRef]
- Liu, Q.; Lu, Z.; Zhu, M.; Yang, Z.; Hu, Z.; Li, J. Experimental and FEM analysis of the compressive behavior of 3D random fibrous materials with bonded networks. J. Mater. Sci. 2014, 49, 1386–1398. [Google Scholar] [CrossRef]
- Ortiz-Longo, C.R.; White, K.W. Elevated-temperature fracture characterization of advanced fibrous ceramic thermal Insulators. J. Am. Ceram. Soc. 1994, 77, 2703–2711. [Google Scholar] [CrossRef]
- Clyne, T.W.; Golosnoy, I.O.; Tan, J.C.; Markaki, A.E. Porous materials for thermal management under extreme conditions. Philos. Trans. 2006, 364, 125–146. [Google Scholar] [CrossRef] [PubMed]
- Gogotsi, G.A. Fracture toughness of ceramics and ceramic composites. Ceram. Int. 2003, 29, 777–784. [Google Scholar] [CrossRef]
- Sun, B.A.; Wang, W.H. The fracture of bulk metallic glasses. Prog. Mater. Sci. 2015, 74, 211–307. [Google Scholar] [CrossRef]
- Ast, J.; Ghidelli, M.; Durst, K.; Göken, M.; Sebastiani, M.; Korsunsky, A. A review of experimental approaches to fracture toughness evaluation at the micro-scale. Mater. Des. 2019, 173, 107762. [Google Scholar] [CrossRef]
- Jaya, B.N.; Wheeler, J.M.; Wehrs, J.; Best, J.P.; Soler, R.; Michler, J.; Kirchlechner, C.; Dehm, G. Microscale fracture behavior of single crystal silicon beams at elevated temperatures. Nano Lett. 2016, 16, 7597–7603. [Google Scholar] [CrossRef]
- Best, J.P.; Zechner, J.; Wheeler, J.M.; Schoeppner, R.; Morstein, M.; Michler, J. Small-scale fracture toughness of ceramic thin films: The effects of specimen geometry, ion beam notching and high temperature on chromium nitride toughness evaluation. Philos. Mag. 2016, 96, 3552–3569. [Google Scholar] [CrossRef]
- Marshall, D.; Cox, B. A J-integral method for calculating steady-state matrix cracking stresses in composites. Mech. Mater. 1988, 7, 127–133. [Google Scholar] [CrossRef]
- Petti, J.P.; Dodds, R.H., Jr. Coupling of the Weibull stress model and macroscale models to predict cleavage fracture. Eng. Fract. Mech. 2004, 71, 2079–2103. [Google Scholar] [CrossRef]
- Droillard, C.; Lamon, J. Fracture Toughness of 2-D Woven SiC/SiC CVI-Composites with Multilayered Interphases. J. Am. Ceram. Soc. 1996, 79, 849–858. [Google Scholar] [CrossRef]
- Pinho, S.T.; Robinson, P.; Iannucci, L. Fracture toughness of the tensile and compressive fibre failure modes in laminated composites. Compos. Sci. Technol. 2006, 66, 2069–2079. [Google Scholar] [CrossRef] [Green Version]
- Rice, J.R. A path independent integral and the approximate analysis of strain concentration by notches and cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef] [Green Version]
- Laffan, M.; Pinho, S.; Robinson, P.; McMillan, A. Translaminar fracture toughness testing of composites: A review. Polymer Testing 2012, 31, 481–489. [Google Scholar] [CrossRef]
- Pinho, S.; Iannucci, L.; Robinson, P. Physically based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking. Part II: FE implementation. Compos. Part A Appl. Sci. Manufacturing 2006, 37, 766–777. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Zheng, J. Recent developments on damage modeling and finite element analysis for composite laminates: A review. Mater. Des. 2010, 31, 3825–3834. [Google Scholar] [CrossRef]
- Matzenmiller, A.; Lubliner, J.; Taylor, R. A constitutive model for anisotropic damage in fiber-composites. Mech. Mater. 1995, 20, 125–152. [Google Scholar] [CrossRef]
- Kwon, Y.; Liu, C. Study of damage evolution in composites using damage mechanics and micromechanics. Compos. Struct. 1997, 38, 133–139. [Google Scholar] [CrossRef]
- Maa, R.-H.; Cheng, J.-H. A CDM-based failure model for predicting strength of notched composite laminates. Compos. Part B Eng. 2002, 33, 479–489. [Google Scholar] [CrossRef]
- Camanho, P.P.; Maimí, P.; Dávila, C. Prediction of size effects in notched laminates using continuum damage mechanics. Compos. Sci. Technol. 2007, 67, 2715–2727. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.-K.; Joyce, J. Review of fracture toughness (G, K, J, CTOD, CTOA) testing and standardization. Eng. Fract. Mech. 2012, 85, 1–46. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Yu, W.; Xia, W.; Fang, Q.; Shen, S. Fracture toughness of random fibrous materials with ultrahigh porosity at elevated temperatures. J. Am. Ceram. Soc. 2018, 101, 1323–1332. [Google Scholar] [CrossRef]
- Li, D.T.; Xia, W.; Yu, W.S.; Fang, Q.Z.; Shen, S.P. Investigations on the compressive behavior of 3D random fibrous materials at elevated temperatures. Ceram. Int. 2017, 43, 5195–5203. [Google Scholar] [CrossRef]
- Li, D.T.; Yu, W.S.; Xia, W.; Fang, Q.Z.; Shen, S.P. Investigations on fracture toughness and fracture surface energy of 3D random fibrous materials at elevated temperatures. Eng. Fract. Mech. 2018, 190, 288–298. [Google Scholar] [CrossRef]
- Li, D.T.; Yu, W.S.; Xia, W.; Fang, Q.Z.; Shen, S.P. Porosity Effects on Mechanical Properties of 3D Random Fibrous Materials at Elevated Temperatures. Acta Mech. Solida Sinica 2020, 33, 14–30. [Google Scholar] [CrossRef]
- Shinkai, N.; Bradt, R.; Rindone, G.E. Fracture toughness of fused SiO2 and float glass at elevated temperatures. J. Am. Ceram. Soc. 1981, 64, 426–430. [Google Scholar] [CrossRef]
- Kourtides, D.A.; Pitts, W.C.; Araujo, M.; Zimmerman, R. High-temperature properties of ceramic fibers and insulations for thermal protection of atmospheric entry and hypersonic cruise vehicles. J. Fire Sci. 1988, 6, 313–332. [Google Scholar] [CrossRef] [Green Version]
- Li, D.T.; Xia, W.; Fang, Q.Z.; Yu, W.S.; Shen, S.P. Experimental and numerical investigations on the tensile behavior of 3D random fibrous materials at elevated temperature. Compos. Struct. 2017, 160, 292–299. [Google Scholar] [CrossRef]
- Lyons, J.S.; Starr, T.L. Strength and toughness of slip-cast fused-silica composites. J. Am. Ceram. Soc. 1994, 77, 1673–1675. [Google Scholar] [CrossRef]
- Brueckner, R. Properties and structure of vitreous silica. J. Non Cryst. Solids 1970, 5, 123–175. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Li, Y.; Yu, W. Temperature Dependence of the Fracture Toughness JC of Random Fibrous Material. Appl. Sci. 2020, 10, 941. https://doi.org/10.3390/app10030941
Li D, Li Y, Yu W. Temperature Dependence of the Fracture Toughness JC of Random Fibrous Material. Applied Sciences. 2020; 10(3):941. https://doi.org/10.3390/app10030941
Chicago/Turabian StyleLi, Datao, Yan Li, and Wenshan Yu. 2020. "Temperature Dependence of the Fracture Toughness JC of Random Fibrous Material" Applied Sciences 10, no. 3: 941. https://doi.org/10.3390/app10030941





