The Impact of Single- and Multicomponent Liquid Drops on a Heated Wall: Child Droplets
Abstract
:1. Introduction
2. Experimental Procedures
3. Results and Discussion
3.1. Patterns, Observations, and Outcomes of Drop Impact on a Wall
3.2. Effect of a Group of the Governing Parameters
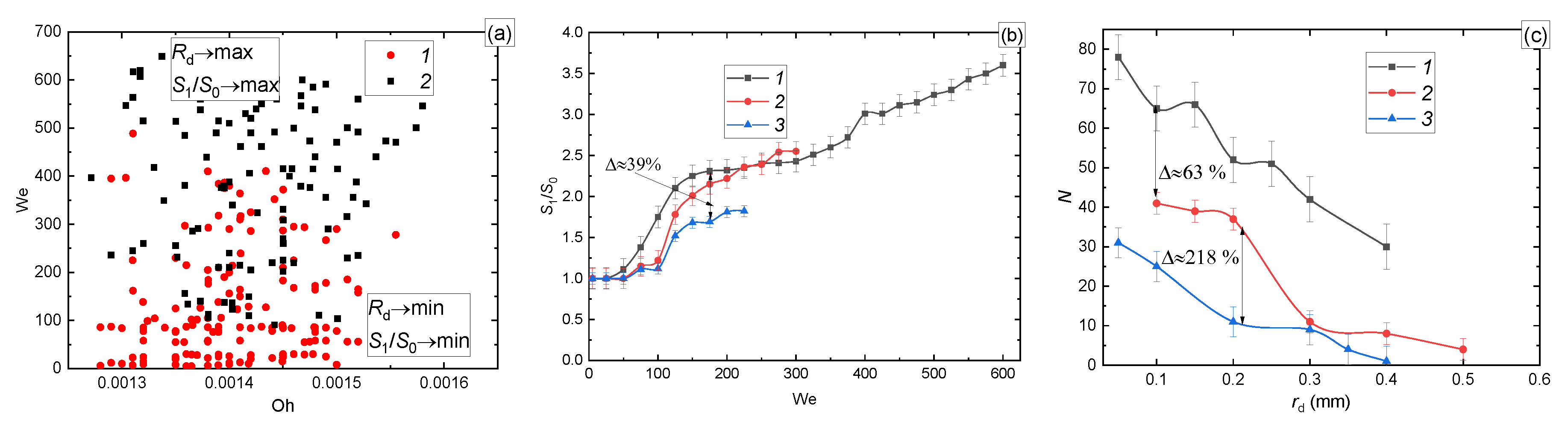
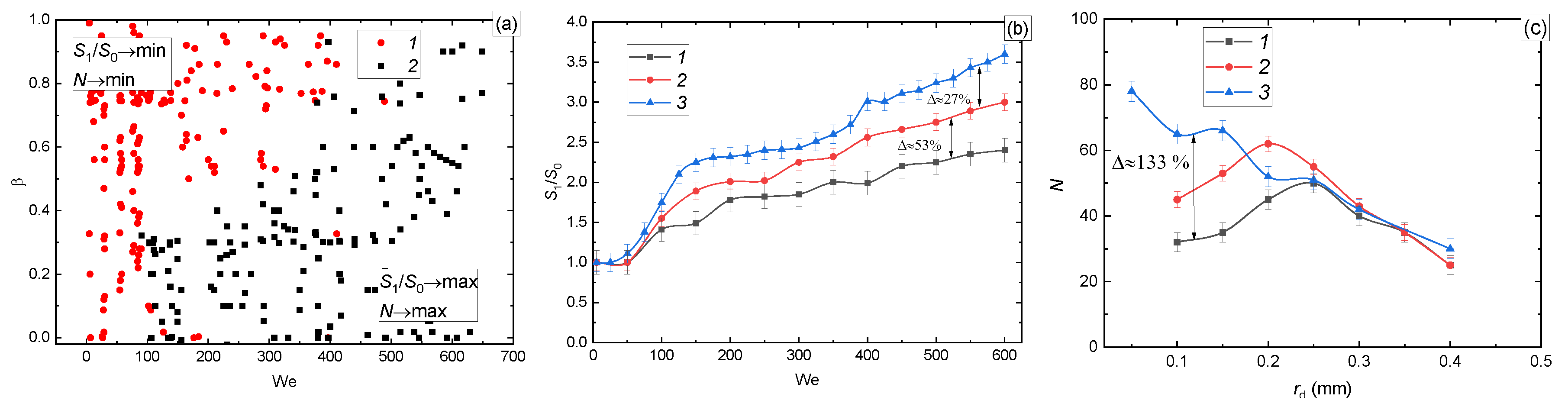
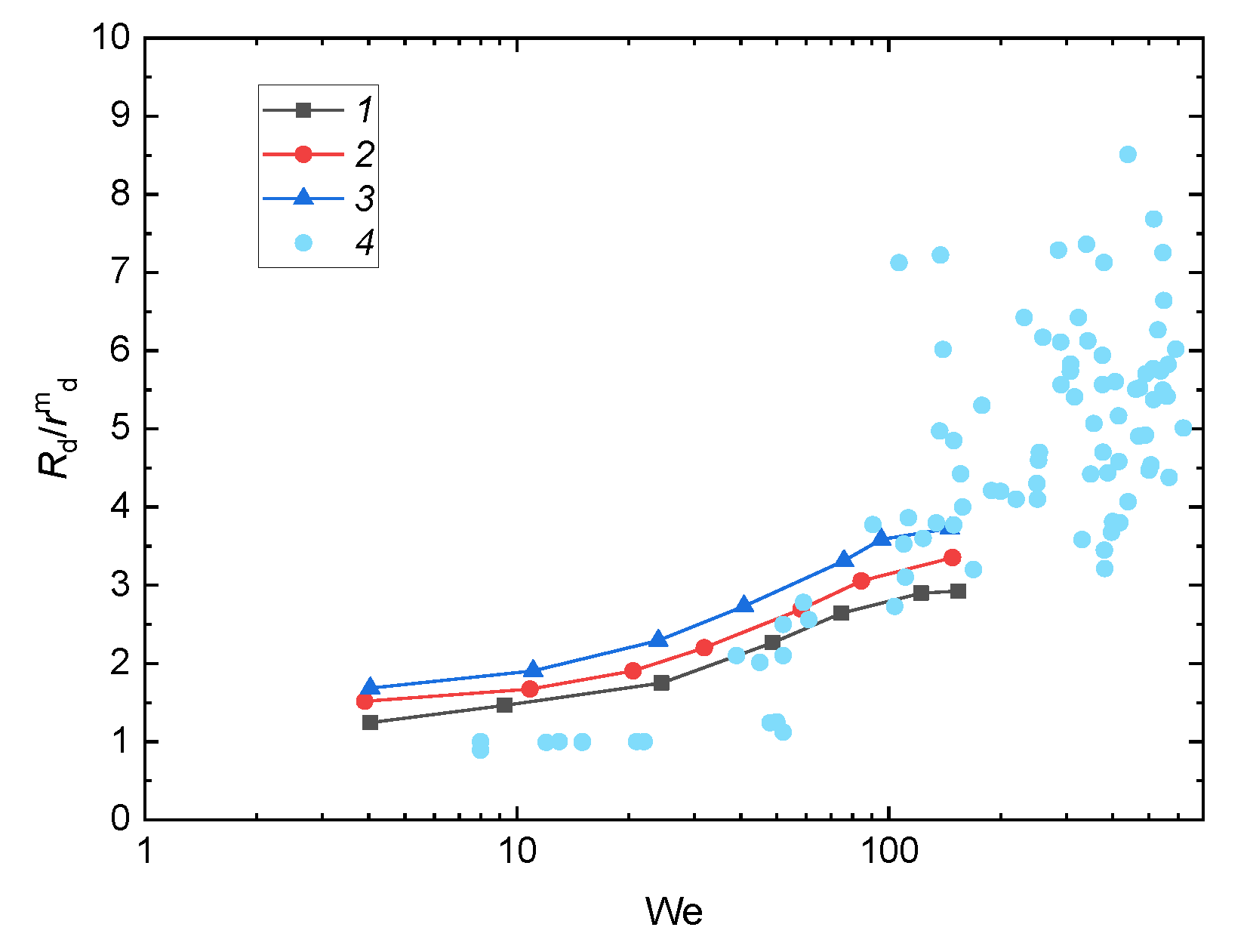
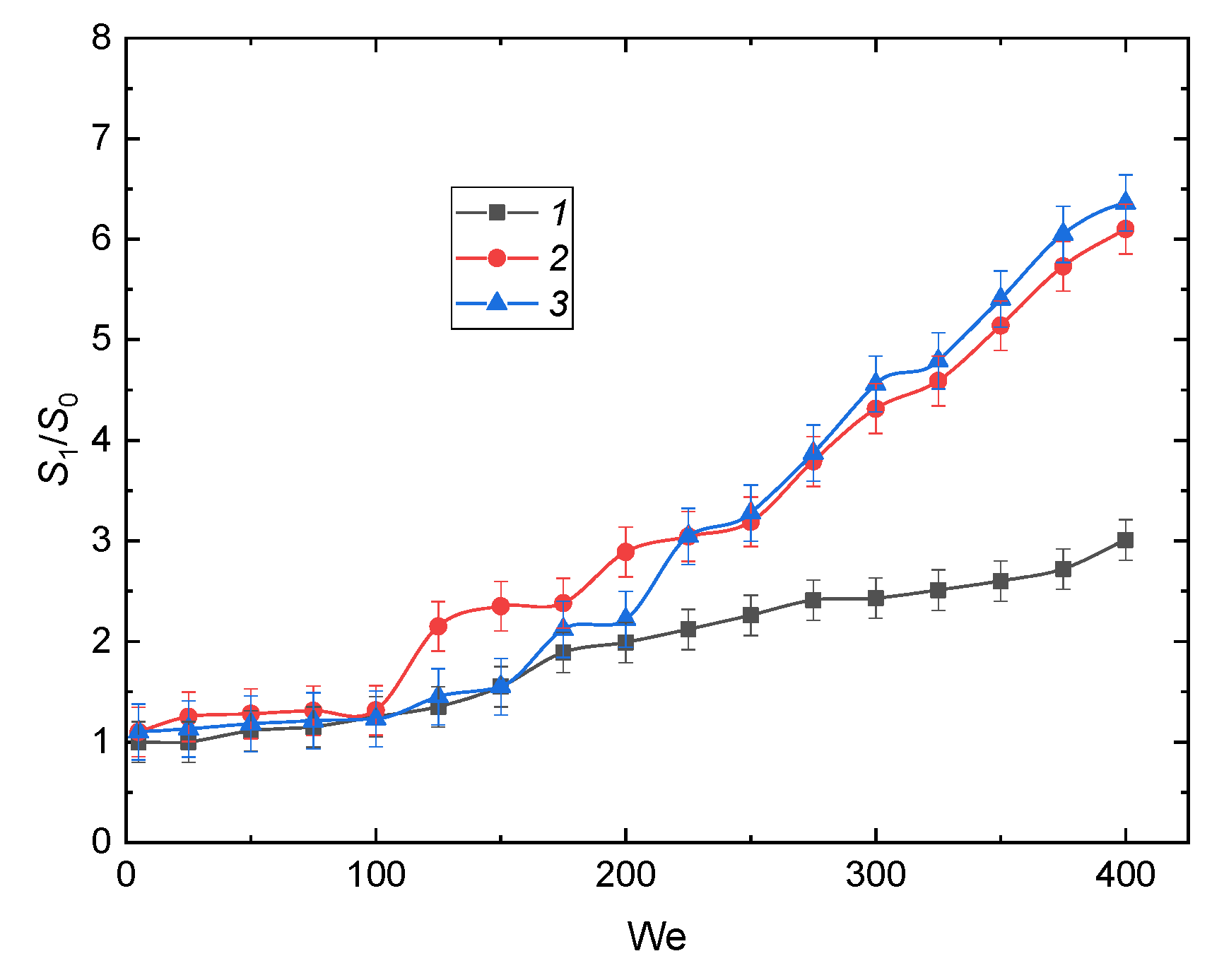
3.2.1. Velocity, Size, and Impinging Angle
3.2.2. Wall Heating
3.2.3. Wall Material
3.2.4. Surface Roughness and Hydrophilicity
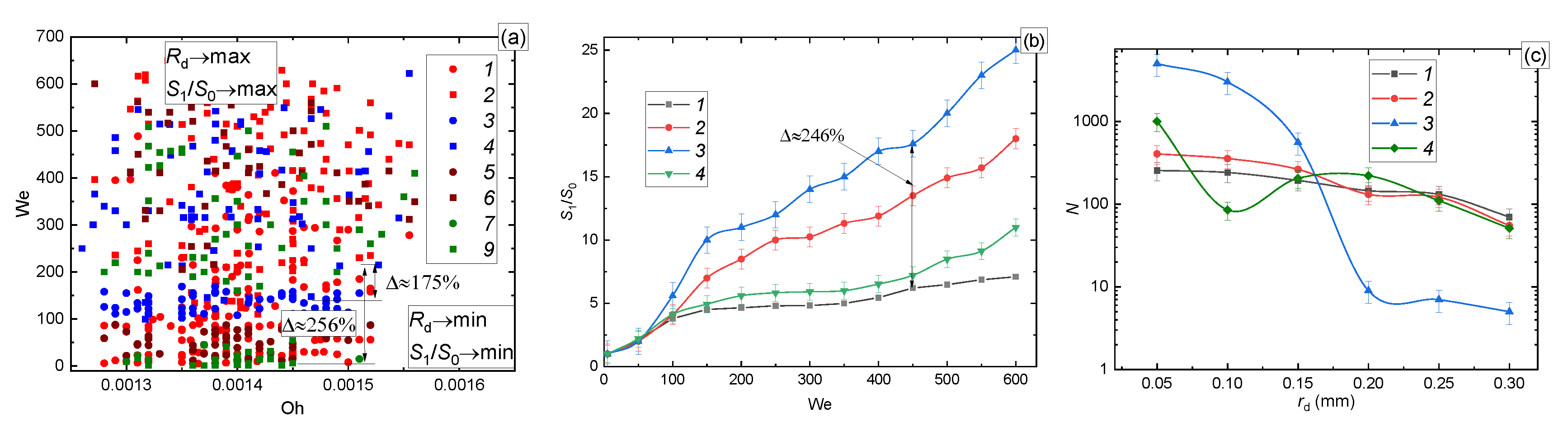
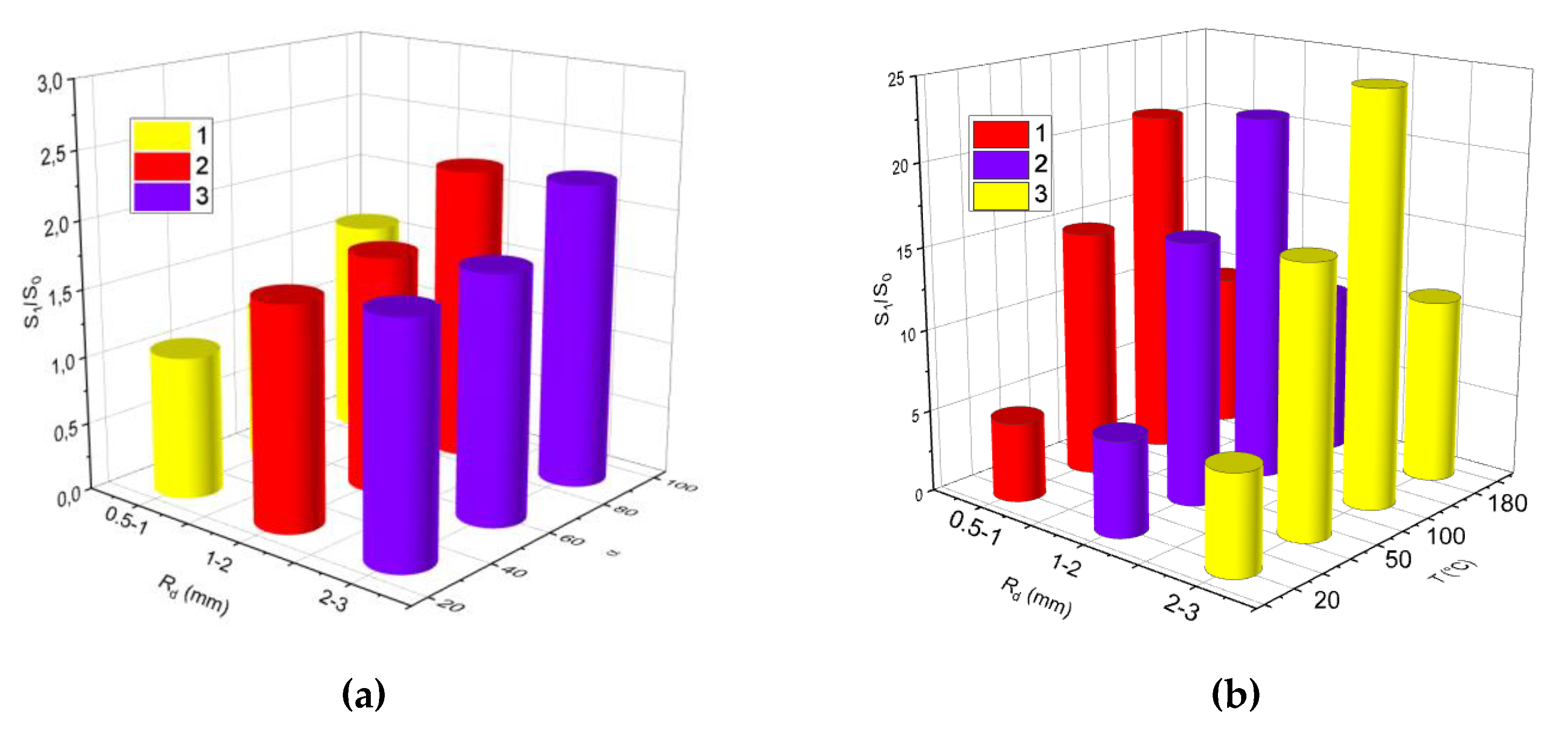
3.2.5. Drop Homogeneity and Heterogeneity; Liquid Viscosity and Surface Tension
3.3. Prospects of the Drop Breakup When Impacting onto a Surface
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liang, G.; Mudawar, I. Review of drop impact on heated walls. Int. J. Heat Mass Transf. 2017, 106, 103–126. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Review of mass and momentum interactions during drop impact on a liquid film. Int. J. Heat Mass Transf. 2016, 101, 577–599. [Google Scholar] [CrossRef]
- Šikalo, Š.; Marengo, M.; Tropea, C.; Ganić, E.N. Analysis of impact of droplets on horizontal surfaces. Exp. Therm. Fluid Sci. 2002, 25, 503–510. [Google Scholar] [CrossRef]
- Xie, J.; Wong, T.N.; Duan, F. Modelling on the dynamics of droplet impingement and bubble boiling in spray cooling. Int. J. Therm. Sci. 2016, 104, 469–479. [Google Scholar] [CrossRef]
- Tang, C.; Qin, M.; Weng, X.; Zhang, X.; Zhang, P.; Li, J.; Huang, Z. Dynamics of droplet impact on solid surface with different roughness. Int. J. Multiph. Flow 2017, 96, 56–69. [Google Scholar] [CrossRef]
- Clavijo, C.E.; Crockett, J.; Maynes, D. Hydrodynamics of droplet impingement on hot surfaces of varying wettability. Int. J. Heat Mass Transf. 2017, 108, 1714–1726. [Google Scholar] [CrossRef] [Green Version]
- Fujimoto, H.; Tong, A.Y.; Takuda, H. Interaction phenomena of two water droplets successively impacting onto a solid surface. Int. J. Therm. Sci. 2008, 47, 229–236. [Google Scholar] [CrossRef]
- Negeed, E.-S.R.; Ishihara, N.; Tagashira, K.; Hidaka, S.; Kohno, M.; Takata, Y. Experimental study on the effect of surface conditions on evaporation of sprayed liquid droplet. Int. J. Therm. Sci. 2010, 49, 2250–2271. [Google Scholar] [CrossRef]
- Senda, J.; Kanda, T.; Al-Roub, M.; Farrell, P.V.; Fukami, T.; Fujimoto, H. Modeling Spray Impingement Considering Fuel Film Formation on the Wall. SAE Tech. Pap. 1997. [Google Scholar] [CrossRef]
- Roisman, I. Inertia dominated drop collisions. II. An analytical solution of the Navier–Stokes equations for a spreading viscous film. Phys. Fluids 2009, 21, 52104. [Google Scholar] [CrossRef]
- Williams, Y.O.; Roas-Escalona, N.; Rodríguez-Lopez, G.; Villa-Torrealba, A.; Toro-Mendoza, J. Modeling droplet coalescence kinetics in microfluidic devices using population balances. Chem. Eng. Sci. 2019, 201, 475–483. [Google Scholar] [CrossRef]
- Lunkenheimer, K.; Wantke, K.D. On the applicability of the du Nouy (ring) tensiometer method for the determination of surface tensions of surfactant solutions. J. Colloid Interface Sci. 1978, 66, 579–581. [Google Scholar] [CrossRef]
- Orme, M. Experiments on droplet collisions, bounce, coalescence and disruption. Prog. Energy Combust. Sci. 1997, 23, 65–79. [Google Scholar] [CrossRef]
- Krishnan, K.G.; Loth, E. Effects of gas and droplet characteristics on drop-drop collision outcome regimes. Int. J. Multiph. Flow 2015, 77, 171–186. [Google Scholar] [CrossRef]
- Pawar, S.K.; Henrikson, F.; Finotello, G.; Padding, J.T.; Deen, N.G.; Jongsma, A.; Innings, F.; Kuipers, J.A.M.H. An experimental study of droplet-particle collisions. Powder Technol. 2016, 300, 157–163. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Gratadeix, A.; Do-Quang, M.; Amberg, G. Events and conditions in droplet impact: A phase field prediction. Int. J. Multiph. Flow 2016, 87, 54–65. [Google Scholar] [CrossRef]
- Charalampous, G.; Hardalupas, Y. Collisions of droplets on spherical particles. Phys. Fluids 2017, 29, 103305. [Google Scholar] [CrossRef] [Green Version]
- Finotello, G.; De, S.; Vrouwenvelder, J.C.R.; Padding, J.T.; Buist, K.A.; Jongsma, A.; Innings, F.; Kuipers, J.A.M. Experimental investigation of non-Newtonian droplet collisions: The role of extensional viscosity. Exp. Fluids 2018, 59, 113. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; Zhao, B.; Zou, S.; Guo, J.; Wei, Z.; Chen, L. Impact of viscous droplets on different wettable surfaces: Impact phenomena, the maximum spreading factor, spreading time and post-impact oscillation. J. Colloid Interface Sci. 2018, 516, 86–97. [Google Scholar] [CrossRef]
- Li, D.; Duan, X. Numerical analysis of droplet impact and heat transfer on an inclined wet surface. Int. J. Heat Mass Transf. 2019, 128, 459–468. [Google Scholar] [CrossRef]
- Unnikrishnan, P.K.; Vaikuntanathan, V.; Sivakumar, D. Impact dynamics of high Weber number drops on chemically modified metallic surfaces. Colloids Surfaces A Physicochem. Eng. Asp. 2014, 459, 109–119. [Google Scholar] [CrossRef]
- Negeed, E.-S.R.; Albeirutty, M.; Takata, Y. Dynamic behavior of micrometric single water droplets impacting onto heated surfaces with TiO2 hydrophilic coating. Int. J. Therm. Sci. 2014, 79, 1–17. [Google Scholar] [CrossRef]
- Roisman, I.V.; Breitenbach, J.; Tropea, C. Thermal atomisation of a liquid drop after impact onto a hot substrate. J. Fluid Mech. 2018, 842, 87–101. [Google Scholar] [CrossRef]
- Solomatin, Y.; Shlegel, N.; Strizhak, P. Secondary atomization of firefighting liquid droplets by their collisions. At. Sprays 2019, 29, 429–454. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Shlegel, N.E.; Solomatin, Y.; Strizhak, P.A. Combined techniques of secondary atomization of multi-component droplets. Chem. Eng. Sci. 2019, 209, 115199. [Google Scholar] [CrossRef]
- Solomatin, Y.; Shlegel, N.E.; Strizhak, P.A. Atomization of promising multicomponent fuel droplets by their collisions. Fuel 2019, 255, 115751. [Google Scholar] [CrossRef]
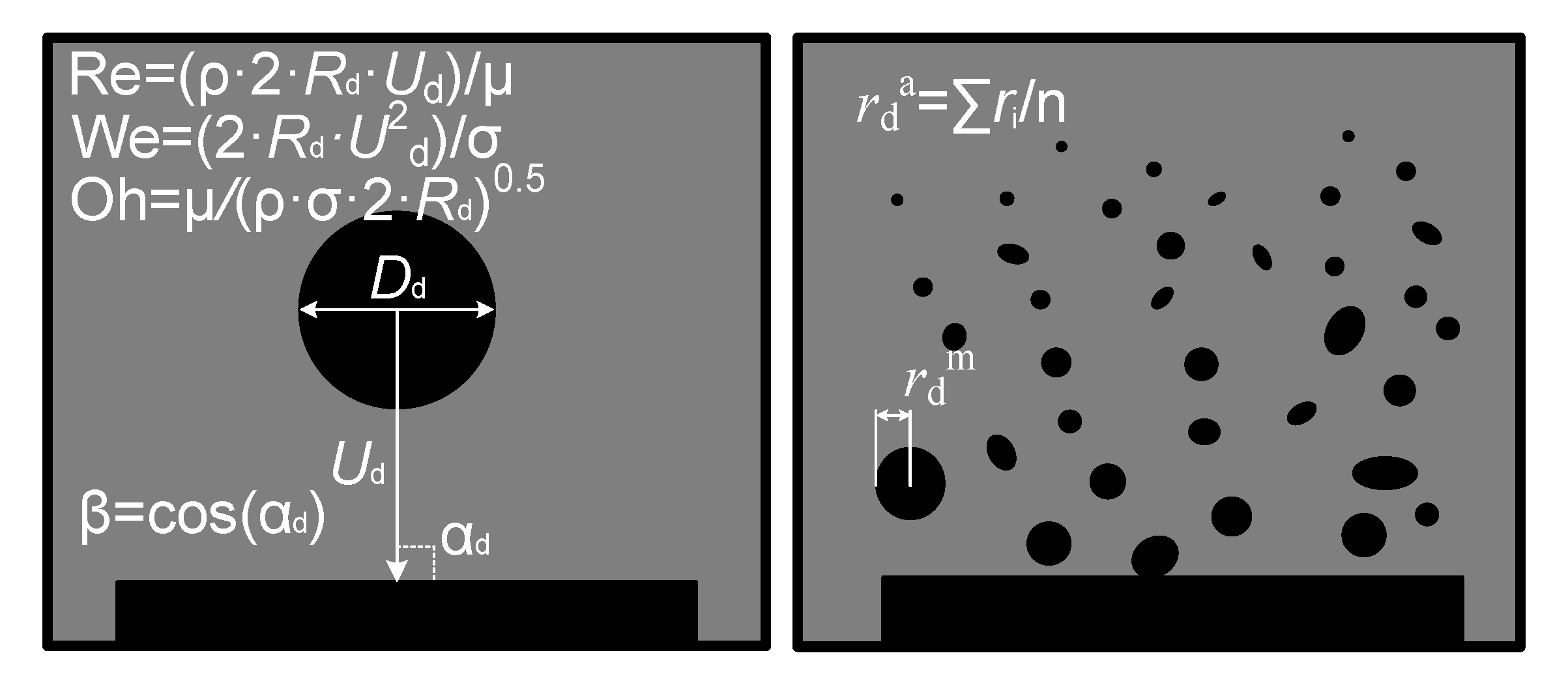



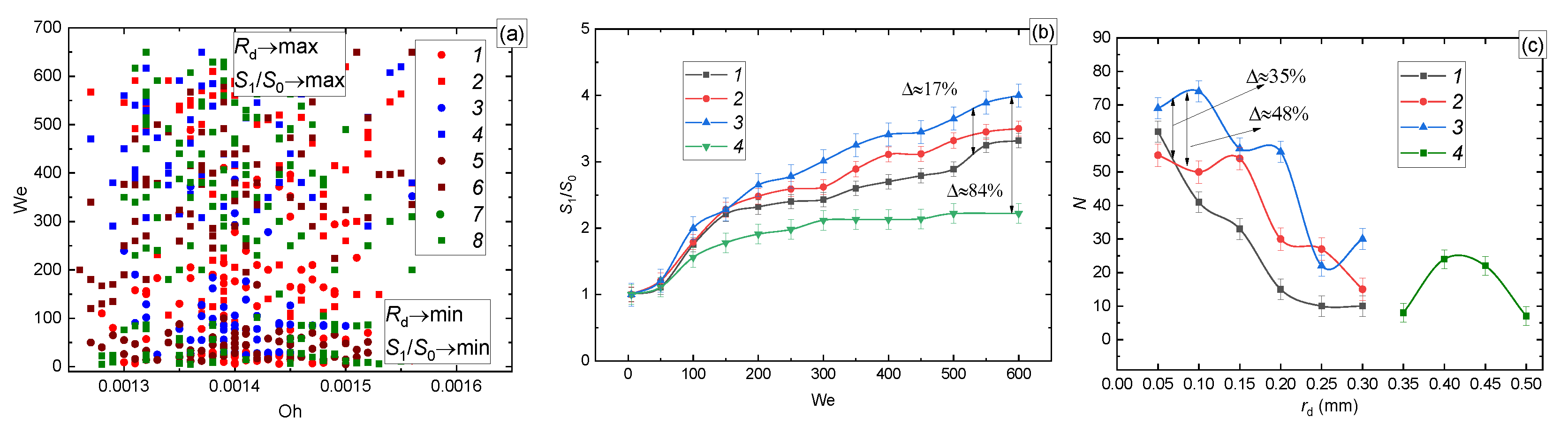
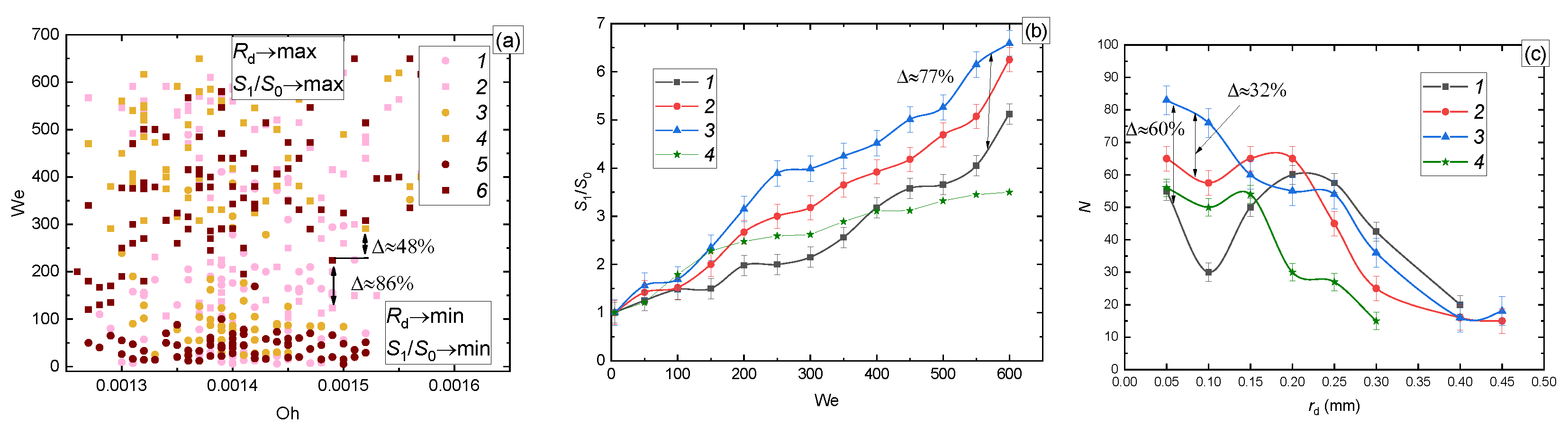

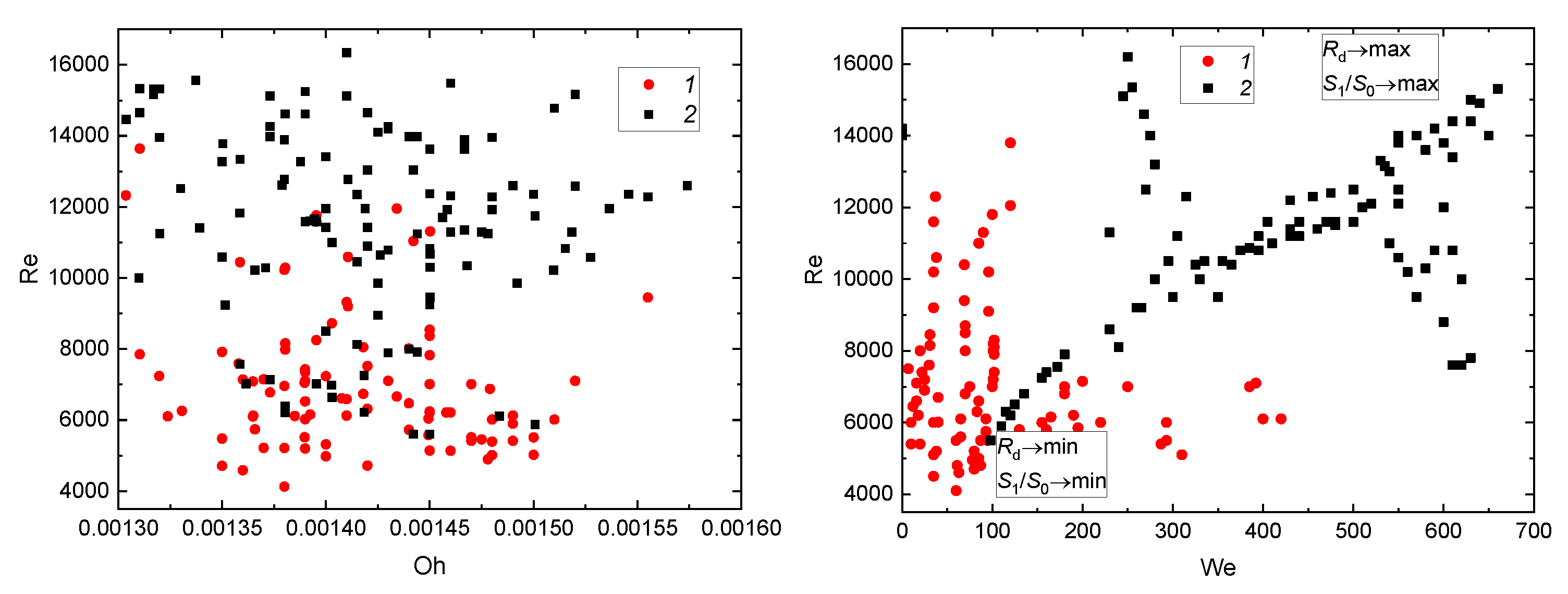
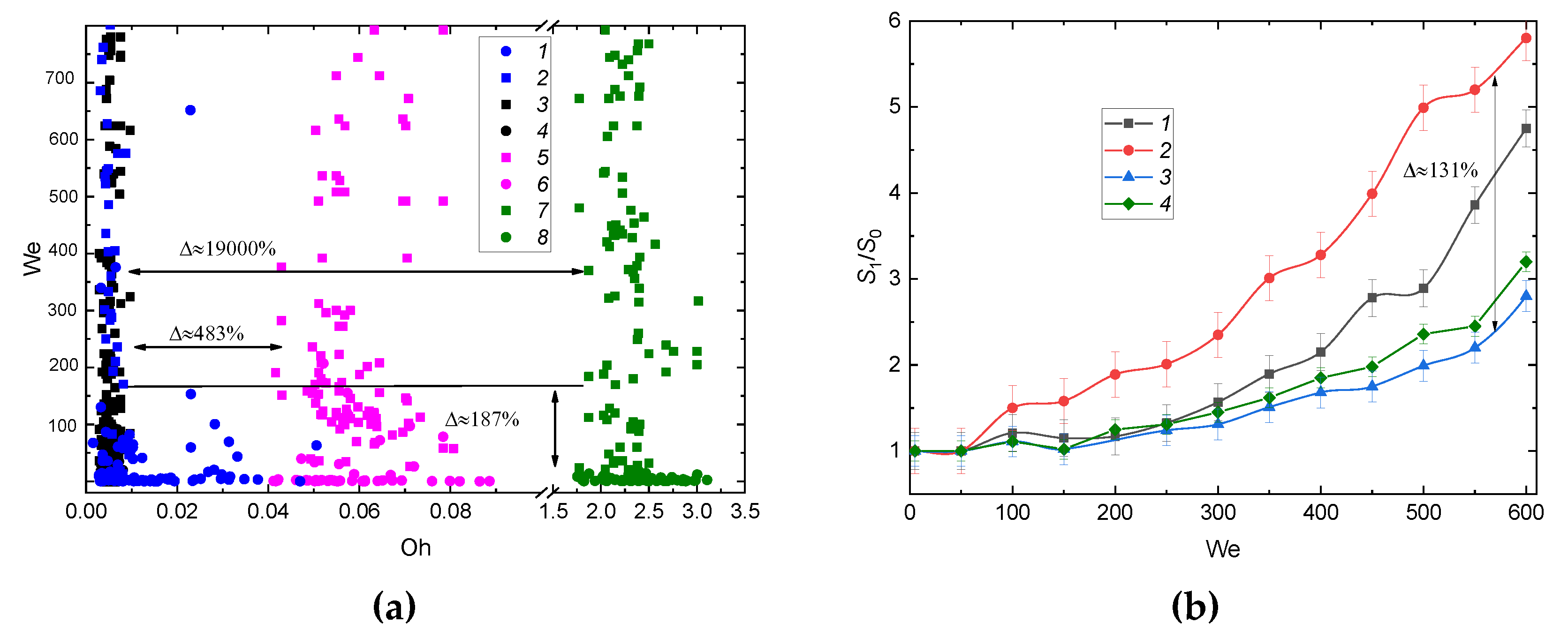

| Liquid (Volume or Mass Concentrations of the Admixtures to Water) | Temperature [°C] | Density [kg/m3] | Surface Tension [N/m] | Dynamic Viscosity [Pa∙s] |
|---|---|---|---|---|
| Water | 20 | 998 | 0.0726 | 0.0014 |
| Coal slurry (30 wt%) | 20 | 1126 | 0.2472 | 0.0033 |
| Transformer oil emulsion (30 vol%) | 20 | 963 | 0.0567 | 0.0069 |
| Castor oil emulsion (30 vol%) | 20 | 987 | 0.0615 | 0.2857 |
| Composition | Water | Water | Water | |
|---|---|---|---|---|
| No. of impingement | 1 | 2 | 546 | |
| αd—impingement angle [°] | 91.2 | 89.4 | … | 30.1 |
| Rd—drop radius [mm] | 2.5 | 2.2 | … | 2.6 |
| Ud—drop velocity [m/s] | 1.3 | 2.3 | … | 2.6 |
| Impact outcome | spreading | breakup | … | breakup |
| No. of frame | 54 | 126 | … | 14568 |
| Drop shape | sphere | sphere | … | sphere |
| N—number of child droplets | 1 | 50 | … | 13 |
| We·[(2·Rd·Ud^2)/σ | 126.3 | 341.7 | … | 508 |
| Oh·[μ/(ρ·σ·2·Rd)^1/2 | 0.0013 | 0.0015 | … | 0.0013 |
| Re [(ρ·2·Rd·Ud)/μ | 6776.9 | 10,433.5 | … | 13,867.8 |
| β·[cos(ɑd)] | 0.02 | 0.01 | … | 0.87 |
| rda—mean diameter of child droplets | – | 0.05 | … | 0.23 |
| S0—surface area of the parent drop [mm2] | 79.1 | 66.3 | … | 85.6 |
| Sf—surface area of the liquid film [mm2] | 79.1 | 57.6 | 76.4 | |
| S—surface area of child droplets [mm2] | – | 105.3 | … | 121.3 |
| S1—total surface area of child droplets and liquid film [mm2] | 79.1 | 162.9 | 197.7 | |
| S1/S0 | 1 | 2.4 | … | 2.3 |
| Parameter | Systematic Error [%] | Random Error [%] |
|---|---|---|
| Rd | 1.6 | 2.1 |
| Ud | 2.1 | 3.4 |
| αd | 2.3 | 3.1 |
| Rd [mm] | Weber Numbers | Threshold Velocities [m/s] | Impingement Angles | |||
|---|---|---|---|---|---|---|
| Deposition | Breakup | Deposition | Breakup | Deposition | Breakup | |
| 0.5–1 | 0–195 | 195–630 | 0–2.28 | 2.28–3 | 0–π/3 | π/3–π/2 |
| 1–2 | 0–163 | 163–630 | 0–2.14 | 2.14–3 | 0–π/4 | π/4–π/2 |
| 2–2.5 | 0–442 | 442–630 | 0–2.51 | 2.51–3 | 0–π/5 | π/5–π/2 |
| 2.5–3 | 0–300 | 300–630 | 0–1.89 | 1.89–3 | 0–π/8 | π/8–π/2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demidovich, A.V.; Kropotova, S.S.; Piskunov, M.V.; Shlegel, N.E.; Vysokomornaya, O.V. The Impact of Single- and Multicomponent Liquid Drops on a Heated Wall: Child Droplets. Appl. Sci. 2020, 10, 942. https://doi.org/10.3390/app10030942
Demidovich AV, Kropotova SS, Piskunov MV, Shlegel NE, Vysokomornaya OV. The Impact of Single- and Multicomponent Liquid Drops on a Heated Wall: Child Droplets. Applied Sciences. 2020; 10(3):942. https://doi.org/10.3390/app10030942
Chicago/Turabian StyleDemidovich, Anastasia V., Svetlana S. Kropotova, Maxim V. Piskunov, Nikita E. Shlegel, and Olga V. Vysokomornaya. 2020. "The Impact of Single- and Multicomponent Liquid Drops on a Heated Wall: Child Droplets" Applied Sciences 10, no. 3: 942. https://doi.org/10.3390/app10030942
APA StyleDemidovich, A. V., Kropotova, S. S., Piskunov, M. V., Shlegel, N. E., & Vysokomornaya, O. V. (2020). The Impact of Single- and Multicomponent Liquid Drops on a Heated Wall: Child Droplets. Applied Sciences, 10(3), 942. https://doi.org/10.3390/app10030942






