Numerical Simulation of the Effect of Injected CO2 Temperature and Pressure on CO2-Enhanced Coalbed Methane
Abstract
:1. Introduction
2. Theory
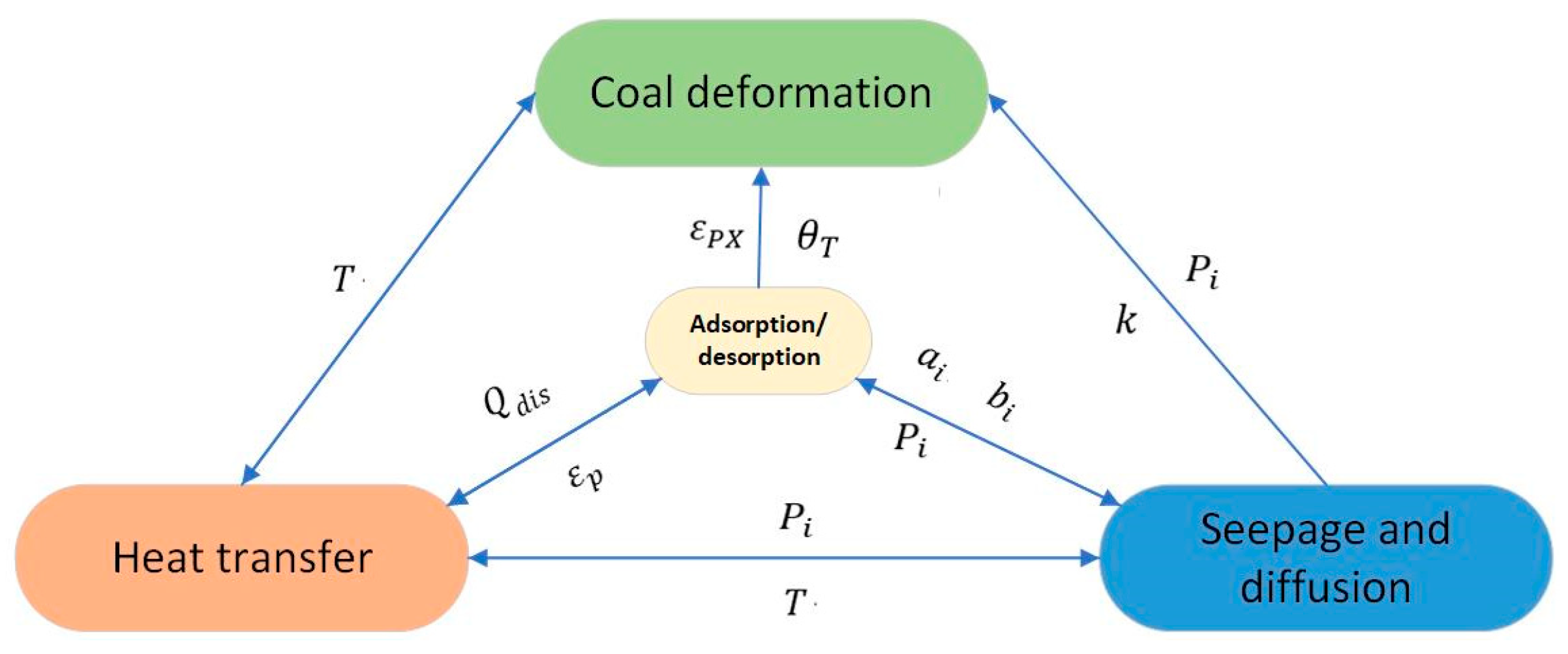
2.1. Desorption–Seepage–Diffusion Principle of CO2 Displacement of CH4
2.2. THM Coupling Equation of CO2 Displacement CBM
- (1)
- The coal seam is a heterogeneous porous medium;
- (2)
- The binary gas adsorption and desorption models conform to the Langmuir equation [27];
- (3)
- The influence of water and vapor on gas transport is not considered [28];
- (4)
- (5)
- (6)
- The initial state of the coal seam’s only free adsorption state of CBM sets CO2 content to 0 with binary gas in the boundary around the coal seam as no flux.
2.2.1. Stress–Strain Equation
2.2.2. Coupling Equation of Permeation and Diffusion of Binary Gas
2.2.3. Temperature Field Equation of Binary Gas Flow
2.2.4. Porosity and Permeability
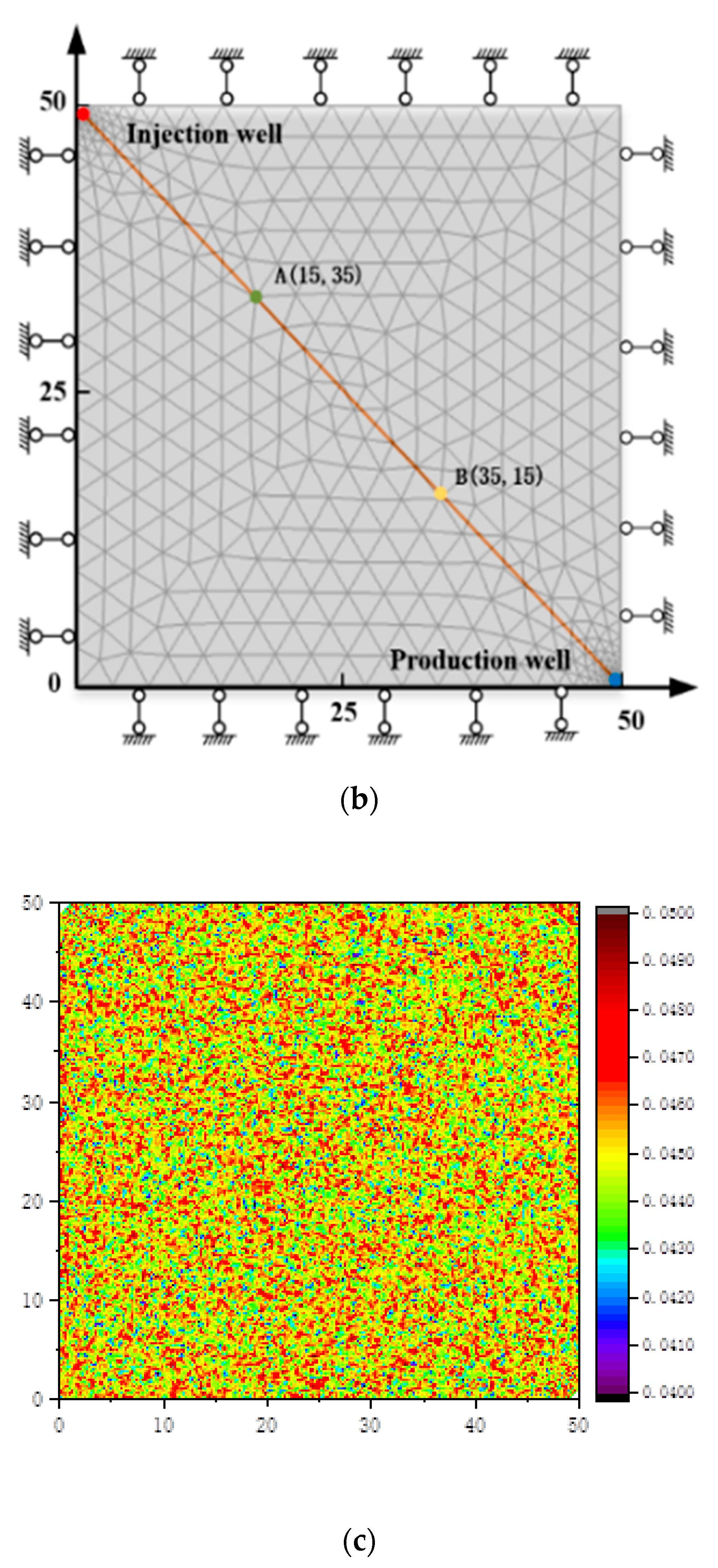
3. Geometric Model and Solution Conditions
4. Results
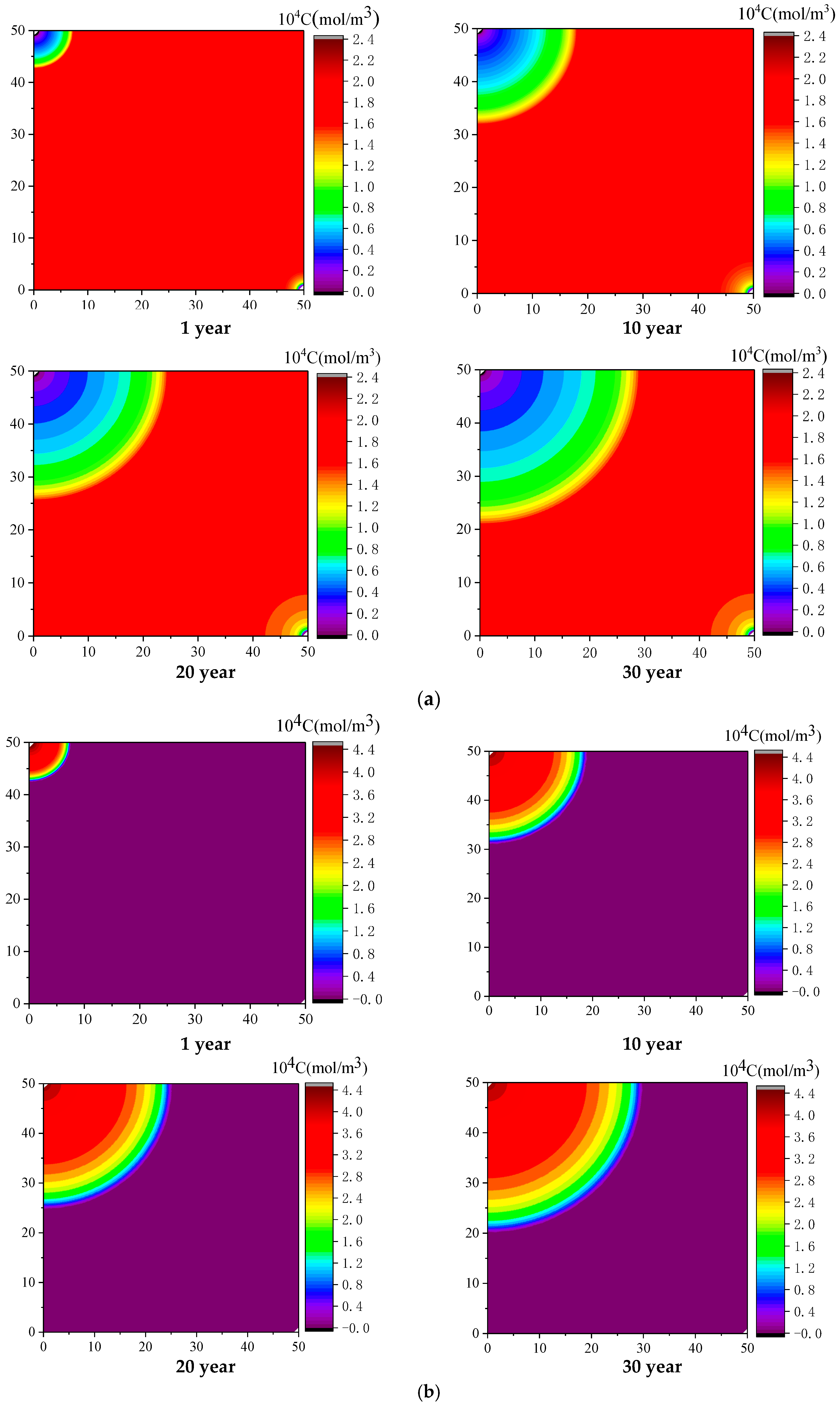
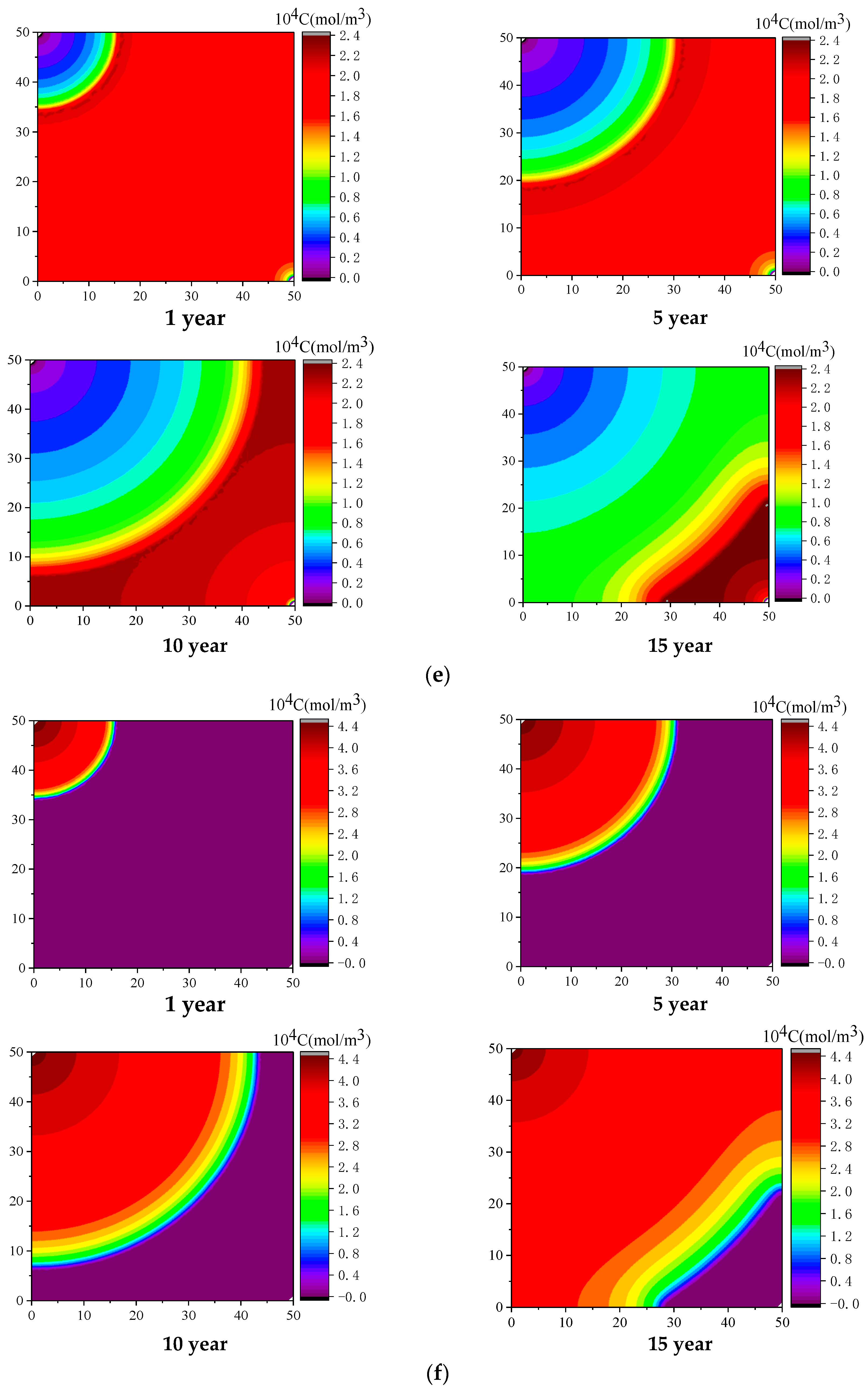
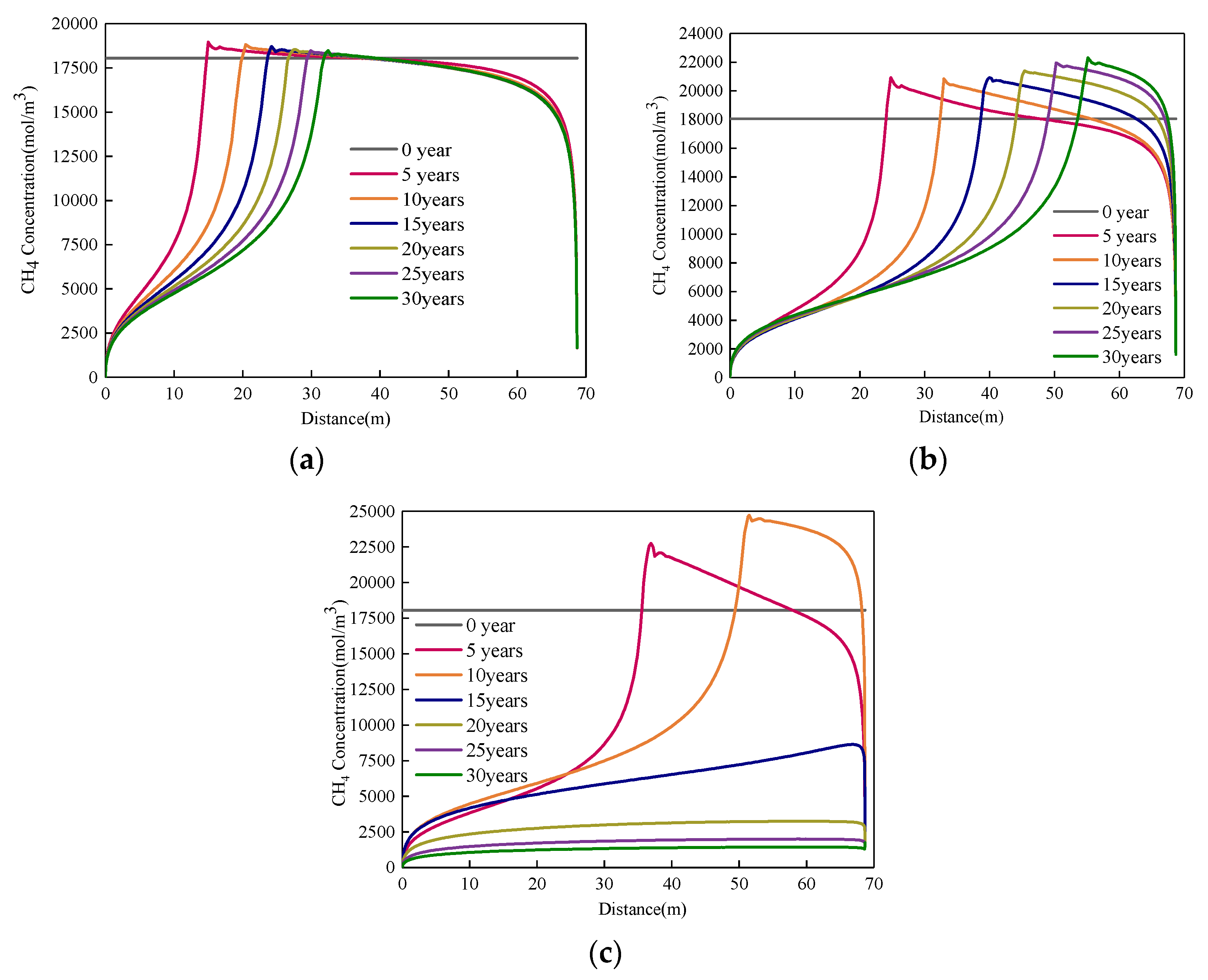
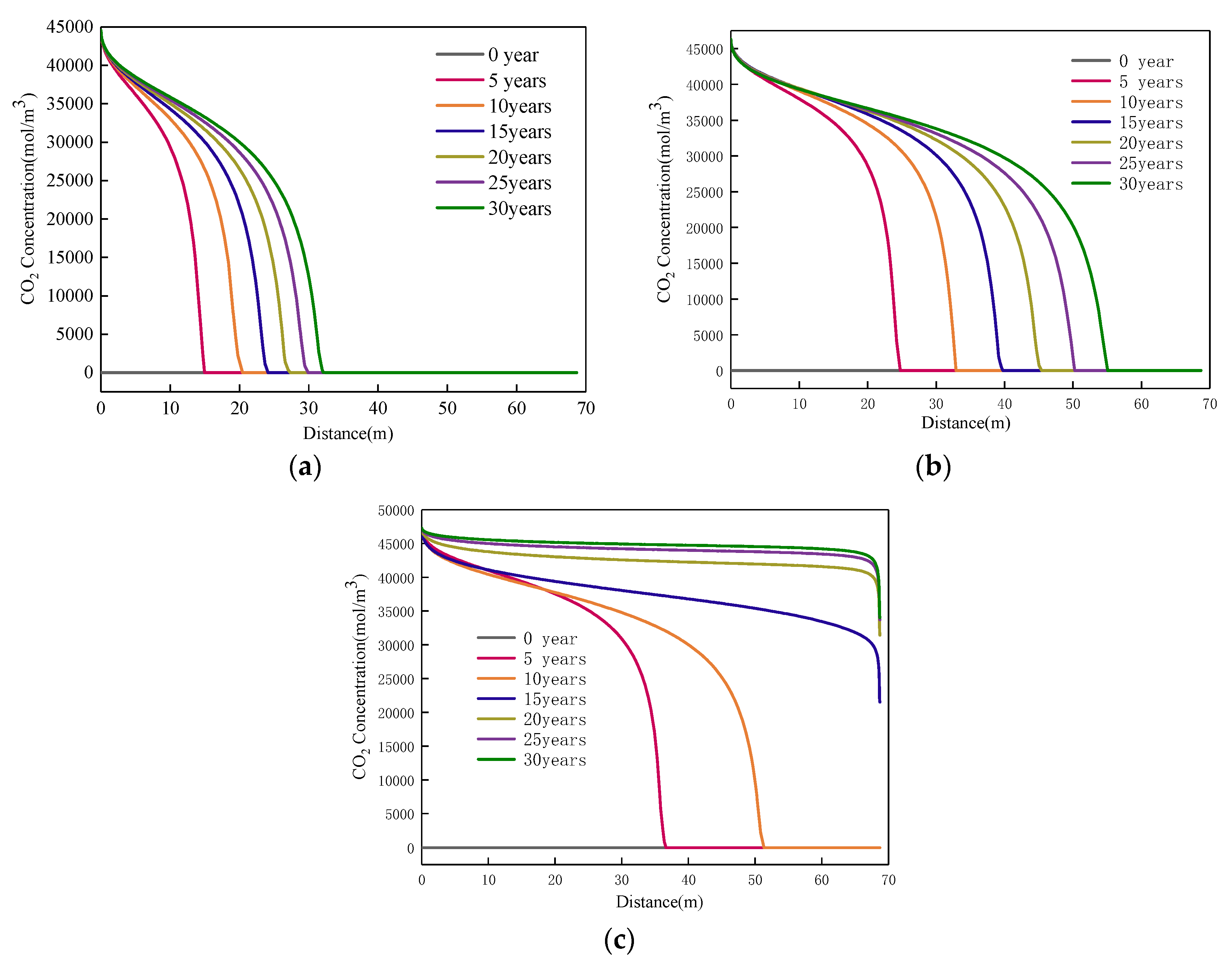
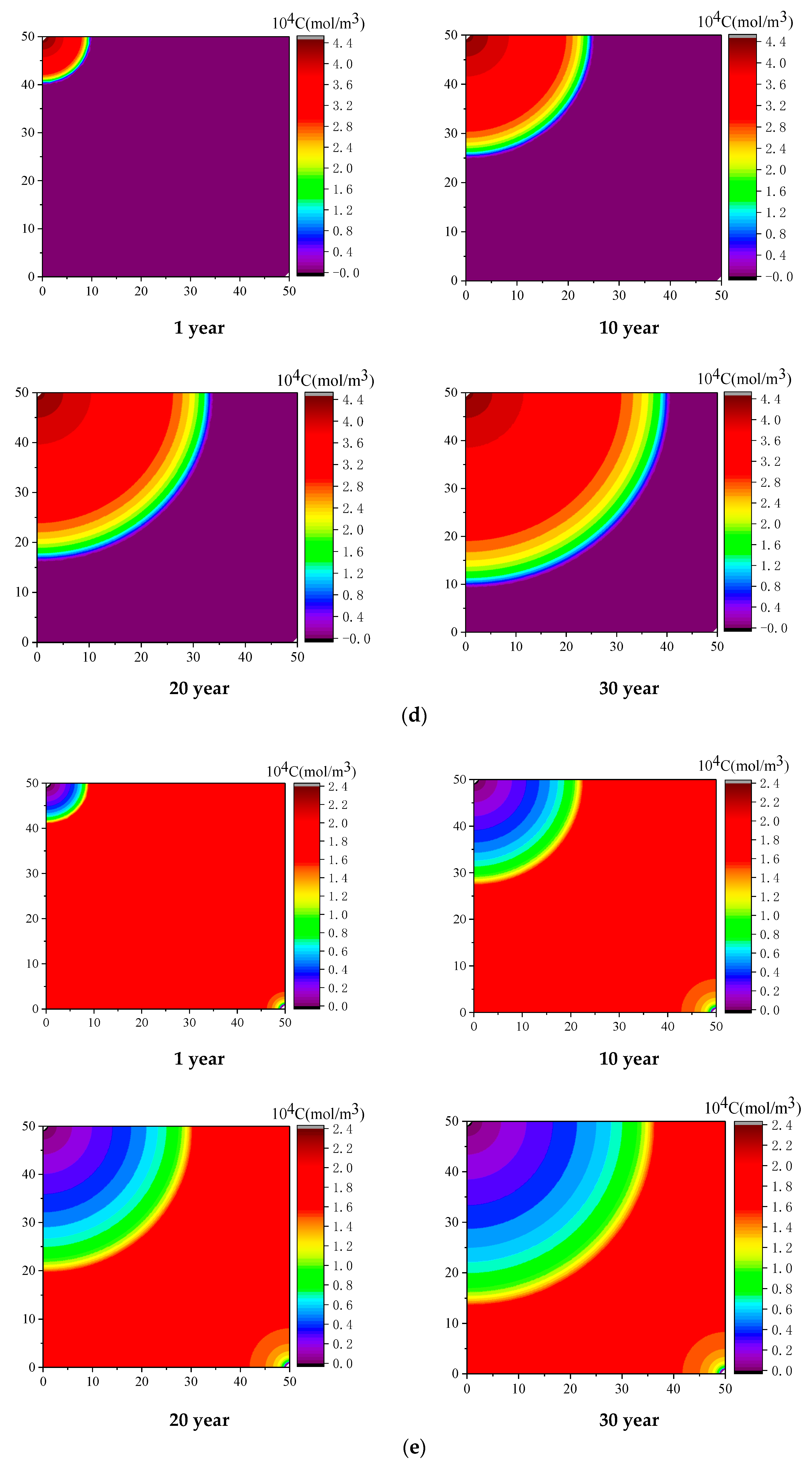
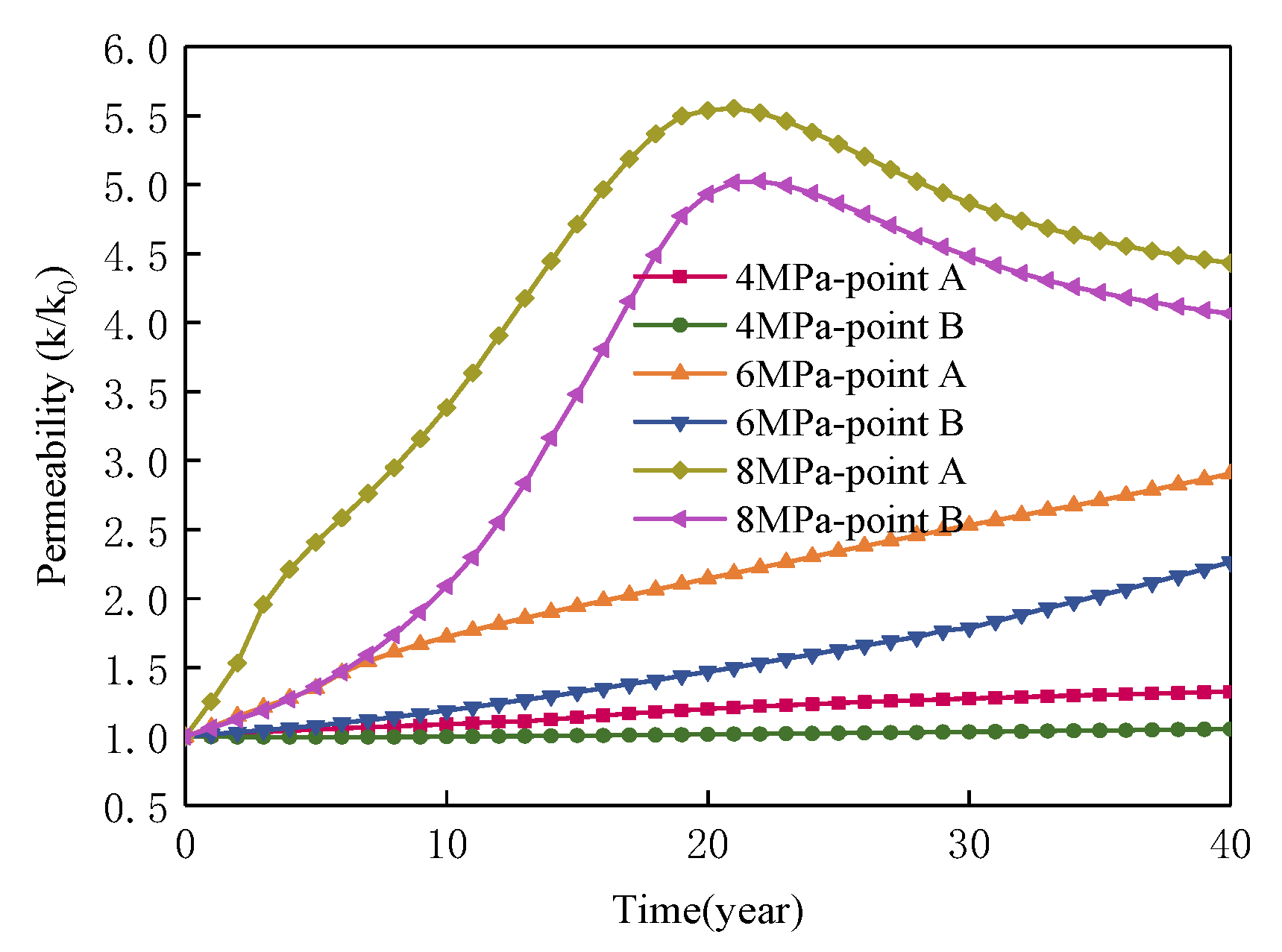
4.1. Effect of Injected CO2 Pressure on CO2-ECBM
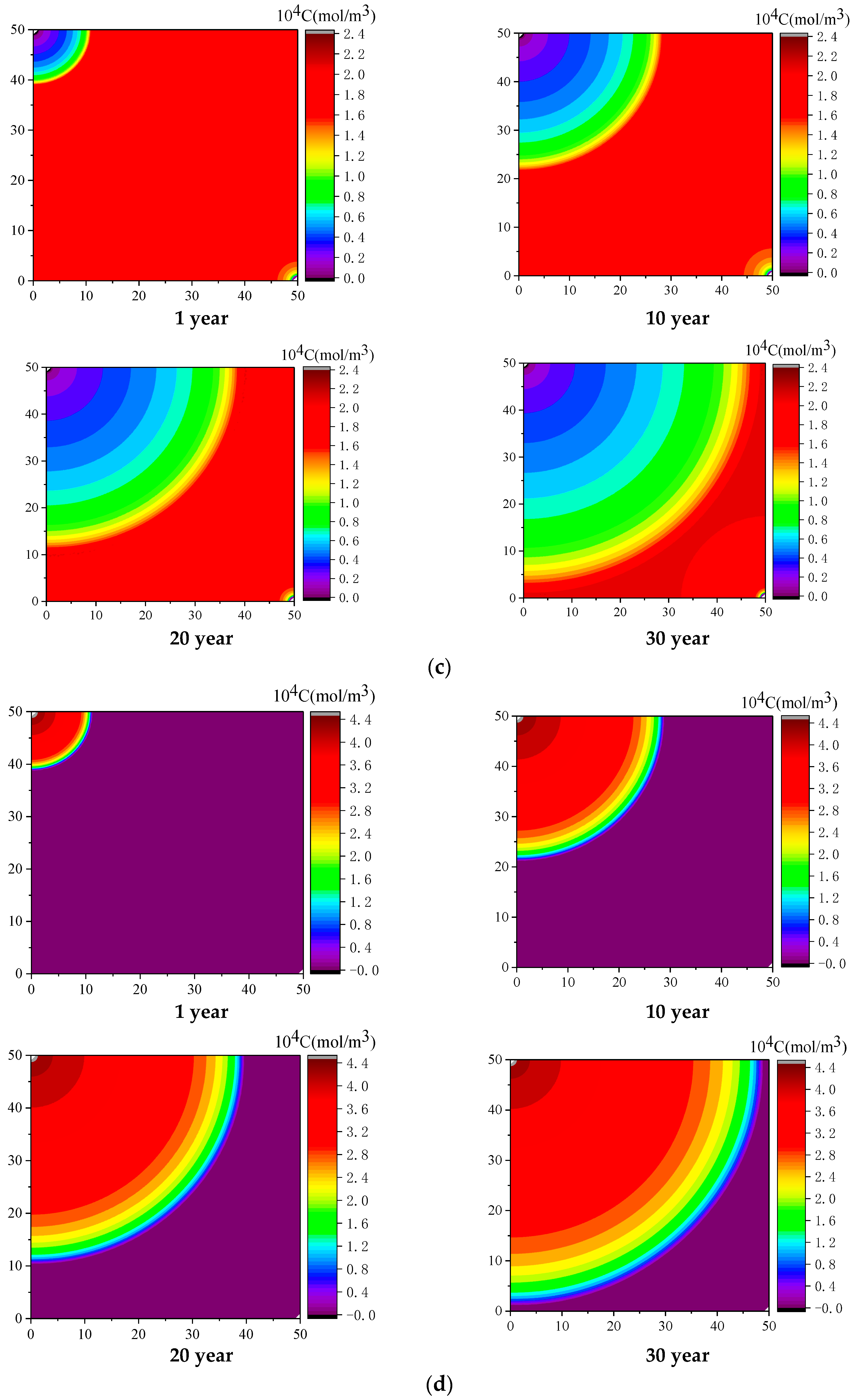
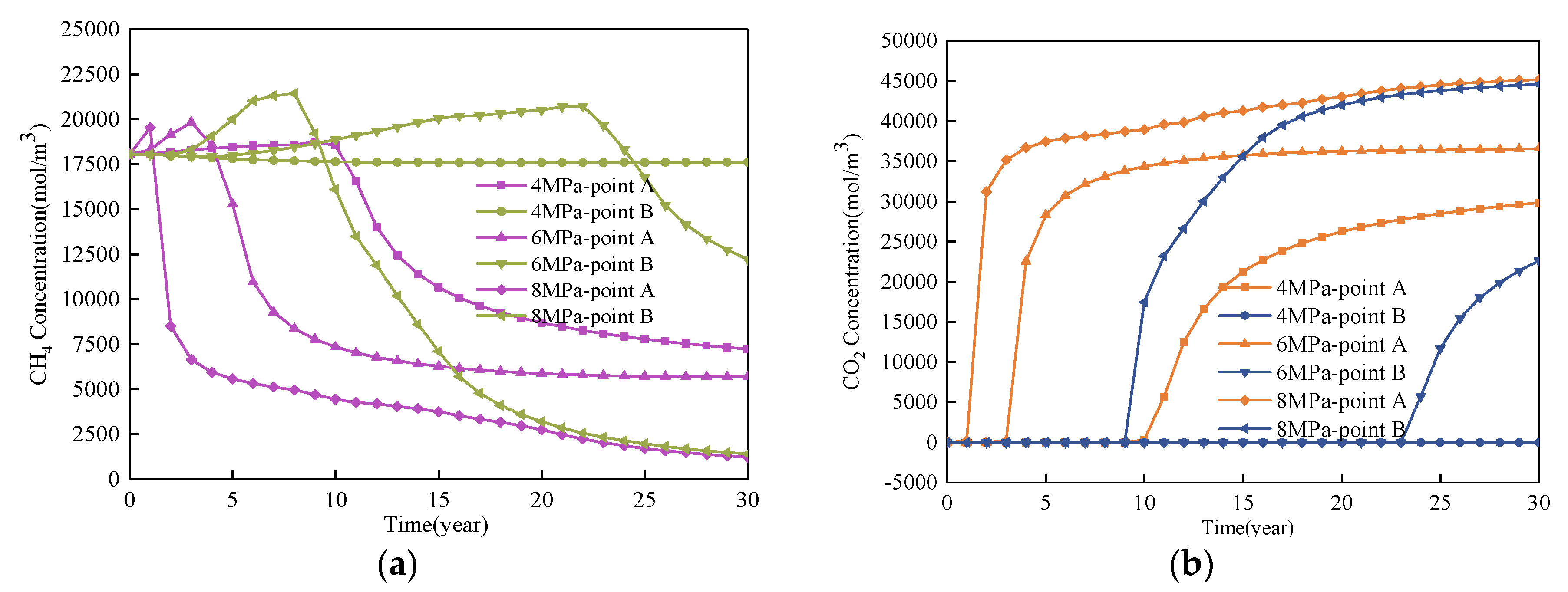
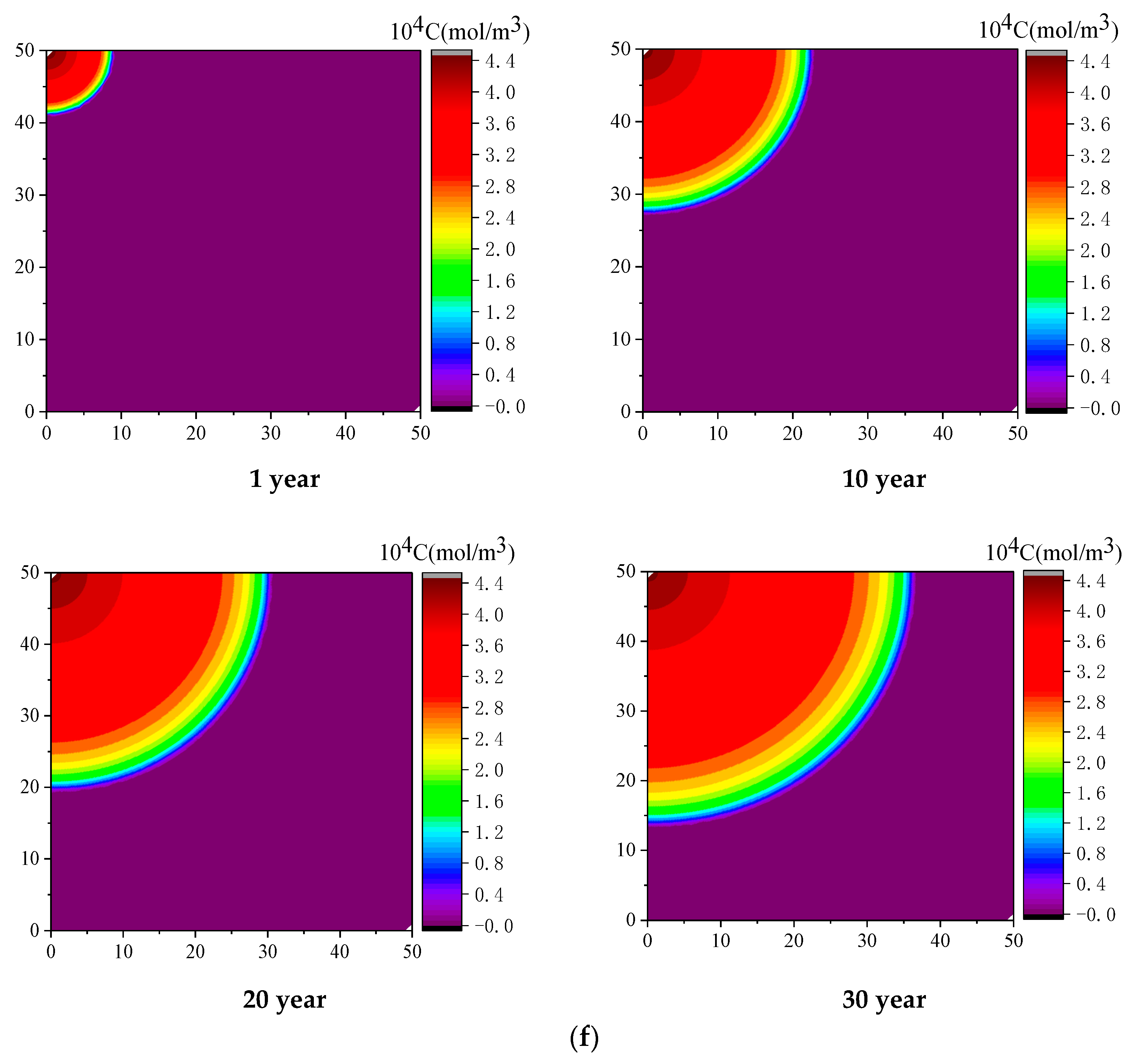
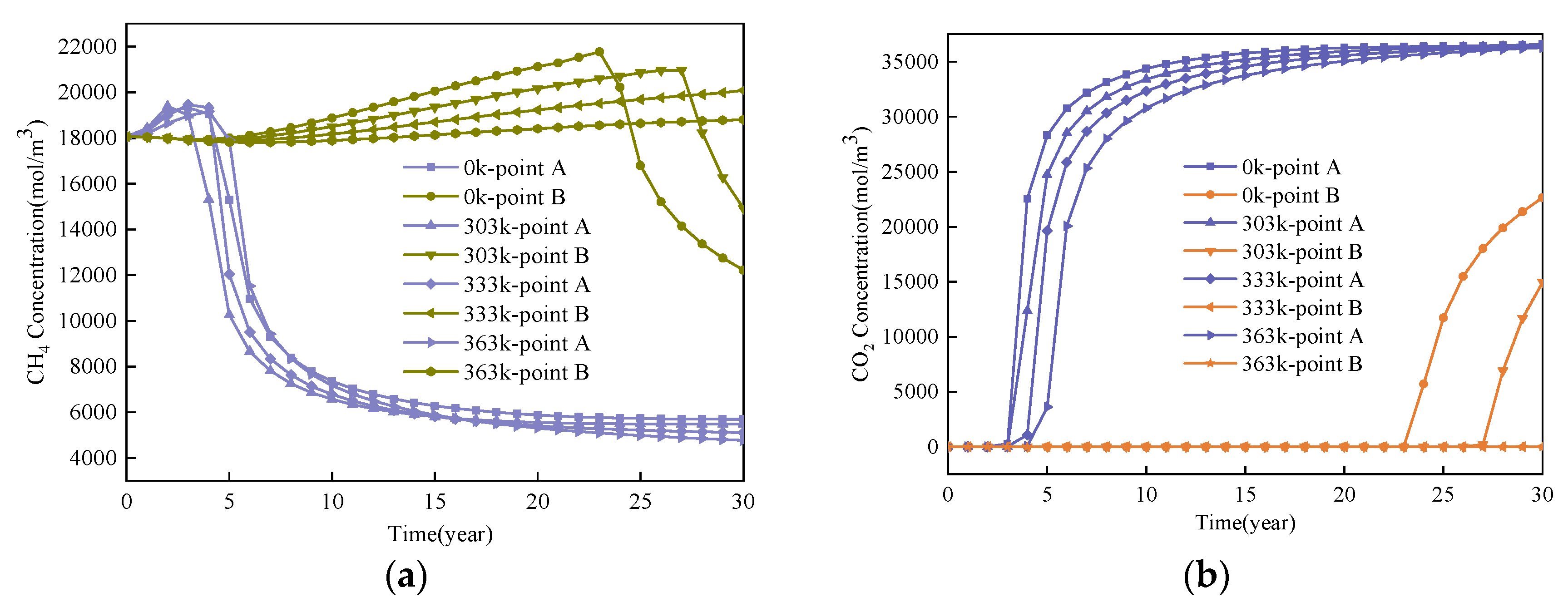
4.2. Effect of Injected CO2 Temperature on CO2-ECBM
5. Conclusions
- (1)
- Higher CO2 injection pressure is associated with higher gas seepage velocities. CO2 reserves and CH4 production increase with increasing CO2 injection pressure. When the injected CO2 pressure is 8 MPa, the storage capacity of CO2 is the highest, the radius of effected by CO2 injection of 5, 10 and 30 years are 31, 44, and 58 m, respectively. After 30 years with injected CO2 pressure of 4, 6, and 8 MPa, the productivity of CH4 in the coal seam is 28%, 43%, and 92%, respectively. Therefore, storage of CO2 and production of CH4 can be significantly increased by increasing pressure.
- (2)
- Coal seam temperature has a significant impact on CO2-ECBM. Under the same CO2 injection pressure, CO2 reserves, CH4 production, and coal seam permeability all decrease with increasing coal seam temperature. The coal seam matrix shrinks at the beginning due to the desorption of CH4, and then it expands due to the adsorption of CO2 and high temperature. This hinders the seepage and displacement of CO2. Therefore, reserve of CO2, production of CH4, and permeability of coal seam all decrease with increasing coal seam temperature. When the injected CO2 temperature is 363 K, the storage capacity of CO2 is the lowest, the radius of effected by CO2 injection of 10, 20, and 30 years are 22, 30, and 36 m, respectively. After 30 years with injected CO2 temperature of 303, 333, and 363 K, the productivity of CH4 in the coal seam is 25%, 22%, and 20%, respectively. The radius of effected by CO2 injection reduces 10 m when the temperature of CO2 injection increases from 303 to 363 K. Therefore, high temperatures are not conducive for CO2 displacement of CH4, and the injection temperature should be reduced.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| The shear modulus, Pa | |
| The bulk modulus of coal, Pa | |
| The Young’s modulus, Pa | |
| Bulk modulus of coal skeleton | |
| Molar constant of gas | |
| Universal gas constant, J/mol·k | |
| Gas pressure, MPa | |
| Temperature of the coal, K | |
| Stress coefficient caused by gas pressure | |
| Stress coefficient caused by gas adsorption | |
| Coefficient of thermal stress | |
| Seepage velocity(m3/s) | |
| Diffusion component of single phase | |
| Diffusion coefficient of single phase, m2/s | |
| Gas mass of each component, kg | |
| Molar concentration of a single component, mol/m3 | |
| Permeability, m2 | |
| Source term, kg/(m3·s) | |
| Molar mass of each component, kg/mol | |
| Heat source for thermal expansion | |
| The internal energy per unit volume | |
| Specific heat at constant volume of coal seam | |
| Differential heat source. | |
| Initial volume of coal skeleton | |
| The coal skeleton volume changes | |
| Bulk expansion and deformation of coal caused by pressure | |
| Bulk expansion and deformation of coal caused by temperature | |
| The initial permeability, m2 | |
| Poisson’s ratio | |
| Thermal expansion coefficient, K−1 | |
| Kronecker function | |
| Langmuir volume constant, m3/kg | |
| Langmuir pressure constant, Pa−1 | |
| Density of coal, kg/m3 | |
| Thermal expansion strain | |
| Strain caused by gas pressure | |
| Gas strain | |
| Train component | |
| Displacement component | |
| Biot coefficient | |
| Stress tensor(i, j = 1, 2) | |
| Viscosity coefficient of single phase | |
| Density of a single component, kg/m3 | |
| Porosity | |
| Density of gas at standard conditions, kg/m3 | |
| Thermal conductivity of coal | |
| Initial porosity of coal | |
| Volumetric strain of coal | |
| Effective diameter of particle |
References
- Sun, H.; Yao, J.; Gao, S.H.; Fan, D.Y.; Wang, C.C.; Sun, Z.X. Numerical study of CO2 enhanced natural gas recovery and sequestration in shale gas reservoirs. Int. J. Greenh. Gas Control 2013, 19, 406–419. [Google Scholar] [CrossRef]
- Xia, T.; Zhou, F.; Liu, J.; Hu, S.; Liu, Y. A fully coupled coal deformation and compositional flow model for the control of the pre-mining coal seam gas extraction. Int. J. Rock Mech. Min. Sci. 2014, 72, 138–148. [Google Scholar] [CrossRef]
- Sobczyk, J. A comparison of the influence of adsorbed gases on gas stresses leading to coal and gas outburst. Fuel 2014, 115, 288–294. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, Y.; Zhang, X. Selective adsorption and selective transport diffusion of CO2–CH4 binary mixture in coal ultramicropores. Environ. Sci. Technol. 2016, 50, 9380–9389. [Google Scholar] [CrossRef] [PubMed]
- Orr, F.M. Onshore Geologic Storage of CO2. Science 2009, 325, 1656–1658. [Google Scholar] [CrossRef] [PubMed]
- Sreenivasulu, B.; Suresh, P.; Sreedhar, I.; Raghavan, K.V. Development trends in porous adsorbents for carbon capture. Environ. Sci. Technol. 2015, 49, 12641–12661. [Google Scholar] [CrossRef]
- Shahtalebi, A.; Shukla, P.; Farmahini, A.H.; Bhatia, S.K. Barriers to diffusion of CO2 in microporous carbon derived from silicon carbide. Carbon 2015, 88, 1–15. [Google Scholar] [CrossRef]
- Karacan, C.; Ruiz, F.A.; Michael, C.; Phipps, S. Coal mine methane: A review of capture and utilization practices with benefits to mining safety and to greenhouse gas reduction. Int. J. Coal Geol. 2011, 86, 121–156. [Google Scholar] [CrossRef]
- Zhou, F.; Hussain, F.; Cinar, Y. Injecting pure N2 and CO2 to coal for enhanced coalbed methane: Experimental observations and numerical simulation. Int. J. Coal Geol. 2013, 116, 53–62. [Google Scholar] [CrossRef]
- Liu, J.; Xie, L.; Elsworth, D.; Gan, Q. CO2/CH4 Competitive Adsorption in Shale: Implications for Enhancement in Gas Production and Reduction in Carbon Emissions. Environ. Sci. Technol. 2019, 53, 9328–9336. [Google Scholar] [CrossRef]
- Liu, X.; Wu, C.; Zhao, K. Feasibility and applicability analysis of CO2-ECBM based on CO2-H2O-coal interactions. Energy Fuels 2017, 31, 9268–9274. [Google Scholar] [CrossRef]
- Pratama, E.; Ismail, M.S.; Ridha, S. Identification of coal seams suitability for carbon dioxide sequestration with enhanced coalbed methane recovery: A case study in South Sumatera Basin, Indonesia. Clean Technol. Environ. Policy. 2017, 20, 581–587. [Google Scholar] [CrossRef]
- Zhang, R.; Yin, X.; Winterfeld, P.H.; Wu, Y.S. A fully coupled thermal-hydrological-mechanical-chemical model for CO2 geological sequestration. J. Nat. Gas Sci. Eng. 2016, 28, 280–304. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Xie, L.; Yao, Y.; Gan, Q.; Zhao, P.; Du, L. Preliminary study of influence factors and estimation model of the enhanced gas recovery stimulated by carbon dioxide utilization in shale. ACS Sustain. Chem. Eng. 2019, 7, 20114–20125. [Google Scholar] [CrossRef]
- White, C.M.; Smith, D.H.; Jones, K.L.; Goodman, A.L.; Schroeder, K.T. Sequestration of carbon dioxide in coal with enhanced coalbed methane recovery a review. Energy Fuels 2005, 19, 659–724. [Google Scholar] [CrossRef]
- Gentzis, T. Subsurface sequestration of carbon dioxide-an overview from an Alberta (Canada) perspective. Int. J. Coal Geol. 2000, 43, 287–305. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J.; Elsworth, D.; Chen, Z.; Pan, Z. Dual poroelastic response of coal seam to CO2 injection. Int. J. Greenh. Gas Control 2010, 4, 668–678. [Google Scholar] [CrossRef]
- Charrière, D.; Pokryszka, Z.; Behra, P. Effect of pressure and temperature on diffusion of CO2 and CH4 into coal from the Lorraine basin. Int. J. Coal Geol. 2010, 81, 373–380. [Google Scholar] [CrossRef]
- Mazumder, S.; Wolf, K.H. Differential swelling and permeability change of coal in response to CO2 injection for ECBM. Int. J. Coal Geol. 2008, 74, 123–138. [Google Scholar] [CrossRef]
- Wei, X.R.; Wang, G.X.; Massarotto, P.; Golding, S.D.; Rudolph, V. Numerical simulation of multicomponent gas diffusion and flow in coals for enhanced coalbed methane recovery. Chem. Eng. Sci. 2007, 62, 4193–4203. [Google Scholar] [CrossRef]
- Fujioka, M.; Yamaguchi, S.; Nako, M. CO2-ECBM field tests in the Ishikari Coal Basin of Japan. Int. J. Coal Geol. 2010, 82, 287–298. [Google Scholar] [CrossRef]
- Luo, F.; Xu, R.N.; Jiang, P.X. Numerical investigation of the influence of vertical permeability heterogeneity in stratified formation and of injection/production well perforation placement on CO2 geological storage with enhanced CH4 recovery. Appl. Energy 2013, 102, 1314–1323. [Google Scholar] [CrossRef]
- Vishal, V.; Singh, T.N.; Ranjith, P.G. Influence of sorption time in CO2-ECBM process in Indian coals using coupled numerical simulation. Fuel 2015, 139, 51–58. [Google Scholar] [CrossRef]
- Wang, G.; Ren, T.; Qi, Q.; Zhang, L.; Liu, Q. Prediction of Coalbed Methane (CBM) Production Considering Bidisperse Diffusion: Model Development, Experimental Test, and Numerical Simulation. Energy Fuels 2017, 31, 5785–5797. [Google Scholar] [CrossRef]
- Fan, Y.; Deng, C.; Zhang, X.; Li, F.; Wang, X.; Qiao, L. Numerical study of CO2-enhanced coalbed methane recovery. Int. J. Greenh. Gas Control 2018, 76, 12–23. [Google Scholar] [CrossRef]
- Fang, H.H.; Sang, S.X.; Liu, S.Q. Numerical simulation of enhancing coalbed methane recovery by injecting CO2 with heat injection. Pet. Sci. 2019, 16, 32–43. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.; Elsworth, D.; Li, S.; Zhou, L.; Yang, Z.; Song, Y. Thermo-hydro-mechanical-chemical couplings controlling CH4 production and CO2 sequestration in enhanced coalbed methane recovery. Energy 2019, 173, 1054–1077. [Google Scholar] [CrossRef]
- Li, H.; Lin, B.; Yang, W.; Hong, Y.; Wang, Z. A fully coupled electromagnetic-thermal-mechanical model for coalbed methane extraction with microwave heating. J. Nat. Gas Sci. Eng. 2017, 46, 830–844. [Google Scholar] [CrossRef]
- Fan, C.; Elsworth, D.; Li, S.; Chen, Z.; Luo, M.; Song, Y.; Zhang, H. Modelling and optimization of enhanced coalbed methane recovery using CO2/N2 mixtures. Fuel 2019, 253, 1114–1129. [Google Scholar] [CrossRef]
- Li, S.; Fan, C.; Han, J.; Luo, M.; Yang, Z.; Bi, H. A fully coupled thermal-hydraulic-mechanical model with two-phase flow for coalbed methane extraction. J. Nat. Gas Sci. Eng. 2016, 33, 324–336. [Google Scholar] [CrossRef] [Green Version]
- Teng, T.; Zhao, Y.; Gao, F.; Wang, J.G.; Wang, W. A fully coupled thermo-hydro-mechanical model for heat and gas transfer in thermal stimulation enhanced coal seam gas recovery. Int. J. Heat Mass Transf. 2018, 125, 866–875. [Google Scholar] [CrossRef]
- Xia, T.; Zhou, F.; Gao, F.; Kang, J.; Liu, J.; Wang, J. Simulation of coal self-heating processes in underground methane-rich coal seams. Int. J. Coal Geol. 2015, 141, 1–12. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Elsworth, D.; Qu, H.; Chen, D. Interactions of multiple processes during CBM extraction: A critical review. Int. J. Coal Geol. 2011, 87, 175–189. [Google Scholar] [CrossRef]
- Qu, H.; Liu, J.; Chen, Z.; Wang, J.; Pan, Z.; Connell, L. Complex evolution of coal permeability during CO2 injection under variable temperatures. Int. J. Greenh. Gas Control 2012, 9, 281–293. [Google Scholar] [CrossRef]
- Huang, S.P. In situ stress distribution and its impact on CBM reservoir properties in the Zhengzhuang area, southern Qinshui Basin, North China. J. Nat. Gas Sci. Eng. 2019, 61, 83–96. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Elsworth, D. How sorption-induced matrix deformation affects gas flow in coal seams: A new FE model. Int. J. Rock Mech. Min. Sci. 2008, 45, 1226–1236. [Google Scholar] [CrossRef]
- Liu, T.; Lin, B.; Yang, W.; Liu, T.; Kong, J.; Huang, Z. Dynamic diffusion-based multifield coupling model for gas drainage. J. Nat. Gas Sci. Eng. 2017, 44, 233–249. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, C.H.; Liu, J.; Qu, H.Y.; Elsworth, D. A model of coal–gas interaction under variable temperatures. Int. J. Coal Geol. 2011, 86, 213–221. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, Y.; Liu, Q.; Jiang, J.; Li, W.; Zhang, K. Numerical assessment of CMM drainage in the remote unloaded coal body: Insights of geostress-relief gas migration and coal permeability. J. Nat. Gas Sci. Eng. 2017, 45, 487–501. [Google Scholar] [CrossRef]
- Kong, X.; Wang, E.; Liu, Q.; Li, Z.; Li, D.; Cao, Z. Dynamic permeability and porosity evolution of coal seam rich in CBM based on the flow-solid coupling theory. J. Nat. Gas Sci. Eng. 2017, 40, 61–71. [Google Scholar] [CrossRef]
- Li, X.C.; Guo, Y.Y.; Wu, S.Y.; Nie, B.S. Mathematical model and numerical simulation of fluid-solid coupled flow of coal-bed gas considering swelling stress of adsorption. Chin. J. Rock Mech. Eng. 2007, 26, 2743–2748. [Google Scholar]
- Zheng, C.; Chen, Z.; Kizil, M.; Aminossadati, S.; Zou, Q.; Gao, P. Characterisation of mechanics and flow fields around in-seam methane gas drainage borehole for preventing ventilation air leakage: A case study. Int. J. Coal Geol. 2016, 162, 123–138. [Google Scholar] [CrossRef] [Green Version]
- Pan, Z.; Connell, L.D. Comparison of adsorption models in reservoir simulation of enhanced coalbed methane recovery and CO2 sequestration in coal. Int. J. Greenh. Gas Control 2009, 3, 77–89. [Google Scholar] [CrossRef]
- Balan, H.O.; Gumrah, F. Assessment of shrinkage–swelling influences in coal seams using rank-dependent physical coal properties. Int. J. Coal Geol. 2009, 77, 203–213. [Google Scholar] [CrossRef]
- Durucan, S.; Shi, J.Q. Improving the CO2 well injectivity and enhanced coalbed methane production performance in coal seams. Int. J. Coal Geol. 2009, 77, 214–221. [Google Scholar] [CrossRef]
- Han, L.F.; Hou, Y.D.; Wang, Y.J.; Liu, X.B.; Han, J.; Xie, R.H.; Mu, H.W.; Fu, C.F. Measurement of Velocity of Sand -Containing Oil–Water Two-Phase Flow with Super High Water Holdup in Horizontal Small Pipe Based on Thermal Tracers. Flow Meas Instrum. 2019, 69, 101622–101631. [Google Scholar] [CrossRef]




| Variable | Parameter | Value |
|---|---|---|
| Gas pressure under standard conditions (MPa) | 2 | |
| Initial temperature of coal seam (K) | 273 | |
| The density of coal (kg/m3) | 1350 | |
| CH4 molar mass (kg/mol) | 0.016 | |
| CO2 molar mass (kg/mol) | 0.044 | |
| CH4 dynamic viscosity coefficient (Pa·s) | ||
| CO2 dynamic viscosity coefficient (Pa·s) | ||
| CH4 density under standard conditions (kg/m3) | 0.717 | |
| Poisson’s ratio | 0.35 | |
| Young’s modulus of coal (MPa) | 2713 | |
| Universal gas constant (J/(mol·k)) | 8.314 | |
| Thermal conductivity (W/(m·k)) | 0.478 | |
| Thermal expansion coefficient (K−1) | 2.4 × 10−5 | |
| Heat capacity at constant stress (J/(kg·k) | 1000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yudong, H.; Saipeng, H.; Jian, H.; Xingbin, L.; Lianfu, H.; Changfeng, F. Numerical Simulation of the Effect of Injected CO2 Temperature and Pressure on CO2-Enhanced Coalbed Methane. Appl. Sci. 2020, 10, 1385. https://doi.org/10.3390/app10041385
Yudong H, Saipeng H, Jian H, Xingbin L, Lianfu H, Changfeng F. Numerical Simulation of the Effect of Injected CO2 Temperature and Pressure on CO2-Enhanced Coalbed Methane. Applied Sciences. 2020; 10(4):1385. https://doi.org/10.3390/app10041385
Chicago/Turabian StyleYudong, Hou, Huang Saipeng, Han Jian, Liu Xingbin, Han Lianfu, and Fu Changfeng. 2020. "Numerical Simulation of the Effect of Injected CO2 Temperature and Pressure on CO2-Enhanced Coalbed Methane" Applied Sciences 10, no. 4: 1385. https://doi.org/10.3390/app10041385
APA StyleYudong, H., Saipeng, H., Jian, H., Xingbin, L., Lianfu, H., & Changfeng, F. (2020). Numerical Simulation of the Effect of Injected CO2 Temperature and Pressure on CO2-Enhanced Coalbed Methane. Applied Sciences, 10(4), 1385. https://doi.org/10.3390/app10041385




