Interval Identification of Thermal Parameters Using Trigonometric Series Surrogate Model and Unbiased Estimation Method
Abstract
:Featured Application
Abstract
1. Introduction
2. Model Structures
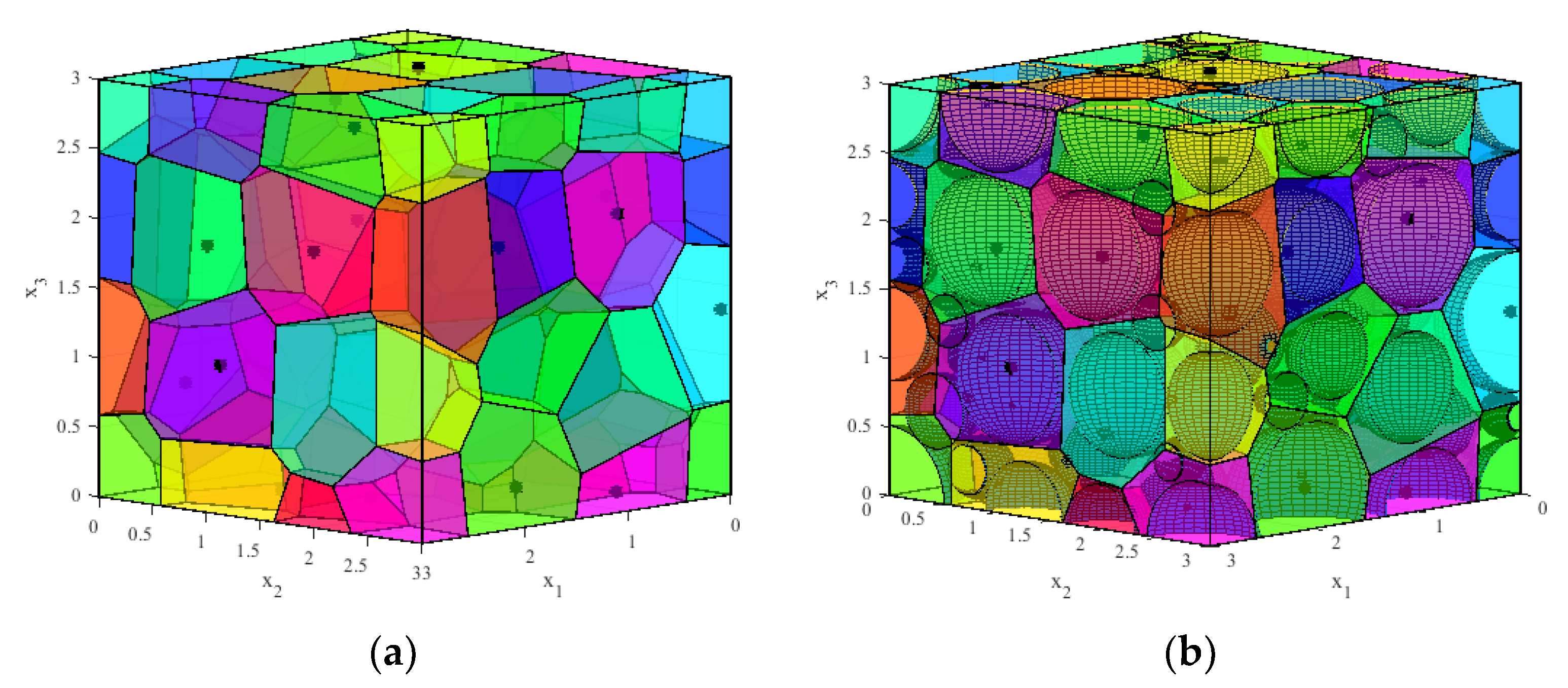
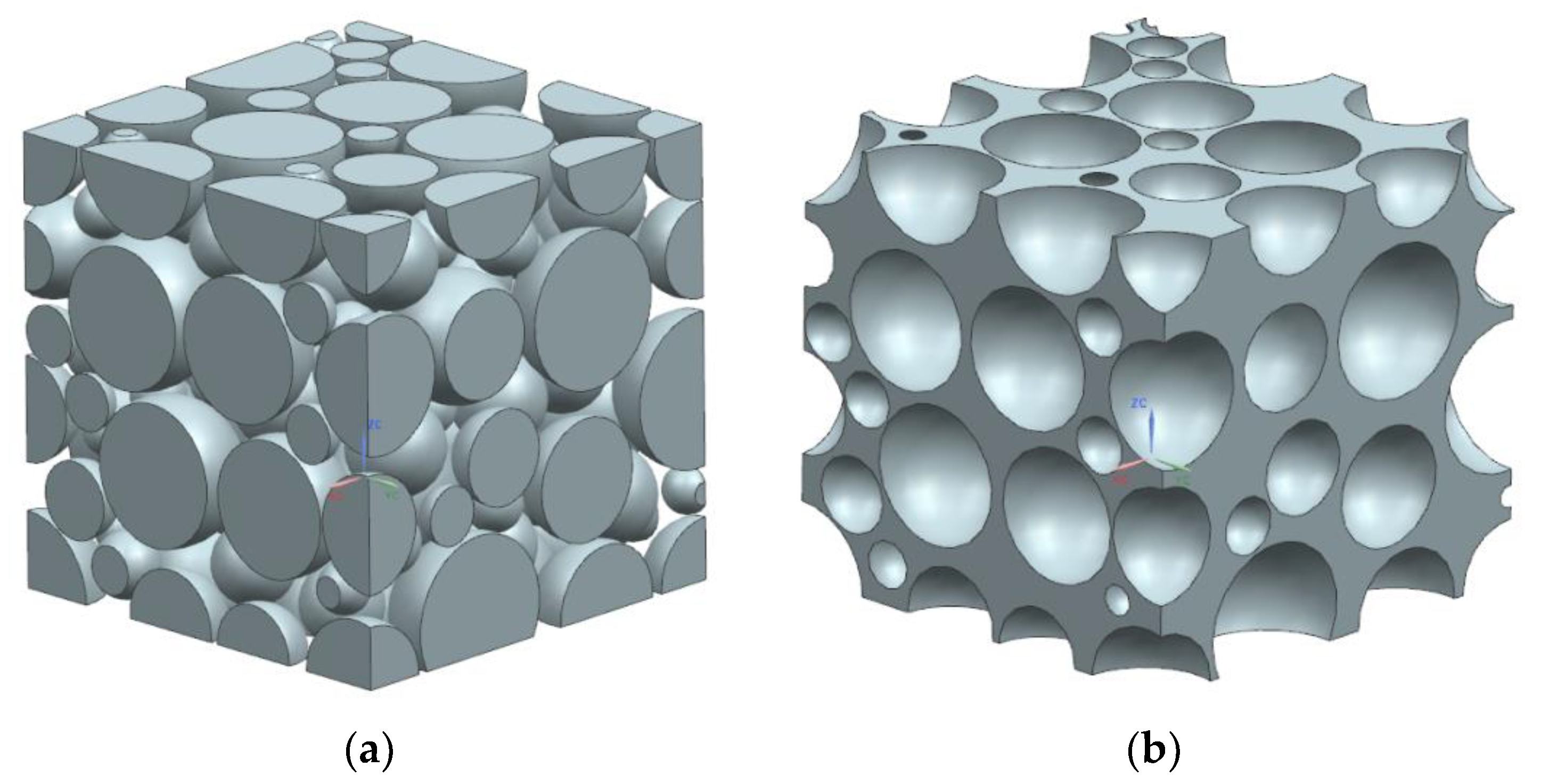
2.1. Generation of a Closed-Cell Foam Structure
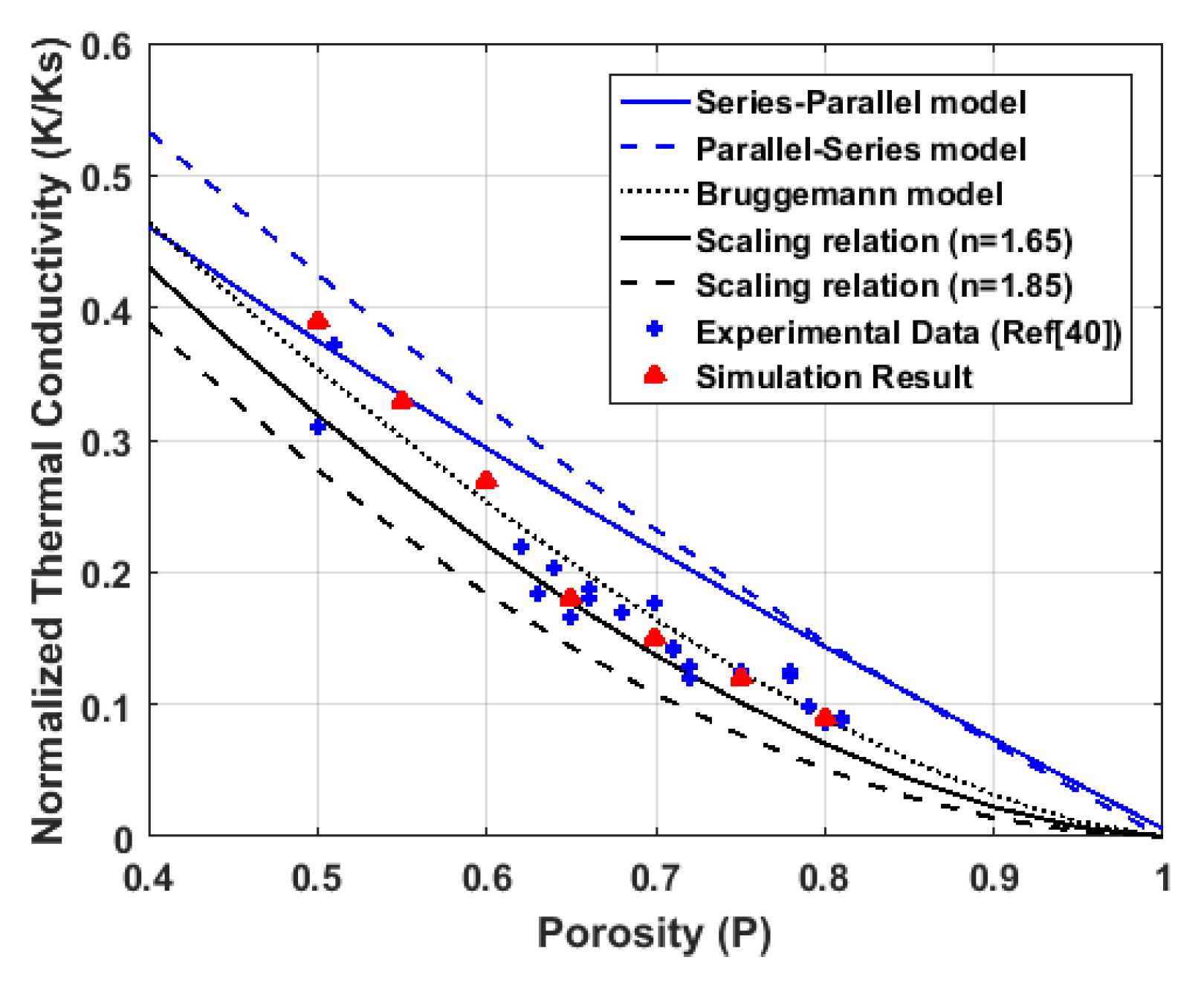
2.2. Effective Thermal Conductivity of the Foam Structure
3. Theory Preparation
3.1. Thermodynamics Computational Model with Uncertainty
3.2. Augmented Trigonometric Polynomial Surrogate Model
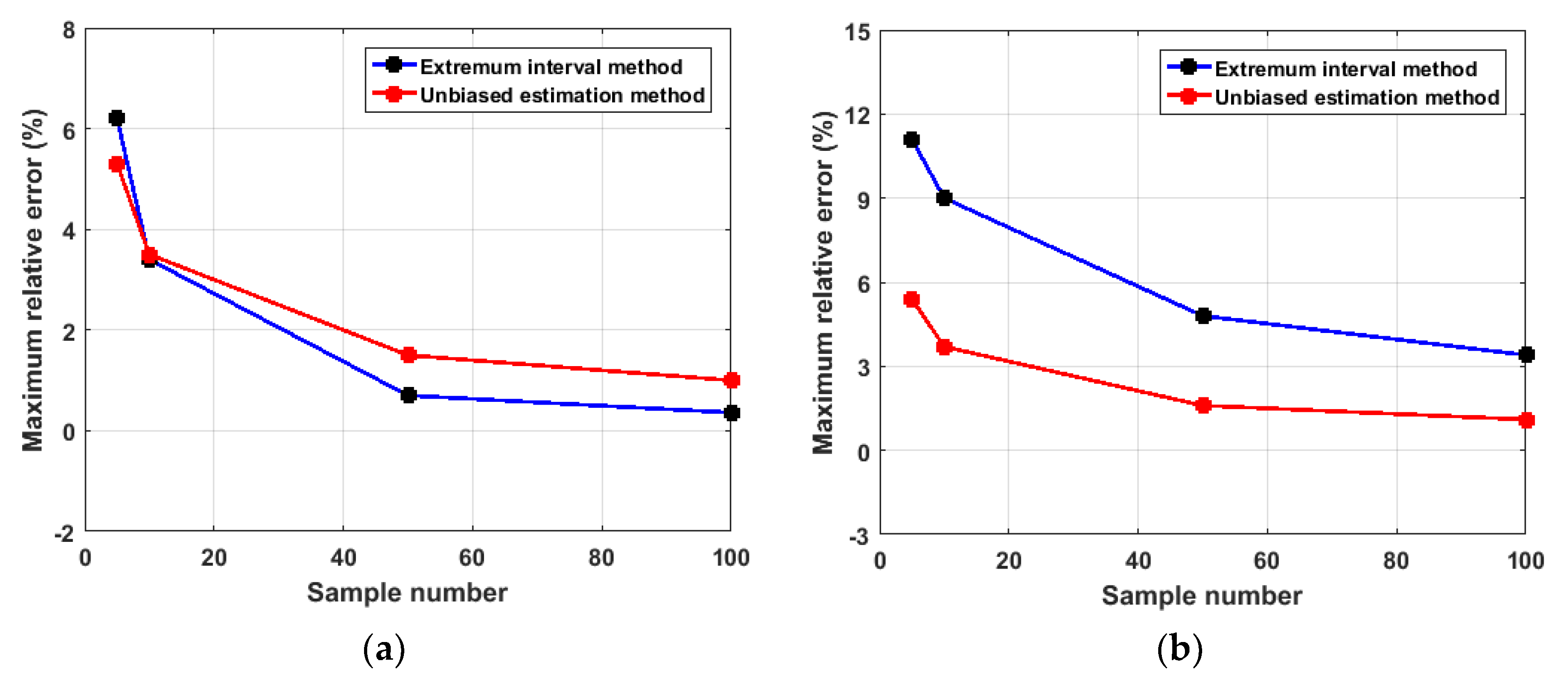
3.3. Unbiased Estimation for Inadequate Interval
3.3.1. Uniformly Distributed
3.3.2. Normal Distribution
3.3.3. Numerical Calculation
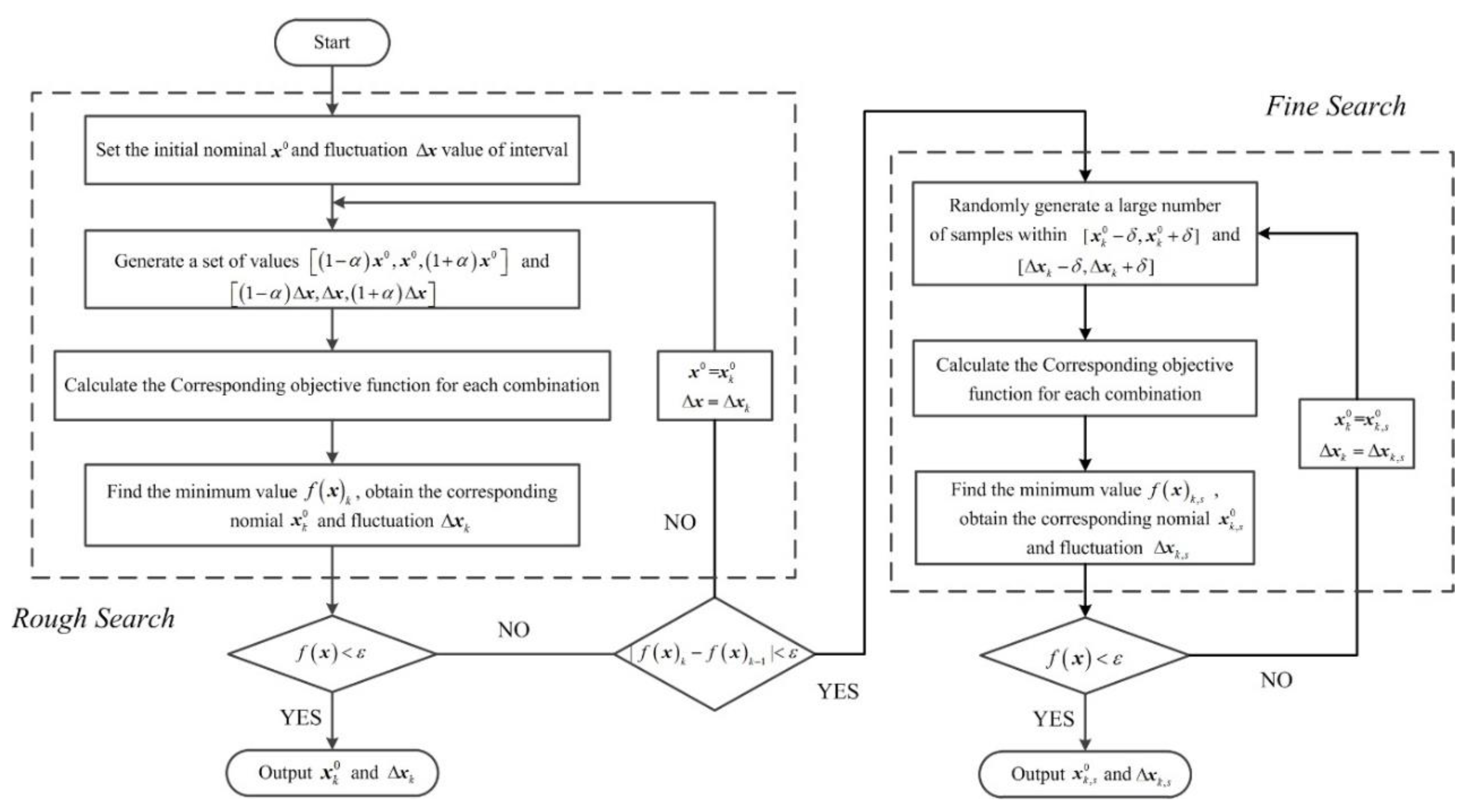
4. Interval Parameter Identification Procedure
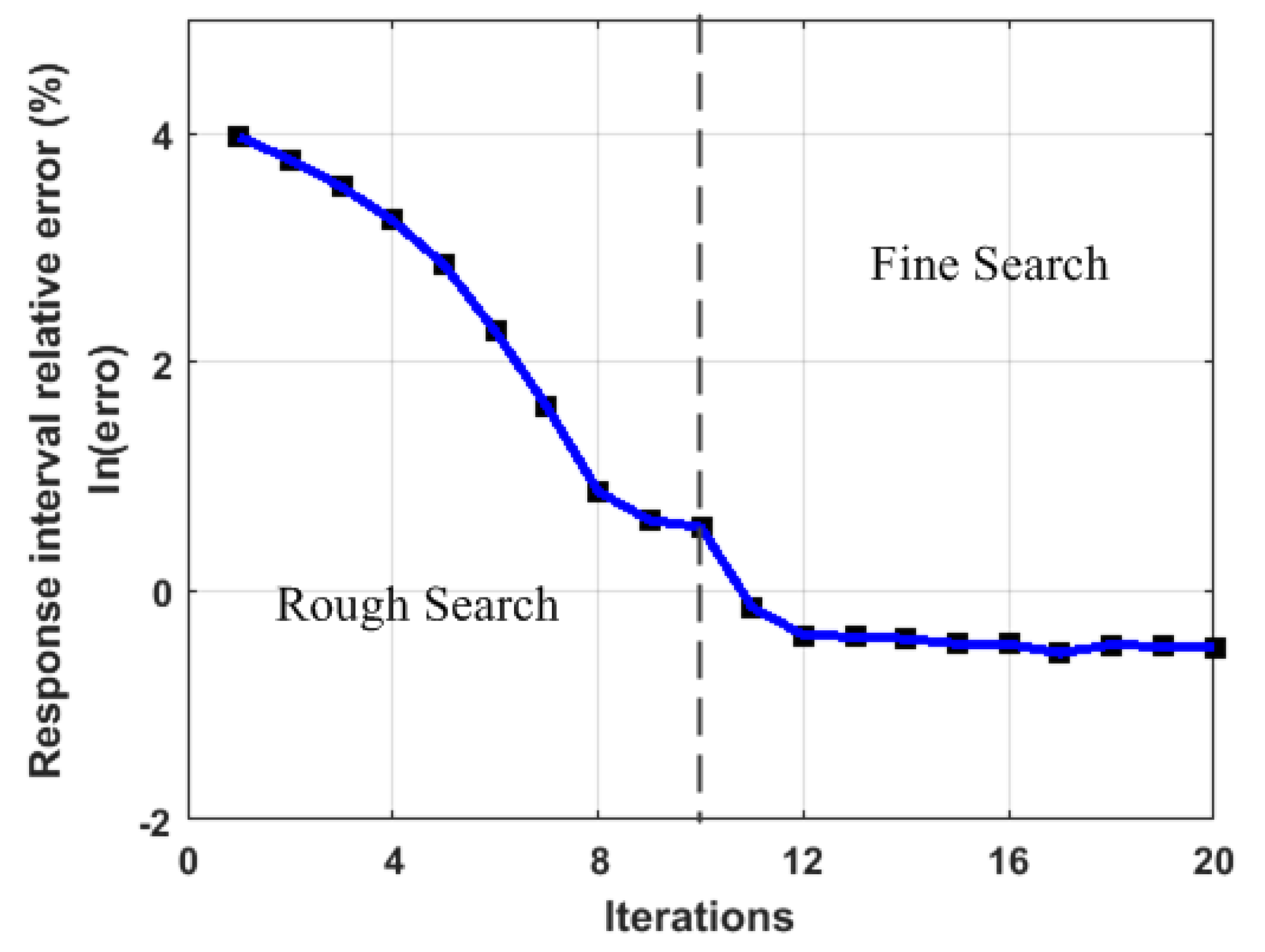
4.1. Searching the Initial Value
4.2. Searching the Eventual Result
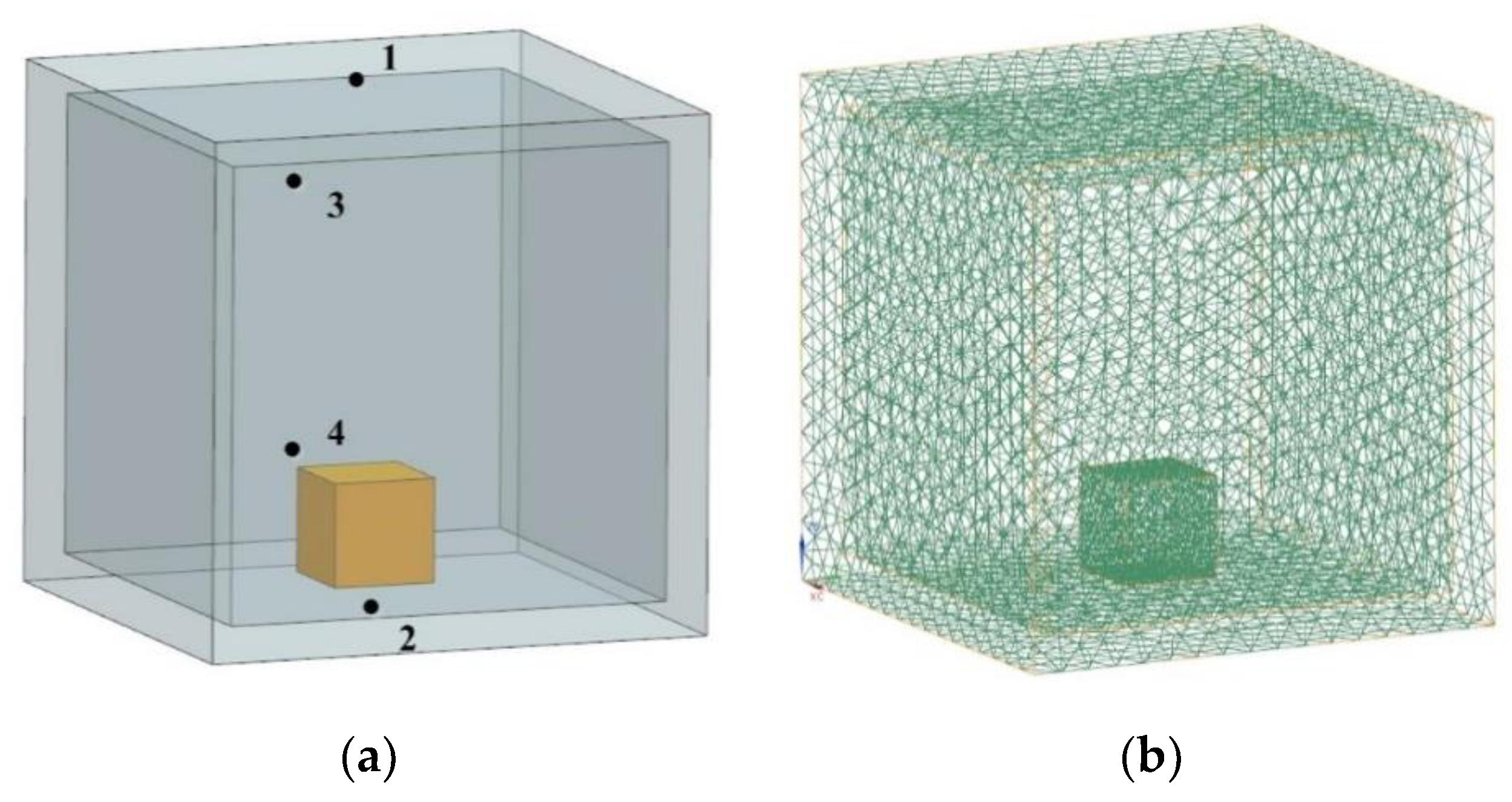
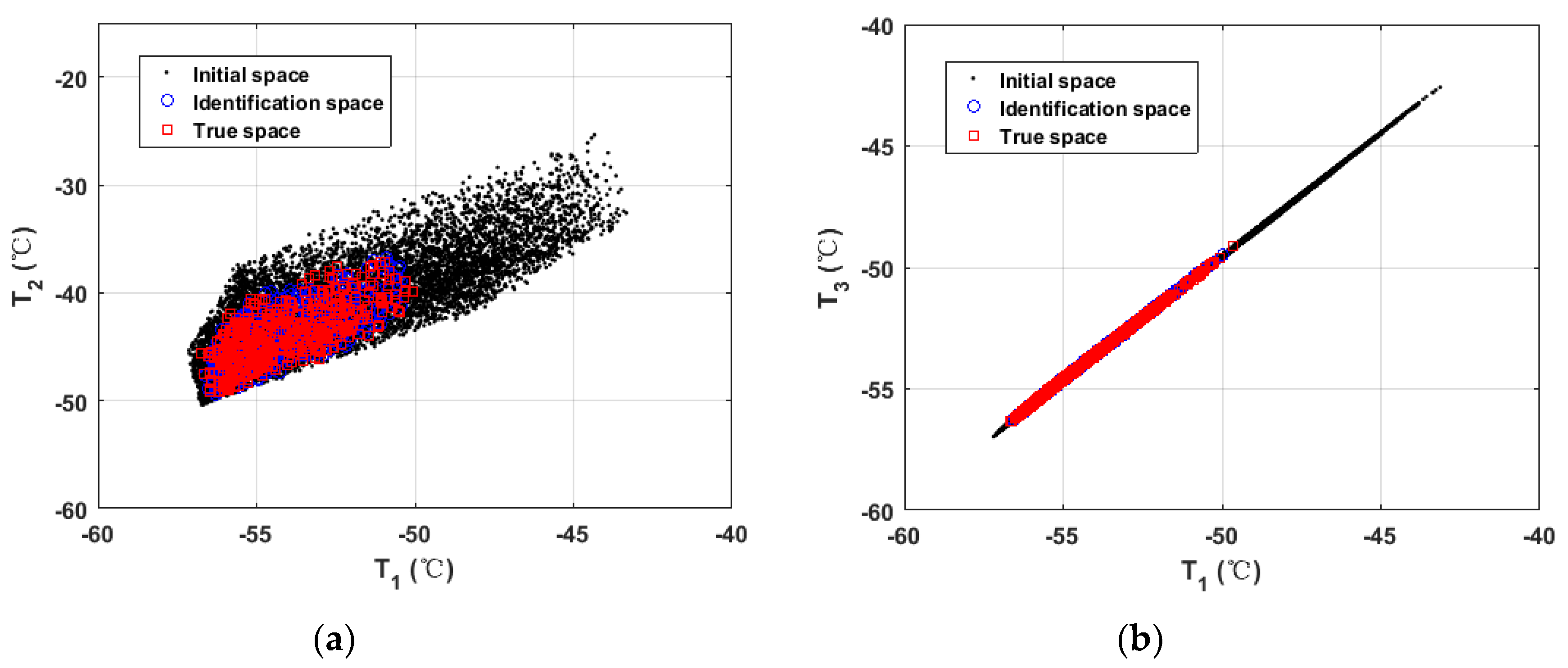
5. Numerical Example
6. Conclusions
- A novel Voronoi-based modelling methodology is proposed for the closed-cell metal-foam in low porosity, by which the realistic pore geometry can be generated concisely and effectively. This method adopts the new algorithm of spheres random packing, which can simplify the calculation program. Moreover, the randomness of the boundary thickness between pores is taken into account in the searching process. Meanwhile, the boundary constraint can be effectively removed when searching the maximum volume sphere of convex polyhedra on boundary surfaces.
- Compared to the probabilistic based parameter identification methods, interval methods can preferably describe uncertainty problems, especially for the case with limited information. Besides, the novel ATP surrogate model was constructed to describe the mapping relationship between variables and responses effectively and accurately. Meanwhile, the unbiased estimations method is adopted to describe the measurement interval of the actual engineering system accurately.
- To executive the parameter identification procedure effectively, the novel multi-level optimization-based strategy was designed, which can identify the unknown parameter of uncertain systems efficiently and accurately in the order of searching the initial value, rough searching, and fine searching.
- An engineering heat transfer example of a box structure made of metal-foam was provided to verify the efficiency of the proposed method without sufficient information. The satisfactory identification results were obtained when applied to the proposed method, which indicated that the proposed interval parameter identification method could quantify the uncertainty of metal-foam structure in the engineering heat transfer system efficiently, especially for the actual case without sufficient measurements.
- The application of the unbiased estimation method was under certain conditions in this study. Furthermore, the validation example just considered a single non-probabilistic uncertainty. In the future, the applicable conditions of the unbiased estimation method will be further studied. Meanwhile, the proposed method will be expanded to complex engineering problems with mixed uncertainties.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Gibson, L.J.; Ashby, M.F. Cellular Solids Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Silva, M.J.; Gibson, L.J. The effects of non-periodic microstructure and defects on the compressive strength of two-dimensional cellular solids. Int. J. Mech. Sci. 1997, 39, 549–563. [Google Scholar] [CrossRef]
- Wang, J.G.; Sun, W.; Anand, S. Amicrostructure analysis for crushable deformation of foammaterials. Comput. Mater. Sci. 2008, 44, 195–200. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. The mechanics of three-dimensional cellularmaterials. Proc. R. Soc. 1982, 382, 43–59. [Google Scholar]
- Demiray, S.; Becker, W.; Hohe, J. Numerical determination of initial and subsequent yield surfaces of open-celled model foams. Int. J. Solids Struct. 2007, 44, 1093–1208. [Google Scholar] [CrossRef]
- Liu, P.S. Failure by buckling mode of the pore-strut for isotropic three-dimensional reticulated porous metal foams under different compressive loads. Mater. Des. 2011, 32, 3493–3498. [Google Scholar] [CrossRef]
- Sassov, A.; Cornelis, E.; Dyck, D. Non-destructive 3D investigation of metal foam microstructure. Mater. Werkst. 2000, 31, 571–573. [Google Scholar] [CrossRef]
- Toda, H.; Ohgaki, T.; Uesugi, K.; Makii, K.; Aruga, Y.; Akahori, T.; Niinomi, M.; Kobayashi, T. In situ observation of fracture of aluminium foam using synchrotron X-ray microtomography. Key Eng. Mater. 2005, 297, 1189–1195. [Google Scholar] [CrossRef]
- Miedzinska, D.; Niezgoda, T.; Gieleta, R. Numerical and experimental aluminum foam microstructure testing with the use of computed tomography. Comput. Mater. Sci. 2012, 64, 90–95. [Google Scholar] [CrossRef]
- Ramirez, J.F.; Cardona, M.; Velez, J.A.; Mariaka, I.; Isaza, J.A.; Mendoza, E.; Betancourt, S.; Fernández-Morales, P. Numerical modeling and simulation of uniaxial compression of aluminum foams using FEM and 3D-CT images. Proc. Mater. Sci. 2014, 4, 227–231. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.A.; Brown, A.D.; Hazell, P.J.; Kader, M.A.; Escobedo, J.P.; Saadatfar, M.; Xu, S.; Ruan, D.; Turner, M. Mechanical response and dynamic deformation mechanisms of closed-cell aluminium alloy foams under dynamic loading. Int. J. Impact Eng. 2018, 114, 111–122. [Google Scholar] [CrossRef]
- Sharma, V.; Zivic, F.; Grujovic, N.; Babcsan, N.; Babcsan, J. Numerical Modeling and Experimental Behavior of Closed-Cell Aluminum Foam Fabricated by the Gas Blowing Method under Compressive Loading. Materials 2019, 12, 1582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wejrzanowski, T.; Skibinski, J.; Szumbarski, J.; Kurzydlowski, K.J. Structure of foams modeled by Laguerre-Voronoi tessellations. Comput. Mater. Sci. 2013, 67, 216–221. [Google Scholar] [CrossRef]
- Tang, L.; Shi, X.; Zhang, L.; Liu, Z.; Jiang, Z.; Liu, Y. Effects of statistics of cell’s size and shape irregularity on mechanical properties of 2D and 3D Voronoi foams. Acta Mech. 2014, 225, 1361–1372. [Google Scholar] [CrossRef]
- Yang, B.; Liu, Z.J.; Tang, L.Q.; Jiang, Z.Y.; Liu, Y.P. Mechanism of the strain rate effect of metal foams with numerical simulations of 3D Voronoi foams during the split Hopkinson pressure bar tests. Int. J. Comput. Methods 2015, 12. [Google Scholar] [CrossRef]
- Zhang, X.T.; Wang, R.Q.; Liu, J.X.; Li, X.; Jia, G. A numerical method for the ballistic performance prediction of the sandwiched open cell aluminum foam under hypervelocity impact. Aerosp. Sci. Technol. 2018, 75, 254–260. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, T.; Li, S.Q.; Ruan, D.; Wang, Z.; Lu, G. Sample size effect on the mechanical behavior of aluminum foam. Int. J. Mech. Sci. 2019, 151, 622–638. [Google Scholar] [CrossRef]
- Skibinski, J.; Cwieka, K.; Ibrahim, S.H.; Wejrzanowski, T. Influence of Pore Size Variation on Thermal Conductivity of Open-Porous Foams. Materials 2019, 12, 12. [Google Scholar] [CrossRef] [Green Version]
- Alexander, Z.; Zinchenko. Algorithm for Random Close Packing of Spheres with Periodic Boundary Conditions. J. Comput. Phys. 1994, 114, 298–307. [Google Scholar]
- Fang, Q.; Zhang, J.H.; Chen, L.; Liu, J.; Fan, J.; Zhang, Y. An algorithm for the grain-level modelling of a dry sand particulate system. Model. Simul. Mater. Sci. Eng. 2014, 22, 5. [Google Scholar] [CrossRef]
- Zheng, Z.J.; Wang, C.F.; Yu, J.L.; Rei, S.R.; Harriga, J.J. Dynamic stress–strain states for metal foams using a 3D cellular model. J. Mech. Phys. Solids 2014, 72, 93–114. [Google Scholar] [CrossRef]
- Khodaparast, H.H.; Mottershead, J.E.; Friswell, M.I. Perturbation methods for the estimation of parameter variability in stochastic model updating. Mech. Syst. Signal Process. 2008, 22, 1751–1773. [Google Scholar] [CrossRef]
- Deng, Z.M.; Bi, S.F.; Atamturktur, S. Stochastic model updating using distance discrimination analysis. Chin. J. Aeronaut. 2014, 27, 1188–1198. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Liu, J.; Cho, C.; Han, X. A hybrid parameter identification method based on Bayesian approach and interval analysis for uncertain structures. Mech. Syst. Signal Process. 2015, 60, 853–865. [Google Scholar] [CrossRef]
- Wu, Z.F.; Huang, B.; Li, Y.J.; Pu, W. A Statistical Model Updating Method of Beam Structures with Random Parameters under Static Load. Appl. Sci. 2017, 7, 6. [Google Scholar] [CrossRef] [Green Version]
- Furukawa, T.; Lim, S.H.; Michopoulos, J.G. Stochastic identification of defects under sensor uncertainties. Int. J. Numer. Methods Eng. 2012, 90, 135–151. [Google Scholar] [CrossRef]
- Wan, H.P.; Ren, W.X. Stochastic model updating utilizing Bayesian approach and Gaussian process model. Mech. Syst. Signal Process. 2016, 70–71, 245–268. [Google Scholar] [CrossRef]
- Wang, C.; Matthies, H.G.; Qiu, Z.P. Optimization-based inverse analysis for membership function identification in fuzzy steady-state heat transfer problem. Struct. Multidiscip. Optim. 2018, 57, 1495–1505. [Google Scholar] [CrossRef]
- Fedele, F.; Muhanna, R.L.; Xiao, N.; Mullen, R.L. Interval-based approach for uncertainty propagation in inverse problems. J. Eng. Mech. 2014, 141, 1–7. [Google Scholar] [CrossRef]
- Chen, X.; Shen, Z.; Liu, X. A Copula-Based and Monte Carlo Sampling Approach for Structural Dynamics Model Updating with Interval Uncertainty. Shock and Vibration. 2018, 2018. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.S.; Wang, X.J.; Wang, L. Interval uncertainty analysis for static response of structures using radial basis functions. Appl. Math. Model. 2019, 69, 425–440. [Google Scholar] [CrossRef]
- Zheng, Z.L.; Jing, Q.; Xie, Y.H.; Zhang, D. An Investigation on the Forced Convection of Al2O3-water Nanofluid Laminar Flow in a Microchannel under Interval Uncertainties. Appl. Sci. 2019, 9, 3. [Google Scholar] [CrossRef] [Green Version]
- Khodaparast, H.H.; Mottershead, J.E.; Badcock, K.J. Interval model updating with irreducible uncertainty using the Kriging predictor. Mech. Syst. Signal Process. 2011, 25, 1204–1226. [Google Scholar] [CrossRef]
- Fang, S.E.; Zhang, Q.H.; Lin, Y.Q.; Ren, W.X. An interval model updating strategy using interval response surface models. Mech. Syst. Signal Process. 2015, 60–61, 909–927. [Google Scholar] [CrossRef]
- Deng, Z.M.; Guo, Z.P. Interval identification of structural parameters using interval overlap ratio and Monte Carlo simulation. Adv. Eng. Softw. 2018, 21, 120–130. [Google Scholar] [CrossRef]
- Deng, Z.M.; Guo, Z.P.; Zhang, X.J. Interval model updating using perturbation method and radius basis function neural networks. Mech. Syst. Signal Process. 2017, 84, 699–716. [Google Scholar] [CrossRef]
- Chong, W.; Hermann, G.M. Novel interval theory-based parameter identification method for engineering heart transfer systems with epistemic uncertainty. Int. J. Numer. Methods Eng. 2018, 115, 756–770. [Google Scholar]
- Wang, X.G.; He, W.L.; Zhao, L.G. Novel Interval Parameter Identification Method Using Augmented Fourier Series-Based Polynomial Surrogate Model. IEEE Access 2019, 7, 70862–70875. [Google Scholar]
- Zhao, A.; Hu, Y.B. Numerical Simulation of Effective Thermal Conductivity Aluminum Foam Sandwich Panel. Thermodynamics 2018, 22, 2827–2834. [Google Scholar] [CrossRef]
- Solorzano, E.; Reglero, J.A.; Rodriguez-Perez, M.A.; Lehmhus, D.; Wichmann, M.; de Saja, J.A. An experimental study on the thermal conductivity of foams by using the transient plane source method. Int. J. Heat Mass Transf. 2008, 51, 6259–6267. [Google Scholar] [CrossRef]
- Wang, H.; Liu, B.; Kang, Y.X.; Qin, Q.H. Analysing effective thermal conductivity of 2D closed-cell foam based on shrunk Voronoi tessellations. Arch. Mech. 2017, 69, 451–470. [Google Scholar]
- Liu, Z.Z.; Wang, T.S.; Li, J.F. A trigonometric interval method of dynamic response analysis of uncertain nonlinear systems. Sci. China Phys. Mech. Astron. 2015, 58, 044501. [Google Scholar] [CrossRef]


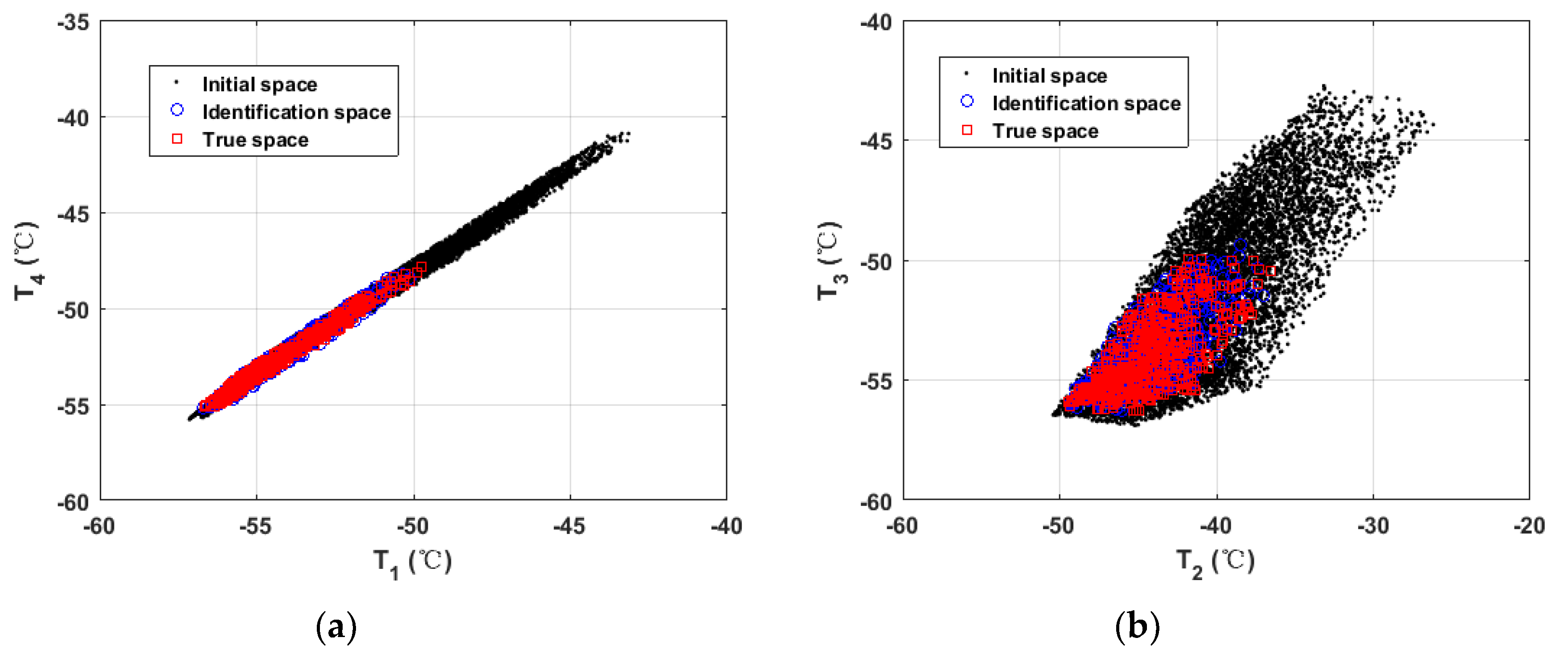

| Parameter | Real Interval | Identification Interval | Error (%) |
|---|---|---|---|
| k(W/(m·°C)) | [10, 20] | [9.62, 19.56] | (3.8, 2.2) |
| ε | [0.4, 0.8] | [0.4159, 0.8241] | (3.9, 3.0) |
| P (W) | [10, 15] | [10.57, 15.21] | (5.7, 1.4) |
| Mean | (4.5, 2.2) |
| Feature | Real Interval | Unbiased Interval | Output Interval | Error (%) |
|---|---|---|---|---|
| Point 1 | [−56.85, −49.57] | [−57.51, −49.91] | [−56.75, −49.83] | (0.1759, −0.5245) |
| Point 2 | [−49.80, −34.97] | [−49.33, −34.74] | [−49.34, −34.72] | (0.9237, 0.7149) |
| Point 3 | [−56.56, −49.11] | [−57.25, −49.36] | [−56.47, −49.36] | (0.1591, −0.5091) |
| Point 4 | [−55.36, −47.83] | [−55.08, −47.35] | [−55.23, −47.83] | (0.2348, 0) |
| Mean | (0.3734, 0.4371) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; He, W.; Zhao, L. Interval Identification of Thermal Parameters Using Trigonometric Series Surrogate Model and Unbiased Estimation Method. Appl. Sci. 2020, 10, 1429. https://doi.org/10.3390/app10041429
Wang X, He W, Zhao L. Interval Identification of Thermal Parameters Using Trigonometric Series Surrogate Model and Unbiased Estimation Method. Applied Sciences. 2020; 10(4):1429. https://doi.org/10.3390/app10041429
Chicago/Turabian StyleWang, Xiaoguang, Weiliang He, and Linggong Zhao. 2020. "Interval Identification of Thermal Parameters Using Trigonometric Series Surrogate Model and Unbiased Estimation Method" Applied Sciences 10, no. 4: 1429. https://doi.org/10.3390/app10041429





