Depth Dependence and Keyhole Stability at Threshold, for Different Laser Welding Regimes
Abstract
:Featured Application
Abstract
1. Introduction
2. Thermal Model for High Aspect Ratio Keyholes
2.1. Model for Deep Penetration Regime
3. Dynamic Model for Low Aspect Ratio Keyholes or High Welding Speeds
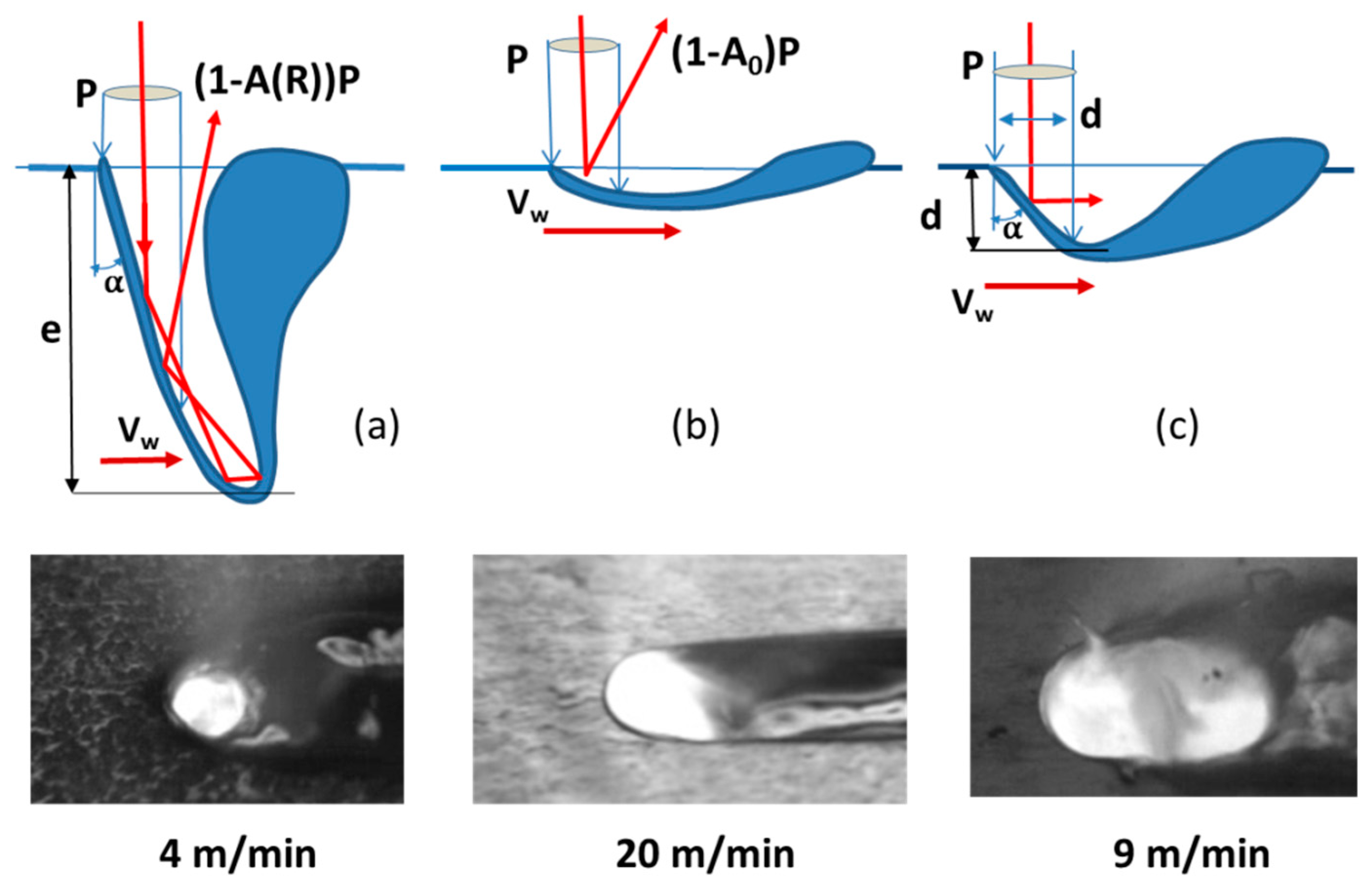
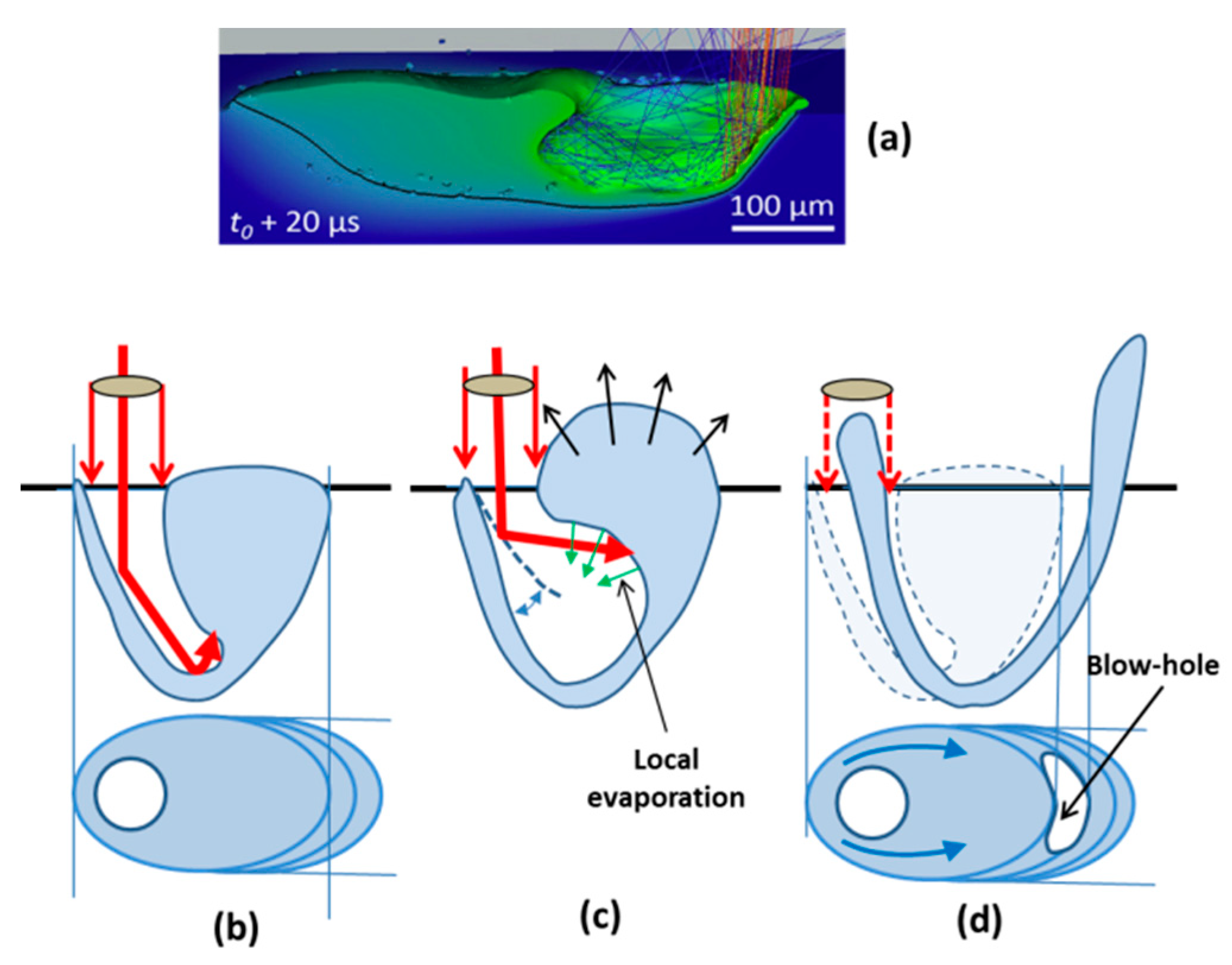
3.1. Geometry of the KH Front at High Welding Speed
3.2. Generalized Piston Model for High Welding Speeds
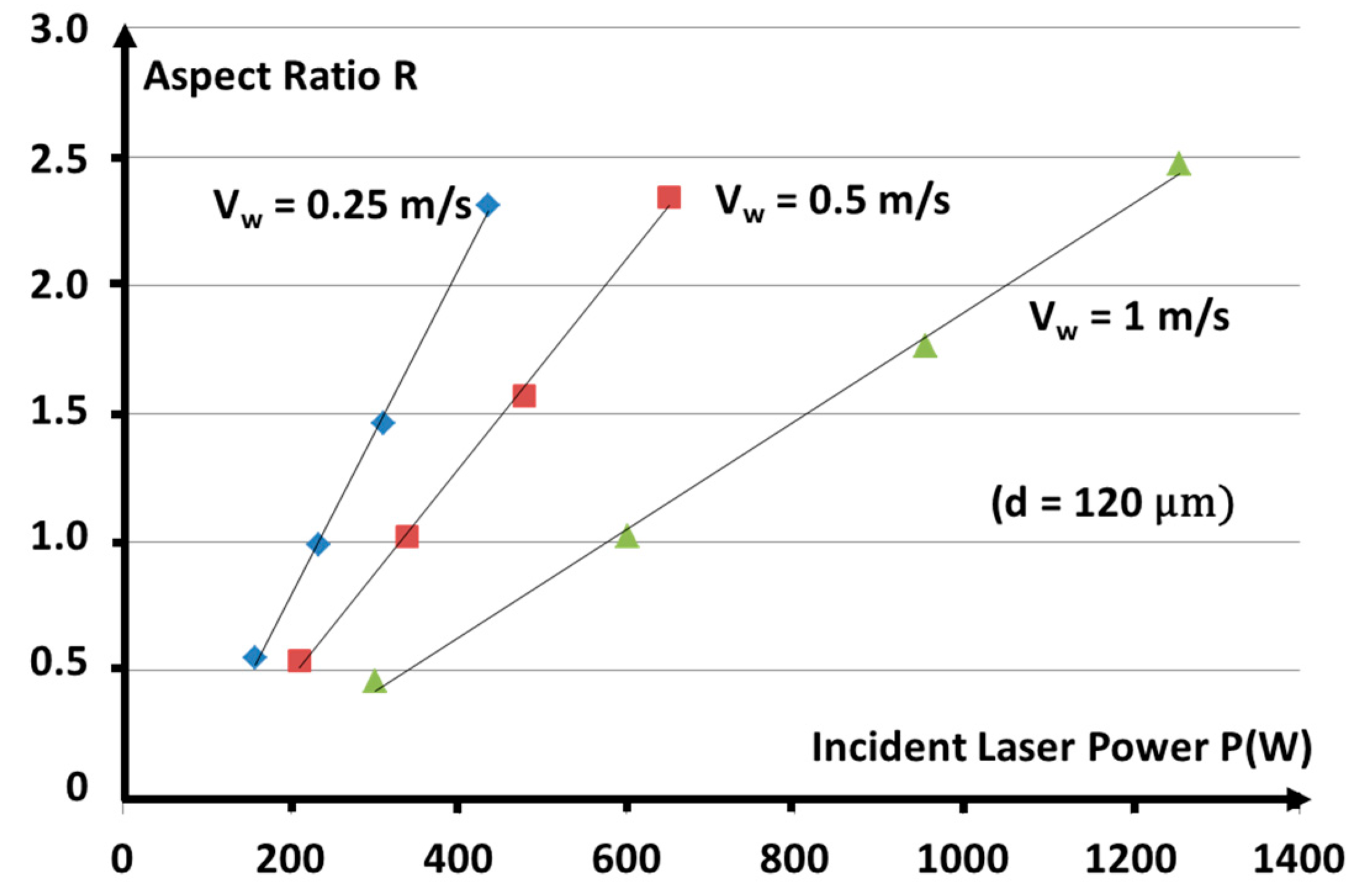
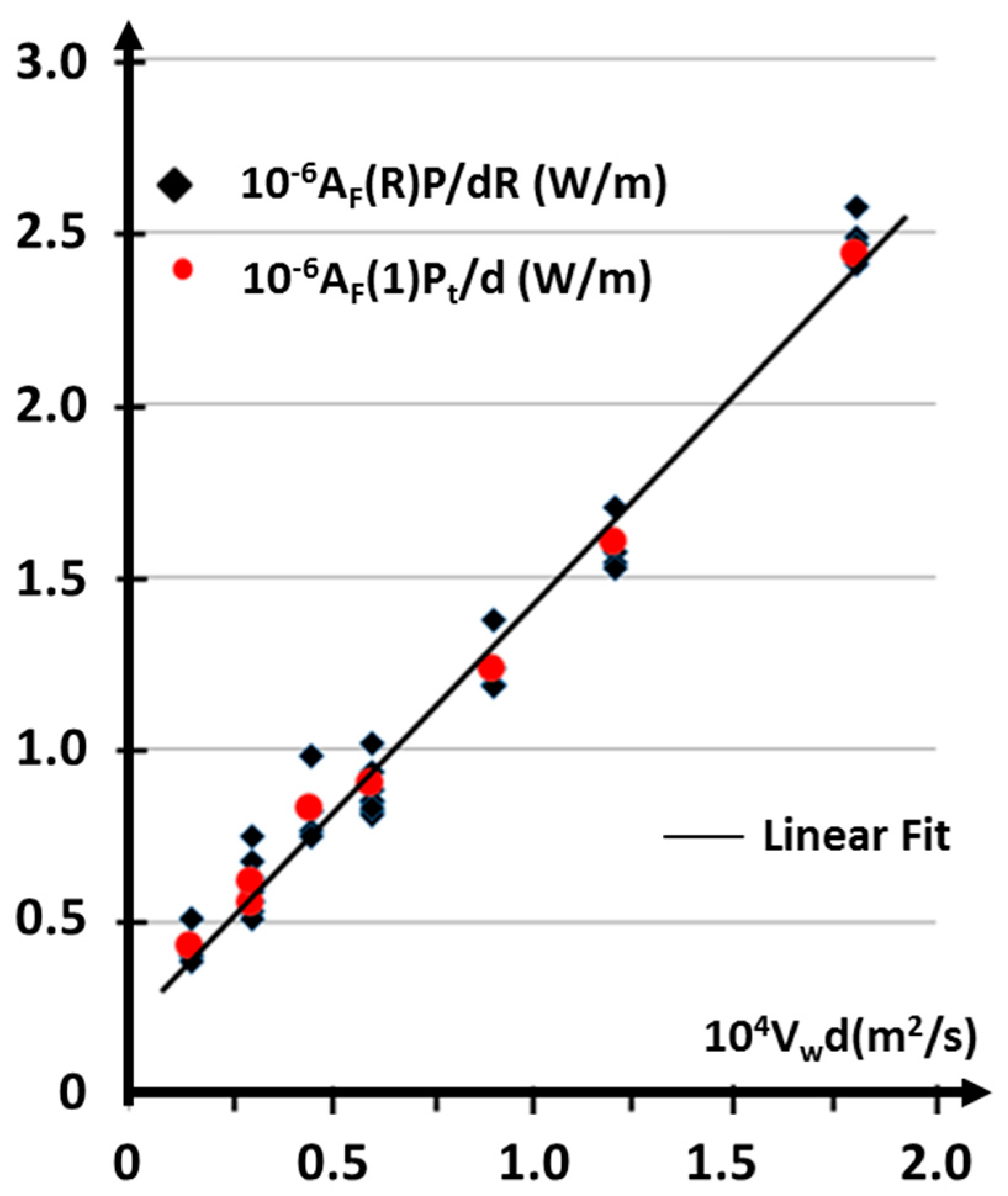
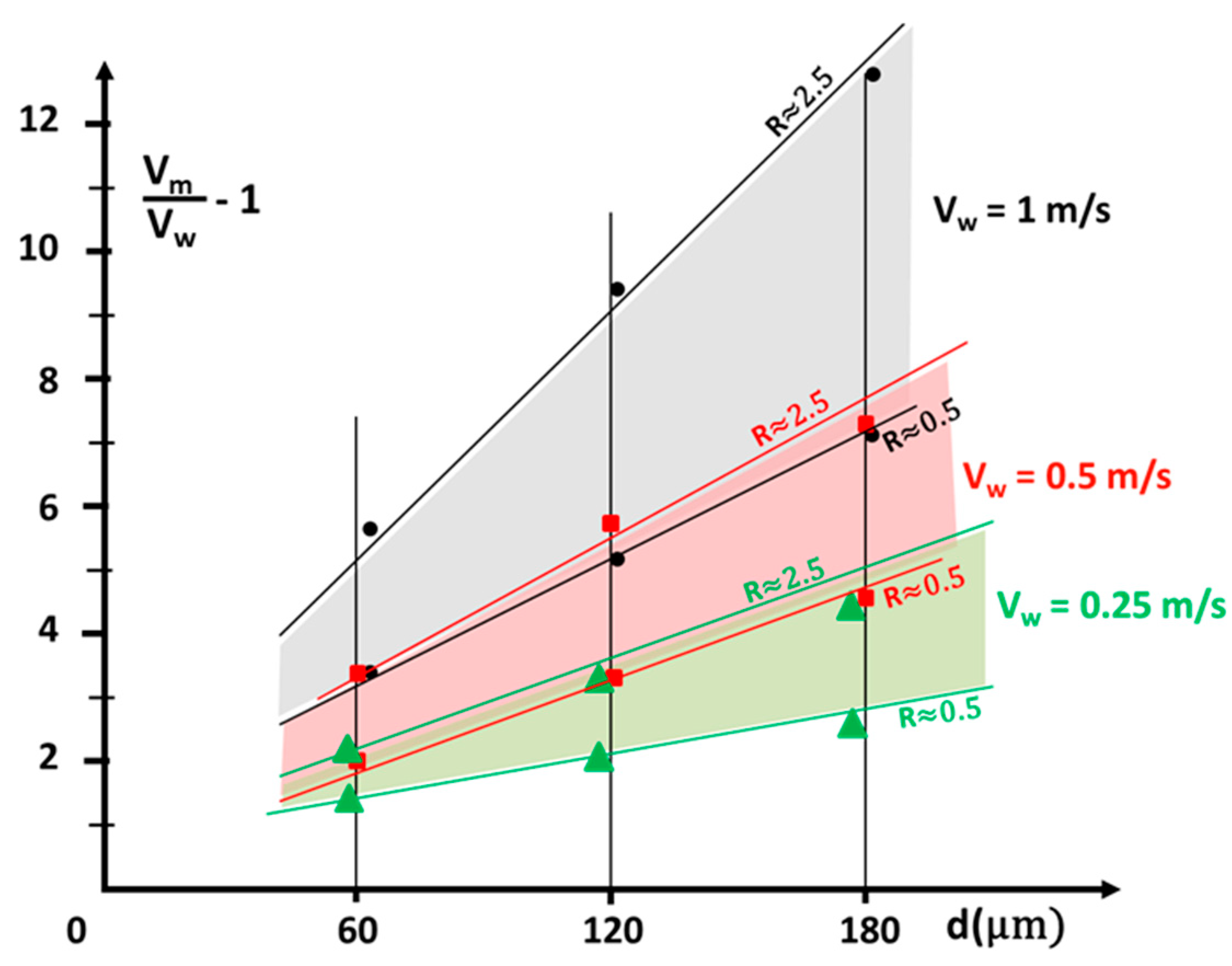
3.3. Results of the Generalized Piston Model for High Welding Speeds
3.4. Example of Application of This Model to the Analysis of Experiments on Ti-6Al-4V
4. Analysis of KH Stability Near Its Threshold Around R ≈ 1
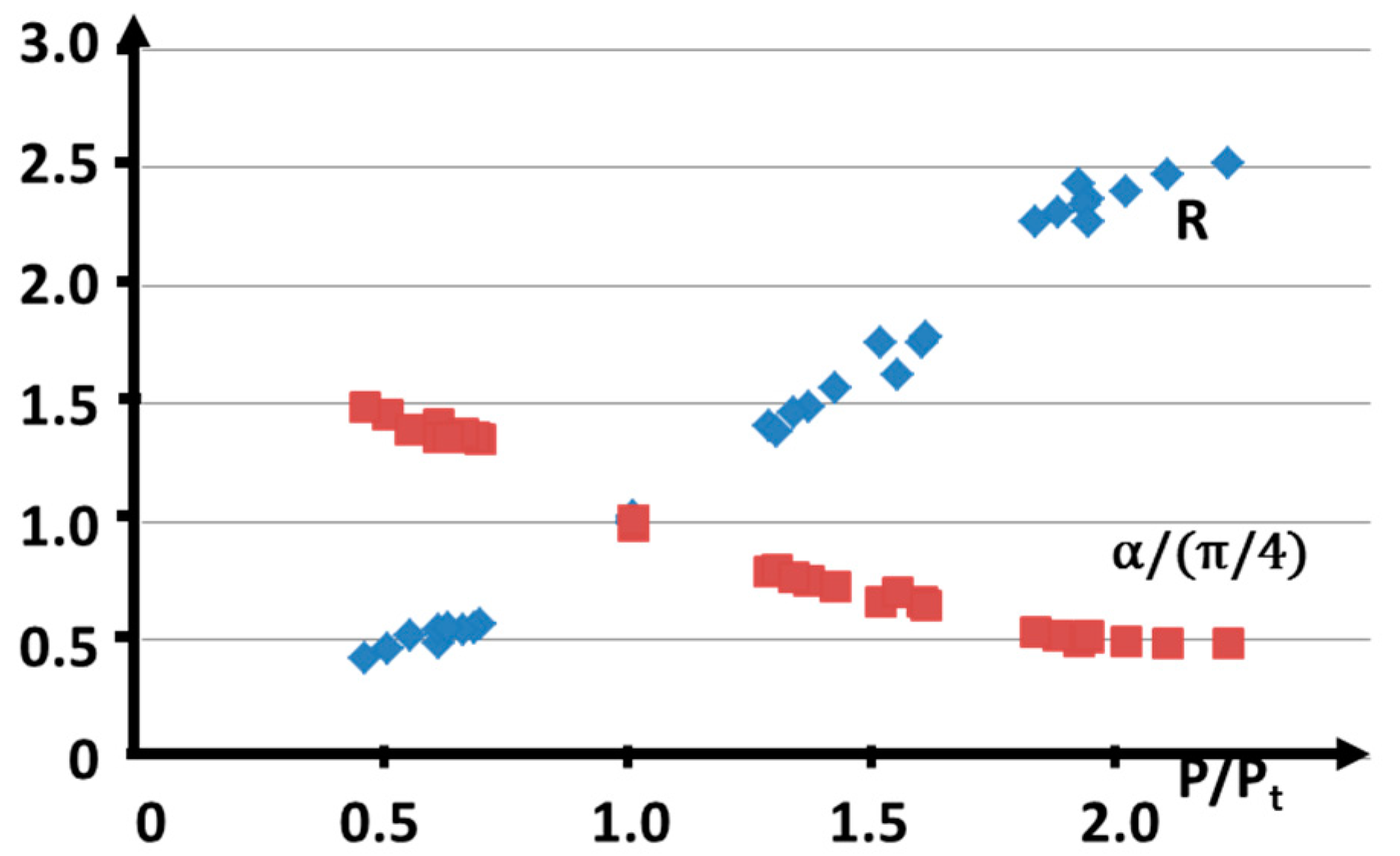
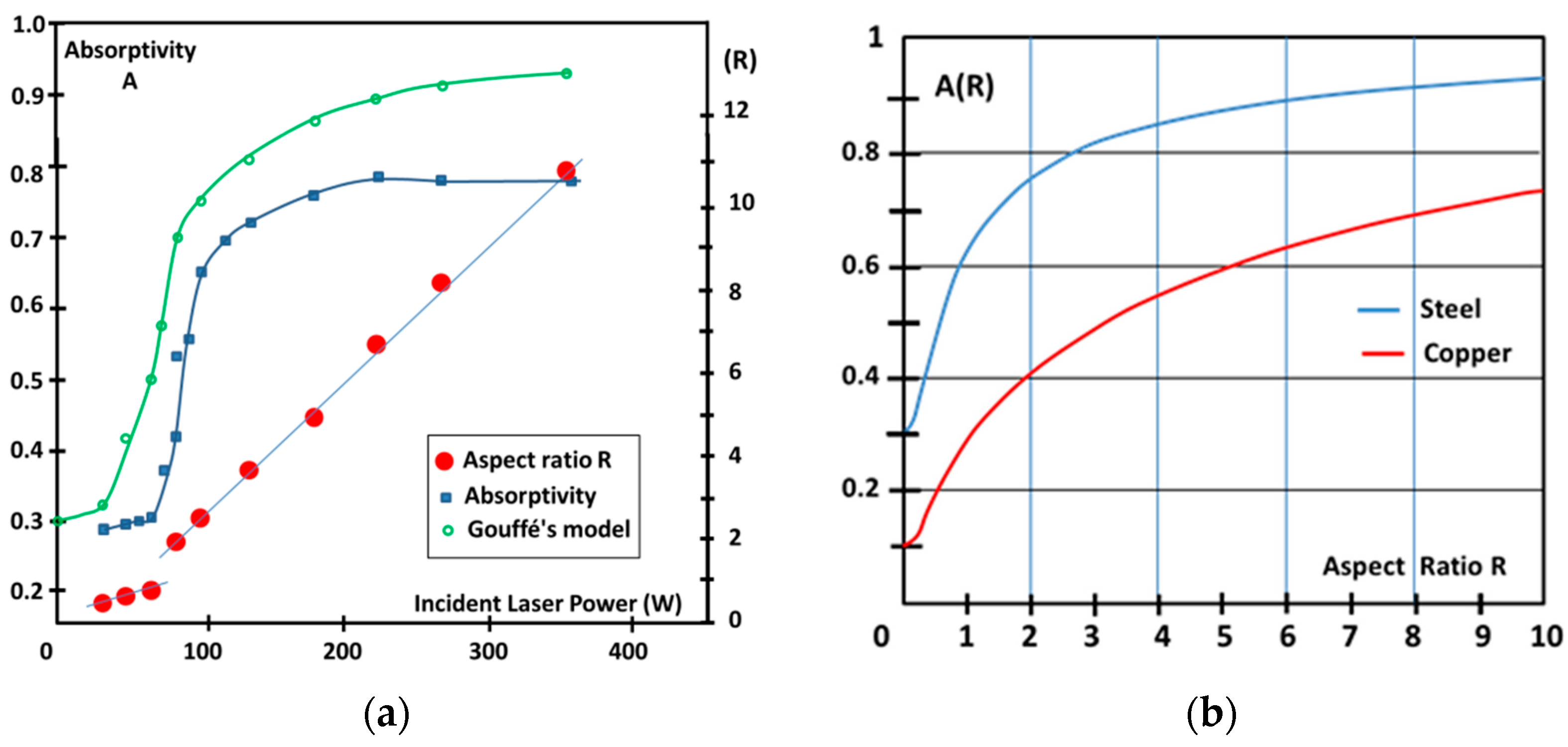
4.1. KH Absorptivity Variations
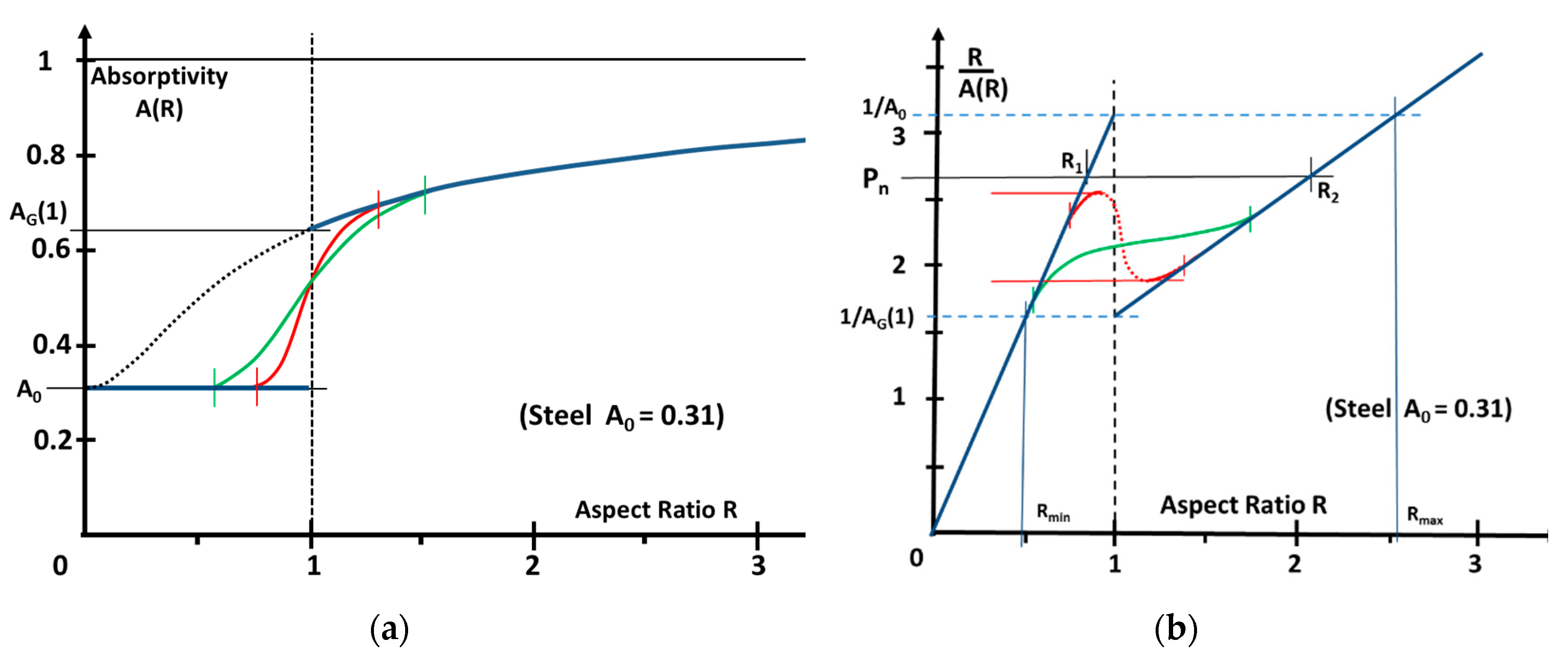
4.2. Dependance of the KH Front Inclination for a Given Incident Laser Power
- -
- For P/Pt < (P/Pt)min = A(1)/AG(1) ≈ 0.8, only one solution with R < 1 is obtained, which does not correspond to a KH. It can be considered as some “forced” conductive regime, where the melt pool surface is depressed with an inclination angle α > π/4.
- -
- For P/Pt > (P/Pt)max = A(1)/A0(≈1.7), only one solution also exists for R such that R > Rmax ≈ 2.6 (with Rmax being the solution of A0Rmax=AG(Rmax)).
- -
- For (P/Pt)min < P/Pt < (P/Pt)max, two solutions, R1 and R2, are such that Rmin = A0/AG(1)(≈0.5) < R1, R2 < Rmax.
4.3. Experimental Observation of These Unstable Behaviors
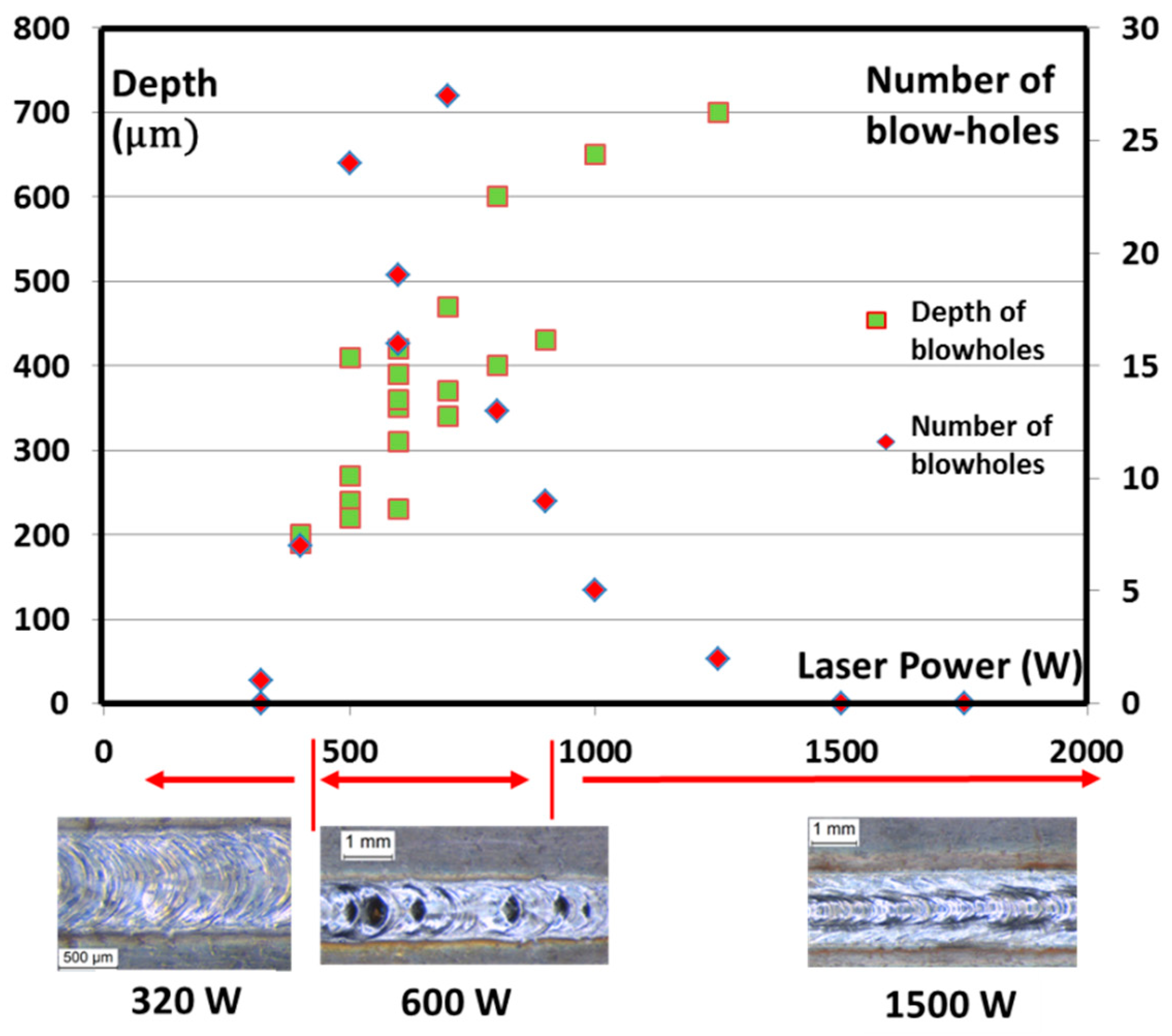
4.3.1. Welding Experiments
4.3.2. Spot-Welding Experiments
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Generalized Piston Model
Numerical Procedure of Resolution
References
- Gu, D.D.; Meiners, W.; Wissenbach, K.; Poprawe, R. Laser additive manufacturing of metallic components: Materials, processes and mechanisms. Int. Mater. Rev. 2012, 57, 133–164. [Google Scholar] [CrossRef]
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E.; Sing, S.L. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2, 041101. [Google Scholar] [CrossRef]
- Rosenthal, D. The theory of moving sources of heat and its application to metal treatments. Trans. ASME 1946, 68, 849–866. [Google Scholar]
- Swift-Hook, D.T.; Gick, A.E.F. Penetration welding with lasers. Weld. Res. Suppl. J. 1973, 52, 492–499. [Google Scholar]
- Dowden, J.; Postacioglu, N.; Davis, M.; Kapadia, P. A keyhole model in penetration welding with a laser. J. Phys. D Appl. Phys. 1987, 20, 36–44. [Google Scholar] [CrossRef]
- Noller, F. The stationary shapes of vapor cavity and molten zone in EB-welding. In Proceedings of the 3rd CISFFEL, International Colloquium on Welding and Melting by Electrons and Laser Beam, Lyon, France, 5–9 September 1983; pp. 89–97. [Google Scholar]
- Kroos, J.; Gratzke, U.; Simon, G. Towards a-self-consistent model of the keyhole in penetration laser beam welding. J. Phys. D Appl. Phys. 1993, 26, 474–480. [Google Scholar] [CrossRef]
- Kaplan, A. A model of deep penetration laser welding based on calculation of the keyhole. J. Phys. D Appl. Phys. 1994, 27, 1805–1814. [Google Scholar] [CrossRef]
- Sudnik, D.; Radaj, D.; Erofeew, W. Computerized simulation of laser beam welding, modelling and verification. J. Phys. D Appl. Phys. 1996, 29, 2811–2817. [Google Scholar] [CrossRef]
- Ki, H.; Mohanty, P.S.; Mazumder, J. Modeling of laser keyhole welding: Part I. Mathematical modeling, numerical methodology, role of recoil pressure, multiple reflections, and free surface evolution. Metall. Mater. Trans. A 2002, 33, 1817–1830. [Google Scholar] [CrossRef]
- Geiger, M.; Leitz, K.H.; Koch, H.; Otto, A. A 3D transient model of keyhole and melt pool dynamics in laser beam welding applied to the joining of zinc coated sheets. Prod. Eng. 2009, 3, 127–136. [Google Scholar] [CrossRef]
- Pang, S.; Chen, L.; Zhou, J.; Yin, Y.; Chen, T. A three-dimensional sharp interface model for self-consistent keyhole and weld pool dynamics in deep penetration laser welding. J. Phys. D Appl. Phys. 2011, 44, 025301. [Google Scholar] [CrossRef]
- Courtois, M.; Carin, M.; Masson, P.; Gaied, S.; Balabane, M. A new approach to compute multi-reflections of laser beam in a keyhole for heat transfer and fluid flow modelling in laser welding. J. Phys. D Appl. Phys. 2013, 46, 505305. [Google Scholar] [CrossRef]
- Tan, W.; Shin, Y.C. Analysis of multi-phase interaction and its effects on keyhole dynamics with a multi-physics numerical model. J. Phys. D: Appl. Phys. 2014, 47, 345501. [Google Scholar] [CrossRef]
- Zhao, H.; Niu, W.; Zhang, B.; Lei, Y.; Kodoma, M.; Ishide, T. Modelling of keyhole dynamics and porosity formation considering the adaptive keyhole shape and three-phase coupling during deep-penetration laser welding. J. Phys. D Appl. Phys. 2011, 40, 5753–5766. [Google Scholar] [CrossRef]
- Fabbro, R.; Dal, M.; Peyre, P.; Coste, F.; Schneider, M.; Gunenthiram, V. Analysis and possible estimation of keyhole depths evolution, using laser operating parameters and material properties. J. Laser Appl. 2018, 30, 032410. [Google Scholar] [CrossRef]
- Rubenchick, A.M.; King, W.E.; Wu, S.S. Scaling laws for additive manufacturing. J. Mater. Process. Technol. 2018, 257, 234–243. [Google Scholar] [CrossRef]
- King, W.E.; Barth, H.D.; Castillo, V.M.; Gallegos, G.F.; Gibbs, J.W.; Hahn, D.E.; Kamath, C.; Rubenchik, A.M. Observation of keyhole-mode laser melting in laser powder-bed fusion additive manufacturing. J. Mater. Process. Technol. 2014, 214, 2915–2925. [Google Scholar] [CrossRef]
- Fabbro, R. Scaling laws for the welding process in keyhole mode. J. Mater. Process. Technol. 2019, 264, 346–351. [Google Scholar] [CrossRef] [Green Version]
- Berger, P.; Hügel, H. Fluid dynamic effect in keyhole welding – an attempt to characterize different regimes. Phys. Procedia 2013, 41, 216–224. [Google Scholar] [CrossRef] [Green Version]
- Cunningham, R.; Zhao, C.; Parab, N.; Kantzos, C.; Pauza, J.; Fezzaa, K.; Sun, T.; Rollett, A.D. Keyhole threshold and morphology in laser melting revealed by ultrahigh-speed x-ray imaging. Science 2019, 363, 849–852. [Google Scholar] [CrossRef]
- Kouraytem, N.; Li, X.; Cunningham, R.; Zhao, C.; Parab, N.; Sun, T.; Rollett, A.D.; Spear, A.D.; Tan, W. Effect of Laser-Matter Interaction on Molten Pool Flow and Keyhole Dynamics. Phys. Rev. Appl. 2019, 11, 064054. [Google Scholar] [CrossRef]
- Semak, V.; Matsunawa, A. The role of recoil pressure in energy balance during laser materials processing. J. Phys. D Appl. Phys. 1997, 30, 2541–2552. [Google Scholar] [CrossRef]
- Lankalapalli, K.N.; Tu, J.T.; Gartner, M. A model for estimating penetration depth of laser welding processes. J. Phys. D Appl. Phys. 1996, 29, 1831–1841. [Google Scholar] [CrossRef]
- Miyazaki, T.; Giedt, W.H. Heat transfer from an elliptical cylinder moving through an infinite plate applied to electron beam welding. Int. J. Heat Mass Transf. Theory Appl. 1982, 25, 807–814. [Google Scholar]
- Suder, W.J.; Williams, S. Power factor model for selection of welding parameters for CW laser welding. Opt. Laser Technol. 2014, 56, 223–229. [Google Scholar] [CrossRef]
- Heider, A.; Stritt, P.; Weber, R.; Graf, T. High power laser sources enable high-quality laser welding of copper. In Proceedings of the ICALEO Conference, San Diego, CA, USA, 19–23 October 2014; pp. 343–348. [Google Scholar]
- Fabbro, R. Melt pool and keyhole behavior analysis for deep penetration laser welding. J. Phys. D Appl. Phys. 2010, 43, 445501. [Google Scholar] [CrossRef]
- Fabbro, R.; Chouf, K. Keyhole modeling during laser welding. J. Appl. Phys. 2000, 87, 4075. [Google Scholar] [CrossRef]
- Trapp, J.; Rubenchik, A.M.; Guss, G.; Matthews, M.J. In situ absorptivity measurements of metallic powders during laser powder-bed fusion additive manufacturing. Appl. Mater. Today 2017, 9, 341–349. [Google Scholar] [CrossRef]
- Ye, J.; Khairallah, S.A.; Rubenchik, A.M.; Crumb, M.F.; Guss, G.; Belak, J.; Matthews, M.J. Energy Coupling Mechanisms and Scaling Behavior Associated with Laser Powder Bed Fusion Additive Manufacturing. Adv. Eng. Mater. 2019, 21, 1900185. [Google Scholar] [CrossRef]
- Gouffe, A. Correction d’ouverture des corps noirs artificiels compte tenu des diffusions multiples internes. Rev. Opt. 1945, 24, 1–10. [Google Scholar]
- Martin, A.A.; Nicholas, P.; Calta, P.; Joshua, A.; Hammons, J.A.; Khairallah, S.A.; Nielsen, M.H.; Shuttlesworth, R.S.; Sinclair, N.; Matthews, M.J.; et al. Ultrafast dynamics of laser-metal interactions in additive manufacturing alloys captured by in situ X-ray imaging. Mater. Today Adv. 2019, 1, 100002. [Google Scholar] [CrossRef]
- Kaplan, A.F.H.; Samarjy, R.S.M. Absorption peaks depending on topology of the keyhole front and wavelength. J. Laser Appl. 2015, 27, S29012. [Google Scholar] [CrossRef]
- Weberpals, J.-P. Nutzen und Grenzen Starker Fokussierung Beim Laserschweißen. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2010. [Google Scholar]
- Simonds, B.J.; Sowards, J.; Hadler, J.; Pfeif, E.; Wiltham, B.; Tanner, J.; Harris, C.; Williams, P.; Lehman, J. Time-Resolved Absorptance and Melt Pool Dynamics during Intense Laser Irradiation of a Metal. Phys. Rev. Appl. 2018, 10, 044061. [Google Scholar] [CrossRef]
- Ki, H.; Mohanty, P.S.; Mazumder, J. Multiple reflection and its influence on keyhole evolution. J. Laser Appl. 2002, 14, 39–45. [Google Scholar] [CrossRef]
- Mas, C.; Fabbro, R.; Gouedard, Y. Steady state laser cutting modeling. J. Laser Appl. 2003, 15, 145–152. [Google Scholar] [CrossRef]
- Dausinger, F.; Shen, J. Energy coupling efficiency in laser surface treatment. ISIJ Int. 1993, 33, 925–933. [Google Scholar] [CrossRef] [Green Version]
- Knight, C.J. Theoretical modeling of rapid surface vaporization with back pressure. AIAA J. 1979, 17, 519–523. [Google Scholar] [CrossRef]
- Samokhin, A.A. First-order Phase Transitions Induced by Laser Radiation in Absorbing Condensed Matter; Effect of Laser Radiation on Absorbing Condensed Matter, Nova Science Publishers: Commack, NY, USA, 1990; pp. 1–161. [Google Scholar]
- Abe, Y.; Mizutani, M.; Kawahito, Y.; Katayama, S. Deep penetration welding with high power laser under vacuum. In Proceedings of the ICALEO, Anaheim, CA, USA, 26–30 September 2010; LIA, Ed.; pp. 648–653. [Google Scholar]
- Borner, C.; Dilger, K.; Rominger, V.; Harrer, T.; Krussel, T.; Lower, T. Influence of ambient pressure on spattering and weld seam quality in laser beam welding with the solid-state laser. In Proceedings of the ICALEO, Orlando, FL, USA, 23–27 October 2011; LIA, Ed.; pp. 621–629. [Google Scholar]
- Rominger, V.; Berger, P.; Hügel, H. Effects of reduced ambient pressure on spattering during the laser beam welding of mild steel. J. Laser Appl. 2019, 31, 042016. [Google Scholar] [CrossRef]
- Fabbro, R.; Hirano, K.; Pang, S. Analysis of the physical processes occurring during deep penetration laser welding under reduced pressure. J. Laser Appl. 2016, 28, 022427. [Google Scholar] [CrossRef] [Green Version]


© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabbro, R. Depth Dependence and Keyhole Stability at Threshold, for Different Laser Welding Regimes. Appl. Sci. 2020, 10, 1487. https://doi.org/10.3390/app10041487
Fabbro R. Depth Dependence and Keyhole Stability at Threshold, for Different Laser Welding Regimes. Applied Sciences. 2020; 10(4):1487. https://doi.org/10.3390/app10041487
Chicago/Turabian StyleFabbro, Remy. 2020. "Depth Dependence and Keyhole Stability at Threshold, for Different Laser Welding Regimes" Applied Sciences 10, no. 4: 1487. https://doi.org/10.3390/app10041487
APA StyleFabbro, R. (2020). Depth Dependence and Keyhole Stability at Threshold, for Different Laser Welding Regimes. Applied Sciences, 10(4), 1487. https://doi.org/10.3390/app10041487




