Study of Lead Rubber Bearings for Vibration Reduction in High-Tech Factories
Abstract
:1. Introduction
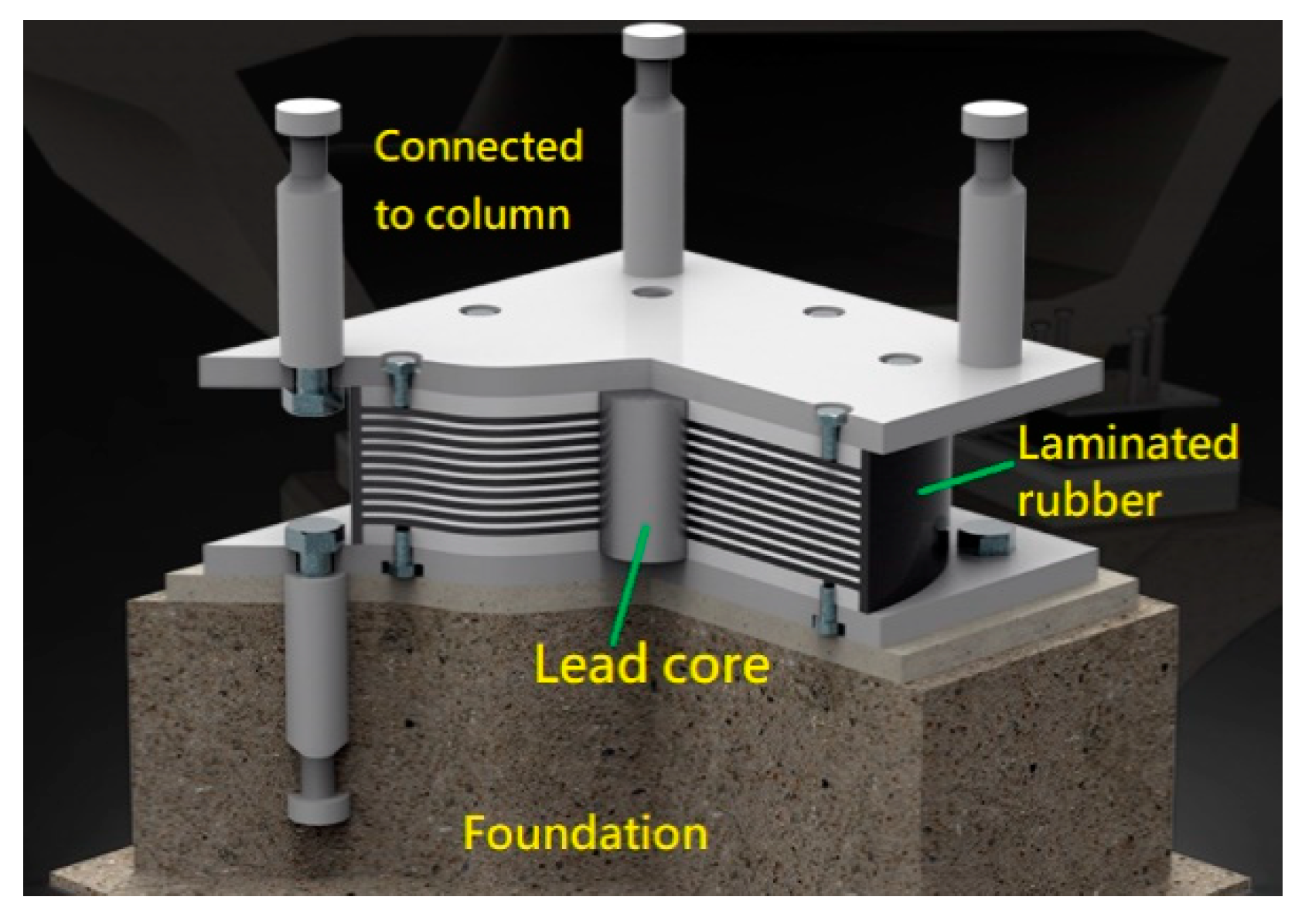
2. Finite Element Modeling of Lead Rubber Bearings
3. High-Tech Factory and Finite Element Model
3.1. Illustration of the Structure of the High-Tech Factory
3.2. Finite Element Model
3.3. Illustration of Seismic Loads
4. Parametric Study Using LRBs in High-Tech Factories
4.1. Earthquake Effect
4.2. Micro-Vibration Induced by Mobile Cranes
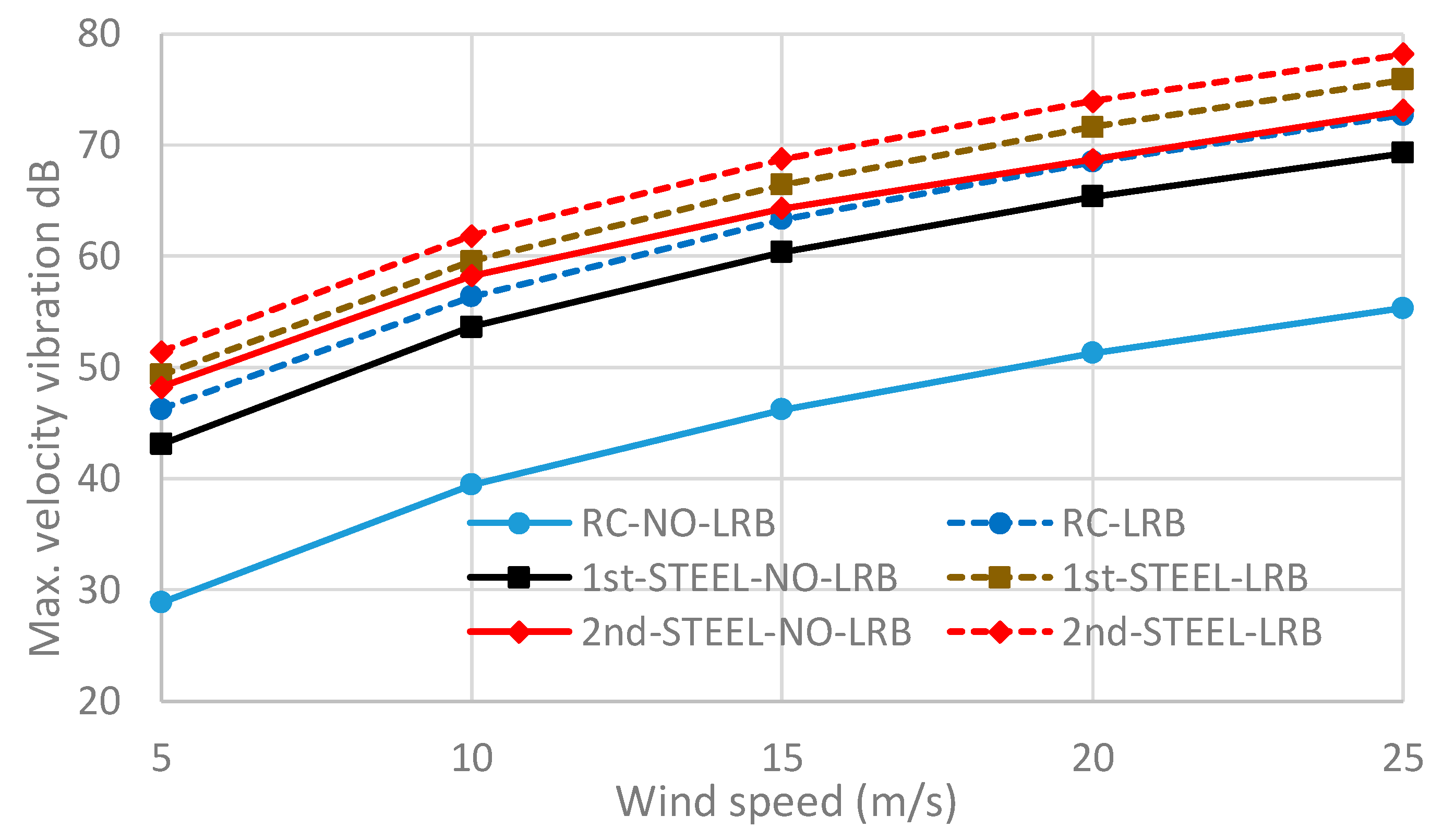
4.3. Micro-Vibration Simulation Under Wind Loads
5. Design of LRBs Concerning the Micro Vibration
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Turkington, D.H.; Carr, A.J.; Cooke, N.; Moss, P.J. Seismic design of bridges on lead-rubber bearings. J. Struct. Eng. 1989, 115, 3000–3016. [Google Scholar] [CrossRef]
- Turkington, D.H.; Carr, A.J.; Cooke, N.; Moss, P.J. Design method for bridges on lead-rubber bearings. J. Struct. Eng. 1989, 115, 3017–3030. [Google Scholar] [CrossRef]
- Fujita, T.; Sasaki, Y.; Fujimoto, S.; Tsuruya, C. Seismic isolation of industrial facilities using lead-rubber bearing. JSME Int. J. Ser. 3 Vib. Control Eng. Eng. Ind. 1990, 33, 427–434. [Google Scholar] [CrossRef]
- Salic, R.B.; Garevski, M.A.; Milutinovic, Z.V. Response of lead-rubber bearing isolated structure. In Proceedings of the 14th World Conference on Earthquake Engineering (14WCEE), Beijing, China, 12–17 October 2008. [Google Scholar]
- Kalpakidis, I.V.; Constantinou, M.C.; Whittaker, A.S. Modeling strength degradation in lead-rubber bearings under earthquake shaking. Earthq. Eng. Struct. Dyn. 2010, 39, 1533–1549. [Google Scholar] [CrossRef]
- Kalpakidis, I.V.; Constantinou, M.C. Principles of scaling and similarity for testing of lead-rubber bearings. Earthq. Eng. Struct. Dyn. 2010, 39, 1551–1568. [Google Scholar] [CrossRef]
- Islam, A.B.M.S.; Hussain, R.R.; Jumaat, M.Z.; Rahman, M.A. Nonlinear dynamically automated excursions for rubber-steel bearing isolation in multi-storey construction. Autom. Constr. 2013, 30, 265–275. [Google Scholar] [CrossRef]
- Li, A.; Yang, C.; Xie, L.; Liu, L.; Zeng, D. Research on the Rational Yield Ratio of Isolation System and Its Application to the Design of Seismically Isolated Reinforced Concrete Frame-Core Tube Tall Buildings. Appl. Sci. 2017, 7, 1191. [Google Scholar] [CrossRef] [Green Version]
- Warn, G.P.; Whittaker, A.S.; Constantinou, M.C. Vertical Stiffness of Elastomeric and Lead–Rubber Seismic Isolation Bearings. J. Struct. Eng. 2007, 133, 1227–1236. [Google Scholar] [CrossRef]
- Weisman, J.; Warn, G.P. Stability of elastomeric and lead-rubber seismic isolation bearings. J. Struct. Eng. 2012, 138, 215–223. [Google Scholar] [CrossRef]
- Al-Kutti, W.; Islam, A.B.M.S. Potential design of seismic vulnerable buildings incorporating lead rubber bearing. Buildings 2019, 9, 37. [Google Scholar] [CrossRef] [Green Version]
- Nagarajaiah, S.; Reinhorn, A.M.; Constantinou, M.C. Nlinear dynamic analysis of 3-d-base-isolated structures. J. Struct. Eng. 1991, 117, 2035–2054. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.H.; Fenves, G.L.; Whittaker, A.S.; Mahin, S.A. Characterization of seismic isolation bearings for bridges from bi-directional testing. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Abe, M.; Yoshida, J.; Fujino, Y. Multiaxial behaviors of laminated rubber bearings and their modeling. I: Experimental study. J. Struct. Eng. 2004, 130, 1119–1132. [Google Scholar] [CrossRef]
- Falborski, T.; Jankowski, R. Experimental study on effectiveness of a prototype seismic isolation system made of polymeric bearings. Appl. Sci. 2017, 7, 808. [Google Scholar] [CrossRef]
- Yuantien, C.C. Application of Biaxial Lead Rubber Bearings in High-Tech Factories. Master’s Thesis, National Cheng-Kung University, Tainan, Taiwan, 2019. Available online: http://etds.lib.ncku.edu.tw/etdservice/view_metadata?etdun=U0026-1408201913481400 (accessed on 22 February 2020).
- Benzoni, G.; Casarotti, C. Effects of vertical load, strain rate and cycling on the response of lead-rubber seismic isolators. J. Earthq. Eng. 2009, 13, 293–312. [Google Scholar] [CrossRef]
- De Domenico, D.; Falsone, G.; Ricciardi, G. Improved response-spectrum analysis of base-isolated buildings: Asubstructure-based response spectrum method. Eng. Struct. 2018, 162, 198–212. [Google Scholar] [CrossRef]
- Gordon, C.G. Generic criteria for vibration sensitive equipment 1991. In Vibration Control in Microelectronics, Optics, and Metrology; SPIE: Bellingham, WA, USA, 1992; Volume 1619, pp. 71–75. [Google Scholar]
- Ju, S.H.; Kuo, H.H.; Yu, S.W.; Ni, S.H. Investigation of vibration induced by moving cranes in high-tech factories. J. Low Freq. Noise Vib. Act. Control 2019. [Google Scholar] [CrossRef]
- Ju, S.H. Development a Nonlinear Finite Element Program with Rigid Link and Contact Element; NSC-86-2213-E-006-063; Taiwan, 1997; Available online: http//myweb.ncku.edu.tw/~juju (accessed on 22 February 2020).
- American Petroleum Institute (API). Planning, Design, Planning, Designing, and Constructing Fixed Offshore Platforms—Load and Resistance Factor Design. In API RP 2A-LRFD, 2nd ed.; American Petroleum Institute: Washington, DC, USA, 2019. [Google Scholar]
- Ju, S.H.; Kuo, H.H. Experimental and numerical study of wind-induced vibration in high-tech factories. J. Perform. Constr. Facil. 2019. [Google Scholar] [CrossRef]
- MIT. SIMQKE: A Program for Artificial Motion Generation: User’s Manual and Documentation; M.I.T. Department of Civil Engineering: Cambridge, MA, USA, 1976. [Google Scholar]
- IBC. International Building Code 2006; International Code Council: Birmingham, AL, USA, 2006. [Google Scholar]
- Idriss, I.M.; Sun, J.I. User’s Manual for SHAKE91: A Computer Program for Conducting Equivalent Linear Seismic Response Analyses of Horizontally Layered Soil Deposits; Center for Geotechnical Modeling, Dept. of Civil and Environmental Engineering; University of California: Davis, CA, USA, 1993. [Google Scholar]
- Jonkman, B.J.; Buhl, M. Turbsim User’s Guide v2.00.00; Technical Report No. NRELEL-500-36970; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2004. [Google Scholar]
- International Electrotechnical Commission. IEC 61400-1: Wind Turbines—Part 1: Wind Energy Generation Systems–Part 1: Design Requirements; International Electrotechnical Commission: Geneva, Switzerland, 2019. [Google Scholar]
















| Member | Axis | Label | Member Dimensions (mm) d×bf×tw×tf |
|---|---|---|---|
| Column | ALL | C1 | BOX 900 × 900 × 35 × 35 |
| Braces | X | B1 | RH 400 × 400 × 13 × 21 |
| Braces | Y | B2 | RH 414 × 405 × 18 × 28 |
| Braces | Y | B3 | RH 428 × 407 × 20 × 35 |
| Girder | X | G1 | RH 588 × 300 × 12 × 20 |
| Girder | Y | G2 | BH 375 × 200 × 10 × 25 |
| Name | Model/Parameter | ||||
|---|---|---|---|---|---|
| LRB1 | EIRL-G4-1000-170 | 1.9732×104 | 196.0850 | 0.0769 | 4.660×106 |
| LRB2 | EIRL-G4-700-130 | 1.4058×104 | 114.8299 | 0.0769 | 3.259×106 |
| Level | VC-D(48dB) | VC-C(54dB) | VC-B(60dB) | VC-A(66dB) | Type |
|---|---|---|---|---|---|
| 1st Without LRB | 16.8 | 23.4 | >25 | >25 | RC |
| 1st With LRB | 5.9 | 8.8 | 12.6 | 17.6 | RC |
| 2nd Without LRB | 7.3 | 10.3 | 14.7 | 20.9 | Steel |
| 2nd With LRB | 4.4 | 7.3 | 10.4 | 14.7 | Steel |
| 3rd Without LRB | 4.9 | 7.9 | 11.5 | 17 | Steel |
| 3rd With LRB | 3.4 | 6.2 | 9.1 | 13 | Steel |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, S.-H.; Yuantien, C.-C.; Hsieh, W.-K. Study of Lead Rubber Bearings for Vibration Reduction in High-Tech Factories. Appl. Sci. 2020, 10, 1502. https://doi.org/10.3390/app10041502
Ju S-H, Yuantien C-C, Hsieh W-K. Study of Lead Rubber Bearings for Vibration Reduction in High-Tech Factories. Applied Sciences. 2020; 10(4):1502. https://doi.org/10.3390/app10041502
Chicago/Turabian StyleJu, Shen-Haw, Cheng-Chun Yuantien, and Wen-Ko Hsieh. 2020. "Study of Lead Rubber Bearings for Vibration Reduction in High-Tech Factories" Applied Sciences 10, no. 4: 1502. https://doi.org/10.3390/app10041502
APA StyleJu, S.-H., Yuantien, C.-C., & Hsieh, W.-K. (2020). Study of Lead Rubber Bearings for Vibration Reduction in High-Tech Factories. Applied Sciences, 10(4), 1502. https://doi.org/10.3390/app10041502






