Motion-Based Design of Passive Damping Systems to Reduce Wind-Induced Vibrations of Stay Cables under Uncertainty Conditions
Abstract
:1. Introduction
2. Motion-Based Design of Structures under Uncertainty Conditions
2.1. Motion-Based Design of Structures under Deterministic Conditions
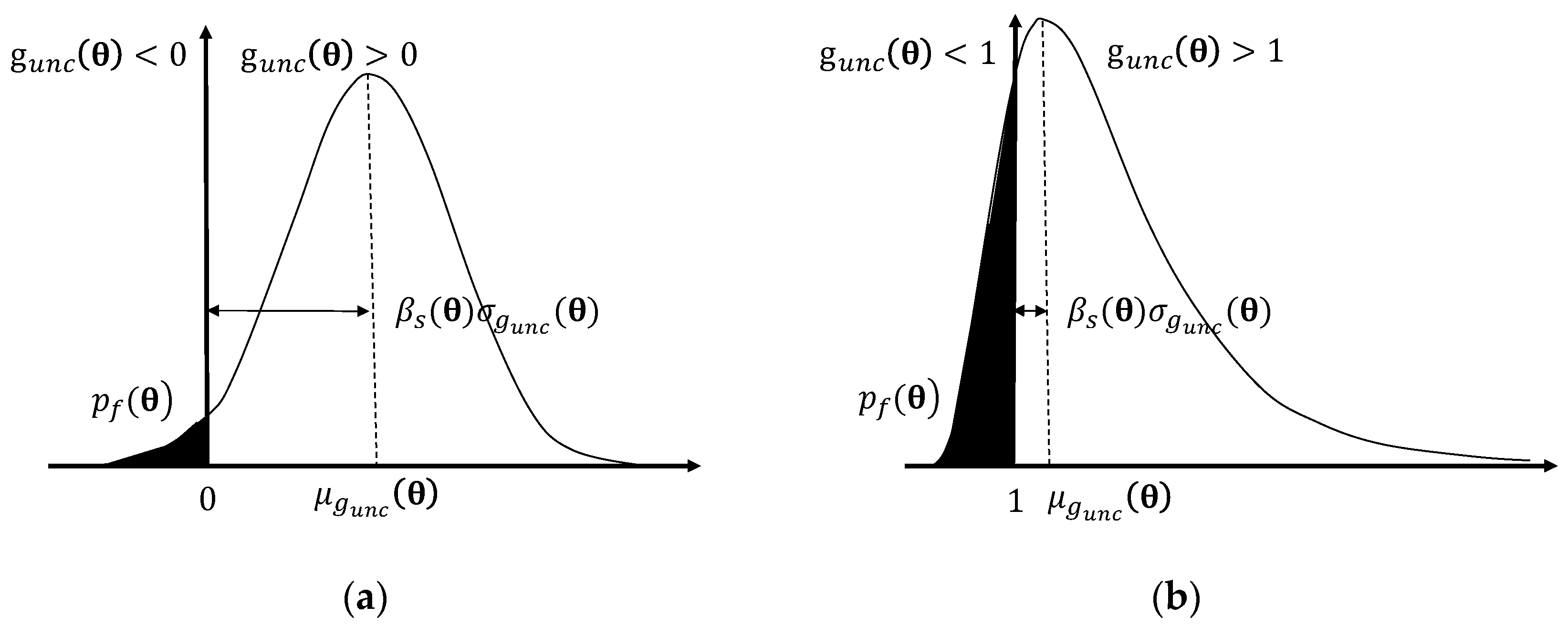
2.2. Motion-Based Design of Structures under Stochastic Conditions
3. Damper-Cable Interaction Model under Wind Action
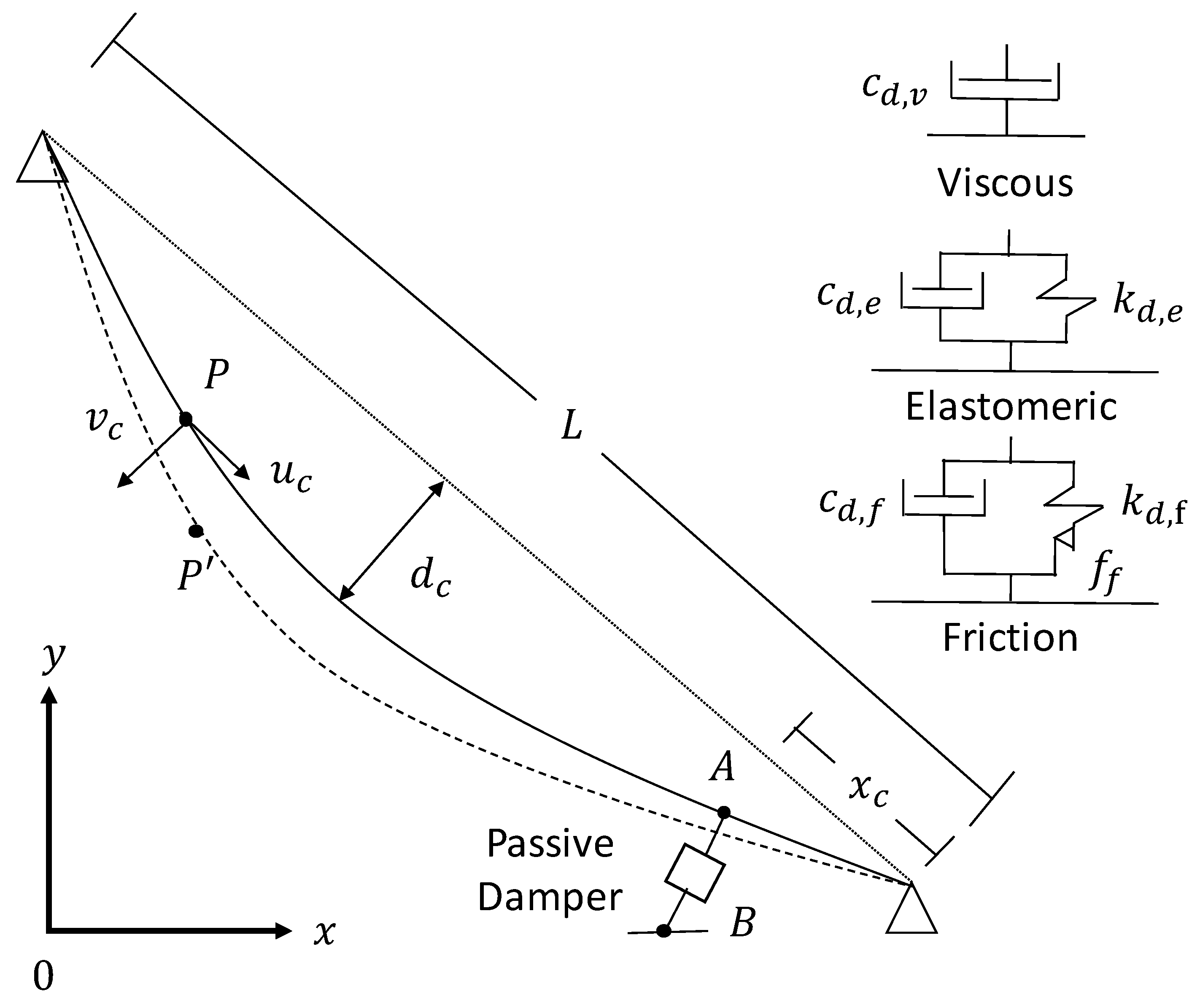
3.1. Modelling the Damper-Cable Interaction
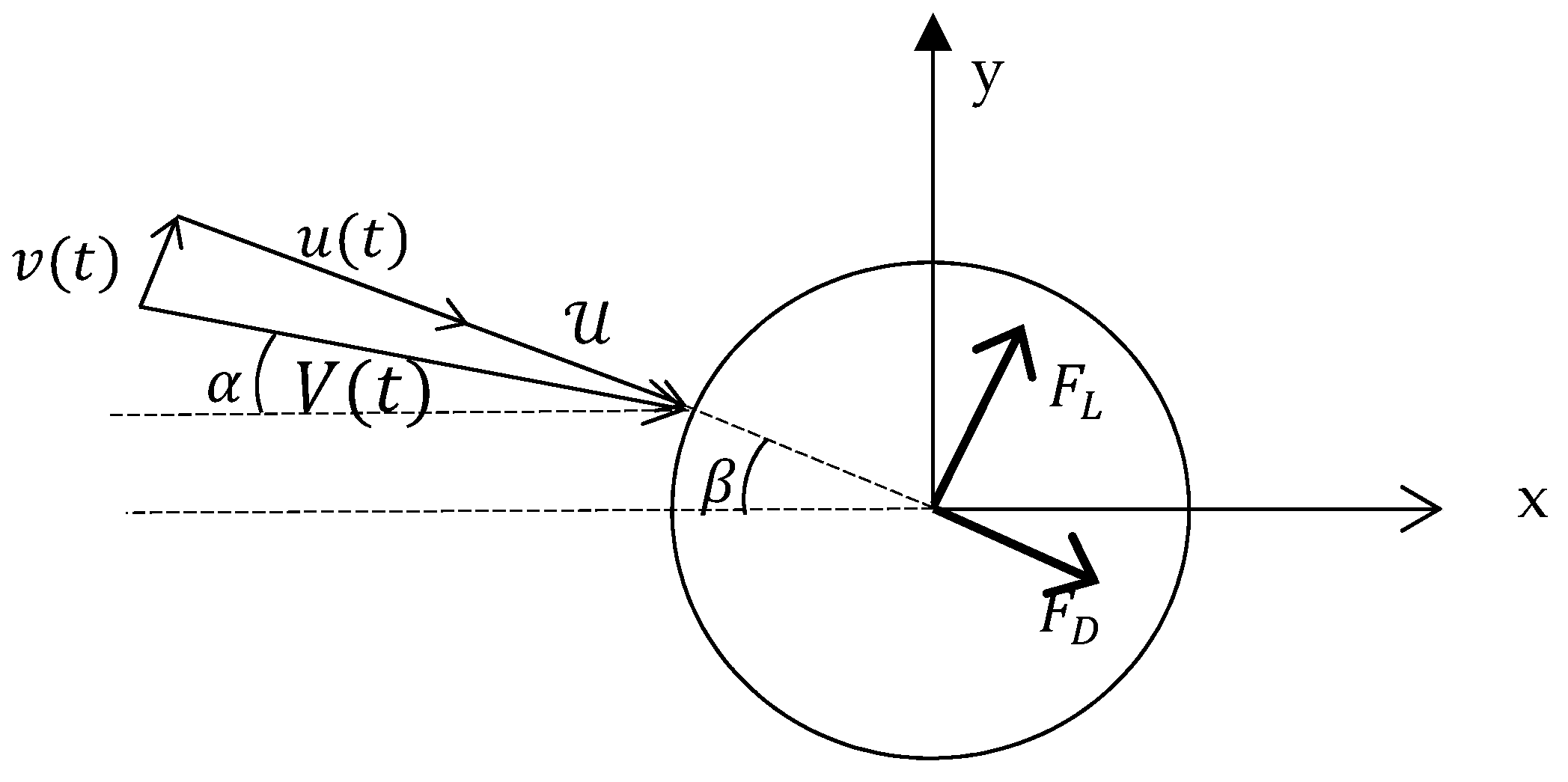
3.2. Modelling the Wind Action
4. Application Example
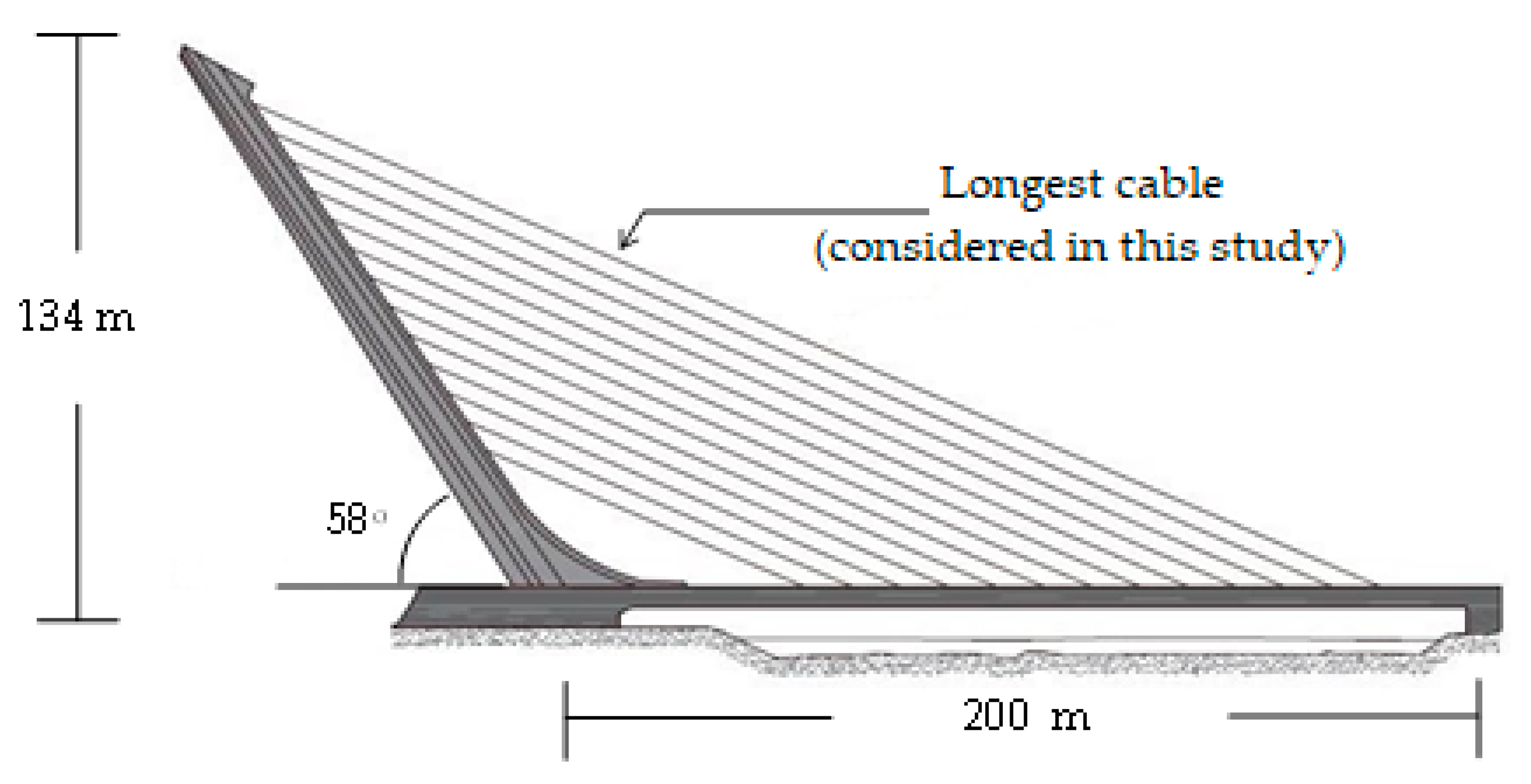
4.1. FE Model and Numerical Modal Analysis
4.2. Assessment of the Vibration Serviceability Limit State of the Cable under Uncertainty Conditions
4.3. Motion-Based Design of Passive Damping Devices under Uncertainty Conditions
4.3.1. Viscous Damper
4.3.2. Elastomeric Damper
4.3.3. Friction Damper
4.4. Discussion of Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abdel-Ghaffar, A.M.; Khalifa, M.A. Importance of Cable Vibration in Dynamics of Cable-Stayed Bridges. J. Eng. Mech. 1991, 117, 2571–2589. [Google Scholar] [CrossRef]
- Caetano, E. Cable Vibrations in Cable-Stayed Bridges; IABSE: Zürich, Switzerland, 2007; Volume 9. [Google Scholar]
- Lepidi, M.; Gattulli, V. Static and dynamic response of elastic suspended cables with thermal effects. Int. J. Solids Struct. 2012, 49, 1103–1116. [Google Scholar] [CrossRef] [Green Version]
- Caetano, E.; Cunha, A.; Gattulli, V.; Lepidi, M. Cable–deck dynamic interactions at the International Guadiana Bridge: On-site measurements and finite element modelling. Struct. Control Health Monit. 2008, 15, 237–264. [Google Scholar] [CrossRef]
- Domaneschi, M.; Martinelli, L. Extending the benchmark cable-stayed bridge for transverse response under seismic loading. J. Bridge Eng. 2013, 19, 04013003. [Google Scholar] [CrossRef]
- Wind-Induced Vibration of Stay Cables; FHWA-HRT-05-083; Federal Highway Administration: New York, NY, USA, 2007.
- Dyke, S.J.; Caicedo, J.M.; Turan, G.; Bergman, L.A.; Hague, S. Phase I benchmark control problem for seismic response of cable-stayed bridges. J. Struct. Eng. 2003, 129, 857–872. [Google Scholar] [CrossRef] [Green Version]
- Cremona, C. Comportement Au Vent Des Ponts; Presses De L’ecole Natinale Des Ponts Et Chaussées; Association Francaise De Génie Civil: Paris, France, 2002. [Google Scholar]
- Caracoglia, L.; Zuo, D. Effectiveness of cable networks of various configurations in suppressing stay-cable vibration. Eng. Struct. 2009, 31, 2851–2864. [Google Scholar] [CrossRef]
- Bossens, F.; Preumont, A. Active tendon control of cable-stayed bridges: A large-scale demonstration. Earthq. Eng. Struct. Dyn. 2001, 30, 961–979. [Google Scholar] [CrossRef]
- Johnson, E.A.; Baker, G.A.; Spencer, B.F., Jr.; Fujino, Y. Semiactive Damping of Stay Cables. J. Eng. Mech. 2007, 133, 1–11. [Google Scholar] [CrossRef]
- Ali, H.-E.M.; Abdel-Ghaffar, A.M. Seismic Passive Control of Cable-Stayed Bridges. Shock Vib. 1995, 2, 918721. [Google Scholar] [CrossRef]
- Rodellar, J.; Mañosa, V.; Monroy, C. An active tendon control scheme for cable-stayed bridges with model uncertainties and seismic excitation. J. Struct. Control 2002, 9, 75–94. [Google Scholar] [CrossRef]
- Huang, P.; Wang, X.; Wen, Q.; Wang, W.; Sun, H. Active Control of Stay Cable Vibration Using a Giant Magnetostrictive Actuator. J. Aerosp. Eng. 2018, 31, 04018074. [Google Scholar] [CrossRef]
- Zhou, H.J.; Sun, L.M. Damping of stay cable with passive-on magnetorheological dampers: A full-scale test. Int. J. Civ. Eng. 2013, 11, 154–159. [Google Scholar]
- Chen, Z.H.; Lam, K.H.; Ni, Y.Q. Enhanced damping for bridge cables using a self-sensing MR damper. Smart Mater. Struct. 2016, 25, 085019. [Google Scholar] [CrossRef]
- YeganehFallah, A.; Attari, N.K.A. Robust control of seismically excited cable stayed bridges with MR dampers. Smart Mater. Struct. 2017, 26, 035056. [Google Scholar] [CrossRef]
- Zhao, Y.-L.; Xu, Z.-D.; Wang, C. Wind vibration control of stay cables using magnetorheological dampers under optimal equivalent control algorithm. J. Sound Vib. 2019, 443, 732–747. [Google Scholar] [CrossRef]
- Xu, Y.L.; Zhou, H.J. Damping cable vibration for a cable-stayed bridge using adjustable fluid dampers. J. Sound Vib. 2007, 306, 349–360. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, S. Magnetic negative stiffness dampers. Smart Mater. Struct. 2015, 24, 072002. [Google Scholar] [CrossRef]
- Zhou, P.; Fang, Q. Match of Negative Stiffness and Viscous Damping in A Passive Damper for Cable Vibration Control. Available online: https://www.hindawi.com/journals/sv/2019/3208321/ (accessed on 30 September 2019).
- Caracoglia, L.; Jones Nicholas, P. Passive hybrid technique for the vibration mitigation of systems of interconnected stays. J. Sound Vib. 2007, 307, 849–864. [Google Scholar] [CrossRef]
- Jiménez-Alonso, J.F.; Sáez, A. Robust optimum design of tuned mass dampers to mitigate pedestrian-induced vibrations using multi-objective genetic algorithms. Struct. Eng. Int. 2017, 27, 492–501. [Google Scholar] [CrossRef]
- Kovacs, I. Zur frage der seilschwingungen und der seildämpfung. Bautechnik 1982, 59, 325–332. [Google Scholar]
- Pacheco, B.M.; Fujino, Y.; Sulekh, A. Estimation curve for modal damping in stay cables with viscous damper. J. Struct. Eng. 1993, 119, 1961–1979. [Google Scholar] [CrossRef]
- Krenk, S. Vibrations of a taut cable with an external damper. J. Appl. Mech. 2000, 67, 772–776. [Google Scholar] [CrossRef]
- Yoneda, M.; Maeda, K. A study on practical estimation method for structural damping of stay cables with dampers. Doboku Gakkai Ronbunshu 1989, 1989, 455–458. [Google Scholar] [CrossRef] [Green Version]
- Ontiveros-Pérez, S.P.; Miguel, L.F.F.; Miguel, L.F.F. Robust Simultaneous Optimization of Friction Damper for the Passive Vibration Control in a Colombian Building. Procedia Eng. 2017, 199, 1743–1748. [Google Scholar] [CrossRef]
- Connor, J.J. Introduction to Structural Motion Control, MIT-Prentice Hall Series on Civil, Environmental and Systems Engineering; Prentice Hall: Bergen, NJ, USA, 2003. [Google Scholar]
- Naranjo-Pérez, J.; Jiménez-Manfredi, J.; Jiménez-Alonso, J.; Sáez, A. Motion-based design of passive damping devices to mitigate wind-induced vibrations in stay cables. Vibration 2018, 1, 269–289. [Google Scholar] [CrossRef] [Green Version]
- Hao, P.; Wang, B.; Li, G.; Meng, Z.; Wang, L. Hybrid Framework for Reliability-Based Design Optimization of Imperfect Stiffened Shells. AIAA J. 2015, 53, 2878–2889. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.; Li, Y.; Lin, G.; Qiu, Z. Structural time-dependent reliability assessment of the vibration active control system with unknown-but-bounded uncertainties. Struct. Control Health Monit. 2017, 24, e1965. [Google Scholar] [CrossRef]
- Rathi, A.K.; Chakraborty, A. Reliability-based performance optimization of TMD for vibration control of structures with uncertainty in parameters and excitation. Struct. Control Health Monit. 2017, 24, e1857. [Google Scholar] [CrossRef]
- EN 1990 Eurocode 0: Basis of Structural Design; European Committee for Standardization: Brussels, Belgium, 2005.
- Wang, L.; Liu, J.; Yang, Y. A nonprobabilistic time-variant reliability-based optimization approach to the reliable active controller design of structural vibration considering convex uncertainties. Struct. Control Health Monit. 2018, 25, e2269. [Google Scholar] [CrossRef]
- Binder, K.; Heermann, D. Monte Carlo Simulation in Statistical Physics: An Introduction; Graduate Texts in Physics, 5th ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-03162-5. [Google Scholar]
- Arora, J.S. Optimization of Structural and Mechanical Systems; World Scientific Publishing Co. Pte. Ltd.: 5 Toh Tuck Link, Singapore, 2007. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer Verlag: New York, NY, USA, 1999. [Google Scholar]
- Holickỳ, M. Reliability Analysis for Structural Design; African Sun Media: Stellenbosch, South Africa, 2009. [Google Scholar]
- Warnitchai, P.; Fujino, Y.; Susumpow, T. A non-linear dynamic model for cables and its application to a cable structure system. J. Sound Vib. 1995, 187, 695–712. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, A.; Taylor, C.A. Investigation of dynamic cable–deck interaction in a physical model of a cable-stayed bridge. Part I: Modal analysis. Earthq. Eng. Struct. Dyn. 2000, 28, 481–498. [Google Scholar] [CrossRef]
- Johnson, E.A.; Christenson, R.E.; Spencer, B.F., Jr. Semiactive damping of cables with sag. Comput. Aided Civ. Infrastruct. Eng. 2003, 18, 132–146. [Google Scholar] [CrossRef]
- Zhou, Q.; Nielsen, S.R.; Qu, W.L. Semiactive control of three-dimensional vibrations of an inclined sag cable with magnetorheological dampers. J. Sound Vib. 2006, 296, 1–22. [Google Scholar] [CrossRef]
- Mehrabi, A.B.; Tabatabai, H. Unified finite difference formulation for free vibration of cables. J. Struct. Eng. 1998, 124, 1313–1322. [Google Scholar] [CrossRef]
- Hoang, N.; Fujino, Y. Analytical study on bending effects in a stay cable with a damper. J. Eng. Mech. 2007, 133, 1241–1246. [Google Scholar] [CrossRef]
- Yu, Z.; Xu, Y.L. Mitigation of three-dimensional vibration of inclined sag cable using discrete oil dampers—I. Formulation. J. Sound Vib. 1998, 214, 659–673. [Google Scholar] [CrossRef]
- Connor, J.; Laflamme, S. Optimal Passive Damping Distribution. In Structural Motion Engineering; Springer: Berlin/Heidelberg, Germany, 2014; pp. 141–197. [Google Scholar]
- Xu, Z.-D.; Shen, Y.-P.; Zhao, H.-T. A synthetic optimization analysis method on structures with viscoelastic dampers. Soil Dyn. Earthq. Eng. 2003, 23, 683–689. [Google Scholar] [CrossRef]
- Zhou, H.; Sun, L.; Xing, F. Free vibration of taut cable with a damper and a spring. Struct. Control Health Monit. 2014, 21, 996–1014. [Google Scholar] [CrossRef]
- Seong, J.-Y.; Min, K.-W. An analytical approach for design of a structure equipped with friction dampers. Procedia Eng. 2011, 14, 1245–1251. [Google Scholar] [CrossRef] [Green Version]
- Hong, S. Time Domain Buffeting Analysis of Large-Span Cable-Stayed Bridge. Master’s Thesis, FEUP. University of Porto, Porto, Portugal, 2009. [Google Scholar]
- Solari, G. Gust-excited vibrations. In Wind-Excited Vibrations of Structures; Springer: Berlin/Heidelberg, Germany, 1994; pp. 195–291. [Google Scholar]
- Davenport, A.G. The Dependence of Wind Loads on Meteorological Parameter. Wind Eff. Build. Struct. 1968, 1, 19–82. [Google Scholar]
- EN 1991-1-4 Eurocode 1. Actions on Structures—Part 1–4: General Actions—Wind Actions; European Committee for Standardization: Brussels, Belgium, 2005.
- Casas, J.R.; Aparicio, A.C. Monitoring of the Alamillo cable-stayed bridge during construction. Exp. Mech. 1998, 38, 24–28. [Google Scholar] [CrossRef]
- Casas, J.R.; Aparicio, A.C. Rain–wind-induced cable vibrations in the Alamillo cable-stayed bridge (Sevilla, Spain). Assessment and remedial action. Struct. Infrastruct. Eng. 2010, 6, 549–556. [Google Scholar] [CrossRef] [Green Version]
- Ansys Mechanical 19.0. Ansys Inc. 2019. Available online: http://www.ansys.com/ (accessed on 1 October 2019).
- Simiu, E.; Scanlan, R.H. Wind Effects on Structures: Fundamentals and Applications to Design, 3rd ed.; John Willey & Sons, Inc.: New York, NY, USA, 1996. [Google Scholar]
- EN 1993-1-11 Eurocode 3: Design of Steel Structures-Part 1–11: Design of Structures with Tension Components; European Committee for Standardization: Brussels, Belgium, 2006.
- Stromquist-LeVoir, G.; McMullen, K.F.; Zaghi, A.E.; Christenson, R. Determining Time Variation of Cable Tension Forces in Suspended Bridges Using Time-Frequency Analysis. Adv. Civ. Eng. 2018, 2018. [Google Scholar] [CrossRef] [Green Version]
- Naranjo-Pérez, J.; Jiménez-Alonso, J.F.; Díaz, I.M.; Sáez, A. Motion-based design of viscous dampers for cable-stayed bridges under uncertainty conditions. In Proceedings of the 5th International Conference on Mechanical Models in Structural Engineering, CMMoST 2019, Alicante, Spain, 23–25 Ocober 2019. [Google Scholar]
- Park, S.; Bosch, H.R. Mitigation of Wind-Induced Vibration of Stay Cables: Numerical Simulations and Evaluations; Federal Highway Administration: Hampton, VA, USA, 2014.
- Jurado, D. Simulación Estocástica De Cargas Para Análisis Dinámico De Estructuras En Ingeniería Civil. Master’s Thesis, Universidad de Sevilla, Seville, Spain, 2017. [Google Scholar]
- Matlab Inc. Matlab R2019b. Available online: http://www.mathworks.com/ (accessed on 15 October 2019).
- Koh, C.G.; Perry, M.J. Structural Identification and Damage Detection Using Genetic Algorithms: Structures and Infrastructures Book Series; CRC Press: Boca Raton, FL, USA, 2017; Volume 6. [Google Scholar]

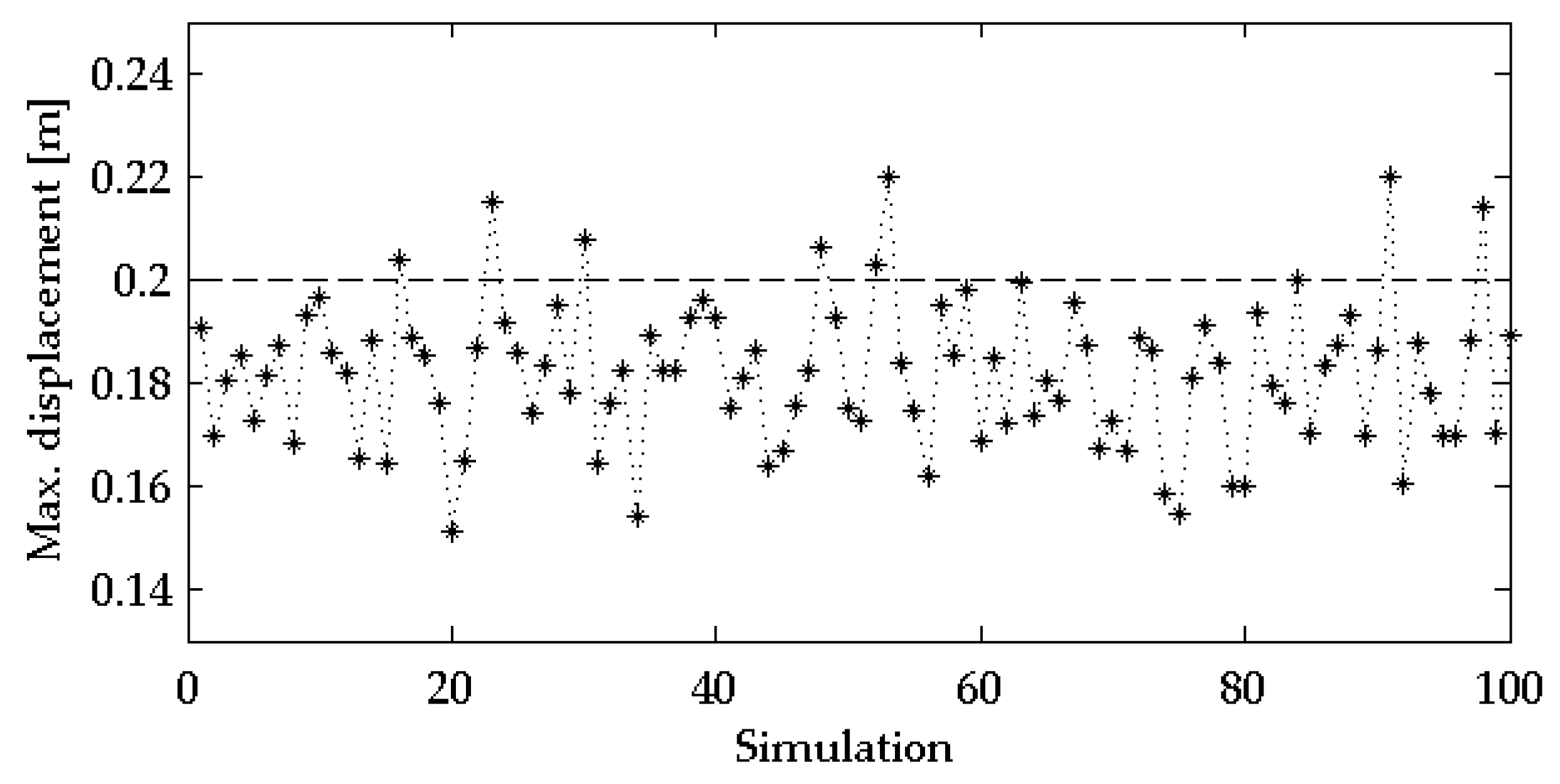
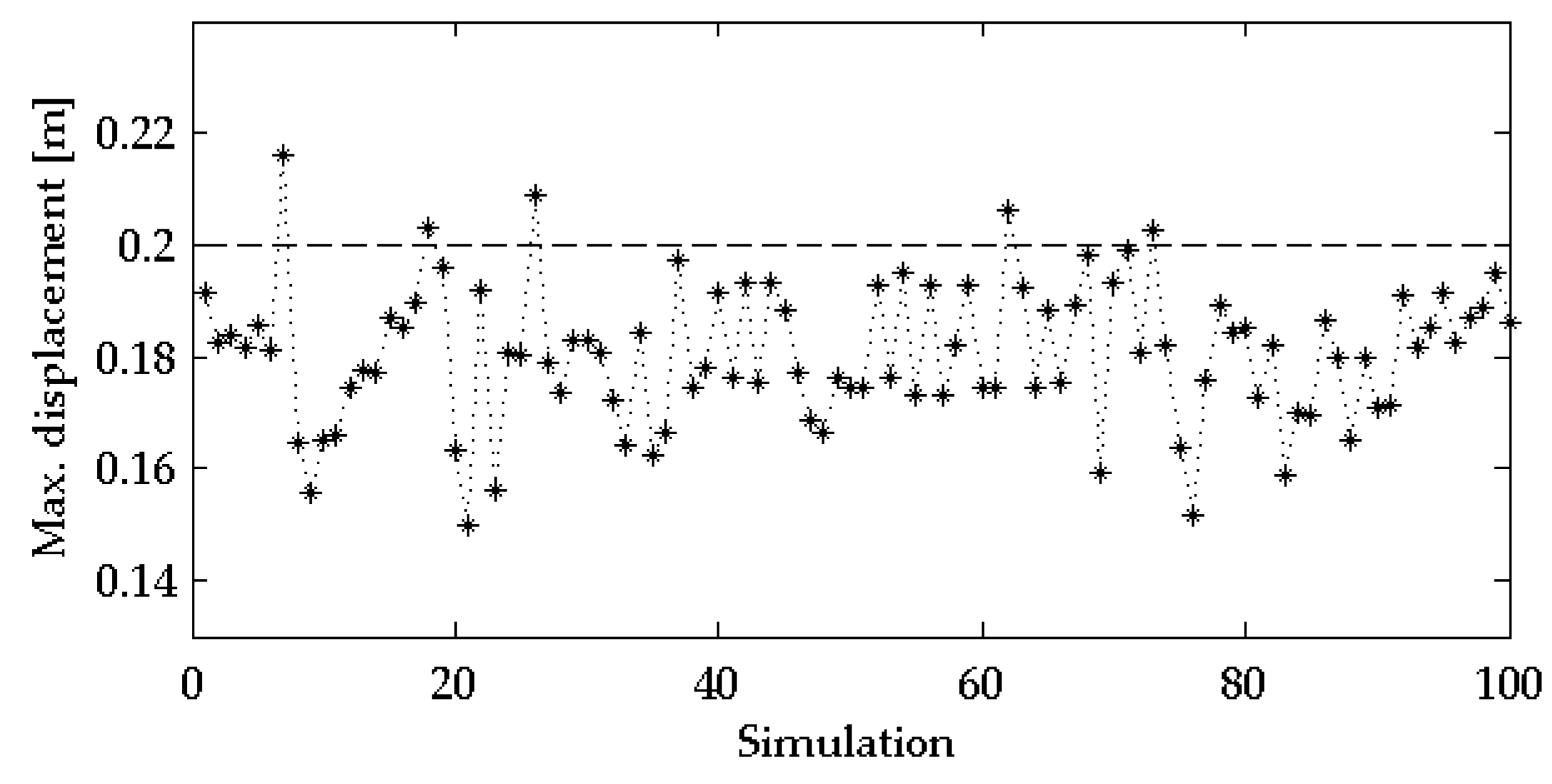
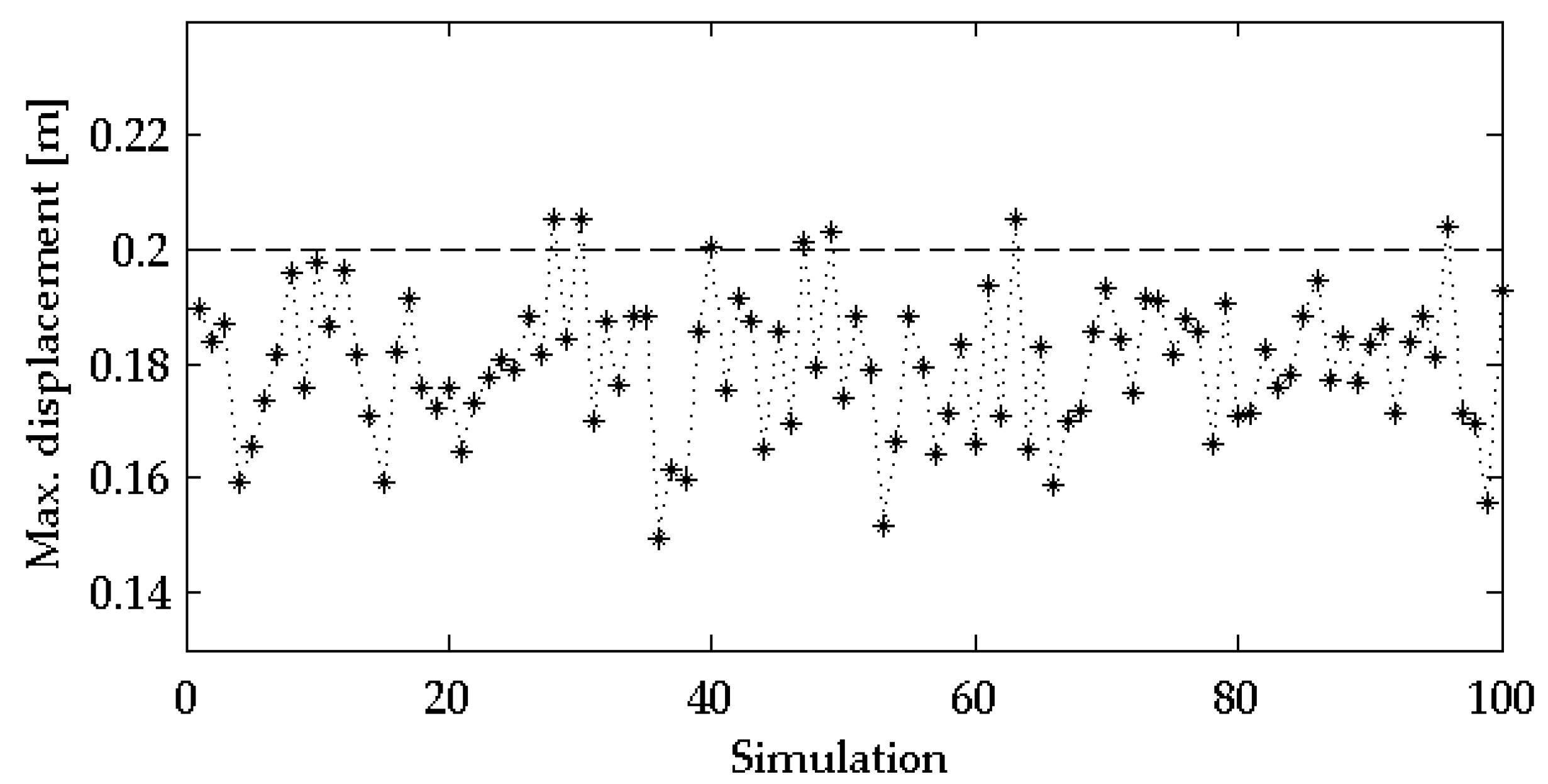
| Natural Frequency | ||||||
|---|---|---|---|---|---|---|
| Value [Hz] | 0.452 | 0.905 | 1.351 | 1.802 | 2.254 | 2.706 |
| Design Level | Allowable Displacement [m] 1 |
|---|---|
| preferred | |
| recommended | |
| not to exceed |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naranjo-Pérez, J.; Jiménez-Alonso, J.F.; M. Díaz, I.; Quaranta, G.; Sáez, A. Motion-Based Design of Passive Damping Systems to Reduce Wind-Induced Vibrations of Stay Cables under Uncertainty Conditions. Appl. Sci. 2020, 10, 1740. https://doi.org/10.3390/app10051740
Naranjo-Pérez J, Jiménez-Alonso JF, M. Díaz I, Quaranta G, Sáez A. Motion-Based Design of Passive Damping Systems to Reduce Wind-Induced Vibrations of Stay Cables under Uncertainty Conditions. Applied Sciences. 2020; 10(5):1740. https://doi.org/10.3390/app10051740
Chicago/Turabian StyleNaranjo-Pérez, Javier, Javier F. Jiménez-Alonso, Iván M. Díaz, Giuseppe Quaranta, and Andrés Sáez. 2020. "Motion-Based Design of Passive Damping Systems to Reduce Wind-Induced Vibrations of Stay Cables under Uncertainty Conditions" Applied Sciences 10, no. 5: 1740. https://doi.org/10.3390/app10051740
APA StyleNaranjo-Pérez, J., Jiménez-Alonso, J. F., M. Díaz, I., Quaranta, G., & Sáez, A. (2020). Motion-Based Design of Passive Damping Systems to Reduce Wind-Induced Vibrations of Stay Cables under Uncertainty Conditions. Applied Sciences, 10(5), 1740. https://doi.org/10.3390/app10051740






