Opal-Like Photonic Structuring of Perovskite Solar Cells Using a Genetic Algorithm Approach
Abstract
:Featured Application
Abstract
1. Introduction
2. Design of the Perovskite Solar Cell
3. Numerical Methods and Figure of Merits
4. Results
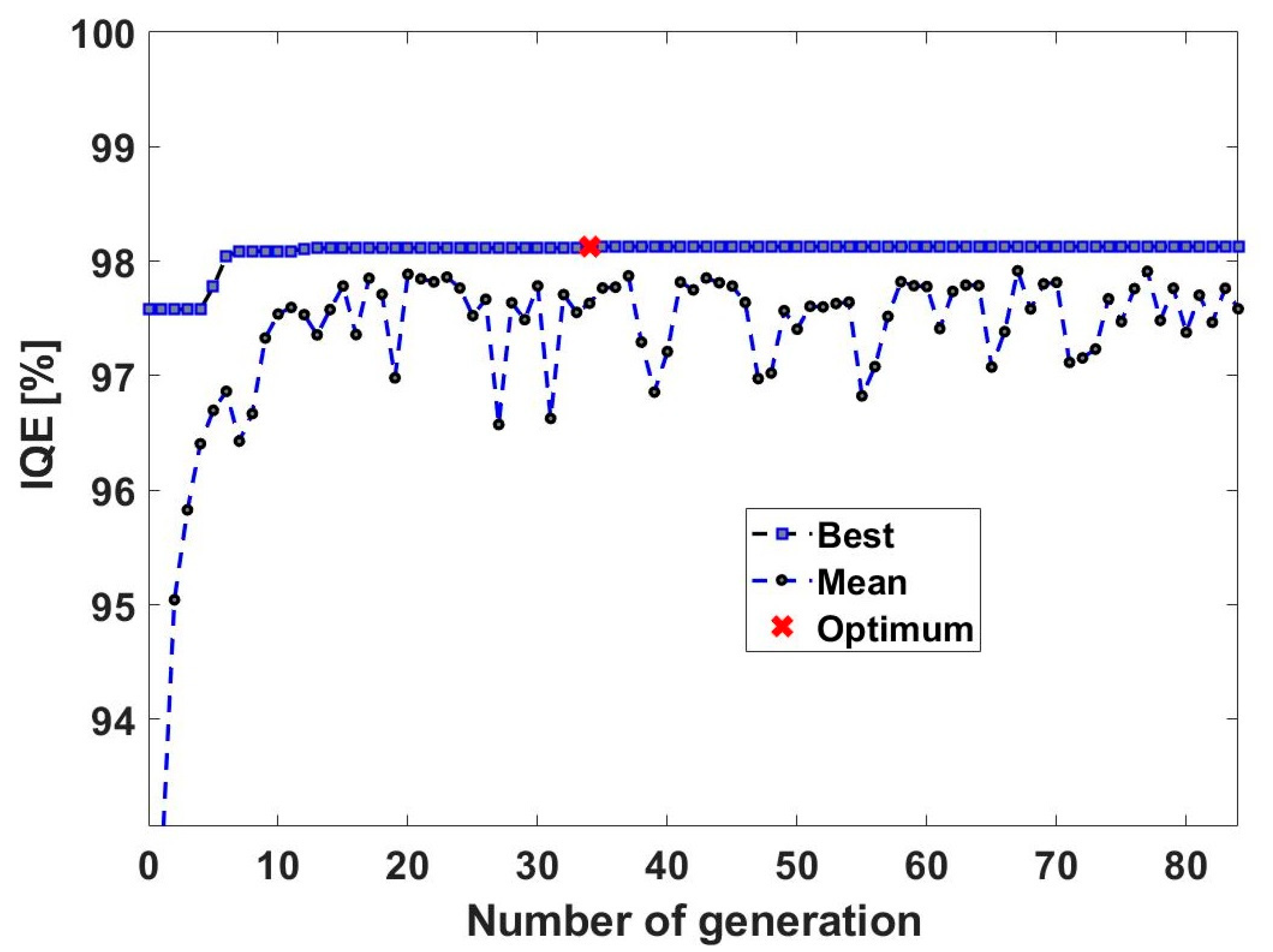
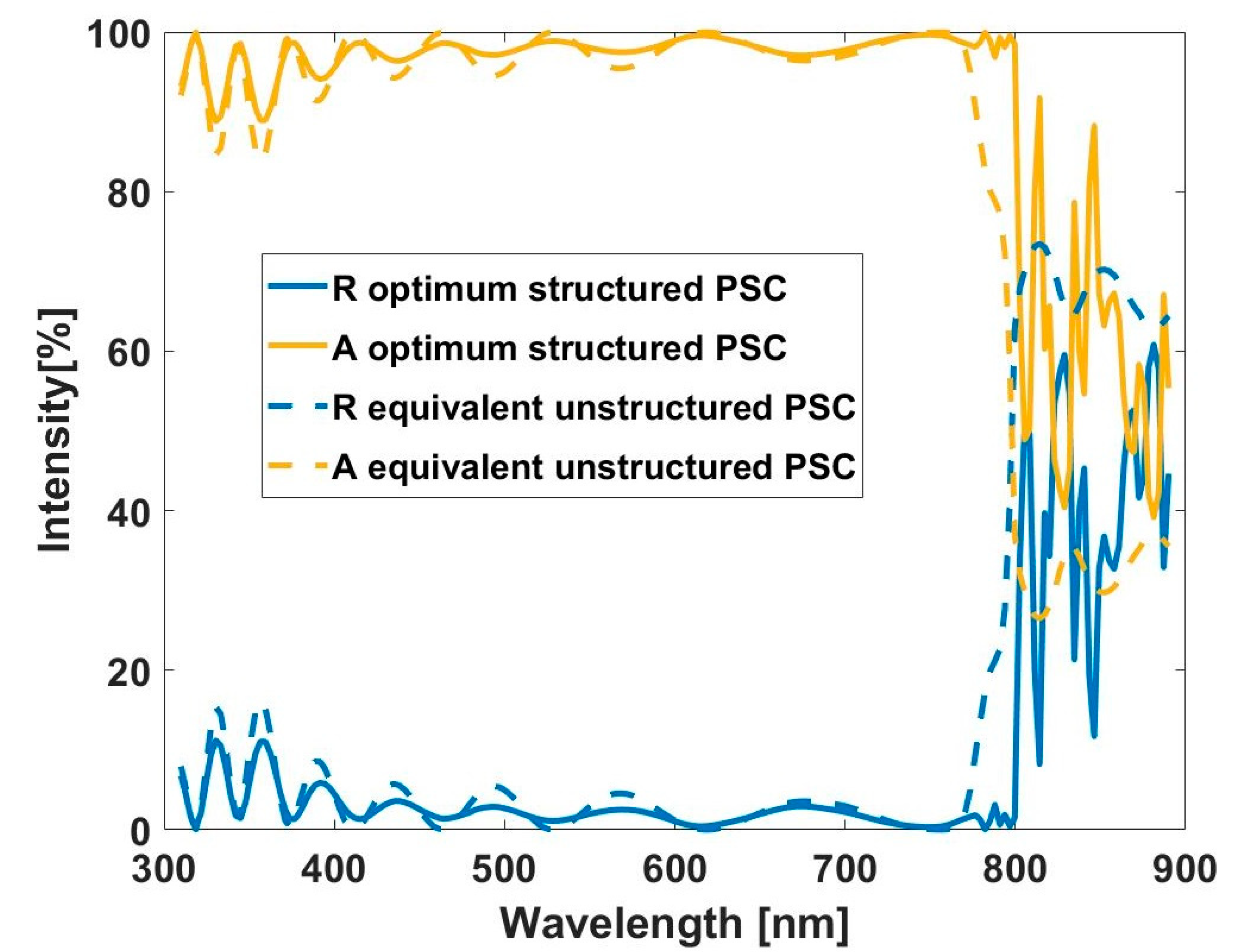
4.1. Optimum
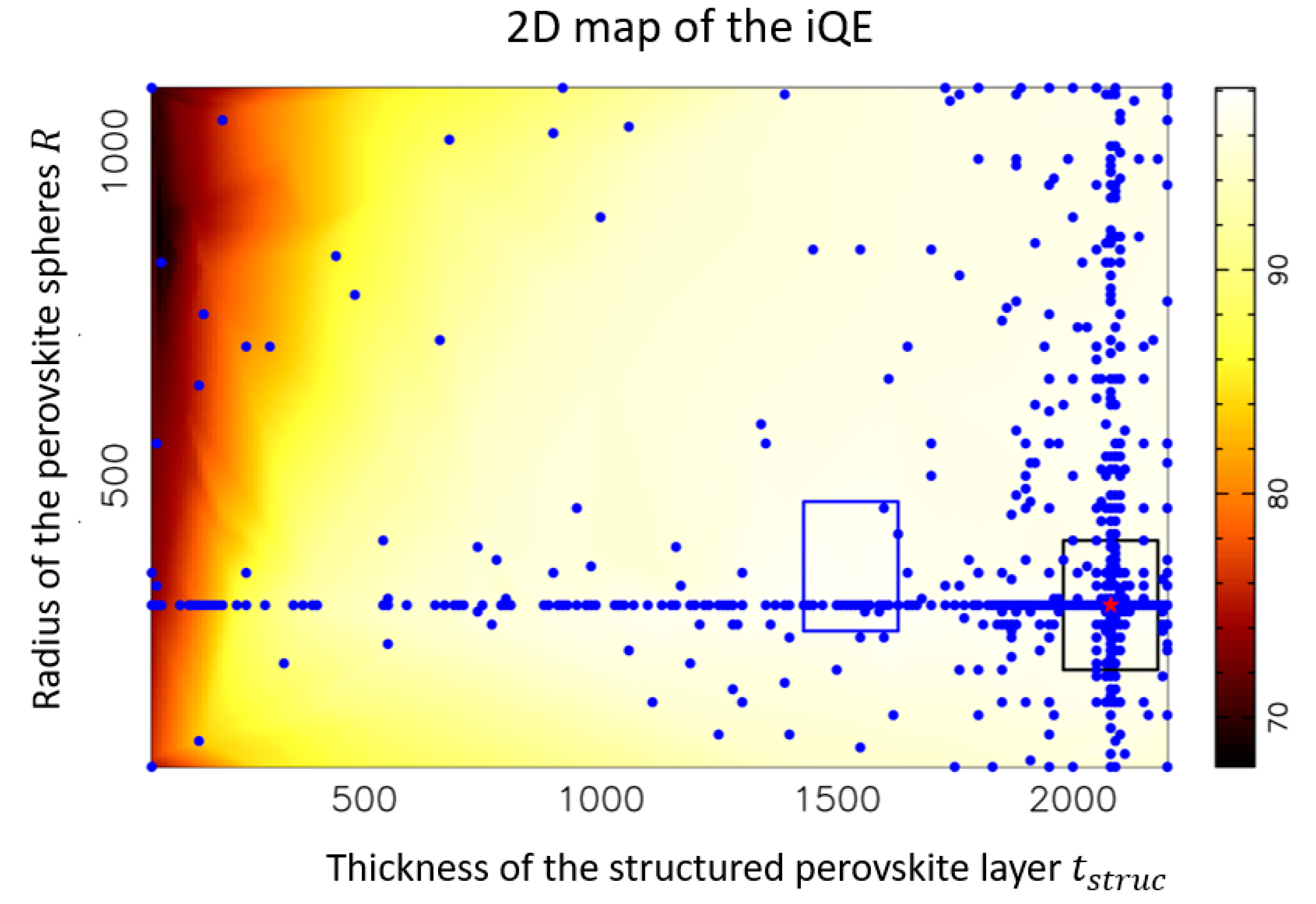
4.2. Robustness of the Optimum
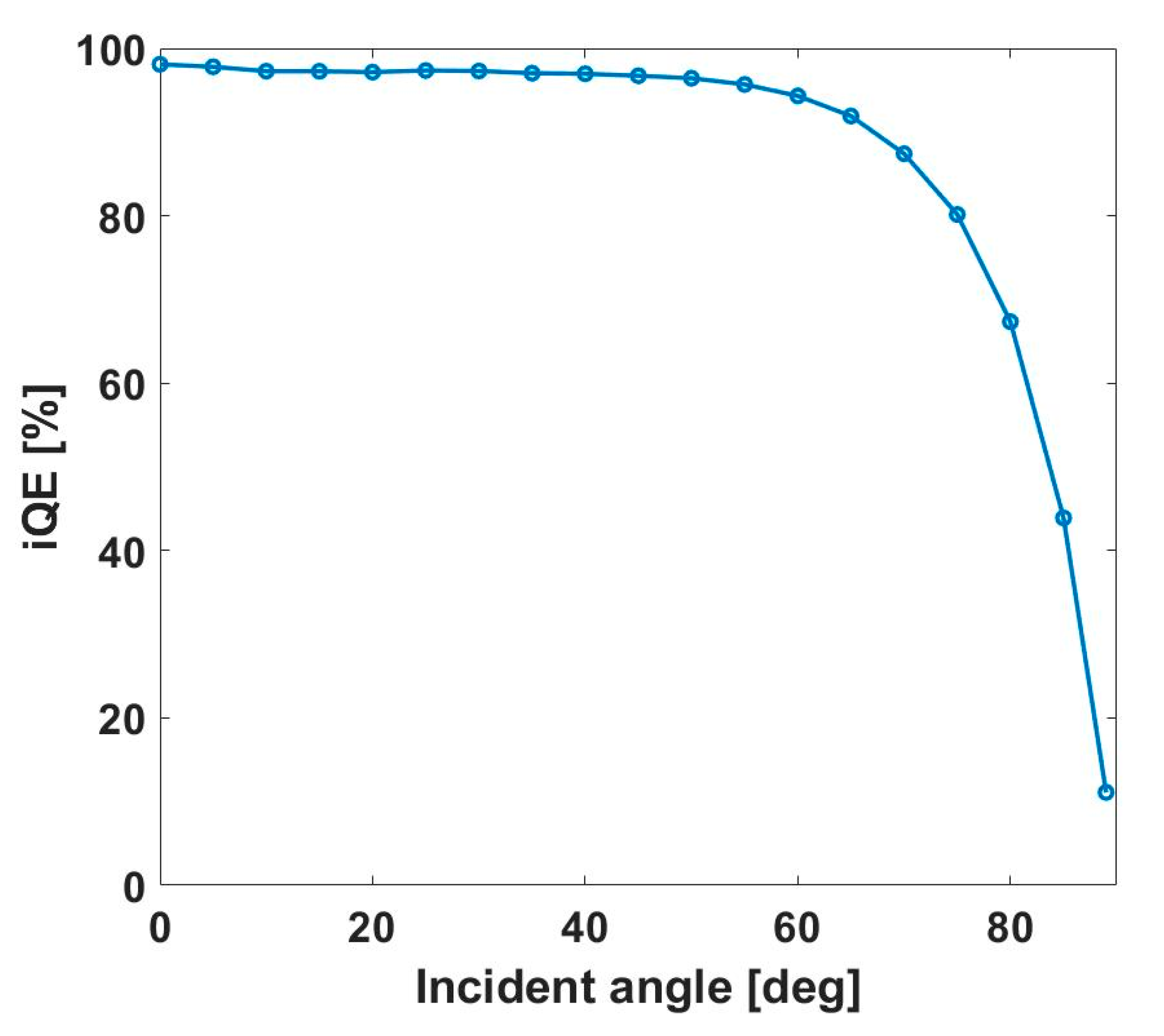
4.3. Angular Dependency
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Best Research-Cell Efficiency Chart|Photovoltaic Research|NREL. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 30 December 2019).
- Streetman, B.; Sanjay, B. Solid State Electronic Devices, 5th ed.; Prentice Hall: Upper New Jersey River, NJ, USA, 2000; p. 524. [Google Scholar]
- Sher, M.-J.; Winkler, M.T.; Mazur, E. Pulsed-laser hyperdoping and surface texturing for photovoltaics. MRS Bull. 2011, 36, 439–445. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, A.; Green, M.A. 19.8% efficient “honeycomb” textured multicrystalline and 24.4% monocrystalline silicon solar cells. Appl. Phys. Lett. 1998, 73, 1991. [Google Scholar] [CrossRef]
- Dewan, R.; Marinkovic, M.; Noriega, R.; Phadke, S.; Salleo, A.; Knipp, D. Light trapping in thin film silicon solar cells with submicron surface texture. Opt. Express 2009, 17, 23058–23065. [Google Scholar] [CrossRef] [PubMed]
- Müller, J.; Rech, B.; Springer, J.; Vanecek, M. TCO and light trapping in silicon thin film solar cells. Sol. Energy 2004, 77, 917–930. [Google Scholar]
- Kumar Raut, H. Anti-reflective coating: A critical, in-depth review. Energy Environ. Sci. 2011, 4, 3779–3804. [Google Scholar] [CrossRef]
- Atwater, H.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Ferry, V.E.; Munday, J.N.; Atwater, H.A. Design considerations for plasmonic photovoltaics. Adv. Mater. 2010, 22, 4794–4808. [Google Scholar] [CrossRef]
- Joannopoulos, J.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University: Princeton, NJ, USA, 2008. [Google Scholar]
- Mihi, A.; Calvo, M.E.; Anta, J.A.; Mi, H. Spectral response of opal-based dye sensitized solar cells. J. Phys. Chem. C 2008, 112, 13–17. [Google Scholar] [CrossRef] [Green Version]
- Mihi, A.; Mi, H. Origin of light-harversting enhancement in colloidal photonic crystal base dye-sensitized solar cells. J. Phys. Chem. B 2005, 109, 15968–15976. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, Y.; Kawamoto, Y.; Fujita, M.; Noda, S. Enhancement of broadband optical absorption in photovoltaic devices by band-edge effect of photonic crystals. Opt. Express 2013, 21, 20111–20118. [Google Scholar] [CrossRef]
- Guldin, S.; Hüttner, S.; Kolle, M.; Welland, M.E.; Müller-Buschbaum, P.; Friend, R.H.; Tétreault, N.; Steiner, U. Dye-sensitized solar cell based on a three-dimensional photonic crystal. Nano Lett. 2010, 10, 2303–2309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ha, L.; Colodrero, S.; Mihi, A.; Häggman, L.; Ocaña, M.; Boschloo, G.; Hagfeldt, A.; Míguez, H. Porous one-dimensional photonic crystals improve the power-conversion efficiency of dye-sensitized solar cells. Adv. Mater. 2009, 21, 764–770. [Google Scholar]
- Fan, S.; Joannopoulos, J.D. Analysis of guided resonances in photonic crystal slabs. Phys. Rev. B 2002, 65, 235112. [Google Scholar] [CrossRef] [Green Version]
- Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Novel photoelectrochemical cell with mesoscopic electrodes sensitized by lead-halide compounds. In Meeting Abstracts; MA2007-02; The Electrochemical Society: Pennington, NJ, USA, 2007. [Google Scholar]
- Lang, L.; Yang, J.-H.; Liu, H.-R.; Xiang, H.J.; Gong, X.G. First-principles study on the electronic and optical properties of cubic ABX3 halide perovskite. Phys. Lett. A 2014, 378, 290–293. [Google Scholar] [CrossRef] [Green Version]
- Green, M.A.; Jiang, Y.; Soufiani, A.M.; Ho-Baillie, A. Optical properties of photovoltaic organic-inorganic lead halide perovskite. J. Phys. Chem. Lett. 2015, 6, 4774–4785. [Google Scholar] [CrossRef]
- Shirayama, M.; Kadowaki, H.; Miyadera, T.; Sugita, T.; Tamakoshi, M.; Kato, M.; Fujiseki, T.; Murata, D.; Hara, S.; Murakami, T.N.; et al. Optical transitions in hybrid perovskite solar cells: Ellipsometry, density functional theory, and quantum efficiency analyses for ch3nh3pbi 3. Phys. Rev. Appl. 2016, 5, 014012. [Google Scholar] [CrossRef] [Green Version]
- Löper, P.; Stuckelberger, M.; Niesen, B.; Werner, J.; Filipič, M.; Moon, S.J.; Yum, J.H.; Topič, M.; De Wolf, S.; Ballif, C. Complex refractive index spectra of CH3NH3PbI3 perovskite thin films determined by spectroscopic ellipsometry and spectrophotometry. J. Phys. Chem. Lett. 2015, 6, 66–71. [Google Scholar]
- Tenutta, E.; Zheng, C.; Rubel, O. Thermodynamic origin of instability in hybrid halide perovskites. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [Green Version]
- Ciccioli, A.; Latini, A. Thermodynamics and the intrinsic stability of lead halide perovskites ch3nh3pbx3. J. Phys. Chem. Lett. 2018, 9, 3756–3765. [Google Scholar] [CrossRef]
- Schünemann, S.; Chen, K.; Brittman, S.; Garnett, E.; Tüysüz, H. Preparation of organometal halide perovskite photonic crystal films for potential optoelectronic applications. ACS Appl. Mater. Interfaces 2016, 8, 25489–25495. [Google Scholar]
- Meng, K.; Gao, S.; Wu, L.; Wang, G.; Liu, X.; Chen, G.; Liu, Z. Two-dimensional organic-inorganic hybrid perovskite photonic films. Nano Lett. 2016, 16, 4166–4173. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.-X.; Rao, H.-S.; Chen, H.-Y.; Li, W.-G.; Kuang, D.-B.; Su, C.-Y. Ordered macroporous CH3NH3PbI3 perovskite semitransparent film for high-performance solar cells. J. Mater. Chem. A 2016, 4, 15662–15669. [Google Scholar] [CrossRef]
- Ha, S.-J.; Heo, J.H.; Im, S.H.; Moon, J.H. Mesoscopic CH 3NH 3PbI 3 perovskite solar cells using TiO2 inverse opal electron-conducting scaffolds. J. Mater. Chem. A 2017, 5, 1972–1977. [Google Scholar] [CrossRef]
- Chen, K.; Tüz, H. Morphology-controlled synthesis of organometal halide perovskite inverse opals. Angew. Chem. 2015, 54, 13806–13810. [Google Scholar] [CrossRef] [PubMed]
- Dewalque, J.; Henrist, C.; Loicq, J. Light-harvesting capabilities of dielectric sphere multilayers. Phot. Phon. Prop. Eng. Nanos. 2018. [Google Scholar] [CrossRef]
- Schmager, R.; Hossain, I.M.; Schackmar, F.; Richards, B.S.; Gomard, G.; Paetzold, U.W. Light coupling to quasi-guided modes in nanoimprinted perovskite solar cells. Sol. Energy Mater. Sol. Cells 2019, 201, 110080. [Google Scholar] [CrossRef]
- Schmager, R.; Gomard, G.; Richards, B.S.; Paetzold, U.W. Nanophotonic perovskite layers for enhanced current generation and mitigation of lead in perovskite solar cells. Sol. Energy Mater. Sol. Cells 2019, 192, 65–71. [Google Scholar] [CrossRef]
- Lobet, M.; Pierre, P.; Jennifer, D.; Anthony, M.; Olivier, D.; Catherine, H.; Jérôme, L. Efficiency enhancement of perovskite solar cells based on opal-like photonic crystals. Opt. Express 2019, 27, 32308–32322. [Google Scholar] [CrossRef]
- Mayer, A.; Bay, A. Optimization by a genetic algorithm of the light-extraction efficiency of a GaN light-emitting diode. J. Opt. 2015, 17, 025002. [Google Scholar] [CrossRef] [Green Version]
- Mayer, A.; Gaouyat, L.; Nicolay, D.; Carletti, T.; Deparis, O. Multi-objective genetic algorithm for the optimization of a flat-plate solar thermal collector. Opt. Express 2014, 22, A1641. [Google Scholar] [CrossRef] [PubMed]
- Mayer, A.; Muller, J.; Herman, A.; Deparis, O. Optimized absorption of solar radiations in nano-structured thin films of crystalline silicon via a genetic algorithm. Proc. SPIE 2015, 9546, 95461N-01. [Google Scholar] [CrossRef]
- Mayer, A.; Lobet, M. UV to near-infrared broadband pyramidal absorbers via a genetic algorithm optimization approach. Proc. SPIE 2018, 10671, 1067127-1-11. [Google Scholar] [CrossRef]
- Mayer, A.; Lobet, M. A genetic algorithm for addressing computationally expensive optimization problems in optical engineering. Jordan J. Phys. 2019, 12, 17–36. [Google Scholar]
- Jung, H.S.; Park, N.-G. Perovskite solar cells: From materials to devices. Small 2015, 11, 10–25. [Google Scholar] [CrossRef]
- Saliba, M.; Correa-Baena, J.-P.; Wolff, C.M.; Stolterfoht, M.; Phung, N.; Albrecht, S.; Neher, D.; Abate, A. How to make over 20% efficient perovskite solar cells in regular n-i-p and inverted p-i-n architectures. Chem. Mater. 2018, 30, 4193–4201. [Google Scholar] [CrossRef]
- Hussain, I.; Tran, H.P.; Jaksik, J.; Moore, J.; Islam, N.; Uddin, M.J. Functional materials, device architecture and flexibility of perovskite solar cell. Emergent Mater. 2018, 1, 133–154. [Google Scholar] [CrossRef] [Green Version]
- Ball, J.M.; Stranks, S.D.; Hörantner, M.T.; Hüttner, S.; Zhang, W.; Ramirez, I.; Riede, M.; Johnston, M.B.; Friend, R.H.; Snaith, H.J.; et al. Optical properties and limiting photocurrent of thin film perovskite solar cells. Energy Environ. Sci. 2015, 8, 602–609. [Google Scholar] [CrossRef]
- Shahbazyan, T.V.; Stockman, M.I. Plasmonics: Theory and Applications; Springer: Berlin, Germany, 2013. [Google Scholar]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1981, 71, 811–818. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Haupt, R.L.; Werner, D.H. Genetic Algorithms in Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing, 2nd ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
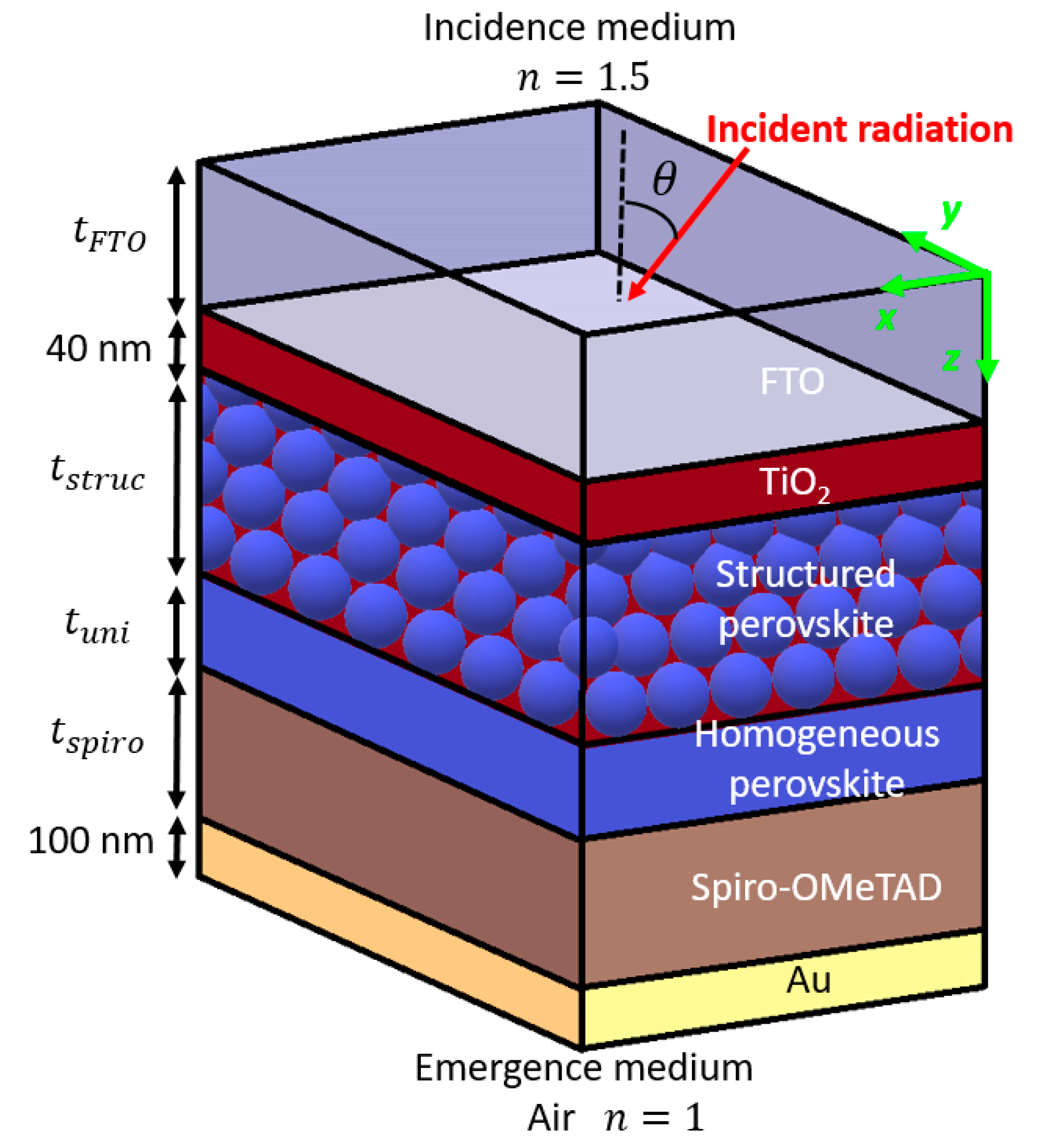

| Parameter Name | Minimum Value | Maximum Value |
|---|---|---|
| Thickness of the transparent conducting electrode fluorine-doped tin oxide FTO layer | 50 nm | 800 nm |
| Thickness of the uniform perovskite layer | 0 nm | 100 nm |
| Radius of the perovskite spheres | 50 nm | 1100 nm |
| Thickness of the structured perovskite layer | 50 nm | 2200 nm |
| Thickness of the hole transporting spiro–OMeTAD layer | 50 nm | 800 nm |
| Parameter Name | Optimum Value |
|---|---|
| Thickness of the transparent conducting electrode fluorine-doped tin oxide FTO layer | 710 nm |
| Thickness of the uniform perovskite layer | 80 nm |
| Radius of the perovskite spheres | 300 nm |
| Thickness of the structured perovskite layer | 2080 nm |
| Thickness of the hole transporting spiro–OMeTAD layer | 240 nm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lobet, M.; Mayer, A.; Maho, A.; Piron, P.; Dewalque, J.; Henrist, C.; Loicq, J. Opal-Like Photonic Structuring of Perovskite Solar Cells Using a Genetic Algorithm Approach. Appl. Sci. 2020, 10, 1783. https://doi.org/10.3390/app10051783
Lobet M, Mayer A, Maho A, Piron P, Dewalque J, Henrist C, Loicq J. Opal-Like Photonic Structuring of Perovskite Solar Cells Using a Genetic Algorithm Approach. Applied Sciences. 2020; 10(5):1783. https://doi.org/10.3390/app10051783
Chicago/Turabian StyleLobet, Michaël, Alexandre Mayer, Anthony Maho, Pierre Piron, Jennifer Dewalque, Catherine Henrist, and Jérôme Loicq. 2020. "Opal-Like Photonic Structuring of Perovskite Solar Cells Using a Genetic Algorithm Approach" Applied Sciences 10, no. 5: 1783. https://doi.org/10.3390/app10051783
APA StyleLobet, M., Mayer, A., Maho, A., Piron, P., Dewalque, J., Henrist, C., & Loicq, J. (2020). Opal-Like Photonic Structuring of Perovskite Solar Cells Using a Genetic Algorithm Approach. Applied Sciences, 10(5), 1783. https://doi.org/10.3390/app10051783





