Abstract
We discuss the implementation of a computer program for accurate calculation of the kinetics of chemical reactions integrated in the user-friendly, multi-purpose Virtual Multifrequency Spectrometer tool. The program is based on the ab initio modeling of the involved molecular species, the adoption of transition-state theory for each elementary step of the reaction, and the use of a master-equation approach accounting for the complete reaction scheme. Some features of the software are illustrated through examples including the interconversion reaction of hydroxyacetone and 2-hydroxypropanal and the production of HCN and HNC from vinyl cyanide.
1. Introduction
Calculation of chemical kinetics in the gas phase by accurate theoretical models is extremely important in research areas like atmospheric chemistry, combustion chemistry, and astrochemistry. As a matter of fact, the accurate prediction of reaction rates and the evolution of the involved species in a given set of physical conditions is a key feature for understanding the presence of a molecular or ionic species in that environment. Sometimes, the reactions involved are too fast to be tracked by laboratory experiment or the associated physical conditions are simply not reproducible, hence the understanding of those reactions relies on accurate theoretical treatments capable of predicting the evolution of the species involved in a reaction network.
A rigorous treatment of the time evolution of a chemical reaction should be based on quantum-dynamics calculations modeling the motion of the involved nuclei on ab initio potential-energy surfaces [1,2,3]. However, exact quantum-dynamics methods are only applicable to very small systems made up of three or four atoms (see, for instance, Refs. [4,5,6]). For the remaining systems—the vast majority—one can either opt for approximate methods, such as the Multi-Configuration Time-Dependent Hartree (MCTDH) [7] or the Ring Polymer Molecular Dynamics [8] (which can however extend this limit only marginally), or for a (quasi-)classical treatment of the nuclear motion [9,10,11].
On the other hand, a less expensive yet reliable route to chemical kinetics is the adoption of statistical models, such as the popular transition-state theory (TST) in one of its variants, which successfully exploits information on the energetics of a limited set of important points of the potential energy surface to predict the kinetics of chemical reactions. The usual procedure in this framework involves the calculation of transition states and intermediates of a given reaction and a description of the motions at molecular level of these species. Then, classical or semiclassical transition state theory (TST) is applied to calculate the reaction rates of each of the elementary steps making up the whole reaction (the Rice–Ramsperger–Kassel–Marcus (RRKM) [12,13,14] theory, shortly summarized in the following, is usually adopted for unimolecular reactions in the gas-phase). Finally, the time evolution of the relative abundances of each of the reactant, intermediate, and product species is calculated using methods based on either master-equation or stochastic approaches.
In this paper, we discuss the implementation of the computer program StarRate for kinetics calculations of multi-step chemical reactions, and its integration in the graphical interface of the user-friendly, multipurpose framework Virtual Multifrequency Spectrometer (VMS) [15]. The Virtual Multifrequency Spectrometer (VMS) is a tool that aims at integrating a wide range of computational and experimental spectroscopic techniques with the final goal of disclosing the static and dynamic physical-chemical properties of molecular systems, and is composed of two parts: VMS-Comp, which provides access to the latest developments in the field of computational spectroscopy [16,17], and VMS-Draw, which provides a powerful graphical user interface (GUI) for an intuitive interpretation of theoretical outcomes and a direct comparison to experiment [18]. We discuss the integration of StarRate within the VMS tool and illustrate some features of the developed software through two important reactions: the single-step interconversion of hydroxyacetone and 2-hydroxypropanal, and the more challenging multi-step dissociation of vinyl cyanide. It is worth mentioning here that the reported calculations were performed for the purpose of illustrating the developed computational software, and that providing new accurate results on the above reactions for comparison with experiment is beyond the scope of this work.
2. Computational Details: StarRate and the VMS Tool
StarRate is an object-based, modern Fortran program for modeling the kinetics of multistep reactions. At its current stage of development, StarRate targets multi-step unimolecular reactions (which can however dissociate, irreversibly, to multiple products). (The implementation of procedures for the treatment of bimolecular entrance channels is currently in progress). From a technical point of view, the program is written in the so-called ‘F language’ [19,20], a carefully crafted subset of Fortran 95, and is conceived in an object-based programming paradigm. As described in deeper detail in Ref. [21], StarRate is structured in three main modules, namely molecules, steps and reactions, which reflect the entities associated with a multi-step chemical reaction. All of these modules contain a defined data-type and some related procedures to access and operate on it. The main program, StarRate, controls the sequences of the calling of the procedures contained in each of the three main modules.
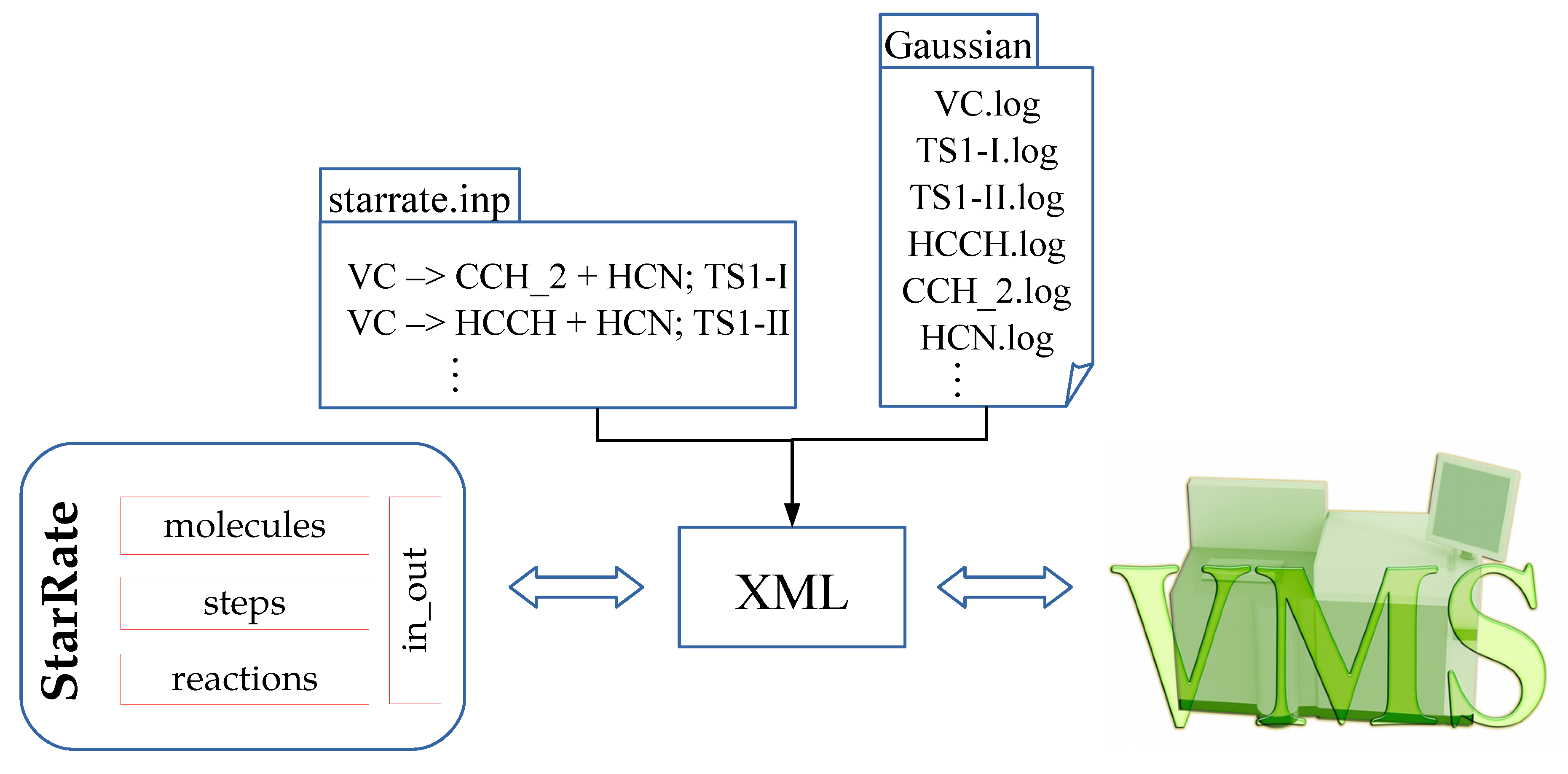
Another important module of StarRate is in_out, which handles the input and output operations of the program. Input data are accessed by StarRate through an XML interface based on the same versatile hierarchical data structure that is adopted by VMS. (The current version of VMS reads data in the JSON format, so that a straightforward conversion from XML to JSON is in order. This can be easily done, for instance, using xml2json (https://github.com/hay/xml2json), or online converters such as https://www.convertjson.com/xml-to-json.htm). At the beginning, the user has to prepare a very simple input file encoding a reaction scheme (see the starrate.inp box in Figure 1) and gather all the files, one for each molecular species, containing data deriving from electronic-structure calculations. These can be either in an internal standard format (similar to that adopted in the EStokTP [22] package) or directly output files of quantum-chemistry packages, as exemplified in Figure 1 for the case of the Gaussian package. Currently StarRate supports output files from this quantum-chemistry package (.log extension), though support for other popular electronic-structure programs is presently being pursued (see also Refs. [23,24] on the issue of interoperability and common data formats in quantum chemistry). Then, a Python script is run which extracts data from the output files generated by the quantum-chemistry calculations and, driven by the reaction scheme, collects the information in the proper sections of the XML file.
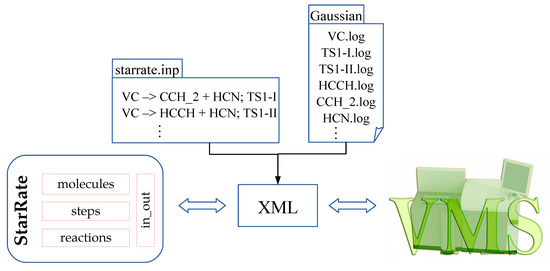
Figure 1.
Diagram showing the interoperability between electronic-structure calculations, StarRate, and Virtual Multifrequency Spectrometer (VMS) through a dedicated hierarchical data structure XML interface (see Figure 2).
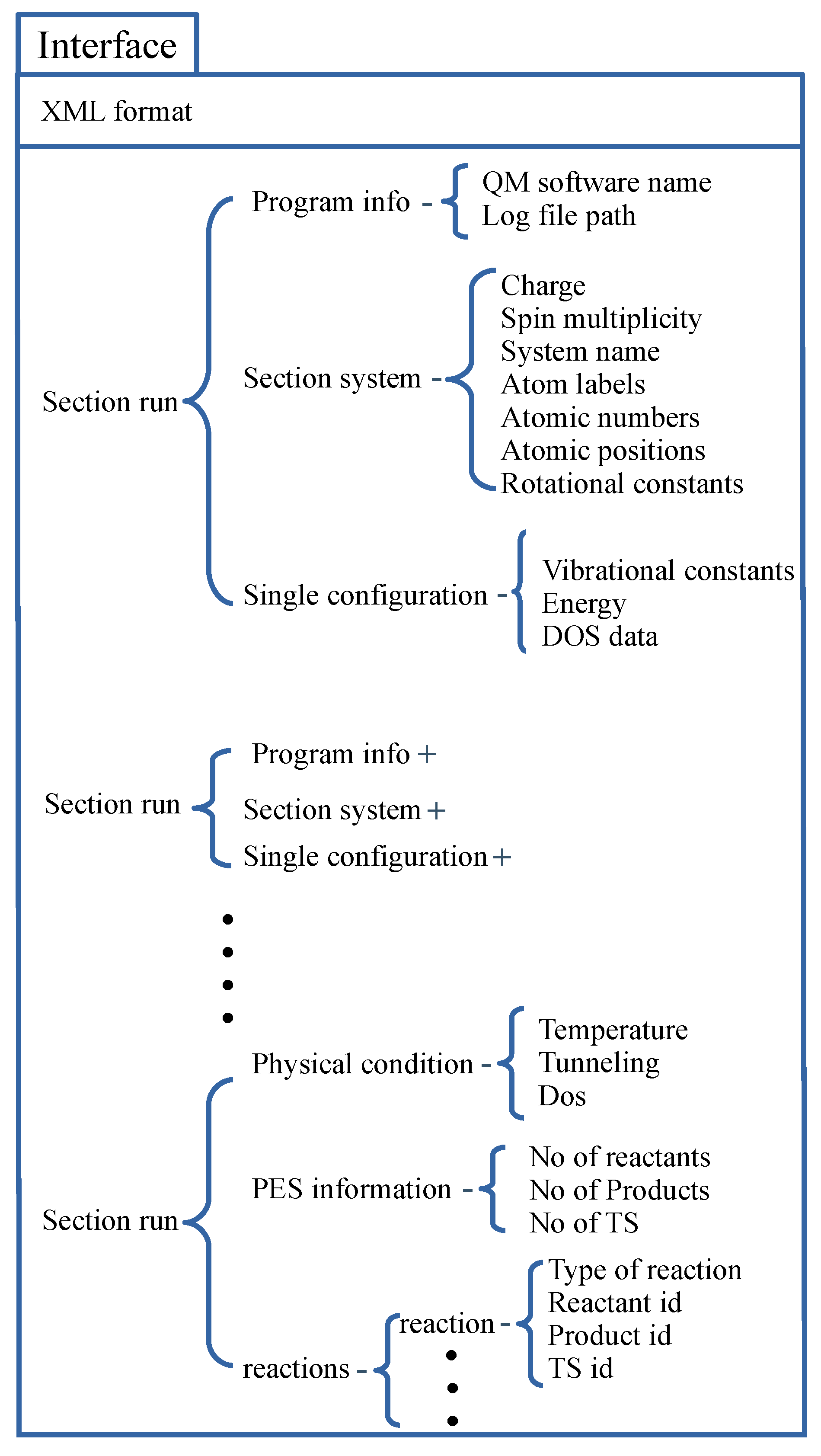
The structure of the XML interface is schematized in Figure 2. The whole XML document develops under a root element named escdata. The escdata has one child element for each molecule named section_run. Each of these elements contains three nodes: program_info, section_system, and system_single_configuration_calculation. All the information regarding a molecule is handled by these three sibling nodes. The program_info node contains two subnodes which keep track of quantum chemical software name and .log file location. The section_system node contains basic information which does not require quantum chemical information (viz., molecular charge, spin multiplicity, atom label, atomic numbers, rotational constants). The last sibling, system_single_configuration_calculation, contains information which requires quantum chemical calculations (viz., vibrational constants, SCF energy, density of state data). Finally, the last section_run collects information on physical conditions and on the reaction under study. For illustrative purposes, the actual .xml file for the reaction studied in Section 3 is given as Supplementary Materials.
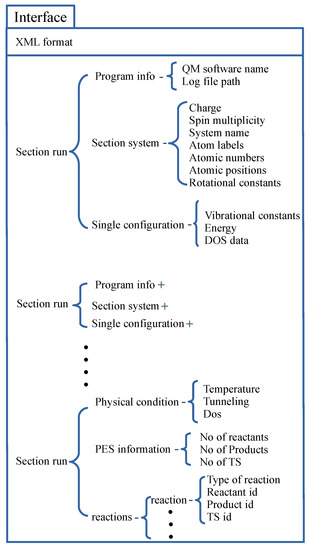
Figure 2.
Hierarchical data structure of the XML interface.
Once the XML has been generated, the StarRate program comes into play. The module in_out reads the XML file (a well-built external Fortran library, FoX_dom [25], is used for XML parsing) and saves the data for each molecule and step as structured arrays of the molecules and steps modules, respectively. Some information, such as vibrational frequencies, rotational constants, and electronic energy, is collected from the electronic-structure calculations; some other information such as densities of states (see later on) and single-step microcanonical rate coefficients are either also read as input data or computed internally to StarRate. Lastly, the reactions module solves the kinetics for the overall reactions using a chemical master equation method. At the end of the calculations, VMS is used to access, visualize and analyze the data produced thanks to the shared XML interface (see Figure 1).
3. Elementary Steps: The Interconversion Reaction of Hydroxyacetone and 2-Hydroxypropanal
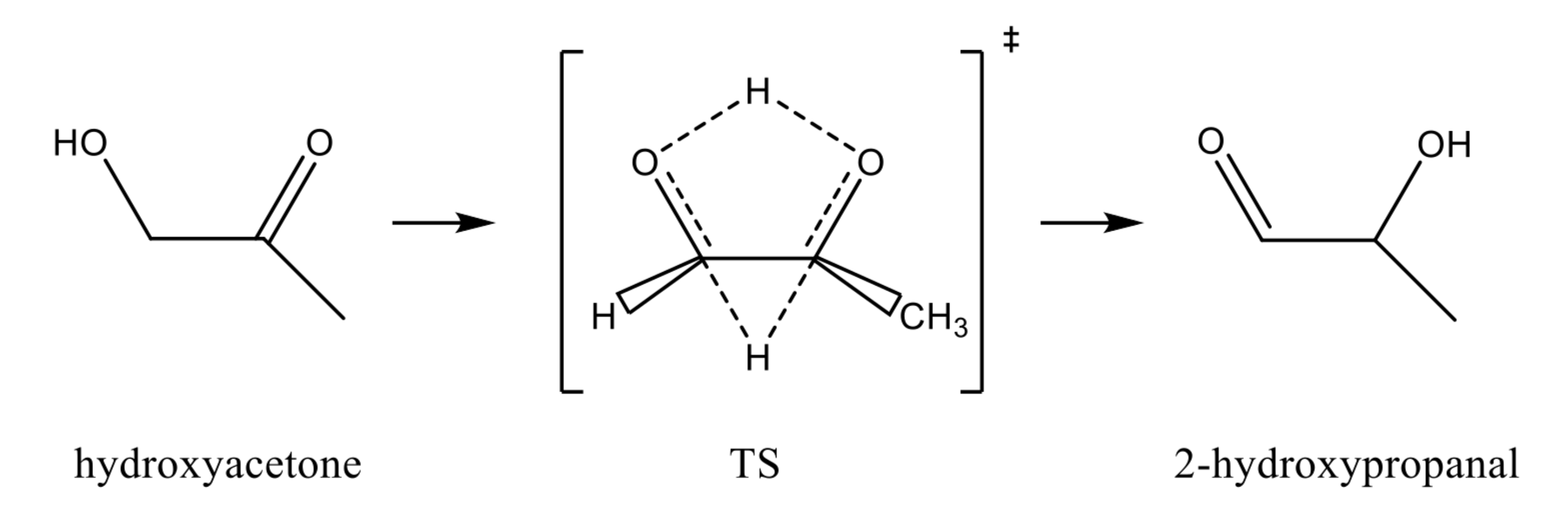
The interconversion reaction between hydroxyacetone and 2-hydroxypropanal is an important reaction in the context of atmospheric chemistry because the hydroxyacetone represent the simplest form of photochemically oxidised volatile organic compounds [26]. In a recent study, Sun et al. [27] have considered the interconversion mechanisms on several hydroxycarbonyl compounds, and much attention has been focused on the interconversion reaction between hydroxyacetone and 2-hydroxypropanal. This isomerization reaction can occur through three different mechanisms, 2 high-barrier multistep processes and, as shown in Figure 3, a direct mechanism via double hydride shift involving a low-barrier concerted transition state.
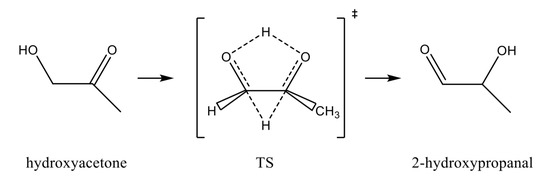
Figure 3.
Direct isomerization reaction mechanism between hydroxyacetone and 2-hydroxypropanal.
In their work, Sun et al. also supposed that hydroxycarbonyl compounds can adsorb solar radiation, as carbonyl compounds, from 320 to 220 nm and then undergo an internal conversion to the vibrationally excited ground state with an energy more than sufficient to overcome the isomerization barrier, and computed RRKM microcanonical rate coefficients in order to understand how much the isomerization reaction is favored with respect to collisional deactivation and fragmentation processes at a given excitation energy.
Within the RRKM theory [12,13,14], the microcanonical rate coefficient for the reaction of Figure 3 is given by the equation [28]
where
In Equations (1) and (2), h is Planck’s constants, is the sum of states of the transition state (TS) (computed by excluding the normal mode with imaginary frequency under the assumption that the motion along the reaction coordinates is separable from that of the other modes), and and are the density of states (DOS, i.e., the number of rovibrational states per energy interval) of the reactant molecule and transition state, respectively. As apparent, a central quantity in this framework is the molecular rovibrational density of states of the involved molecular species. This can be easily worked out by convoluting its rotational and vibrational counterparts [29]. In the present version of the program, a classical expression is used for the rotational DOS (see [21] for details), while the vibrational DOS is evaluated at uncoupled anharmonic level by adoption of the Stein–Rabinovitch [30] extension of the Beyer–Swinehart algorithm [31].
An improved version of Equation (1) accounts for the tunneling correction by using a modified version of the sum of states of the TS. A common and efficient way of including tunneling is by means of the asymmetric Eckart barrier [32]. Within this model, the sum of states of the transition state is redefined by
where is a tunneling-corrected version of the sum of state of the TS and is the classical energy barrier for the forward reaction. The quantity is the tunneling coefficient at the energy , and is given by the expression
where, a, b, and c are parameters defined by:
Here, is the classical energy barrier for the reverse reaction, and is the magnitude of the imaginary frequency of the saddle point (in Equation (5), if the energies are expressed, as in this work, in cm).
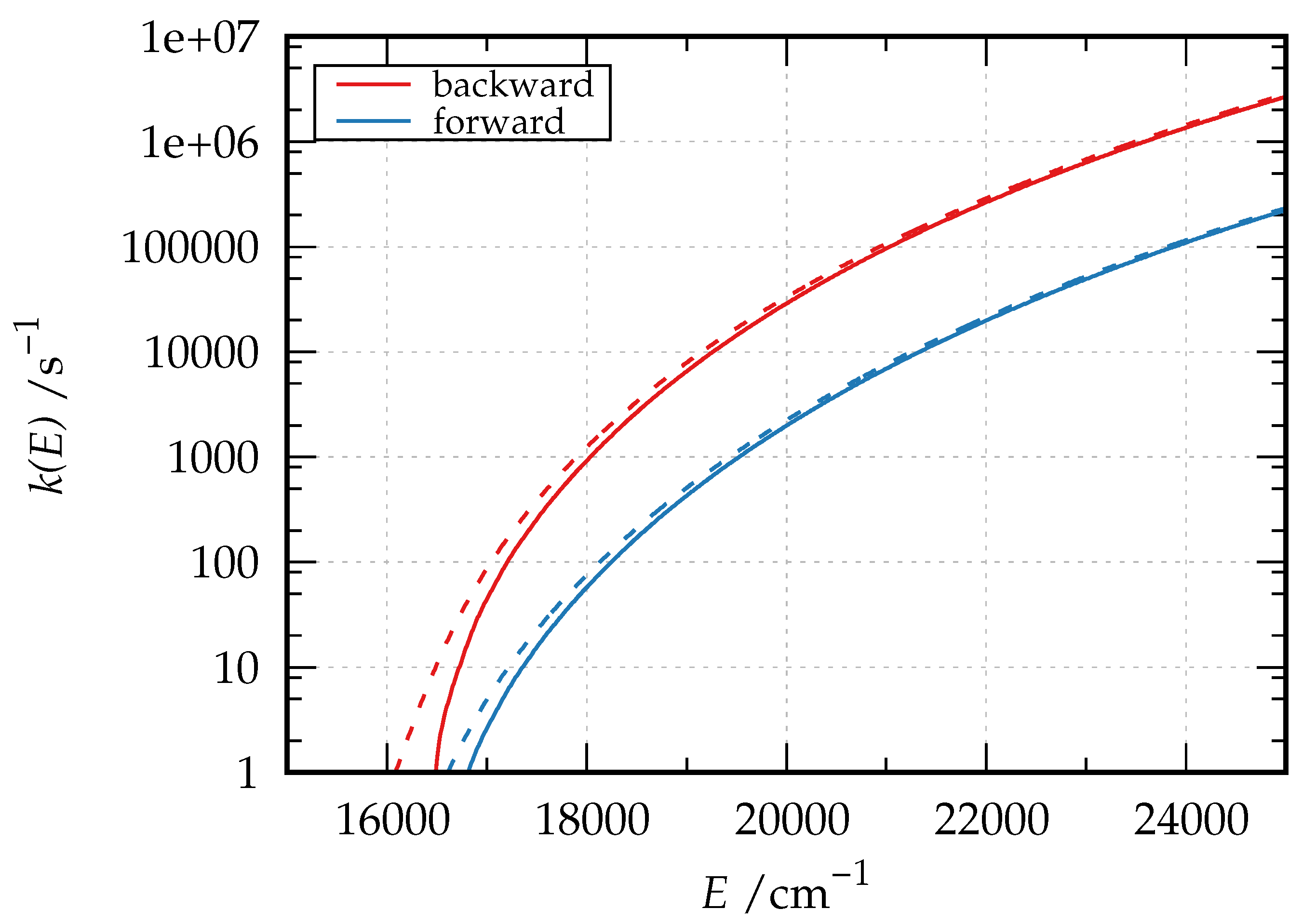
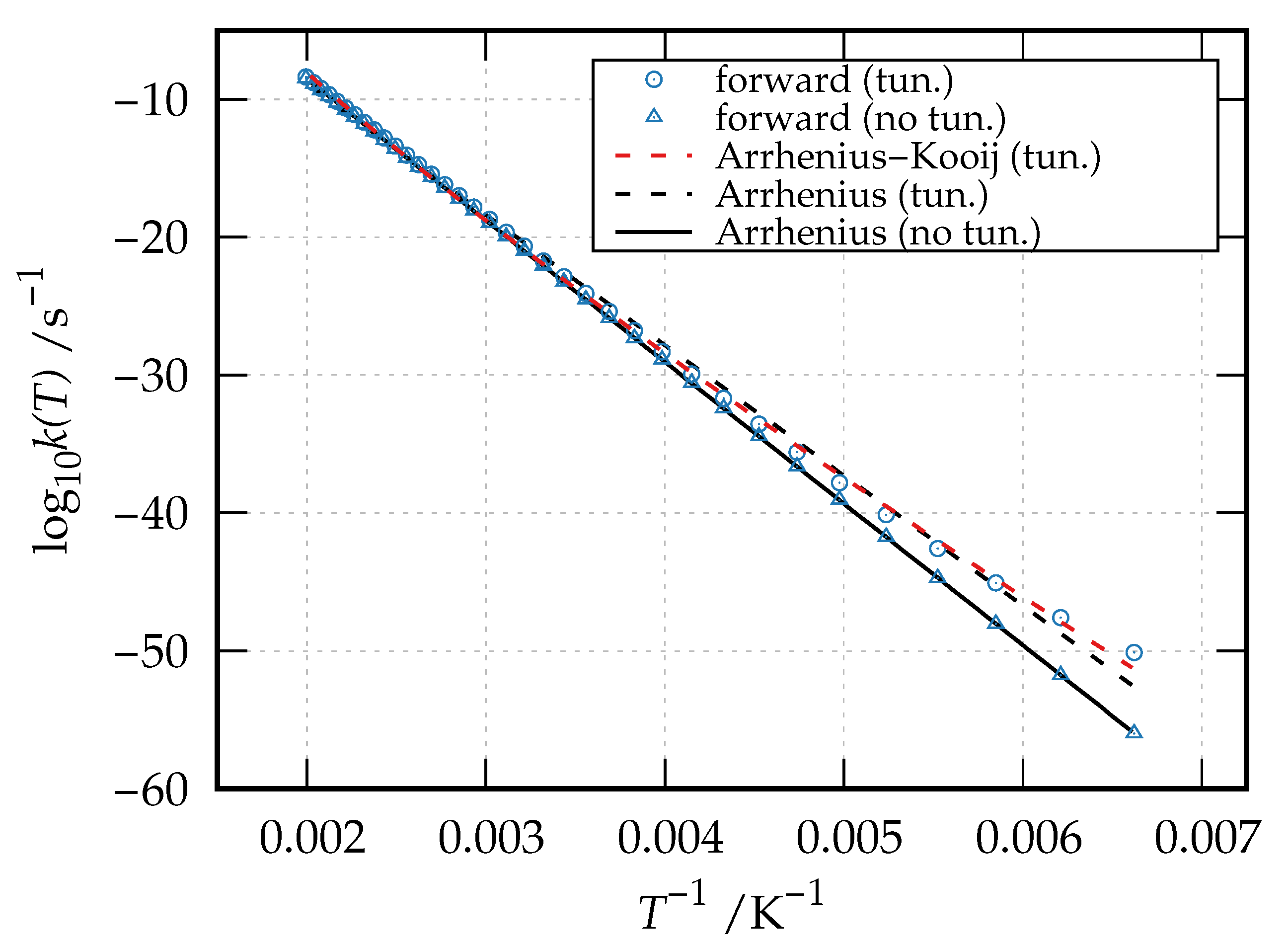
For illustrative purposes, we computed the microcanonical rate coefficient for the direct and inverse reaction of Figure 3, both with and without tunneling correction. To this purpose, the three molecular species were modeled by density-functional theory with the B2PLYP-D3/jun-cc-pVTZ model chemistry. According to our calculations, the forward reaction is exoergic by 1719 cm with a barrier of 16448 cm (the barrier for the backward reaction is 14729 cm). The resulting microcanonical rate coefficients are plotted in Figure 4 (on a logarithmic scale) for the forward (blue line) and backward (red line) reaction as a function of the energy relative to the hydroxyacetone zero-point energy. In the same figure, the dashed curves are the tunneling-corrected ones. As apparent, the tunneling correction enhances the reaction rate both in the forward and backward direction, more visibly nearby the threshold region, thus lowering the actual value of the reaction threshold in both directions.
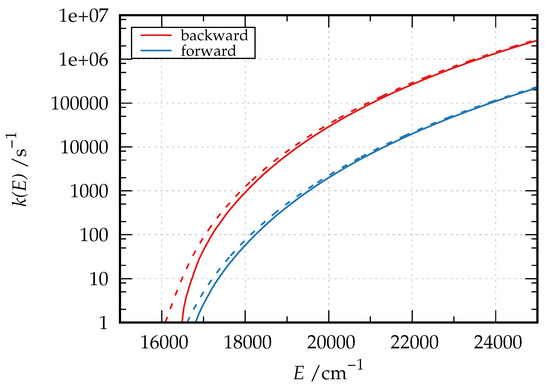
Figure 4.
Microcanonical rate coefficients for the backward (red color) and forward (blue color) isomerization reaction of hydroxyacetone and 2-hydroxypropanal (Figure 3) as a function of the energy relative to the reactant zero-point energy. Dashed lines are the tunneling-corrected versions of the rate coefficients.
The thermal rate coefficient can easily be computed from the microcanonical rate coefficients using the following equation:
with being the partition function of the reactant species. The computed thermal rate coefficients for the forward reaction (isomerization reaction of hydroxyacetone to 2-hydroxypropanal) in the temperature range 151–501 K are given as Arrhenius plot ( versus ) in Figure 5.
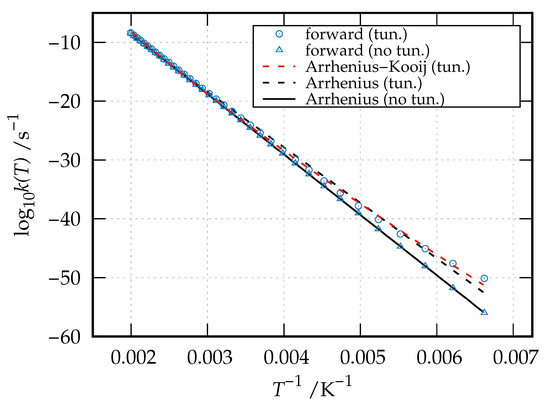
Figure 5.
Arrhenius plot of the computed thermal rate coefficient (both neglecting and including tunneling) for the isomerization reaction of hydroxyacetone to 2-hydroxypropanal (Figure 3) and of the Arrhenius and Arrhenius–Kooij best-fitting curves.
Results are reported both neglecting (blue triangles) and including (blue circles) tunneling. These data can be fitted to the popular Arrhenius equation:
(with A being the pre-exponential factor, the activation energy, and R the gas constant) or to the more refined Arrhenius–Kooij formula [33] (also known as modified Arrhenius equation [34]) allowing for a temperature dependence of the pre-exponential factor:
which essentially implies a linear variation of the activation energy with the temperature, . The Arrhenius best-fitting curve for both the tunneling-corrected and no-tunneling data are shown in Figure 5 as dashed black line and solid black line, respectively. The Arrhenius–Kooij best-fitting curve for the tunneling-corrected data is also reported as a red dashed line in the same figure, while the best-fitting parameters together with the associated coefficient of determination are given in Table 1.

Table 1.
Results of the fit of the Arrhenius and Arrhenius–Kooij equations to the computed thermal rate coefficients for the isomerization reaction of hydroxyacetone to 2-hydroxypropanal in the temperature range 151–501 K.
As evident from Figure 5 and Table 1, the Arrhenius equation perfectly fits the thermal rate coefficients calculated by neglecting tunneling, yielding a and an activation energy of 16428 cm that compares well with the computed reaction barrier. On the contrary, the tunneling-corrected thermal rate coefficients show a deviation from linearity with decreasing temperatures. As a result, the Arrhenius expression yields a worse best-fitting curve () and a lower activation energy of 15120 cm , while a better fitting is obtained through the Arrhenius–Kooij equation (), which gives an activation energy of 14839 cm at K and of 13352 cm at K.
4. Multi-Step Reactions: The Dissociation of Vinyl Cyanide
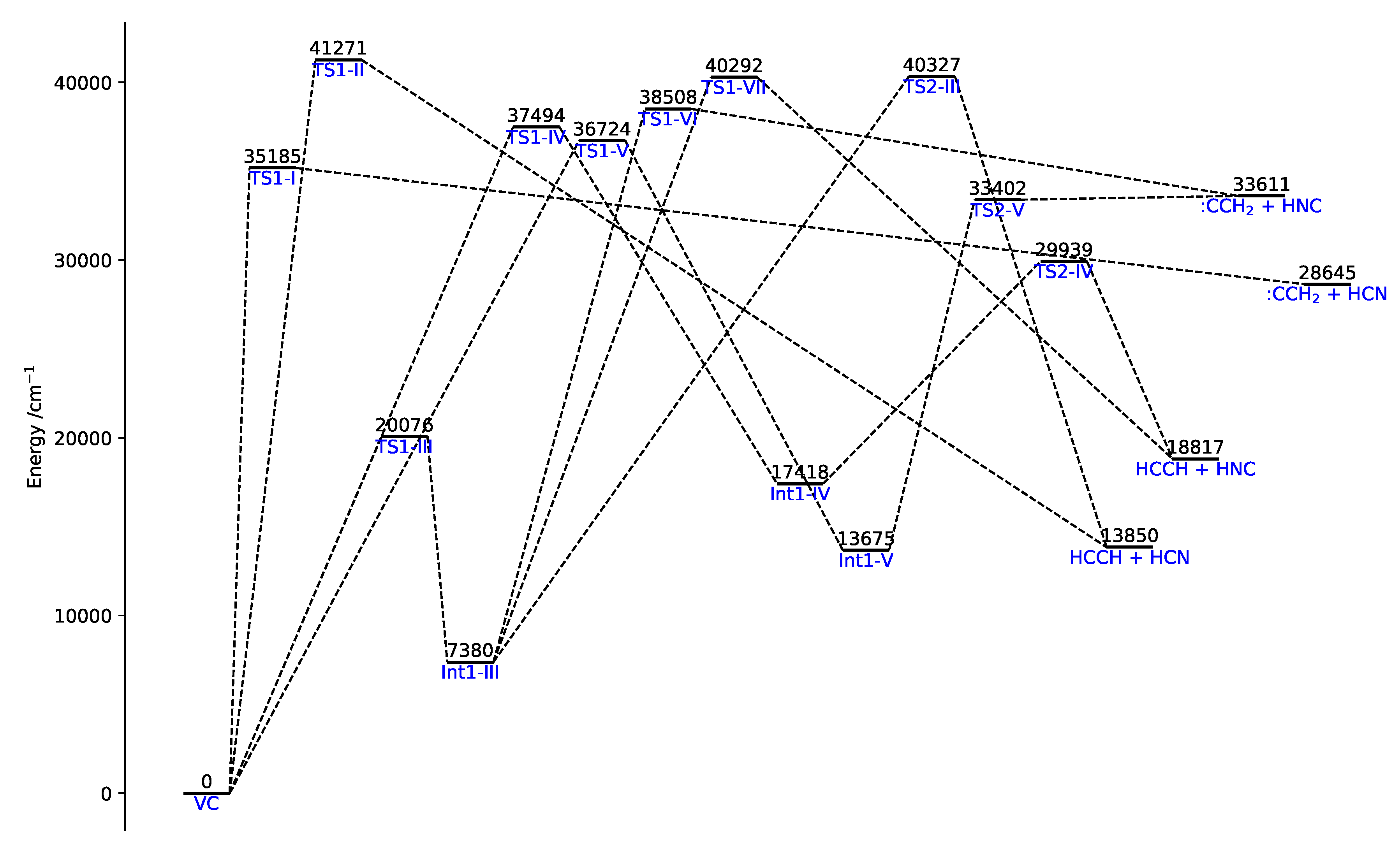
The dissociation of vinyl cyanide (VC, CHN), is particularly interesting because it involves multiple reaction channels and different sets of products (HCN, HNC, HCCH, and :CCH) and hence it serves as a very good test case for master-equation based kinetic models. The potential-energy surface for this reaction has been investigated in a recent work by Homayoon et al. [35] through ab initio CCSD and CCSD(T) calculations with the 6-311+G(2d,2p) and 6-311++G(3df,3pd) basis sets. In the same work, a reaction scheme involving ten unimolecular steps, three of which reversible, was proposed. The ten reaction steps are summarized in Table 2, while the associated reaction diagram is given in Figure 6.

Table 2.
Reaction steps involved in the dissociation mechanism of vinyl cyanide considered in this work. The associated activation energies (relative to the zero-point energy of the reactant of each step) are also given.
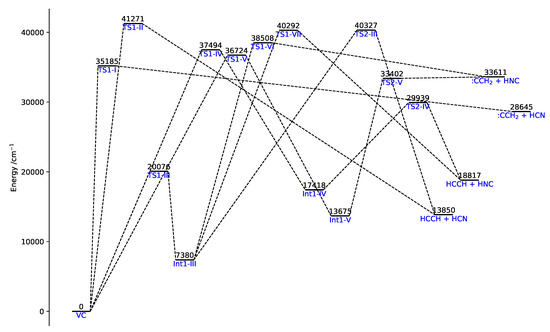
Figure 6.
Reaction diagram for the dissociation of vinyl cyanide yielding HCN, HNC, :CCH, and HCCH. All energies are relative to the reactant zero-point energy.
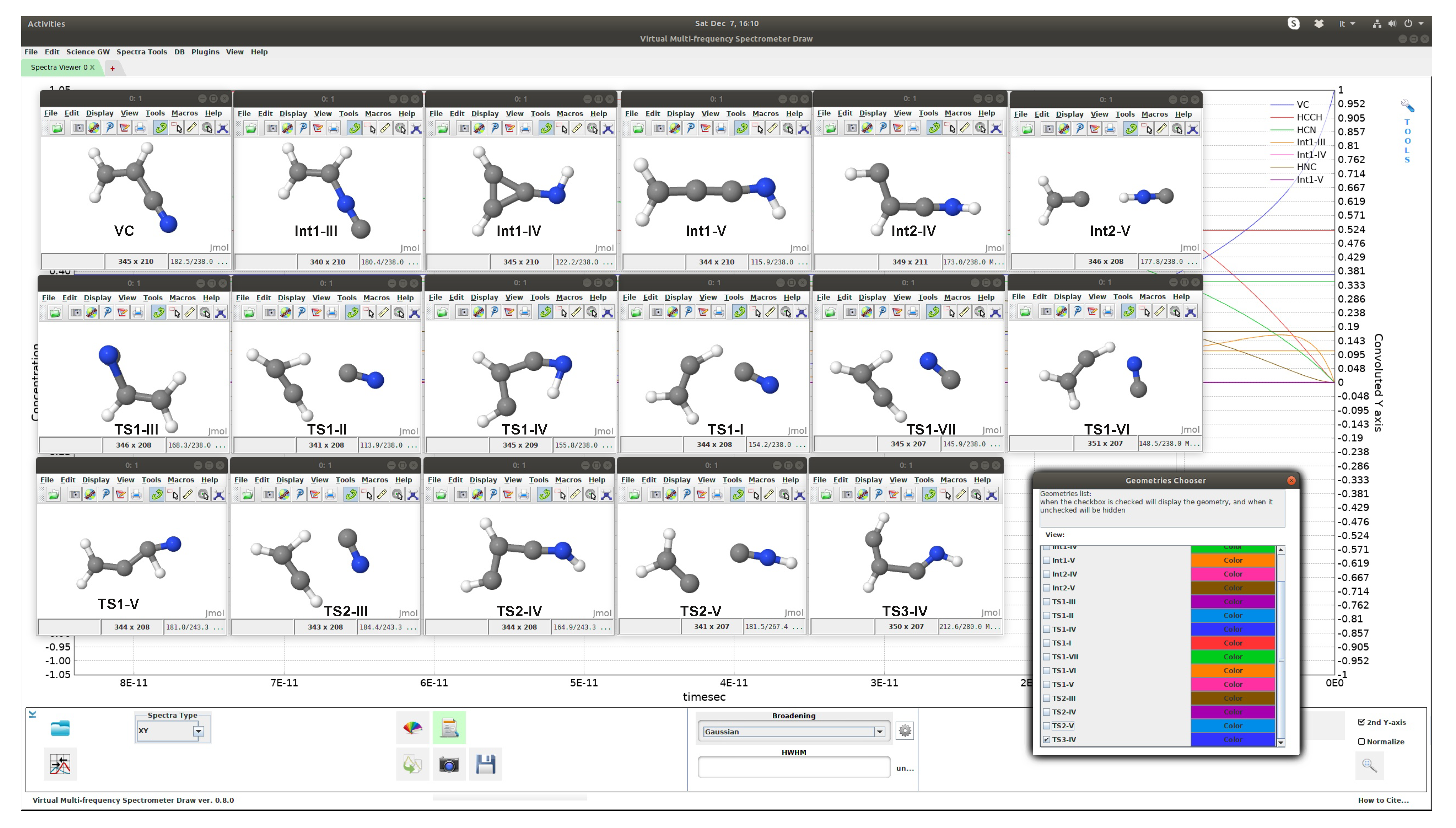
As shown in Figure 6 and Table 2, VC can directly dissociate to product sets :CCH + HCN and HCCH + HCN through steps 1 and 2 (the only direct dissociation paths), or lead to formation of reaction intermediates Int1-III (the most stable one), Int1-IV, and Int1-V, further evolving to products. On the other hand, product HNC can only be formed via indirect dissociation paths involving the above-mentioned intermediates. A screenshot of VMS showing the structures of all the molecular species involved in this reaction is given in Figure 7.
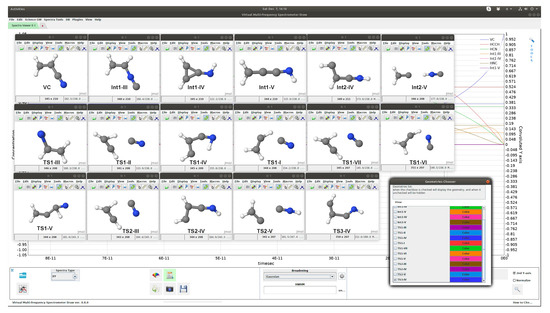
Figure 7.
Structures of the reactant molecule (top left corner), intermediates (remaining frames in the top row), and transition states (second and third rows) visualized through the VMS software.
Within a master-equation approach (see for instance [36]), to determine the time evolution of the relative abundance of the involved species, initially a matrix, , is set up by opportunely combining the microcanonical rate coefficients at a specified energy. In particular, the diagonal elements contain the loss rate of species i, while the off-diagonal elements contain the rate of formation of species i from species j. The rate of change in the concentration of each species is given by the vector differential equation:
where is the vector of the concentrations of the species at time t. This is a linear differential equation and can be solved by diagonalization of . In terms of the eigenvector matrix and eigenvalue vector , the solution of Equation (9) reads:
where is the concentration vector at . In this model, a fundamental hypothesis is that collisional relaxation occurs on time scales much shorter than those that characterize phenomenological kinetics [37]. It is worth mentioning here that a more general version of the master equation would involve diagonalizing a much larger matrix explicitly including collisional relaxation [36]. However, if the above-mentioned hypothesis holds, the resulting eigenvalues would appear in two separated sets: one made up by so-called internal energy relaxation eigenvalues (IEREs) and one made up by so-called chemically significant eigenvalues (CSEs). These last eigenvalues that relate to the phenomenological kinetics of interest in interstellar space and atmospheric studies would be identical to those obtained by solving Equation (9).
By using the methodology described, we computed the evolution of species with respect to time through the StarRate program using the structural parameters of the species given in Ref. [35], and computing the microcanonical rate coefficients through Equation (1). For the reader’s convenience, we give the full form of the matrix for this reaction (please note that expressions in square brackets, though spanning several rows, relate to single matrix elements and are shown as such to give a compact picture of the matrix):
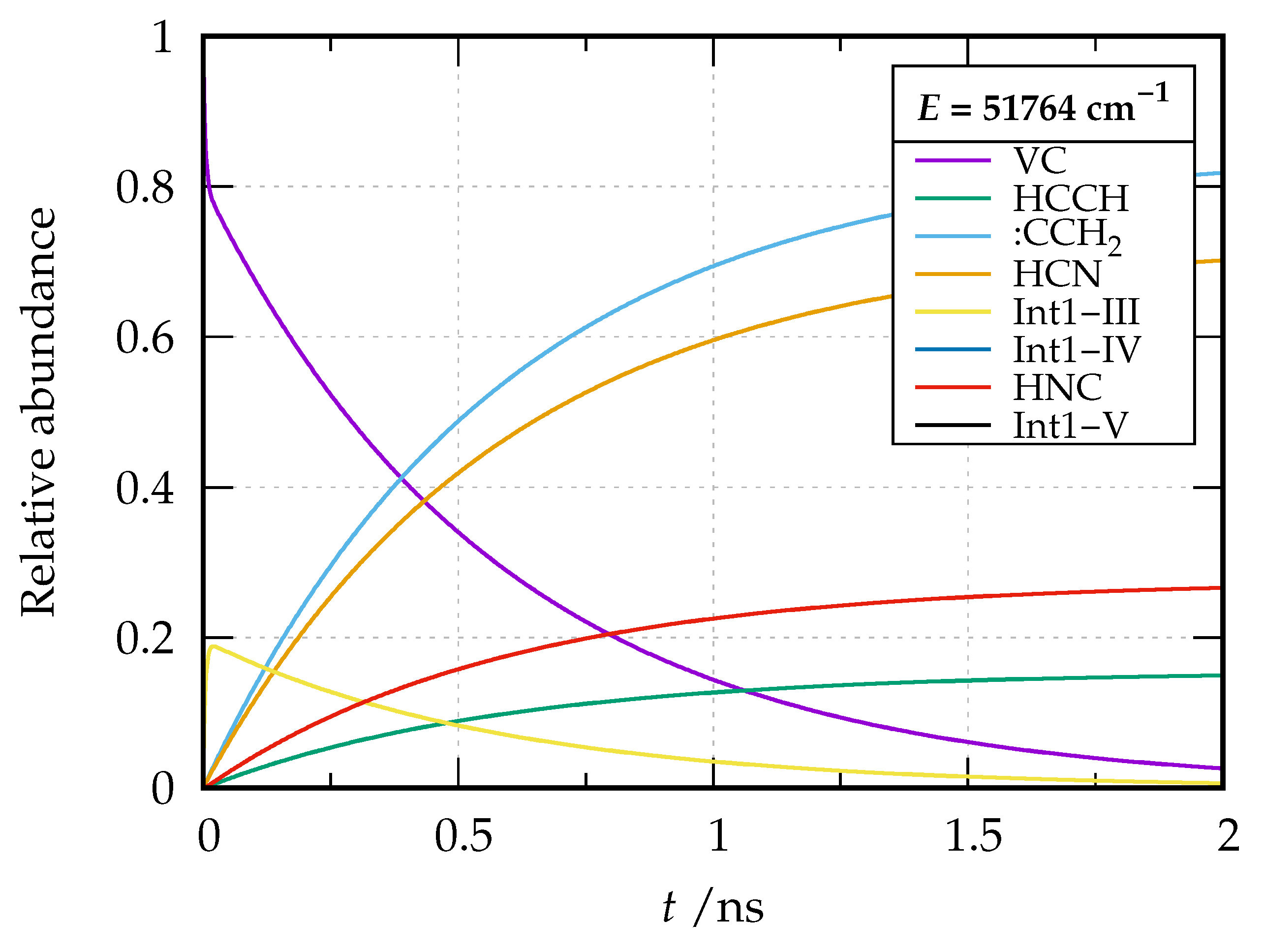
In our calculations, the initial concentration of VC was taken as 1.0 and the concentration of other species was set to 0.0. The relative abundances of the involved species as a function of time are plotted for two energies, namely cm and cm, in Figure 8 and Figure 9, respectively.
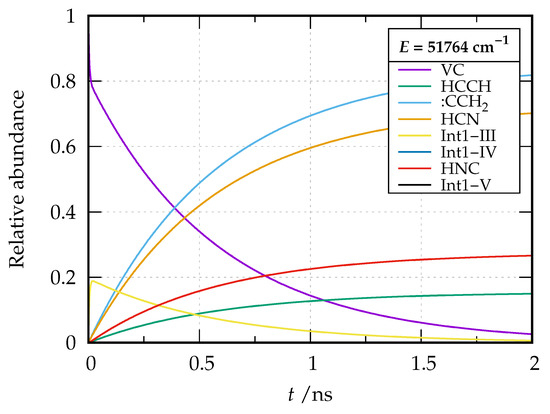
Figure 8.
Relative abundance of the species involved in the dissociation of vinyl cyanide as a function of time at energy cm relative to the reactant zero-point energy.
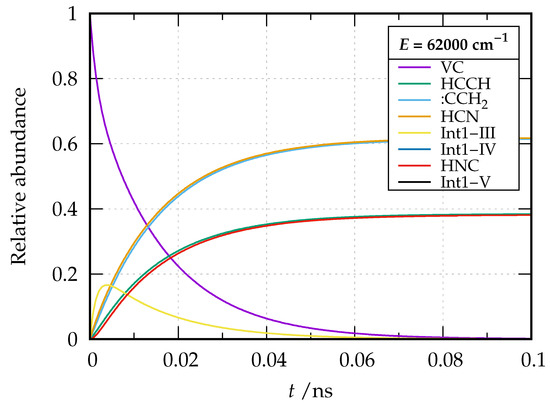
Figure 9.
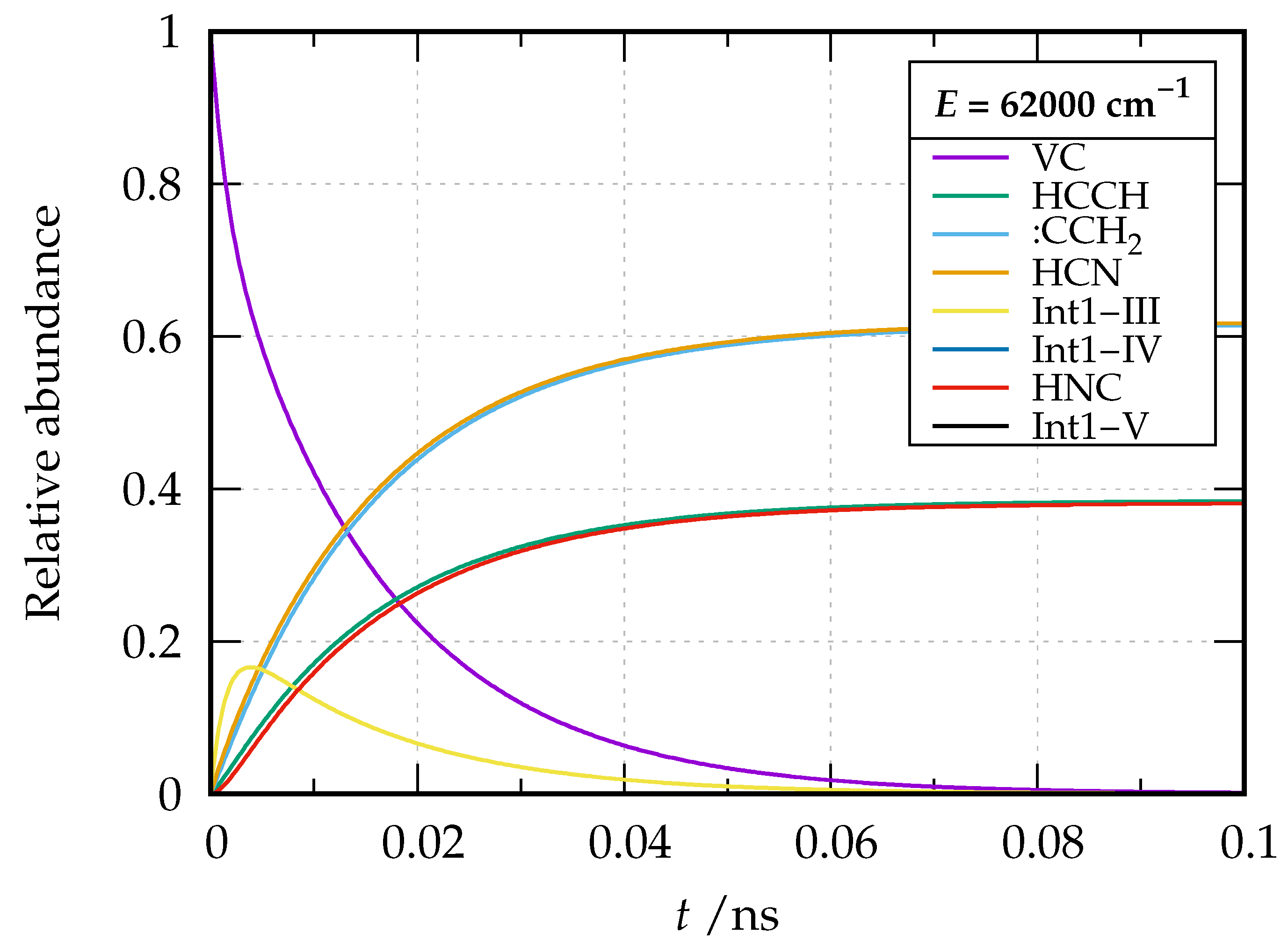
Relative abundance of the species involved in the dissociation of vinyl cyanide as a function of time at energy E = 62000 cm relative to the reactant zero-point energy.
By inspection of the plots, a first remark is that there is a sudden spike of the concentration for Int1-III in a very small time range for both energies. This is because Step 3 involves a low activation energy (20076 cm) compared to Int1-IV (37494 cm) and Int1-V (36724 cm), and the intermediate Int1-III is relatively stable compared to the other two (the stability of Int1-III is also reflected by the long sigmoidal tail of the plot). At the considered energies, these last two species are virtually never present and as soon as formed evolve into products. The reaction paths involving these two intermediates (the only ones leading to formation of HNC) become increasingly important at E = 62000 cm; in fact, while the branching ratio HCN/HNC tends to a value of about 2.5 at cm, a branching ratio of 1.9 is obtained at cm. The predicted branching ratio at cm nicely compares with the experimental estimate of 3.3 of Ref. [38] and the theoretical one of 1.9 of Ref. [35] (where, however, only vibrational densities and sum of states were taken into account in the calculation of the microcanonical rate coefficients), substantially improving over former theoretical calculations yielding a branching ratio of over 120 [39].
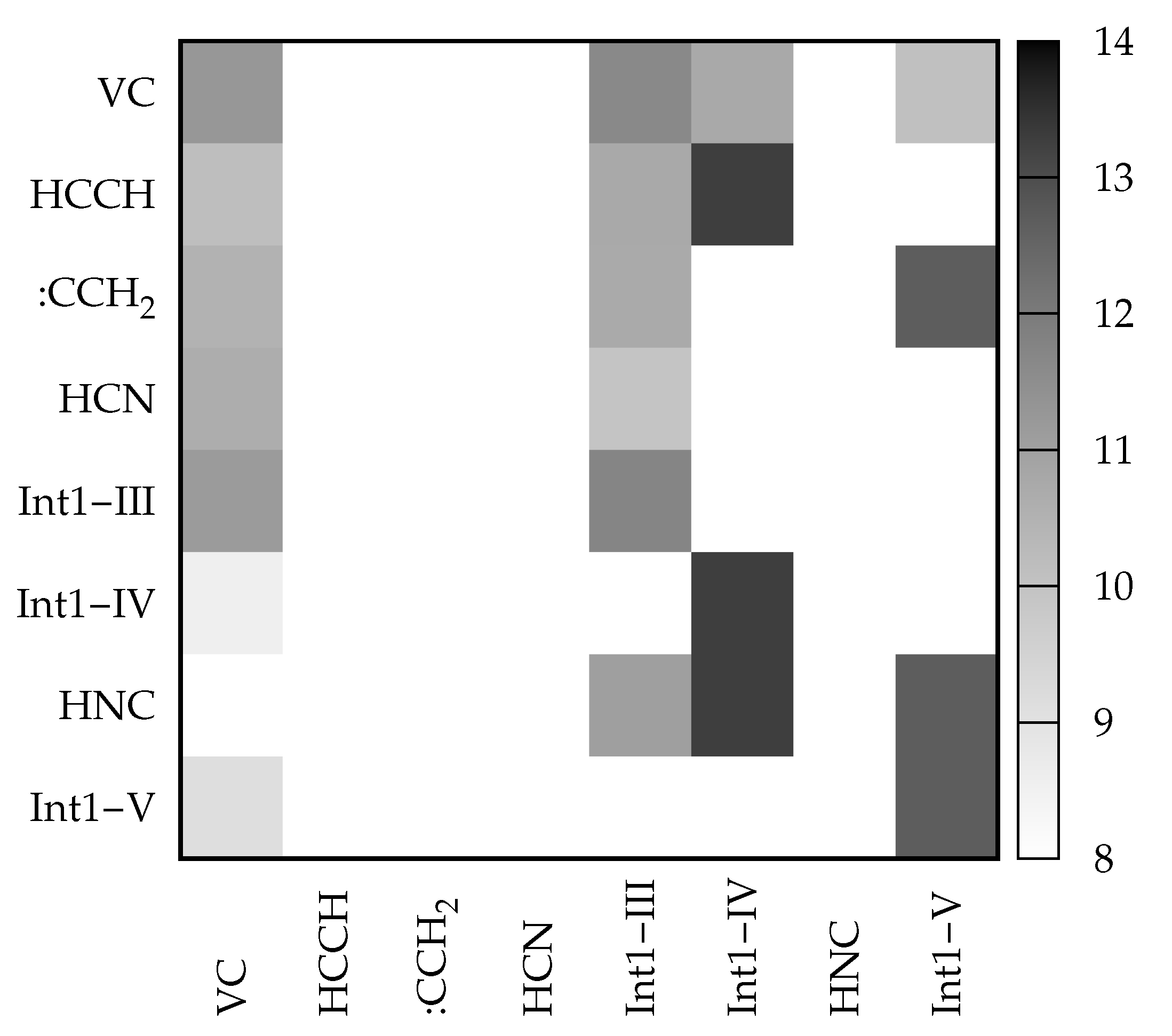
An interesting feature offered by VMS is that of visualizing matrices in a ‘heat-map’ fashion through a color palette reflecting the actual value of the elements. A heat-map of for the rate coefficient at E = 62000 cm is given in Figure 10. Looking at the first column and recalling the meaning of the elements, one can see that VC is directly converted to all the remaining species except HNC. The highest conversion rate (darkest gray) is towards Int1-III, while the rate of formation of the other two intermediates from VC is slower due to higher activation energies. Direct conversion to product sets containing HCN is also fast. On the contrary, as already mentioned, HNC is not formed directly from VC (blank square in position 7,1). Looking at the whole matrix, the darkest squares are those of the matrix elements connecting Int1-IV and Int1-V to products, due to the associated lowest activation energy. This is in line with the fact that, as also shown by Figure 8, these intermediates evolve rapidly to products.
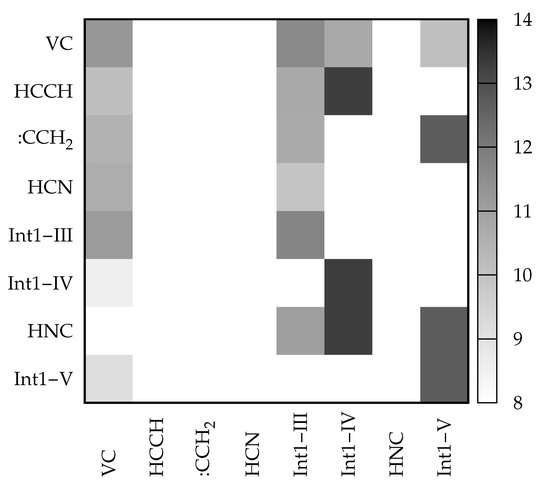
Figure 10.
Color map of the transition matrix at energy cm relative to the reactant zero-point energy as visualized in the VMS software. For each element of the matrix, the value of in s is plotted according to the gray scale on the right-hand-side of the plot area.
5. Conclusions
In this paper, the implementation of a computer program for chemical kinetics of multi-step reactions and its integration with the graphical interface of the Virtual Multifrequency Spectrometer has been discussed. The developed computational machinery is built around an input/output interface using a hierarchical data structure based on the XML language and shared in common with VMS. Details are given on the implementation of the calculation of microcanonical rate coefficients for the single steps of a unimolecular reaction, and on the modeling of the time evolution of the relative abundance of the involved species. The main features of the program have been illustrated through two example reactions, namely the atmospherically relevant interconversion between hydroxyacetone and 2-hydroxypropanal, and the production of HCN and HNC by dissociation of vinyl cyanide. Work is ongoing in our laboratory to account for bimolecular entrance channels, enhance the potentialities of the program, and integrate it in virtual-reality environments [40,41].
Supplementary Materials
The following are available online at https://www.mdpi.com/2076-3417/10/5/1872/s1, Sample XML file for the interconversion reaction of hydroxyacetone and 2-hydroxypropanal.
Author Contributions
Conceptualization, S.R. and V.B.; methodology, S.N. and S.R.; software, S.N. and S.R.; validation, S.N. and B.B.; formal analysis, S.N. and B.B.; investigation, B.B.; writing—original draft preparation, S.N., B.B. and S.R.; writing—review and editing, S.R. and V.B.; supervision, S.R. and V.B.; funding acquisition, S.R. and V.B. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results has received funding from Scuola Normale Superiore through project “DIVE: Development of Immersive approaches for the analysis of chemical bonding through Virtual-reality Environments” (SNS18_B_RAMPINO) and program “Finanziamento a supporto della ricerca di base” (SNS_RB_RAMPINO).
Acknowledgments
The authors are grateful to Daniele Licari for fruitful discussions and to the technical staff of the SMART Laboratory for managing the computational facilities at the Scuola Normale Superiore.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Althorpe, S.C.; Clary, D.C. Quantum Scattering Calculations on chemical reactions. Ann. Rev. Phys. Chem. 2003, 54, 493–529. [Google Scholar] [CrossRef] [PubMed]
- Rampino, S.; Faginas Lago, N.; Laganà, A.; Huarte-Larrañaga, F. An extension of the grid empowered molecular simulator to quantum reactive scattering. J. Comput. Chem. 2012, 33, 708–714. [Google Scholar] [CrossRef] [PubMed]
- Rampino, S. Configuration-Space Sampling in Potential Energy Surface Fitting: A Space-Reduced Bond-Order Grid Approach. J. Phys. Chem. A 2016, 120, 4683–4692. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Rampino, S.; Skouteris, D.; Laganà, A. Microscopic branching processes: The O + O2 reaction and its relaxed potential representations. Int. J. Quantum Chem. 2010, 110, 358–367. [Google Scholar] [CrossRef]
- Rampino, S.; Skouteris, D.; Laganà, A. The O + O2 reaction: Quantum detailed probabilities and thermal rate coefficients. Theor. Chem. Acc. Theory Comput. Model. 2009, 123, 249–256. [Google Scholar] [CrossRef]
- Laganà, A.; Faginas Lago, N.; Rampino, S.; Huarte Larrañaga, F.; García, E. Thermal rate coefficients in collinear versus bent transition state reactions: The N + N2 case study. Phys. Scr. 2008, 78, 058116. [Google Scholar] [CrossRef]
- Beck, M.H.; Jäckle, A.; Worth, G.A.; Meyer, H.D. The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1–105. [Google Scholar] [CrossRef]
- Craig, I.R.; Manolopoulos, D.E. Chemical reaction rates from ring polymer molecular dynamics. J. Chem. Phys. 2005, 122, 084106. [Google Scholar] [CrossRef]
- Rampino, S.; Pastore, M.; Garcia, E.; Pacifici, L.; Laganà, A. On the temperature dependence of the rate coefficient of formation of from C + CH+. Mon. Not. R. Astron. Soc. 2016, 460, 2368–2375. [Google Scholar] [CrossRef]
- Pacifici, L.; Pastore, M.; Garcia, E.; Laganà, A.; Rampino, S. A dynamics investigation of the C + CH+→ + H reaction on an ab initio bond-order like potential. J. Phys. Chem. A 2016, 120, 5125–5135. [Google Scholar] [CrossRef]
- Rampino, S.; Suleimanov, Y.V. Thermal Rate Coefficients for the Astrochemical Process C + CH+→ C2+ + H by Ring Polymer Molecular Dynamics. J. Phys. Chem. A 2016, 120, 9887–9893. [Google Scholar] [CrossRef] [PubMed]
- Rice, O.K.; Ramsperger, H.C. Theories of Unimolecular Gas Reactions at Low Pressures. J. Am. Chem. Soc. 1927, 49, 1617–1629. [Google Scholar] [CrossRef]
- Kassel, L.S. Studies in Homogeneous Gas Reactions. I. J. Phys. Chem. 1927, 32, 225–242. [Google Scholar] [CrossRef]
- Marcus, R.A. Unimolecular Dissociations and Free Radical Recombination Reactions. J. Chem. Phys. 1952, 20, 359–364. [Google Scholar] [CrossRef]
- Barone, V. The virtual multifrequency spectrometer: A new paradigm for spectroscopy. WIREs Comput. Mol. Sci. 2016, 6, 86–110. [Google Scholar] [CrossRef] [PubMed]
- Bloino, J.; Biczysko, M.; Barone, V. General Perturbative Approach for Spectroscopy, Thermodynamics, and Kinetics: Methodological Background and Benchmark Studies. J. Chem. Theory Comput. 2012, 8, 1015–1036. [Google Scholar] [CrossRef] [PubMed]
- Bloino, J.; Barone, V. A second-order perturbation theory route to vibrational averages and transition properties of molecules: General formulation and application to infrared and vibrational circular dichroism spectroscopies. J. Chem. Phys. 2012, 136, 124108. [Google Scholar] [CrossRef]
- Licari, D.; Baiardi, A.; Biczysko, M.; Egidi, F.; Latouche, C.; Barone, V. Implementation of a graphical user interface for the virtual multifrequency spectrometer: The VMS-Draw tool. J. Comput. Chem. 2015, 36, 321–334. [Google Scholar] [CrossRef]
- F Syntax Rules. Available online: http://www.fortran.com/F/F_bnf.html (accessed on 5 February 2020).
- Metcalf, M.; Reid, J. The F Programming Language; Oxford University Press, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Nandi, S.; Calderini, D.; Bloino, J.; Rampino, S.; Barone, V. A Modern-Fortran Program for Chemical Kinetics on Top of Anharmonic Vibrational Calculations. Lect. Notes Comput. Sci. 2019, 11624, 401–412. [Google Scholar]
- Cavallotti, C.; Pelucchi, M.; Georgievskii, Y.; Klippenstein, S.J. EStokTP: Electronic Structure to Temperature- and Pressure-Dependent Rate Constants–A Code for Automatically Predicting the Thermal Kinetics of Reactions. J. Chem. Theory Comput. 2019, 15, 1122–1145. [Google Scholar] [CrossRef]
- Rossi, E.; Evangelisti, S.; Laganà, A.; Monari, A.; Rampino, S.; Verdicchio, M.; Baldridge, K.K.; Bendazzoli, G.L.; Borini, S.; Cimiraglia, R.; et al. Code interoperability and standard data formats in quantum chemistry and quantum dynamics: The Q5/D5Cost data model. J. Comput. Chem. 2014, 35, 611–621. [Google Scholar] [CrossRef] [PubMed]
- Rampino, S.; Monari, A.; Rossi, E.; Evangelisti, S.; Laganà, A. A priori modeling of chemical reactions on computational grid platforms: Workflows and data models. Chem. Phys. 2012, 398, 192–198. [Google Scholar] [CrossRef]
- FoX in Fortran Wiki. Available online: http://fortranwiki.org/fortran/show/FoX (accessed on 5 February 2020).
- Butkovskaya, N.I.; Pouvesle, N.; Kukui, A.; Mu, Y.; Le Bras, G. Mechanism of the OH-Initiated Oxidation of Hydroxyacetone over the Temperature Range 236–298 K. J. Phys. Chem. A 2006, 110, 6833–6843. [Google Scholar] [CrossRef]
- Sun, J.; Thus, S.; da Silva, G. The gas phase aldose-ketone isomerization mechanism: Direct interconversion of the model hydroxycarbonyls 2-hydroxypropanal and hydroxyacetone. Int. J. Quantum Chem. 2017, 117, e25434. [Google Scholar] [CrossRef]
- Brouard, M. Reaction Dynamics; Oxford Chemistry Primers, OUP Oxford: Oxford, UK, 1998. [Google Scholar]
- Green, N.J.B. Chapter 1—Introduction. In Unimolecular Kinetics; Green, N.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2003; Volume 39, pp. 1–53. [Google Scholar]
- Stein, S.; Rabinovitch, B.S. Accurate evaluation of internal energy level sums and densities including anharmonic oscillators and hindered rotors. J. Chem. Phys. 1973, 58, 2438–2445. [Google Scholar] [CrossRef]
- Beyer, T.; Swinehart, D.F. Algorithm 448: Number of Multiply-restricted Partitions. Commun. ACM 1973, 16, 379. [Google Scholar] [CrossRef]
- Miller, W.H. Tunneling corrections to unimolecular rate constants, with application to formaldehyde. J. Am. Chem. Soc. 1979, 101, 6810–6814. [Google Scholar] [CrossRef]
- Kooij, D.M. Über die Zersetzung des Gasförmigen Phosphorwasserstoffs. Zeitschrift für Physikalische Chemie Abteilung B 1893, 12, 155–161. [Google Scholar]
- Laidler, K. A glossary of terms used in chemical kinetics, including reaction dynamics (IUPAC Recommendations 1996). Pure Appl. Chem. 1996, 68, 149–192. [Google Scholar] [CrossRef]
- Homayoon, Z.; Vázquez, S.A.; Rodríguez-Fernández, R.; Martínez-Núñez, E. Ab Initio and RRKM Study of the HCN/HNC Elimination Channels from Vinyl Cyanide. J. Phys. Chem. A 2011, 115, 979–985. [Google Scholar] [CrossRef]
- Robertson, S.H.; Pilling, M.J.; Jitariu, L.C.; Hillier, I.H. Master equation methods for multiple well systems: Application to the 1-,2-pentyl system. Phys. Chem. Chem. Phys. 2007, 9, 4085–4097. [Google Scholar] [CrossRef] [PubMed]
- Barker, J.R.; Weston, R.E. Collisional Energy Transfer Probability Densities P(E, J; E′, J′) for Monatomics Colliding with Large Molecules. J. Phys. Chem. A 2010, 114, 10619–10633. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, M.J.; Nikow, M.; Letendre, L.; Dai, H.L. Photodissociation of vinyl cyanide at 193 nm: Nascent product distributions of the molecular elimination channels. J. Chem. Phys. 2009, 130, 044307. [Google Scholar] [CrossRef] [PubMed]
- Derecskei-Kovacs, A.; North, S.W. The unimolecular dissociation of vinylcyanide: A theoretical investigation of a complex multichannel reaction. J. Chem. Phys. 1999, 110, 2862–2871. [Google Scholar] [CrossRef]
- Salvadori, A.; Fusè, M.; Mancini, G.; Rampino, S.; Barone, V. Diving into chemical bonding: An immersive analysis of the electron charge rearrangement through virtual reality. J. Comput. Chem. 2018, 39, 2607–2617. [Google Scholar] [CrossRef]
- Martino, M.; Salvadori, A.; Lazzari, F.; Paoloni, L.; Nandi, S.; Mancini, G.; Barone, V.; Rampino, S. Chemical Promenades: Exploring Potential-energy Surfaces with Immersive Virtual Reality. J. Comput. Chem. 2020. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).