Compressed-Sensing Magnetic Resonance Image Reconstruction Using an Iterative Convolutional Neural Network Approach
Abstract
:1. Introduction
2. Materials and Methods
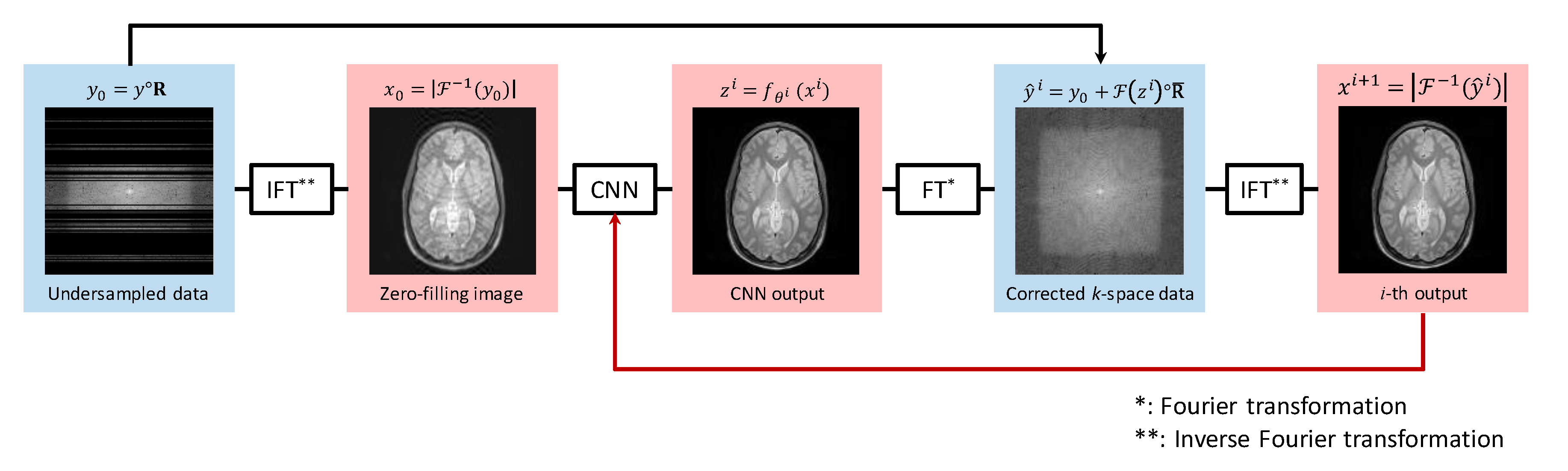
2.1. Proposed Method
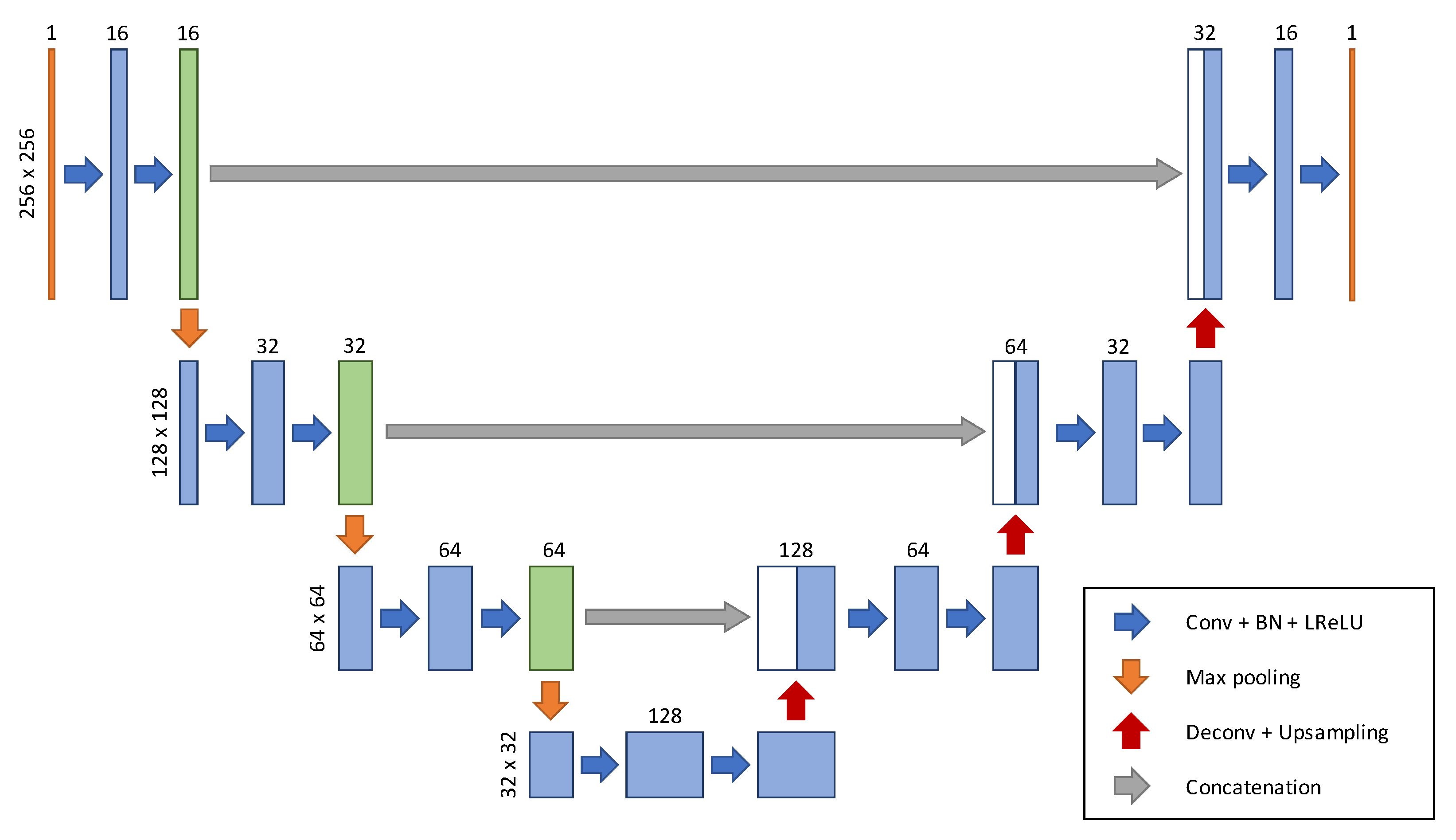
2.2. Network Architecture
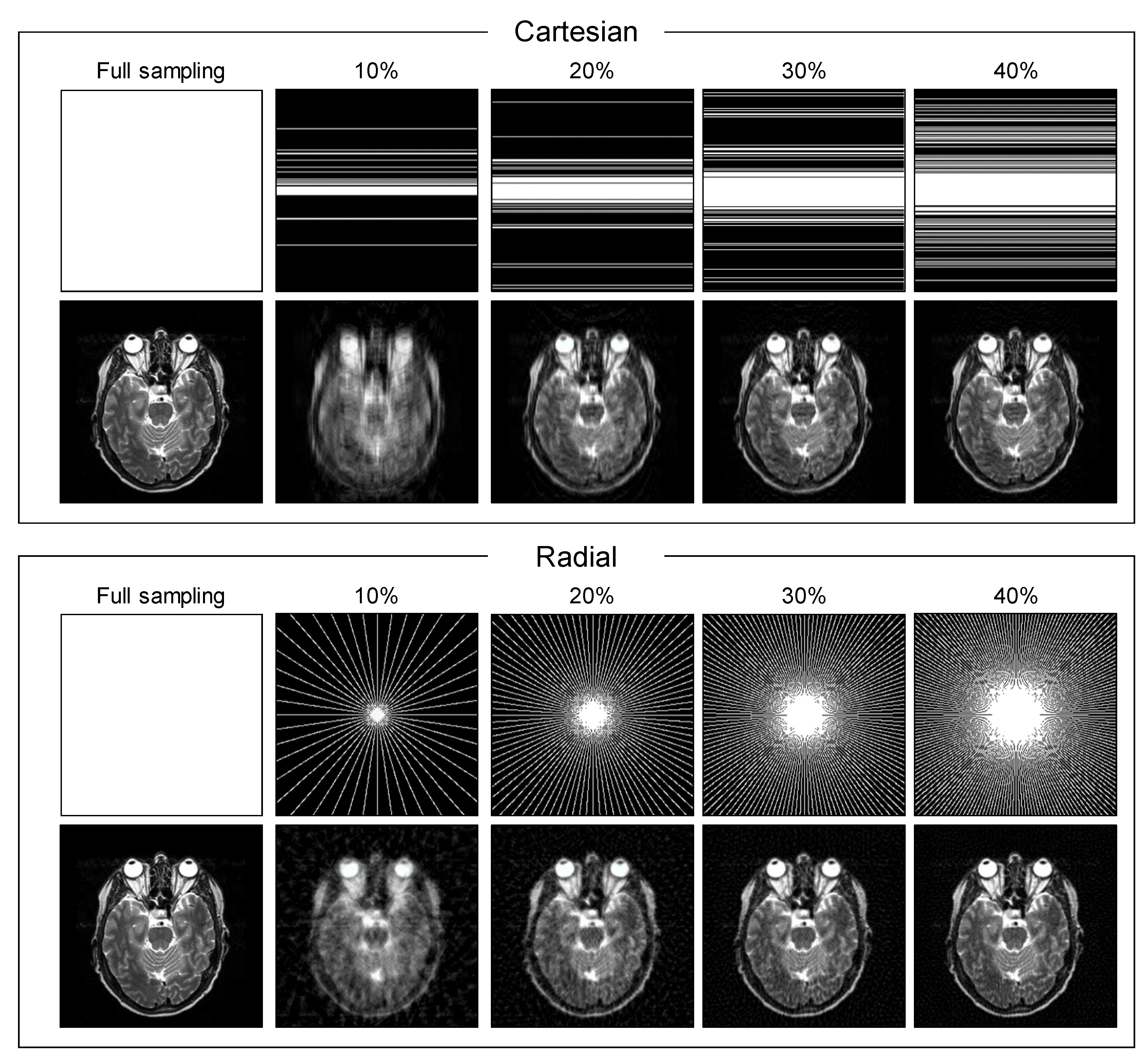
2.3. Experimental Setup
- The standalone image-based U-net was trained by the same architecture as that of this study, expressed by the following:
- The noniterative k-space correction method was implemented based on Hyun’s method [23], expressed by the following:
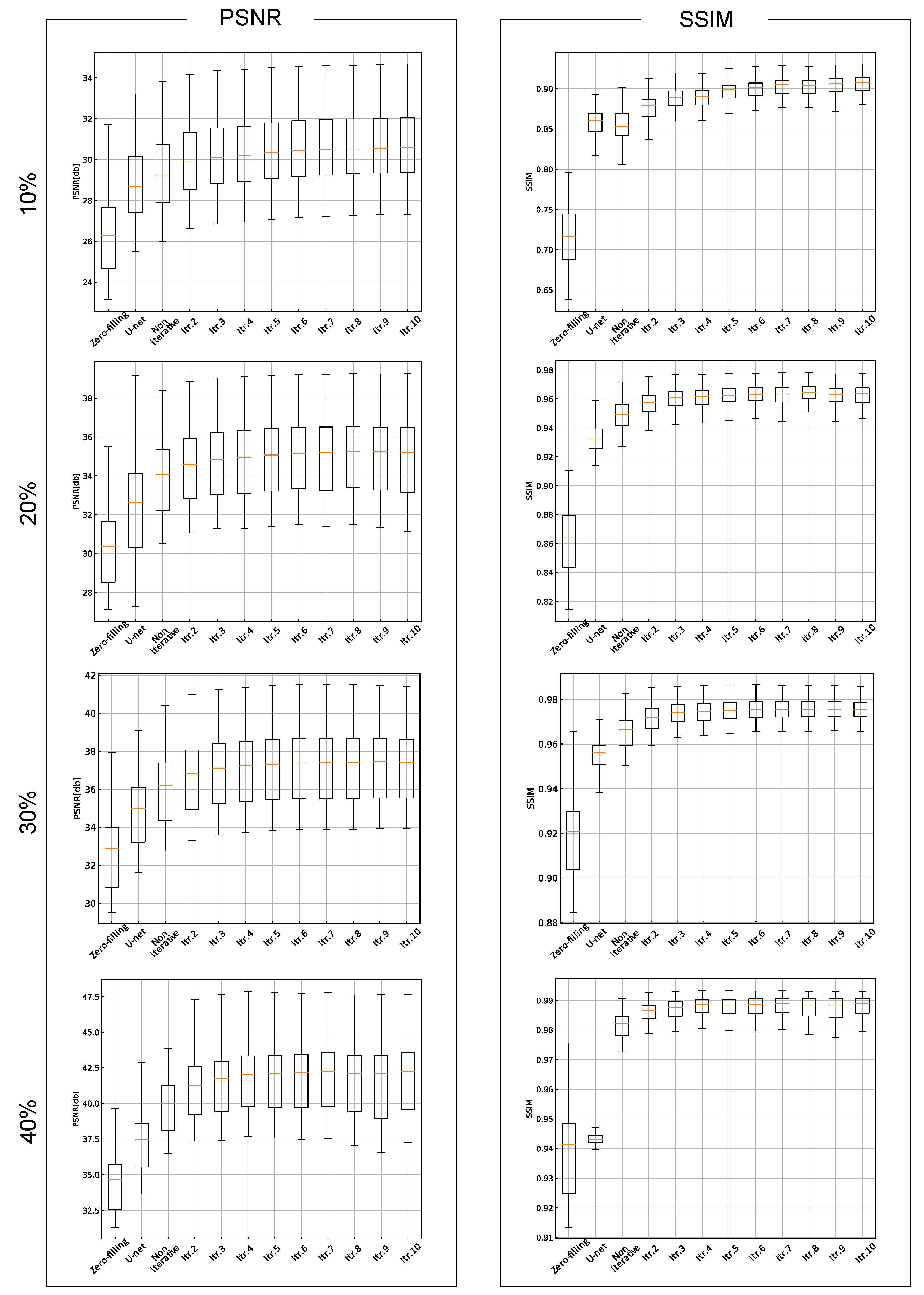
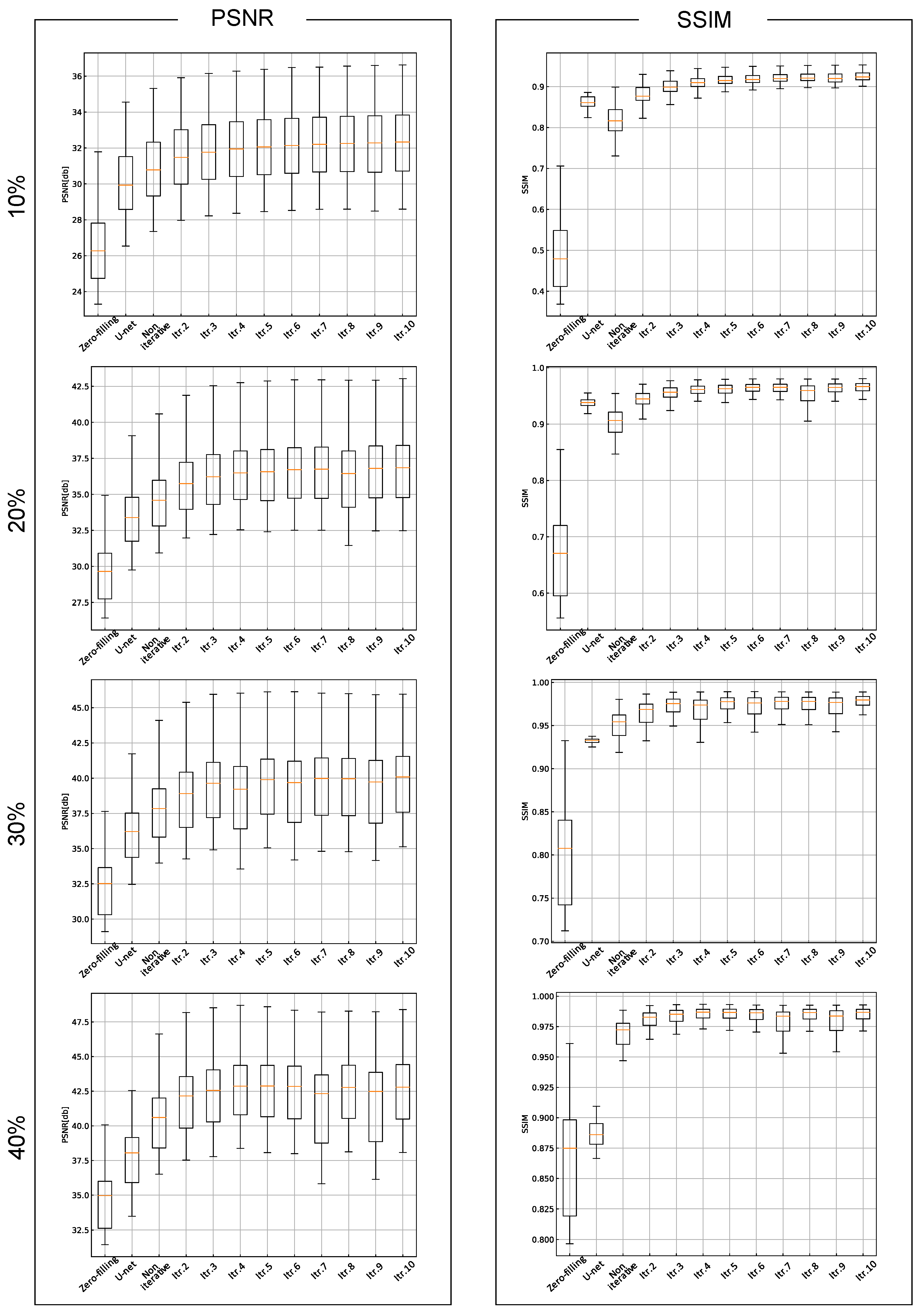
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McGibney, G.; Smith, M.R.; Nichols, S.T.; Crawley, A. Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI. Magn. Reson. Med. 1993, 30, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Sodickson, D.K.; Manning, W.J. Simultaneous acquisition of spatial harmonics (SMASH): Fast imaging with radiofrequency coil arrays. Magn. Reson. Med. 1997, 38, 591–603. [Google Scholar] [CrossRef] [PubMed]
- Pruessmann, K.P.; Weiger, M.; Scheidegger, M.B.; Boesiger, P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999, 42, 952–962. [Google Scholar] [CrossRef]
- Griswold, M.A.; Jakob, P.M.; Heidemann, R.M.; Nittka, M.; Jellus, V.; Wang, J.; Kiefer, B.; Haase, A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002, 47, 1202–1210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stehling, M.K.; Turner, R.; Mansfield, P. Echo-planar imaging: Magnetic resonance imaging in a fraction of a second. Science 1991, 254, 43–50. [Google Scholar] [CrossRef] [Green Version]
- Schmitt, F.; Stehling, M.K.; Turner, R. Echo-Planar Imaging: Theory, Technique and Application; Springer: Heidelberg, Germany, 1998. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef]
- Gamper, U.; Boesiger, P.; Kozerke, S. Compressed sensing in dynamic MRI. Magn. Reson. Med. 2008, 59, 365–373. [Google Scholar] [CrossRef]
- Haldar, J.P.; Hernando, D.; Liang, Z.P. Compressed-sensing MRI with random encoding. IEEE Trans. Med. Imaging. 2010, 30, 893–903. [Google Scholar] [CrossRef] [Green Version]
- Ma, J. Improved iterative curvelet thresholding for compressed sensing and measurement. IEEE Trans. Instrum. Meas. 2010, 60, 126–136. [Google Scholar] [CrossRef] [Green Version]
- Ravishankar, S.; Bresler, Y. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans. Med. Imaging. 2010, 30, 1028–1041. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Dou, W.; Vosters, L.; Xu, X.; Sun, Y.; Tan, T. Denoising of 3D magnetic resonance images with multi-channel residual learning of convolutional neural network. Jpn. J. Radiol 2018, 36, 566–574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ran, M.; Hu, J.; Chen, Y.; Chen, H.; Sun, H.; Zhou, J.; Zhang, Y. Denoising of 3D magnetic resonance images using a residual encoder–decoder Wasserstein generative adversarial network. Med. Image Anal. 2019, 55, 165–180. [Google Scholar] [CrossRef] [Green Version]
- Kidoh, M.; Shinoda, K.; Kitajima, M.; Isogawa, K.; Nambu, M.; Uetani, H.; Morita, K.; Nakaura, T.; Tateishi, M.; Yamashita, Y.; et al. Deep Learning Based Noise Reduction for Brain MR Imaging: Tests on Phantoms and Healthy Volunteers. Magn. Reson. Med. Sci. 2019. [Google Scholar] [CrossRef] [Green Version]
- Hashimoto, F.; Ohba, H.; Ote, K.; Teramoto, A.; Tsukada, H. Dynamic PET Image Denoising Using Deep Convolutional Neural Networks Without Prior Training Datasets. IEEE Access 2019, 7, 96594–96603. [Google Scholar] [CrossRef]
- Du, X.; He, Y. Gradient-Guided Convolutional Neural Network for MRI Image Super-Resolution. Appl. Sci. 2019, 9, 4874. [Google Scholar] [CrossRef] [Green Version]
- Shanshan, W.; Zhenghang, S.; Leslie, Y.; Xi, P.; Shun, Z.; Feng, L.; Dagan, F.; Dong, L. Accelerating magnetic resonance imaging via deep learning. In Proceedings of the IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic, 13–16 April 2016; pp. 514–517. [Google Scholar] [CrossRef]
- Kyong, H.J.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Li, H.; Xu, Z. Deep ADMM-Net for compressive sensing MRI. In Proceedings of the Neural Information Processing Systems (NIPS), IEEE, Barcelona, Spain, 5–10 December 2016; pp. 10–18. [Google Scholar]
- Quan, T.M.; Nguyen-Duc, T.; Jeong, W.K. Compressed sensing MRI reconstruction using a generative adversarial network with a cyclic loss. IEEE Trans. Med. Imaging 2018, 37, 1488–1497. [Google Scholar] [CrossRef] [Green Version]
- Eo, T.; Jun, Y.; Kim, T.; Jang, J.; Lee, H.J.; Hwang, D. KIKI-net: Cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images. Magn. Reson. Med. 2018, 80, 2188–2201. [Google Scholar] [CrossRef]
- Hyun, C.M.; Kim, H.P.; Lee, S.M.; Lee, S.; Seo, J.K. Deep learning for undersampled MRI reconstruction. Phys. Med. Biol. 2018, 63, 135007. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, F.; Gan, Y. Reference-Driven Compressed Sensing MR Image Reconstruction Using Deep Convolutional Neural Networks without Pre-Training. Sensors 2020, 20, 308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef] [Green Version]
- Hashimoto, F.; Kakimoto, A.; Ota, N.; Ito, S.; Nishizawa, S. Automated segmentation of 2D low-dose CT images of the psoas-major muscle using deep convolutional neural networks. Radiol. Phys. Technol. 2019, 12, 210–215. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, L.J. ADAM: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; p. 11. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the Symposium on Operating Systems Design and Implementation (OSDI), Savannah, GA, USA, 16 November 2016; Volume 16, pp. 265–283. [Google Scholar]
- Keras: The Python Deep Learning Library. Available online: http://keras.io/ (accessed on 22 January 2020).
- IXI Dataset. Available online: http://brain-development.org/ixi-dataset/ (accessed on 22 January 2020).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zbontar, J.; Knoll, F.; Sriram, A.; Muckley, M.J.; Bruno, M.; Defazio, A.; Parente, M.; Geras, K.; Katsnelson, J.; Chandarana, H.; et al. fastMRI: An open dataset and benchmarks for accelerated MRI. arXiv 2018, arXiv:1811.08839. [Google Scholar]
- Uecker, M.; Virtue, P.; Ong, F.; Murphy, M.J.; Alley, M.T.; Vasanawala, S.S.; Lustig, M. Software toolbox and programming library for compressed sensing and parallel imaging. In Proceedings of the ISMRM Workshop on Data Sampling and Image Reconstruction, Sedona, AZ, USA, 3–6 February 2013; p. 41. [Google Scholar]

| Cartesian Sampling | Radial Sampling | |||
|---|---|---|---|---|
| PSNR (dB) | SSIM | PSNR (dB) | SSIM | |
| Zero-filling | 26.31 ± 2.13 | 0.717 ± 0.040 | 26.45 ± 2.16 | 0.481 ± 0.080 |
| U-net | 28.77 ± 1.96 | 0.859 ± 0.016 | 30.07 ± 2.03 | 0.861 ± 0.015 |
| Noniterative | 29.33 ± 2.00 | 0.855 ± 0.020 | 30.86 ± 2.06 | 0.816 ± 0.039 |
| 2 iterations | 29.94 ± 1.94 | 0.878 ± 0.016 | 31.53 ± 2.06 | 0.879 ± 0.025 |
| 3 iterations | 30.19 ± 1.93 | 0.889 ± 0.014 | 31.81 ± 2.06 | 0.900 ± 0.019 |
| 4 iterations | 30.30 ± 1.92 | 0.889 ± 0.014 | 31.97 ± 2.06 | 0.909 ± 0.017 |
| 5 iterations | 30.44 ± 1.92 | 0.897 ± 0.013 | 32.08 ± 2.06 | 0.915 ± 0.015 |
| 6 iterations | 30.54 ± 1.92 | 0.901 ± 0.013 | 32.17 ± 2.07 | 0.917 ± 0.015 |
| 7 iterations | 30.60 ± 1.91 | 0.903 ± 0.013 | 32.24 ± 2.06 | 0.920 ± 0.015 |
| 8 iterations | 30.64 ± 1.90 | 0.903 ± 0.012 | 32.27 ± 2.07 | 0.921 ± 0.014 |
| 9 iterations | 30.68 ± 1.90 | 0.905 ± 0.012 | 32.27 ± 2.11 | 0.920 ± 0.016 |
| 10 iterations | 30.72 ± 1.90 | 0.906 ± 0.012 | 32.33 ± 2.09 | 0.923 ± 0.015 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashimoto, F.; Ote, K.; Oida, T.; Teramoto, A.; Ouchi, Y. Compressed-Sensing Magnetic Resonance Image Reconstruction Using an Iterative Convolutional Neural Network Approach. Appl. Sci. 2020, 10, 1902. https://doi.org/10.3390/app10061902
Hashimoto F, Ote K, Oida T, Teramoto A, Ouchi Y. Compressed-Sensing Magnetic Resonance Image Reconstruction Using an Iterative Convolutional Neural Network Approach. Applied Sciences. 2020; 10(6):1902. https://doi.org/10.3390/app10061902
Chicago/Turabian StyleHashimoto, Fumio, Kibo Ote, Takenori Oida, Atsushi Teramoto, and Yasuomi Ouchi. 2020. "Compressed-Sensing Magnetic Resonance Image Reconstruction Using an Iterative Convolutional Neural Network Approach" Applied Sciences 10, no. 6: 1902. https://doi.org/10.3390/app10061902
APA StyleHashimoto, F., Ote, K., Oida, T., Teramoto, A., & Ouchi, Y. (2020). Compressed-Sensing Magnetic Resonance Image Reconstruction Using an Iterative Convolutional Neural Network Approach. Applied Sciences, 10(6), 1902. https://doi.org/10.3390/app10061902





