The Influence of the Load Term of the Strain Energy Sensitivity in the Shell Shape Optimization
Abstract
:Featured Application
Abstract
1. Introduction
2. Formula of Surface Shape Optimization Problem
3. The Derivation of the Strain Energy Sensitivity
3.1. The Sensitivity Derivation by the Traditional Way
3.2. The Derivation of the Strain Energy Sensitivity Including the Load Term
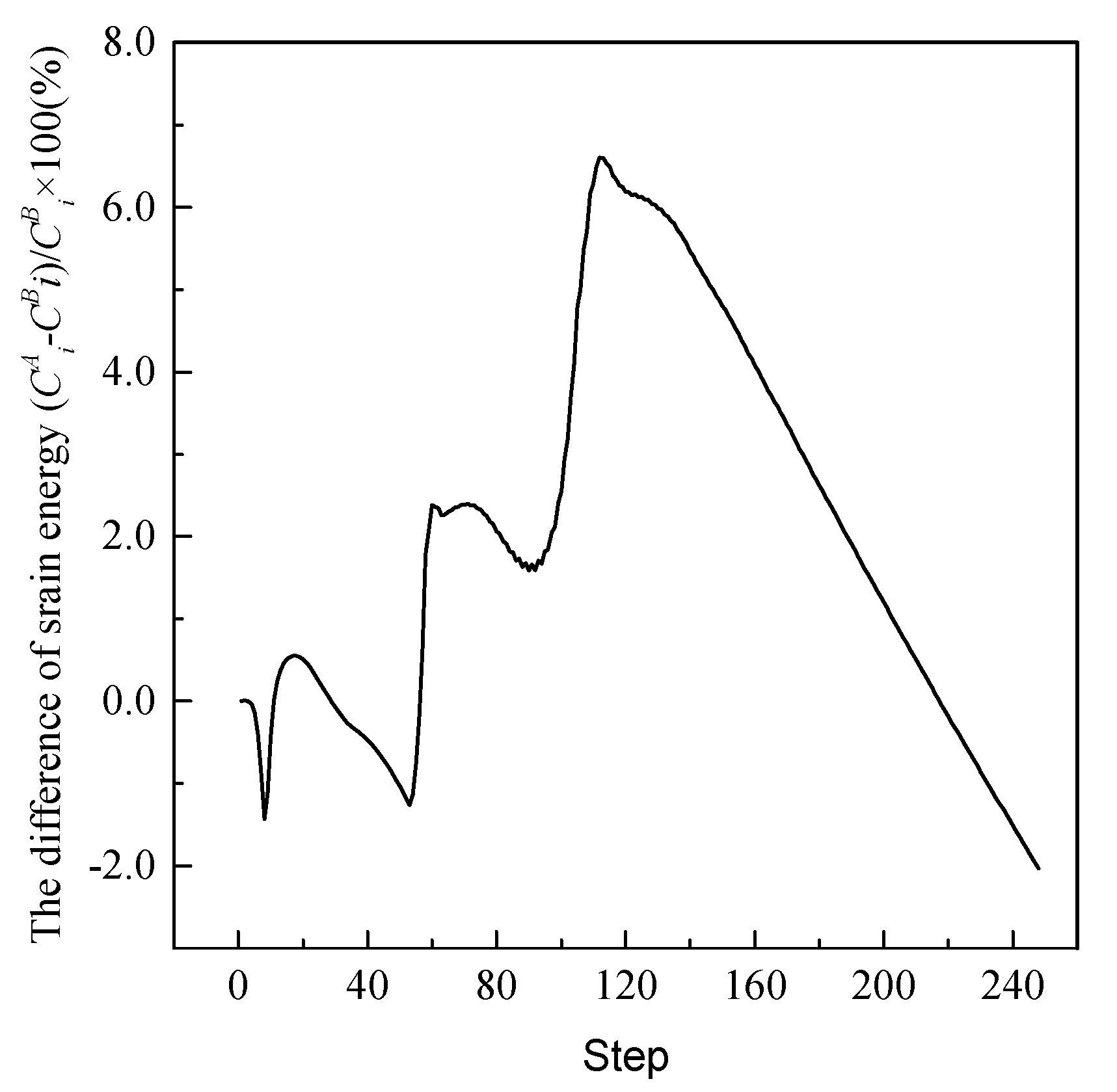
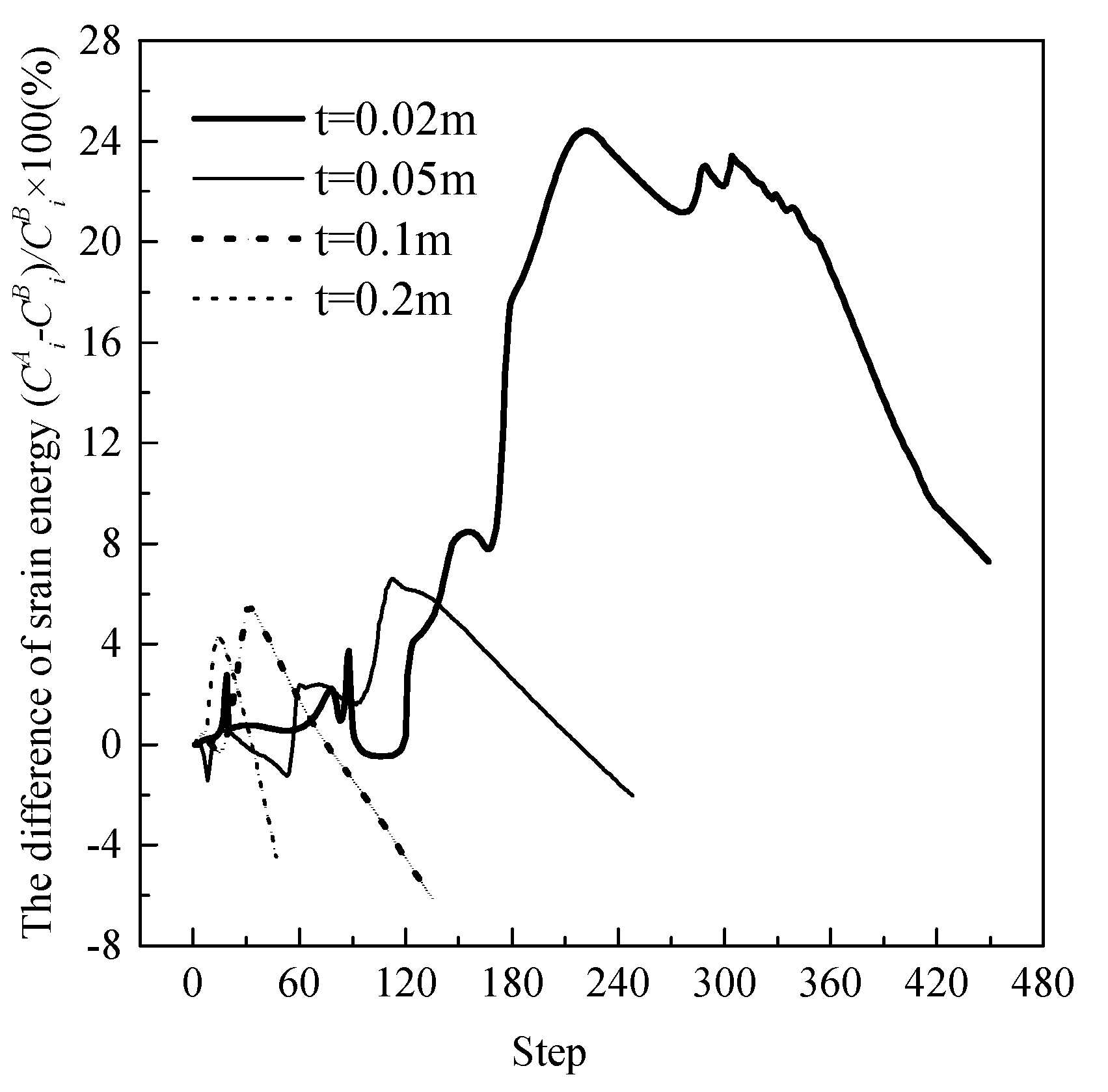
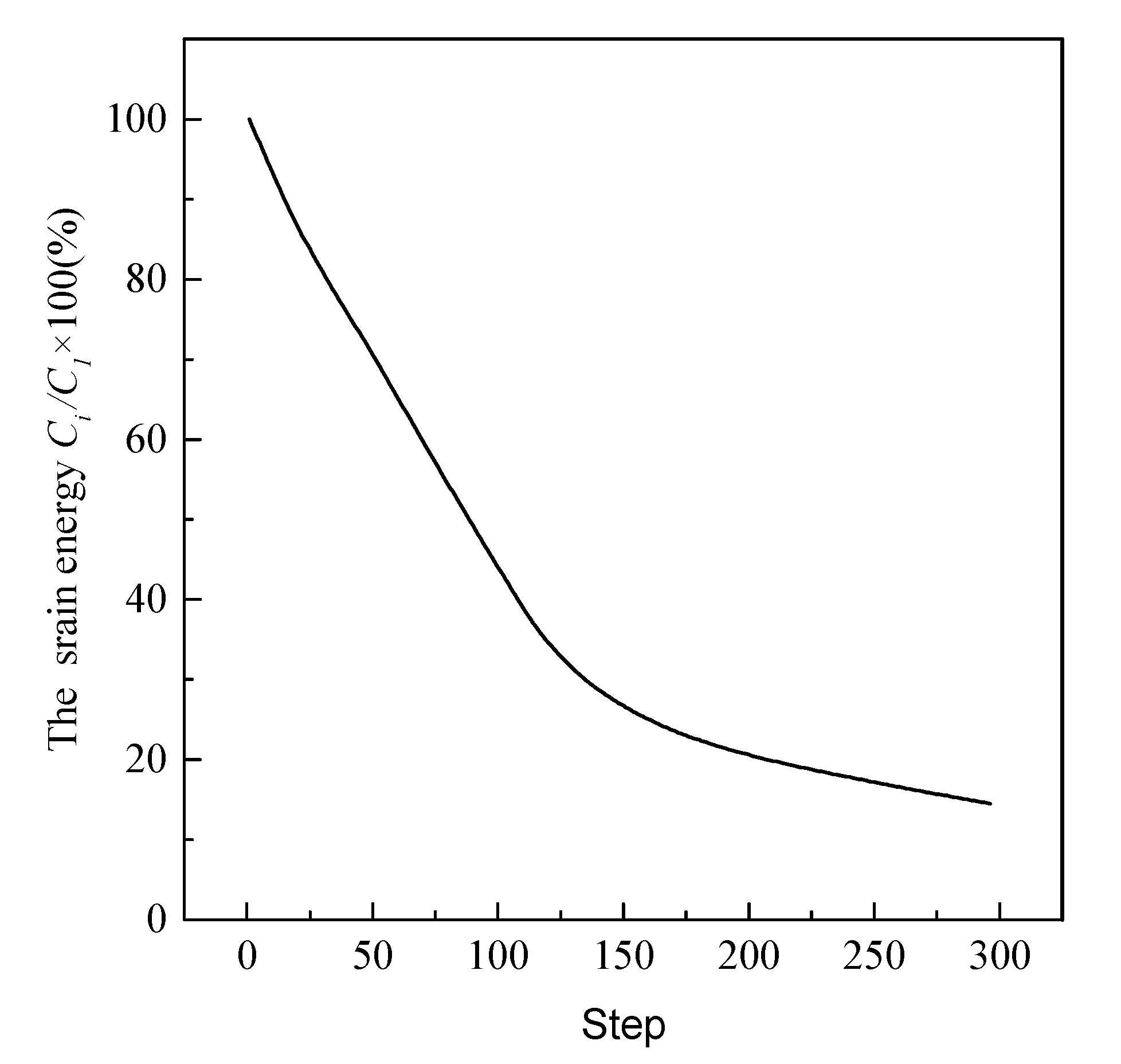
4. Effect of the Load Term on Strain Energy Sensitivity
5. Structure Iteration
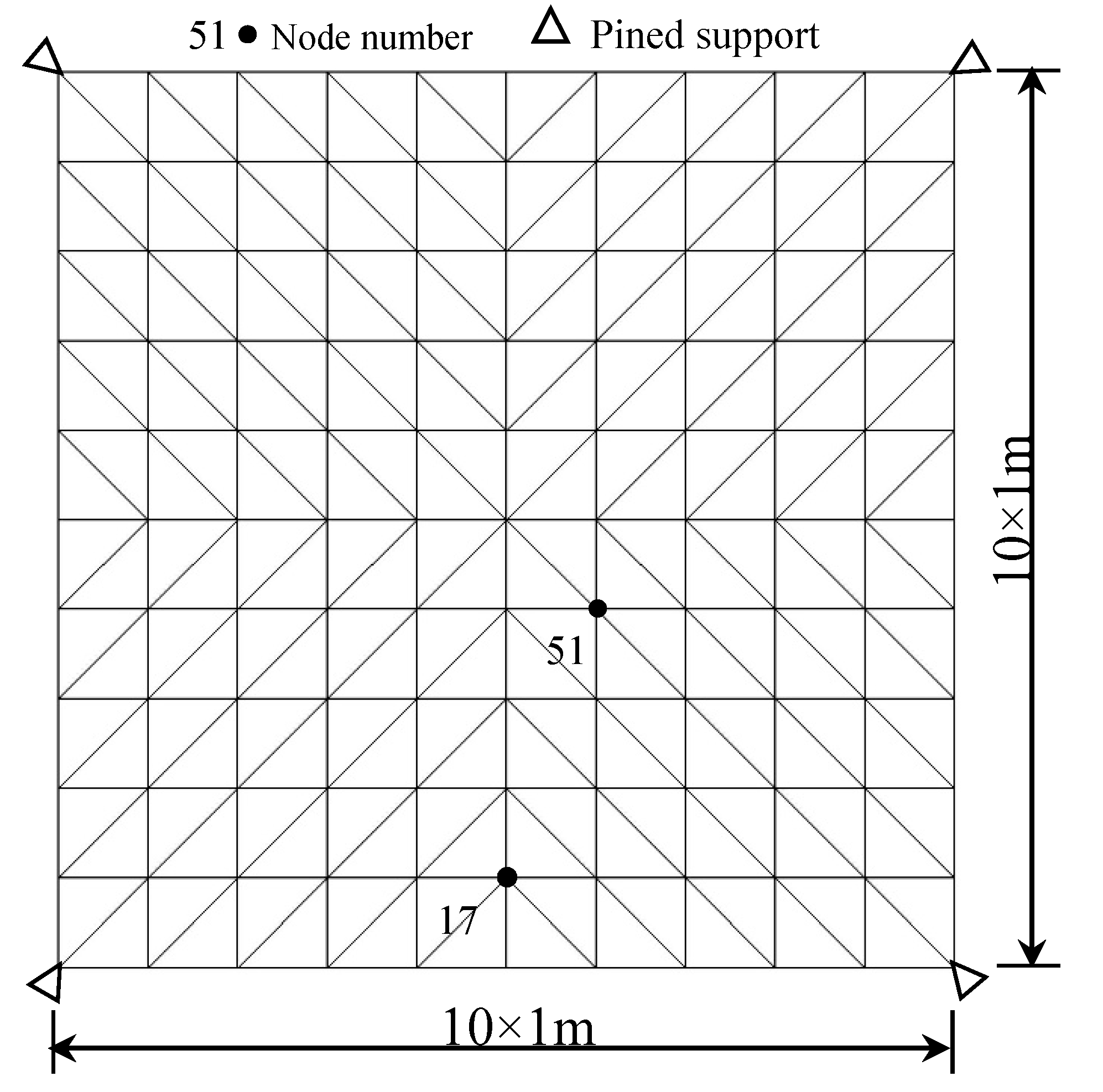
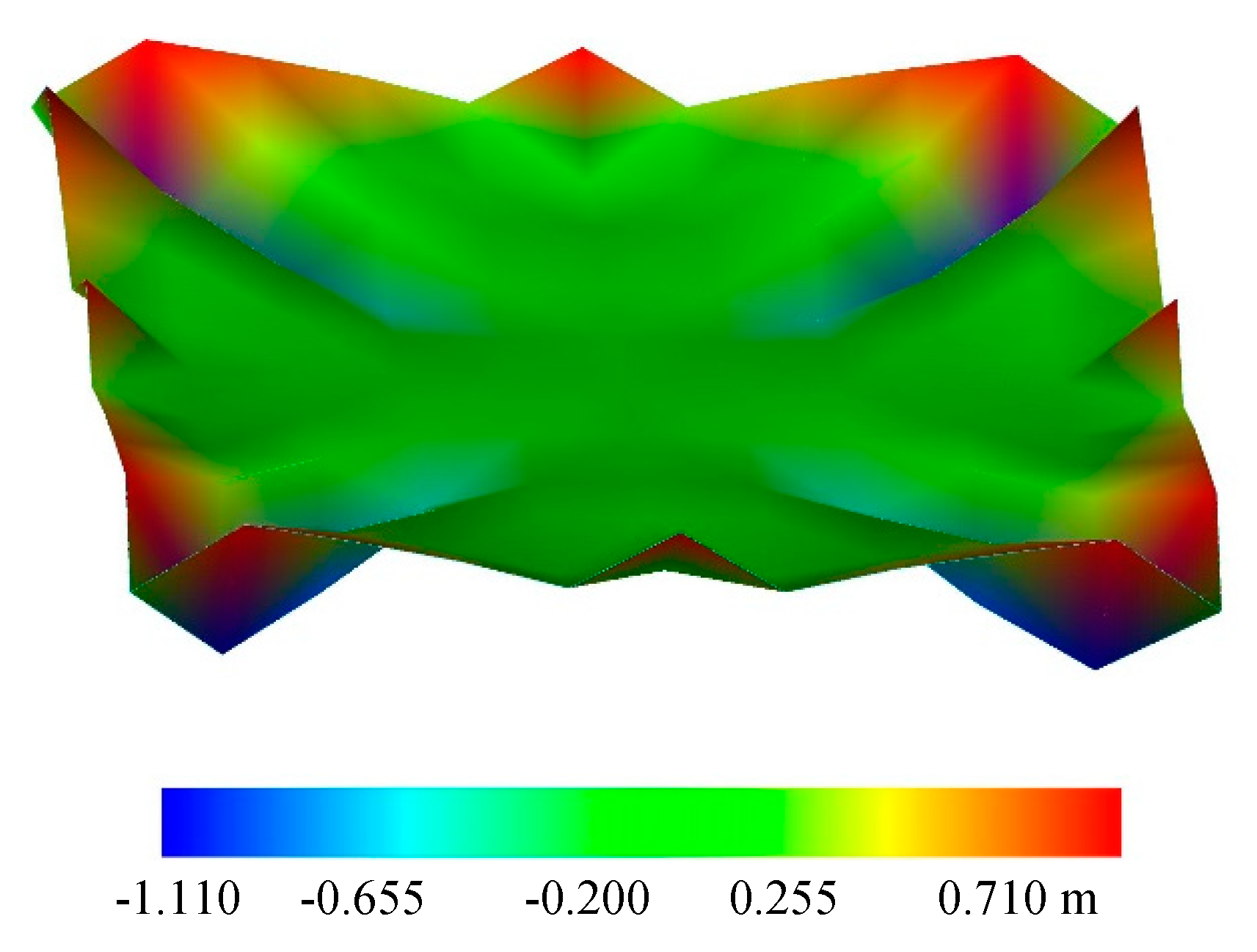
6. Case Study
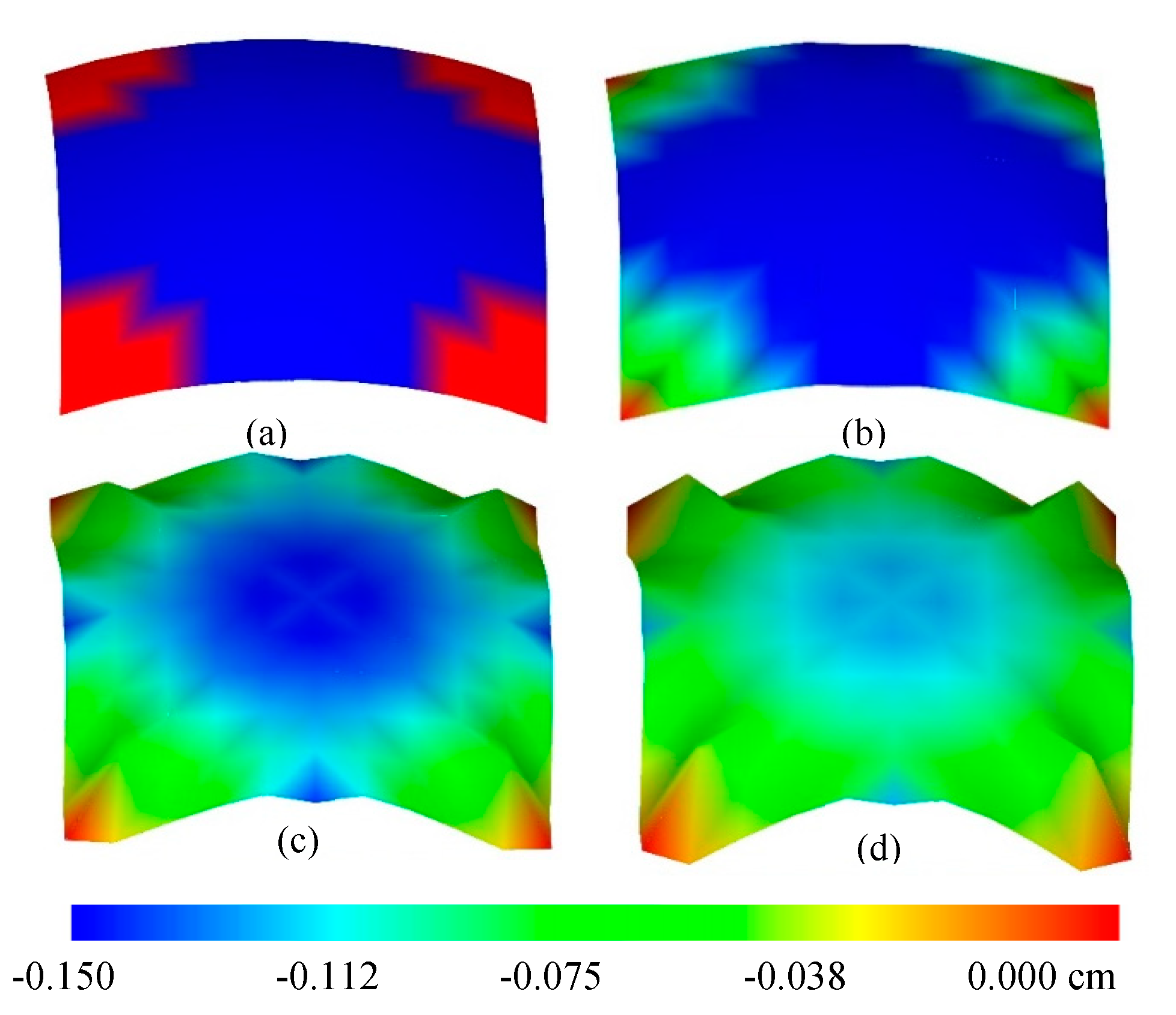
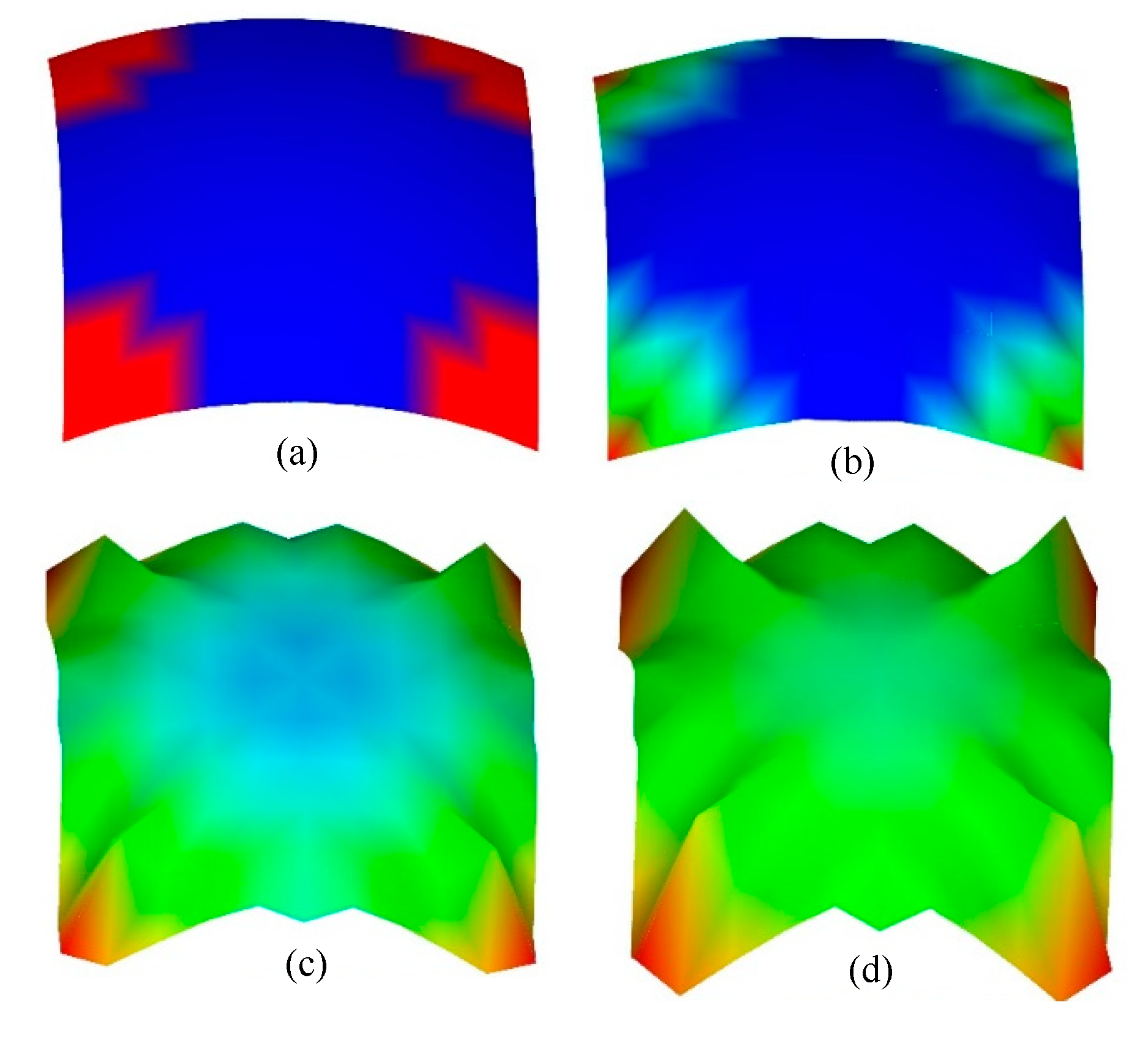
6.1. Example 1: the Shape Optimization of A Spherical Shell
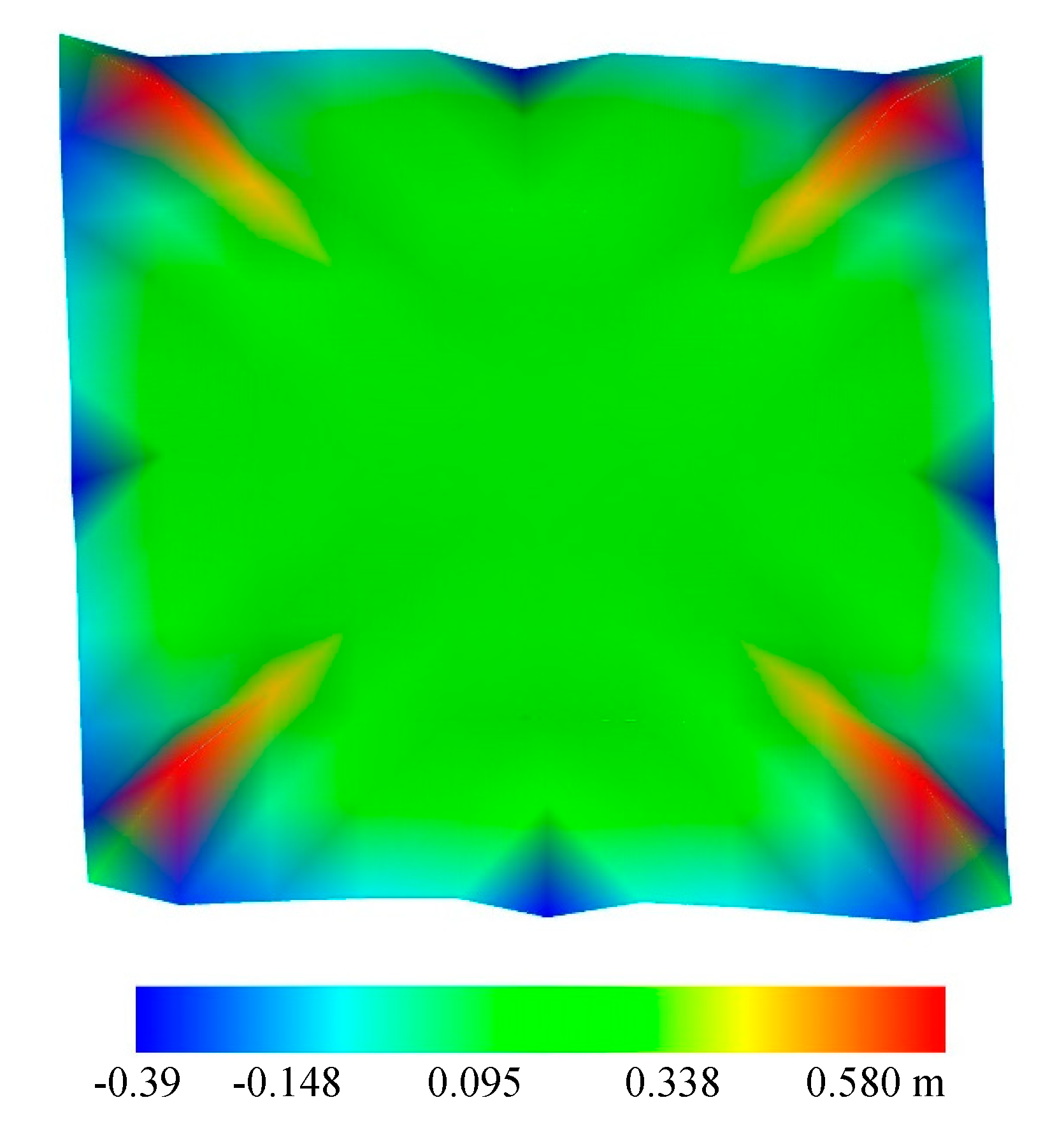
6.2. Example 2: The Shape Optimization of the Shell Roof In the Rolex Learning Center
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- San, B.; Waisman, H.; Harari, I. Analytical and numerical shape optimization of a class of structures under mass constraints and self-weight. J. Eng. Mech. 2020, 146, 1–17. [Google Scholar] [CrossRef]
- Ramm, E.; Bletzinger, K.U.; Reitinger, R. Shape optimization of shell structures. Revue Européenne des Éléments Finis 1993, 2, 377–398. [Google Scholar] [CrossRef]
- Kiendl, J.; Schmidt, R.; Wüchner, R.; Bletzinger, K.U. Isogeometric shape optimization of shells using semi-analytical sensitivity analysis and sensitivity weighting. Comput. Methods Appl. Mech. Eng. 2014, 274, 148–167. [Google Scholar] [CrossRef]
- Tanaka, N.; Honma, T.; Yokosuka, Y. Structural shape optimization of free-form surface shell and property of solution search using firefly algorithm. J. Mech. Sci. Technol. 2015, 29, 1449–1455. [Google Scholar] [CrossRef]
- Su, Y.; Ohsaki, M.; Wu, Y.; Zhang, J. A numerical method for form finding and shape optimization of reciprocal structures. Eng. Struct. 2019, 198, 109510. [Google Scholar] [CrossRef]
- Xia, Y.; Wu, Y.; Hendriks, M.A.N. Simultaneous optimization of shape and topology of free-form shells based on uniform parameterization model. Autom. Constr. 2019, 102, 148–159. [Google Scholar] [CrossRef]
- Cui, C.; Cui, G.; Tu, G.; Chi, X. Structure morphogenesis of free-form surfaces based on B-spline. Jianzhu Jiegou Xuebao J. Build. Struct. 2017, 38, 164–172. [Google Scholar]
- Cui, C.; Yan, H. A morphosis technique for curved-surface structures of arbitrary geometries-height adjusting method and its engineering applications. China Civ. Eng. J. 2006, 39, 1–6. [Google Scholar]
- Cui, C.; Zheng, H.; Jiang, B. The engineering applications of free form curved-surface by the height adjusting method. In Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium, Shanghai, China, 10–12 December 2010. [Google Scholar]
- Sasaki, M. Structural design of free-curved RC shells—An overview of built works. In Shell Structures for Architecture; Adriaenssens, S., Block, P., Eds.; Routledge Taylor & Francis Group: London, UK; New York, NY, USA, 2014; pp. 259–270. [Google Scholar]
- Cui, C.; Jiang, B. A morphogenesis method for shape optimization of framed structures subject to spatial constraints. Eng. Struct. 2014, 77, 109–118. [Google Scholar] [CrossRef]
- Cui, C.; Jiang, B.; Wang, Y. Node shift method for stiffness-based optimization of single-layer reticulated shells. J. Zhejiang Univ. Sci. A 2014, 15, 97–107. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Wu, M. Global shape optimization of free-form cable-stiffened latticed shell based on local optimal solutions. Eng. Struct. 2018, 168, 576–588. [Google Scholar] [CrossRef]
- Wei, L.; Zhao, M.; Wu, G.; Meng, G. Truss optimization on shape and sizing with frequency constraints based on genetic algorithm. Comput. Mech. 2005, 35, 361–368. [Google Scholar] [CrossRef]
- Papadopoulos, V.; Papadrakakis, M. The effect of material and thickness variability on the buckling load of shells with random initial imperfections. Comput. Methods Appl. Mech. Eng. 2005, 194, 1405–1426. [Google Scholar] [CrossRef]
- Shimoda, M.; Okada, T.; Nagano, T.; Shi, J.X. Free-form optimization method for buckling of shell structures under out-of-plane and in-plane shape variations. Struct. Multidiscip. Optim. 2016, 54, 275–288. [Google Scholar] [CrossRef]
- Falco, S.A.; Afonso, S.M.B.; Vaz, L.E. Analysis and optimal design of plates and shells under dynamic loads—II: Optimization. Struct. Multidiscip. Optim. 2004, 27, 197–209. [Google Scholar] [CrossRef]
- Mi, D.; Yang, R.; Zhou, L.; Liu, Y.; Guo, D. Optimal structural frequency design of stiffened shell. Appl. Mech. Mater. 2012, 157–158, 1636–1639. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y. Structural topology optimization on dynamic compliance at resonance frequency in thermal environments. Struct. Multidiscip. Optim. 2014, 49, 81–91. [Google Scholar] [CrossRef]
- Bletzinger, K.; Ramm, E. Computational form finding and optimization. In Shell Structures for Architecture: Form Finding and Optimization; Adriaenssens, S., Block, P., Eds.; Routledge Taylor & Francis Group: London, UK; New York, NY, USA, 2014; pp. 45–55. [Google Scholar]
- Yang, X.Y.; Xie, Y.M.; Steven, G.P. Evolutionary methods for topology optimisation of continuous structures with design dependent loads. Comput. Struct. 2005, 83, 956–963. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Q.; Huang, J. The influence of structural mass on optimization effect of rational criterion methods. Chin. J. Comput. Mech. 2015, 32, 33–40. [Google Scholar]
- Bandara, K.; Cirak, F. Isogeometric shape optimisation of shell structures using multiresolution subdivision surfaces. CAD Comput. Aided Des. 2018, 95, 62–71. [Google Scholar] [CrossRef] [Green Version]
- Ding, C.; Seifi, H.; Dong, S.; Xie, Y.M. A new node-shifting method for shape optimization of reticulated spatial structures. Eng. Struct. 2017, 152, 727–735. [Google Scholar] [CrossRef]




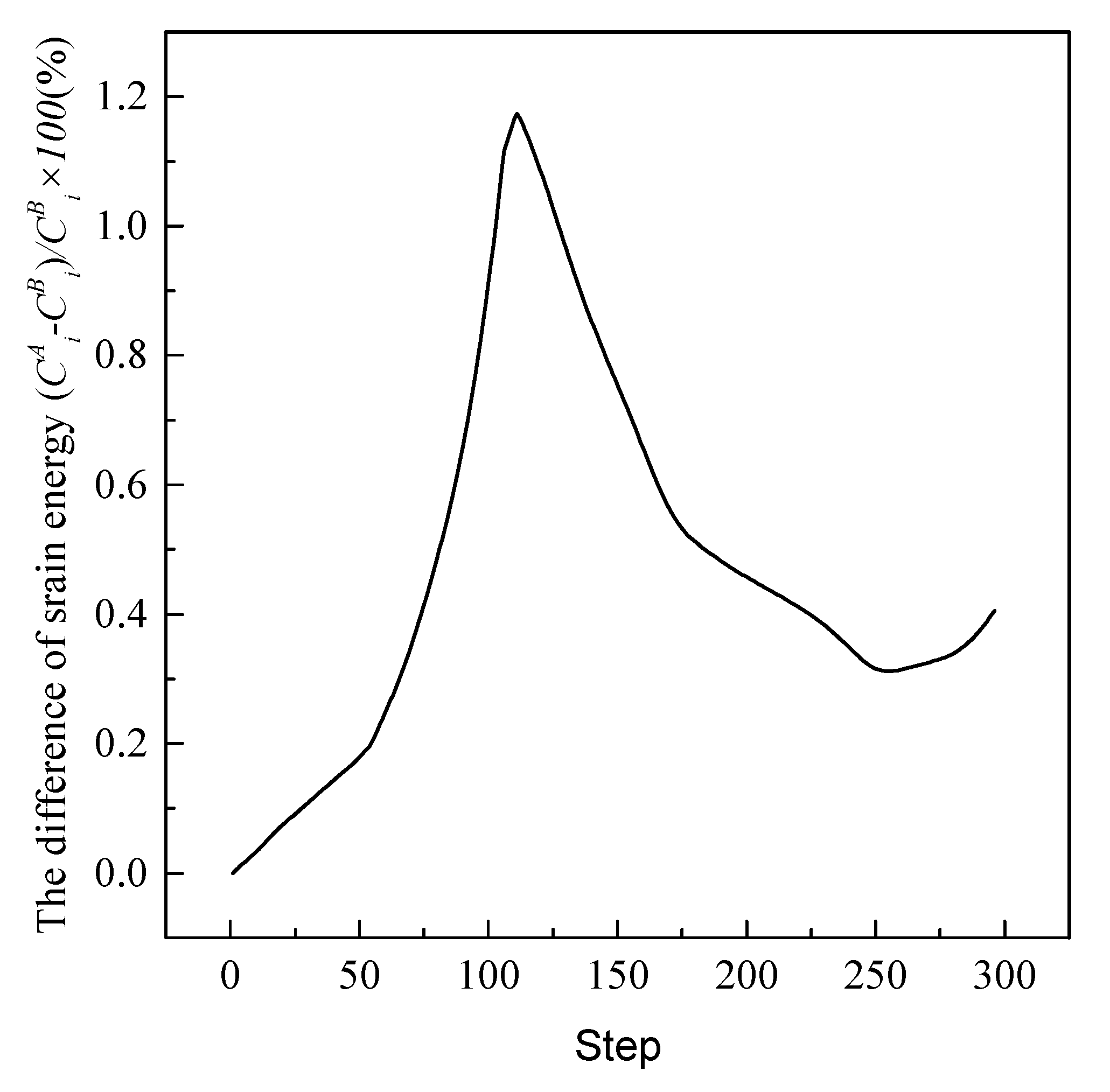

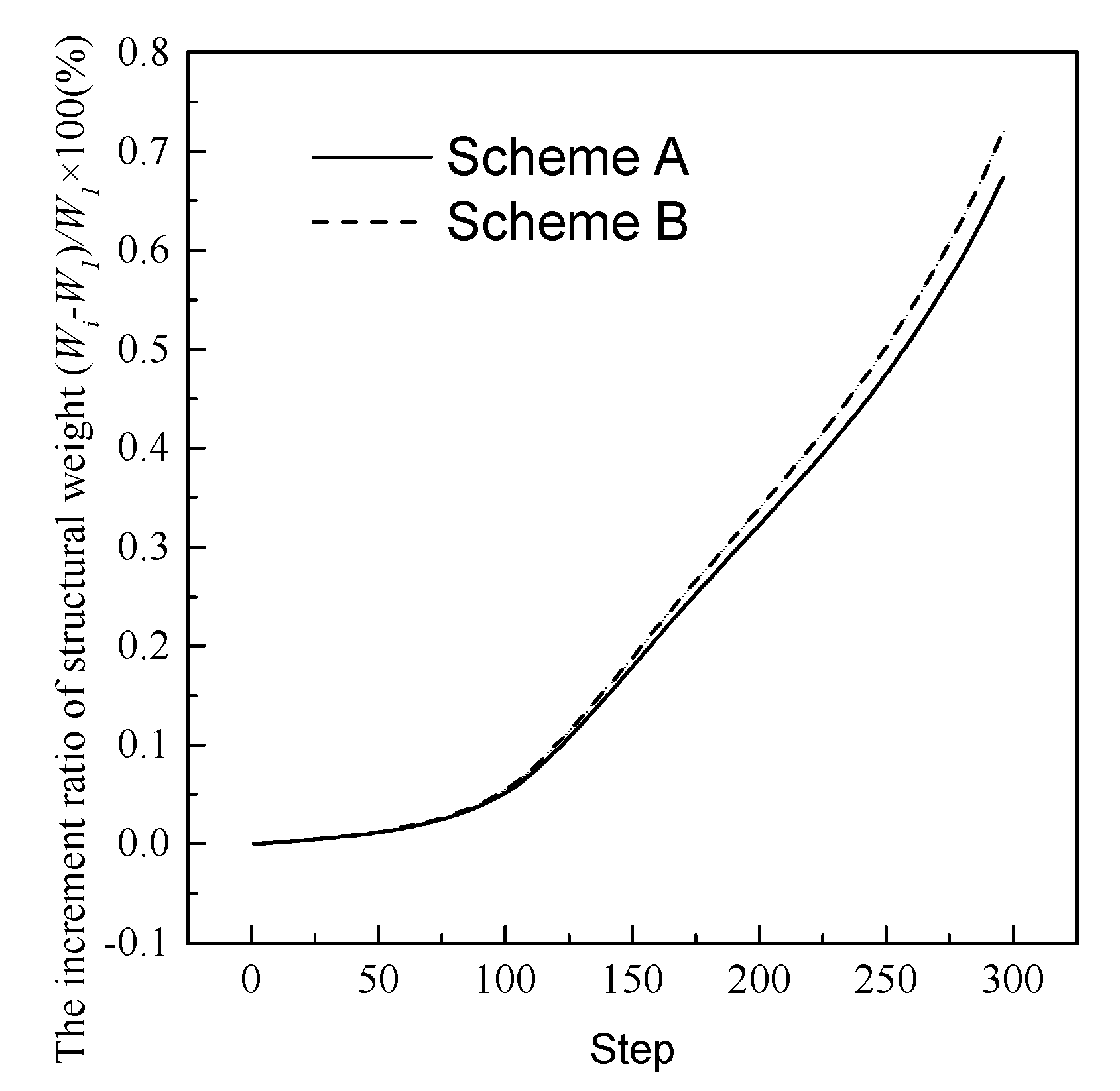
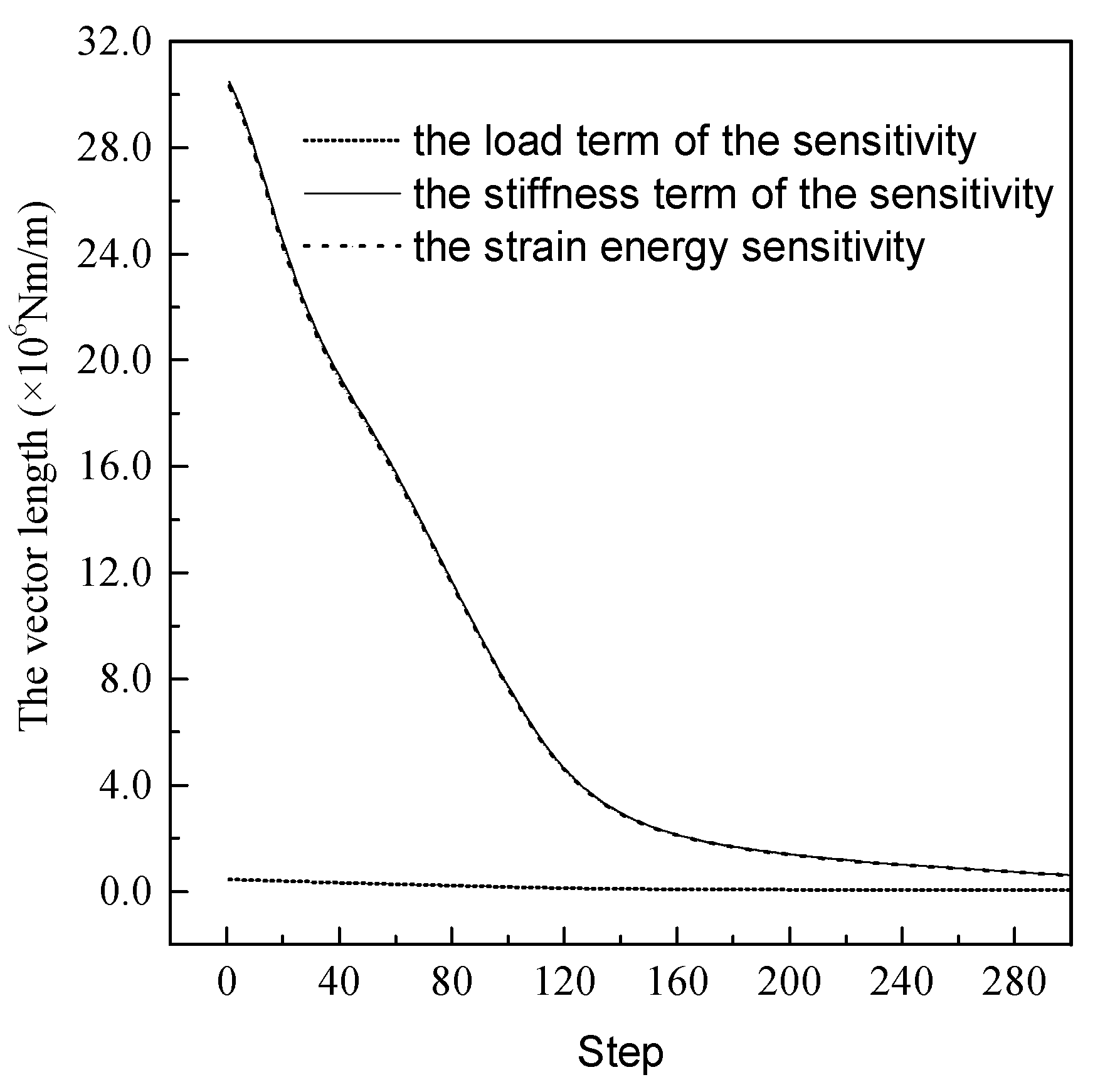
| Step | Load Term SNF | Stiffness Term SNG | Whole Sensitivity SNT | SNF/SNT × 100 (%) |
|---|---|---|---|---|
| 1 | 116.54 | −1486.47 | −1369.92 | −8.51 |
| 10 | 55.22 | −555.56 | −500.34 | −11.04 |
| 20 | 27.67 | −149.31 | −121.64 | −22.75 |
| 30 | 16.18 | −31.12 | −14.94 | −108.30 |
| 40 | 9.68 | −26.25 | −16.57 | −58.41 |
| 120 | 6.18 | −8.74 | −2.56 | −241.40 |
| 248 | 5.18 | −6.37 | −1.19 | −435.29 |
| Step | Load Term SNF | Stiffness Term SNG | Whole Sensitivity SNT | SNF/SNT × 100 (%) |
|---|---|---|---|---|
| 1 | 34.04 | −20.59 | 13.45 | 253.09 |
| 10 | 11.94 | −6.57 | 5.37 | 222.35 |
| 20 | 5.93 | −3.09 | −2.83 | −209.54 |
| 30 | 4.55 | −5.24 | −0.69 | −659.42 |
| 40 | 3.98 | −5.95 | −1.97 | −202.03 |
| 120 | 3.35 | −1.99 | 5.35 | 62.74 |
| 248 | 2.97 | −1.31 | 1.66 | 178.92 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Cui, C.; Wang, J. The Influence of the Load Term of the Strain Energy Sensitivity in the Shell Shape Optimization. Appl. Sci. 2020, 10, 1947. https://doi.org/10.3390/app10061947
Jiang B, Cui C, Wang J. The Influence of the Load Term of the Strain Energy Sensitivity in the Shell Shape Optimization. Applied Sciences. 2020; 10(6):1947. https://doi.org/10.3390/app10061947
Chicago/Turabian StyleJiang, Baoshi, Changyu Cui, and Jianghong Wang. 2020. "The Influence of the Load Term of the Strain Energy Sensitivity in the Shell Shape Optimization" Applied Sciences 10, no. 6: 1947. https://doi.org/10.3390/app10061947




