In-flight Wind Field Identification and Prediction of Parafoil Systems
Abstract
:1. Introduction
2. Parafoil System Model
3. Wind Field Identification
4. Wind Field Prediction
4.1. Average Wind Field Prediction Model
4.2. Identification-predictive Method
- According to the flight states of parafoil systems, the average wind field at current altitude is identified by the wind field identification method.
- Let , according to Equation (22), can be obtained.
- Substituting the predicted altitude that to be and into Equation (24), the average wind field at the corresponding altitude can be predicted.
5. Simulation and Analysis
5.1. Simulation Settings
5.2. Simulation of Parafoil System
5.3. Simulation of Wind Field Identification
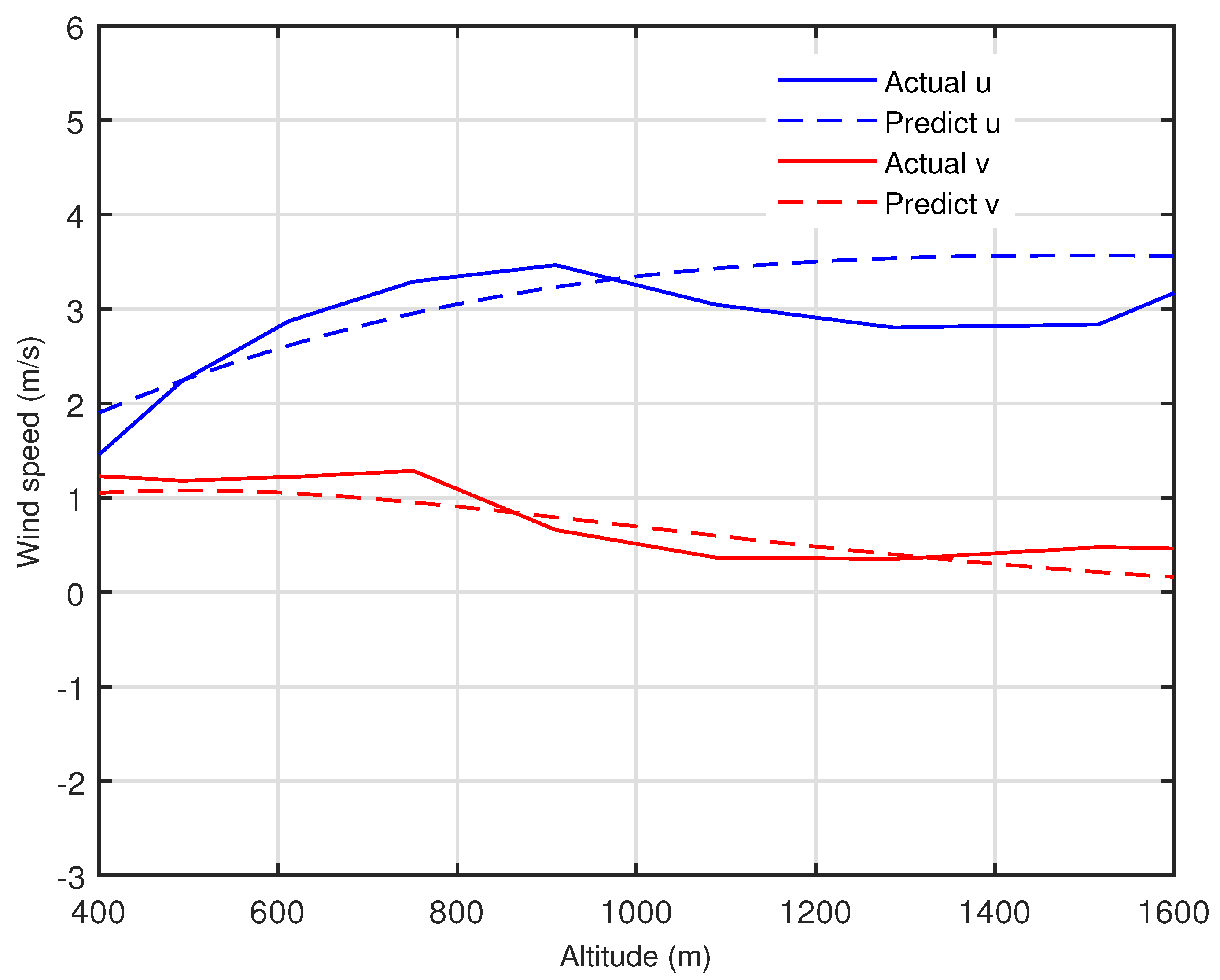
5.4. Simulation of Wind Field Prediction
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Yakimenk, O.A. Precision Aerial Delivery Systems: Modeling, Dynamics, and Control; AIAA: Reston, VA, USA, 2015; pp. 2–44. [Google Scholar]
- Tao, J.; Sun, Q.L.; Liang, W.; Chen, Z.Q.; He, Y.P.; Dehmer, M.; Sun, M.W. Dynamic modeling and trajectory tracking control of parafoil system in wind environments. IEEE-ASME Trans. Mechatron. 2017, 22, 2736–2745. [Google Scholar] [CrossRef]
- Slegers, N.; Costello, M. Model predictive control of a parafoil and payload system. J. Guid. Control Dyn. 2005, 28, 816–821. [Google Scholar] [CrossRef]
- Tao, J.; Sun, Q.L.; Liang, W.; Chen, Z.Q.; He, Y.P.; Dehmer, M. Computational fluid dynamics based dynamic modeling of parafoil system. Appl. Math. Model. 2018, 54, 136–150. [Google Scholar] [CrossRef]
- Slegers, N.; Yakimenko, O.A. Terminal Guidance of Autonomous Parafoils in High Wind-to-Airspeed Ratios. Proc. Inst. Mech. Eng. Part G-J. Aerosp. Eng. 2010, 225, 336–346. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Sun, Y.X.; Zhao, M.; Liu, M. A Virtual Structure Formation Guidance Strategy for Multi-Parafoil Systems. IEEE Access 2019, 7, 123592–123603. [Google Scholar] [CrossRef]
- Tao, J.; Sun, Q.L.; Tan, P.L.; Chen, Z.Q.; He, Y.P. Active disturbance rejection control (ADRC)-based autonomous homing control of powered parafoils. Nonlinear Dyn. 2016, 86, 1461–1476. [Google Scholar] [CrossRef]
- Tao, J.; Sun, Q.L.; Tan, P.L.; Chen, Z.Q.; He, Y.P. Autonomous homing control of a powered parafoil with insufficient altitude. ISA Trans. 2016, 65, 516–524. [Google Scholar] [CrossRef]
- Chiel, B.S.; Dever, C. Autonomous parafoil guidance in high winds. J. Guid. Control Dyn. 2015, 38, 588–597. [Google Scholar] [CrossRef] [Green Version]
- Tao, J.; Liang, W.; Sun, Q.L.; Luo, S.Z.; Chen, Z.Q.; Tan, P.L.; He, Y.P. Modeling and control of a powered parafoil in wind and rain environments. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1642–1659. [Google Scholar] [CrossRef]
- Tao, J.; Dehmer, M.; Xie, G.M.; Zhou, Q. A generalized predictive control-based path following method for parafoil systems in wind environments. IEEE Access 2019, 7, 42586–42595. [Google Scholar] [CrossRef]
- Ward, M.; Costello, M.; Slegers, N. On the Benefits of In-Flight System Identification for Autonomous Airdrop Systems. J. Guid. Control Dyn. 2010, 33, 1313–1326. [Google Scholar] [CrossRef]
- Gao, H.T.; Zhang, L.M.; Sun, Q.L.; Chen, Z.Q. Fault-tolerance Design of Homing Trajectory for Parafoil System Based on Pseudo-spectral Method. Control Theory Appl. 2013, 30, 142–149. [Google Scholar] [CrossRef]
- Sun, H.; Sun, Q.L.; Luo, S.Z.; Chen, Z.Q.; Wu, W.N.; Tao, J.; He, Y.P. In-flight compound homing methodology of parafoil delivery systems under multiple constraints. Aerosp. Sci. Technol. 2018, 79, 85–104. [Google Scholar] [CrossRef]
- Zhang, L.M.; Gao, H.T.; Chen, Z.Q.; Sun, Q.L.; Zhang, X.H. Multi-objective global optimal parafoil homing trajectory optimization via Gauss pseudospectral method. Nonlinear Dyn. 2013, 72, 1–8. [Google Scholar] [CrossRef]
- Cacan, M.R.; Scheuermann, E.; Ward, M.; Costello, M.; Slegers, N. Autonomous airdrop systems employing ground wind measurements for improved landing accuracy. IEEE-ASME Trans. Mechatron. 2015, 20, 3060–3070. [Google Scholar] [CrossRef]
- Wu, K. Homing Criterion and Principle of Measuring Wind for Gliding Parachute Systems. Spacecr. Recovery Remote Sens. 1996, 17, 10–16. [Google Scholar]
- Koehl, A.; Boutayeb, M.; Rafaralahy, H.; Martinez, B. Wind-disturbance and aerodynamic parameter estimation of an experimental Launched Micro Air Vehicle using an EKF-like observer. In Proceedings of the 49th IEEE Conference on Decision and Control Symposium on Plasma Chemistry, Atlanta, GA, USA, 15–17 December 2010; pp. 6383–6388. [Google Scholar]
- Herrmann, T.; Ward, M.; Costello, M.; Slegers, N. Utilizing Ground-based LIDAR for Autonomous Airdrop. In Proceedings of the 22nd AIAA Aerodynamic Decelerator Systems(ADS) Conference, Daytona Beach, FL, USA, 25–28 March 2013; pp. 1288–1300. [Google Scholar]
- Kelly, K.; Pena, B. Wind study and GPS dropsonde applicability to airdrop testing. In Proceedings of the 16th AIAA aerodynamic decelerator systems technology conference and seminar, AIAA 2001–2022, Boston, MA, USA, 21–24 May 2001. [Google Scholar]
- Altmann, H. An enhanced GNC functionality combining pre-flight wind forecast and in-flight identified wind. In Proceedings of the 21st AIAA aerodynamic decelerator systems technology conference and seminar, AIAA 2011–2531, Dublin, Ireland, 23–26 May 2011. [Google Scholar]
- Rogers, J.; Slegers, N. Robust parafoil terminal guidance using massively parallel processing. J Guid. Dyn. 2013, 36, 336–1345. [Google Scholar] [CrossRef] [Green Version]
- Hunt, K.; Nason, G.P. Wind speed modelling and short-term prediction using wavelets. Wind Eng. 2001, 25, 55–61. [Google Scholar] [CrossRef]
- Rodriguez, L.; Cobano, J.; Ollero, A. Small uas-based wind feature identification system part 1: Integration and validation. Sensors 2017, 17, 8. [Google Scholar] [CrossRef] [Green Version]
- Neumann, P.; Bartholmai, M. Real-time wind estimation on a micro unmanned aerial vehicle using its inertial measurement unit. Sens. Actuators A Phys. 2015, 235, 300–310. [Google Scholar] [CrossRef]
- Tao, J.; Sun, Q.L.; Tan, P.L.; Chen, Z.Q.; He, Y.P. Homing control of parafoil systems in unknown wind environments. Acta Aeronaut. Astronaut. Sin. 2017, 38, 320523. [Google Scholar]
- Jun, L.; Wang, Y.; Chen, J.Y. Noise attenuation based on wave vector characteristics. Appl. Sci. 2018, 8, 672. [Google Scholar]
- Tae-Gu, K.; Ahmad, S.F.; Yun, B.J.; Kim, H.D. Cutting Blade Measurement of an Ultrasonic Cutting Machine Using Multi-Step Detection. Appl. Sci. 2019, 9, 3338. [Google Scholar]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Tort, M.; Dubos, T. Dynamically consistent shallow-atmosphere equations with a complete Coriolis force. Q. J. R. Meteorol. Soc. 2014, 140, 2388–2392. [Google Scholar] [CrossRef]
- Lueck, R.; Laurrent, L.S.; Moum, J.N. Turbulence in the Benthic Boundary Layer. Encyclopedia of Ocean Sciences: Elements of Physical Oceanography; Academic Press: Cambridge, UK, 2009; pp. 311–316. [Google Scholar]
- China Meteorological Adeministration. Available online: Http://www.cma.gov.cn/ (accessed on 2 December 2013).









| Parameter | Value (Unit) |
|---|---|
| Aspect ratio | 1.73 |
| Area of canopy | 22 m |
| Length of lines | 3.7 m |
| Rigging angle | 7 |
| Length of riser | 0.5 m |
| Mass of payload | 80 kg |
| Characteristic area of drag of payload | 0.5 m |
| No. | Deflection (Left, Right) | Wind Velocity Vector (m/s) | Identification Result (m/s) | Relative Error |
|---|---|---|---|---|
| 1 | (10%, 0%) | (2.0, 4.0) | (2.1510, 3.8600) | (7.55%, 3.5%) |
| 2 | (30%, 0%) | (−2.0, −5.0) | (−2.0735, −4.9470) | (3.68%, 1.06%) |
| 3 | (60%, 0%) | (2.0, −4.0) | (1.7385, −4.8084) | (13.07%, 20.21%) |
| 4 | (0%, 20%) | (2.0, 4.0) | (2.0150, 3.9757) | (0.75%, 0.61%) |
| 5 | (0%, 30%) | (2.0, 4.0) | (2.1546, 3.7059) | (7.73%, 7.35%) |
| 6 | (0%, 60%) | (2.0, 4.0) | (1.7385, 4.8084) | (13.08%, 20.21%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Tao, J.; Dehmer, M.; Emmert-Streib, F.; Sun, Q.; Chen, Z.; Xie, G.; Zhou, Q. In-flight Wind Field Identification and Prediction of Parafoil Systems. Appl. Sci. 2020, 10, 1958. https://doi.org/10.3390/app10061958
Gao H, Tao J, Dehmer M, Emmert-Streib F, Sun Q, Chen Z, Xie G, Zhou Q. In-flight Wind Field Identification and Prediction of Parafoil Systems. Applied Sciences. 2020; 10(6):1958. https://doi.org/10.3390/app10061958
Chicago/Turabian StyleGao, Haitao, Jin Tao, Matthias Dehmer, Frank Emmert-Streib, Qinglin Sun, Zengqiang Chen, Guangming Xie, and Quan Zhou. 2020. "In-flight Wind Field Identification and Prediction of Parafoil Systems" Applied Sciences 10, no. 6: 1958. https://doi.org/10.3390/app10061958
APA StyleGao, H., Tao, J., Dehmer, M., Emmert-Streib, F., Sun, Q., Chen, Z., Xie, G., & Zhou, Q. (2020). In-flight Wind Field Identification and Prediction of Parafoil Systems. Applied Sciences, 10(6), 1958. https://doi.org/10.3390/app10061958










