Failure Prediction of the Rotating Machinery Based on CEEMDAN-ApEn Feature and AR-UKF Model
Abstract
:1. Introduction
- (1)
- The complete ensemble empirical mode decom-posetion with adaptive noise (CEEMDAN), which can overcome shortages of EMD and EEMD on modal aliasing and calculation efficiency, is adopted to decompose the original vibration signals of the rotating machinery into a number of IMFs and a residual.
- (2)
- The maximal information coefficient (MIC), which can reveal the degree of association between two variables, is utilized to select eligible IMFs and get the reconstructed signals.
- (3)
- The approximate entropy (ApEn) is employed to achieve fault features of the reconstructed signals and track the degradation process of the rotating machinery.
- (4)
- A remaining useful life (RUL) prediction model by combing the auto regress (AR) model and the unscented Kalman filter (UKF) algorithm is developed to achieve the RUL of the rotating machinery accurately.
2. Methodology
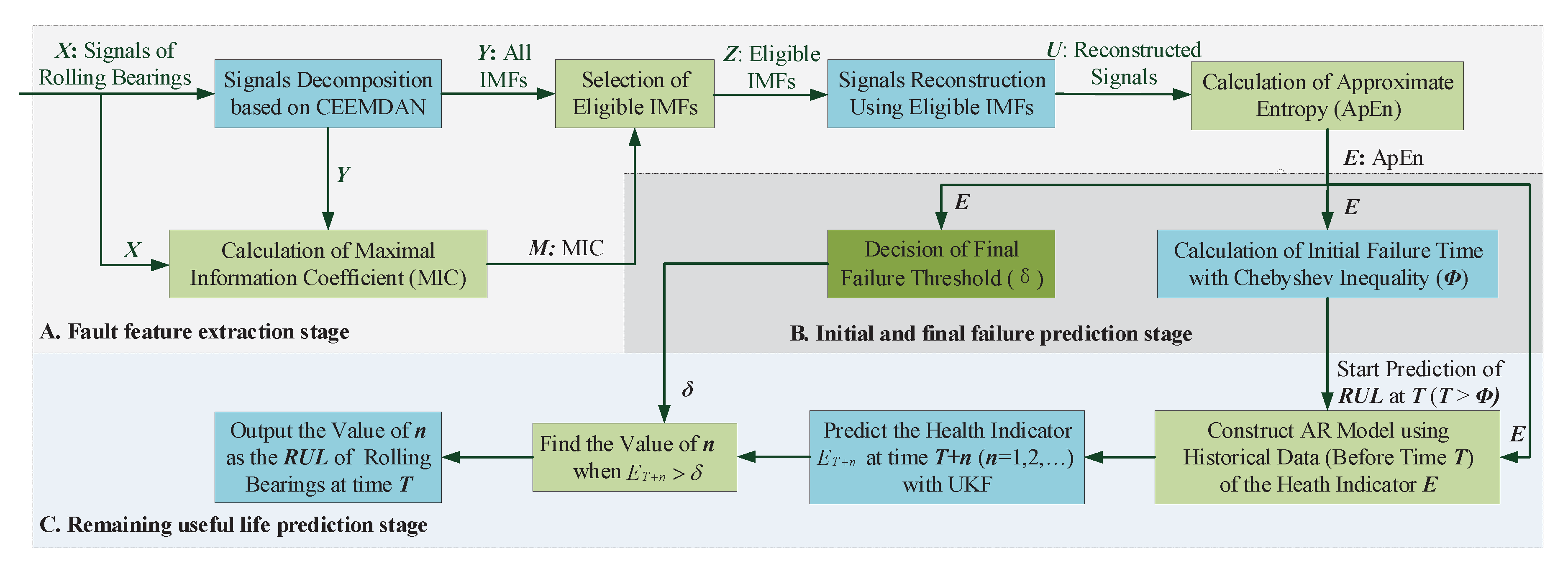
2.1. Overview
2.2. Fault Feature Extraction Stage
2.2.1. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise
- (1)
- Add to the original signals X:where is the k-th IMF processing Gaussian white noise, and is the signal-to-noise radio for each procedure.
- (2)
- Use EMD to obtain the local mean of to get the first residual :where N is total number of sets, and is a function used to estimate the local mean of signals.
- (3)
- Calculate the first IMF:
- (4)
- Decompose and delimit the second IMF:
- (5)
- Calculate the k-th residual :
- (6)
- Get k-th IMF:
- (7)
2.2.2. Maximal Information Coefficient
- (1)
- Denote as a joint probability distribution function of two variables and , and mutual information of and is defined as:where and denote the marginal probability distribution function of and , respectively. is non-negative and iff . It is obviously that the value of I is higher than zero when and are correlated, and the stronger the correlation is, the larger the value of .
- (2)
- Suppose Y is consisted of a number of elements which are ordered value pairs of and , and N is the amount of pairs. A grid G is defined as a partition on Y, which can partition the values of in Y into a number of bins and that of in Y into a number of bins, respectively. Denote as the mutual information of and on grid G with rows and columns. The feature matrix of Y is defined as:where represents the maximum mutual information of and on grid G.
- (3)
- Furthermore, MIC of and in set Y with N samples is defines as follows.where is the upper bound of the grid size required to be selected carefully, and its suitable value is .
2.2.3. Approximate Entropy
- (1)
- The sequence is sequentially composed into an m-dimensional vector :
- (2)
- Calculate the distance between the vector and the remaining vectors for each i.
- (3)
- Given a threshold , for each value of i, count the number n of and calculate the ratio of n to the total number .
- (4)
- Calculate the logarithm of and get it average value :
- (5)
- Add the dimension to , and repeat steps (1)–(4) to get .
- (6)
- The value of ApEn for this sequence is:
2.3. Initial and Final Failure Prediction Stage
2.4. RUL Prediction
2.4.1. Unscented Kalman Filter
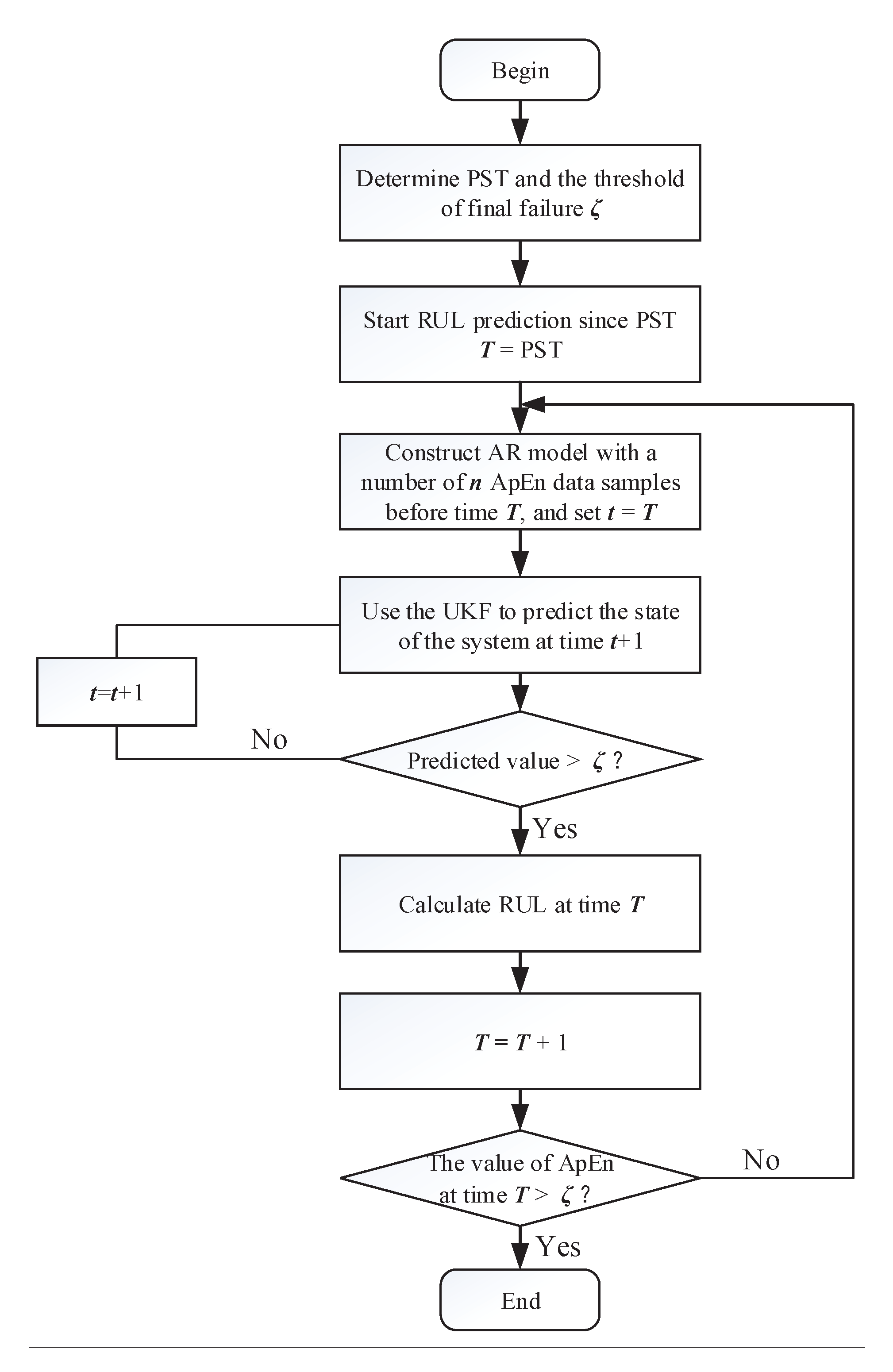
2.4.2. AR-UKF Prediction Model
- (1)
- Calculate the proposed CEEMDAN-ApEn feature according to the method proposed in Section 2.2. Obtain the prediction starting time (PST) and the threshold of the final failure using the method proposed in Section 2.3.
- (2)
- Start RUL prediction by setting .
- (3)
- At the time T, select n data samples of the CEEMDAN-ApEn feature on time slots to construct the AR model.
- (4)
- Use UKF to perform multiple steps prediction on time slots until the predicted value is greater than the threshold of final failure . Suppose the time corresponding to above predicted value is ; thus, m is the predicted RUL at the time T.
- (5)
- (6)
- Finally, the predicted RUL value obtained at each time is used to plot a RUL curve.
3. Experiment and Results
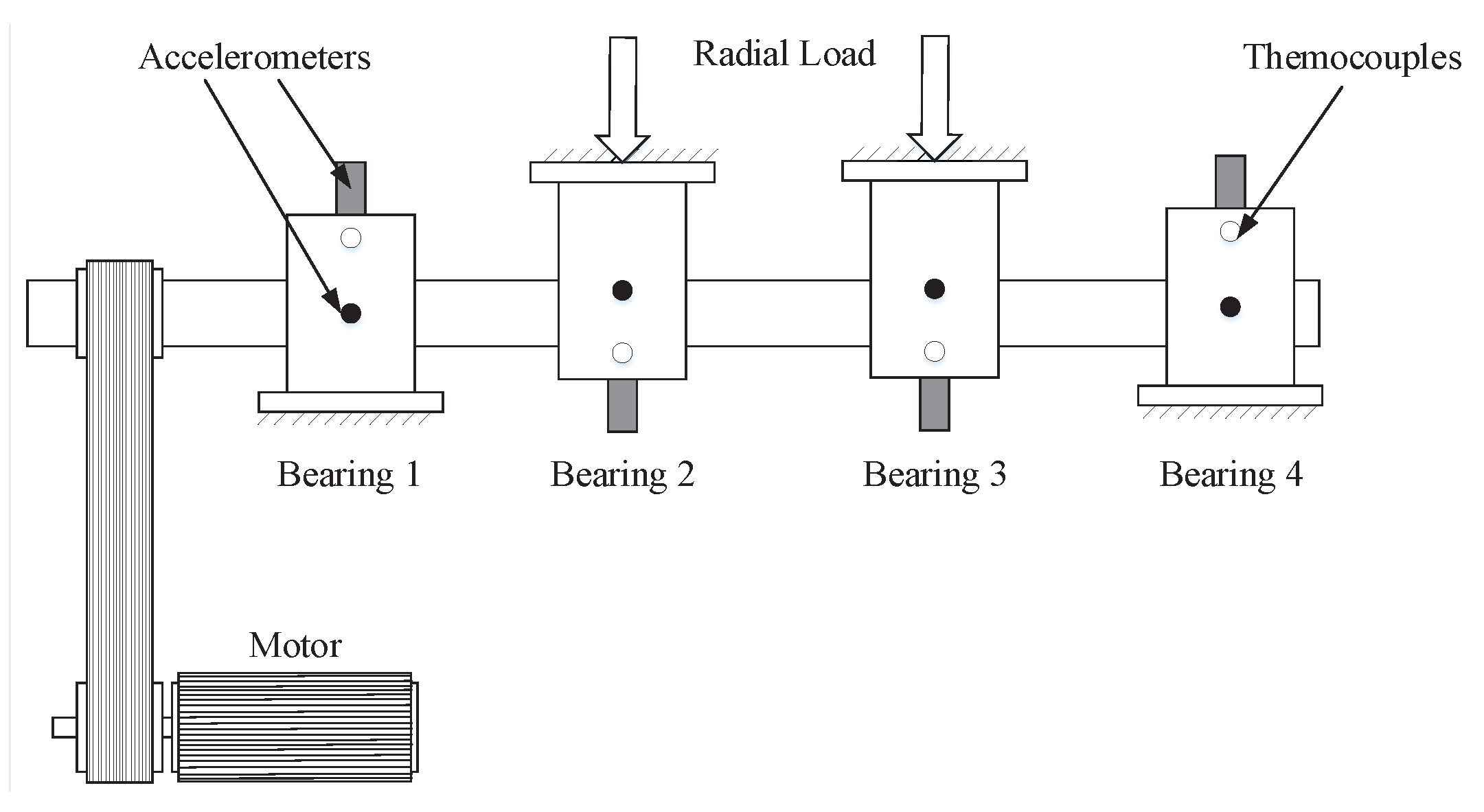
3.1. Experimental Setup
3.2. Fault Feature Extraction and Selection
- (1)
- The feature should vary with degradation process gradually, thus maintaining a certain correlation with time.
- (2)
- The feature should show a consistent increasing or decreasing characteristics throughout the life cycle.
- (3)
- The feature should be robust to outliers.
3.3. Initial and Final Failure Prediction
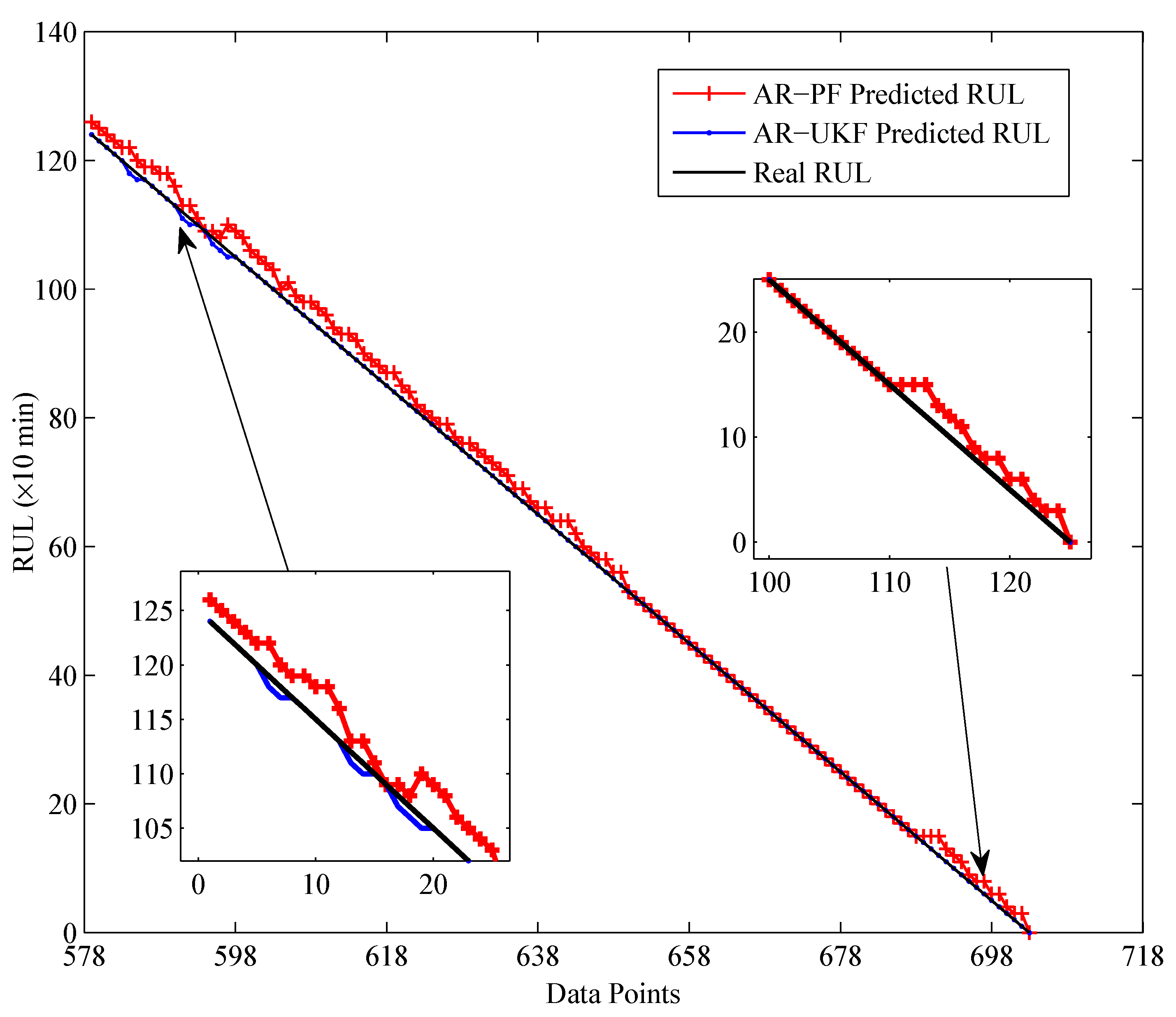
3.4. RUL Prediction
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhong, Q.; Zhang, Z. Several issues of scientific development of safety production (Including safety manufacturing) in China. Chin. J. Mech. Eng. 2007, 43, 7–18. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y. Development of fault detection and diagnosis technology of rolling bearing. Eng. Test 2009, 49, 1–5. [Google Scholar]
- Huang, Z. Historical review and future expectation of dimensionless diagnosis in China. China Plant Eng. 2000, 10, 30–35. [Google Scholar]
- Pan, Q.; He, T. Fault diagnosis of gears based on local mean decomposition combing with kurtosis. J. Vibroeng. 2014, 16, 2639–2648. [Google Scholar]
- Qiu, H.; Lee, J. Robust performance degradation assessment methods for enhanced rolling element bearings prognostics. Adv. Eng. Inform. 2003, 17, 127–140. [Google Scholar] [CrossRef]
- Heng, R.; Nor, M. Statistical analysis of sound and vibration signals for monitoring rolling element bearing condition. Appl. Acoust. 1998, 53, 211–226. [Google Scholar] [CrossRef]
- Li, Y.; Lin, J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Dong, H.; Qi, K.; Chen, X. Shifting process of EMD and its application in rolling element bearing fault diagnosis. J. Mech. Sci. Technol. 2009, 23, 2000–2007. [Google Scholar] [CrossRef]
- Wang, J.; Gao, X.; Yan, R. Integration of EEMD and ICA for wind turbine gearbox diagnosis. Wing Energy 2014, 17, 757–773. [Google Scholar] [CrossRef]
- Zhao, X.; Patel, T.H.; Zuo, M.J. Multivariate EMD and full spectrum based condition monitoring for rotating machinery. Mech. Syst. Signal Process. 2012, 27, 712–728. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. Multi-scale enveloping spectrogram for vibration analysis in bearing defect diagnosis. Neural Comput. 2009, 42, 293–302. [Google Scholar] [CrossRef]
- Wang, C.; Yan, R.; Gao, R. Unified time-scale-frequency analysis for machine defect signature extraction: Theoretical framework. Mech. Syst. Signal Process. 2009, 23, 226–235. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. An efficient approach to machine health evaluation based on harmonic wavelet packet transform. Robot. Comput. Integr. Manuf. 2005, 21, 291–301. [Google Scholar] [CrossRef]
- Chen, H.; Chen, X.; Zi, Y. An effective approach to rolling bearing diagnosis based on adaptive redundant second-generation wavelet. Int. J. Mater. Prod. Technol. 2008, 33, 65–78. [Google Scholar] [CrossRef]
- Dong, S.J.; Wu, W.L. Rolling bearing performance degradation assessment based on improved convolutional neural network with anti-interference. Measurement 2020, 151, 107219. [Google Scholar] [CrossRef]
- Zhao, X.L.; Jia, M.P. A new local-global deep neural network and its application in rotating machinery fault diagnosis. Neurocomputing 2019, 366, 215–233. [Google Scholar] [CrossRef]
- Wu, C.; Feng, F.; Wu, S.; Jiang, P.; Wang, J. A method for constructing rolling bearing lifetime health indicator based on multi-scale convolutional neural networks. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 526. [Google Scholar] [CrossRef]
- Qian, Y.; Yan, R. Remaining useful life prediction of mechanical rotary components using an enhanced particle filter. IEEE Trans. Instrum. Meas. 2015, 64, 2696–2707. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. An integrated approach to bearing prognostics based on EEMD-multi feature extraction, Gaussian mixture models and Jensen-Renyi divergence. Appl. Soft Comput. 2018, 71, 36–50. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, B.; Vachtsevanos, G. Prediction of machine health condition using neuro-fuzzy and Bayesian algorithms. IEEE Trans. Instrum. Meas. 2012, 61, 297–306. [Google Scholar] [CrossRef]
- Donga, M.; He, D. A segmental hidden semi-Markov model (HSMMS)-based diagnostics and prognostics framework and methodology. Mech. Syst. Signal Process. 2007, 21, 2248–2266. [Google Scholar] [CrossRef]
- Liao, L. Discovering prognostic features using genetic programming in remaining useful life prediction. IEEE Trans. Ind. Electron. 2014, 61, 2464–2472. [Google Scholar] [CrossRef]
- Oppenheimer, C.H.; Loparo, K.A. Physically based diagnosis and prognosis of cracked rotor shafts. In Proceedings of the SPIE—The International Society for Optical Engineering, Orlando, FL, USA, 24–27 July 2002; pp. 122–132. [Google Scholar]
- Qian, Y.; Yan, R.; Hu, S. Bearing degradation evaluation using recurrence quantification analysis and Kalman filter. IEEE Trans. Instrum. Meas. 2014, 63, 2599–2610. [Google Scholar] [CrossRef]
- Swanson, D.C.; Spencer, J.M.; Arzoumanian, S.H. Prognostic modelling of crack growth in a tensioned steel band. Mech. Syst. Signal Process. 2000, 14, 789–803. [Google Scholar] [CrossRef]
- Chen, X.; Shen, Z.; He, Z.; Sun, C.; Liu, Z. Remaining life prognostics of rolling bearing based on relative features and multivariable support vector machine. J. Mech. Eng. Sci. 2013, 227, 2849–2860. [Google Scholar] [CrossRef]
- Bustos, A.; Rubio, H.; Castejón, C.; García-Prada, J.C. EMD-Based methodology for the identification of a high-speed train running in a gear operating state. Sensors 2018, 18, 793. [Google Scholar] [CrossRef] [Green Version]
- Bustos, A.; Rubio, H.; Castejón, C.; García-Prada, J.C. Condition monitoring of critical mechanical elements through graphical representation of state configurations and chromogram of bands of frequency. Measurement 2019, 135, 71–82. [Google Scholar] [CrossRef]
- Torres, A.; Colominas, M.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [Green Version]
- Pincus, S.M. Approximate entropy as a measure of system-complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [Green Version]
- Yu, J. Health condition monitoring of machines based on hidden Markov model and contribution analysis. IEEE Trans. Instrum. Meas. 2012, 61, 2200–2211. [Google Scholar] [CrossRef]
- Qian, Y.; Yan, R.; Gao, R.X. A multi-time scale approach to remaining useful life prediction in rolling bearing. Mech. Syst. Signal Process. 2017, 83, 549–567. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Zhang, L.J.; Xu, J.X. Degradation feature selection for remaining useful life prediction of rolling element bearings. Qual. Reliab. Eng. Int. 2016, 32, 547–554. [Google Scholar] [CrossRef]
- Camci, F.; Medjaher, K. Features evaluation for effective bearing prognostics. Qual. Reliab. Eng. Int. 2013, 29, 477–486. [Google Scholar] [CrossRef] [Green Version]
- Orchard, M.E.; Vachtsevanos, G.J. A particle-filtering approach for on-line fault diagnosis and failure prognosis. Trans. Inst. Meas. Control 2009, 31, 221–246. [Google Scholar] [CrossRef]
- Rigatos, G.G. Particle filtering for state estimation in nonlinear industrial systems. IEEE Trans. Instrum. Meas. 2009, 58, 3885–3900. [Google Scholar] [CrossRef]
- Chen, C.; Vachtsevanos, G.; Orchard, M.E. Machine remaining useful life prediction: An integrated adaptive neuro-fuzzy and highorder particle filtering approach. Mech. Syst. Signal Process. 2012, 28, 597–607. [Google Scholar] [CrossRef]
- Zhao, W.; Tao, T.; Ding, Z.; Zio, E. A dynamic particle filter-support vector regression method for reliability prediction. Reliab. Eng. Syst. Saf. 2013, 119, 109–116. [Google Scholar]

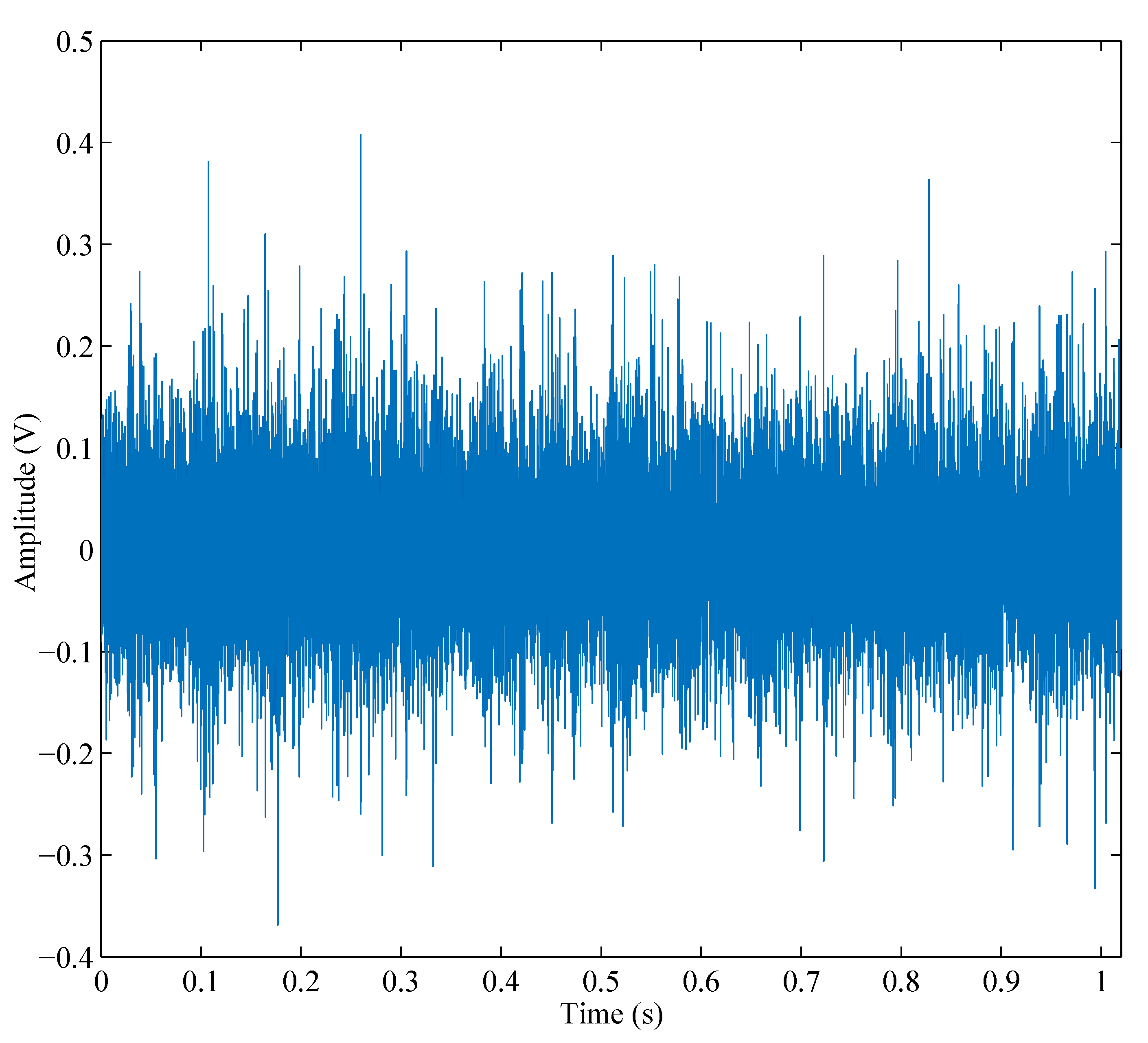

| IMFs | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| MIC | 0.2939 | 0.1643 | 0.1767 | 0.0987 | 0.0574 | 0.0502 | 0.0576 |
| IMFs | 8 | 9 | 10 | 11 | 12 | 13 | |
| MIC | 0.0610 | 0.0514 | 0.0535 | 0.0587 | 0.0688 | 0.0685 |
| Features | J | |||
|---|---|---|---|---|
| Kurtosis | 0.5589 | 0.0356 | 0.9573 | 0.4221 |
| RMS | 0.6596 | 0.0945 | 0.9837 | 0.4743 |
| EEMD-EMTR | 0.7266 | 0.0193 | 0.9748 | 0.4474 |
| ENTR | 0.7431 | 0.0051 | 0.8315 | 0.4006 |
| ApEn | 0.7509 | 0.0234 | 0.9666 | 0.4518 |
| CEEMDAN-ApEn | 0.8321 | 0.0641 | 0.9802 | 0.4925 |
| Metrics | AR-PF | AR-UKF |
|---|---|---|
| (unit: hour) | 0.2240 | 0.0093 |
| (unit: hour) | 0.2959 | 0.0394 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Chang, Y.; Gao, T.; Wang, J. Failure Prediction of the Rotating Machinery Based on CEEMDAN-ApEn Feature and AR-UKF Model. Appl. Sci. 2020, 10, 2056. https://doi.org/10.3390/app10062056
Yang J, Chang Y, Gao T, Wang J. Failure Prediction of the Rotating Machinery Based on CEEMDAN-ApEn Feature and AR-UKF Model. Applied Sciences. 2020; 10(6):2056. https://doi.org/10.3390/app10062056
Chicago/Turabian StyleYang, Jingli, Yongqi Chang, Tianyu Gao, and Jianfeng Wang. 2020. "Failure Prediction of the Rotating Machinery Based on CEEMDAN-ApEn Feature and AR-UKF Model" Applied Sciences 10, no. 6: 2056. https://doi.org/10.3390/app10062056
APA StyleYang, J., Chang, Y., Gao, T., & Wang, J. (2020). Failure Prediction of the Rotating Machinery Based on CEEMDAN-ApEn Feature and AR-UKF Model. Applied Sciences, 10(6), 2056. https://doi.org/10.3390/app10062056




