Smooth Fractional Order Sliding Mode Controller for Spherical Robots with Input Saturation
Abstract
1. Introduction
- (1)
- A fractional PIλDμ sliding control method based hierarchical sliding control and fractional calculus is proposed to improve the control performance;
- (2)
- A novel fractional PIλDμ sliding controller with an auxiliary system is proposed to deal with input saturation;
- (3)
- Smooth dynamic response is achieved by adding a filter, which can decrease the output of the controller in the initial stage and make full use of the fractional sliding surface.
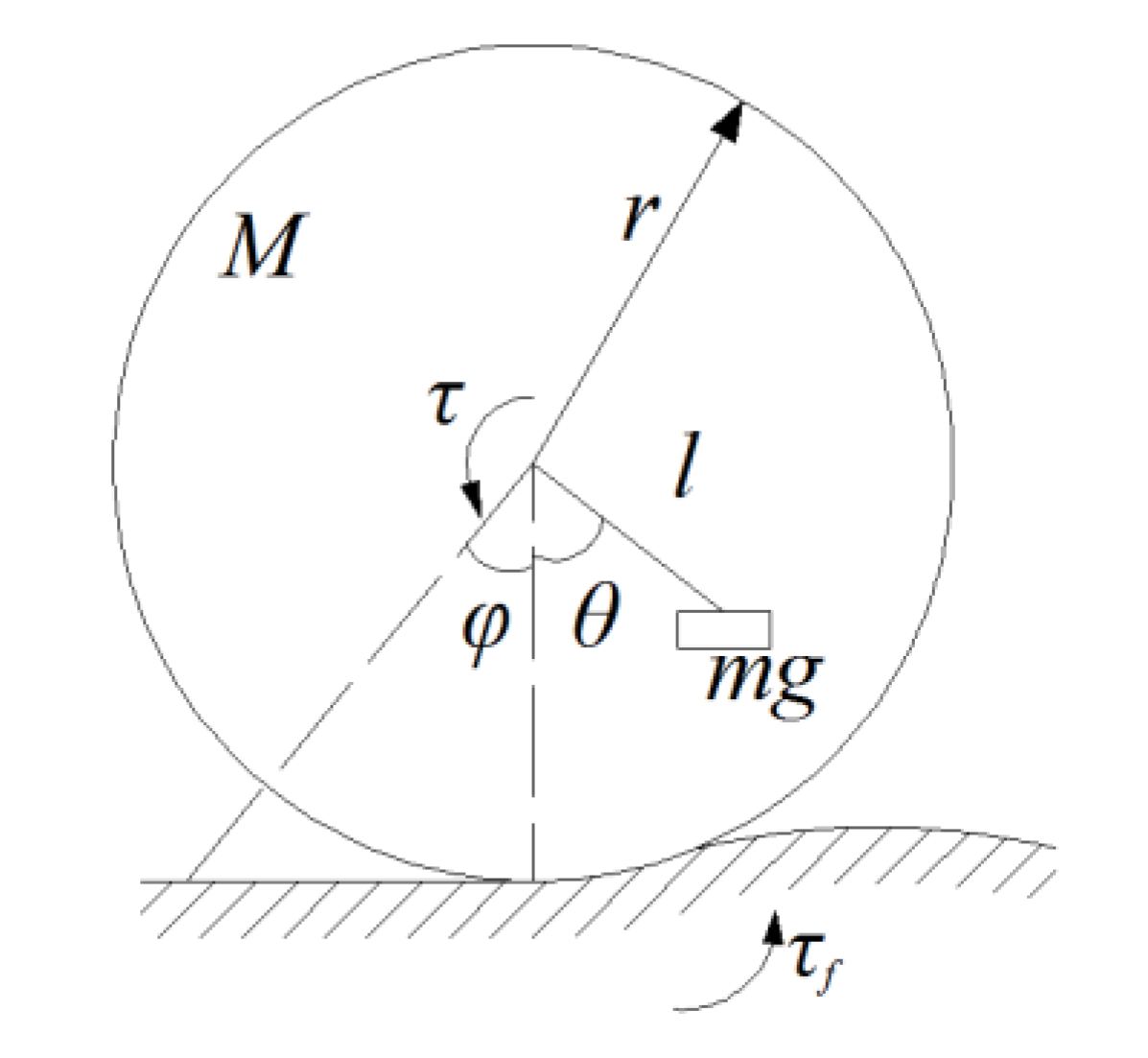
2. Motion Equation and Control System
3. Preliminaries
4. Fractional Order Hierarchical Sliding Mode Controller
4.1. Design of the Fractional Hierarchical Sliding Mode Controller
4.2. A Novel Fractional PIλDμ Sliding Mode Controller
4.3. Stability Analysis of Each Surface
5. Simulation Study
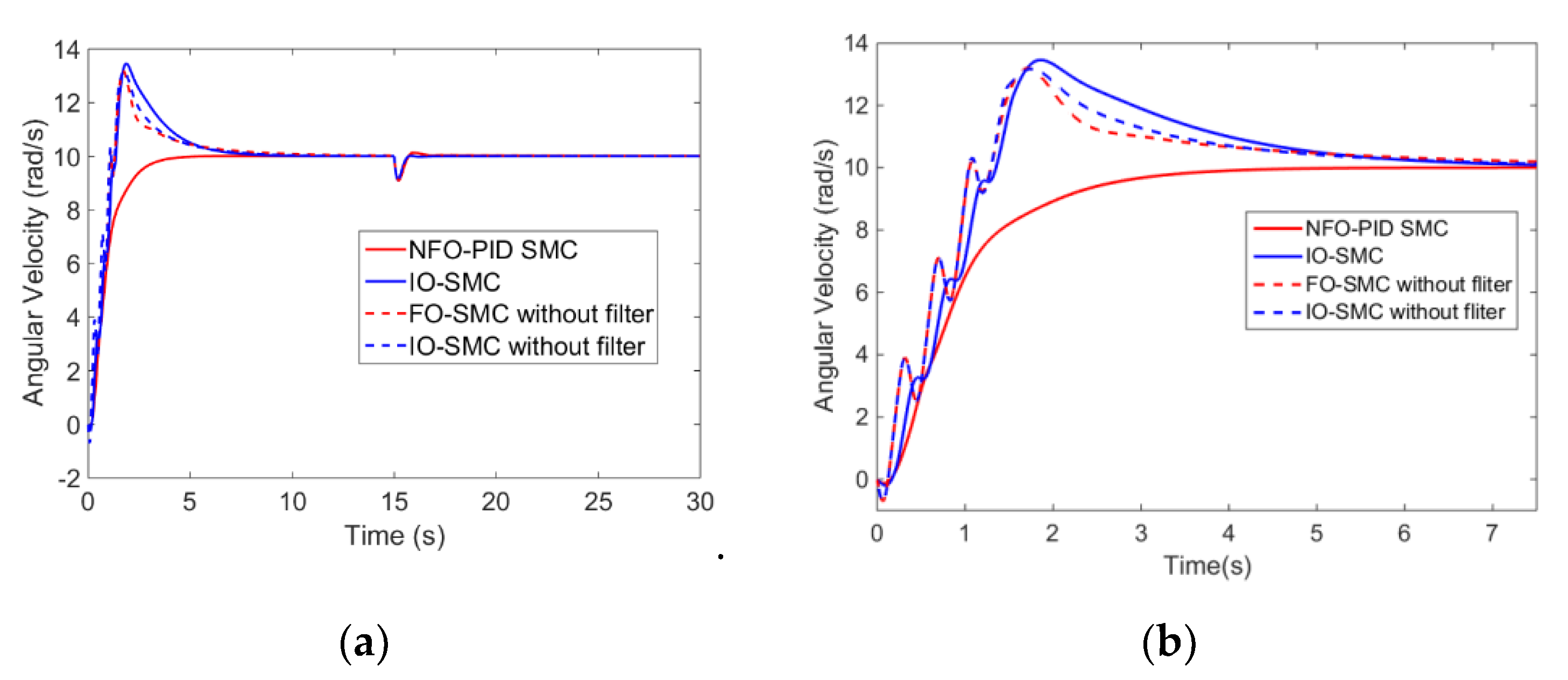
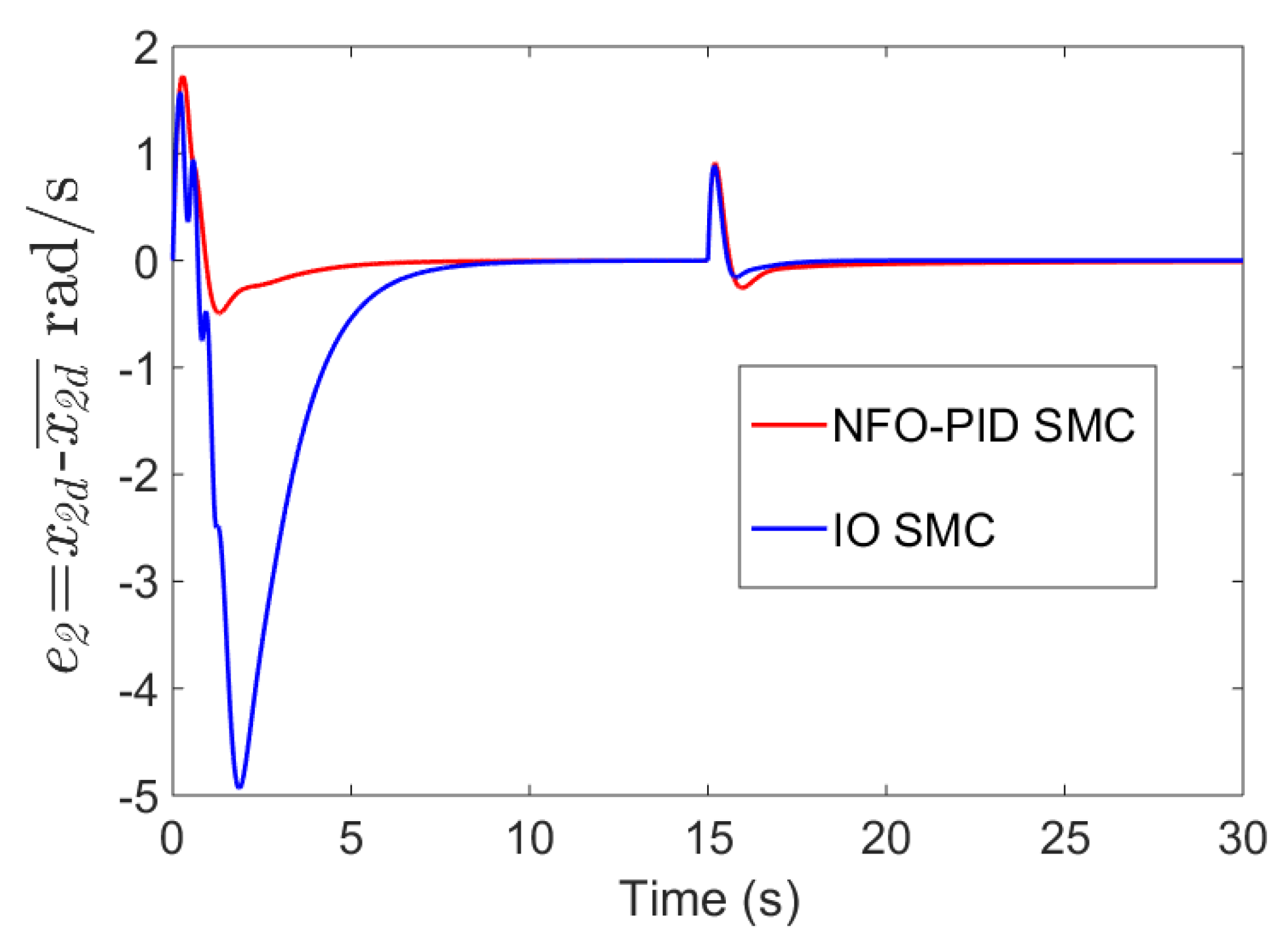
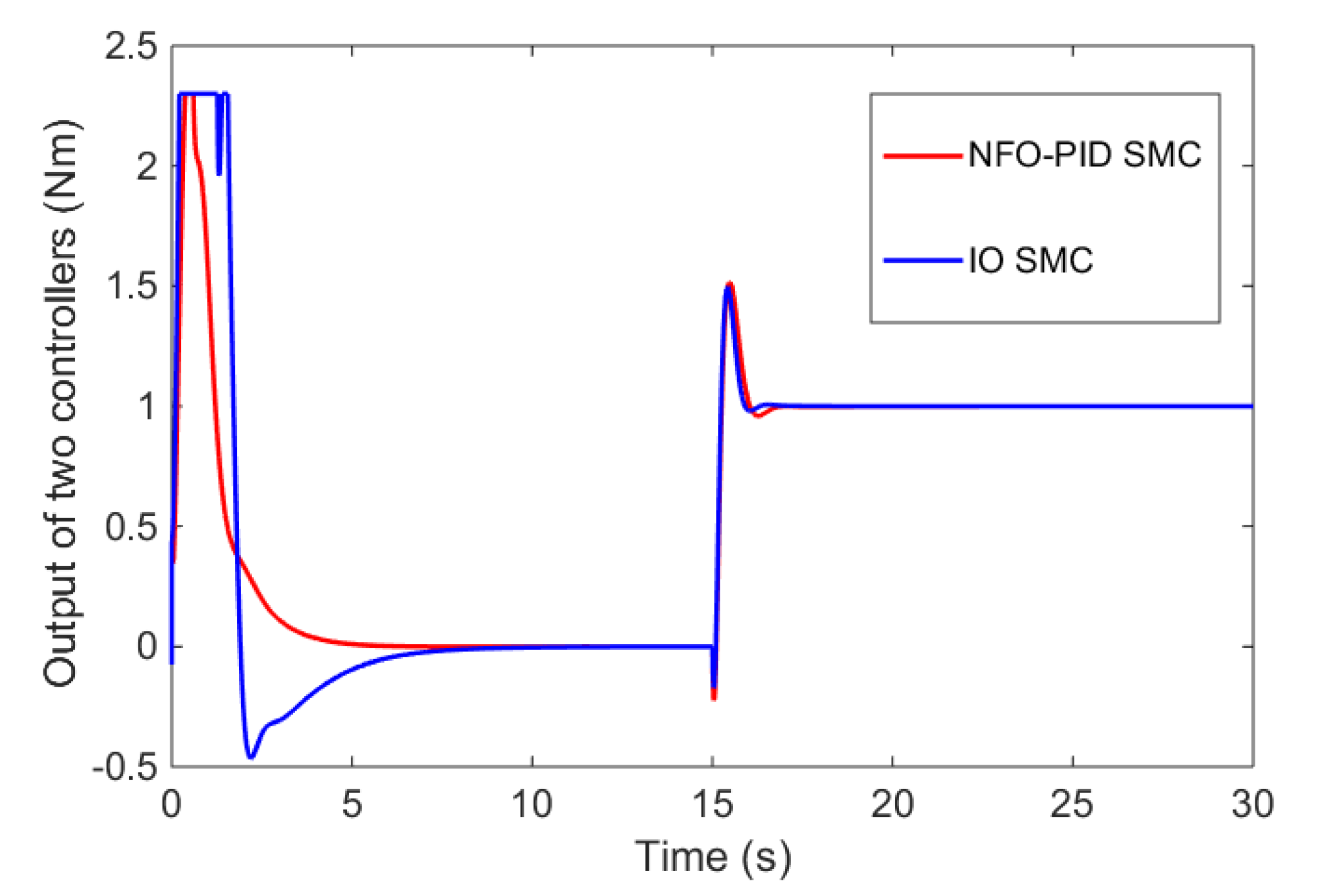
5.1. Tracking Performance Analysis
5.2. Robustness Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Halme, A.; Schonberg, T.; Wang, Y. Motion Control of a Spherical Mobile Robot. In Proceedings of the 4th IEEE International Workshop on Advanced Motion Control, Mie, Japan, 18–21 March 1996; pp. 259–264. [Google Scholar]
- Mojabi, P. Introducing August: A Novel Strategy for an Omnidirectional Spherical Rolling Robot. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; pp. 3527–3533. [Google Scholar]
- Joshi, V.A.; Banavar, R.N. Motion Analysis of a Spherical Mobile Robot. Robotica 2009, 27, 343–353. [Google Scholar] [CrossRef]
- Sugiyama, Y.; Shiotsu, A.; Yamanaka, M.; Hirai, S. Circular/spherical Robots for Crawling and Jumping. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3595–3600. [Google Scholar]
- Zhan, Q.; Cai, Y.; Yan, C. Design, Analysis and Experiments of an Omni-Directional Spherical Robot. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4921–4926. [Google Scholar]
- Karavaev, Y.L.; Kilin, A.A. Nonholonomic Dynamics and Control of a Spherical Robot with an Internal Omniwheel Platform: Theory and Experiments. Proc. Steklov Inst. Math. 2016, 295, 158–167. [Google Scholar] [CrossRef]
- Seeman, M.; Broxvall, M.; Saffiotti, A.; Wide, P. An Autonomous Spherical Robot for Security Tasks. In Proceedings of the 2006 IEEE International Conference on Computational Intelligence for Homeland Security and Personal Safety, Alexandria, VA, USA, 16–17 October 2006; pp. 51–55. [Google Scholar]
- Mukherjee, R.; Minor, M.A.; Pukrushpan, J.T. Simple Motion Planning Strategies for Spherobot: A Spherical Mobile Robot. In Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 7–10 December 1999; pp. 2132–2137. [Google Scholar]
- Wang, H.; Liu, P.X.; Xie, X.; Liu, X.; Hayat, T.; Alsaadi, F.E. Adaptive Fuzzy Asymptotical Tracking Control of Nonlinear Systems with Unmodeled Dynamics and Quantized Actuator. Inf. Sci. 2018. [Google Scholar] [CrossRef]
- Roozegar, M.; Mahjoob, M.J.; Ayati, M. Adaptive Estimation of Nonlinear Parameters of a Nonholonomic Spherical Robot Using a Modified Fuzzy-based Speed Gradient Algorithm. Regul. Chaotic Dyn. 2017, 22, 226–238. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, H.; Xia, W.; Wang, X. Adaptive Fuzzy Hierarchical Sliding Mode Control for a Class of MIMO Nonlinear Time-delay Systems with Input Saturation. IEEE Trans. Fuzzy Syst. 2017, 25, 1062–1077. [Google Scholar] [CrossRef]
- Liu, D.L.; Sun, H.X.; Jia, Q.X. A Family of Spherical Mobile Robot: Driving Ahead Motion Control by Feedback Linearization. In Proceedings of the 2008 2nd International Symposium on Systems and Control in Aerospace and Astronautics, Shenzhen, China, 10–12 December 2008; pp. 1–6. [Google Scholar]
- Borisov, A.V.; Kilin, A.A.; Karavaev, Y.L.; Klekovkin, A.V. Stabilization of the Motion of a Spherical Robot Using Feedbacks. Appl. Math. Model. 2019, 69, 583–592. [Google Scholar]
- Xu, R.; Özgüner, Ü. Sliding Mode Control of a Class of Underactuated Systems. Automatica 2008, 44, 233–241. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, N.; Chen, H.; Zhang, J.; Fang, Y. Nonlinear Time-optimal Trajectory Planning for Varying-rope-length Overhead Cranes. Assem. Autom. 2018, 38, 587–594. [Google Scholar] [CrossRef]
- Bai, Y.; Svinin, M.; Yamamoto, M. Dynamics-Based Motion Planning for a Pendulum-Actuated Spherical Rolling Robot. Regul. Chaotic Dyn. 2018, 23, 372–388. [Google Scholar] [CrossRef]
- Ivanova, T.B.; Kilin, A.A.; Pivovarova, E.N. Controlled Motion of a Spherical Robot with Feedback. II. J. Dyn. Control. Syst. 2019, 25, 1–16. [Google Scholar] [CrossRef]
- Yang, C.; Li, Z.; Cui, R.; Xu, B. Neural Network-Based Motion Control of an Underactuated Wheeled Inverted Pendulum Model. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 2004–2016. [Google Scholar] [CrossRef] [PubMed]
- Yao, C.; Qiang, Z.; Xi, X. Neural Network Control for the Linear Motion of a Spherical Mobile Robot. Int. J. Adv. Robot. Syst. 2011, 8, 79–87. [Google Scholar]
- Utkin, V. Variable Structure Systems with Sliding Modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Lin, C.M.; Mon, Y.J. Decoupling Control by Hierarchical Fuzzy Sliding-mode Controller. IEEE Trans. Control. Syst. Technol. 2005, 13, 593–598. [Google Scholar] [CrossRef]
- Wang, W.; Yi, J.; Zhao, D.; Liu, D. Design of a Stable Sliding-mode Controller for a Class of Second-order Underactuated Systems. IEE Proc. Control Theory Appl. 2004, 151, 683–690. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.D.; Yi, J.Q. Structure Design of Two Types of Sliding-mode Controllers for a Class of Under-actuated Mechanical Systems. IET Control Theory Appl. 2007, 1, 163–172. [Google Scholar] [CrossRef]
- Yue, M.; Liu, B. Adaptive Control of an Underactuated Spherical Robot with a Dynamic Stable Equilibrium Point Using Hierarchical Sliding Mode Approach. Int. J. Adapt. Control Signal 2014, 28, 523–535. [Google Scholar] [CrossRef]
- Yue, M.; Liu, B.; An, C.; Sun, X. Extended State Observer-based Adaptive Hierarchical Sliding Mode Control for Longitudinal Movement of a Spherical robot. Nonlinear Dyn. 2014, 78, 1233–1244. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order Systems and PIλDμ Controllers. IEEE Trans. Autom. Contol 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Yin, C.; Chen, Y.Q.; Zhong, S.M. Fractional-order Sliding Mode Based Extremum Seeking Control of a Class of Nonlinear Systems. Automatica 2014, 50, 3173–3181. [Google Scholar] [CrossRef]
- Delavari, H.; Ghaderi, R.; Ranjbar, A.; Momani, S. Fuzzy Fractional Order Sliding Mode Controller for Nonlinear Systems. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 963–978. [Google Scholar] [CrossRef]
- Ebrahimkhani, S. Robust Fractional Order Sliding Mode Control of Doubly-fed Induction Generator (DFIG)-based Wind Turbines. ISA TRANS 2016, 63, 343–354. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Pi, Y.; Luo, Y. Fractional Order Sliding-mode Control Based on Parameters Auto-tuning for Velocity Control of Permanent Magnet Synchronous Motor. ISA TRANS 2012, 51, 649–656. [Google Scholar] [CrossRef]
- Rahmani, M.; Ghanbari, A.; Ettefagh, M.M. Hybrid Neural Network Fraction Integral Terminal Sliding Mode Control of an Inchworm Robot Manipulator. Mech. Syst. Signal Process. 2016, 80, 117–136. [Google Scholar] [CrossRef]
- Arunshankar, J. Control of Nonlinear Two-tank Hybrid System Using Sliding Mode Controller with Fractional-order PI-D Sliding Surface. Comput. Electr. Eng. 2018, 71, 953–965. [Google Scholar]
- Noureddine, B.; Djamel, B.; Boudjema, F. Tuning Fuzzy Fractional Order PID Sliding-mode Controller Using PSO Algorithm for Nonlinear Systems. In Proceedings of the 3rd International Conference on Systems and Control, Algiers, Algeria, 29–31 October 2013; pp. 797–803. [Google Scholar]
- Bouarroudj, N. A Hybrid Fuzzy Fractional Order PID Sliding-mode Controller Design Using PSO Algorithm for Interconnected Nonlinear Systems. Control Eng. Appl. Inform. 2015, 17, 41–51. [Google Scholar]
- Zhong, G.; Deng, H.; Li, J. Chattering-Free Variable Structure Controller Design via Fractional Calculus Approach and Its Application. Nonlinear Dyn. 2015, 81, 679–694. [Google Scholar] [CrossRef]
- Aghababa, M.P. Design of Hierarchical Terminal Sliding Mode Control Scheme for Fractional-order Systems. IET Sci. Meas. Technol. 2015, 9, 122–133. [Google Scholar] [CrossRef]
- Narayan, S.; Kaur, S. Finite Time Fractional-Order Sliding Mode-Based Tracking for a Class of Fractional-Order Nonholonomic Chained System. J. Comput. Nonlinear Dyn. 2018, 13, 051006. [Google Scholar]
- Mujumdar, A.; Tamhane, B.; Kurode, S. Fractional Order Modeling and Control of a Flexible Manipulator Using Sliding Modes. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 2011–2016. [Google Scholar]
- Bouarroudj, N.; Boukhetala, D.; Boudjema, F. Sliding-Mode Controller Based on Fractional Order Calculus for a Class of Nonlinear Systems. Int. J. Electr. Comput. Eng. 2016, 6, 2239–2250. [Google Scholar]
- Chen, M.; Ge, S.S.; Ren, B. Adaptive Tracking Control of Uncertain MIMO Nonlinear Systems with Input Constraints. Automatica 2011, 47, 452–465. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Chen, C.L.P. Adaptive Neural Control of Uncertain MIMO Nonlinear Systems with State and Input Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 1318–1330. [Google Scholar] [CrossRef]
- Lu, P.; Gan, C.; Liu, X. Finite-Time Distributed Cooperative Attitude Control for Multiple Spacecraft with Actuator Saturation. IET Control Theory Appl. 2014, 8, 2186–2198. [Google Scholar] [CrossRef]
- Polycarpou, M.; Farrell, J.; Sharma, M. On-Line Approximation Control of Uncertain Nonlinear Systems: Issues with Control Input Saturation. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 543–548. [Google Scholar]
- Ming, Y.; Zongquan, D.; Xinyi, Y.; Weizhen, Y. Introducing Hit Spherical Robot: Dynamic Modeling and Analysis Based on Decoupled Subsystem. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 181–186. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; pp. 62–73. [Google Scholar]
- Qian, D.; Li, C.; Agarwal, R.P.; Wong, P.J. Stability Analysis of Fractional Differential System with Riemann-Liouville Derivative. Math. Comput. Model. 2010, 52, 862–874. [Google Scholar] [CrossRef]
- Kilbas, A.A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science Limited: Amsterdam, The Netherlands, 2006; pp. 72–73. [Google Scholar]
- Deng, W.; Li, C.; Lu, J. Stability Analysis of Linear Fractional Differential System with Multiple Time Delays. Nonlinear Dyn. 2007, 48, 409–416. [Google Scholar] [CrossRef]
- Kun, Y.; Mou, C.; Qingxian, W.; Ronggang, Z. Robust Adaptive Compensation Control for Unmanned Autonomous Helicopter with Input Saturation and Actuator Faults. Chin. J. Aeronaut. 2019, 32, 2299–2310. [Google Scholar]
- Tao, G. A Simple Alternative to the Barbalat lemma. IEEE Trans. Autom. Control 1997, 42, 698. [Google Scholar] [CrossRef]
- Aghababa, M.P. Control of Non-linear Non-integer-order Systems Using Variable Structure Control Theory. Trans. Inst. Meas. Control 2014, 36, 425–432. [Google Scholar] [CrossRef]
- Bartolini, G.; Ferrara, A.; Usai, E. Chattering Avoidance by Second-order Sliding Mode Control. IEEE Trans. Autom. Control 1998, 43, 241–246. [Google Scholar] [CrossRef]
- Lee, H.; Utkin, V.I. Chattering Suppression Methods in Sliding Mode Control Systems. Annu. Rev. Control 2007, 31, 179–188. [Google Scholar] [CrossRef]
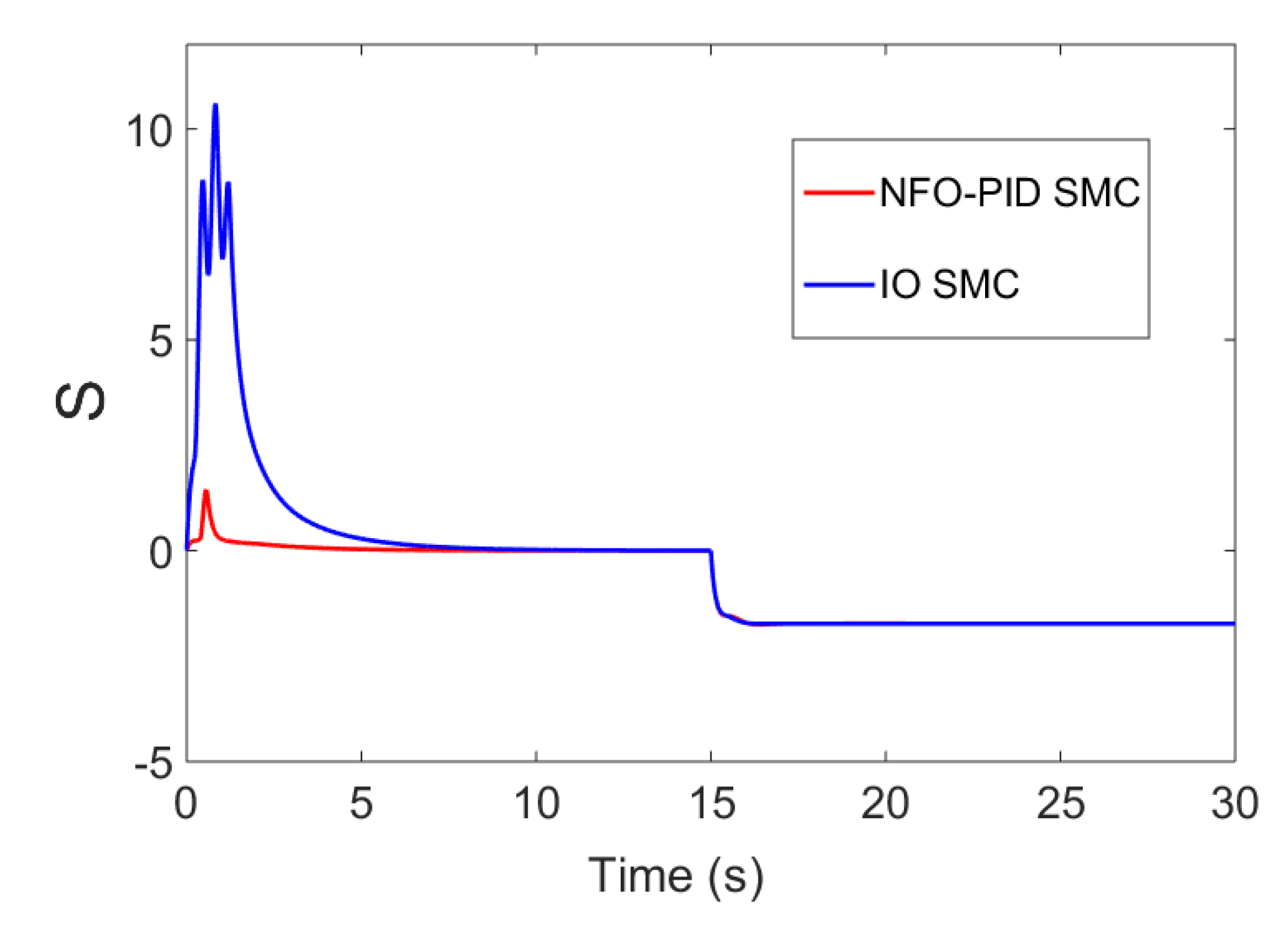

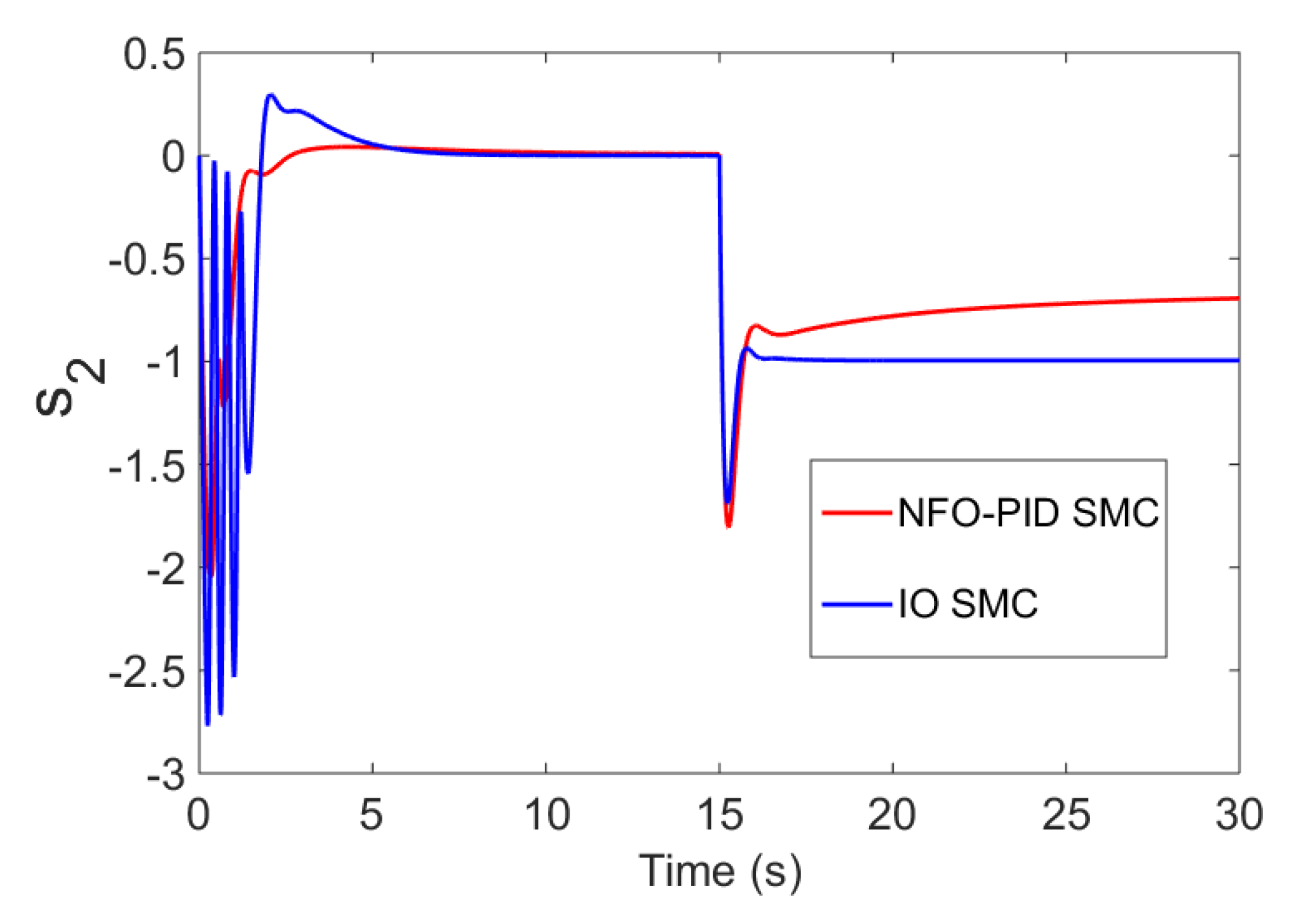
| Parameter | M/kg | m/kg | r/m | l/m | ||
|---|---|---|---|---|---|---|
| Value | 2.5 | 8 | 0.15 | 0.09 | 2.3 | −2.3 |
| Parameter | k1 | k2 | k3 | η | ζ | α | β | λ | μ | ε |
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 1 | 0.3 | 12 | 2 | 2 | 5 | 5 | 0.1 | 0.1 | 1 |
| Controller | Overshoot (%) | Adjustment Time (s) |
|---|---|---|
| NFO-PID SMC | 0 | 3.4 |
| IO-PI SMC | 35 | 6.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Xu, Y.-g.; Wu, B. Smooth Fractional Order Sliding Mode Controller for Spherical Robots with Input Saturation. Appl. Sci. 2020, 10, 2117. https://doi.org/10.3390/app10062117
Zhou T, Xu Y-g, Wu B. Smooth Fractional Order Sliding Mode Controller for Spherical Robots with Input Saturation. Applied Sciences. 2020; 10(6):2117. https://doi.org/10.3390/app10062117
Chicago/Turabian StyleZhou, Ting, Yu-gong Xu, and Bin Wu. 2020. "Smooth Fractional Order Sliding Mode Controller for Spherical Robots with Input Saturation" Applied Sciences 10, no. 6: 2117. https://doi.org/10.3390/app10062117
APA StyleZhou, T., Xu, Y.-g., & Wu, B. (2020). Smooth Fractional Order Sliding Mode Controller for Spherical Robots with Input Saturation. Applied Sciences, 10(6), 2117. https://doi.org/10.3390/app10062117




