A Method of On-Site Describing the Positional Relation between Two Horizontal Parallel Surfaces and Two Vertical Parallel Surfaces
Abstract
1. Introduction
2. Principle of the Measurement Mechanism
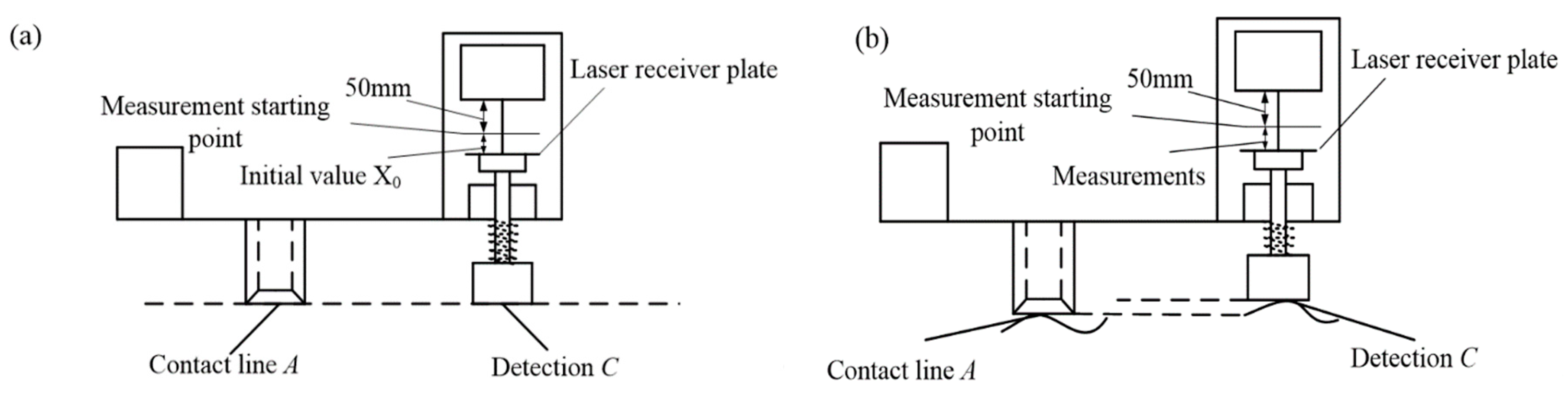
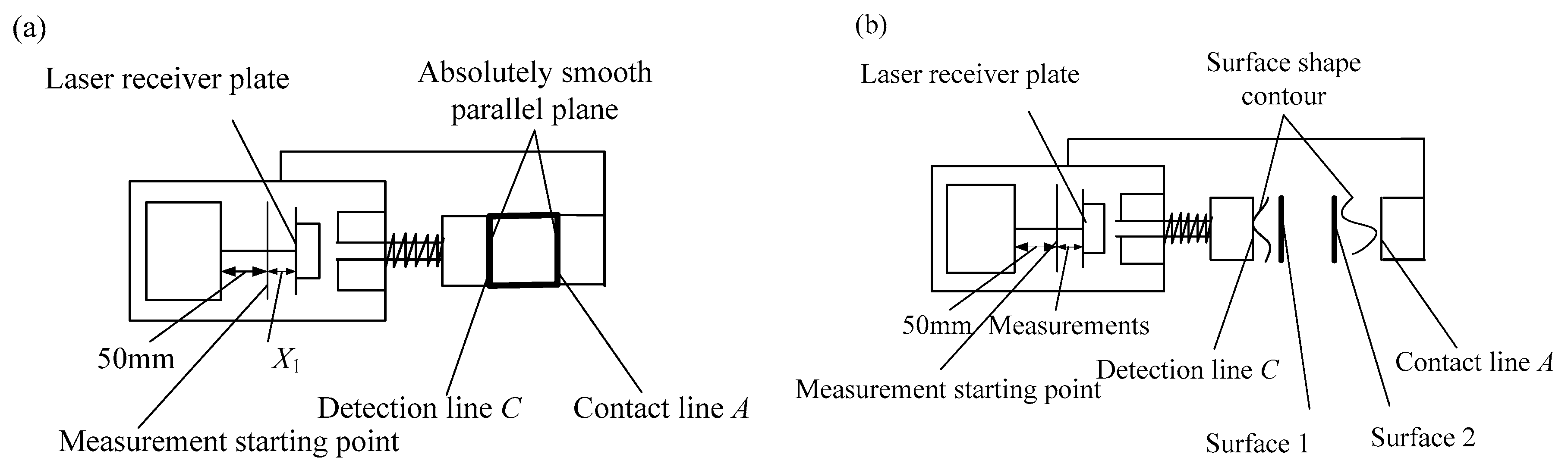
2.1. Measuring Mechanism for Measuring Two Horizontal Parallel Surfaces
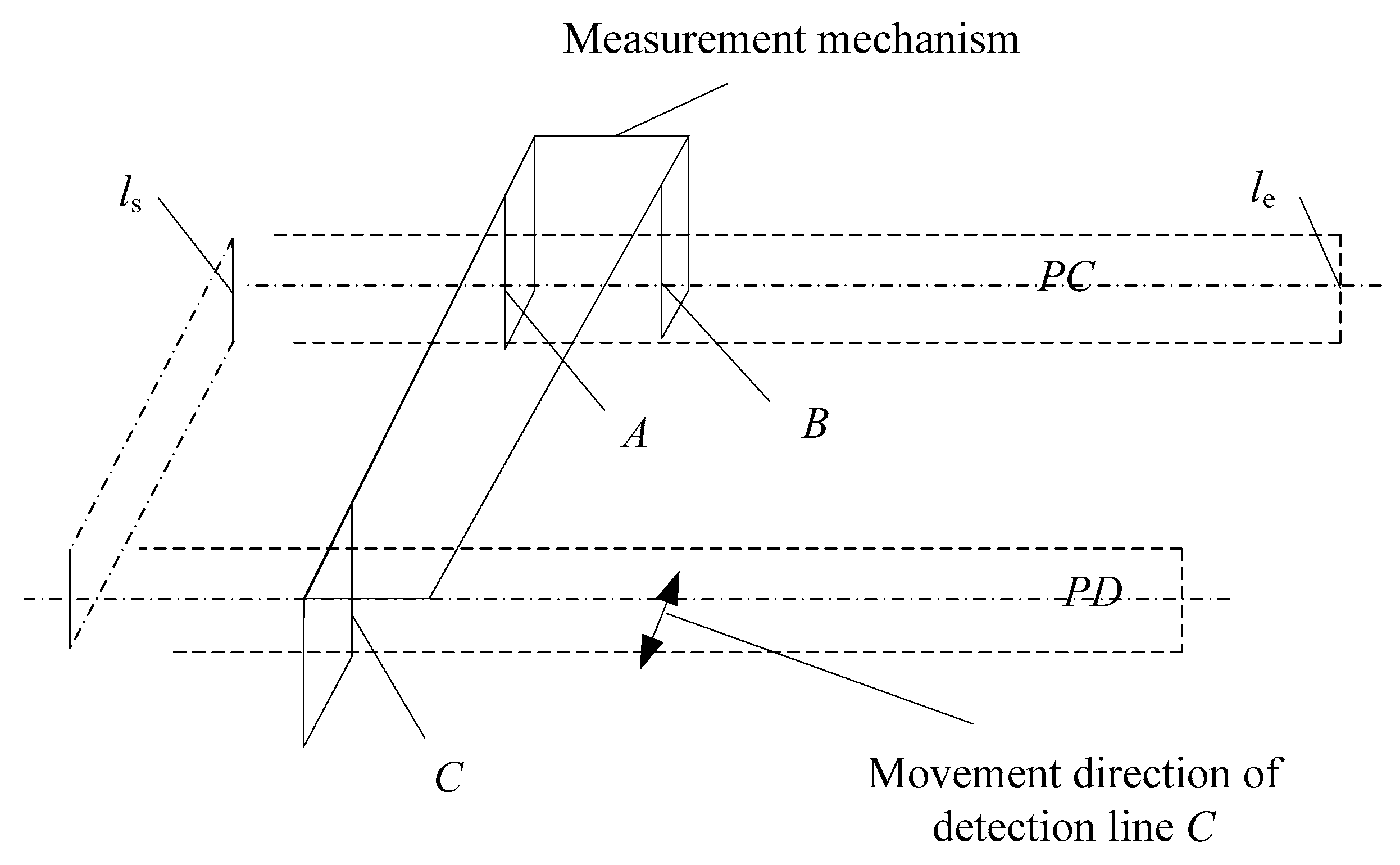
2.2. Measuring Mechanism for Measuring Two Vertical Parallel Surfaces
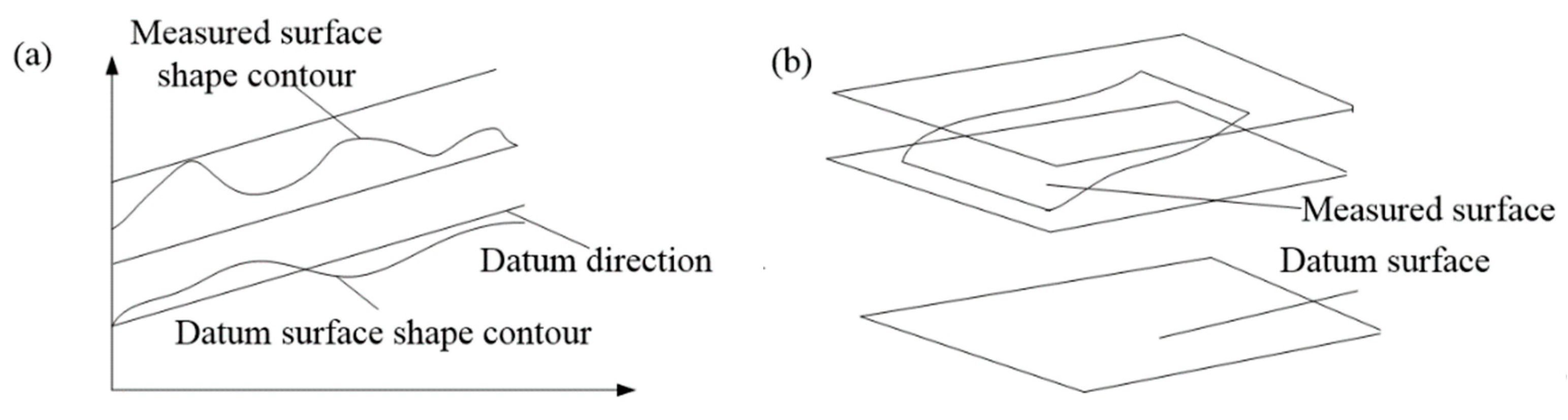
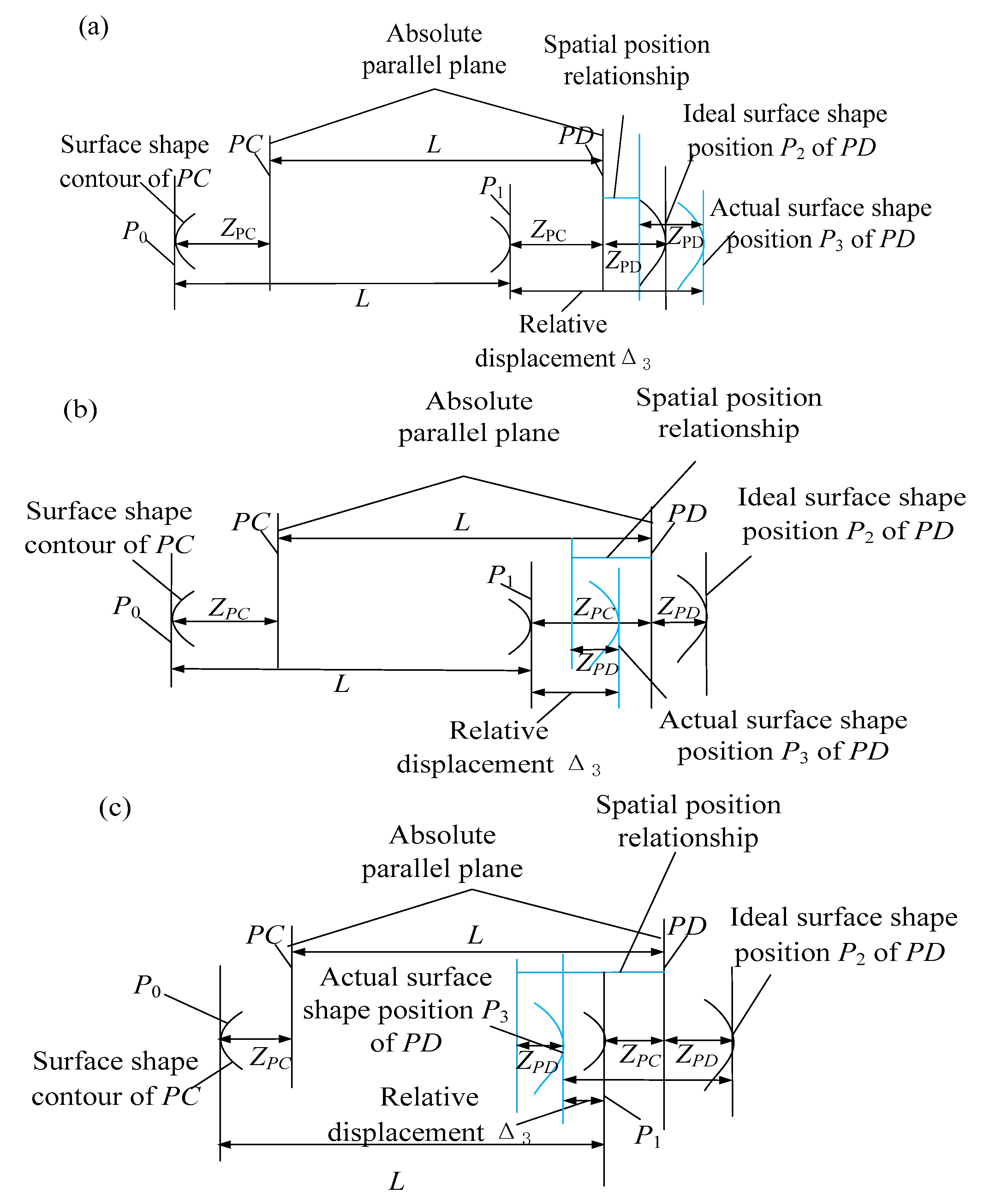
3. The Method for Describing the Positional Relation of Two Parallel Surfaces
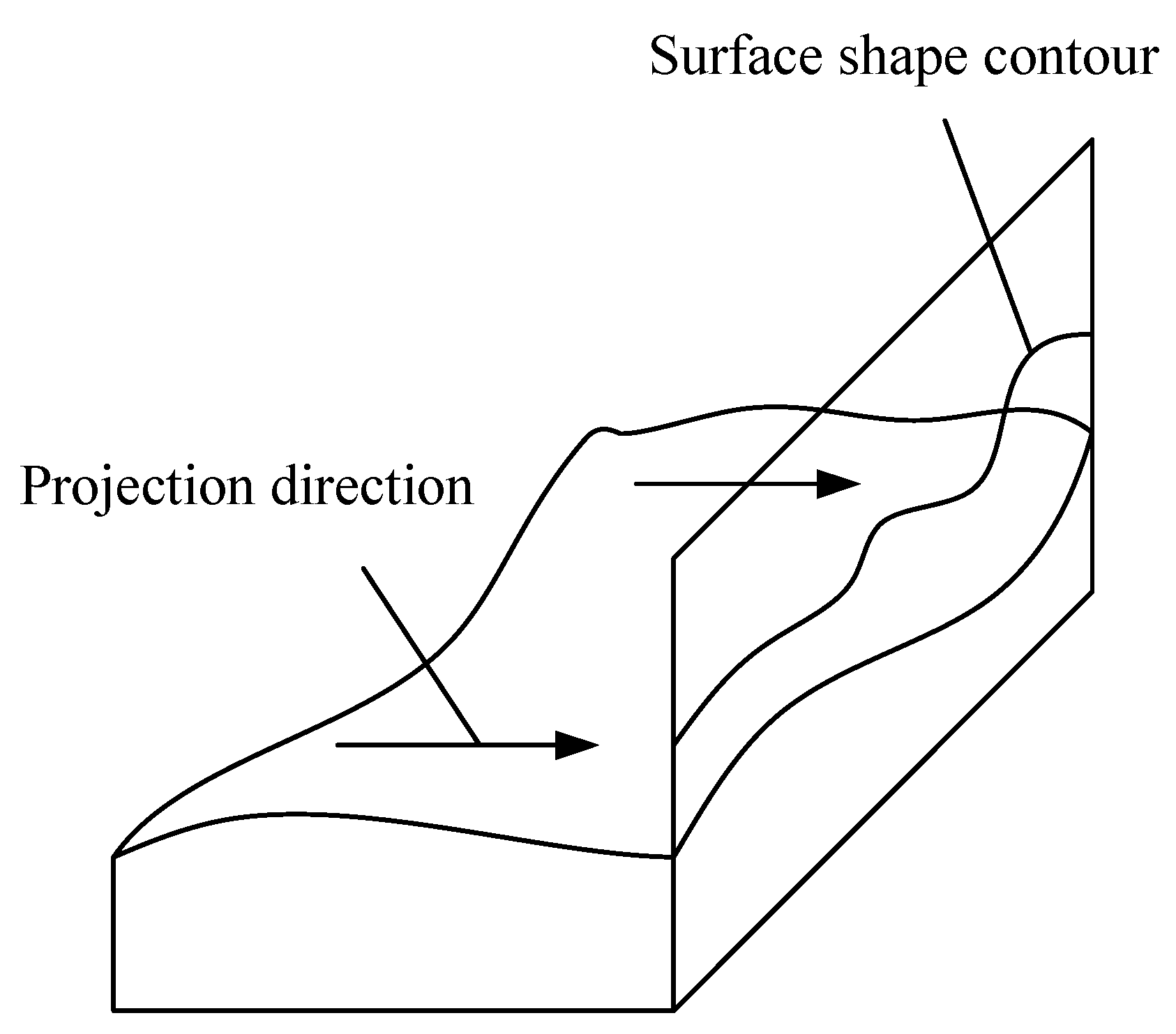
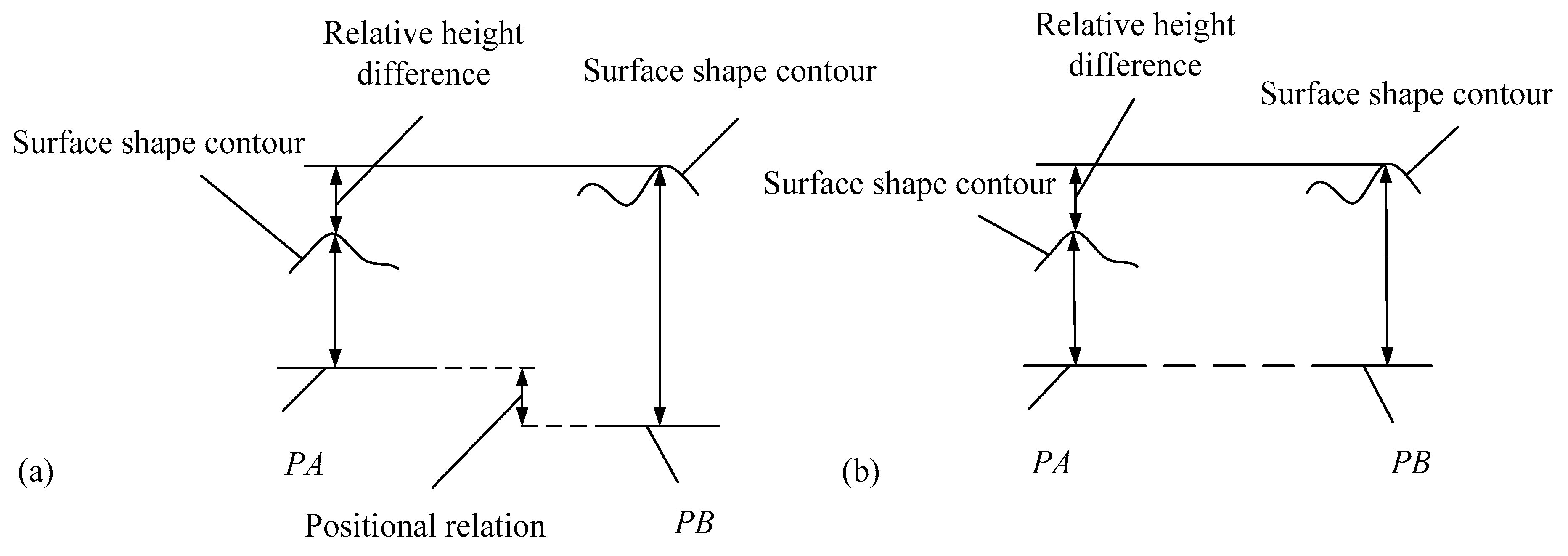
3.1. The Description Method of Positional Relation between Two Horizontal Parallel Surfaces
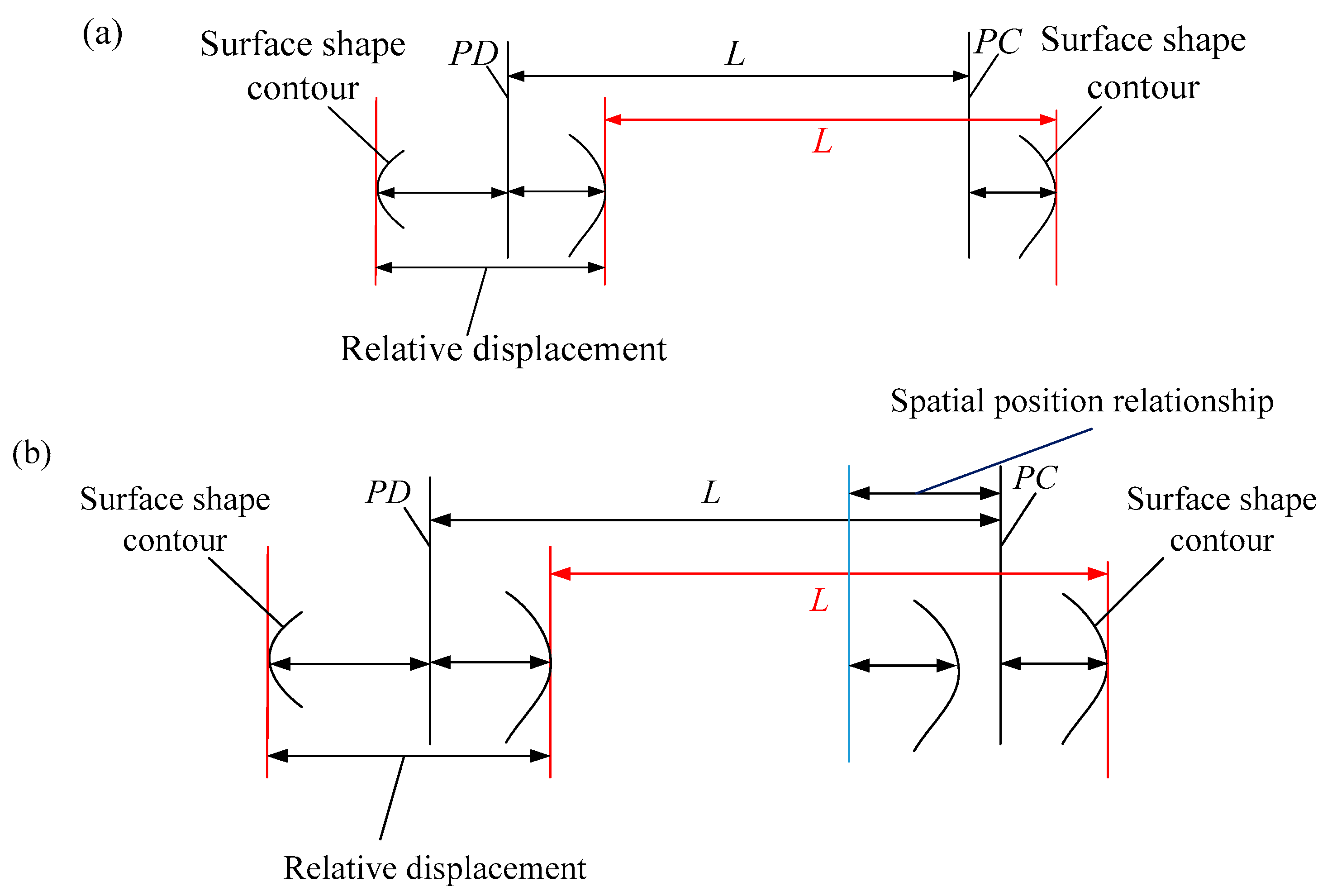
3.2. The Description Method of Positional Relation between Two Vertical Parallel Surfaces
4. Mathematical Model of the Algorithm
4.1. Mathematical Model for Describing Positional Relation between Two Horizontal Parallel Surfaces
4.1.1. Extraction Algorithm for Combined Projection Waveform
4.1.2. Time-Space Conversion Algorithm
4.1.3. Separation Algorithm for Combined Projection Curve
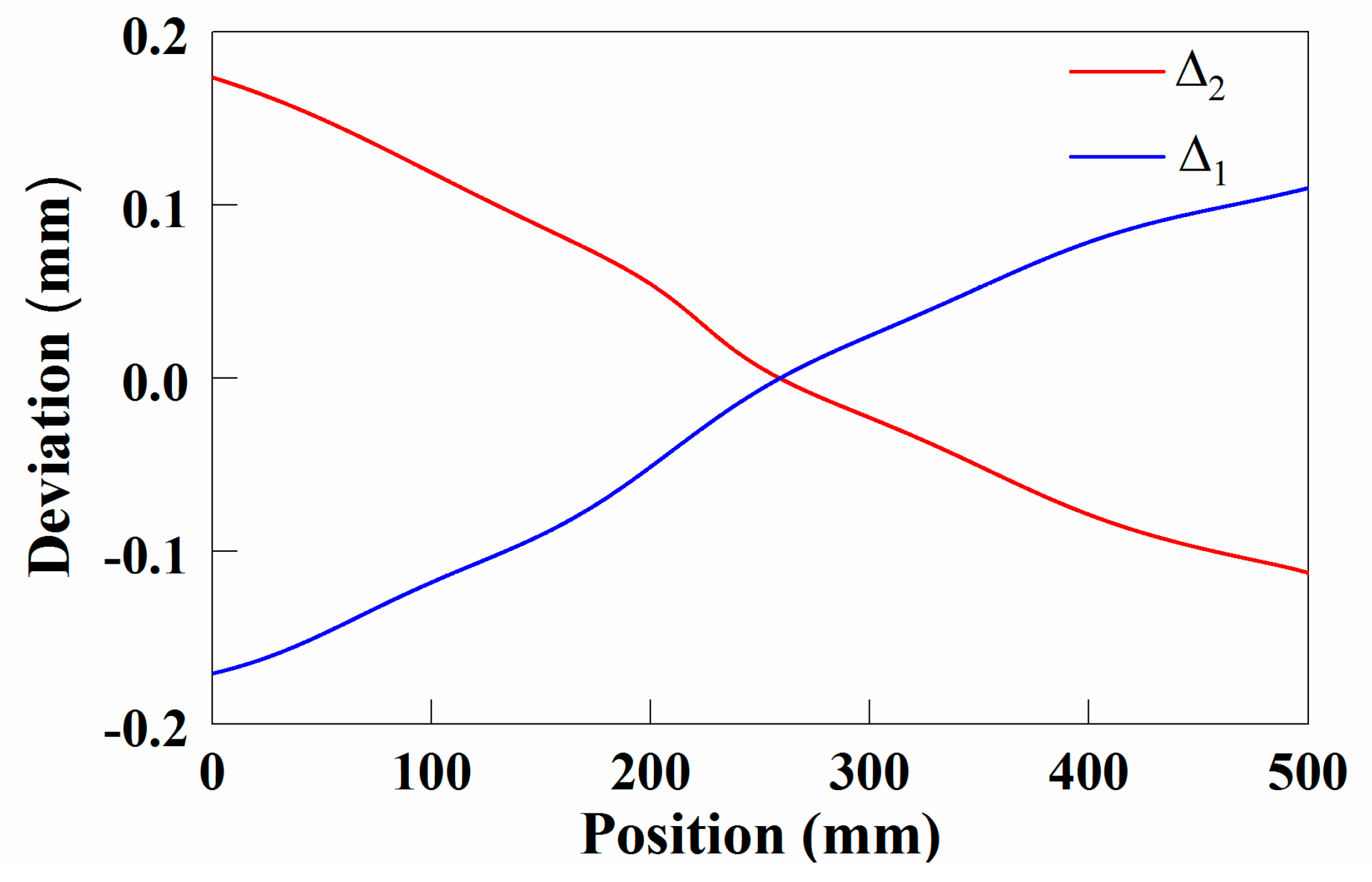
4.1.4. Description Algorithm for Positional Relation
4.2. Mathematical Model for Describing Positional Relation between Two Vertical Parallel Surfaces
4.2.1. Extraction Algorithm for Combined Projection Waveform
4.2.2. Separation Algorithm for Combined Projection Curve
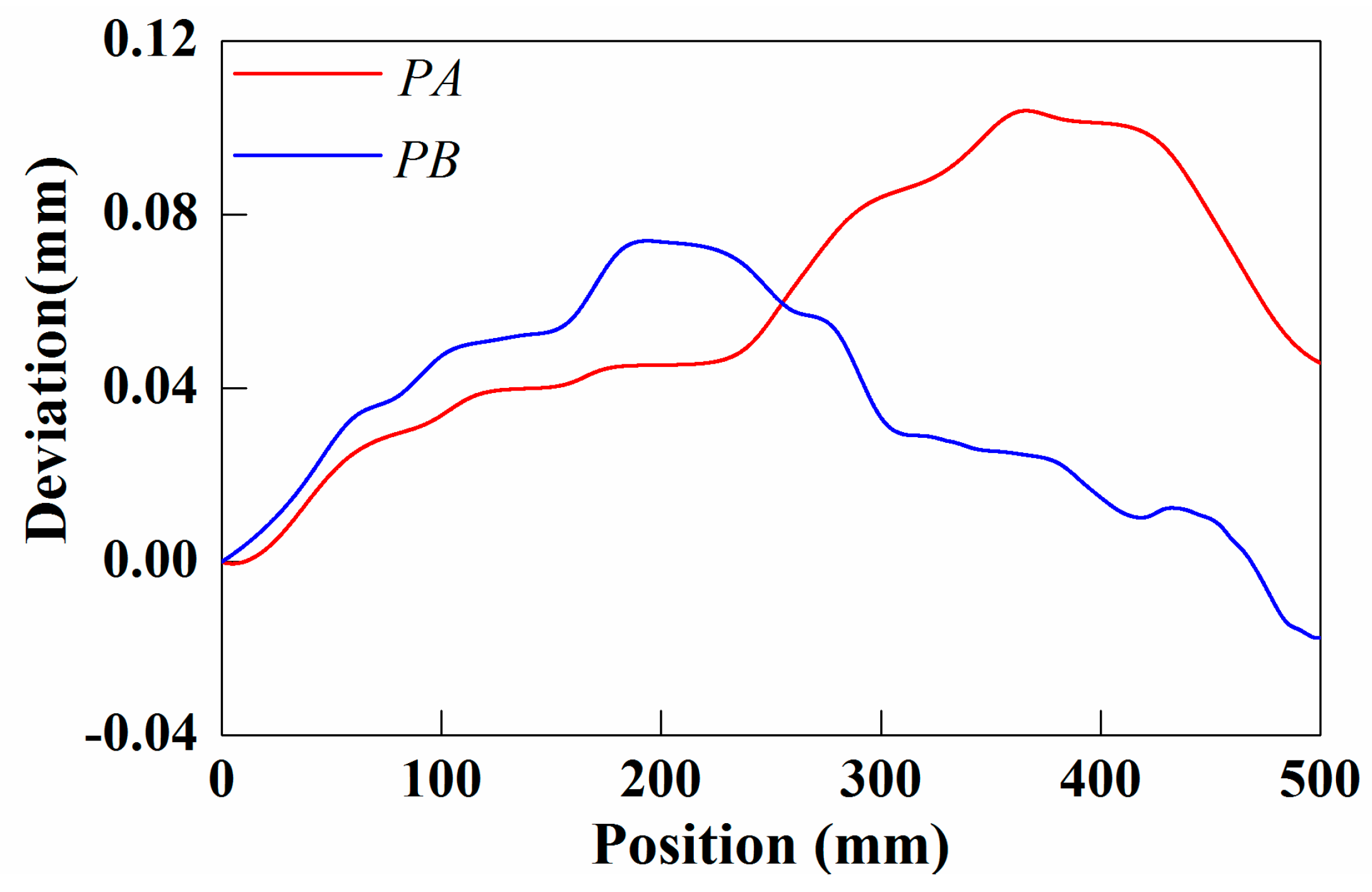
4.2.3. Description Algorithm for Positional Relation
5. Experimental Validation
5.1. Measuremen Texperiment of Two Horizontal Parallel Surfaces
5.1.1. Experimental Step
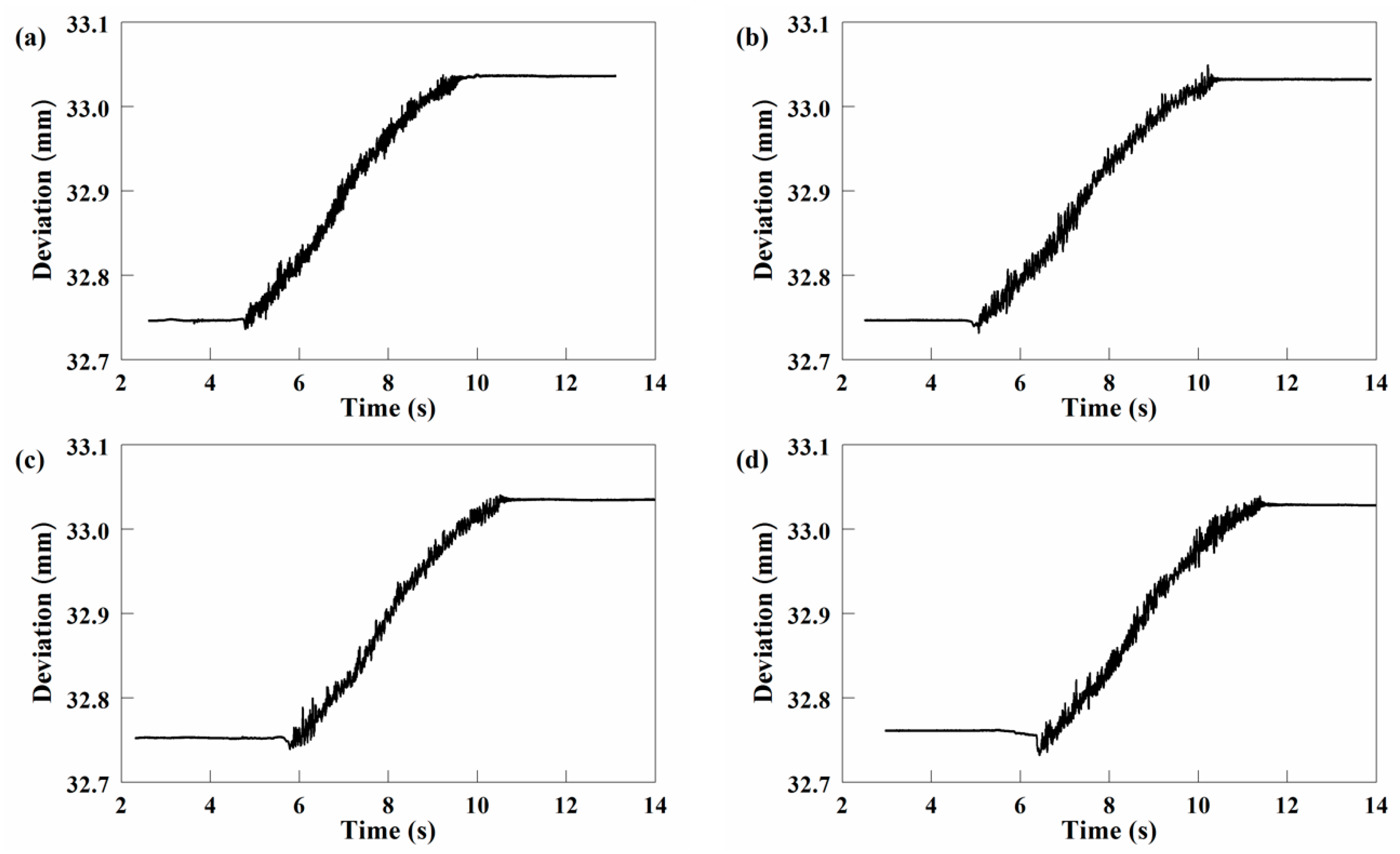
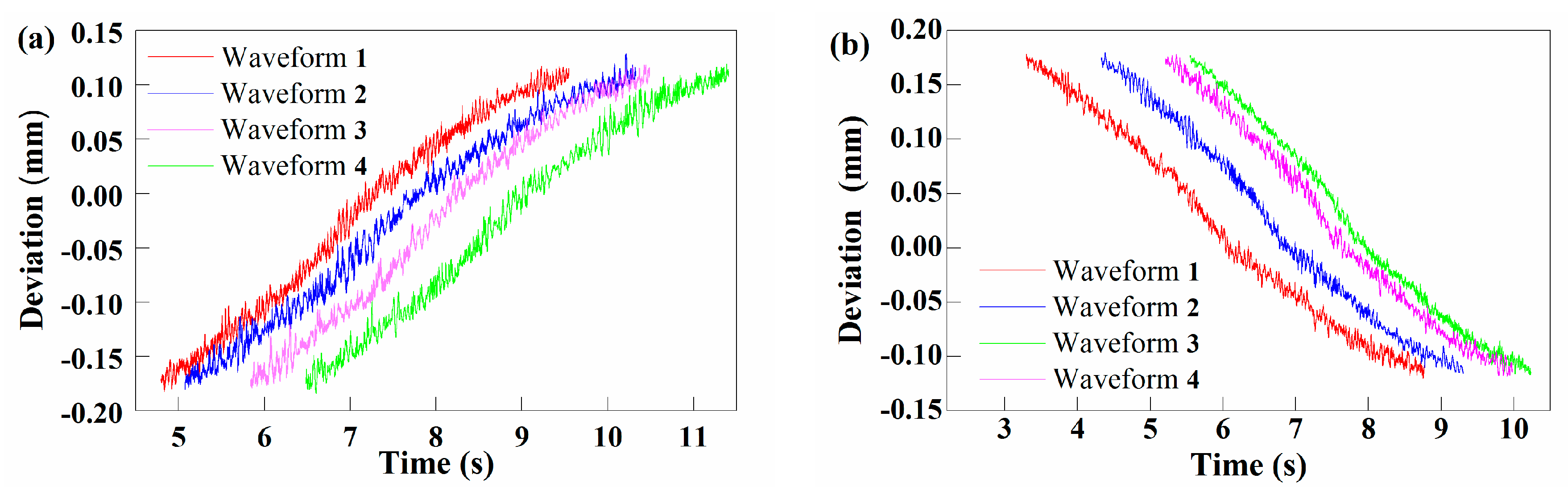
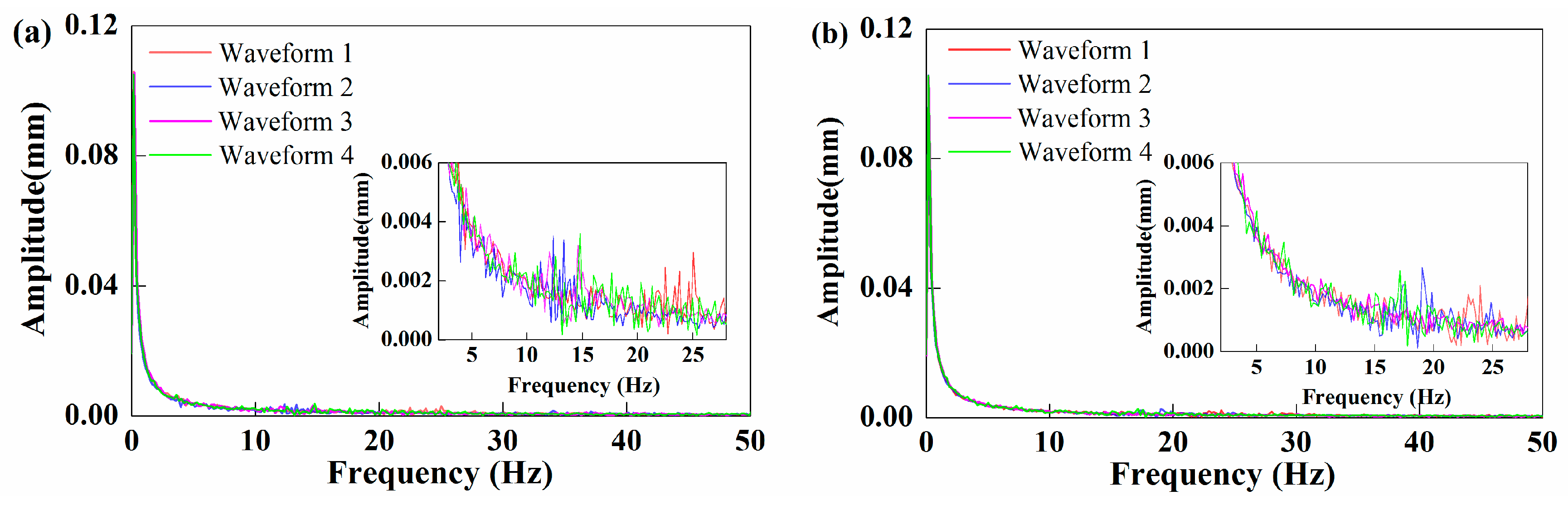
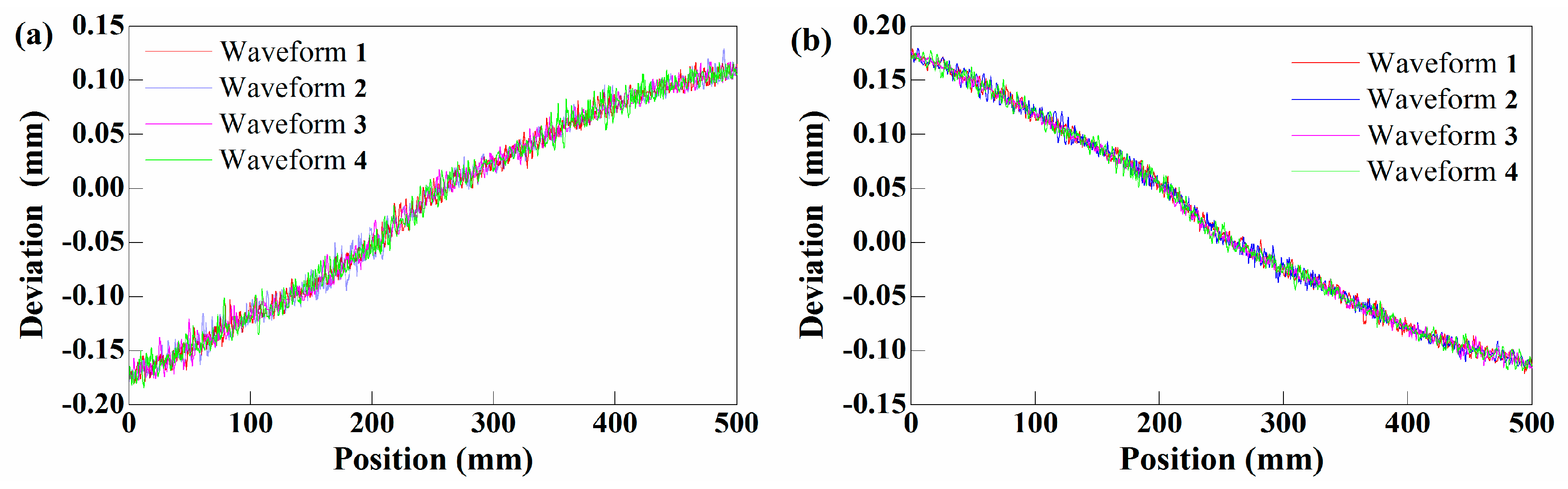
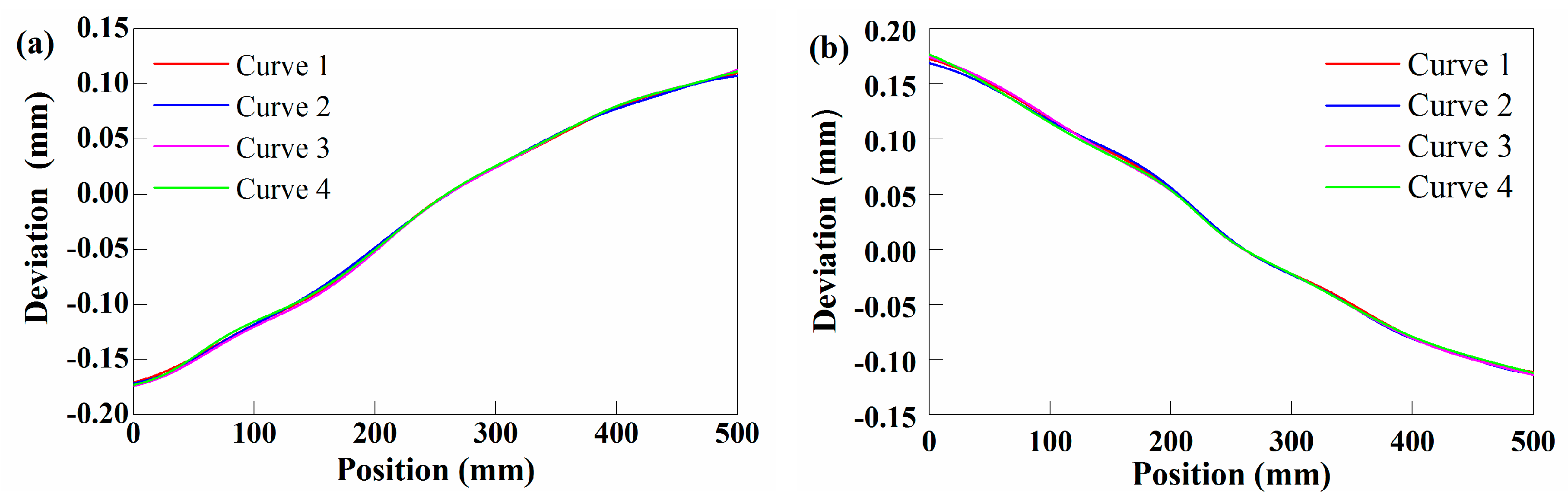
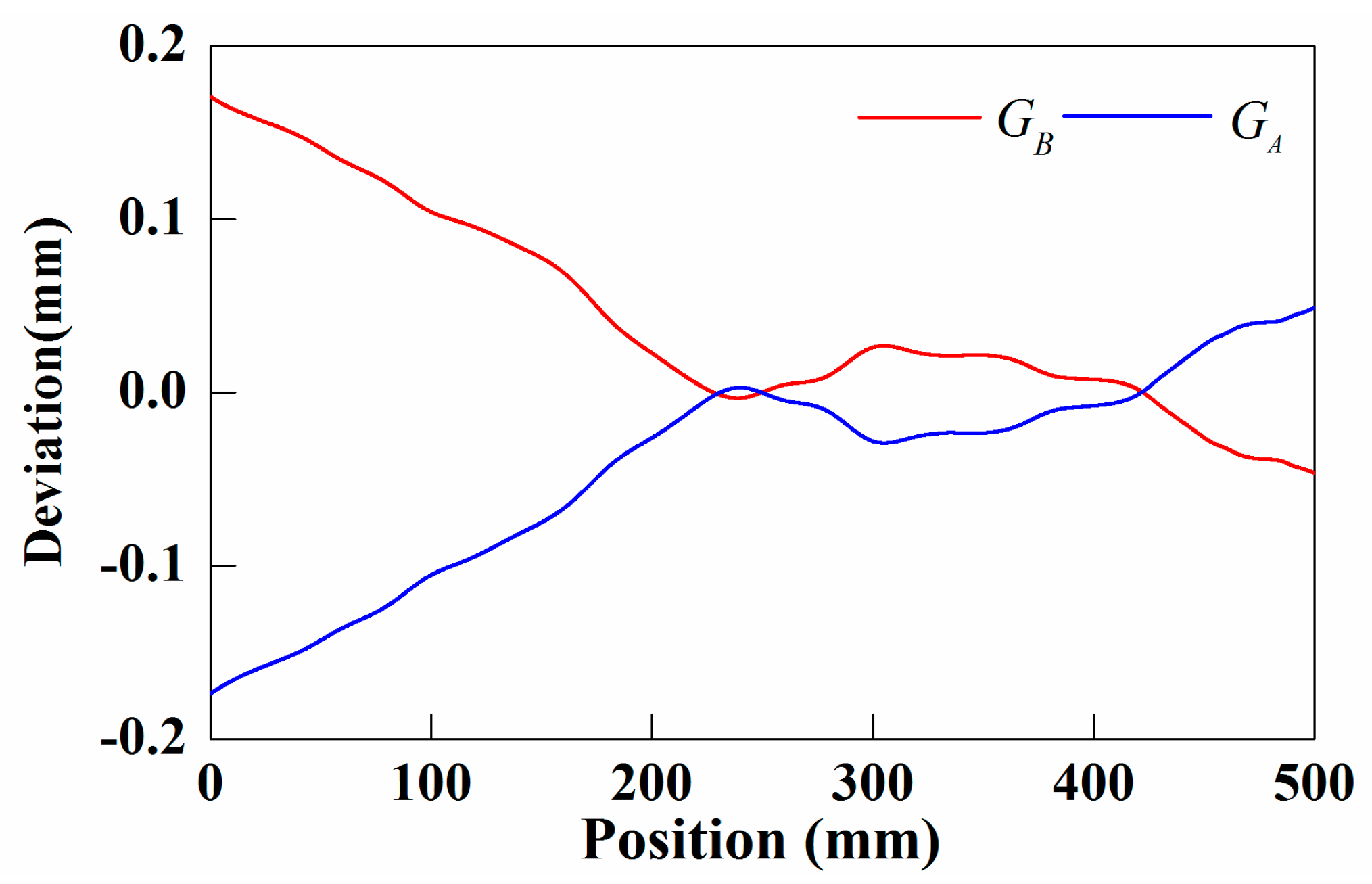
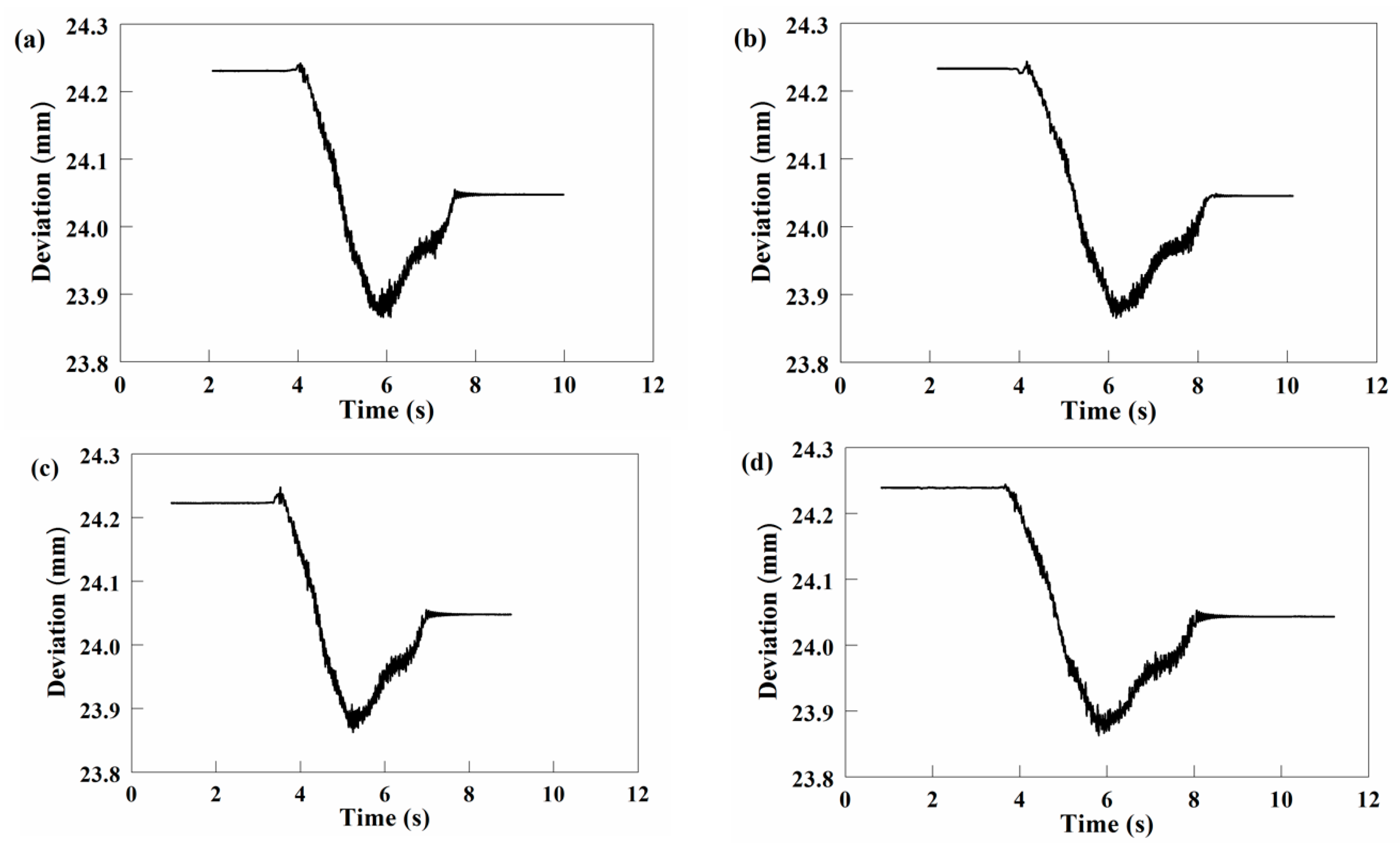
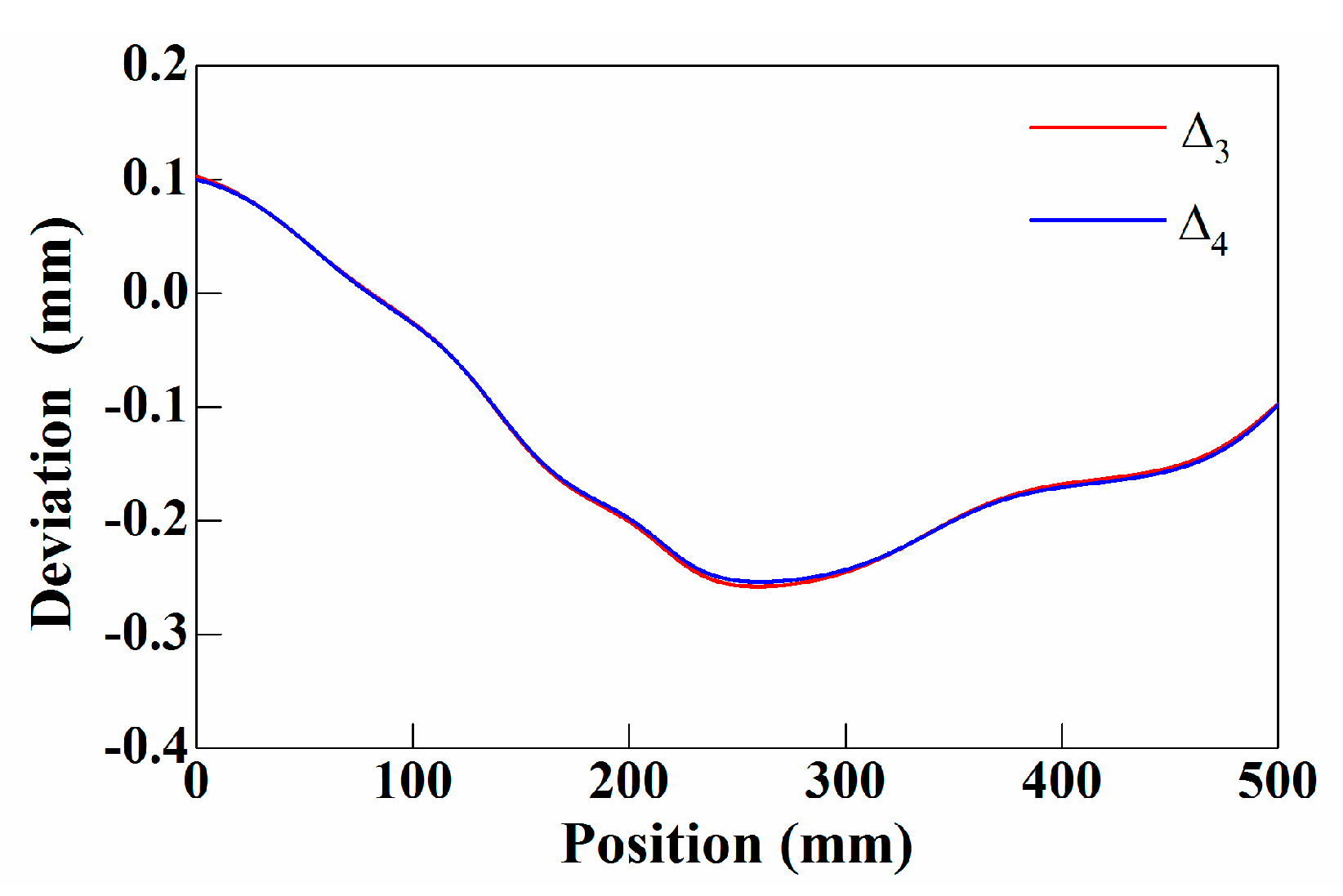
5.1.2. Results and Analysis
5.2. Measuremen Texperiment of Two Vertical Parallel Surfaces
5.2.1. Experimental Step
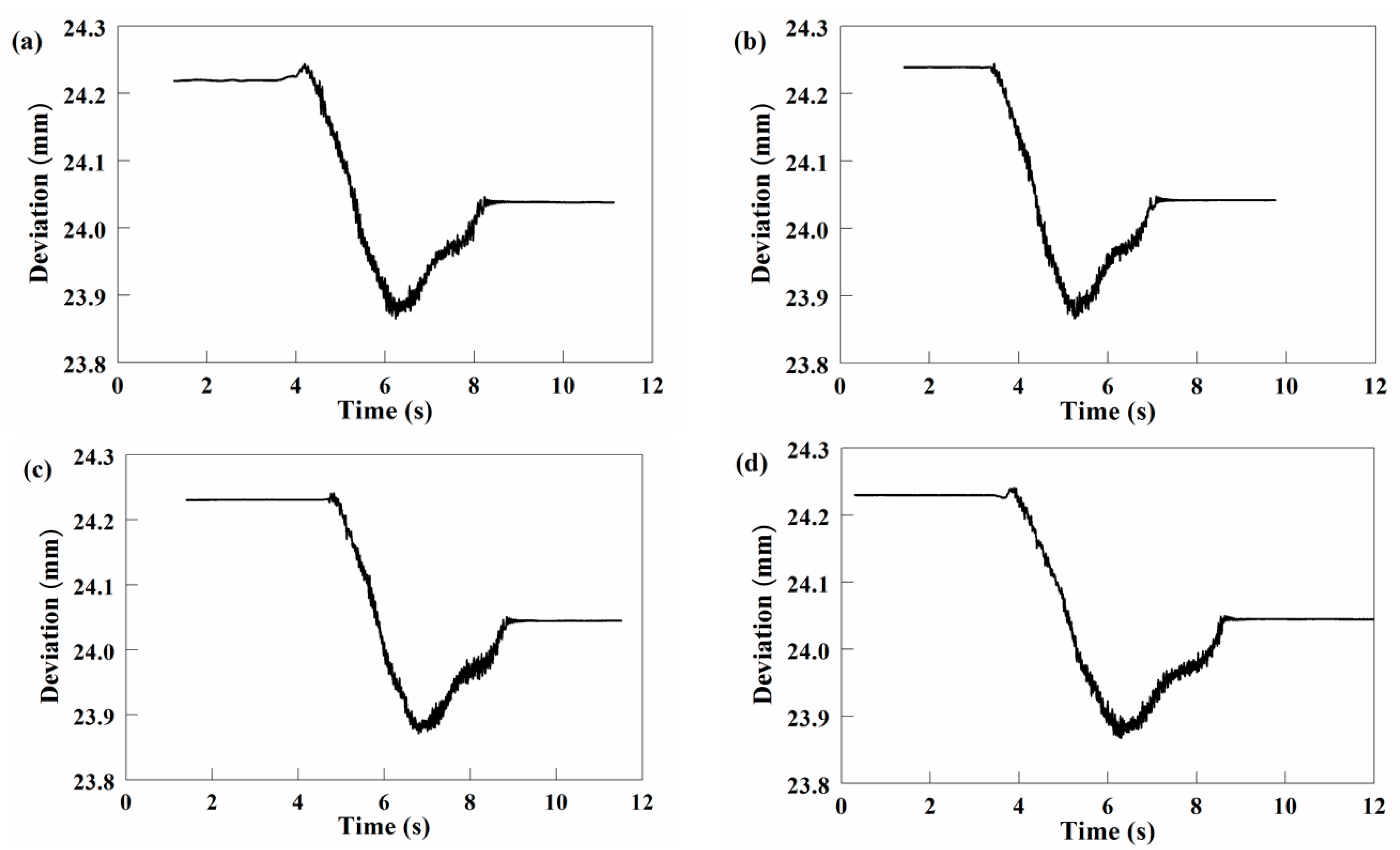
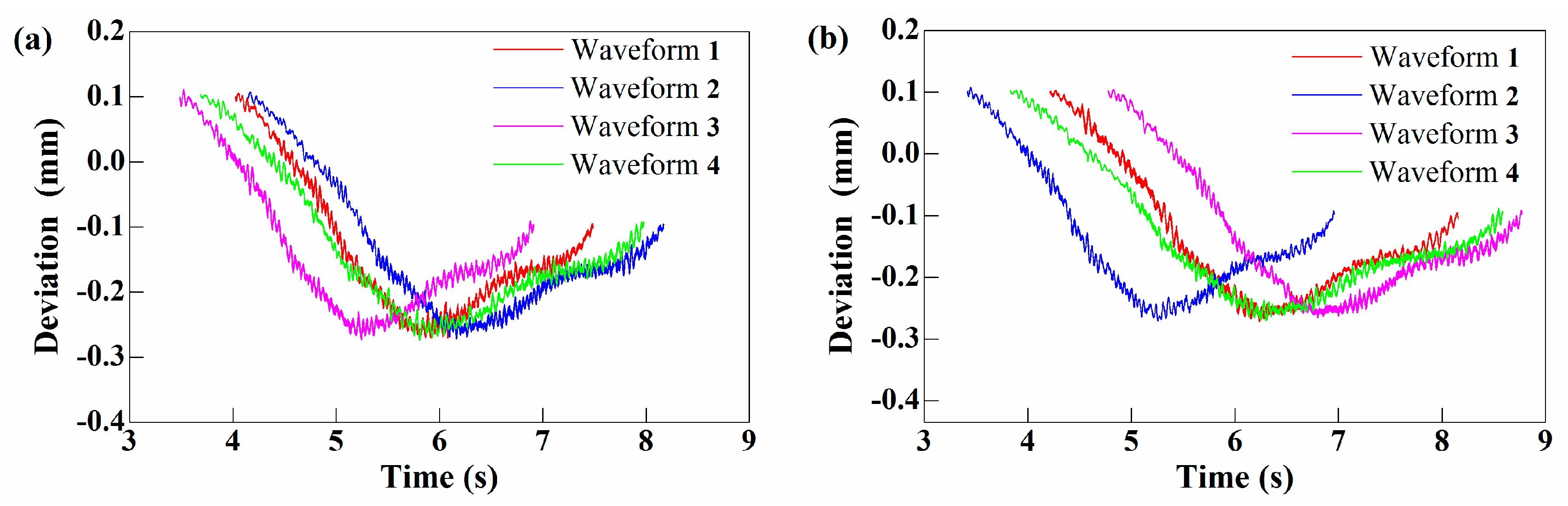
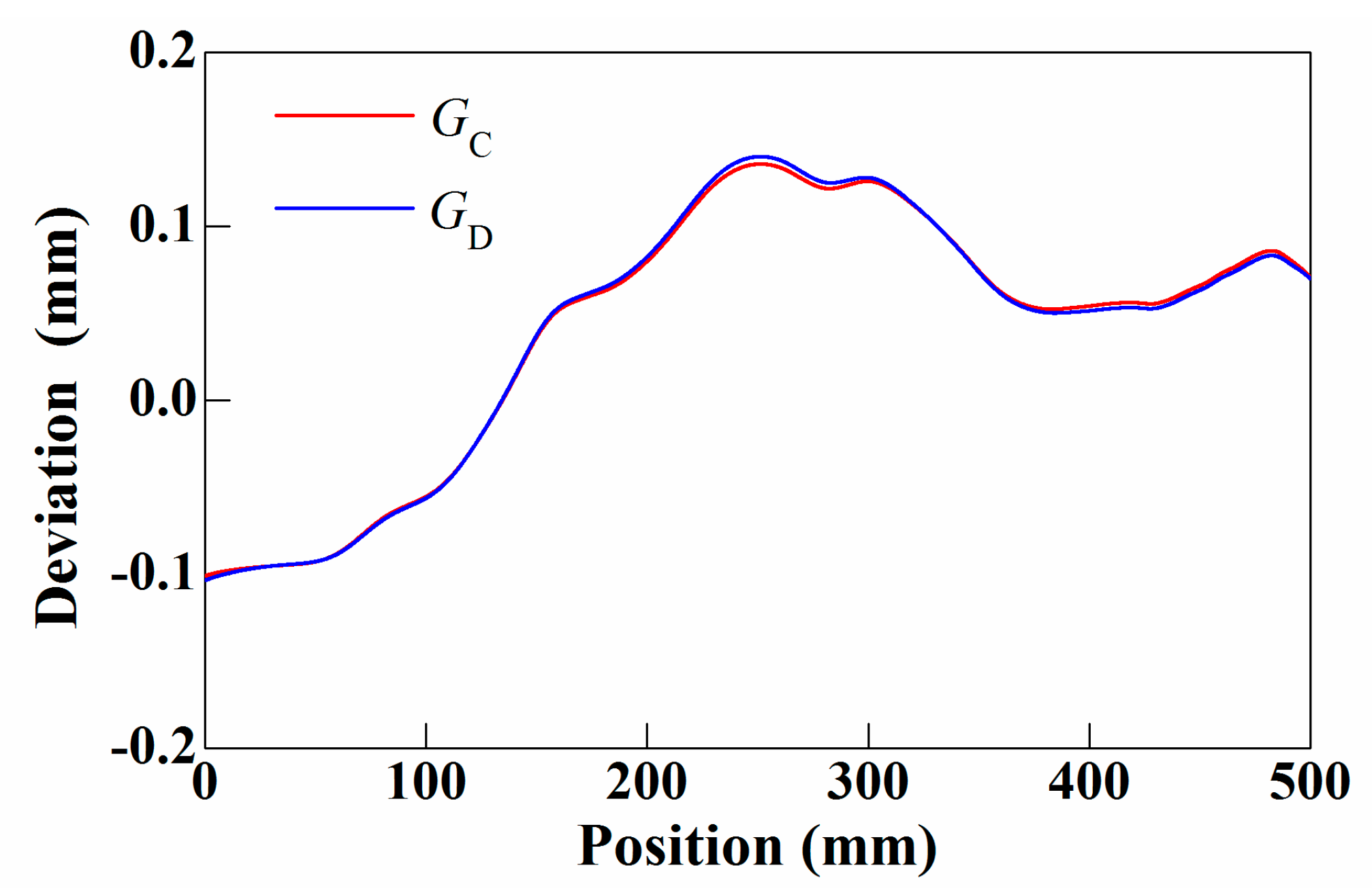
5.2.2. Results and Analysis
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Data Availability
References
- Zha, J.; Xue, F.; Chen, Y. Straightness error modeling and compensation for gantry type open hydrostatic guideways in grinding machine. Int. J. Mach. Tools Manuf. 2017, 112, 1–6. [Google Scholar] [CrossRef]
- Kang, C.S.; Kim, J.A.; Jin, J. An optical straightness measurement sensor for the KRISS watt balance. Measurement 2015, 61, 257–262. [Google Scholar] [CrossRef]
- Borisov, O.; Fletcher, S.; Longstaff, A. New low cost sensing head and taut wire method for automated straightness measurement of machine tool axes. Opt. Lasers Eng. 2013, 51, 978–985. [Google Scholar] [CrossRef]
- Wei, X.; Su, Z.; Yang, X.; Lv, Z.; Yang, Z.; Zhang, H.; Li, X.; Fang, F. A Novel Method for the Measurement of Geometric Errors in the Linear Motion of CNC Machine Tools. Appl. Sci. 2019, 9, 3357. [Google Scholar] [CrossRef]
- Li, P.; Ding, X.M.; Tan, J.B. A hybrid method based on reduced constraint region and convex-hull edge for surface evaluation. Precis. Eng. 2016, 45, 168–175. [Google Scholar] [CrossRef]
- Radlovački, V.; Hadžistević, M.; Štrbac, B. Evaluating minimum zone surface using new method—Bundle of plains through one point. Precis. Eng. 2016, 43, 554–562. [Google Scholar] [CrossRef]
- Giusca, C.L.; Claverley, J.D.; Sun, W. Practical estimation of measurement noise and flatness deviation on focus variation microscopes. CIRP Ann. Manuf. Technol. 2014, 63, 545–548. [Google Scholar] [CrossRef]
- Han, Z.; Chen, L.; Wulan, T. The absolute flatness measurements of two aluminum coated mirrors based on the skip flat test. Opt. Int. J. Light Electron Opt. 2013, 124, 3781–3785. [Google Scholar] [CrossRef]
- Haijun, L.; Zhigang, D.; Han, H. A new method for measuring the flatness of large and thin silicon substrates using a liquid immersion technique. Meas. Sci. Technol. 2015, 26, 115008. [Google Scholar]
- Zhou, P.; Xu, K.; Wang, D. Rail Profile Measurement Based on Line-structured Light Vision. IEEE Access 2018, 6, 16423–16431. [Google Scholar] [CrossRef]
- Srinivasu, D.S.; Venkaiah, N. Minimum zone evaluation of roundness using hybrid global search approach. Int. J. Adv. Manuf. Technol. 2017, 92, 2743–2754. [Google Scholar] [CrossRef]
- Cao, Z.; Wu, Y.; Han, J. Roundness deviation evaluation method based on statistical analysis of local least square circles. Meas. Sci. Technol. 2017, 28, 105017. [Google Scholar]
- Hsieh, T.H.; Huang, H.L.; Jywe, W.Y. Development of a machine for automatically measuring static/dynamic running parallelism in linear guideways. Rev. Sci. Instrum. 2014, 85, 035115. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.; Park, C.H.; Gao, W. A three-probe system for measuring the parallelism and straightness of a pair of rails for ultra-precision guideways. Int. J. Mach. Tools Manuf. 2017, 47, 1053–1058. [Google Scholar] [CrossRef]
- Bhattacharya, J.C. Measurement of parallelism of the surfaces of a transparent sample. Opt. Lasers Eng. 2001, 35, 27–31. [Google Scholar] [CrossRef]
- Lee, K.I.; Shin, D.H.; Yang, S.H. Parallelism error measurement for the spindle axis of machine tools by two circular tests with different tool lengths. Int. J. Adv. Manuf. Technol. 2017, 88, 2883–2887. [Google Scholar] [CrossRef]
- Vannoni, M.; Bertozzi, R. Parallelism error characterization with mechanical and interferometric methods. Opt. Lasers Eng. 2007, 45, 719–722. [Google Scholar] [CrossRef]
- Jywe, W.Y.; Hsieh, T.H.; Chen, P.Y.; Wang, M.S. An Online Simultaneous Measurement of the Dual-Axis Straightness Error for Machine Tools. Appl. Sci. 2018, 8, 2130. [Google Scholar] [CrossRef]
- Hsieh, T.H.; Chen, P.Y.; Jywe, W.Y.; Chen, G.W.; Wang, M.S. A Geometric Error Measurement System for Linear Guideway Assembly and Calibration. Appl. Sci. 2019, 9, 574. [Google Scholar] [CrossRef]




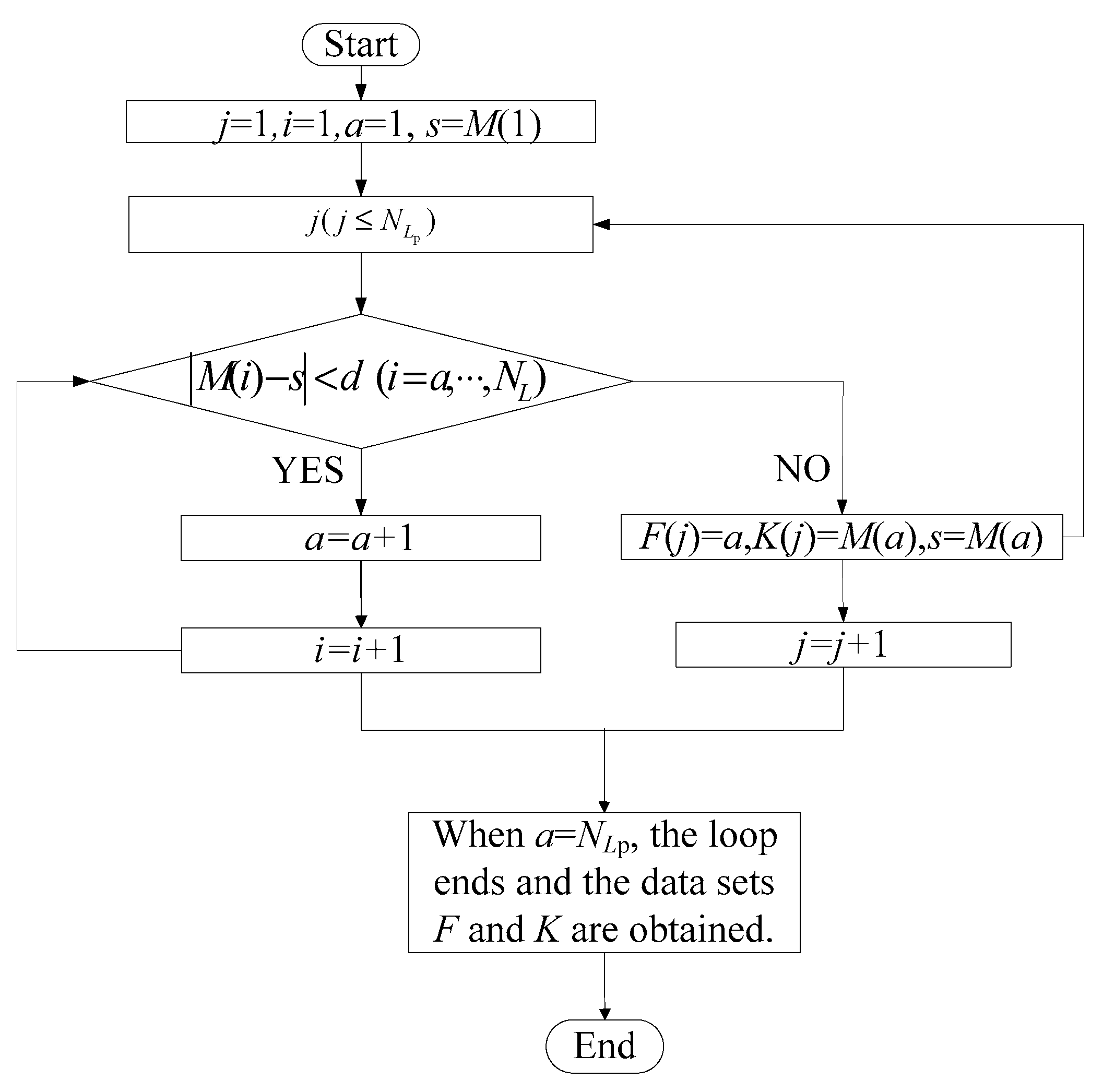









| Model | Parameter |
|---|---|
| Frequency | 20 kHz |
| Resolution | 0.3 μm |
| Absolute error | 4 μm (≤±0.02%) full scale |
| Starting measurement range | 50 mm |
| Light source | semiconductor laser (1 mW, 670 nm red) |
| Impact resistance | 15 g/6 ms |
| Operating temperature | 0–50 °C |
| Power requirements | 24 VDC (11…30 VDC), Max 150 mA |
| Security Level | Class 2 according to DIN EN 60825-1: 2001-11 |
| Spot diameter | SMR140 × 200 μm, MMR46 × 45 μm, EMR140 × 200 μm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Zhang, B.; Li, Z.; Zhao, C. A Method of On-Site Describing the Positional Relation between Two Horizontal Parallel Surfaces and Two Vertical Parallel Surfaces. Appl. Sci. 2020, 10, 2152. https://doi.org/10.3390/app10062152
Lu Z, Zhang B, Li Z, Zhao C. A Method of On-Site Describing the Positional Relation between Two Horizontal Parallel Surfaces and Two Vertical Parallel Surfaces. Applied Sciences. 2020; 10(6):2152. https://doi.org/10.3390/app10062152
Chicago/Turabian StyleLu, Zechen, Bao Zhang, Zhenjun Li, and Chunyu Zhao. 2020. "A Method of On-Site Describing the Positional Relation between Two Horizontal Parallel Surfaces and Two Vertical Parallel Surfaces" Applied Sciences 10, no. 6: 2152. https://doi.org/10.3390/app10062152
APA StyleLu, Z., Zhang, B., Li, Z., & Zhao, C. (2020). A Method of On-Site Describing the Positional Relation between Two Horizontal Parallel Surfaces and Two Vertical Parallel Surfaces. Applied Sciences, 10(6), 2152. https://doi.org/10.3390/app10062152





