Estimation of Hand Motion from Piezoelectric Soft Sensor Using Deep Recurrent Network
Abstract
1. Introduction
2. Interface System
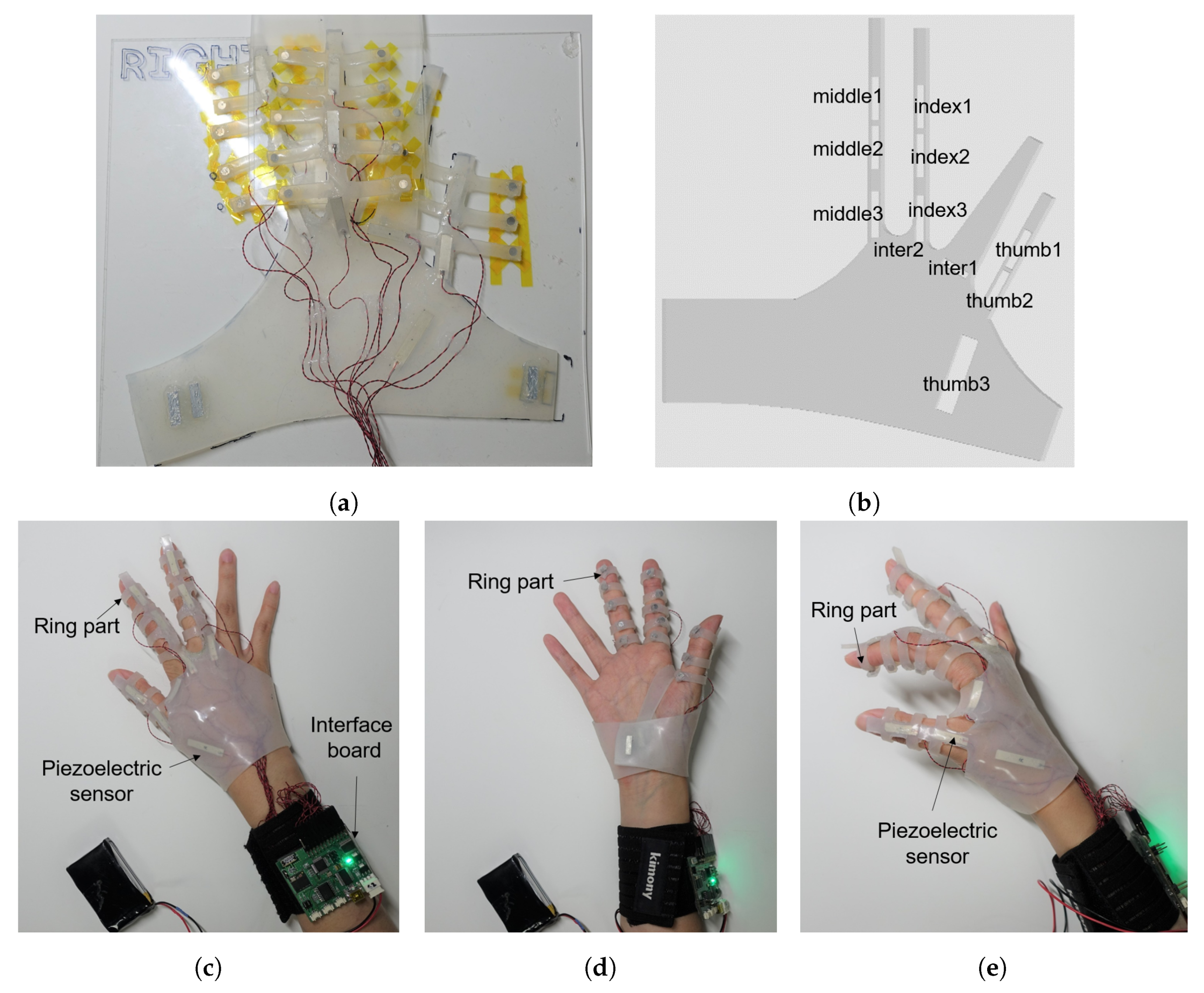
2.1. Glove Structure
2.2. System Setup
3. Application of Recurrent Network
3.1. Conventional Angle Recognition Method
3.2. Estimation of Moving State and Offset Voltage
- If noise is added to v, it is hard to distinguish noise from curvature change.
- Input noise can be random value in case that the system is operated in different environment.
- When noise is random, is hard to determine.
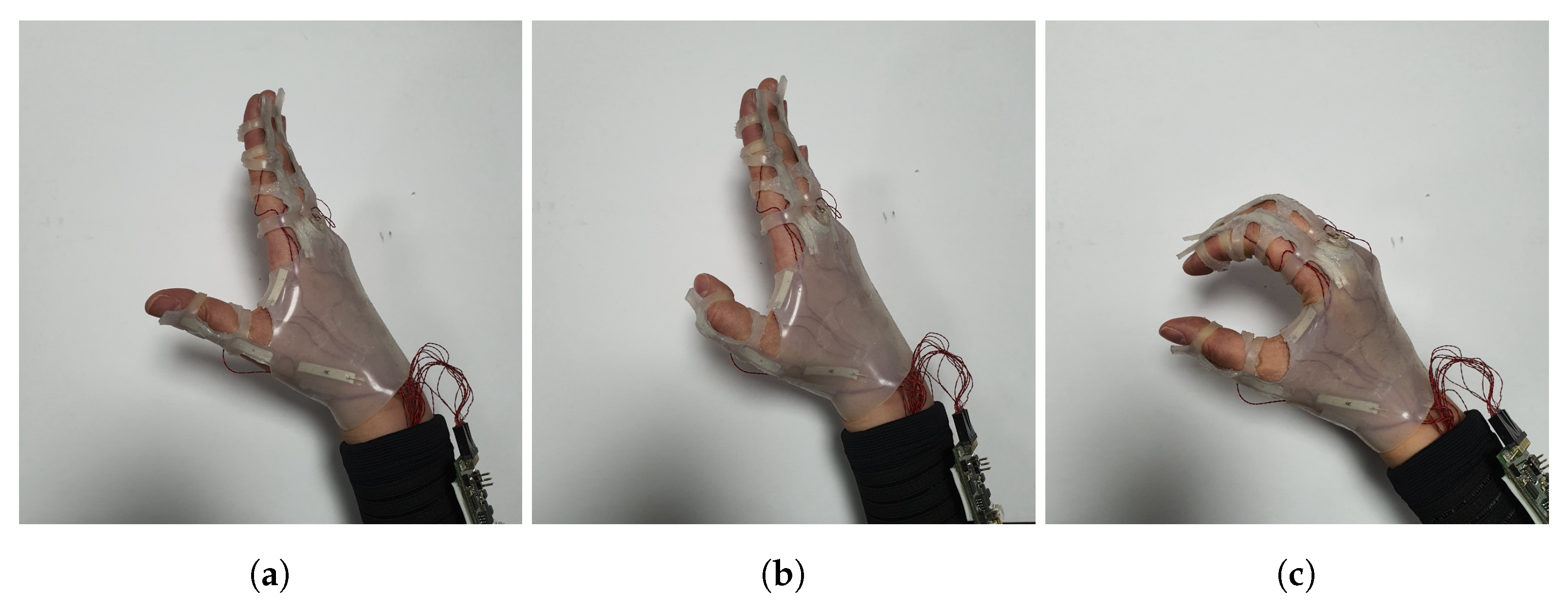
3.3. Data Acquisition
- We used the soft sensor located on the glove, and its piezoelectric voltage was measured with the interface board.
- Joint angle for acquiring moving state was simultaneously measured with leap motion controller.
- Single movement was composed with flexion and extension.
- The range of flexion angle was determined randomly between 30 degrees and 90 degrees.
- Movements for training set were conducted 1080 times, and those for the test set were conducted 270 times.
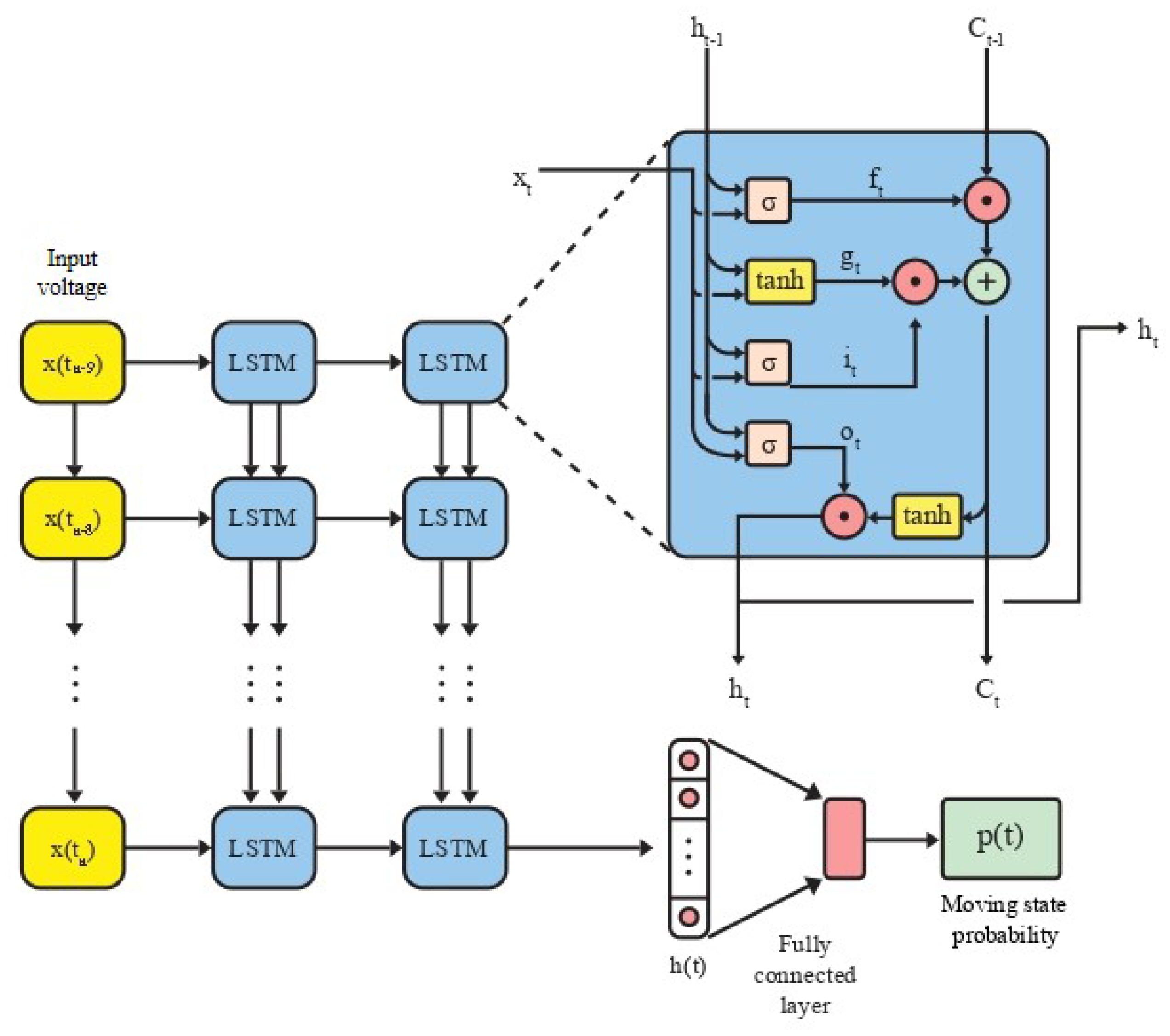
3.4. Proposed Network
4. Result and Discussion
4.1. Moving State Estimation
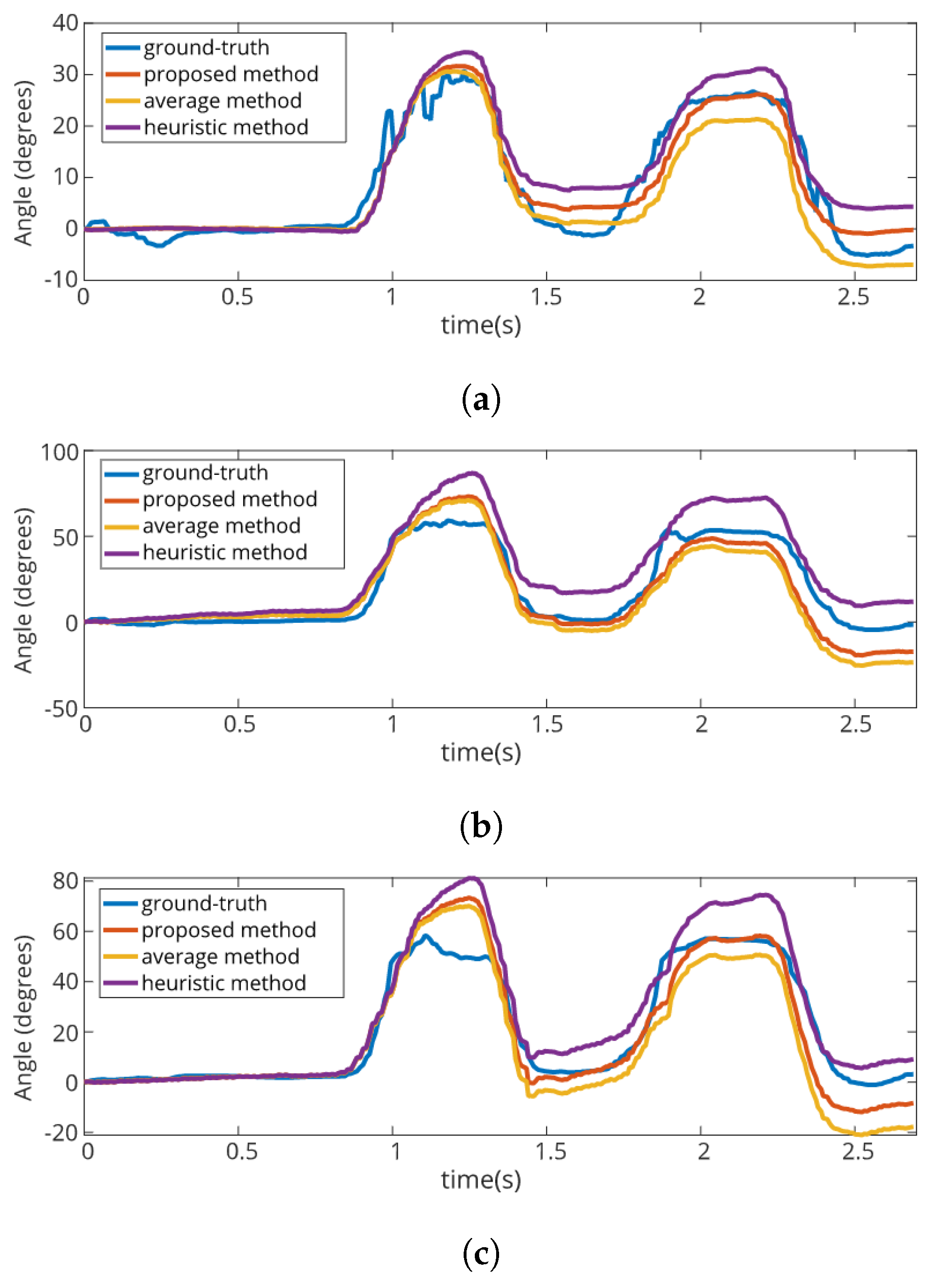
4.2. Angle Value Estimation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LSTM | Long-Short Term Memory |
| RNN | Recurrenct Neural Network |
| SGD | Stochastic Gradient Descent |
References
- Yang, C.C.; Hsu, Y.L. A review of accelerometry-based wearable motion detectors for physical activity monitoring. Sensors 2010, 10, 7772–7788. [Google Scholar] [CrossRef]
- Liu, Y.; Nie, L.; Liu, L.; Rosenblum, D.S. From action to activity: Sensor-based activity recognition. Neurocomputing 2016, 181, 108–115. [Google Scholar] [CrossRef]
- Yap, H.K.; Lim, J.H.; Nasrallah, F.; Goh, J.C.; Yeow, R.C. A soft exoskeleton for hand assistive and rehabilitation application using pneumatic actuators with variable stiffness. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Piscatawa, NJ, USA, 2015; pp. 4967–4972. [Google Scholar]
- Polygerinos, P.; Wang, Z.; Galloway, K.C.; Wood, R.J.; Walsh, C.J. Soft robotic glove for combined assistance and at-home rehabilitation. Robot. Auton. Syst. 2015, 73, 135–143. [Google Scholar] [CrossRef]
- Mengüç, Y.; Park, Y.L.; Pei, H.; Vogt, D.; Aubin, P.M.; Winchell, E.; Fluke, L.; Stirling, L.; Wood, R.J.; Walsh, C.J. Wearable soft sensing suit for human gait measurement. Int. J. Robot. Res. 2014, 33, 1748–1764. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Hao, S.; Peng, X.; Hu, L. Deep learning for sensor-based activity recognition: A survey. Pattern Recognit. Lett. 2019, 119, 3–11. [Google Scholar] [CrossRef]
- Chen, Y.; Xue, Y. A deep learning approach to human activity recognition based on single accelerometer. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Kowloon, Hong Kong, China, 9–12 October 2015; IEEE: Piscatawa, NJ, USA, 2015; pp. 1488–1492. [Google Scholar]
- Kim, Y.; Toomajian, B. Hand gesture recognition using micro-Doppler signatures with convolutional neural network. IEEE Access 2016, 4, 7125–7130. [Google Scholar] [CrossRef]
- Pourbabaee, B.; Roshtkhari, M.J.; Khorasani, K. Deep convolutional neural networks and learning ECG features for screening paroxysmal atrial fibrillation patients. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 2095–2104. [Google Scholar] [CrossRef]
- Park, Y.L.; Tepayotl-Ramirez, D.; Wood, R.J.; Majidi, C. Influence of cross-sectional geometry on the sensitivity and hysteresis of liquid-phase electronic pressure sensors. Appl. Phys. Lett. 2012, 101, 191904. [Google Scholar] [CrossRef]
- Han, S.; Kim, T.; Kim, D.; Park, Y.L.; Jo, S. Use of deep learning for characterization of microfluidic soft sensors. IEEE Robot. Autom. Lett. 2018, 3, 873–880. [Google Scholar] [CrossRef]
- Kim, D.; Kwon, J.; Han, S.; Park, Y.L.; Jo, S. Deep Full-Body Motion Network for a Soft Wearable Motion Sensing Suit. IEEE/ASME Trans. Mechatron. 2018, 24, 56–66. [Google Scholar] [CrossRef]
- Yuan, W.; Zhu, C.; Owens, A.; Srinivasan, M.A.; Adelson, E.H. Shape-independent hardness estimation using deep learning and a gelsight tactile sensor. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscatawa, NJ, USA, 2017; pp. 951–958. [Google Scholar]
- Dong, W.; Xiao, L.; Hu, W.; Zhu, C.; Huang, Y.; Yin, Z. Wearable human–machine interface based on PVDF piezoelectric sensor. Trans. Inst. Meas. Control. 2017, 39, 398–403. [Google Scholar] [CrossRef]
- Swallow, L.; Luo, J.; Siores, E.; Patel, I.; Dodds, D. A piezoelectric fibre composite based energy harvesting device for potential wearable applications. Smart Mater. Struct. 2008, 17. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, J.; Ren, G.; Zhang, P.; Xu, C. A flexible piezoelectric force sensor based on PVDF fabrics. Smart Mater. Struct. 2011, 20. [Google Scholar] [CrossRef]
- Akiyama, M.; Morofuji, Y.; Kamohara, T.; Nishikubo, K.; Tsubai, M.; Fukuda, O.; Ueno, N. Flexible piezoelectric pressure sensors using oriented aluminum nitride thin films prepared on polyethylene terephthalate films. J. Appl. Phys. 2006, 100, 114318. [Google Scholar] [CrossRef]
- Cha, Y.; Seo, J.; Kim, J.S.; Park, J.M. Human–computer interface glove using flexible piezoelectric sensors. Smart Mater. Struct. 2017, 26. [Google Scholar] [CrossRef]
- Song, K.; Kim, S.H.; Jin, S.; Kim, S.; Lee, S.; Kim, J.S.; Park, J.M.; Cha, Y. Pneumatic actuator and flexible piezoelectric sensor for soft virtual reality glove system. Sci. Rep. 2019, 9, 8988. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wang, S.; Zhang, X.; Yao, L.; Yue, L.; Qian, B.; Li, X. EEG-based motion intention recognition via multi-task RNNs. In Proceedings of the 2018 SIAM International Conference on Data Mining, San Diego, CA, USA, 3–5 May 2018; SIAM: Philadelphia, PA, USA, 2018; pp. 279–287. [Google Scholar]
- Ordóńez, F.; Roggen, D. Deep convolutional and lstm recurrent neural networks for multimodal wearable activity recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef] [PubMed]
- Cha, Y.; Hong, S. Energy harvesting from walking motion of a humanoid robot using a piezoelectric composite. Smart Mater. Struct. 2016, 25, 10LT01. [Google Scholar] [CrossRef]
- Chophuk, P.; Chumpen, S.; Tungjitkusolmun, S.; Phasukkit, P. Hand postures for evaluating trigger finger using leap motion controller. In Proceedings of the 2015 8th Biomedical Engineering International Conference (BMEiCON), Pattaya, Thailand, 25–27 November 2015; IEEE: Piscatawa, NJ, USA, 2015; pp. 1–4. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Sak, H.; Senior, A.W.; Beaufays, F. Long Short-Term Memory Recurrent Neural Network Architectures for Large Scale Acoustic Modeling. 2014. Available online: https://static.googleusercontent.com/media/research.google.com/en//pubs/archive/43905.pdf (accessed on 24 March 2020).






| Number of the Data | Number of the Movement | |
|---|---|---|
| Training Set | 214,775 | 1080 |
| Test set | 59,660 | 270 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training | RNN | 85.51% | 85.57% | 85.87% | 85.91% | 85.88% | 85.84% | 85.90% | 85.54% | 85.54% | 85.49% | 85.71% |
| LSTM | 85.88% | 85.39% | 85.73% | 85.86% | 85.92% | 85.87% | 85.87% | 85.93% | 85.73% | 85.94% | 85.81% | |
| Test | RNN | 86.31% | 86.86% | 86.36% | 85.74% | 86.80% | 87.50% | 86.16% | 86.56% | 87.16% | 86.94% | 86.64% |
| LSTM | 86.95% | 86.93% | 87.06% | 87.23% | 87.24% | 87.27% | 87.02% | 87.31% | 87.06% | 86.97% | 87.10% |
| thumb1 | thumb2 | thumb3 | index1 | index2 | index3 | |
|---|---|---|---|---|---|---|
| proposed method () | 80.02% | 84.44% | 83.25% | 84.47% | 81.12% | 82.62% |
| heuristic method () | 61.25% | 63.58% | 78.41% | 65.79% | 54.31% | 53.90% |
| thumb1 | thumb2 | thumb3 | index1 | index2 | index3 | |
|---|---|---|---|---|---|---|
| proposed method | 6.79 | 5.64 | 9.40 | 8.92 | 12.88 | 13.75 |
| average method | 13.28 | 10.72 | 12.16 | 9.94 | 16.04 | 20.91 |
| heuristic method | 6.28 | 7.07 | 17.23 | 11.76 | 25.66 | 25.91 |
| thumb1 | thumb2 | thumb3 | index1 | index2 | index3 | |
|---|---|---|---|---|---|---|
| proposed method | 5.92 | 4.97 | 7.73 | 7.02 | 10.01 | 10.83 |
| average method | 9.61 | 7.69 | 9.46 | 7.64 | 11.50 | 14.75 |
| heuristic method | 5.62 | 5.21 | 13.10 | 8.99 | 18.82 | 19.19 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.H.; Kwon, Y.; Kim, K.; Cha, Y. Estimation of Hand Motion from Piezoelectric Soft Sensor Using Deep Recurrent Network. Appl. Sci. 2020, 10, 2194. https://doi.org/10.3390/app10062194
Kim SH, Kwon Y, Kim K, Cha Y. Estimation of Hand Motion from Piezoelectric Soft Sensor Using Deep Recurrent Network. Applied Sciences. 2020; 10(6):2194. https://doi.org/10.3390/app10062194
Chicago/Turabian StyleKim, Sung Hee, Yongchan Kwon, KangGeon Kim, and Youngsu Cha. 2020. "Estimation of Hand Motion from Piezoelectric Soft Sensor Using Deep Recurrent Network" Applied Sciences 10, no. 6: 2194. https://doi.org/10.3390/app10062194
APA StyleKim, S. H., Kwon, Y., Kim, K., & Cha, Y. (2020). Estimation of Hand Motion from Piezoelectric Soft Sensor Using Deep Recurrent Network. Applied Sciences, 10(6), 2194. https://doi.org/10.3390/app10062194






