Estimating the Unit Weight of Local Organic Soils from Laboratory Tests Using Artificial Neural Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Initial Recognition of the Subsoil of the Study Area with a Cone Penetration Test (CPTM)
2.2. Determination of Leading Parameters of Organic Soils with a Laboratory Test
2.2.1. Natural Water Content
2.2.2. Organic Content
2.2.3. Soil Unit Weight
2.3. Characteristics of the Study Area at the Rzeszow Site
2.4. Artificial Neural Network
3. Results
4. Evaluation of the Soil Unit Weight Based on Laboratory Test Results
4.1. Standard Regreesion
4.2. Artificial Neural Networks Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lune, T.; Robertson, P.; Powell, J. Cone Penetration Testing in Geotechnical Practice; CRC Press: London, UK, 1997. [Google Scholar]
- Mayne, P. Cone Penetration Testing, A Synthesis of Highway Practice, NCHRP Synthesis 368; Transportation Research Board: Washington, DC, USA, 2007. [Google Scholar]
- Robertson, P.; Cabal, K. Estimating soil unit weight from CPT. In Proceedings of the 2rd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010. [Google Scholar]
- Mayne, P.; Peuchen, J.; Bouwmeester, D. Soil unit weight estimation from CPTs. In Proceedings of the 2rd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010; pp. 169–176. [Google Scholar]
- Cai, G.; Liu, S.; Zhang, T.; Zou, H.; Puppala, A. Evaluation of unit weight from SCPTuin soft marine Jiangsu clay. In Proceedings of the 3rd International Symposium on Cone penetration testing, Las Vegas, NV, USA, 12–14 May 2014; Robertson, K., Cabal, K.I., Eds.; ISSMGE technical Committee: Las Vegas, NV, USA, 2014. [Google Scholar]
- Lengkeek, H.J.; de Greef, J.; Joosten, S. CPT based unit weight estimation extended to soft organic soils and peat. In Cone Penetration Testing 2018; Hicks, P., Hicks, P., Eds.; Delft University of Technology: Delft, The Netherlands, 2018; pp. 389–395. ISBN 978-1-138-58449-5. [Google Scholar]
- Straż, G. Estimating soil unit weight from CPT for selected organic soils. In Selected Technical, Economic and Ecological Aspects of Contemporary Construction; Pujer, K., Ed.; Exante Scientific Publisher: Wrocław, Poland, 2016; pp. 63–77. [Google Scholar]
- Sulewska, M.J. Applying Artificial Neural Networks for analysis of geotechnical problems. Comput. Assist. Methods Eng. Sci. 2011, 18, 230–241. [Google Scholar]
- Sulewska, M.J. Artificial Neural modeling of compaction characteristics of cohesionless soil. Comput. Assist. Methods Eng. Sci. 2010, 17, 27–40. [Google Scholar]
- Sulewska, M.J. Artificial Neural Networks in the Evaluation of Non-Cohesive Soil Compaction Parameters; Committee Civil Engineering of the Polish Academy of Sciences: Warsaw, Poland, 2009. [Google Scholar]
- Sulewska, M.J. About usability of the artificial neural networks in embankment compaction estimation. Inżynieria I Budownictwo 2006, 6, 337–338. [Google Scholar]
- Sulewska, M.J. Prediction Models for Minimum and Maximum Dry Density of Non-Cohesive Soils. Pol. J. Environ. Stud. 2010, 19, 797–804. [Google Scholar]
- Lechowicz, Z.; Fukue, M.; Rabarijoely, S.; Sulewska, M.J. Evaluation of the Undrained Shear Strength of Organic Soils from a Dilatometer Test Using Artificial Neural Networks. Appl. Sci. 2018, 8, 1395. [Google Scholar] [CrossRef] [Green Version]
- Ochmański, M.; Bzówka, J. Selected examples of the use of artificial neural networks in geotechnics. Civ. Environ. Eng. 2013, 4, 287–294. [Google Scholar]
- Ochmański, M.; Bzówka, J. Back analysis of SCL tunnels based on Artificial Neural Network. Archit. Civ. Eng. Environ. 2012, 3, 73–81. [Google Scholar]
- Ochmański, M. The use of artificial neural networks for influence analysis of selected parameters on the jet grouting columns diameters. In Proceedings of the XIII Scientific Conference for Civil Engineering Ph.D. Students, Szczyrk, Poland, 12–13 September 2013. [Google Scholar]
- Borowiec, A.; Wilk, K. Prediction of consistency parameters of fen soils by neural networks. Comput. Assist. Methods Eng. Sci. 2014, 21, 67–75. [Google Scholar]
- Klos, M.; Sulewska, M.J.; Waszczyszyn, Z. Neural identification of compaction characteristics for granular soils. Comput. Assist. Methods Eng. Sci. 2011, 18, 265–273. [Google Scholar]
- Kłos, M.; Waszczyszyn, Z. Prediction of Compaction Characteristics of Granular Soils by Neural Networks. Artif. Neural Netw. 2010, 42–45. [Google Scholar] [CrossRef]
- Wrzesiński, G.; Sulewska, M.J.; Lechowicz, Z. Evaluation of the Change in Undrained Shear Strength in Cohesive Soils due to Principal Stress Rotation Using an Artificial Neural Network. Appl. Sci. 2018, 8, 781. [Google Scholar] [CrossRef] [Green Version]
- Zabielska-Adamska, K.; Sulewska, M.J. Ann-based modelling of fly ash compaction curve. Arch. Civ. Eng. 2012, 1, 57–69. [Google Scholar] [CrossRef] [Green Version]
- Zhiming, C.H.; Guotao, M.; Ye, Z.; Yanjie, Z.; Hengyang, H. The application of artificial neural network in geotechnical engineering. In Proceedings of the 2018 International Conference on Civil and Hydraulic Engineering (IConCHE 2018), Qingdao, China, 23–25 November 2018; IOP Publishing: Bristol, UK, 2018. [Google Scholar] [CrossRef]
- Shahin, M.; Jaksa, M.; Maier, H. Artificial neural network applications in geotechnical engineering. Aust. Geomech. 2001, 36, 49–62. [Google Scholar]
- Cal, Y. Soil classification by neural-network. Adv. Eng. Softw. 1995, 22, 95–97. [Google Scholar] [CrossRef]
- Ferentinou, M.; Hasiotis, T. Application of computational intelligence tools for the analysis of marine geotechnical properties in the head of Zakynthos canyon. Greece Comput. Geosci. 2012, 40, 166–174. [Google Scholar] [CrossRef]
- Ferentinou, M.; Sakellariou, M. Computational intelligence tools for the prediction of slope performance. Comput. Geotech. 2007, 34, 362–384. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y. Correction of soil parameters in calculation of embankment settlement using a BP network back-analysis model. Eng. Geol. 2007, 91, 168–177. [Google Scholar] [CrossRef]
- Ylmaz, I.; Yuksek, A. An example of artificial neural network (ANN) application for indirect estimation of rock parameters. Rock Mech. Rock Eng. 2008, 41, 781–795. [Google Scholar] [CrossRef]
- Nawari, N.; Liang, R.; Nusairat, J. Artificial intelligence techniques for the design and analysis of deep foundations. Electron. J. Geotech. Eng. 1999, 4, 1–21. [Google Scholar]
- Goh, A. Empirical design in geotechnics using neural networks. Geotechnique 1995, 45, 709–714. [Google Scholar] [CrossRef]
- Penumadu, D.; Jean-Lou, C. Geomaterial modeling using artificial neural networks. In Artificial Neural Networks for Civil Engineers: Fundamentals and Applications; ASCE: Reston, WV, USA, 1997; pp. 160–184. [Google Scholar]
- PN-EN ISO 22476-12:2009. Geotechnical Investigation and Testing—Field Testing—Part 12: Mechanical Cone Penetration Test; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- Młynarek, Z.; Tschuschke, W.; Wierzbicki, J. Geotechnics in construction and transport. In Proceedings of the 11th National Conference on Soil Mechanics and Foundation Engineering, Gdańsk, Poland, 25–27 June 1997; pp. 119–126. [Google Scholar]
- Douglas, B.J.; Olsen, R.S. Soil classification using electric cone penetrometer. American Society of Civil Engineers, ASCE. In Proceedings of the Conference on Cone Penetration Testing and Experience, St. Louis, MI, USA, 26–30 October 1981; pp. 209–227. [Google Scholar]
- Schmertmann, J.H. Guidelines for Cone Test, Performance, and Design; Report FHWA-TS-78209; Federal Highway Administration: Washington, DC, USA, 1978; p. 145.
- Eslami, A.; Fellenius, B.H. CPT and CPTu data for soil profile interpretation: Review of method sand proposed new approach. Iran. J. Sci. Technol. 2004, 28, 71–86. [Google Scholar]
- Robertson, P.K.; Capanella, R.G. Interpretation of cone penetration tests—Part II (clay). Can. Geotech. J. 1983, 20, 734–745. [Google Scholar] [CrossRef]
- Searle, I.W. The interpretation of Begemann friction jacket cone results to give soil types and design parameters. In Proceedings of the 7th European Conference on Soil Mechanics and Foundation Engineering, ECSMFE, Brighton, UK, 1–6 September 1979; pp. 2265–2270. [Google Scholar]
- PN-EN ISO 17892-1. Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 1: Determination of Water Content; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- PN-EN 1997-2: 2007. Eurocode 7: Geotechnical Design—Part 1: Ground Investigation and Testing; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- PN-B-04481: 1998. Building Soils. Laboratory Tests; Polish Standard: Warsaw, Poland, 1998. [Google Scholar]
- Marut, M.; Straż, G. Verification of standard guidelines for organic matter content determination in organic soils by the loss on ignition method. Geol. Rev. 2016, 64, 918–924. [Google Scholar]
- Heiri, O.; Lotter, A.F.; Lemcke, G. Loss on ignition as a method for estimating organic and carbonate content in sediments: Reproducibility and comparability of results. J. Paleolimnol. 2001, 25, 101–110. [Google Scholar] [CrossRef]
- PN-EN ISO 17892-2:2014. Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 2: Determination of Bulk Density (ISO 17892-2:2014); ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Geotech, Z.O.O. Department of Geological Services Design and Construction and the Environment, Geological and Engineering Geological Conditions for Recognition—Engineering for the Construction of Multi-Storey Building at UL; Witolda in Rzeszów: Rzeszow, Poland, 2010. [Google Scholar]
- Haykin, S.O. Neural Networks and Learning Machines, 3rd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2009; p. 798. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design; PWS Publishing: Boston, MA, USA, 1996. [Google Scholar]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M. Training feed-forward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Dennis, J.E.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- MacKay, D.J.C. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network ToolboxUser’s Guide; TheMathWorks: Natick, MA, USA, 2010. [Google Scholar]
- PN EN-ISO 14688-1:2018. Geotechnical Investigations and Testing—IDENTIFICATION and Classification of —Part 1: Identification and Description; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- PN EN-ISO 14688-1:2018. Geotechnical Investigations and Testing—Identification and Classification of —Part 2: Principles for a Classification; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- PN-B-02480: 1986. Building Soils. Nomenclature, Symbols, Classification and Description of Soils; Polish Standard: Warsaw, Poland, 1986. [Google Scholar]
- Straż, G. Identification of local organic soils based on cone penetration test results. Civ. Eng. Archit. 2014, 13, 49–56. [Google Scholar]
- Straż, G. Identification, marking and classification methods of organic soils according to Eurocode 7 and related standards. Scientific Review—Engineering and Environmental Sciences. Sci. Rev. Eng. Env. Sci. 2018, 27. [Google Scholar] [CrossRef] [Green Version]







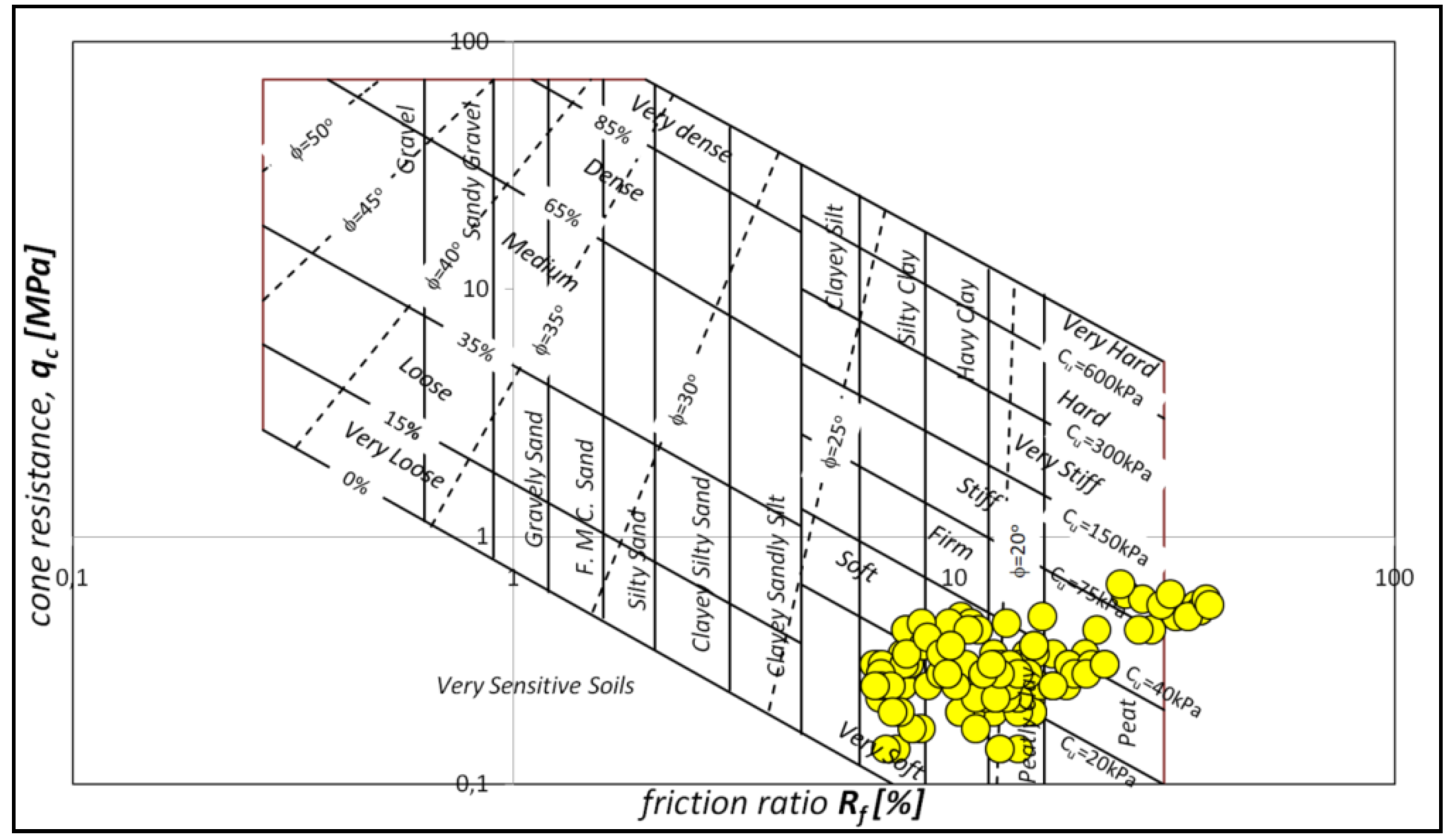






| Material | Organic Content LOIT (%) | Water Content W (%) | Bulk Density ρ (t/m3) | Soil Unit Weight γ (kN/m3) | Specific Density ρd (t/m3) | Specific Density ρs (t/m3) |
|---|---|---|---|---|---|---|
| Various organic soils | 5.02–84.93 | 23.52–417.91 | 1.17–2.25 | 10.27–19.86 | 0.23–1.82 | 1.52–2.59 |
| REγ (w) [%] | REγ (LOIT) [%] | REγ (w; LOIT) [%] | |
|---|---|---|---|
| RE MAX | 21.76 | 121.21 | 22.45 |
| RE MIN | 0.07 | 1.19 | 0.01 |
| Soil Parameter | F1 | F2 | F3 | F4 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Base | Test | Base | Test | Base | Test | Base | Test | ||
| γt (LOIT) | R2 | 0.751 | 0.765 | 0.911 | 0.914 | 0.804 | 0.814 | 0.939 | 0.939 |
| MRE [%] | 7.06 | 7.05 | 3.79 | 3.84 | 6.42 | 6.47 | 2.85 | 2.90 | |
| MSE | 1.664 | 1.664 | 0.608 | 0.608 | 1.315 | 1.315 | 0.413 | 0.413 | |
| γt (w) | R2 | 0.791 | 0.802 | 0.933 | 0.942 | 0.840 | 0.850 | 0.975 | 0.976 |
| MRE [%] | 6.38 | 6.42 | 3.26 | 3.12 | 5.71 | 5.78 | 1.80 | 1.83 | |
| MSE | 1.411 | 1.411 | 0.450 | 0.450 | 1.086 | 1.086 | 0.174 | 0.174 | |
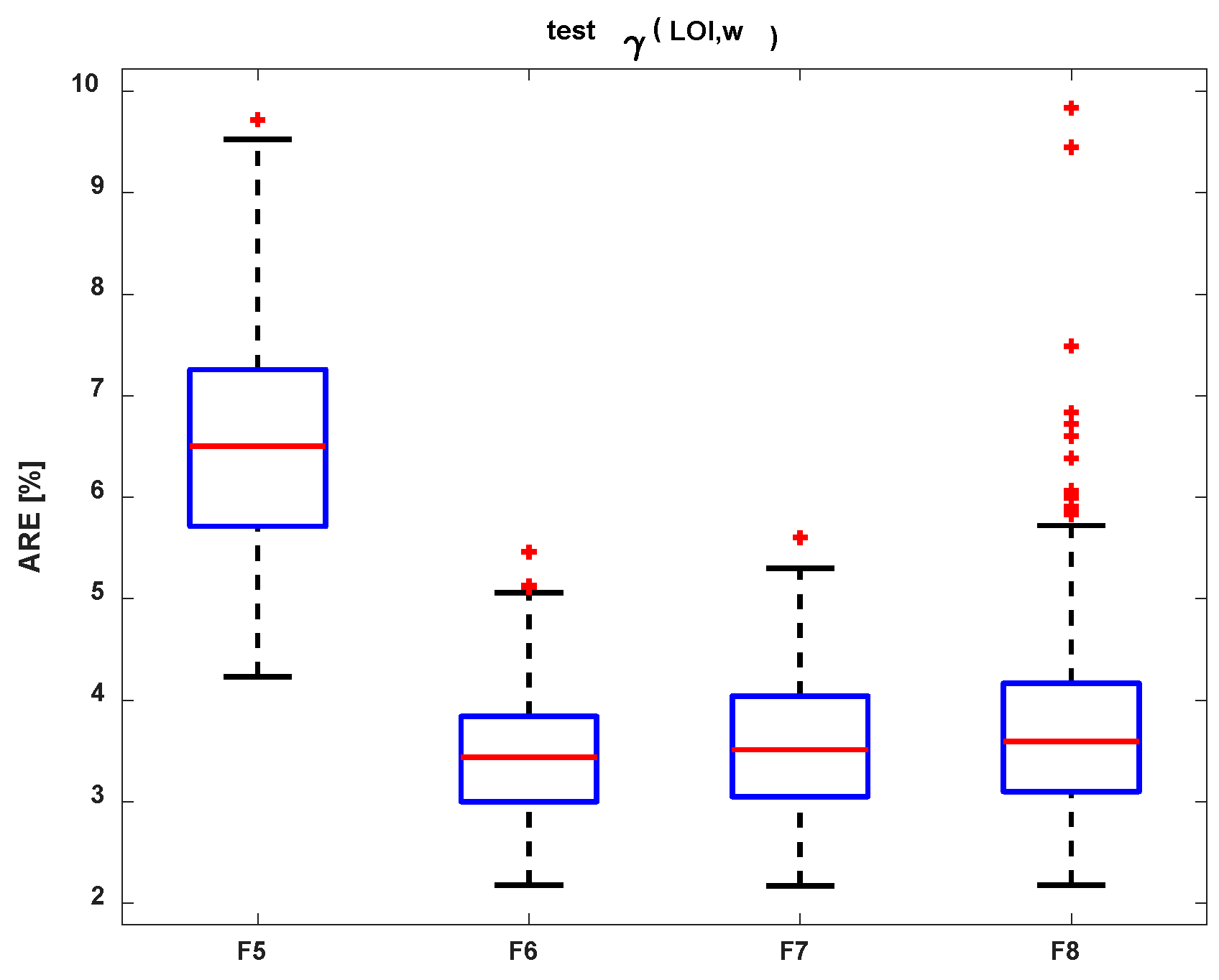
| Soil Parameter | F5 | F6 | F7 | F8 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Base | Test | Base | Test | Base | Test | Base | Test | ||
| γt (LOIT, w) | R2 | 0.798 | 0.798 | 0.938 | 0.936 | 0.938 | 0.935 | 0.939 | 0.932 |
| MRE [%] | 6.22 | 6.50 | 3.19 | 3.44 | 3.22 | 3.51 | 3.17 | 3.59 | |
| MSE | 1.367 | 1.423 | 0.415 | 0.426 | 0.416 | 0.470 | 0.410 | 0.484 | |
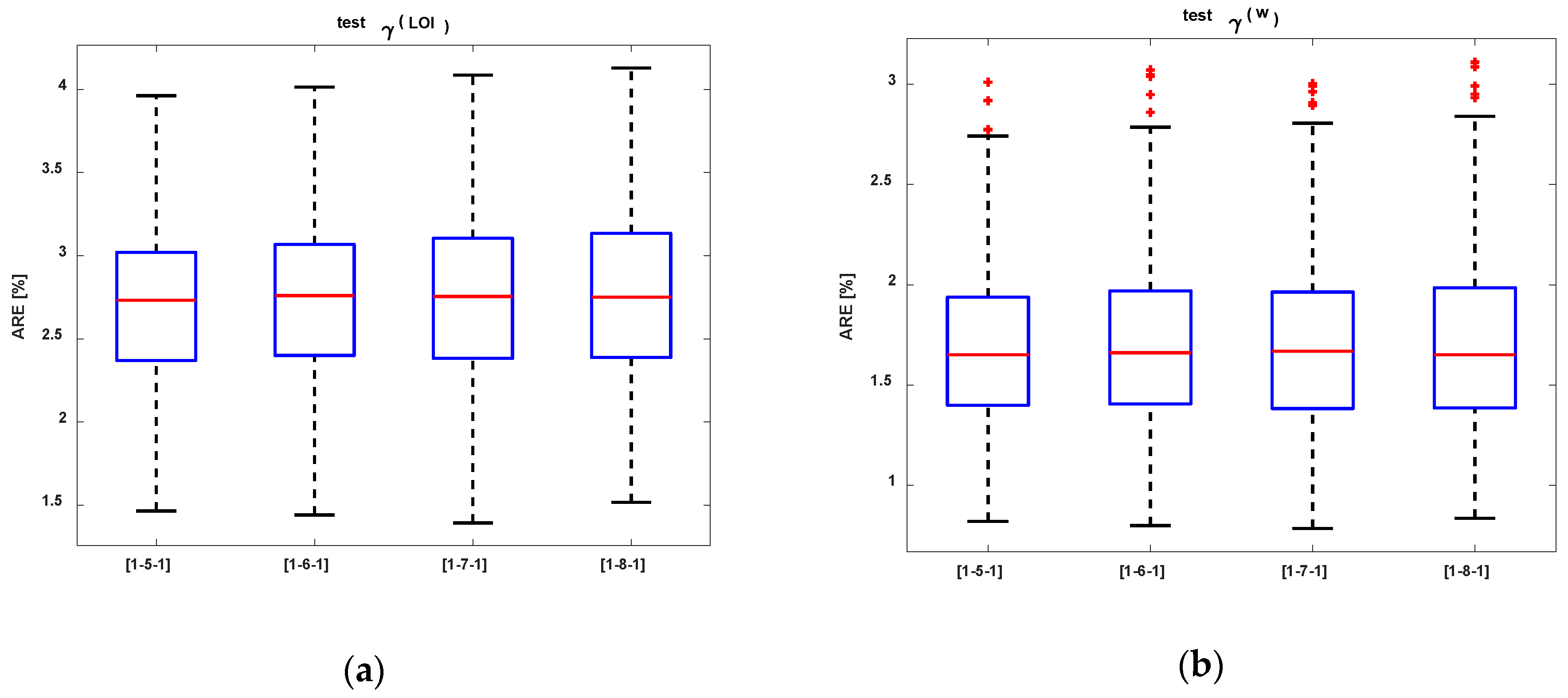
| Soil Parameter | [1-5-1] | [1-6-1] | [1-7-1] | [1-8-1] | |||||
|---|---|---|---|---|---|---|---|---|---|
| Learn | Test | Learn | Test | Learn | Test | Learn | Test | ||
| γt (LOIT) | R2 | 0.945 | 0.948 | 0.944 | 0.947 | 0.945 | 0.947 | 0.945 | 0.947 |
| MRE [%] | 2.70 | 2.73 | 2.69 | 2.76 | 2.68 | 2.76 | 2.64 | 2.75 | |
| MSE | 0.381 | 0.346 | 0.380 | 0.352 | 0.379 | 0.341 | 0.376 | 0.350 | |
| γt (w) | R2 | 0.976 | 0.978 | 0.977 | 0.979 | 0.977 | 0.979 | 0.977 | 0.979 |
| MRE [%] | 1.63 | 1.65 | 1.62 | 1.66 | 1.60 | 1.67 | 1.56 | 1.65 | |
| MSE | 0.160 | 0.146 | 0.160 | 0.143 | 0.159 | 0.144 | 0.158 | 0.144 | |
| Soil Parameter | [2-5-1] | [2-6-1] | [2-7-1] | [2-8-1] | |||||
|---|---|---|---|---|---|---|---|---|---|
| Learn | Test | Learn | Test | Learn | Test | Learn | Test | ||
| γt (LOIT, w) | R2 | 0.982 | 0.986 | 0.982 | 0.986 | 0.982 | 0.986 | 0.983 | 0.986 |
| MRE [%] | 1.39 | 1.44 | 1.39 | 1.42 | 1.36 | 1.40 | 1.36 | 1.42 | |
| MSE | 0.125 | 0.095 | 0.125 | 0.094 | 0.122 | 0.093 | 0.121 | 0.093 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Straż, G.; Borowiec, A. Estimating the Unit Weight of Local Organic Soils from Laboratory Tests Using Artificial Neural Networks. Appl. Sci. 2020, 10, 2261. https://doi.org/10.3390/app10072261
Straż G, Borowiec A. Estimating the Unit Weight of Local Organic Soils from Laboratory Tests Using Artificial Neural Networks. Applied Sciences. 2020; 10(7):2261. https://doi.org/10.3390/app10072261
Chicago/Turabian StyleStraż, Grzegorz, and Artur Borowiec. 2020. "Estimating the Unit Weight of Local Organic Soils from Laboratory Tests Using Artificial Neural Networks" Applied Sciences 10, no. 7: 2261. https://doi.org/10.3390/app10072261
APA StyleStraż, G., & Borowiec, A. (2020). Estimating the Unit Weight of Local Organic Soils from Laboratory Tests Using Artificial Neural Networks. Applied Sciences, 10(7), 2261. https://doi.org/10.3390/app10072261





