Experimental Analysis of a Visual-Recognition Control for an Autonomous Underwater Vehicle in a Towing Tank
Abstract
:1. Introduction
2. Autonomous Underwater Vehicle (AUV) Architecture
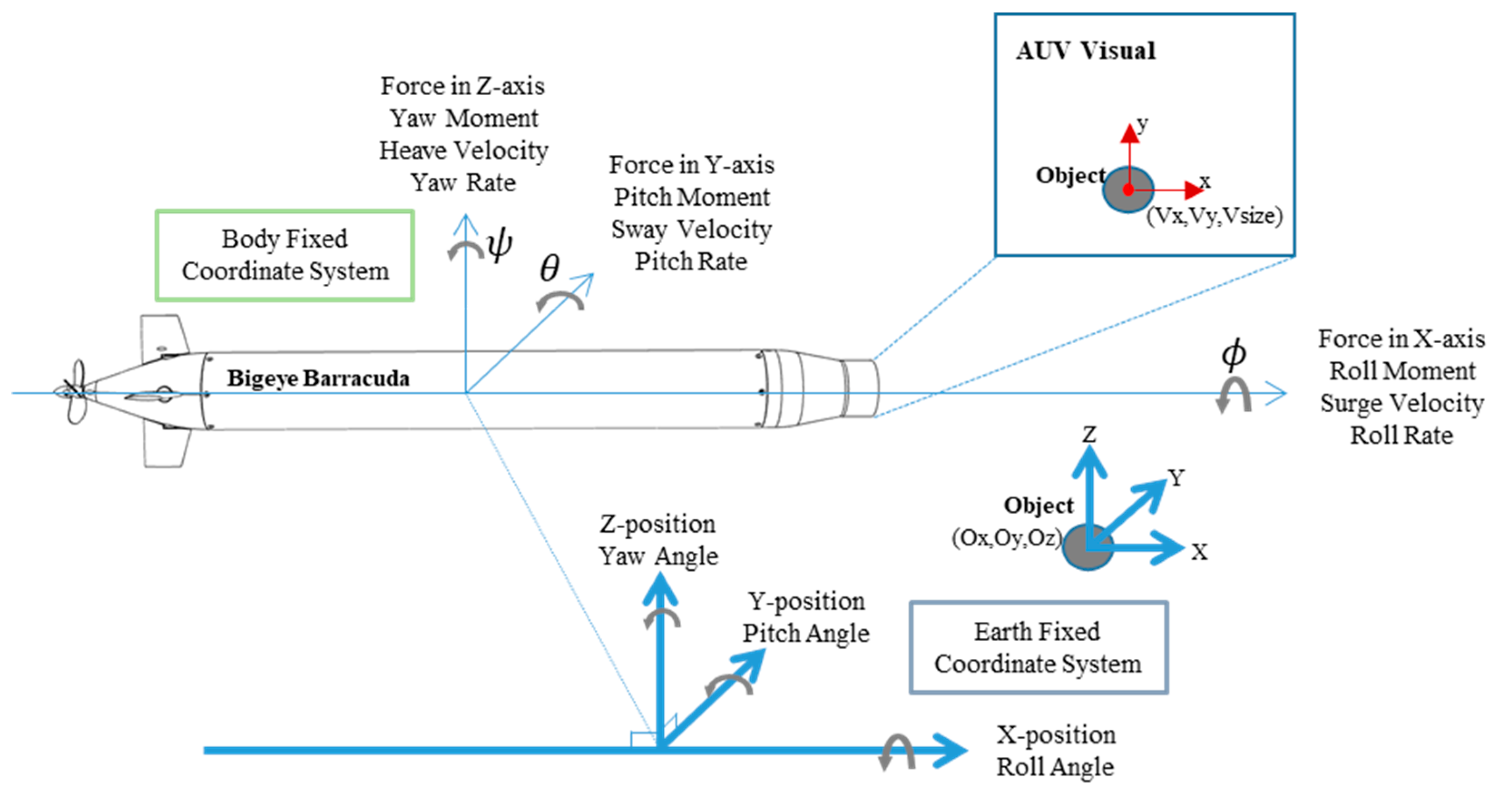
2.1. Autonomous Underwater Vehicle (AUV) Configuration
2.2. Hardware
2.3. Software
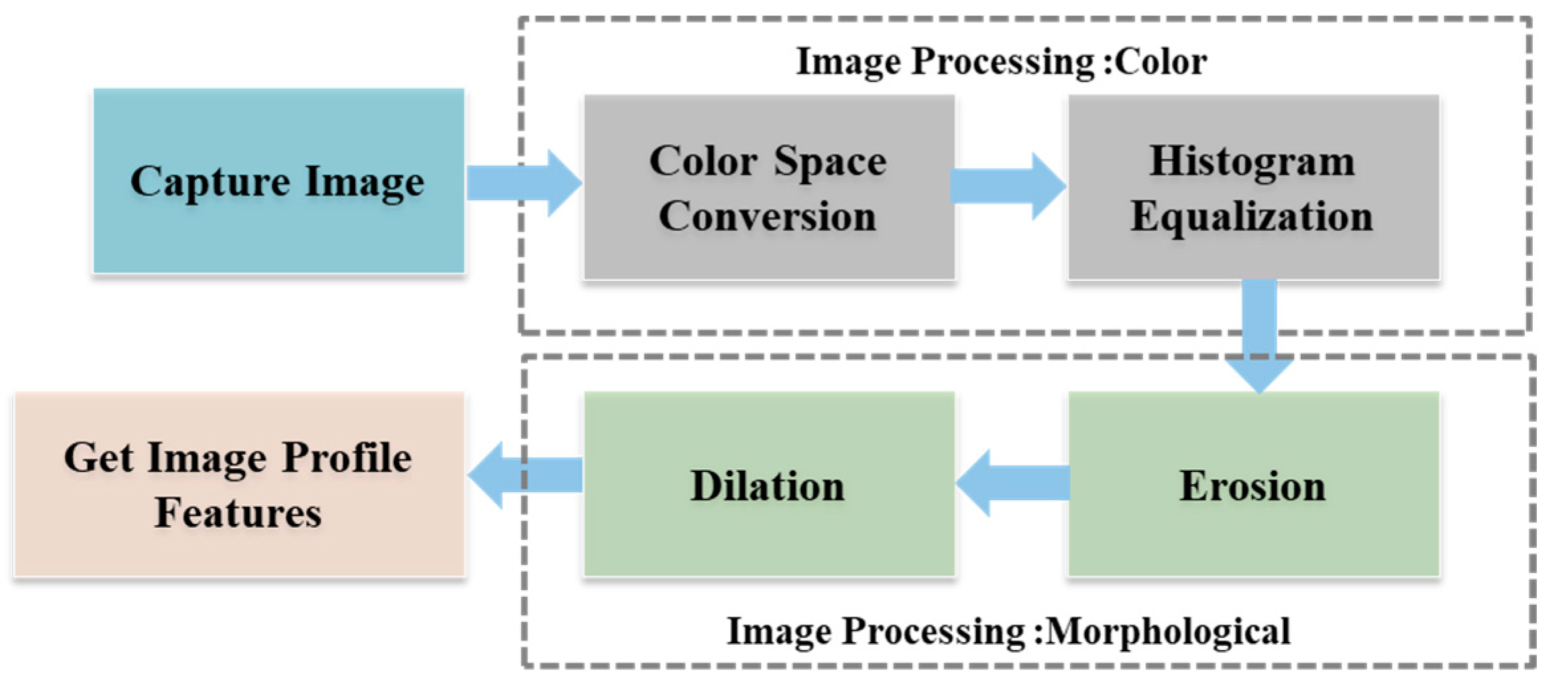
3. Visual-Based System
3.1. Visual-Recognition Procedure
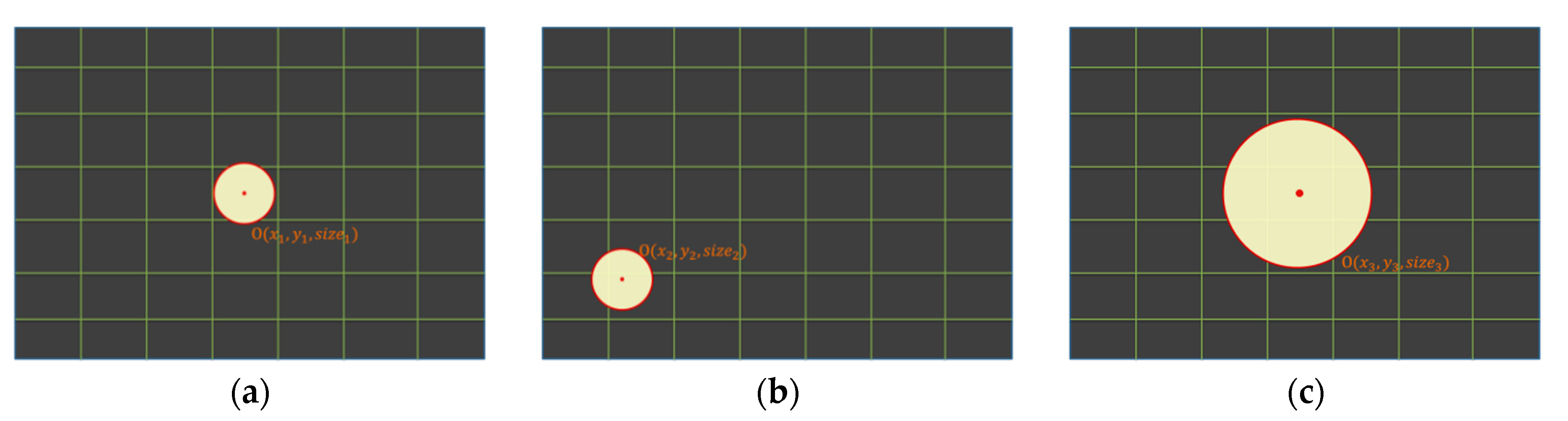
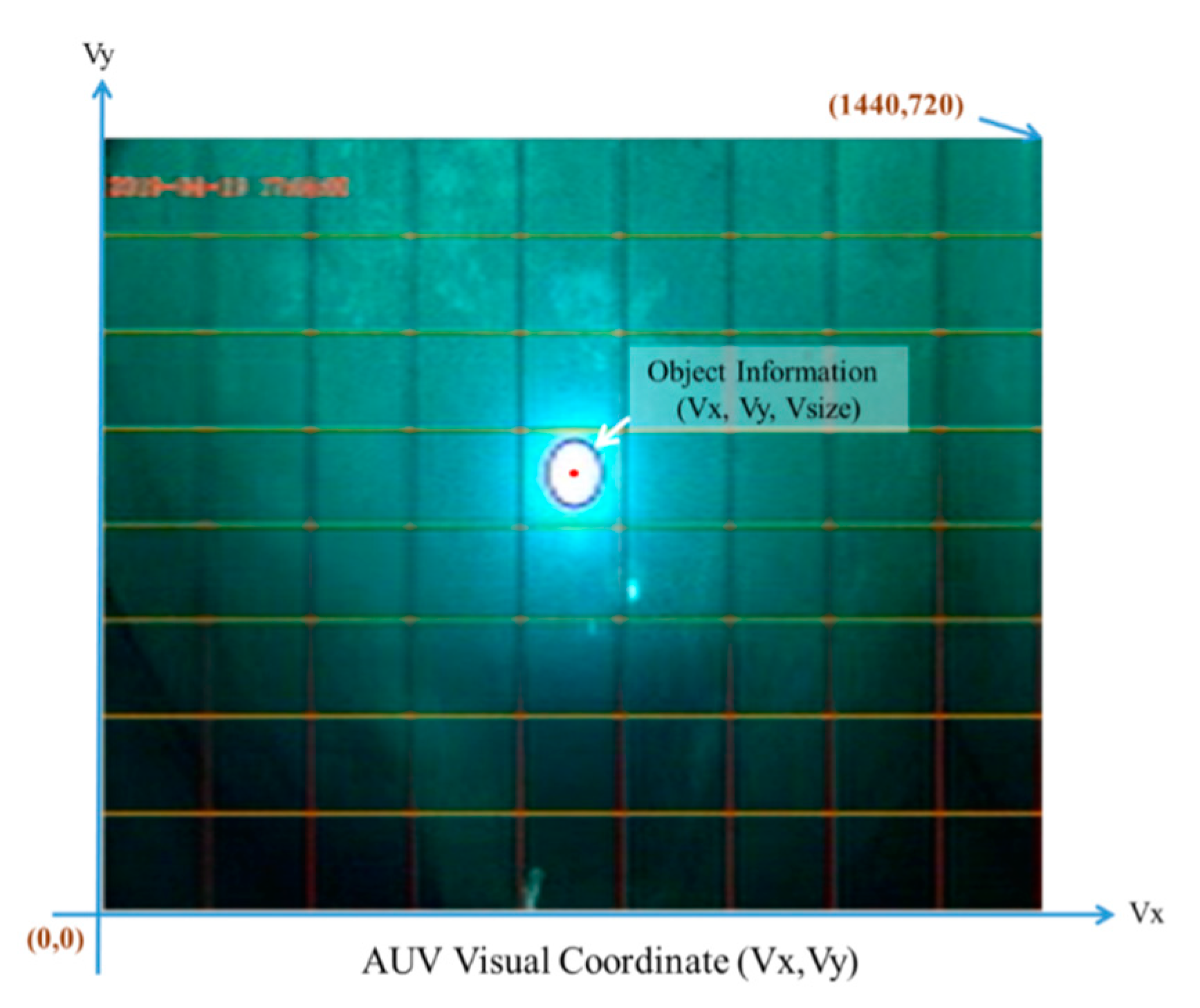
3.2. Visual Recognition and Object Tracking
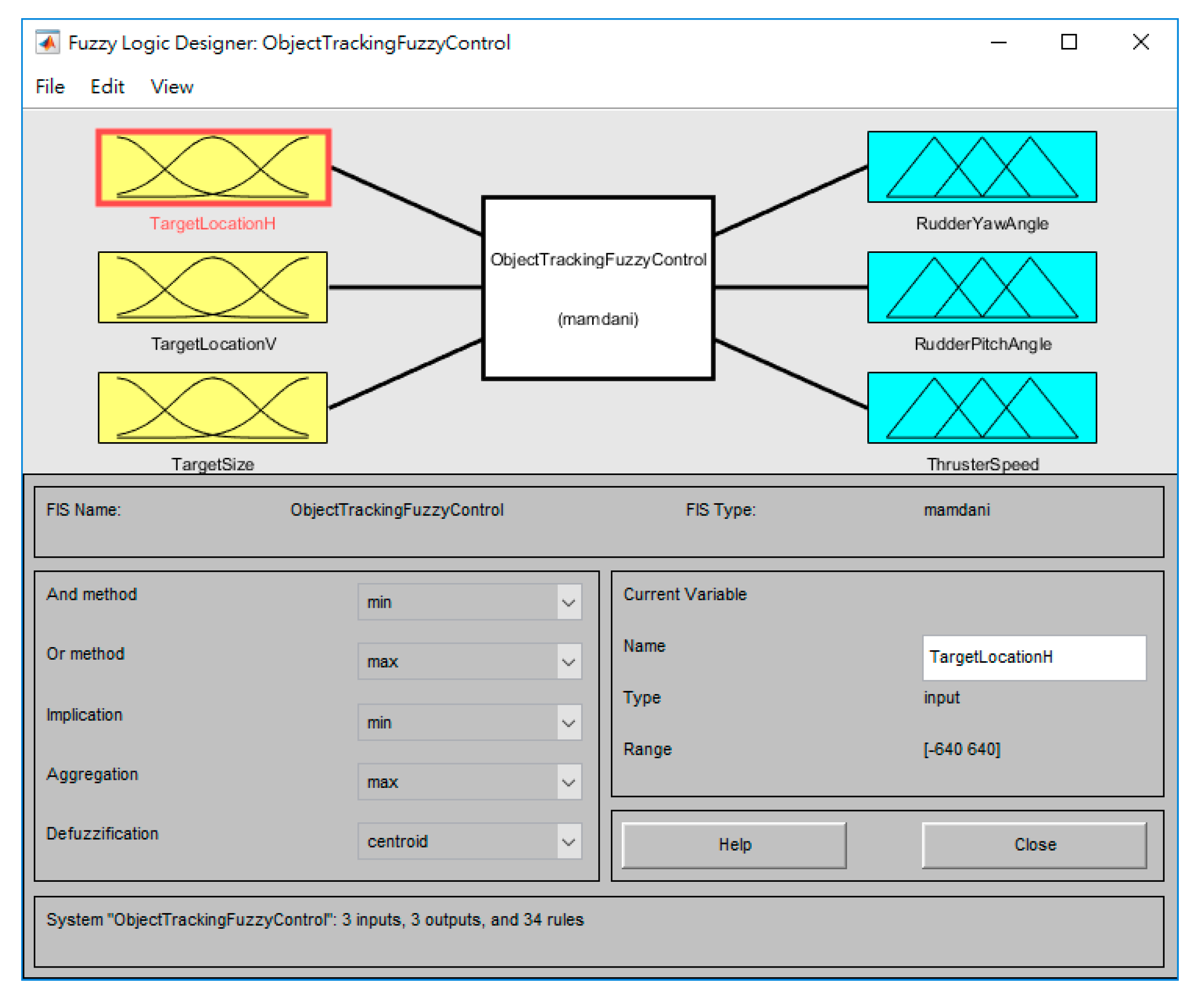
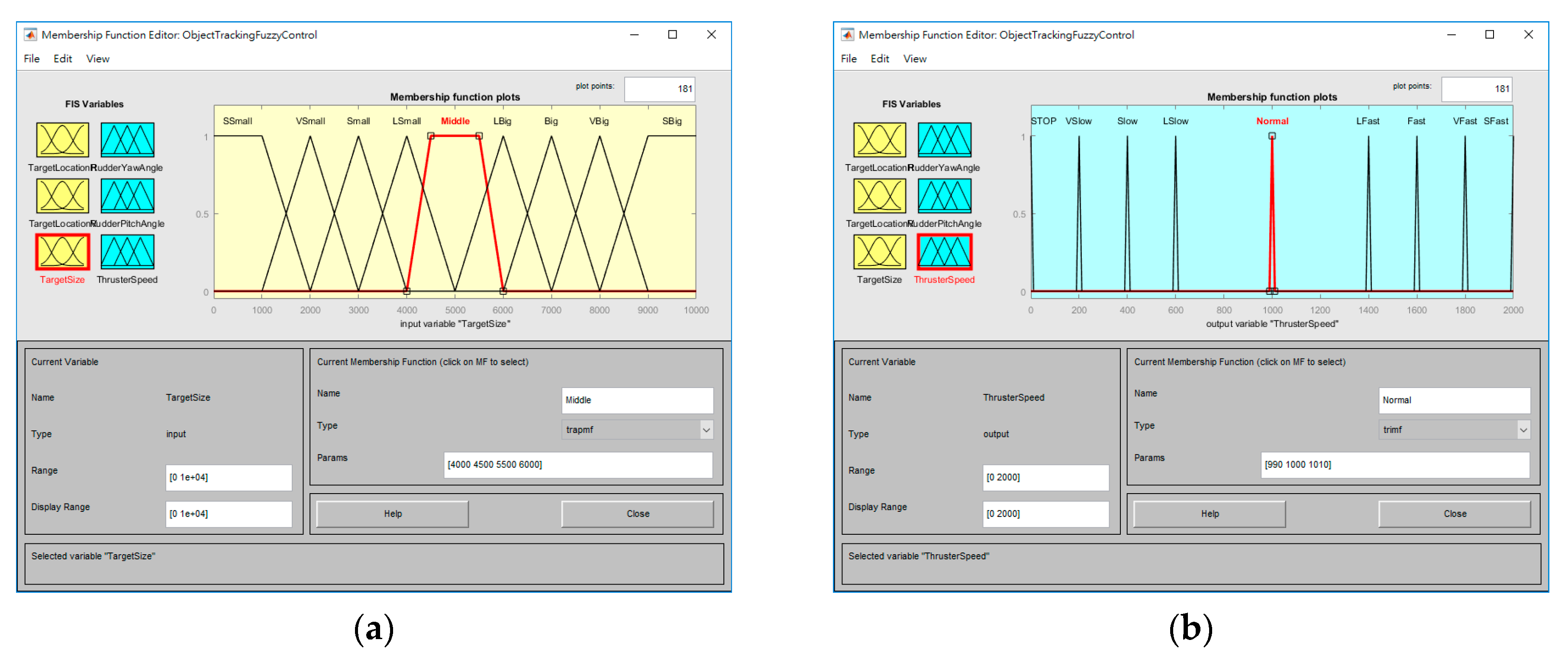
4. Fuzzy Control System
5. Results
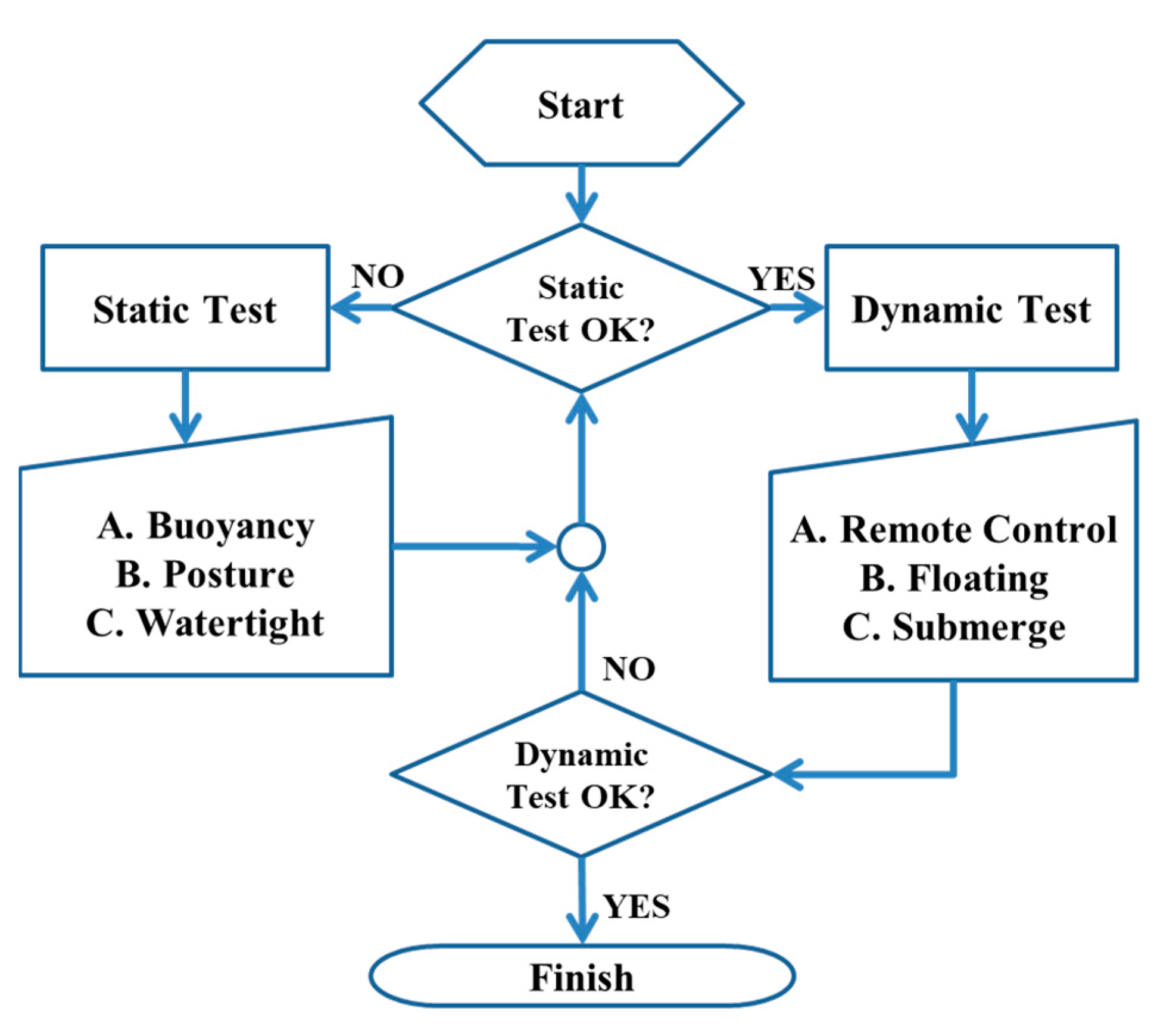
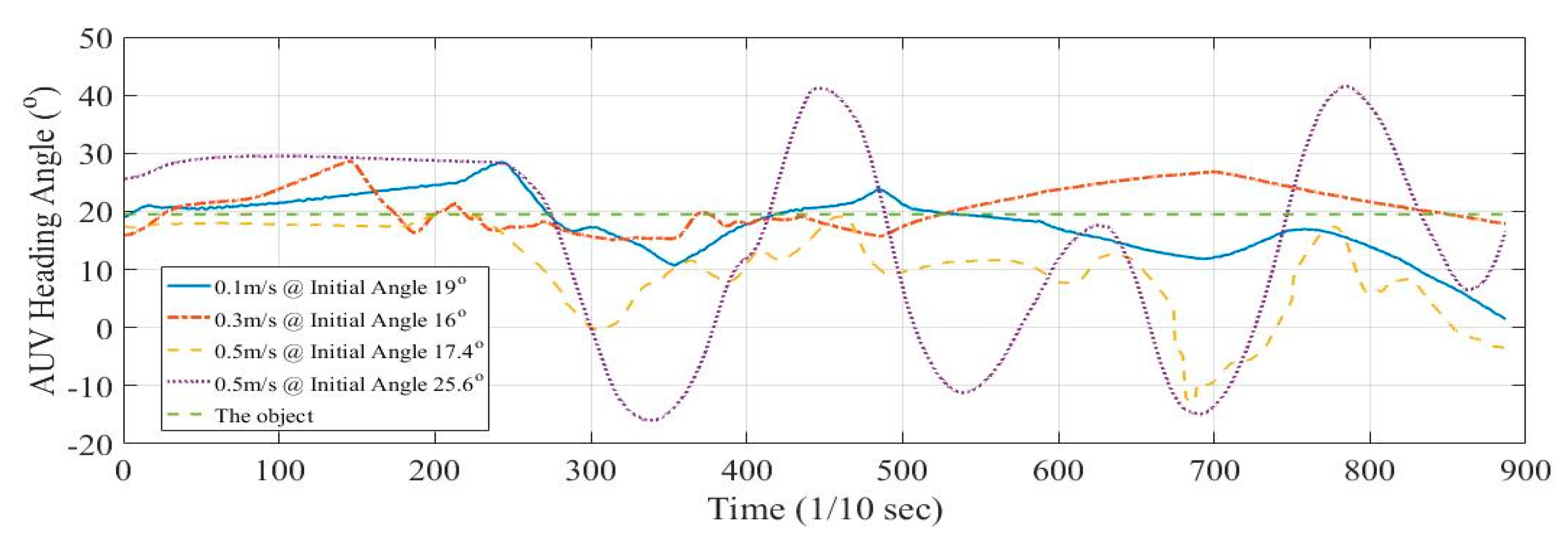
5.1. Fundamental Tests
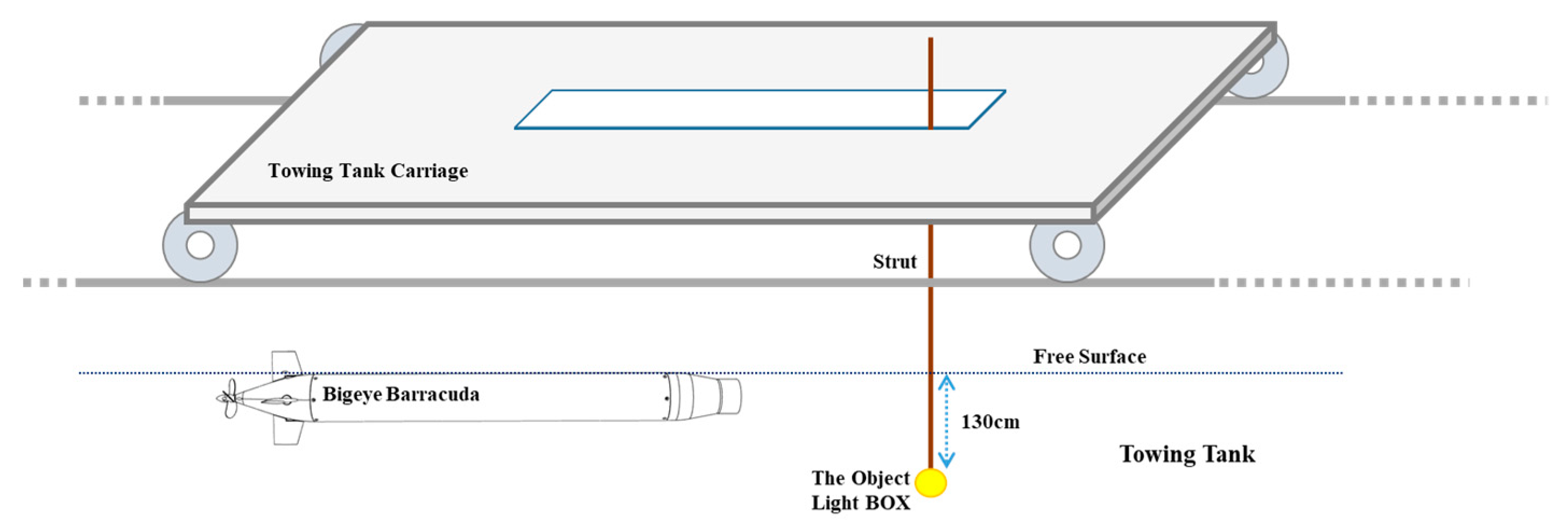
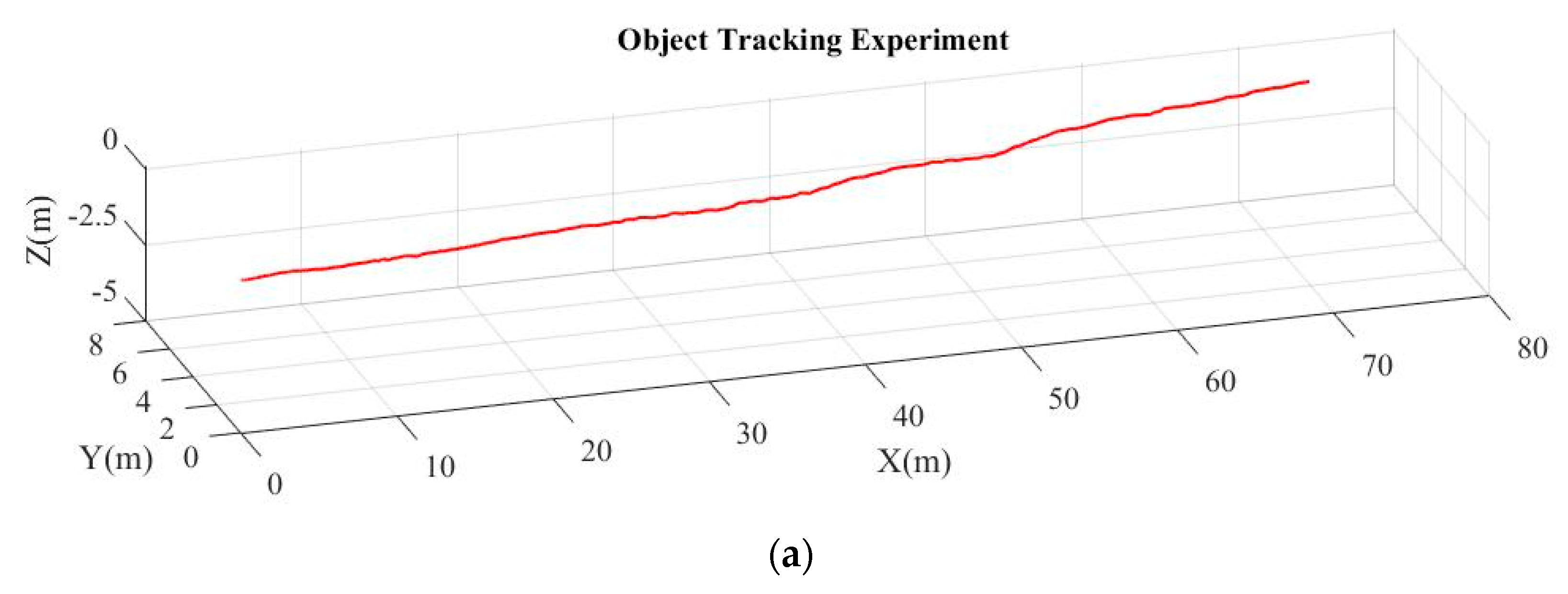
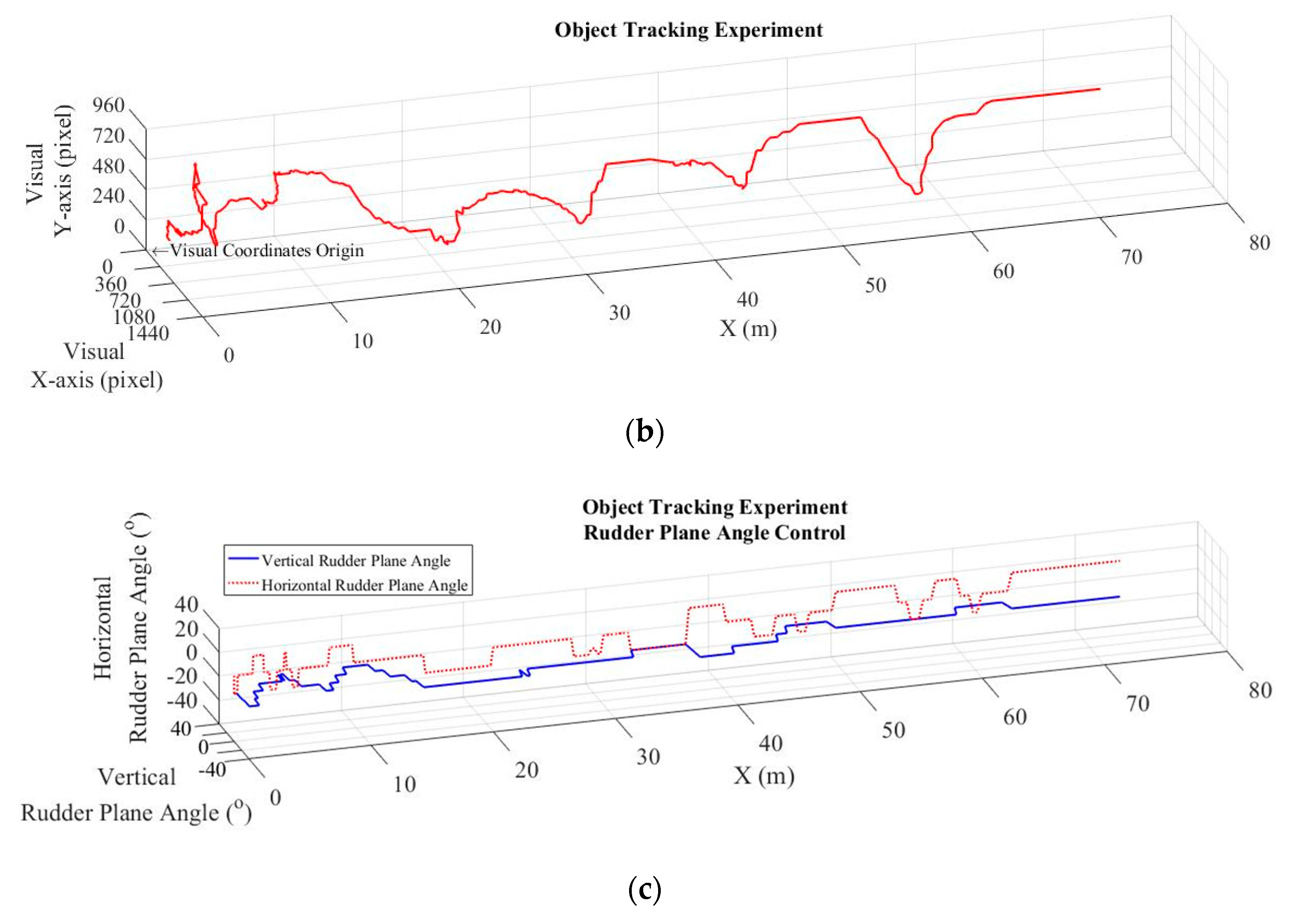
5.2. Visual-Recognition and Object-Tracking Tests
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Silverstone, P. The New Navy, 1883–1922; Taylor & Francis: Milton, UK, 2013. [Google Scholar]
- Michel, J.-L.; Le Roux, H. Epaulard:-Deep Bottom Surveys Now with Acoustic Remote Controlled Vehicle-First Operational Experience. In Proceedings of the OCEANS 81, Boston, MA, USA, 16–18 September 1981; pp. 99–103. [Google Scholar]
- Matsumoto, S.; Ito, Y. Real-time vision-based tracking of submarine-cables for AUV/ROV. In Proceedings of the Challenges of Our Changing Global Environment, San Diego, CA, USA, 9–12 October 1995; pp. 1997–2002. [Google Scholar]
- Santos-Victor, J.; Sentieiro, J. The role of vision for underwater vehicles. In Proceedings of the IEEE Symposium on Autonomous Underwater Vehicle Technology (AUV’94), Cambridge, MA, USA, 19–20 July 1994; pp. 28–35. [Google Scholar]
- Zingaretti, P.; Tascini, G.; Puliti, P.; Zanoli, S. Imaging approach to real-time tracking of submarine pipeline. In Proceedings of the Real-Time Imaging, San Jose, CA, USA, 5 March 1996; pp. 129–137. [Google Scholar]
- Karabchevsky, S.; Braginsky, B.; Guterman, H. AUV real-time acoustic vertical plane obstacle detection and avoidance. In Proceedings of the Autonomous Underwater Vehicles (AUV), 2012 IEEE/OES, Southampton, UK, 24–27 September 2012; pp. 1–6. [Google Scholar]
- Ito, Y.; Kato, N.; Kojima, J.; Takagi, S.; Asakawa, K.; Shirasaki, Y. Cable tracking for autonomous underwater vehicle. In Proceedings of the IEEE Symposium on Autonomous Underwater Vehicle Technology (AUV’94), Cambridge, MA, USA, 19–20 July 1994; pp. 218–224. [Google Scholar]
- Nguyen, H.G.; Kaomea, P.K.; Heckman Jr, P.J. Machine visual guidance for an autonomous undersea submersible. In Proceedings of the Underwater Imaging, San Diego, CA, USA, 16 December 1988; pp. 82–89. [Google Scholar]
- Balasuriya, B.; Takai, M.; Lam, W.; Ura, T.; Kuroda, Y. Vision based autonomous underwater vehicle navigation: Underwater cable tracking. In Proceedings of the Oceans’ 97, MTS/IEEE Conference Proceedings, Halifax, NS, Canada, 6–9 October 1997; pp. 1418–1424. [Google Scholar]
- Foresti, G.L. Visual inspection of sea bottom structures by an autonomous underwater vehicle. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2001, 31, 691–705. [Google Scholar] [CrossRef] [PubMed]
- Lee, P.-M.; Jeon, B.-H.; Kim, S.-M. Visual servoing for underwater docking of an autonomous underwater vehicle with one camera. In Proceedings of the Oceans 2003. Celebrating the Past... Teaming Toward the Future (IEEE Cat. No. 03CH37492), San Diego, CA, USA, 22–26 September 2003; pp. 677–682. [Google Scholar]
- Smith, S.; Rae, G.; Anderson, D. Applications of fuzzy logic to the control of an autonomous underwater vehicle. In Proceedings of the Second IEEE International Conference on Fuzzy Systems, San Francisco, CA, USA, 28 March–1 April 1993; pp. 1099–1106. [Google Scholar]
- Song, F.; Smith, S.M. Design of sliding mode fuzzy controllers for an autonomous underwater vehicle without system model. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition. Conference Proceedings (Cat. No. 00CH37158), Providence, RI, USA, 11–14 September 2000; pp. 835–840. [Google Scholar]
- Teo, K.; An, E.; Beaujean, P.-P.J. A robust fuzzy autonomous underwater vehicle (AUV) docking approach for unknown current disturbances. IEEE J. Ocean. Eng. 2012, 37, 143–155. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Wang, S.-M.; Huang, L.-C.; Fang, M.-C. Applying the stereo-vision detection technique to the development of underwater inspection task with PSO-based dynamic routing algorithm for autonomous underwater vehicles. Ocean. Eng. 2017, 139, 127–139. [Google Scholar] [CrossRef]
- Leonard, J.J.; Bahr, A. Autonomous underwater vehicle navigation. In Springer Handbook of Ocean Engineering; Springer: Berlin, Germany, 2016; pp. 341–358. [Google Scholar]
- Schechner, Y.Y.; Karpel, N. Clear underwater vision. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004. [Google Scholar]
- Park, J.-Y.; Jun, B.-h.; Lee, P.-m.; Oh, J. Experiments on vision guided docking of an autonomous underwater vehicle using one camera. Ocean. Eng. 2009, 36, 48–61. [Google Scholar] [CrossRef]
- Fan, Y.; Balasuriya, A. Optical flow based speed estimation in AUV target tracking. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference Proceedings (IEEE Cat. No. 01CH37295), Honolulu, HI, USA, 5–8 November 2001; pp. 2377–2382. [Google Scholar]
- Kim, D.; Lee, D.; Myung, H.; Choi, H.-T. Object detection and tracking for autonomous underwater robots using weighted template matching. In Proceedings of the 2012 Oceans-Yeosu, Yeosu, Korea, 21–24 May 2012; pp. 1–5. [Google Scholar]
- Prestero, T. Development of a six-degree of freedom simulation model for the REMUS autonomous underwater vehicle. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference Proceedings (IEEE Cat. No. 01CH37295), Honolulu, HI, USA, 5–8 November 2001; pp. 450–455. [Google Scholar]
- Woods, R.; Gonzalez, R. Real-time digital image enhancement. Proc. IEEE 1981, 69, 643–654. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Image processing. Digit. Image Process. 2007, 2, 1. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Gander, W.; Golub, G.H.; Strebel, R. Least-squares fitting of circles and ellipses. BIT Numer. Math. 1994, 34, 558–578. [Google Scholar] [CrossRef]
- Ahn, S.J.; Rauh, W.; Warnecke, H.-J. Least-squares orthogonal distances fitting of circle, sphere, ellipse, hyperbola, and parabola. Pattern Recognit. 2001, 34, 2283–2303. [Google Scholar] [CrossRef]
- Weber, S. A general concept of fuzzy connectives, negations and implications based on t-norms and t-conorms. Fuzzy Set Syst. 1983, 11, 115–134. [Google Scholar] [CrossRef]










| Type | Torpedo |
|---|---|
| Diameter | 17 cm |
| Total length | 180 cm |
| Weight (in the air) | 35 kg |
| Max. operating depth (ideal) | 200 m |
| Power source | Lithium battery |
| Max. velocity (ideal) | 5 Knot |
| Endurance (ideal) | 12 h at 2.5 knot |
| Propeller type | Four-blade propeller |
| Rudder control | Four independent servo control interfaces |
| Attitude sensor | High precision INS |
| Communication | 2.4 GHz wireless |
| Image module | Dual-lens camera and wind-angle camera |
| Processing | Inter ATOM SoC E3845 |
| HDD | 64 GB SSD HD |
| SD card | 32 GB |
| Vertical Rudder Plane | Vision Plant Object Location | |||||
|---|---|---|---|---|---|---|
| Strong Left | Left | Middle | Right | Strong Right | ||
| Rudder Angle | Strong Left | Keep | Right | Strong Right | Strong Right | Strong Right |
| Left | Left | Keep | Right | Strong Right | Strong Right | |
| Middle | Strong Left | Left | Keep | Right | Strong Right | |
| Right | Strong Left | Strong Left | Left | Keep | Right | |
| Strong Right | Strong Left | Strong Left | Strong Left | Left | Keep | |
| Horizontal Rudder Plane | Vision Plant Object Location | |||||
|---|---|---|---|---|---|---|
| Strong Up | Up | Middle | Down | Strong Down | ||
| Rudder Angle | Strong Up | Keep | Up | Strong Up | Strong Up | Strong Up |
| UP | Down | Keep | Up | Strong Up | Strong Up | |
| Middle | Strong Down | Down | Keep | Up | Strong Up | |
| Down | Strong Down | Strong Down | Down | Keep | Up | |
| Strong Down | Strong Down | Strong Down | Strong Down | Down | Keep | |
| Thruster Velocity Plane | Vision Plant Object Size | |||||
| Ssmall | VSmall | Small | LSmall | Normal | ||
| Thruster Rate | SFast | Normal | LFast | Fast | VFast | SFast |
| VFast | LSlow | Normal | LFast | Fast | VFast | |
| Fast | Slow | LSlow | Normal | LFast | Fast | |
| LFast | VSlow | Slow | LSlow | Normal | LFast | |
| Normal | SSlow | VSlow | Slow | LSlow | Normal | |
| LSlow | STOP | SSlow | VSlow | Slow | LSlow | |
| Slow | STOP | STOP | SSlow | VSlow | Slow | |
| VSlow | STOP | STOP | STOP | SSlow | VSlow | |
| Stop | STOP | STOP | STOP | STOP | SSlow | |
| Thruster Velocity Plane | Vision Plant Object Size | |||||
| Lbig | Big | Vbig | Sbig | |||
| Thruster Rate | SFast | SFast | SFast | SFast | SFast | |
| VFast | SFast | SFast | SFast | SFast | ||
| Fast | VFast | SFast | SFast | SFast | ||
| LFast | Fast | VFast | SFast | SFast | ||
| Normal | LFast | Fast | VFast | SFast | ||
| LSlow | Normal | LFast | Fast | VFast | ||
| Slow | LSlow | Normal | LFast | Fast | ||
| VSlow | Slow | LSlow | Normal | LFast | ||
| Stop | VSlow | Slow | LSlow | Normal | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.-M.; Lin, Y.-H. Experimental Analysis of a Visual-Recognition Control for an Autonomous Underwater Vehicle in a Towing Tank. Appl. Sci. 2020, 10, 2480. https://doi.org/10.3390/app10072480
Yu C-M, Lin Y-H. Experimental Analysis of a Visual-Recognition Control for an Autonomous Underwater Vehicle in a Towing Tank. Applied Sciences. 2020; 10(7):2480. https://doi.org/10.3390/app10072480
Chicago/Turabian StyleYu, Chao-Ming, and Yu-Hsien Lin. 2020. "Experimental Analysis of a Visual-Recognition Control for an Autonomous Underwater Vehicle in a Towing Tank" Applied Sciences 10, no. 7: 2480. https://doi.org/10.3390/app10072480
APA StyleYu, C.-M., & Lin, Y.-H. (2020). Experimental Analysis of a Visual-Recognition Control for an Autonomous Underwater Vehicle in a Towing Tank. Applied Sciences, 10(7), 2480. https://doi.org/10.3390/app10072480





