Experimental Investigation of Stochastic Mechanical Behavior of Cement Emulsified Asphalt Mortar under Monotonic Compression
Abstract
1. Introduction
2. Experimental Program
2.1. Raw Materials
2.2. Specimens Preparation
2.3. Experimental Setup
3. Experimental Results and Discussion
3.1. Failure Mode
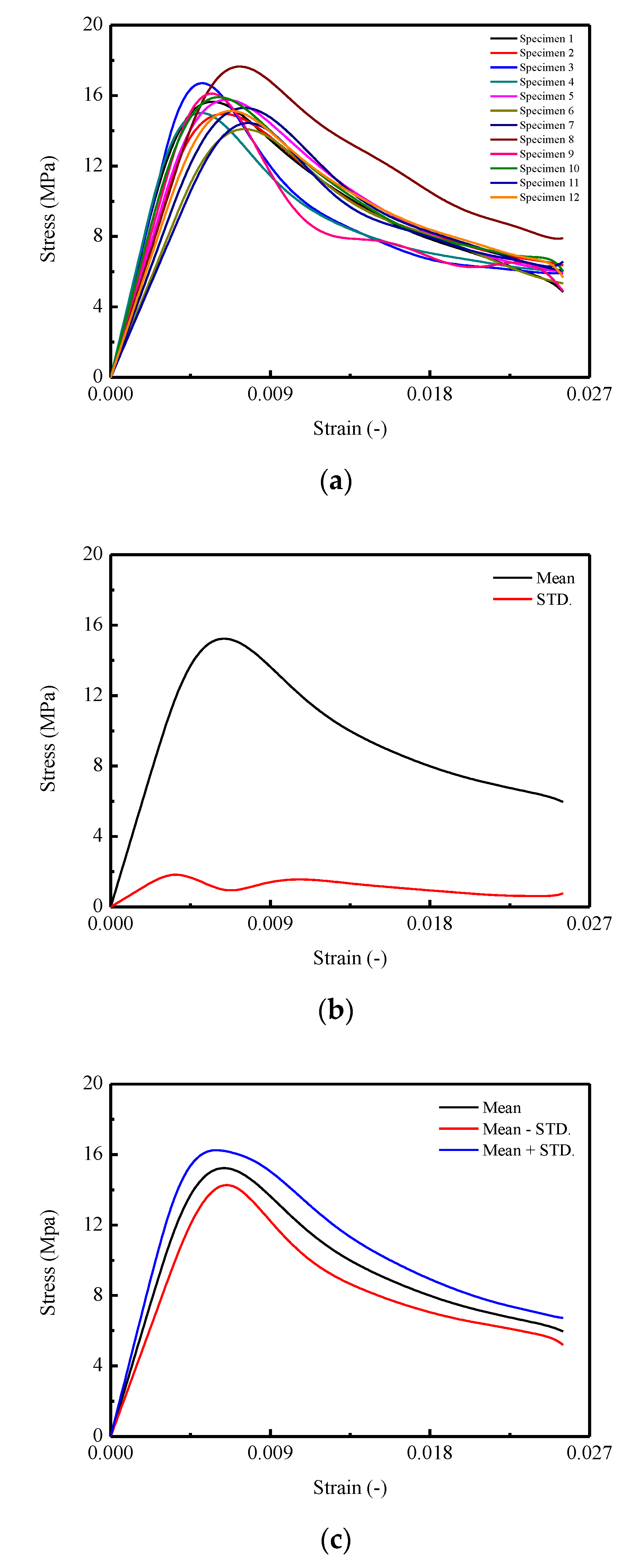
3.2. Strengths and Critical Strain
3.3. Young’s Modulus
3.3.1. Initial Young’s Modulus
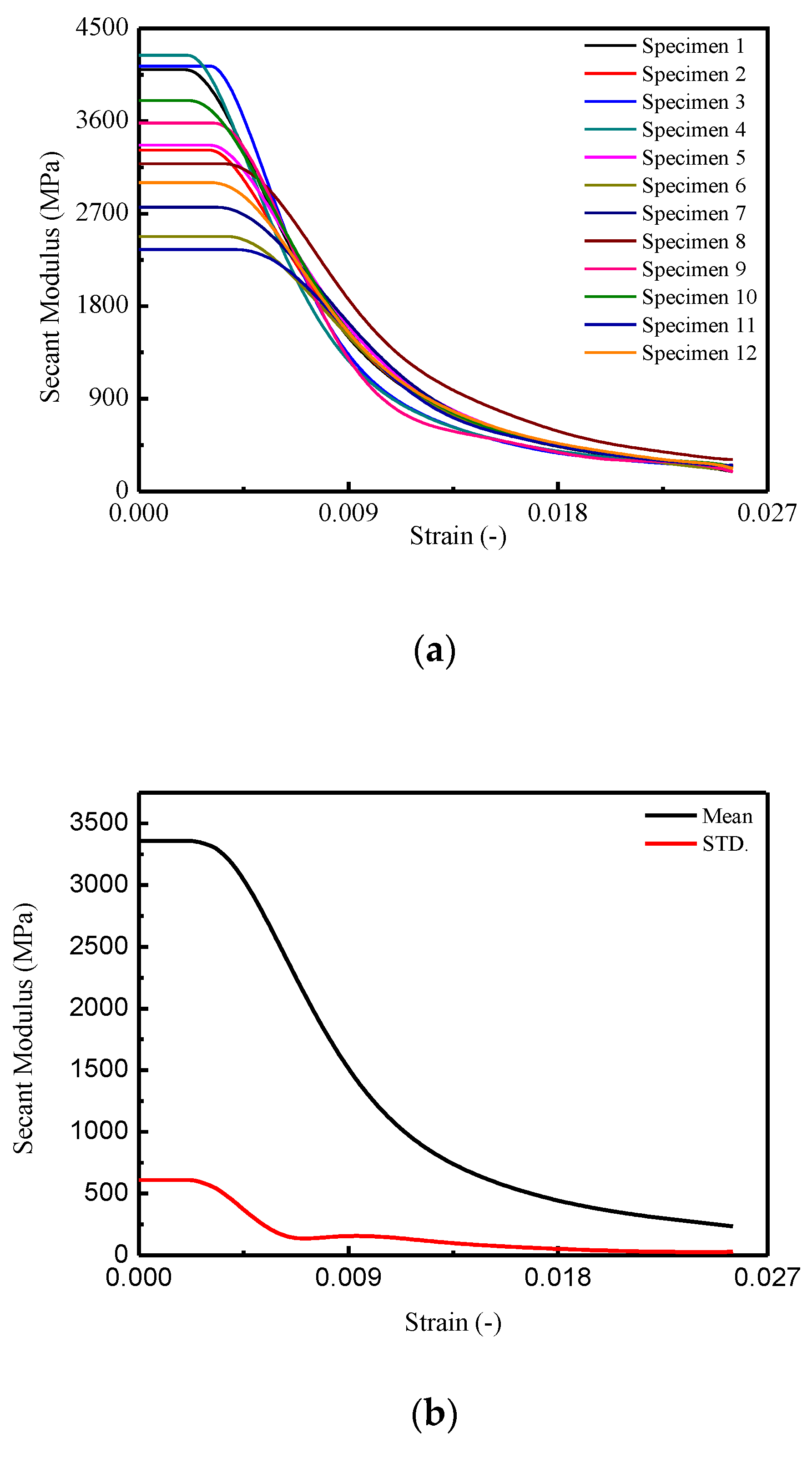
3.3.2. Secant Young’s Modulus
3.4. Complete Stress–Strain Curves
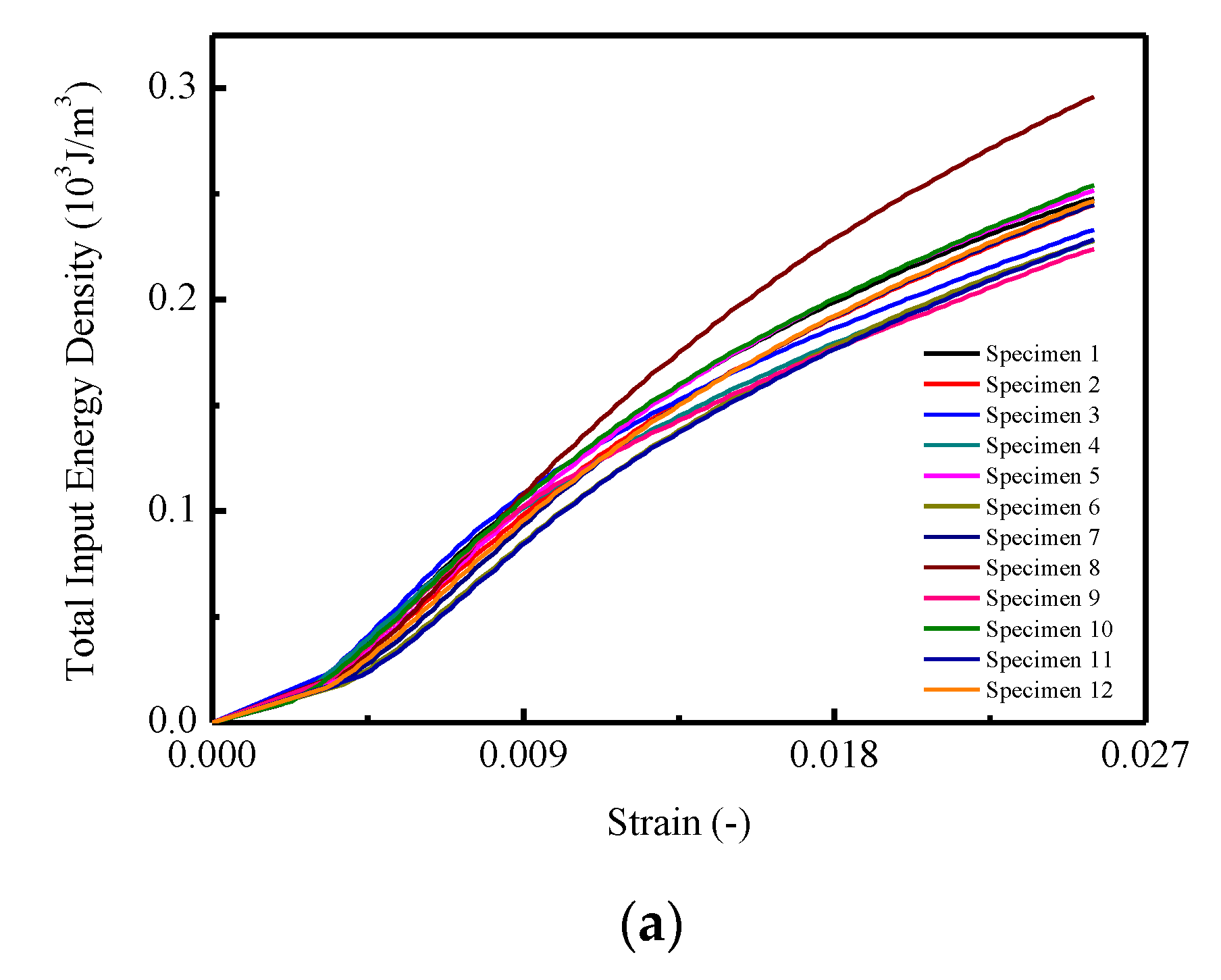
3.5. Energy Dissipation
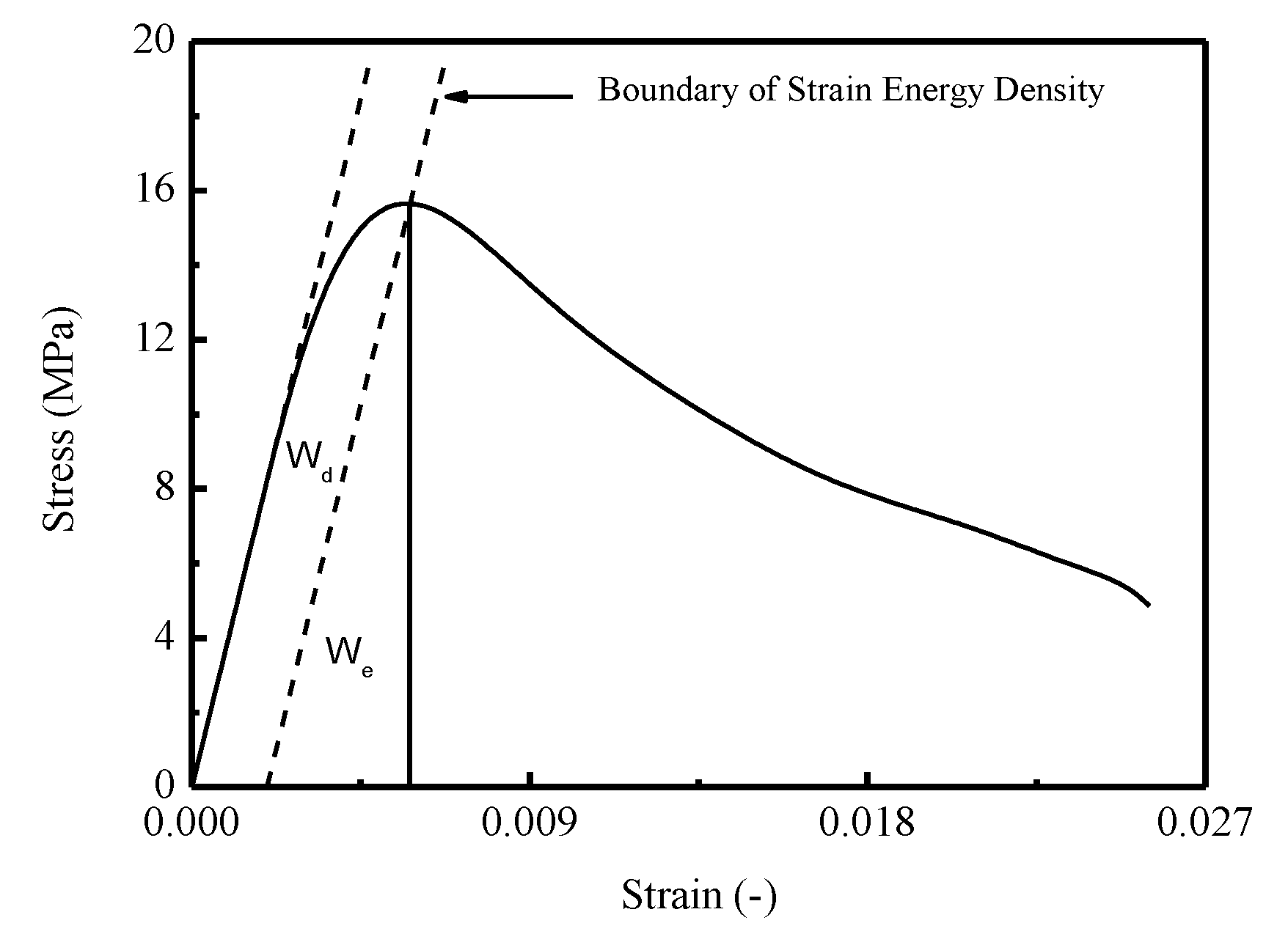
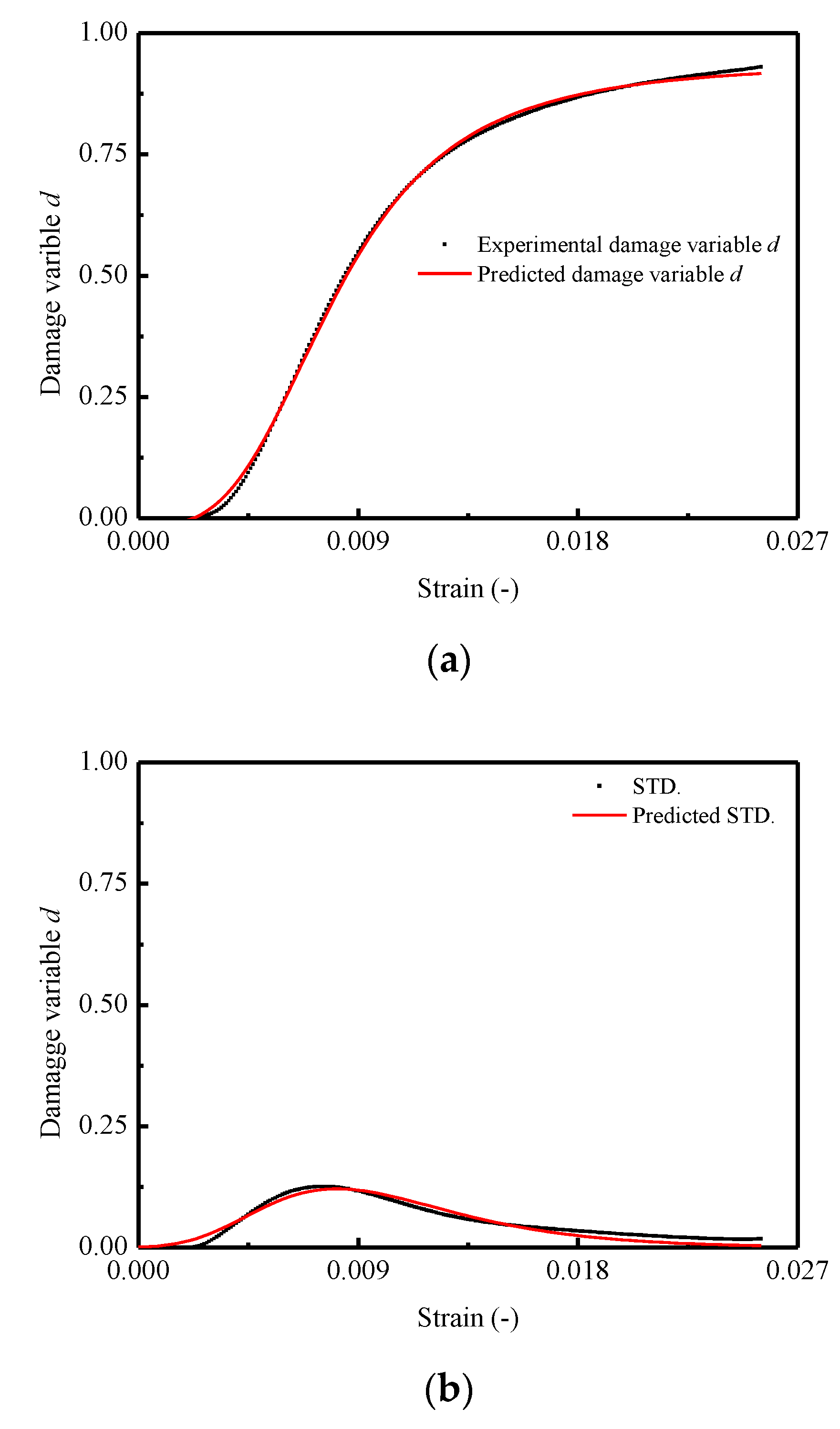
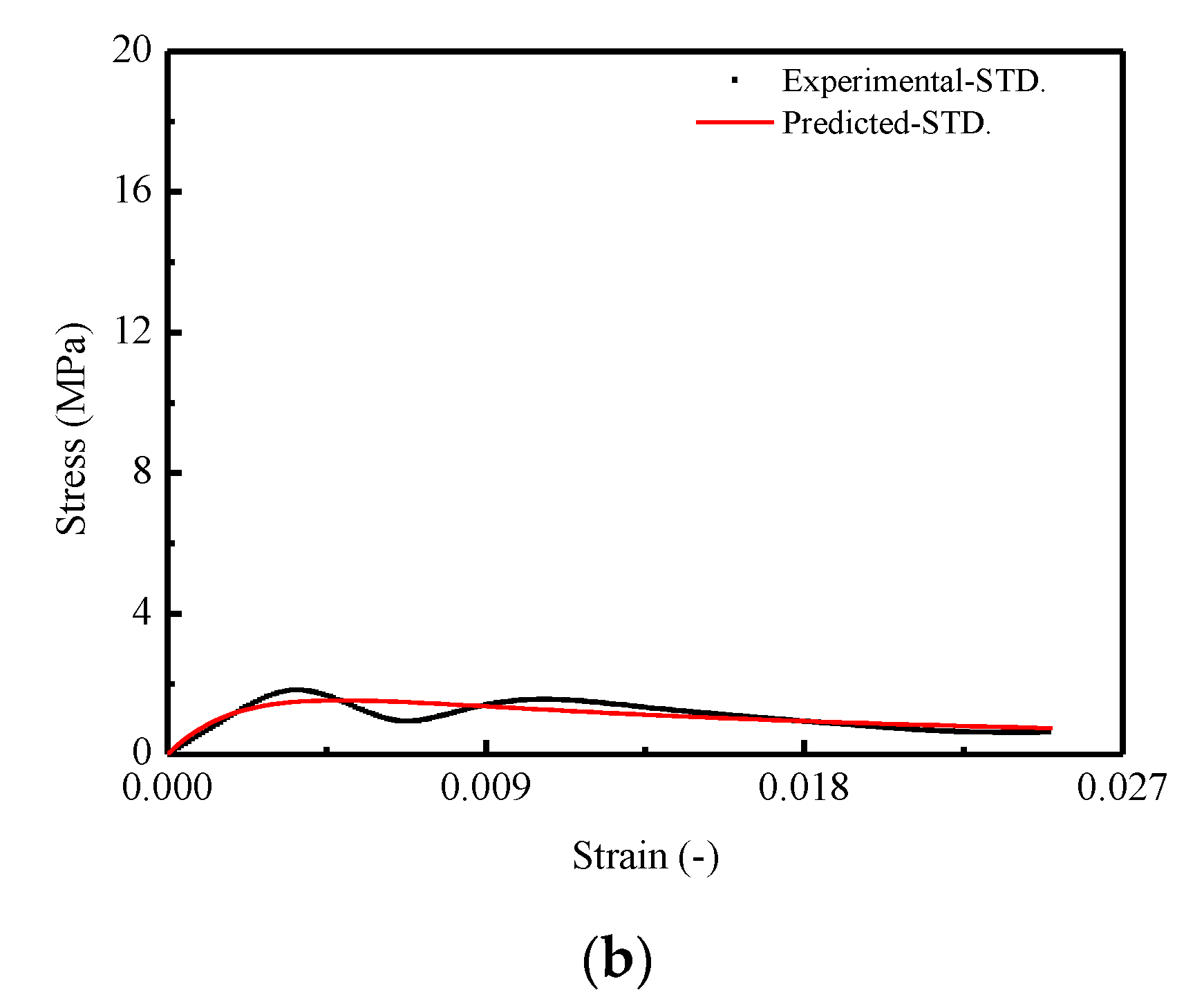
3.6. Damage Model of Stress–Strain Relationship
3.6.1. Brief Review of BCM
3.6.2. Analytical Model of CA Mortar
3.6.3. Model Verification
4. Further Discussion
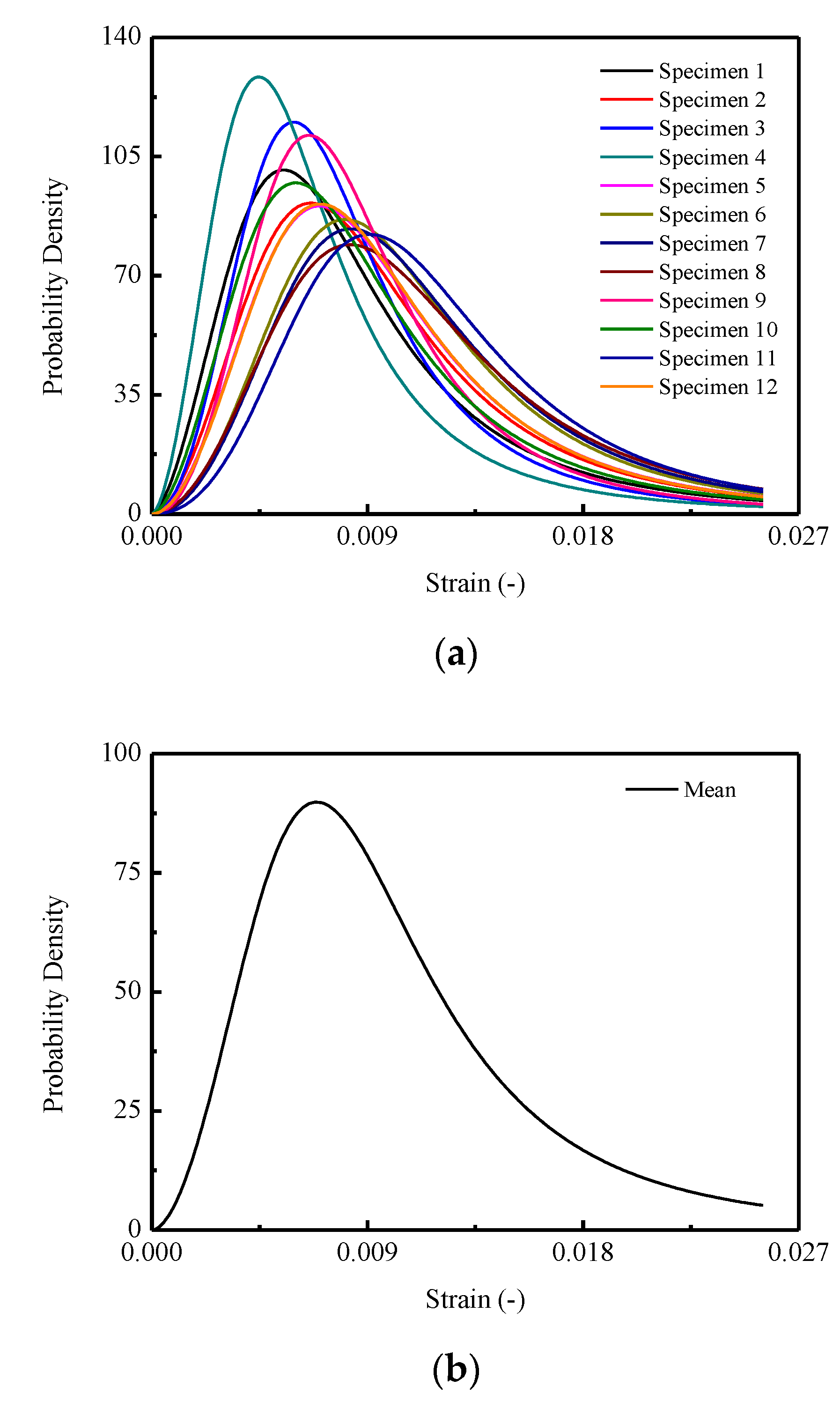
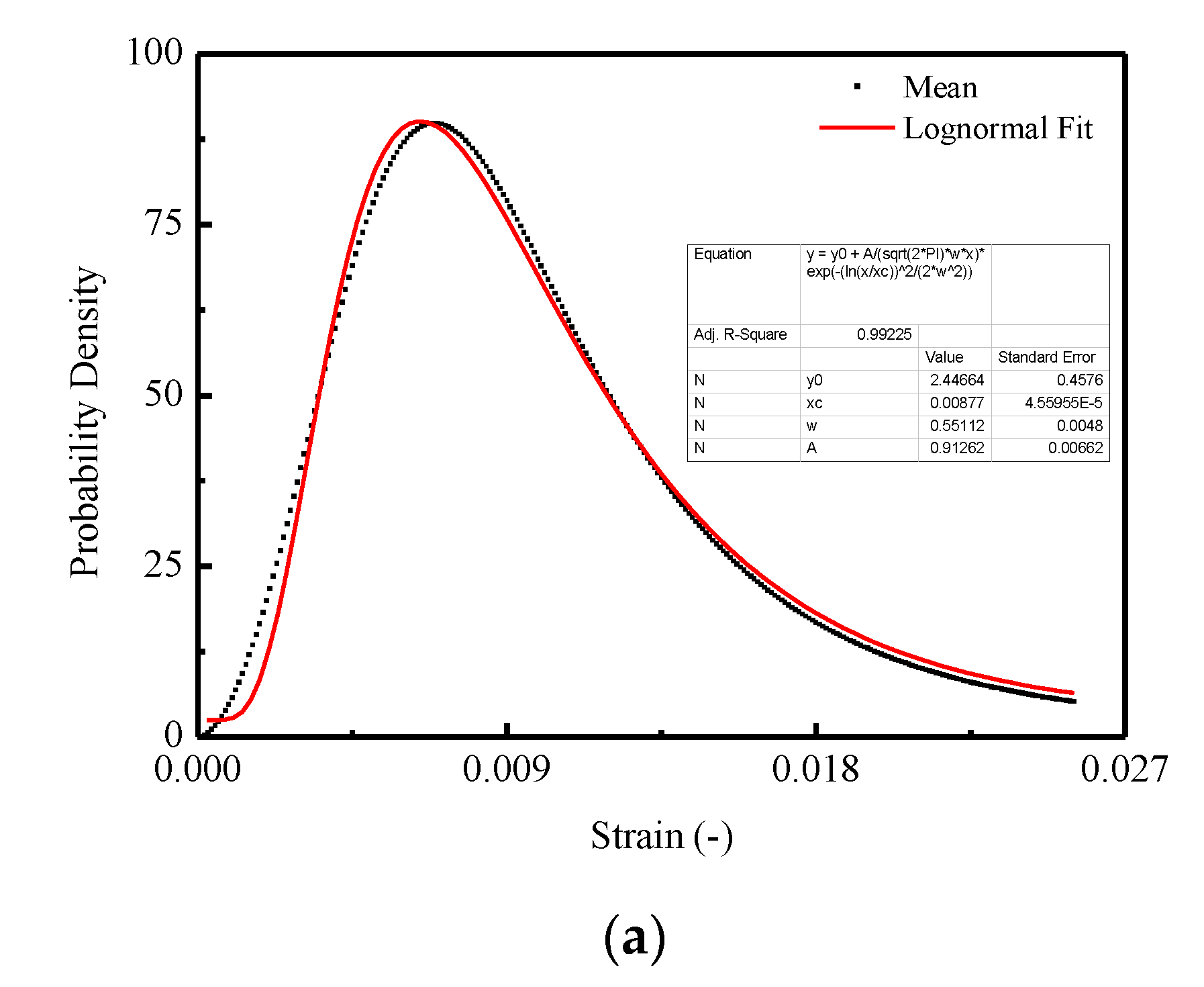
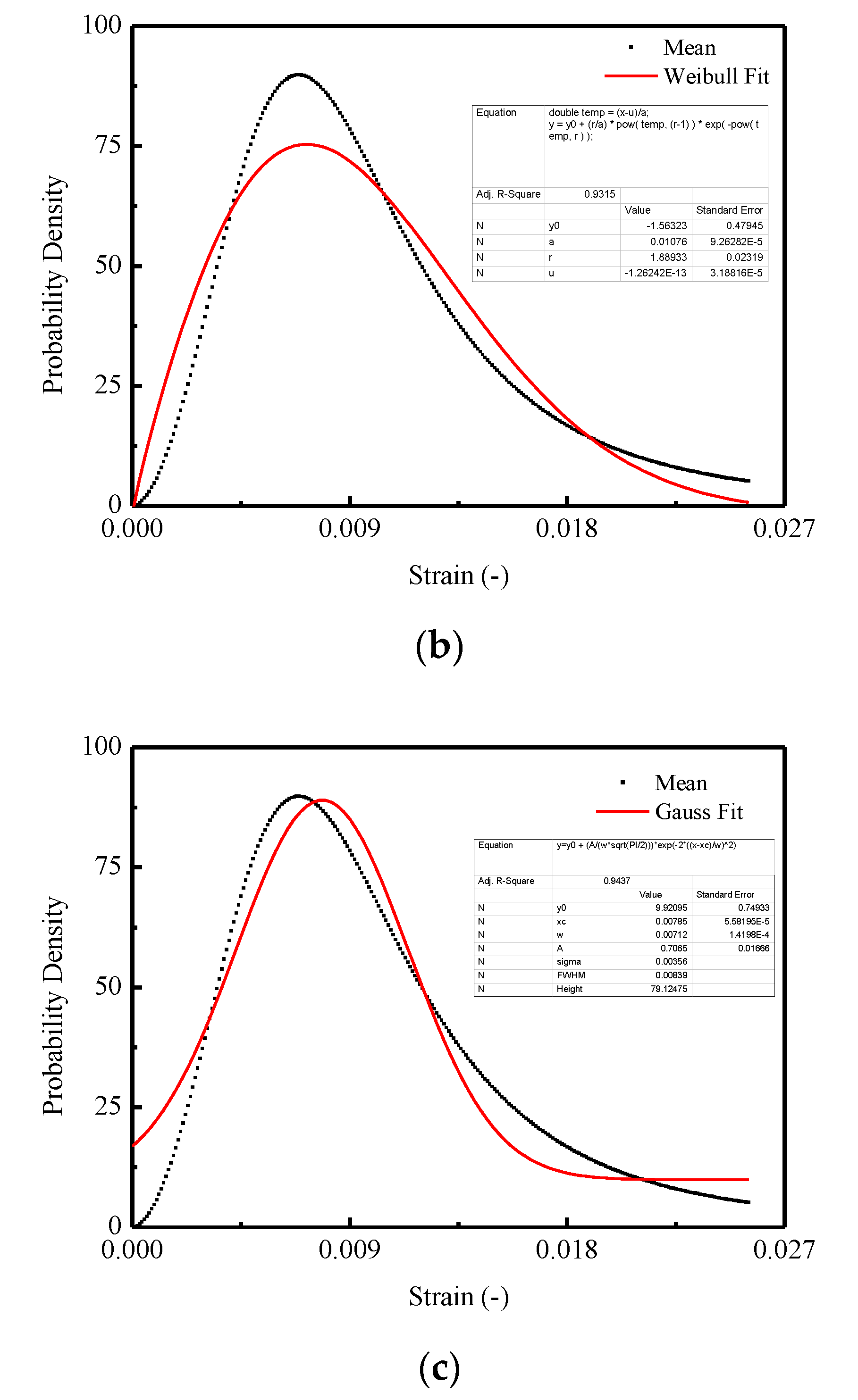
4.1. Transition from Microscale to Macroscale
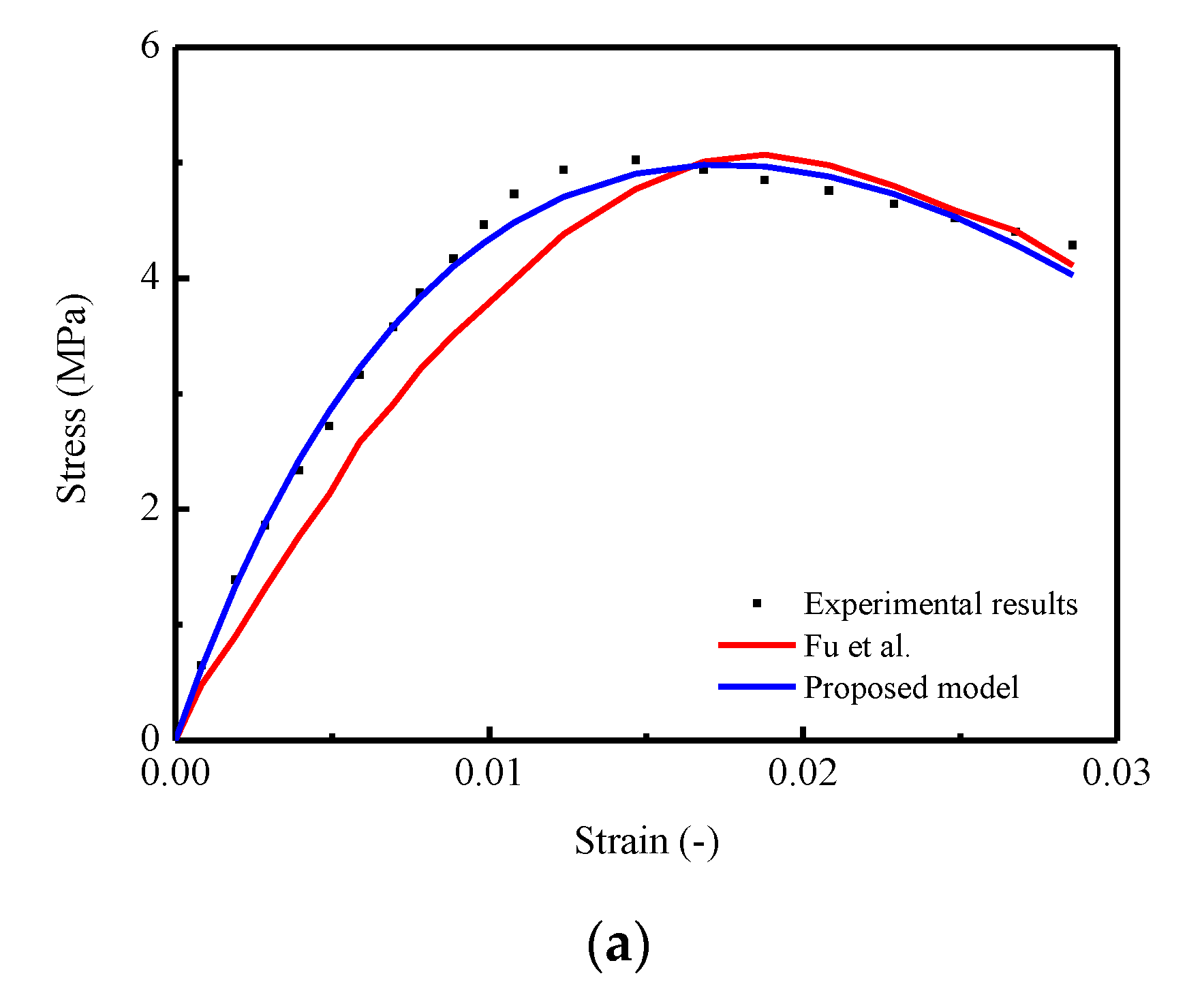
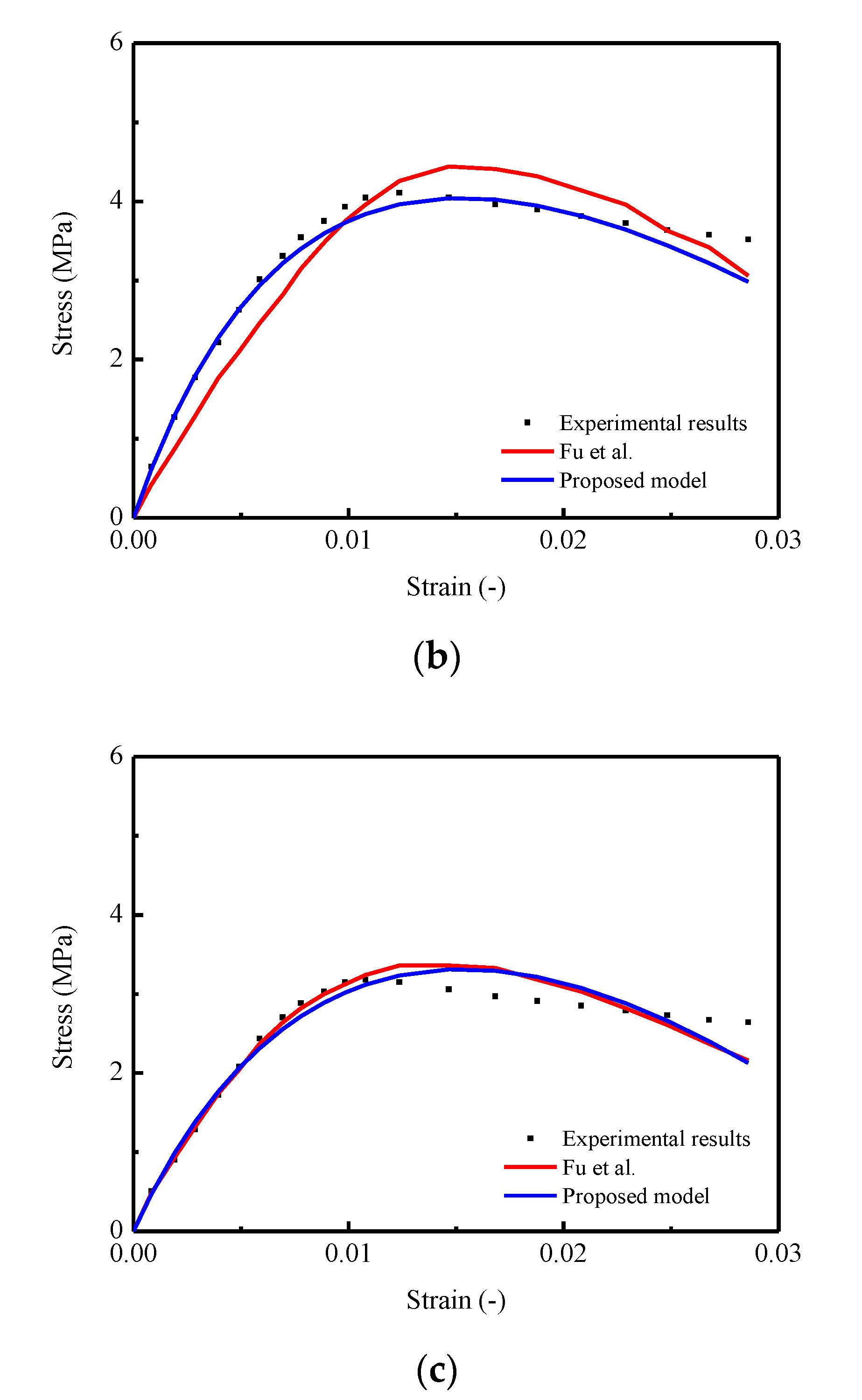
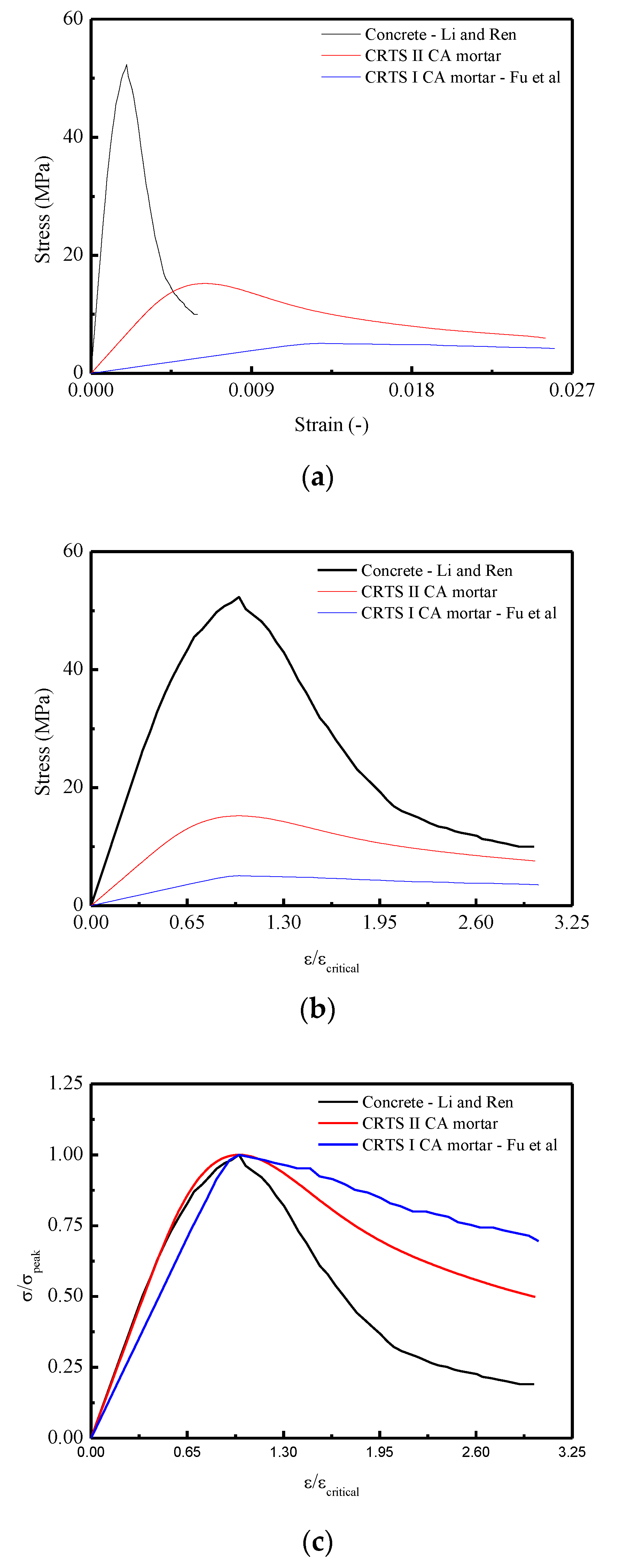
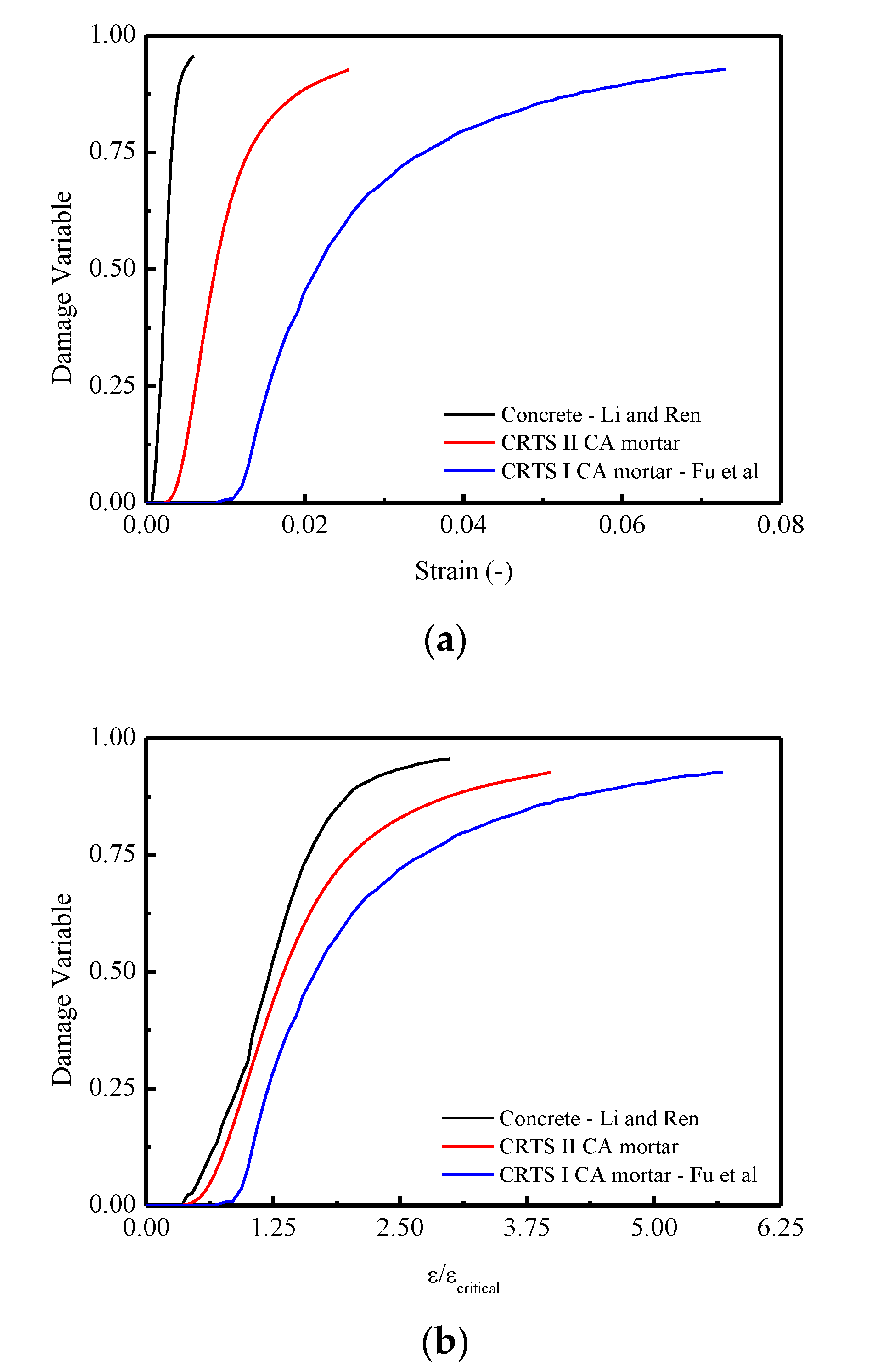
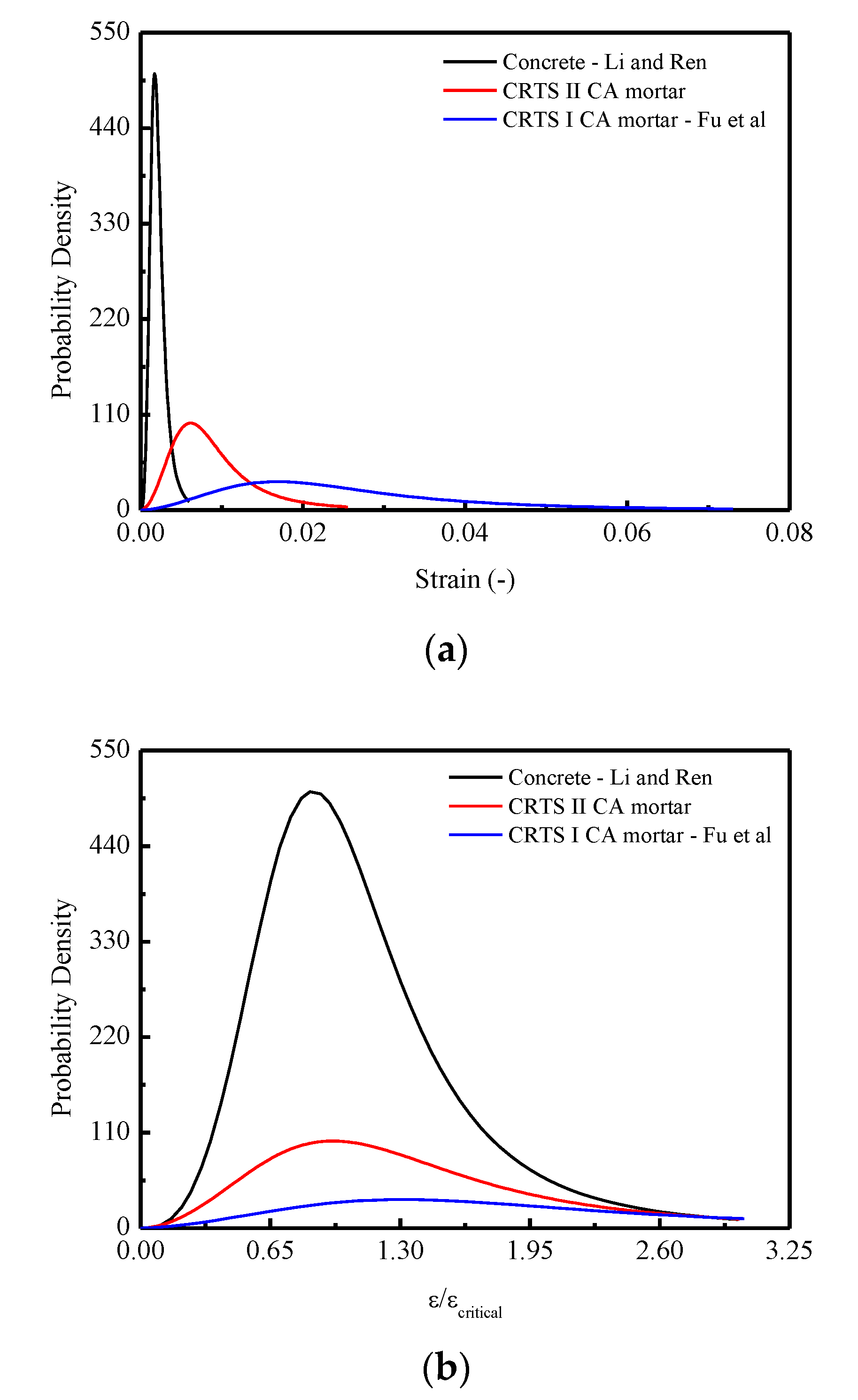
4.2. Comparison of Constitutive Relationships among CA Mortar for CRTS I, II and Concrete under Monotonic Uniaxial Compression
5. Conclusions
- (1)
- The experimental results indicate that there are considerable variations in the mechanical responses including: compressive strength, critical strain, Young’s modulus, and stress–strain curve for CA mortar specimens with the same mix proportions, even when identically prepared.
- (2)
- An analytical model based on the statistical damage approach was developed to describe the stochastic constitutive stress–strain relationship of CA mortar. The proposed model is capable of evaluating the mean and the standard deviation of stress–strain curves. The validation of the proposed model was performed by comparison between the predictions and the experimental results. It was shown that there is a relatively good coincidence between the predictions and the experimental results. In addition, a comparison of predictions in terms of the mean stress–strain curve by the proposed model and those obtained by the model in a previous study was also conducted, which revealed that by adopting the proposed model, the accuracy of prediction is improved.
- (3)
- Further exploration of the behaviors of CA mortar was obtained by examining the media process in terms of transition from microscale (microstructure) to macroscale (macroresponse). It is found that the Lognormal distribution density function can well represent the damage probability density for CA mortar under compression when compared to the Weibull and Gauss distribution density functions. It is also summarized that the stochastic behaviors that emerged for CA mortar are attributed to the randomness of the damage probability density at the microscale. The media process of the transition during the loading process is represented by the stochastic evolution (SE) of specific variables at the macroscale.
- (4)
- Comparisons of the constitutive relationships among the CA mortar used in this work, typical CRTS-I type CA mortar, and concrete were conducted. It was demonstrated that the most ductile stress–strain response was obtained by CRTS-I CA mortar due to its lowest concentration in the probability density curve induced by the microstructure.
Author Contributions
Funding
Conflicts of Interest
References
- Esveld, C. Recent development in slab track. Eur. Railw. Rev. 2003, 9, 81–85. [Google Scholar]
- Miura, S.; Takai, H.; Uchida, M.; Fukada, Y. The mechanism of railway tracks. Jpn. Railw. Transp. Rev. 1998, 15, 38–45. [Google Scholar]
- Katsuoshi, A. Development of slab tracks for Hokuriku Shinkaren line, Quarterly Report of RITI. Railw. Tech. Res. Inst. 2003, 42, 35–41. [Google Scholar]
- Du, J.C.; Kuo, M.F.; Yeh, J.C. Properties of cement asphalt emulsion mortar for pavement. Cem. Concr. Res. Adv. Mater. Res. 2013, 723, 466–473. [Google Scholar] [CrossRef]
- Li, G.; Zhao, Y.; Pang, S.S.; Huang, W. Experimental study of cement-asphalt emulsion composite. Cem. Concr. Res. 1998, 5, 635–641. [Google Scholar] [CrossRef]
- Wang, J.; Molenaar, A.A.A.; van de Ven, M.F.C.; Wu, S. Behaviour of asphalt concrete mixtures under tri-axial compression. Constr. Build. Mater. 2016, 105, 269–274. [Google Scholar] [CrossRef]
- Ouyang, J.; Han, B.G.; Cao, Y.; Zhou, W.J.; Li, W.; Shah, S.P. The role and interaction of superplasticizer and emulsifier in fresh cement asphalt emulsion paste through rheology study. Constr. Build. Mater. 2016, 125, 643–653. [Google Scholar] [CrossRef]
- Xie, Y.J.; Fu, Q.; Zheng, K.R.; Yuan, Q.; Song, H. Dynamic mechanical properties of cement and asphalt mortar based on SHPB test. Constr. Build. Mater. 2014, 70, 217–225. [Google Scholar] [CrossRef]
- Zeng, X.H.; Xie, Y.J.; Deng, D.H. Conductivity behavior of the fresh CA mortar and its relationship with the fluidity properties. Constr. Build. Mater. 2012, 36, 890–894. [Google Scholar] [CrossRef]
- Wang, F.Z.; Liu, Z.C.; Hu, S.G. Early age volume change of cement asphalt mortar in the presence of aluminum powder. Mater. Struct. 2010, 43, 493–498. [Google Scholar] [CrossRef]
- Wang, Z.J.; Shu, X.; Rutherford, T.; Huang, B.S.; Clake, D. Effects of asphalt emulsion on properties of fresh cement emulsified asphalt mortar. Constr. Build. Mater. 2015, 75, 25–30. [Google Scholar] [CrossRef]
- Tan, Y.Q.; Ouyang, J.; Li, Y.L. Factors influencing rheological properties of fresh cement asphalt emulsion paste. Constr. Build. Mater. 2014, 68, 611–617. [Google Scholar] [CrossRef]
- Peng, J.W.; Deng, D.H.; Huang, H.; Yuan, Q.; Peng, J.G. Influence of superplasticizer on the rheology of fresh cement asphalt paste. Case Stud. Constr. Mater. 2015, 3, 9–18. [Google Scholar] [CrossRef]
- Peng, J.W.; Deng, D.H.; Liu, Z.Q.; Yuan, Q.; Ye, T. Rheological models for fresh cement asphalt paste. Constr. Build. Mater. 2014, 71, 254–262. [Google Scholar] [CrossRef]
- Ouyang, J.; Tan, Y.Q. Rheology of fresh cement asphalt emulsion pastes. Constr. Build. Mater. 2015, 80, 236–243. [Google Scholar] [CrossRef]
- Peng, J.W.; Deng, D.H.; Yuan, Q.; Liu, Z.Q.; Fang, L. Study of the rheological behavior of fresh cement emulsified asphalt paste. Constr. Build. Mater. 2014, 66, 348–355. [Google Scholar] [CrossRef]
- Zhang, Y.R.; Kong, X.M.; Hou, S.S.; Liu, Y.L.; Han, S. Study on the rheological properties of fresh cement asphalt paste. Constr. Build. Mater. 2012, 27, 534–544. [Google Scholar] [CrossRef]
- Ouyang, J.; Tan, Y.Q.; Corr, D.J.; Shah, S.P. The thixotropic behavior of fresh cement asphalt emulsion paste. Constr. Build. Mater. 2016, 114, 906–912. [Google Scholar] [CrossRef]
- Wang, T.; Jia, H.Q.; Li, H.G.; Li, H.Y.; Shao, P.Y. Research on water seepage of cement asphalt emulsified (CA) mortar. Constr. Build. Mater. 2016, 125, 595–599. [Google Scholar] [CrossRef]
- Song, H.; Do, J.; Soh, Y. Feasibility study of asphalt-modified mortars using asphalt emulsion. Constr. Build. Mater. 2006, 20, 332–337. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.J.; Song, H.; Zhou, X.L. Model for Mechanical Properties of Cement and Asphalt Mortar. J. Chin. Ceram. Soc. 2014, 42, 1396–1403. (In Chinese) [Google Scholar]
- Rutherford, T.; Wang, Z.J.; Shu, X.; Huang, B.S.; Clarke, D. Laboratory investigation into mechanical properties of cement emulsified asphalt mortar. Constr. Build. Mater. 2014, 65, 76–83. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.J.; Zheng, K.R.; Song, H.; Zhou, X.L. Strain Rate Effect and Modeling of Mechanical Properties of CRTS II Type Cement and Asphalt Mortar. J. Chin. Ceram. Soc. 2014, 42, 989–995. (In Chinese) [Google Scholar]
- Wang, J.F.; Chen, Y.R.; Fan, X.L.; Li, J.Z. Effects of strain rate and confining pressure on compressive behavior of cement asphalt mortar. Mater. Des. 2015, 65, 772–779. [Google Scholar] [CrossRef]
- Wang, J.F.; Wu, X.; Fan, X.L.; Chen, Y.R. Stress-strain model of cement asphalt mortar subjected to temperature and loading rate. Constr. Build. Mater. 2016, 111, 164–174. [Google Scholar] [CrossRef]
- Wang, F.Z.; Liu, Z.C.; Hu, S.G. Influence of loading rate on compressive strength of CA mortar. Beijing Univ. Technol. 2008, 34, 59–65. (In Chinese) [Google Scholar]
- Liu, X.Y.; Wang, P. Dynamics of Vehicle-Track-Subgrade System; SWJT University Press: Chengdu, China, 2010. (In Chinese) [Google Scholar]
- Zeng, X.H.; Xie, Y.J.; Deng, D.H.; Wang, P.; Qu, F.L. A study of the dynamic mechanical properties of CRTS I type CA mortar. Constr. Build. Mater. 2016, 112, 93–99. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.J.; Long, G.C.; Niu, D.T.; Song, H. Dynamic mechanical thermo-analysis of cement and asphalt mortar. Powder Technol. 2017, 313, 36–43. [Google Scholar] [CrossRef]
- Cao, J.Y.; Chung, D.D.L. Effect of strain rate on cement mortar under compression, studied by electrical resistivity measurement. Cem. Concr. Res. 2002, 32, 817–819. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.J.; Long, G.C.; Niu, D.T.; Song, H.; Liu, X.G. Impact characterization and modelling of cement and asphalt mortar based on SHPB experiments. Int. J. Impact Eng. 2017, 106, 44–52. [Google Scholar] [CrossRef]
- Liu, Y.L.; Kong, X.M.; Zhang, Y.R.; Yan, P.Y. Static and dynamic mechanical properties of cement-asphalt composites. J. Mater. Civ. Eng. 2013, 25, 1489–1497. [Google Scholar]
- Kong, X.M.; Liu, Y.L.; Zhang, Y.R.; Zhang, Z.L.; Yan, P.Y.; Bai, Y. Influences of temperature on mechanical properties of cement asphalt mortars. Mater. Struct. 2014, 47, 285–292. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.J.; Zheng, K.; Song, H.; Zhou, X.L. Influence of asphalt on mechanical properties of cement and asphalt mortar. J. Chin. Ceram. Soc. 2014, 42, 642–647. (In Chinese) [Google Scholar]
- Fu, Q.; Xie, Y.J.; Zheng, K.; Zeng, X.H. Statistical damage constitutive model of cement and asphalt mortar. J. Southwest Jiao Tong Univ. 2014; 49, 111–118. (In Chinese) [Google Scholar]
- Xie, Y.J.; Fu, Q.; Long, G.C.; Zheng, K.R.; Song, H. Creep properties of cement and asphalt mortar. Constr. Build. Mater. 2014, 70, 9–16. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.J.; Long, G.C.; Meng, F.; Song, H. Temperature sensitivity and model of stress relaxation properties of cement and asphalt mortar. Constr. Build. Mater. 2015, 84, 1–11. [Google Scholar] [CrossRef]
- Wang, F.Z.; Liu, Z.C. Research on the fatigue behavior of CA mortar used in ballastless slab track of high speed railway. J. Wuhan Univ. Technol. 2008, 30, 79–81. (In Chinese) [Google Scholar]
- Li, Y.; Xie, B.; Hu, S.G.; Zhou, F.Z. The influences of fatigue load types on the residual strength of CRTS II CA mortar. China Civ. Eng. J. 2010, 43, 358–362. (In Chinese) [Google Scholar]
- Mao, J.D. Frost and Fatigue Resistance of CA Mortar in Ballastless Slab Track. Master’s Thesis, Zhejiang University of Technology, Hangzhou, China, 2012. (In Chinese). [Google Scholar]
- Tian, D.M. Research on Degradation and Invalidation Mechanism of Cement Emulsified Asphalt mortar in Slab Track. Ph.D. Thesis, Central South University, Changsha, China, 2013. (In Chinese). [Google Scholar]
- Sun, H.Y.; Li, Y.; Wang, P.; Zeng, X.H. Research on temperature fatigue of CA mortar used for CRTS II slab-type ballastless track. Railw. Eng. 2015, 2, 134–136. (In Chinese) [Google Scholar]
- Li, Y.; Sun, H.Y.; Zeng, X.H.; Wang, P. Study of the effects of water immersion and temperature on mechanical properties of CA mortar. Railw. Stand. Des. 2015, 59, 40–42. (In Chinese) [Google Scholar]
- Yi, X.W.; Fu, Q.; Dong, C.Z.; Zhao, C.Y.; Yang, J.; Gao, Y. Influence of drying and wetting cycles on the mechanical properties of CA motar. J. Yangtze River Sci. Res. Inst. 2013, 30, 91–96. (In Chinese) [Google Scholar]
- Qiu, K.C.; Chen, H.S.; Ye, H.P.; Hong, J.X.; Sun, W.; Jiang, J.Y. Thermo-mechanical coupling effect on fatigue behavior of cement asphalt mortar. Int. J. Fatigue 2013, 51, 116–120. [Google Scholar] [CrossRef]
- Ye, Y.; Yang, X.H.; Chen, C.Y. Experimental researches on visco-elastoplastic constitutive model of asphalt mastic. Constr. Build. Mater. 2009, 23, 3161–3165. [Google Scholar] [CrossRef]
- Li, J.; Wu, J.Y.; Chen, J.B. Stochastic Damage Mechanics of Concrete Structures; Science Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Li, H.B.; Zhao, J.; Li, J.R.; Liu, Y.Q.; Zhou, Q.C. Experimental studies on the strength of different rock types under dynamic compression. Int. J. Rock Mech. Min. Sci. 2004, 41. [Google Scholar] [CrossRef]
- Li, J. Research on the stochastic damage mechanics for concrete. J. Tongji Univ. (Nat. Sci.) 2004, 32, 1270–1277. (In Chinese) [Google Scholar]
- Kandarpa, S.; Kirkner, D.J. Stochastic damage model for brittle material subjected to monotonic loading. J. Eng. Mech. ASCE 1996, 126, 788–795. [Google Scholar] [CrossRef]
- Li, J.; Ren, X.D. Stochastic damage model for concrete based on energy equivalent strain. Int. J. Solids Struct. 2009, 46, 2407–2419. [Google Scholar] [CrossRef]
- Ren, X.D.; Yang, W.Z.; Zhou, Y.; Li, J. Behavior of high-performance concrete under uniaxial and biaxial loading. ACI Mater. J. 2008, 105, 548–557. [Google Scholar]
- Shan, Z.; Yu, Z.W. A fiber bundle-plastic chain model for quasi-brittle materials under uniaxial loading. J. Stat. Mech. Theory Exp. 2015, 2015, 11010. [Google Scholar] [CrossRef]
- Li, X.; Shan, Z.; Yu, Z.W.; Gao, J.; Mao, J.F. Stochastic constitutive relationship of self-compacting concrete under uniaxial compression. Adv. Civ. Eng. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Chinese National Standard GB/T 2085.1-2007, 2007. Aluminium Powder-Part 1: Air Atomized Aluminium Powder; Standards Press of China: Beijing, China, 2017. [Google Scholar]
- Provisional Technical Specifications of Cement-Emulsified Asphalt Mortar of CRTS II Ballastless Track on Passenger Dedicated Line No.74; The Science and Technology Department of the Ministry of Railways: Beijing, China, 2008.
- Chinese National Standard GB/T 17671-1999, 1999. Method of Testing Cements-Determination of Strength; Standards Press of China: Beijing, China, 2019. [Google Scholar]
- Kupfer, H.B.; Hilsdorf, H.K.; Rush, H. Behavior of concrete under biaxial stresses. ACI J. Proc. 1969, 66, 656–666. [Google Scholar]
- Ferdous, W.; Manolo, A.; Wong, H.S.; Abousnina, R.; Alajarmeh, O.S.; Zhuge, Y.; Schubel, P. Optimal design for epoxy polymer concrete based on mechanical properties and durability aspects. Constr. Build. Mater. 2020, 232, 117229. [Google Scholar] [CrossRef]
- Khotbehsara, M.M.; Manalo, A.; Aravinthan, T.; Reddy, K.R.; Ferdous, W.; Wong, H.; Nazari, A. Effect of elevated in-service temperature on the mechanical properties and microstructure of particulate-filled epoxy polymers. Polym. Degrad. Stab. 2019, 170, 108994. [Google Scholar] [CrossRef]
- Xie, H.P.; Ju, Y.; Li, L.Y. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles. Chin. J. Rock Mech. Eng. 2005, 24, 3003–3010. (In Chinese) [Google Scholar]
- Fu, Q.; Xie, Y.J.; Zeng, X.H. Energy mechanism of mechanical property of cement-emulsified asphalt mortar. J. South China Univ. Technol. (Nat. Sci. Ed.) 2014, 42, 107–113. (In Chinese) [Google Scholar]
- Breccolotti, M.; Bonfigli, M.F.; D’Alessandro, A.; Materazzi, A.L. Constitutive modeling of plan concrete subjected to cyclic uniaxial compressive loading. Constr. Build. Mater. 2015, 94, 172–180. [Google Scholar] [CrossRef]
- Elaqra, H.; Godin, N.; Peix, G.; R’Mili, M.; Fantozzi, G. Damage evolution analysis in mortar, during compressive loading using acoustic emission and X-ray tomography: Effects of the sand/cement ratio. Cem. Concr. Res. 2007, 37, 703–713. [Google Scholar] [CrossRef]
- Qin, X.T.; Zhu, S.Y.; Chen, S.F.; Li, X.; Dou, H.B. Comparative study on the deformation behaviors of cement emulsified asphalt mortars. Mater. Struct. 2015, 48, 3241–3247. [Google Scholar] [CrossRef]
- Zhang, H.T.; Meng, L.; Zhang, G.K. Comparative study on mechanical performance of asphalt-cement mortar and emulsified asphalt-cement mortar. Road Mater. Pavement Des. 2017, 5, 1239–1250. [Google Scholar] [CrossRef]
- Miljkovic, M.; Radenberg, M. Effect of compaction energy on physical and mechanical performance of bitumen emulsion mortar. Mater. Struct. 2016, 49, 193–205. [Google Scholar] [CrossRef]
- Al-Khateeb, G.G.; Al-Akhras, N.M. Properties of Portland cement-modified asphalt binder using Superpave tests. Constr. Build. Mater. 2011, 25, 926–932. [Google Scholar] [CrossRef]
- Fu, Q. Study on Viscoelastic Mechanical Properties of Cement and Asphalt Mortar. Ph.D. Thesis, Central South University, Changsha, China, 2014. (In Chinese). [Google Scholar]




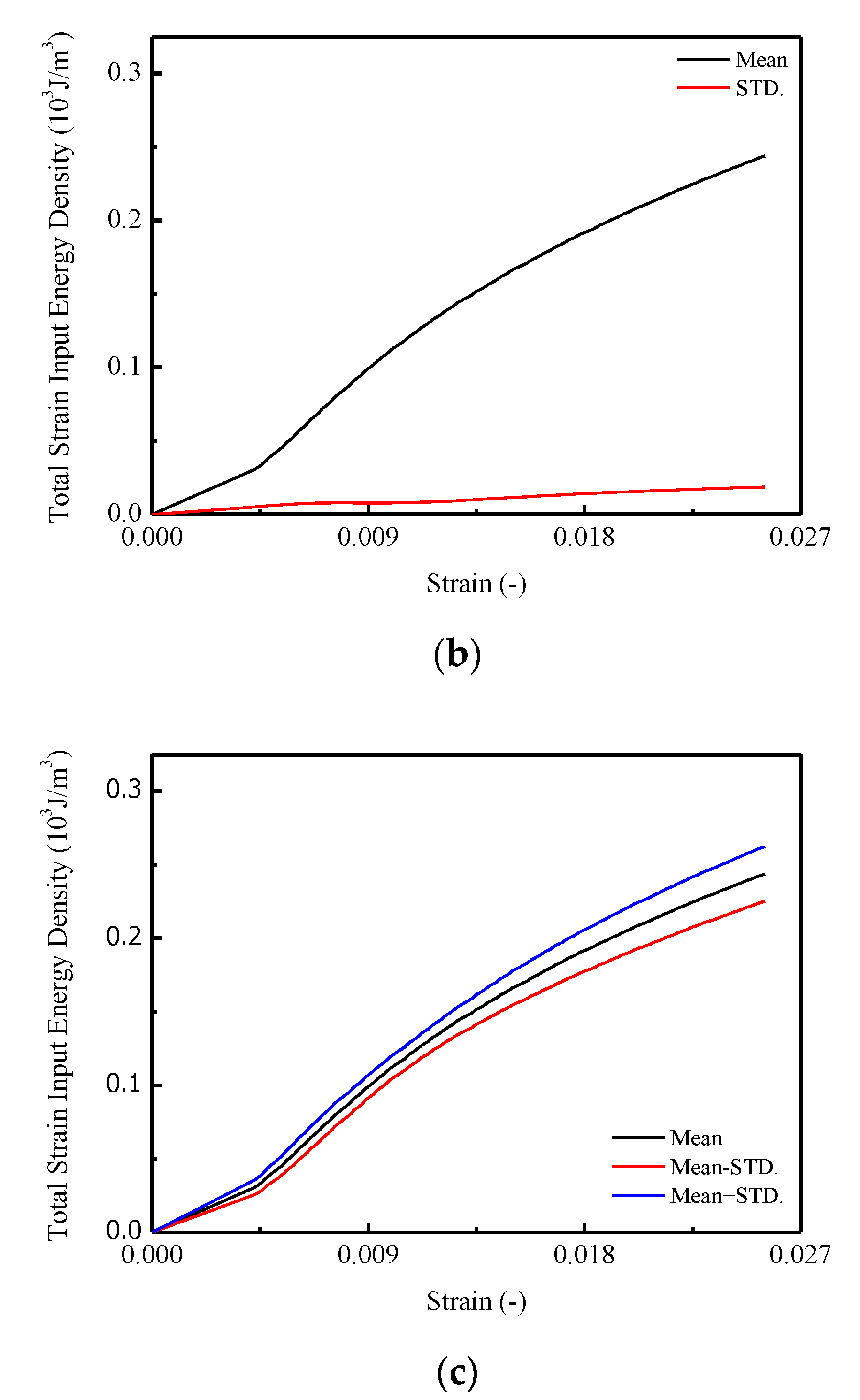
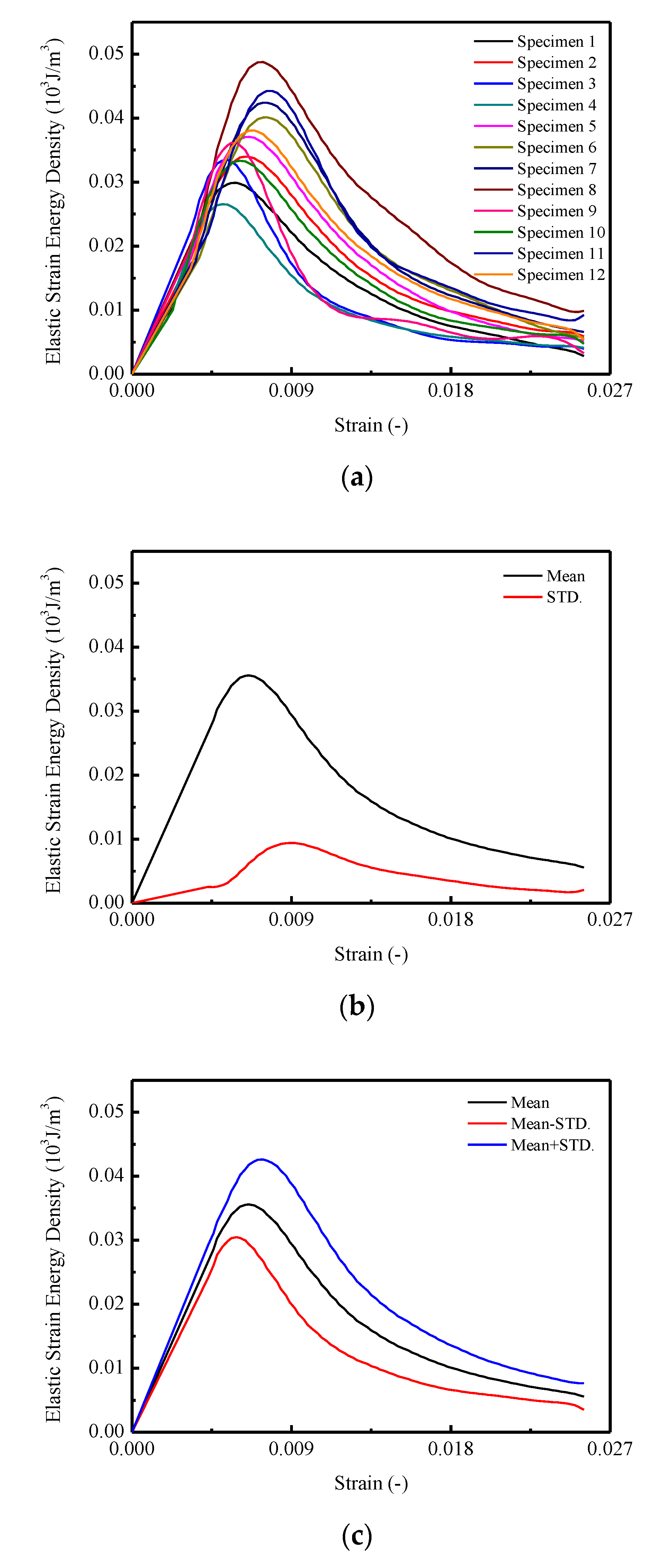

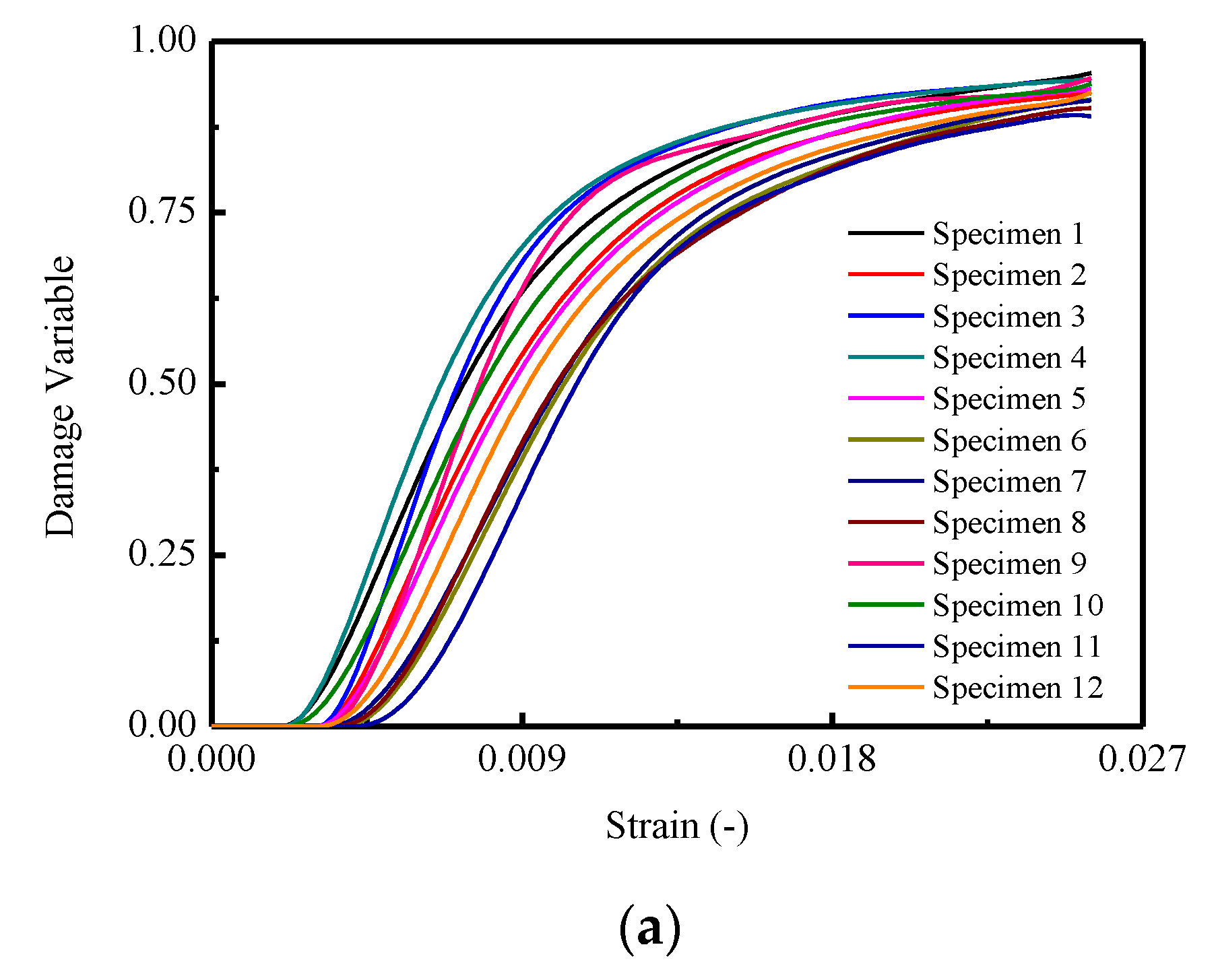
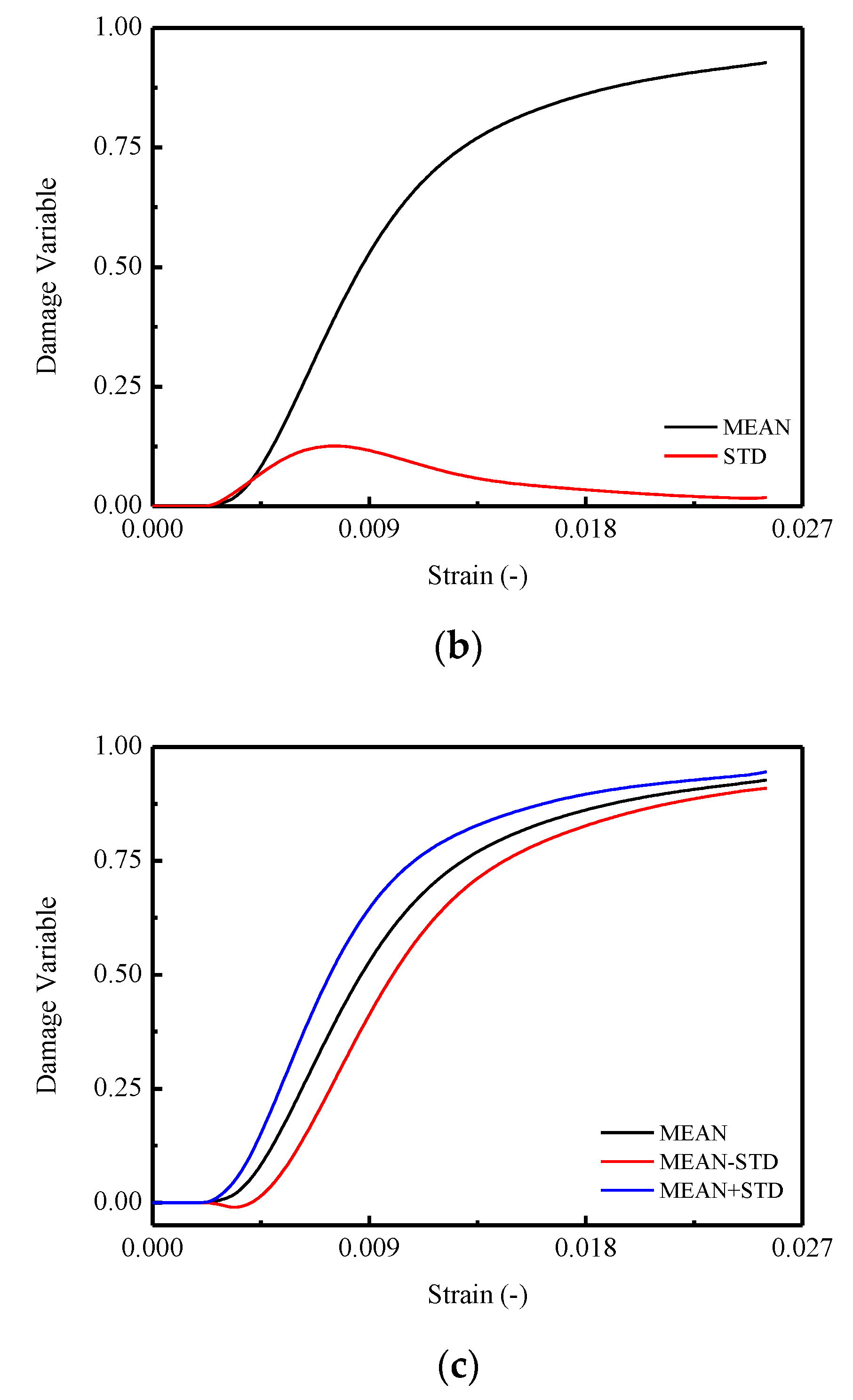

| Type | Solid Content (%) | Engler Viscosity (25 °C) | Sieve Residue (1.18 mm) | Storage Stability (25 °C) | Evaporation Residues Penetration (25 °C)/0.1 mm | Evaporation Residues Ductility (25 °C) (cm) | |
|---|---|---|---|---|---|---|---|
| 1d | 5d | ||||||
| Anionic | 60 | 5.6 | 0.005% | 0.32 | 1.94 | 81 | 104 |
| Specific Surface Area (m2 kg−1) | Loss on Ignition (%) | Compressive Strength on 3 d and 28 d (MPa) | Volume Stability | Flexural Strength on 3 d and 28 d (MPa) |
|---|---|---|---|---|
| 316 | 1.8 | 33.3 and 61.9 | Up to standard | 5.9 and 8.5 |
| Apparent Density (g/cm3) | Moisture Content (%) | Water Absorption Rate (%) | Clay Content (%) | Mud Content (%) | Ruggedness (%) | Organic Matter (Colorimetric Method) | Chloride Content (%) |
|---|---|---|---|---|---|---|---|
| 2.64 | 0.04 | 0.4 | 0 | 0 | 2.0 | Up to standard | 0 |
| Component | Al | Fe | Si | Cu | H2O | Other |
|---|---|---|---|---|---|---|
| Content (%) | 99.80 | 0.076 | 0.046 | 0.0019 | 0.015 | 0.0611 |
| Component | Cement | Sand | Emulsified Asphalt | Water Reducing Admixture | Thickening Agent | Aluminate Powder | Antifoaming Agent | Water |
|---|---|---|---|---|---|---|---|---|
| Mix proportion (g/L) | 606 | 909 | 303 | 12.13 | 1.21 | 0.05 | 5 | 100 |
| Specimen No. | Strength (MPa) | Critical Strain (mm/mm) |
|---|---|---|
| 1 | 15.65 | 0.0057 |
| 2 | 14.96 | 0.0064 |
| 3 | 16.70 | 0.0052 |
| 4 | 15.02 | 0.0051 |
| 5 | 15.76 | 0.0065 |
| 6 | 14.09 | 0.0075 |
| 7 | 15.30 | 0.0075 |
| 8 | 17.65 | 0.0073 |
| 9 | 16.11 | 0.0057 |
| 10 | 15.91 | 0.0061 |
| 11 | 14.44 | 0.0077 |
| 12 | 15.13 | 0.0068 |
| Mean | 15.23 | 0.0064 |
| STD. | 1.83 | 0.0037 |
| Specimen No. | Young’s Modulus (MPa) |
|---|---|
| 1 | 4100.23 |
| 2 | 3316.96 |
| 3 | 4135.15 |
| 4 | 4239.79 |
| 5 | 3365.67 |
| 6 | 2477.80 |
| 7 | 2761.34 |
| 8 | 3186.02 |
| 9 | 3579.87 |
| 10 | 3799.22 |
| 11 | 2350.86 |
| 12 | 3001.41 |
| Mean | 3359.53 |
| STD | 611.00 |
| −0.013 | 0.939 | 0.0081 | 3.2578 |
| 0.12125 | 0.00814 | 0.00393 |
| 0.001 | 0.237 | 42.592 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yu, Z.; Liu, P.; Shan, Z.; Meng, Z. Experimental Investigation of Stochastic Mechanical Behavior of Cement Emulsified Asphalt Mortar under Monotonic Compression. Appl. Sci. 2020, 10, 2860. https://doi.org/10.3390/app10082860
Li X, Yu Z, Liu P, Shan Z, Meng Z. Experimental Investigation of Stochastic Mechanical Behavior of Cement Emulsified Asphalt Mortar under Monotonic Compression. Applied Sciences. 2020; 10(8):2860. https://doi.org/10.3390/app10082860
Chicago/Turabian StyleLi, Xiao, Zhiwu Yu, Peng Liu, Zhi Shan, and Zilong Meng. 2020. "Experimental Investigation of Stochastic Mechanical Behavior of Cement Emulsified Asphalt Mortar under Monotonic Compression" Applied Sciences 10, no. 8: 2860. https://doi.org/10.3390/app10082860
APA StyleLi, X., Yu, Z., Liu, P., Shan, Z., & Meng, Z. (2020). Experimental Investigation of Stochastic Mechanical Behavior of Cement Emulsified Asphalt Mortar under Monotonic Compression. Applied Sciences, 10(8), 2860. https://doi.org/10.3390/app10082860





