TF Entropy and RFE Based Diagnosis for Centrifugal Pumps Subject to the Limitation of Failure Samples
Abstract
:1. Introduction
- A novel feature extraction called TfEn is proposed to jointly quantify the robust nonlinear characteristics from both time and frequency dimensions, which overcomes the limitations of existing entropy based on 1D sequence and thus being more suitable for non-stationary signals;
- RFE-based feature selection is applied to select the optimal feature subset form the high-dimensional feature vector, which achieves better performance on improving the classification accuracy and retaining the feature interpretability compared with mainstream methods;
- The proposed two-stage fault representation has the capability of highlighting and depicting the intrinsic differences among vibration signals, which presents the stability against the variable sizes of training samples, and obtains the satisfied results even with extremely few failure data;
- Compared with the existing entropy variants and mainstream deep models, the experiments with the real vibration signals of centrifugal pumps illustrate the validity and superiority of our proposed fault diagnosis method.
2. Preliminaries
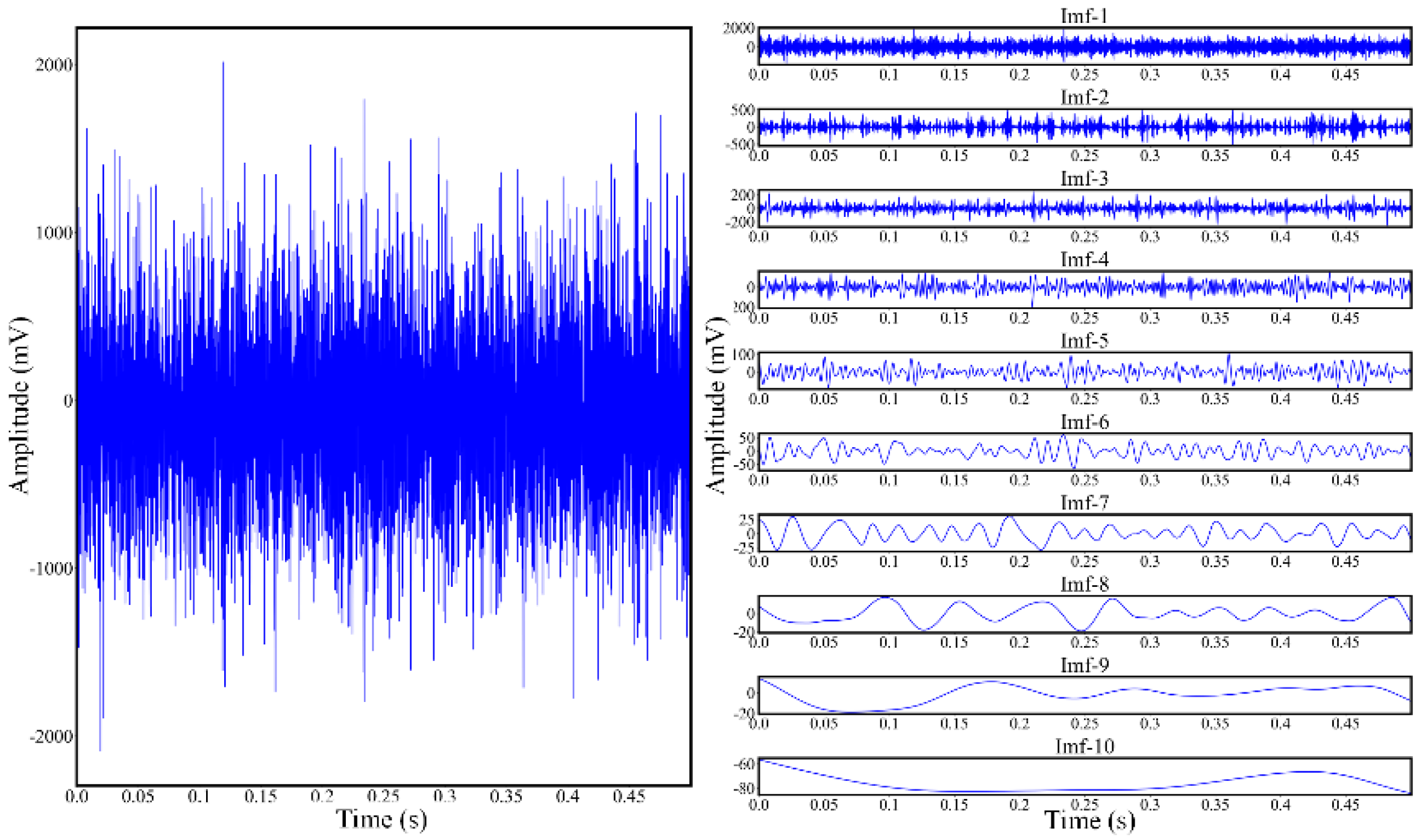
- Given a raw signal . First, add the particular white noise into the signal and decompose it. Repeat the decomposition under different noise realizations and average these results as the first sub-signal :where is the average time, is the defined operator which produces the 1th mode obtained from the given signal using the EMD, is the ratio coefficient and is the particular white noise in each time.
- Compute the first-order residual as follows:
- Set as the new signal and compute the :
- Repeating step (1) to step (3) until the is obtained, and the raw signal is finally decomposed into sub-signals and a residual :
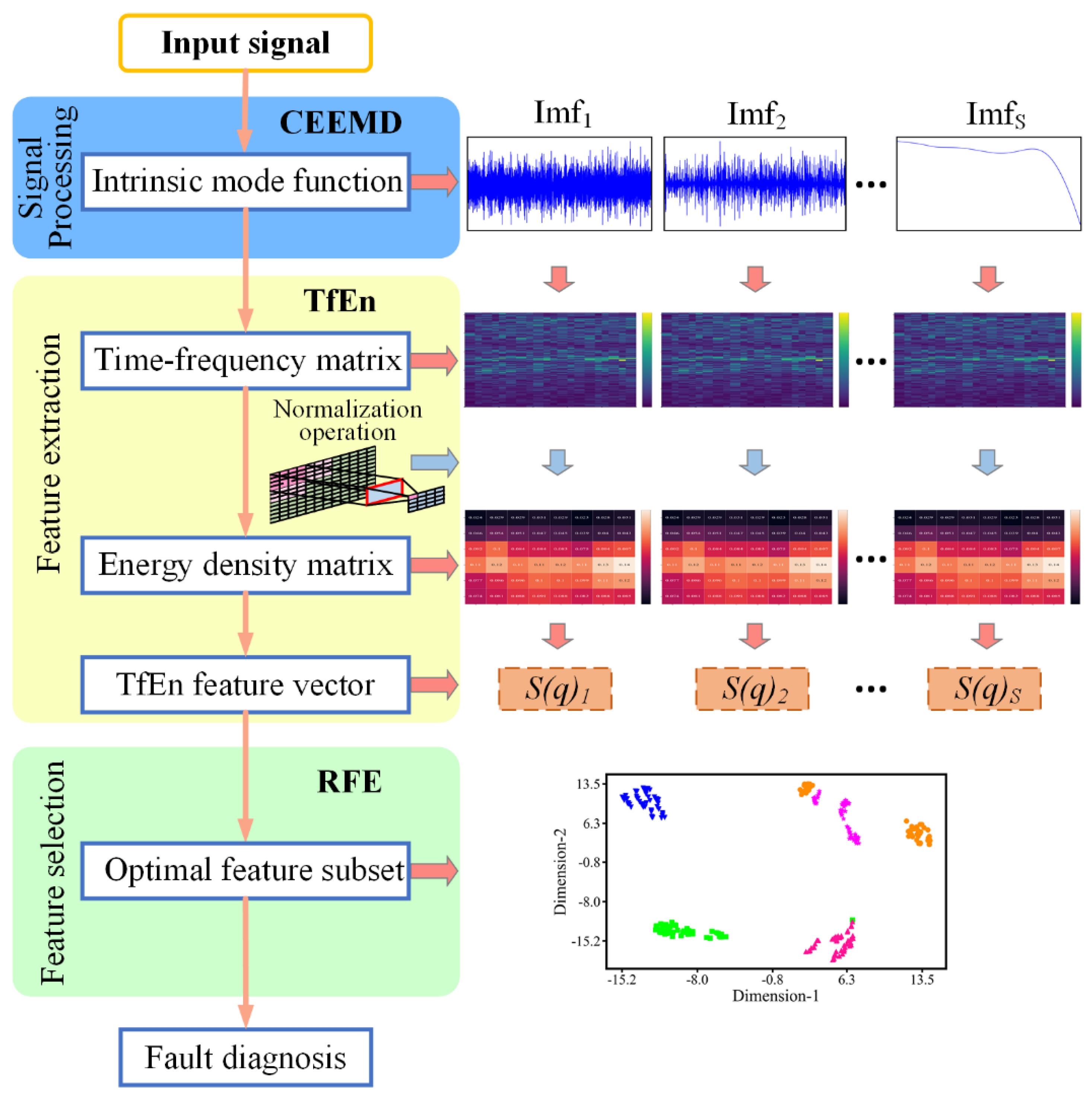
3. Proposed Fault Diagnosis Method
3.1. Procedure of Fault Diagnosis
- Decompose the non-stationary signal into several sub-signals using CEEMD to obtain the multiple-scale components;
- Using our proposed TfEn, transform each non-stationary or approximately stationary component into the 2D time-frequency matrix, and construct their fault representation by taking into account nonlinear behaviors from both the time and frequency domain;
- Select the optimal TfEn feature subset from the high-dimensional feature set using the RFE, where the redundant components are eliminated automatically;
- Choose classifier models to implement the fault diagnosis for centrifugal pumps, based on the optimal TFIE feature subset.
3.2. CEEMD-Based Signal Processing
3.3. Proposed TfEn-Based Feature Extraction
- Given a 1D time series . For the purpose of measuring its complexity both in time and frequency domain, should be first extended into the 2D time-frequency matrix. In this paper, short-time Fourier transform (STFT) [25], a classical time-frequency analysis method, is applied to achieve the above target considering its balance of calculation efficiency and performance.where is the window function, and are both the time variables and is the frequency variable. can be illustrated as the correlation between and .
- Further, through the square operation, the will be transformed into the energy matrix.where the is a 2D matrix consisting of elements , and can be interpreted as the energy located at frequency and time .
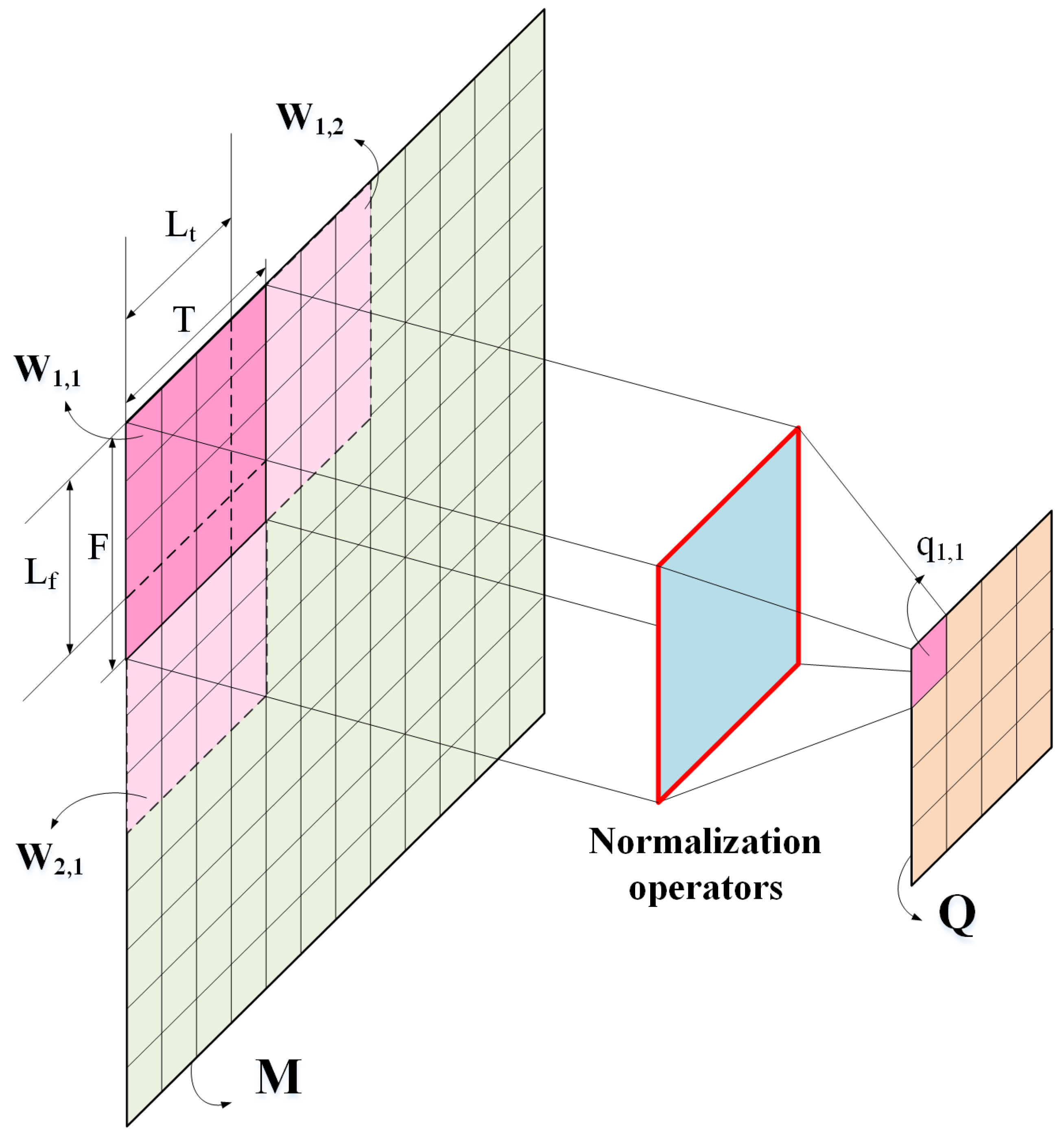
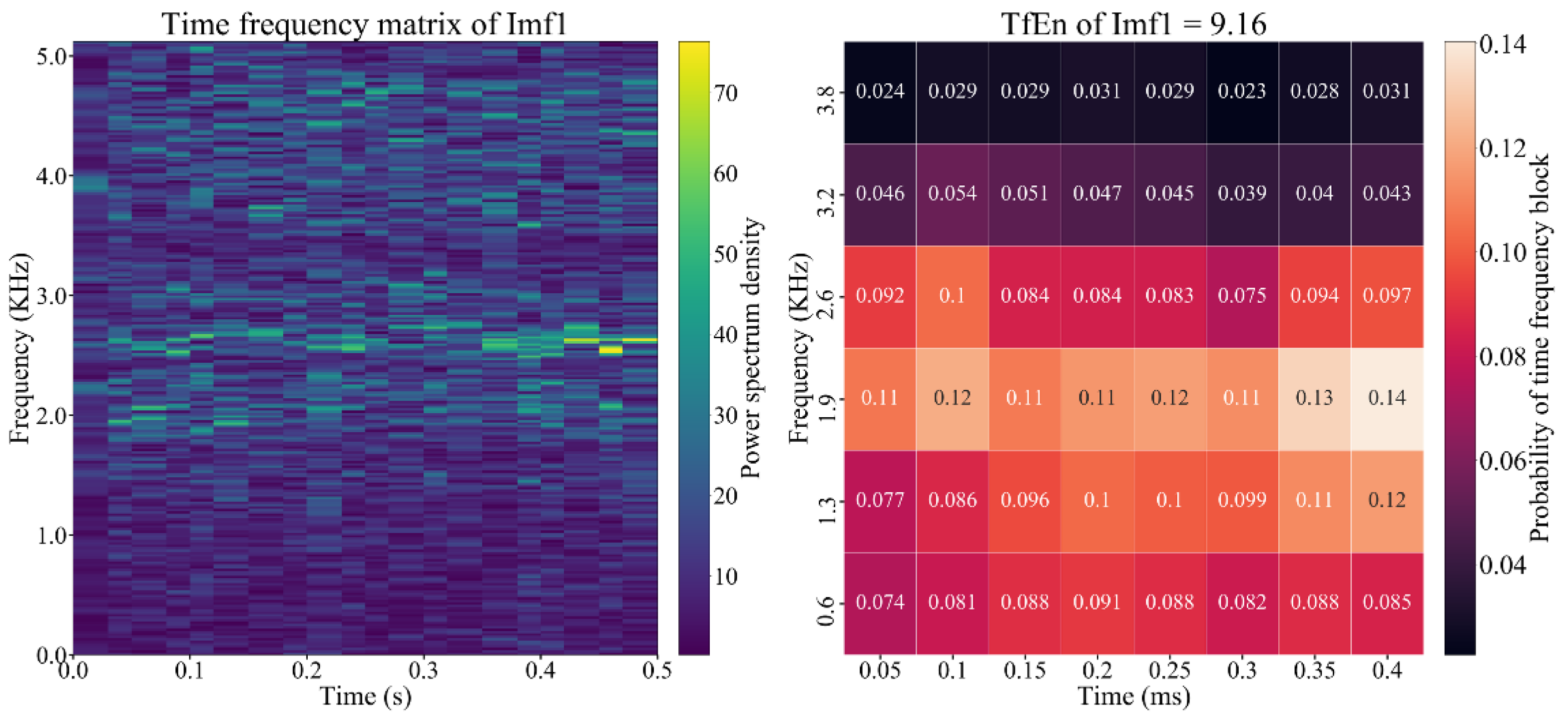
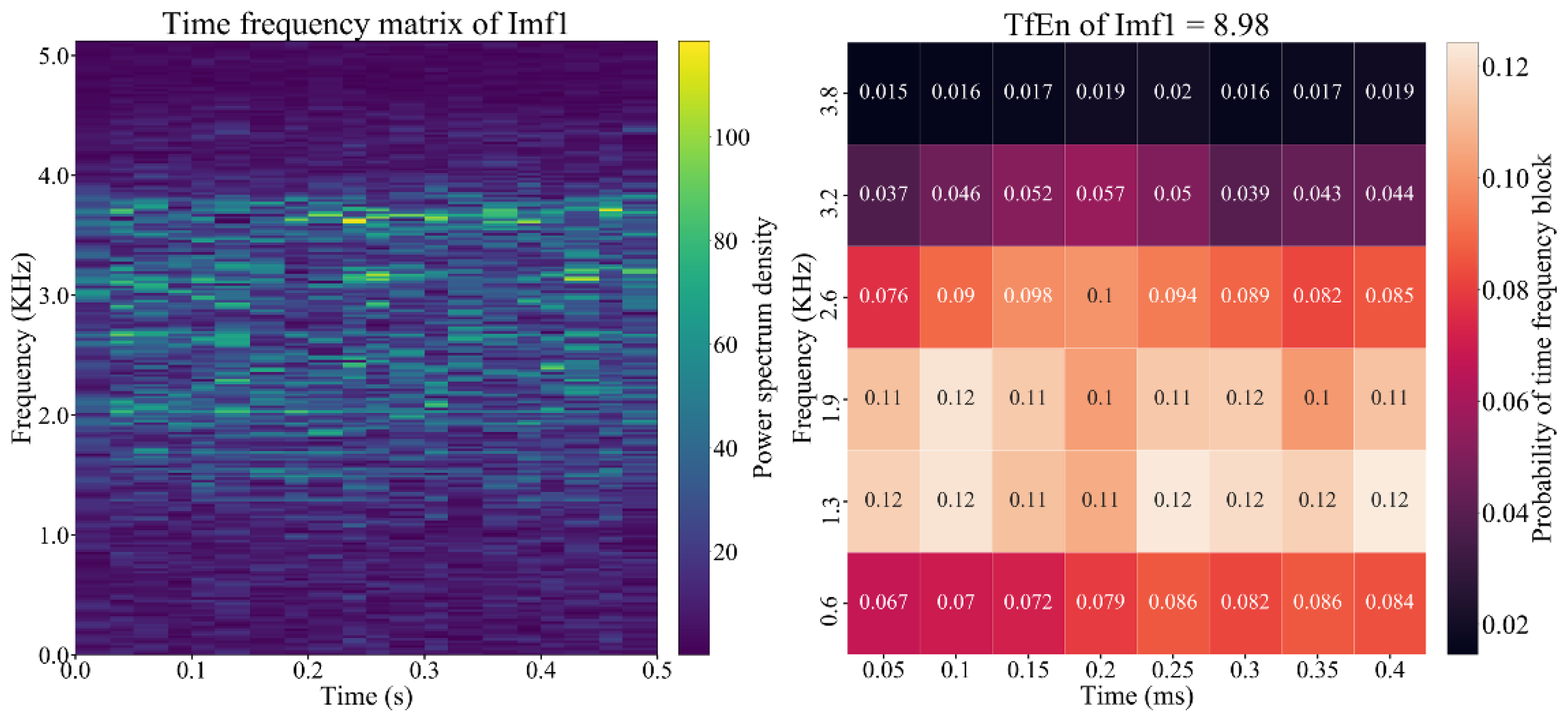
- According to the Shannon methodology, the average degree of uncertainty depicts the irregularity of probability system. In this case, to obtain the robust representation of the time-frequency energy matrix , we utilize a sliding window of size to divide the into blocks . Then a normalization operator will process these blocks one by one and transform them into a probability density matrix . The above operation can be illustrated in Figure 3.As shown in Figure 3, the , , and are 4 hyper-parameters of our proposed TfEn, which respectively represent the span of frequency-axis, span of time-axis, translation span of frequency-axis and translation span of time-axis of each time-frequency block.
- As shown in Figure 3, through the normalization operators, each time-frequency energy block will be transformed into a probability density reflecting its irregularity. The calculation of the normalization operators is described as follows:where is an energy element of the matrix at coordinate , is defined as the sum of energy values in the block , and is defined as the total sum of energy elements of all blocks. is the normalized probability density for the block , which quantifies the concentration of energy in each local time-frequency block.
- According to the normalized probability density of all these blocks, the TfEn feature of the given time series can be extracted as follows:where is an arbitrary constant and it is generally set as one, is the TfEn feature of 1D time series, which jointly represent its complexity and irregularity from both time and frequency domains.
- Repeating the above operations for all the sequences decomposed by CEEMD, we will finally obtain the TfEn feature vector of size :with the help of , we obtain the multi-scale representations reflecting the complexity and dynamic change of nonlinear and non-stationary vibration signals. Besides that, it is worth noting that TfEn requires no state space reconstruction and a large amount of loop comparisons, so it has higher computational efficiency than the methods such as SampleEn and ApEn.
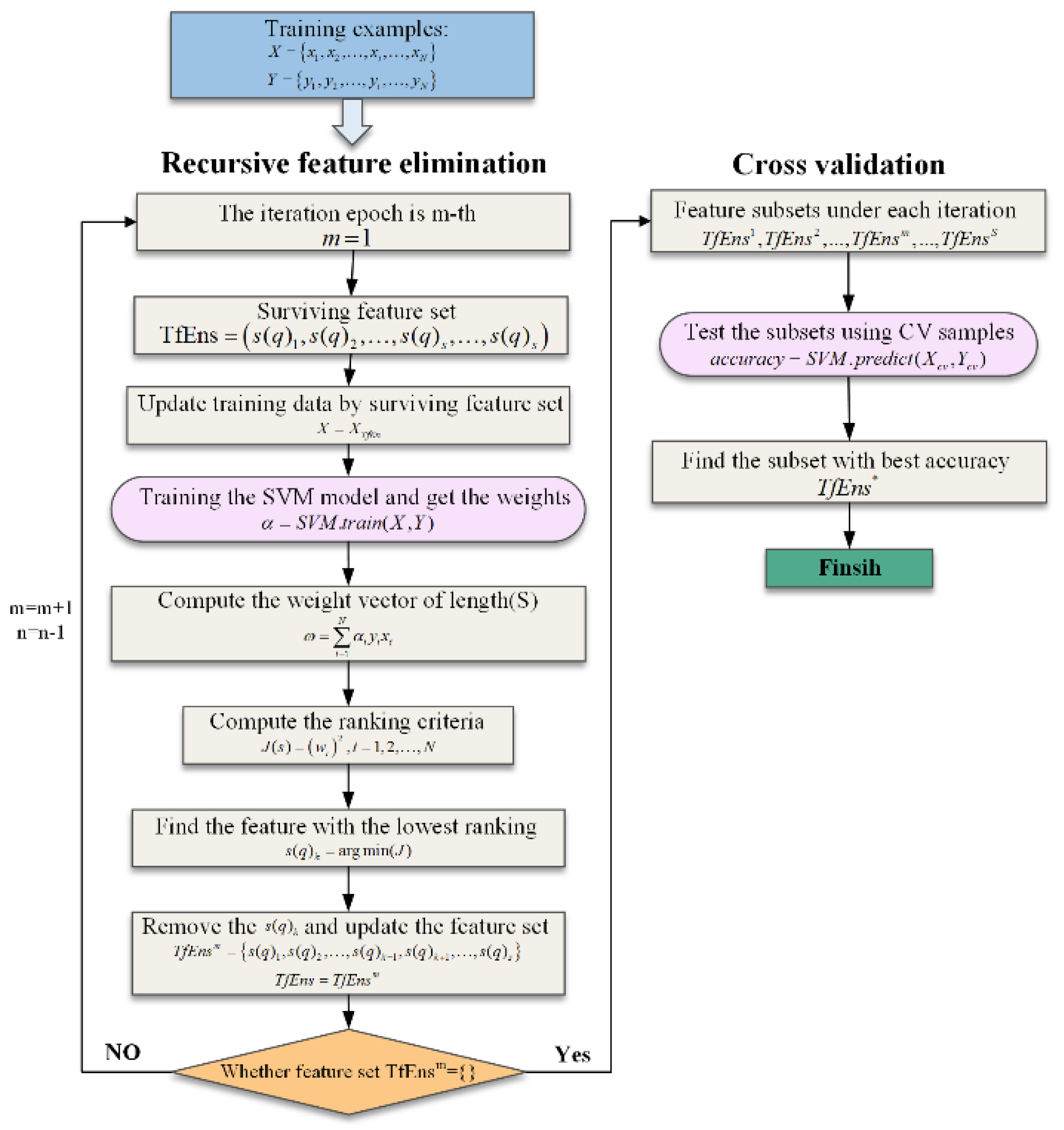
3.4. RFE-Based Feature Selection
- Given a set of training samples , where is the feature vector sample with features, is the status label of centrifugal pumps. A linear SVM model is trained using these training samples, and its decision function is:
- According to the trained SVM model, the ranking criterion of features can be calculated as follows:where is the Lagrange multiplier, is the weight vector of the trained SVM model with elements , is the ranking criterion for the feature .
- Eliminate the feature with the lowest criterion from the feature set:where is the feature subset with features in the first iteration of feature selection.
- Repeating the above operations until all the features are eliminated from the feature set, we will obtain the feature subsets:using the cross-validation technique [27], the feature subset with the best accuracy will be selected as the optimal feature subset for the subsequent fault diagnosis.
4. Experiments
4.1. Description of Dataset
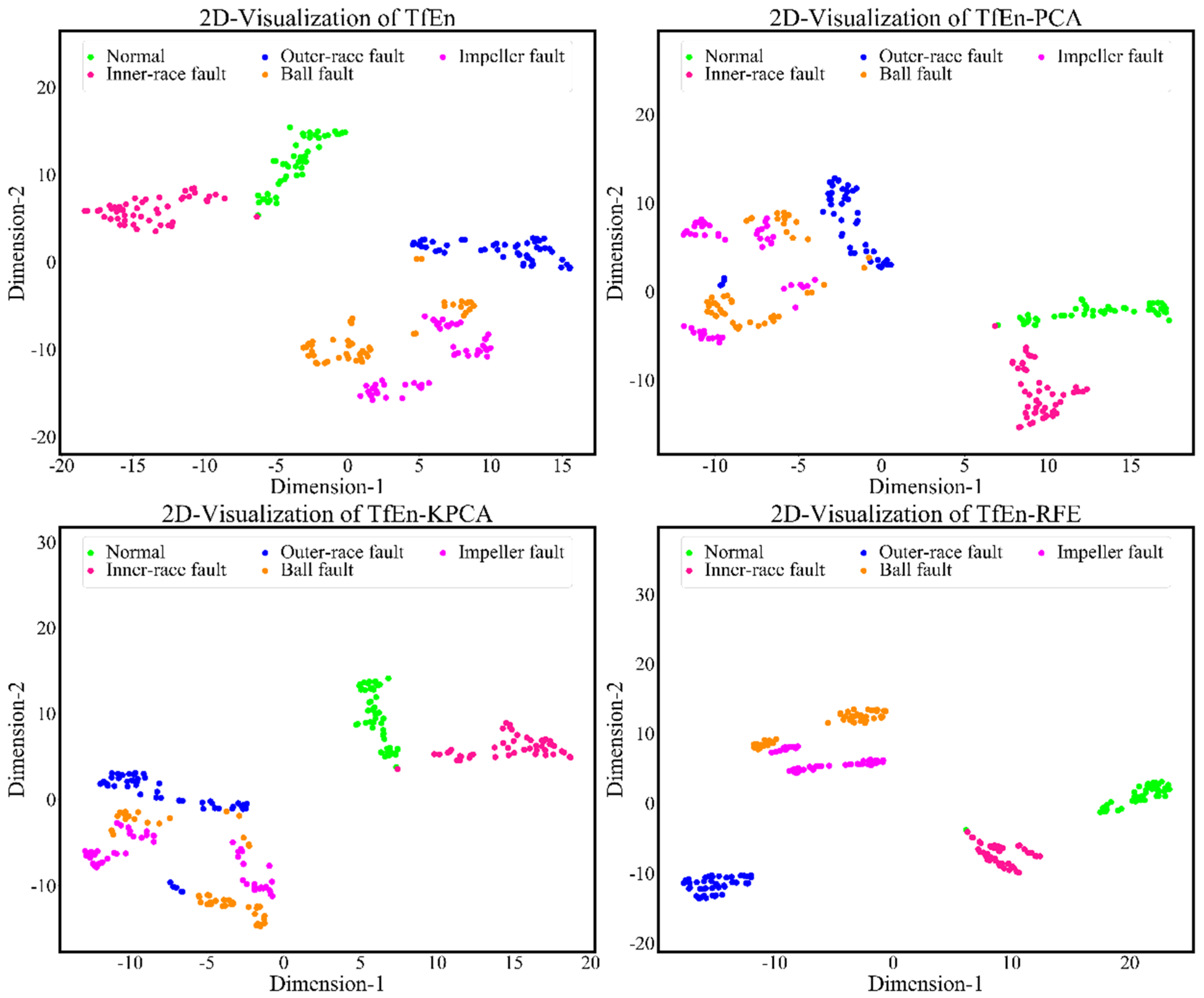
4.2. Fault Diagnosis Using the Proposed Method
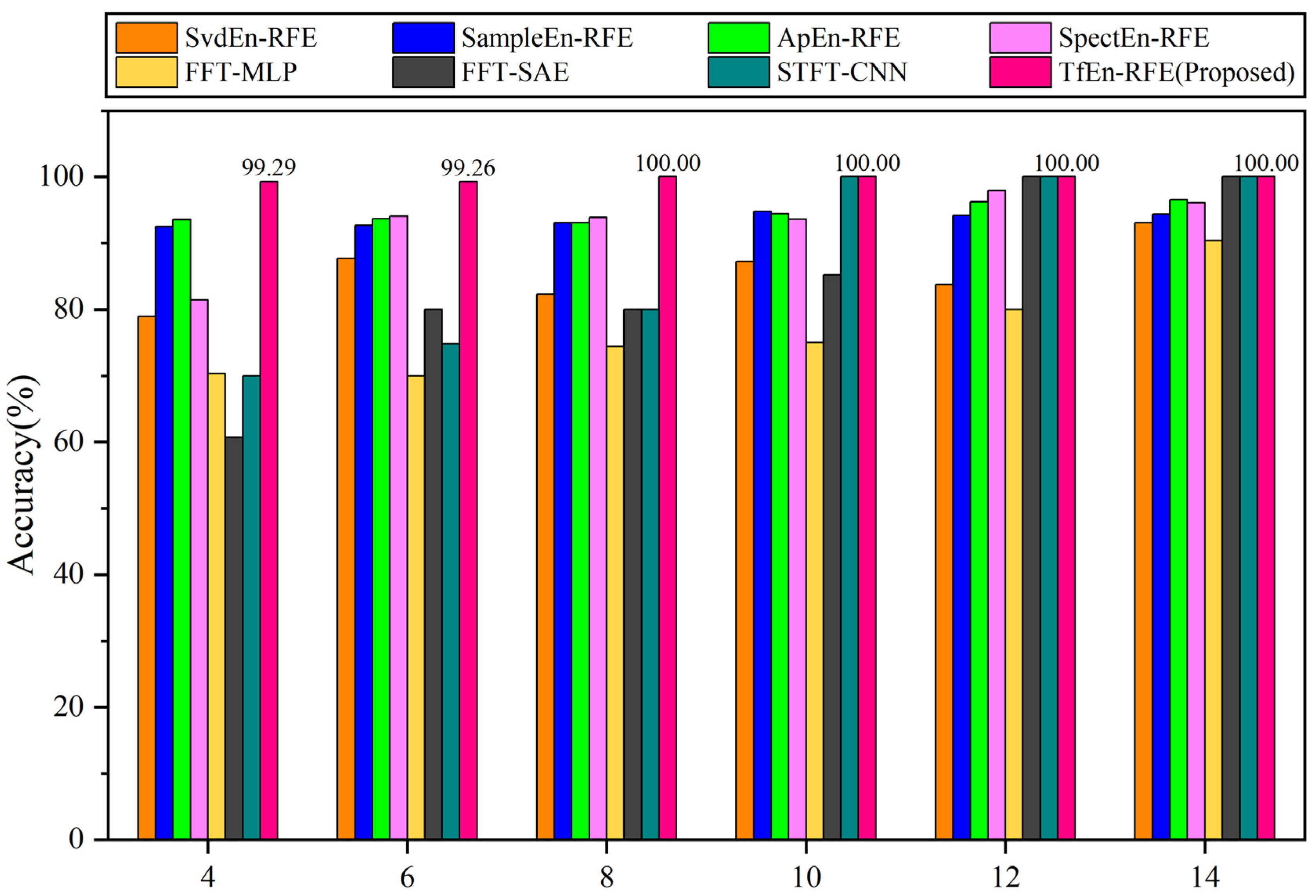
4.3. Comparisons with Variable Taining Sample Sizes
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Irfan, M.; Alwadie, A.; Glowacz, A. Design of a Novel Electric Diagnostic Technique for Fault Analysis of Centrifugal Pumps. Appl. Sci. 2019, 9, 5093. [Google Scholar] [CrossRef] [Green Version]
- Azadeh, A.; Saberi, M.; Kazem, A.; Ebrahimipour, V.; Nourmohammadzadeh, A.; Saberi, Z. A flexible algorithm for fault diagnosis in a centrifugal pump with corrupted data and noise based on ANN and support vector machine with hyper-parameters optimization. Appl. Soft Comput. 2013, 13, 1478–1485. [Google Scholar] [CrossRef]
- Cao, P.; Zhang, S.; Tang, J. Preprocessing-Free Gear Fault Diagnosis Using Small Datasets with Deep Convolutional Neural Network-Based Transfer Learning. IEEE Access 2018, 6, 26241–26253. [Google Scholar] [CrossRef]
- Pathirage, C.S.N.; Li, J.; Li, L.; Hao, H.; Liu, W.; Ni, P. Structural damage identification based on autoencoder neural networks and deep learning. Eng. Struct. 2018, 172, 13–28. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, Y.; Wan, J.; Liu, X.; Song, Z. Industrial Big Data for Fault Diagnosis: Taxonomy, Review, and Applications. IEEE Access 2017, 5, 17368–17380. [Google Scholar] [CrossRef]
- Hui, K.H.; Ooi, C.S.; Lim, M.H.; Leong, M.S.; Al-Obaidi, S.M. An improved wrapper-based feature selection method for machinery fault diagnosis. PLoS ONE 2017, 12, e0189143. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The Entropy Algorithm and Its Variants in the Fault Diagnosis of Rotating Machinery: A Review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. ENSEMBLE EMPIRICAL MODE DECOMPOSITION: A NOISE-ASSISTED DATA ANALYSIS METHOD. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Li, G.; Deng, C.; Wu, J.; Chen, Z.; Xu, X. Rolling Bearing Fault Diagnosis Based on Wavelet Packet Transform and Convolutional Neural Network. Appl. Sci. 2020, 10, 770. [Google Scholar] [CrossRef] [Green Version]
- Mu, Z.; Hu, J.; Min, J.-L. Driver Fatigue Detection System Using Electroencephalography Signals Based on Combined Entropy Features. Appl. Sci. 2017, 7, 150. [Google Scholar] [CrossRef] [Green Version]
- An, X.; Pan, L. Wind turbine bearing fault diagnosis based on adaptive local iterative filtering and approximate entropy. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 3228–3237. [Google Scholar] [CrossRef]
- Kumar, M.; Pachori, R.B.; Acharya, U.R. Automated Diagnosis of Myocardial Infarction ECG Signals Using Sample Entropy in Flexible Analytic Wavelet Transform Framework. Entropy 2017, 19, 488. [Google Scholar] [CrossRef]
- Lechner, M.; Miquel, R.; Wunsch, C. The Curse and Blessing of Training the Unemployed in a Changing Economy: The Case of East Germany After Unification. Ger. Econ. Rev. 2007, 8, 468–509. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Chen, J.; Li, J. Decision tree and PCA-based fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2007, 21, 1300–1317. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Saad, M.H.M. Optimal BP neural network algorithm for state of charge estimation of lithium-ion battery using PSO with PCA feature selection. J. Renew. Sustain. Energy 2017, 9, 064102. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Sánchez-Maroño, N.; Alonso-Betanzos, A. Recent advances and emerging challenges of feature selection in the context of big data. Knowl. Based Syst. 2015, 86, 33–45. [Google Scholar] [CrossRef]
- Yan, K.; Zhang, L. Feature selection and analysis on correlated gas sensor data with recursive feature elimination. Sens. Actuators B Chem. 2015, 212, 353–363. [Google Scholar] [CrossRef]
- Yeh, J.-R.; Shieh, J.-S.; Huang, N.E. complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Yang, J.; Li, P.; Yang, Y.; Xu, D. An improved EMD method for modal identification and a combined static-dynamic method for damage detection. J. Sound Vib. 2018, 420, 242–260. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, S.; Zhao, H.; Yang, X. A Novel Fault Diagnosis Method Based on Integrating Empirical Wavelet Transform and Fuzzy Entropy for Motor Bearing. IEEE Access 2018, 6, 35042–35056. [Google Scholar] [CrossRef]
- Kwok, H.; Jones, D. Improved instantaneous frequency estimation using an adaptive short-time Fourier transform. IEEE Trans. Signal Process. 2000, 48, 2964–2972. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, Z.; Wu, J. Functional connectivity-based classification of autism and control using SVM-RFECV on rs-fMRI data. Phys. Medica 2019, 65, 99–105. [Google Scholar] [CrossRef] [PubMed]
- Tipping, M.E.; Bishop, C.M. Probabilistic Principal Component Analysis. J. R. Stat. Soc. Ser. B (Stat. Methodol. 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.-R. Kernel principal component analysis. In International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 1997; pp. 583–588. [Google Scholar]
- Lameski, P.; Zdravevski, E.; Mingov, R.; Kulakov, A. SVM Parameter Tuning with Grid Search and Its Impact on Reduction of Model Over-fitting. In Lecture Notes in Computer Science; Springer Science and Business Media LLC: Berlin, Germany, 2015; Volume 9437, pp. 464–474. [Google Scholar]
- Yentes, J.M.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The appropriate use of approximate entropy and sample entropy with short data sets. Ann. Biomed. Eng. 2012, 41, 349–365. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Shi, T.; Chen, F.; Huang, S. New method of fault diagnosis of rotating machinery based on distance of information entropy. Front. Mech. Eng. 2011, 6, 249. [Google Scholar] [CrossRef]
- Gardner, M.; Dorling, S. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmospheric Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.-Y.; Qin, W.-L.; Ma, J. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification. Signal Process. 2017, 130, 377–388. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Pdf ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Chen, Z.; Deng, S.; Chen, X.-D.; Li, C.; Sánchez, R.-V.; Qin, H. Deep neural networks-based rolling bearing fault diagnosis. Microelectron. Reliab. 2017, 75, 327–333. [Google Scholar] [CrossRef]
- Verstraete, D.; Ferrada, A.; Droguett, E.L.; Meruane, V.; Modarres, M. Deep Learning Enabled Fault Diagnosis Using Time-Frequency Image Analysis of Rolling Element Bearings. Shock. Vib. 2017, 2017, 1–17. [Google Scholar] [CrossRef]




| Feature No. | Ranking |
|---|---|
| 1 | |
| 1 | |
| 1 | |
| 1 | |
| 6 | |
| 5 | |
| 4 | |
| 3 | |
| 2 | |
| 1 |
| Method | Mode | Accuracy | Errors | Rights |
|---|---|---|---|---|
| TfEn | Normal | 100.00% | 0 | 50 |
| Inner-race fault | 100.00% | 0 | 50 | |
| Outer-race fault | 100.00% | 0 | 50 | |
| Ball fault | 100.00% | 0 | 47 | |
| Impeller fault | 94.34% | 3 | 50 | |
| Average/Total | 98.80% | 3 | 247 | |
| TfEn-PCA | Normal | 100.00% | 0 | 50 |
| Inner-race fault | 100.00% | 0 | 50 | |
| Outer-race fault | 75.00% | 13 | 39 | |
| Ball fault | 73.91% | 12 | 34 | |
| Impeller fault | 94.23% | 3 | 49 | |
| Average/Total | 88.80% | 28 | 222 | |
| TfEn-KPCA | Normal | 91.11% | 4 | 41 |
| Inner-race fault | 100.00% | 0 | 46 | |
| Outer-race fault | 60.24% | 33 | 50 | |
| Ball fault | 86.49% | 5 | 32 | |
| Impeller fault | 94.87% | 2 | 37 | |
| Average/Total | 82.40% | 44 | 206 | |
| TfEn-RFE (proposed) | Normal | 100.00% | 0 | 50 |
| Inner-race fault | 100.00% | 0 | 50 | |
| Outer-race fault | 100.00% | 0 | 50 | |
| Ball fault | 100.00% | 0 | 50 | |
| Impeller fault | 100.00% | 0 | 50 | |
| Average/Total | 100.00% | 0 | 250 |
| Method | SvdEn | SampleEn | ApEn | SpectEn | TfEn(Proposed) |
|---|---|---|---|---|---|
| Running time(s) per 50 samples | 0.24 | 2862.31 | 2740.10 | 0.14 | 1.61 |
| Method | Preprocessing | Type of Layer | Hidden Size | Layer Num |
| MLP | Fast Fourier transform (FFT) | Fully connection layer | 512-128; 128-64; 64-5 | 3 |
| SAE | FFT | Encoder layer | 512-128; 128-64 | 2 |
| Decoder layer | 64-128; 128-512 | 2 | ||
| Fully connection layer | 64-16; 16-5 | 2 | ||
| CNN | STFT | Conv layer | 1-2-5; 2-3-5; 3-3-5 | 3 |
| Max pool layer | 2-2 | 1 | ||
| Fully connection layer | 1980-32; 32-5 | 2 | ||
| Dropout | Optimizer | Training Epochs | Learning Rate | Batch Size |
| 0.5 | Adam | 100 | 0.02 | 15 |
| Training Size/ Methods | 4 | 6 | 8 | 10 | 12 | 14 |
|---|---|---|---|---|---|---|
| SvdEn-RFE | 78.93% | 87.69% | 82.31% | 87.20% | 83.78% | 93.04% |
| SampleEn-RFE | 91.43% | 92.22% | 92.69% | 94.80% | 93.75% | 95.22% |
| ApEn-RFE | 93.57% | 93.71% | 93.08% | 94.40% | 96.25% | 96.52% |
| SpectEn-RFE | 81.43% | 94.07% | 93.85% | 93.60% | 97.92% | 96.09% |
| FFT-MLP | 70.36% | 70.00% | 74.40% | 75.00% | 80.00% | 90.37% |
| FFT-SAE | 60.71% | 80.00% | 80.00% | 85.20% | 100.00% | 100.00% |
| STFT-CNN | 70.00% | 74.82% | 80.00% | 100.00% | 100.00% | 100.00% |
| TfEn-RFE (proposed) | 99.29% | 99.26% | 100.00% | 100.00% | 100.00% | 100.00% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, X.; Liu, H.; Tao, L. TF Entropy and RFE Based Diagnosis for Centrifugal Pumps Subject to the Limitation of Failure Samples. Appl. Sci. 2020, 10, 2932. https://doi.org/10.3390/app10082932
Su X, Liu H, Tao L. TF Entropy and RFE Based Diagnosis for Centrifugal Pumps Subject to the Limitation of Failure Samples. Applied Sciences. 2020; 10(8):2932. https://doi.org/10.3390/app10082932
Chicago/Turabian StyleSu, Xuanyuan, Hongmei Liu, and Laifa Tao. 2020. "TF Entropy and RFE Based Diagnosis for Centrifugal Pumps Subject to the Limitation of Failure Samples" Applied Sciences 10, no. 8: 2932. https://doi.org/10.3390/app10082932
APA StyleSu, X., Liu, H., & Tao, L. (2020). TF Entropy and RFE Based Diagnosis for Centrifugal Pumps Subject to the Limitation of Failure Samples. Applied Sciences, 10(8), 2932. https://doi.org/10.3390/app10082932






