Nonlinear Control Design of a Half-Car Model Using Feedback Linearization and an LQR Controller
Abstract
:1. Introduction
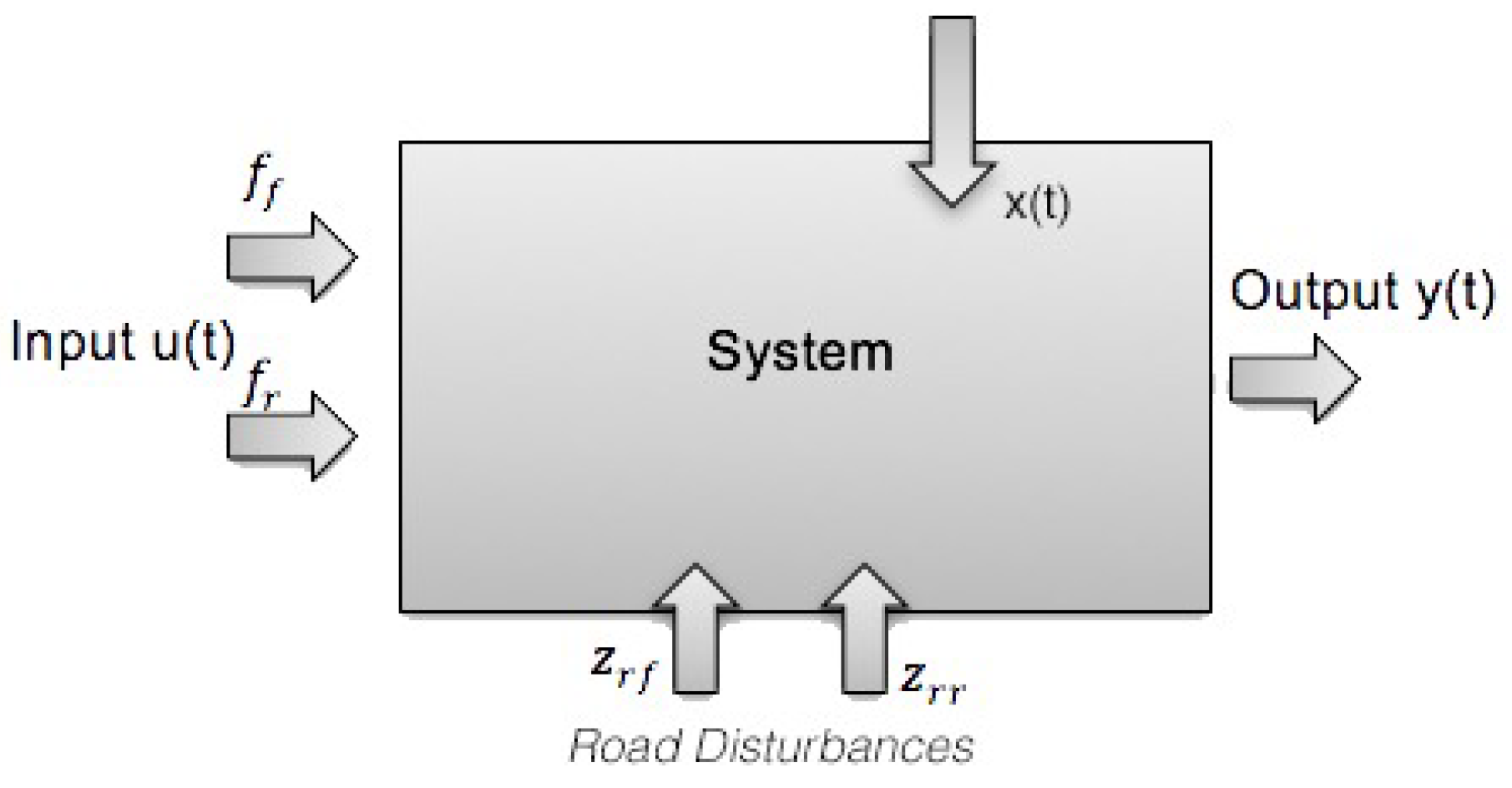
2. Methodology
3. Modelling
3.1. Feedback Linearization
3.2. LQR Controller
3.3. Simulink Modelling
3.3.1. Case 1: Positive Road Disturbances
3.3.2. Case 2: Positive and Negative Road Disturbances
4. Results and Discussions
4.1. Results of Case 1: Positive Road Disturbances
4.2. Results of Case 2: Positive and Negative Road Disturbances
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Karnopp, D. Theoretical Limitations in Active Vehicle Suspensions. Veh. Syst. Dyn. 1986, 15, 41–54. [Google Scholar] [CrossRef]
- Yue, C.; Butsuen, T.; Hedrick, J.K. Alternative Control Laws for Automotive Active Suspensions. J. Dyn. Syst. Meas. Control. 1989, 111, 286–291. [Google Scholar] [CrossRef]
- Hrovat, D. Optimal Active Suspension Structures for Quarter-Car Vehicle Models. Automatica 1990, 26, 845–860. [Google Scholar] [CrossRef]
- Hrovat, D. Applications of Optimal Control to Advanced Automotive Suspension Design. J. Dyn. Syst. Meas. Control. 1993, 115, 328–342. [Google Scholar] [CrossRef]
- KrstiC, M.; Kokotovic, P.V. Adaptive Nonlinear Design with Controller-Identifier Separation and Swapping. IEEE Trans. Autom. Control. 1995, 40, 426–440. [Google Scholar] [CrossRef] [Green Version]
- Cho, B.K.; Ryu, G.; Song, S.J. Control Strategy of An Active Suspension for a Half Car Model with Preview Information. Int. J. Automot. Technol. 2005, 6, 243–249. [Google Scholar]
- Chander, B. Modelling and Analysis of Half Car Vehicle Suspension System Using Fuzzy Logic Controller. Bachelor’s Thesis, Mechancial Engineering Department, Sri Venkateshwara Univeristy College of Engineering, Tirupati, India, 2009. [Google Scholar]
- Huang, C.J.; Lin, J.S.; Chen, C.C. Road-Adaptive Algorithm Design of Half-Car Active Suspension System. Expert Syst. Appl. 2010, 37, 4392–4402. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Hand, S.; Hilton, C. A Study on Half-Vehicle Active Suspension Control using Sampled-Data Control. In Proceedings of the Chinese Conference on Control and Decision, Mianyang, China, 23–25 May 2011; pp. 2635–2640. [Google Scholar]
- Alexandru, C.; Alexandru, P. Dynamic Analysis of a Half-Car Model with Active Suspension. In Proceedings of the 2nd International Conference on Circuits, Systems, Control and Signals, Prague, Czech Republic, 26–28 September 2011; pp. 36–41. [Google Scholar]
- Karuppaiah, N.; Sujatha, C.; Ramamurti, V. Modal vibration/stress analysis of a passenger vehicle by FEM. In Proceedings of the Symposium on International Automotive Technology, Nantes, France, 2–4 July 2012. [Google Scholar]
- Souilem, H.; Mehjoub, S.; Derbel, N. Intelligent Control for a Half-Car Active Suspension by Self-Tunable Fuzzy Inference System. Int. J. Fuzzy Syst. Adv. Appl. 2015, 2, 9–15. [Google Scholar]
- Ata, A.B.; Kunya, A.A. Half Car Suspension System Integrated With PID Controller. In Proceedings of the 29th European Conference on Modelling and Simulation, ECMS, Albena (Varna), Bulgaria, 26–29 May 2015. [Google Scholar]
- Turakhia, T.; Modi, M. Mathematical Modelling and Simulation of a Simple Half—Car Vibration Model. Int. J. Sci. Res. Dev. 2016, 4, 2321. [Google Scholar]
- Rizvi, S.M.H.; Abid, M.; Khan, A.Q.; Satti, S.G.; Latif, J. H∞ control of 8 degrees of freedom vehicle active suspension system. J. King Saud-Univ. Eng. Sci. 2016, 30, 161–169. [Google Scholar] [CrossRef] [Green Version]
- Kadam, R.N.; Gangavane, S.A.; Shaikh, S.M.; Manjarekar, S.S.; Bamankar, P.B. Vibrational Analysis of Half Car Model. J. Int. Eng. Res. (IERJ) 2017, 1, 69–72. [Google Scholar]
- Wang, Z.-F.; Dong, M.-M.; Gu, L.; Rath, J.-J.; Qin, Y.-C.; Bai, B. Influence of Road Excitation and Steering Wheel Input on Vehicle System Dynamic Responses. Appl. Sci. 2017, 7, 570. [Google Scholar] [CrossRef] [Green Version]
- Shelke, G.D.; Mitra, A.C. Analysis and Validation of Linear Half Car Passive Suspension System with Different Road Profiles. In Proceedings of the 7th National Conference on Recent Developments in Mechanical Engineering RDME-2018, Ghent, Belgium, 9–10 July 2018; pp. 14–19. [Google Scholar]
- Nassar, A.; Al-Ghanim, A. Modeling, Simulation, and Control of Half Car Suspension System Using Matlab/Simulink. Int. J. Sci. Res. (IJSR) 2018, 7, 351–362. [Google Scholar]
- Hua, C.; Chen, J.; Li, Y.; Li, L. Adaptive prescribed performance control of half-car active suspension system with unknown dead-zone input. Mech. Syst. Signal Process. 2018, 111, 135–148. [Google Scholar] [CrossRef]
- Ghahremani, A.; Khaloozadeh, H.; Ghahremani, P. Adaptive sliding neural network-based vibration control of a nonlinear quarter car active suspension system with unknown dynamics. Vibroeng. Procedia 2018, 17, 67–72. [Google Scholar] [CrossRef] [Green Version]
- Gopala Rao, L.V.V.; Narayanan, S. Optimal response of half car vehicle model with sky-hook damper based on LQR control. Int. J. Dynam. Control 2019. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Shao, Y.; Chen, C.C. Fast finite-time stability and its application in adaptive control of high-order nonlinear system. Automatica 2019, 106, 339–348. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Zhang, D.; Meng, Q.; Chen, C.C. Feedback stabilization of time-delay nonlinear systems with continuous time-varying output function. Int. J. Syst. Sci. 2019, 50, 244–255. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Dong, Y.Y.; Chen, C.C. Global fast finite-time partial state feedback stabilization of high-order nonlinear systems with dynamic uncertainties. Inf. Sci. 2019, 484, 219–236. [Google Scholar] [CrossRef]
- Hamdoon, F.O.; Faisal, B.M. Simulation of Active Suspension System for Half Vehicle Model under Different Road Profile. Univ. Thi-Qar J. Eng. Sci. 2019, 10, 13–17. [Google Scholar] [CrossRef]
- Rathai, K.M.M.; Sename, O.; Alamir, M. GPU-Based Parameterized NMPC Scheme for Control of Half Car Vehicle With Semi-Active Suspension System. IEEE Control. Syst. Lett. 2019, 3, 631–636. [Google Scholar] [CrossRef]
- Kanchwala, H. Vehicle Suspension Model Development using Test Track Measurements. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2020, 234, 1442–1459. [Google Scholar] [CrossRef]
- Isidori, A. Nonlinear Control Systems, 3rd ed.; Springer: London, UK, 1995; pp. 219–291. [Google Scholar]



















| States | State Variables | Variable Names |
|---|---|---|
| z | Vertical Displacement | |
| Vertical Velocity | ||
| Angular Displacement | ||
| Angular Velocity | ||
| Front Suspension Travel | ||
| Velocity of Front Unsprung Mass | ||
| Rear Wheel Suspension Travel | ||
| Velocity of Rear Unsprung Mass |
| States | Values (m) | Research Papers | Reduction in Amplitude (%) | Reduced rms Values (%) |
|---|---|---|---|---|
| Vertical Displacement | 0.018 | 0.024 [10] | 73.3 | 25 [10] |
| Vertical Acceleration | 1.3 | 2.5 [10] | 76 | 48 [10] |
| Pitch Displacement | 0.014 | 0.0273 [10] | 55.6 | 48 [10] |
| Pitch Acceleration | 0.83 | 1.8 [10] | 45.5 | 53.9 [10] |
| Front Suspension Travel | 0.011 | 0.022 [8] | 85.7 | 50 [8] |
| Rear Suspension Travel | 0.012 | 0.020 [8] | 80 | 40 [8] |
| States | Without Controller (m) | With Controller (m) | Improvement (%) |
|---|---|---|---|
| Vertical Displacement | 0.05 | 0.016 | 68 |
| Vertical Acceleration | 4.4 | 1.3 | 70.4 |
| Pitch Displacement | 0.03 | 0.01 | 66.7 |
| Pitch Acceleration | 2.3 | 0.69 | 70 |
| Front Suspension Travel | 0.022 | 0.013 | 41 |
| Rear Suspension Travel | 0.025 | 0.016 | 36 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.A.; Abid, M.; Ahmed, N.; Wadood, A.; Park, H. Nonlinear Control Design of a Half-Car Model Using Feedback Linearization and an LQR Controller. Appl. Sci. 2020, 10, 3075. https://doi.org/10.3390/app10093075
Khan MA, Abid M, Ahmed N, Wadood A, Park H. Nonlinear Control Design of a Half-Car Model Using Feedback Linearization and an LQR Controller. Applied Sciences. 2020; 10(9):3075. https://doi.org/10.3390/app10093075
Chicago/Turabian StyleKhan, Muhammad Aseer, Muhammad Abid, Nisar Ahmed, Abdul Wadood, and Herie Park. 2020. "Nonlinear Control Design of a Half-Car Model Using Feedback Linearization and an LQR Controller" Applied Sciences 10, no. 9: 3075. https://doi.org/10.3390/app10093075
APA StyleKhan, M. A., Abid, M., Ahmed, N., Wadood, A., & Park, H. (2020). Nonlinear Control Design of a Half-Car Model Using Feedback Linearization and an LQR Controller. Applied Sciences, 10(9), 3075. https://doi.org/10.3390/app10093075







