An ADS-Based Sparse Optimization Method for Sonar Imaging Sensor Arrays
Abstract
:1. Introduction
2. Almost Difference Set and Sparse Optimization of Mills Cross Array
2.1. Almost Difference Sets
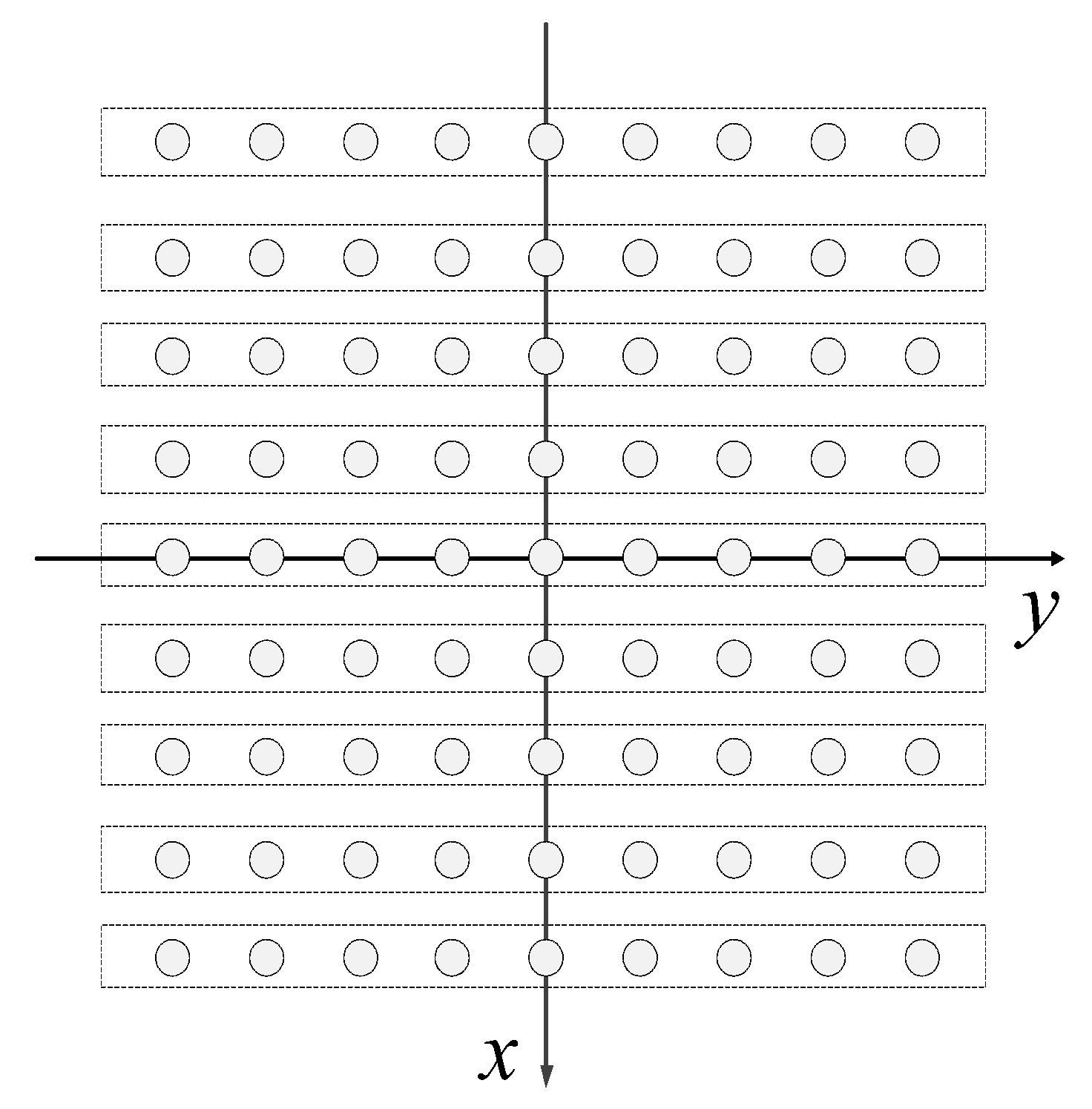
2.2. ADS-Based Arrays
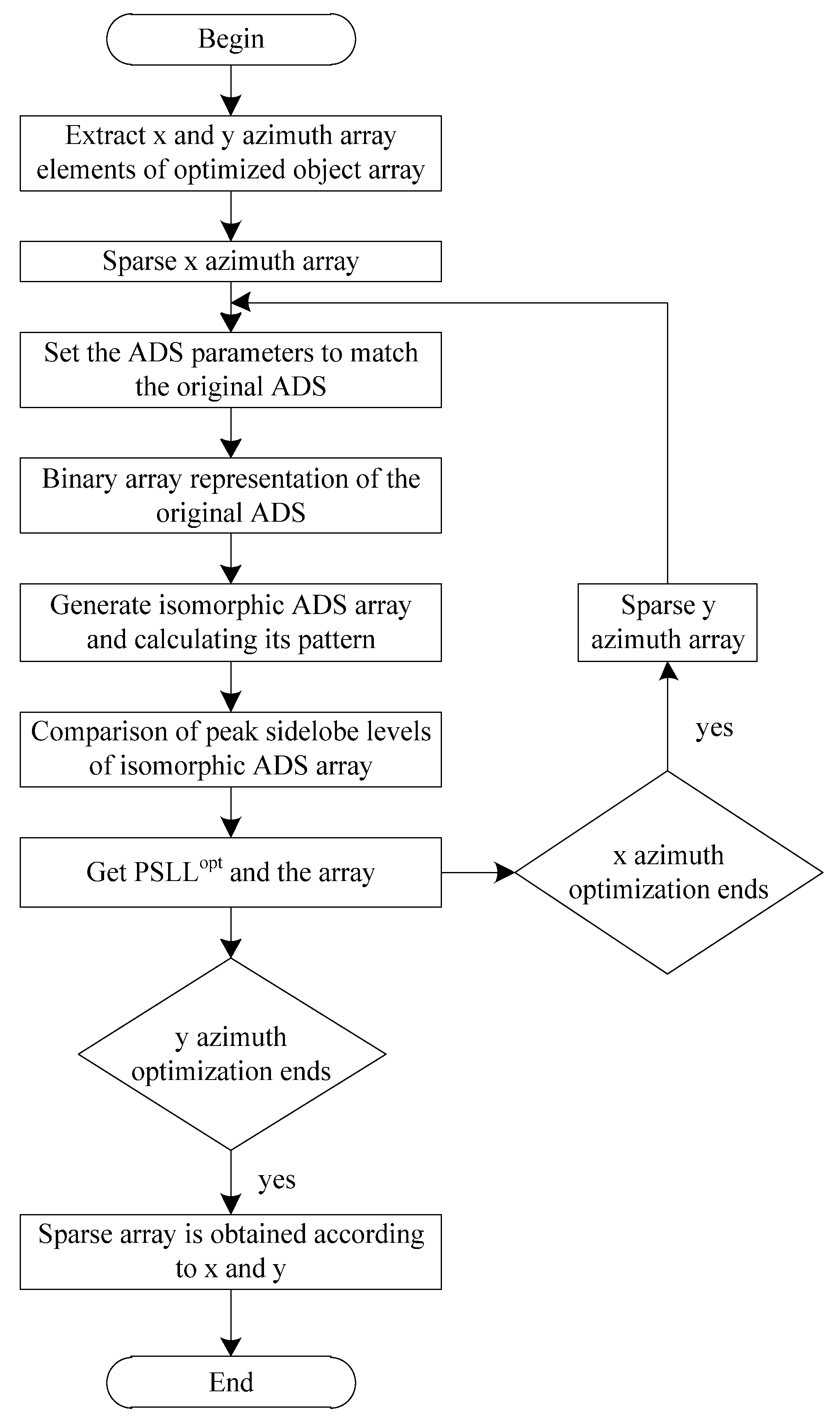
3. Mills Cross Array Optimization Using ADS Method
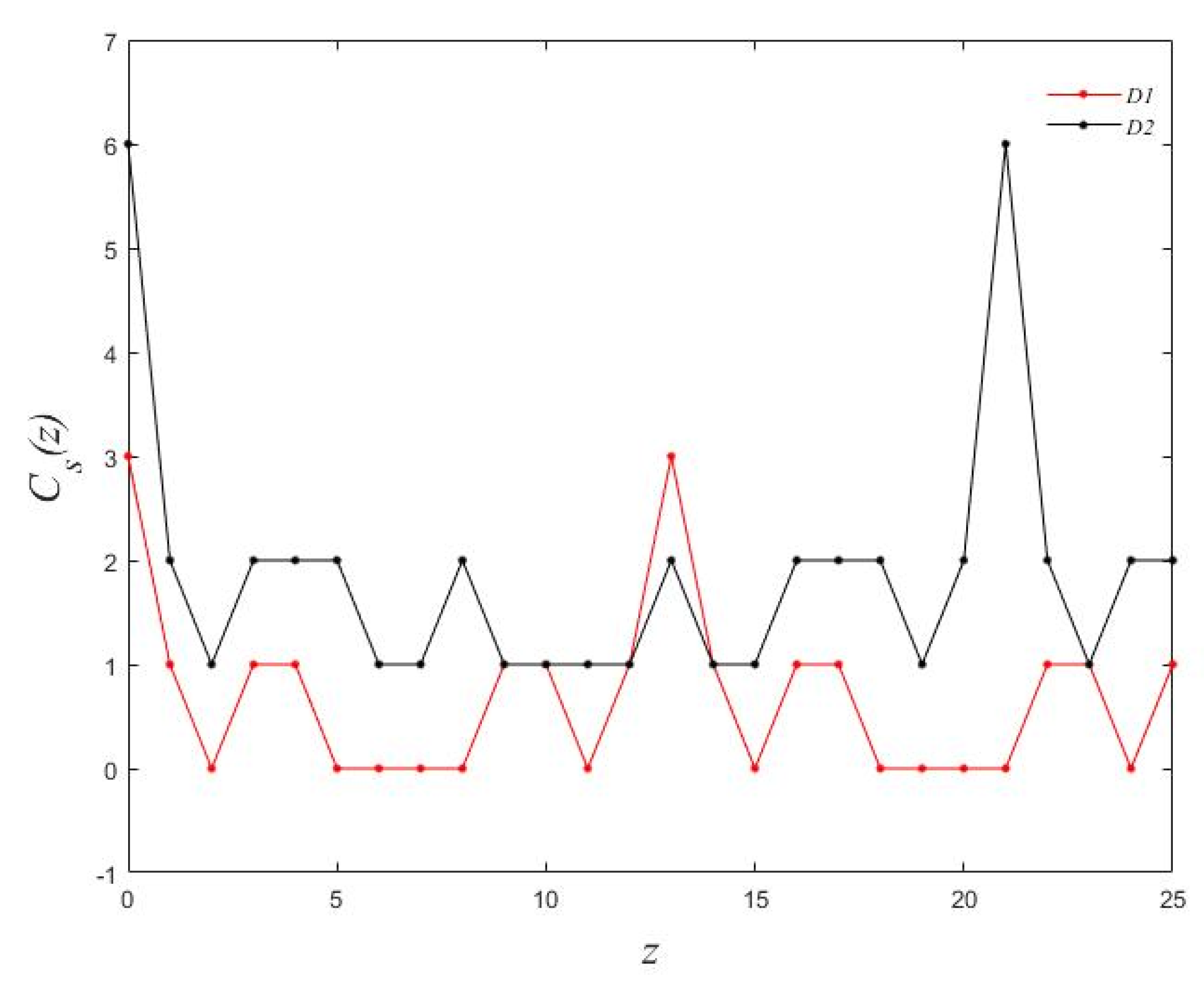
4. Analysis of ADS Thinned Array
4.1. Effect of Cycle Index
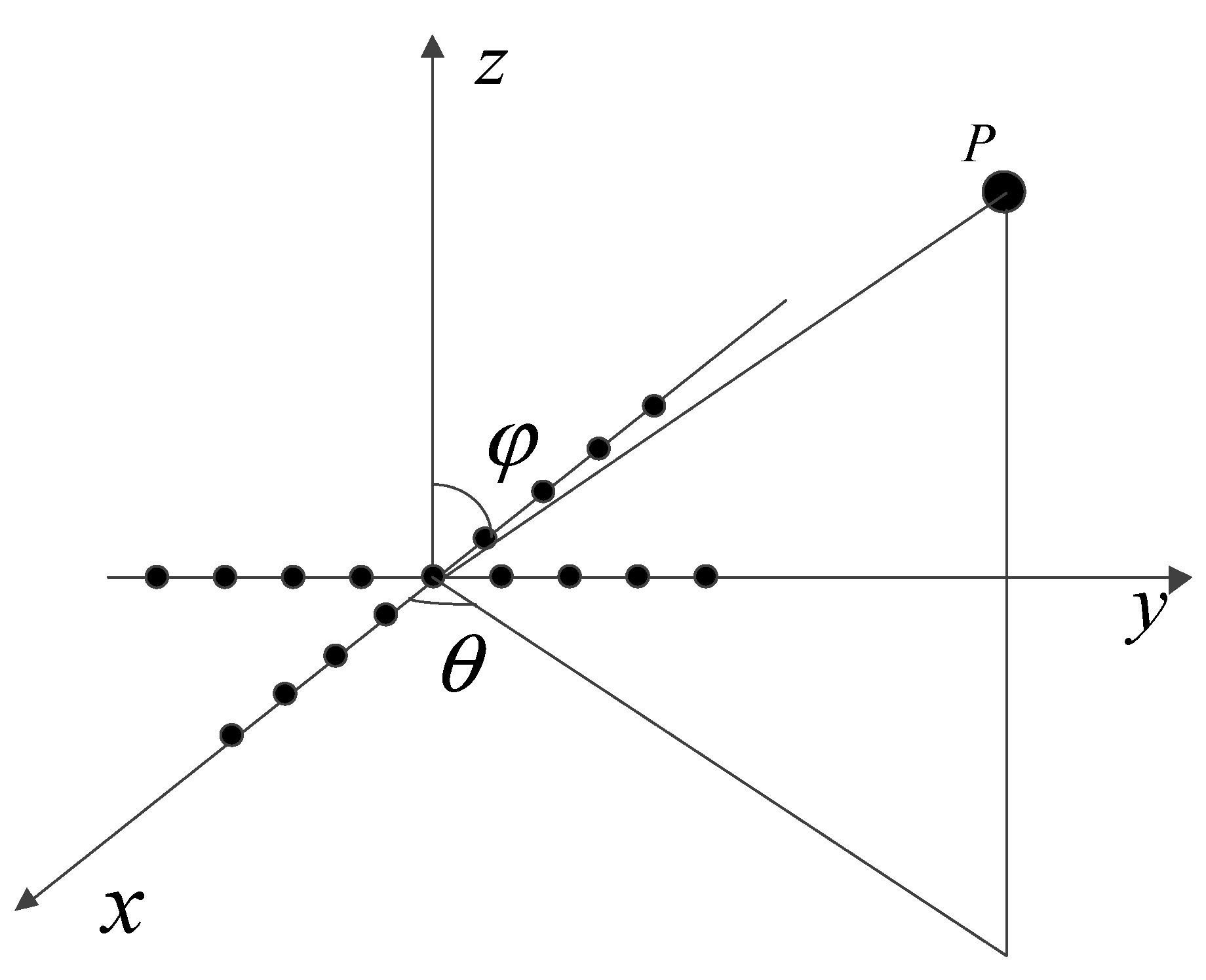
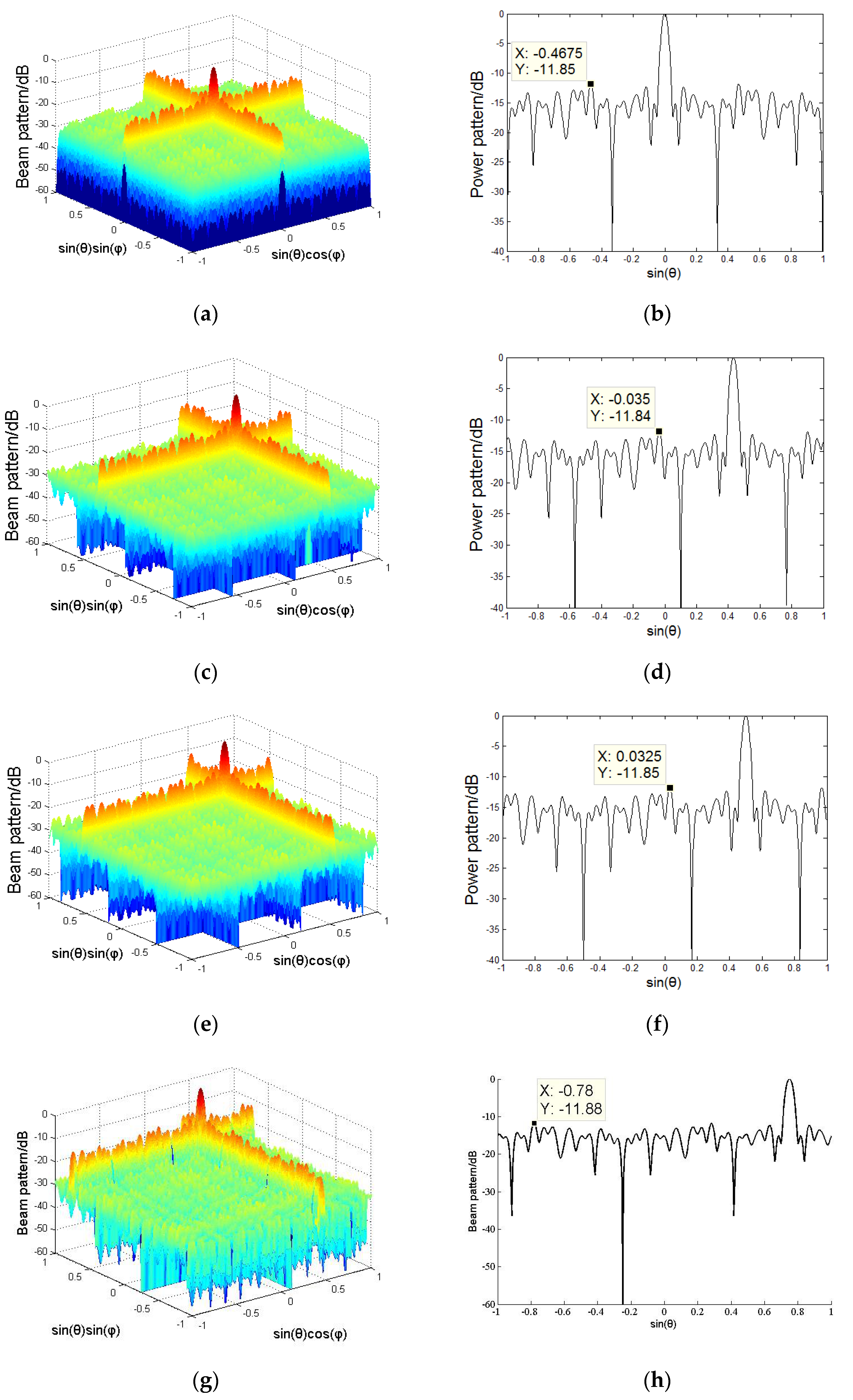
4.2. Azimuth Angle Performance
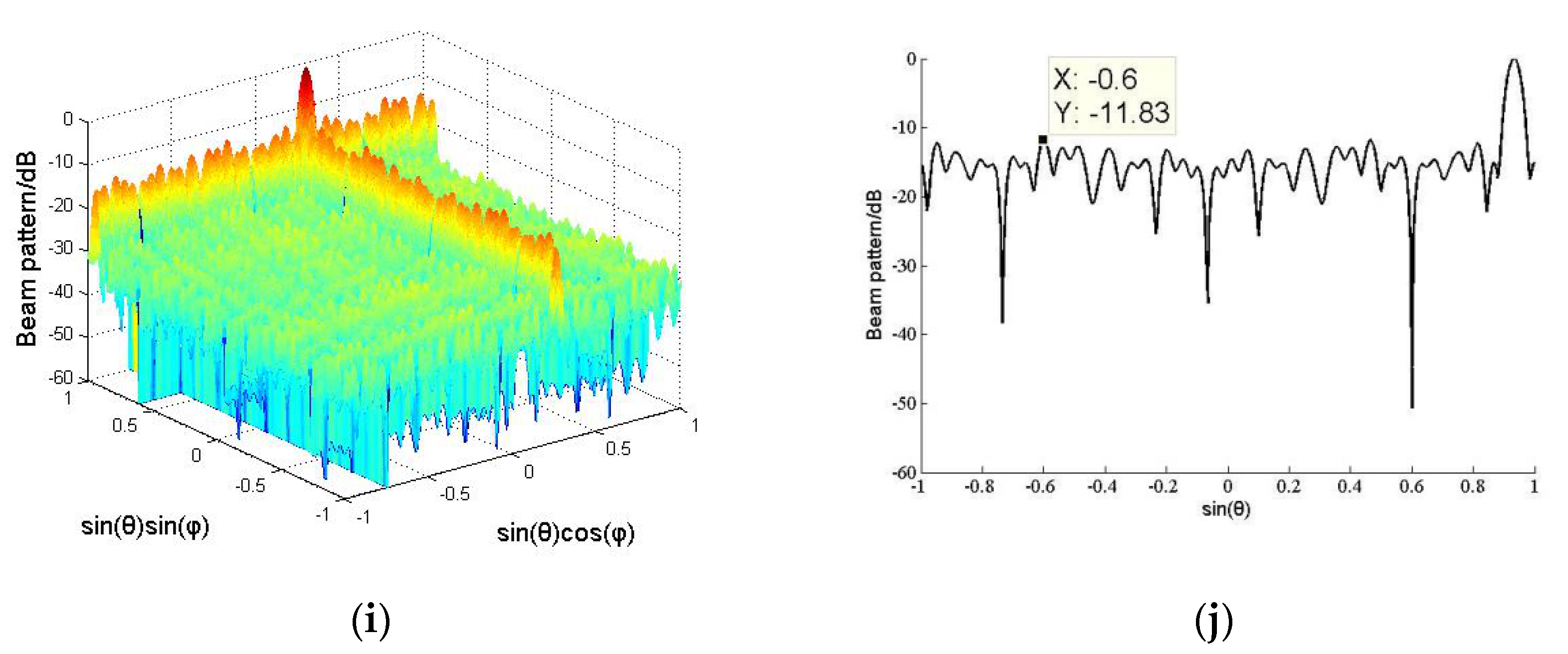
4.3. Azimuth Resolution
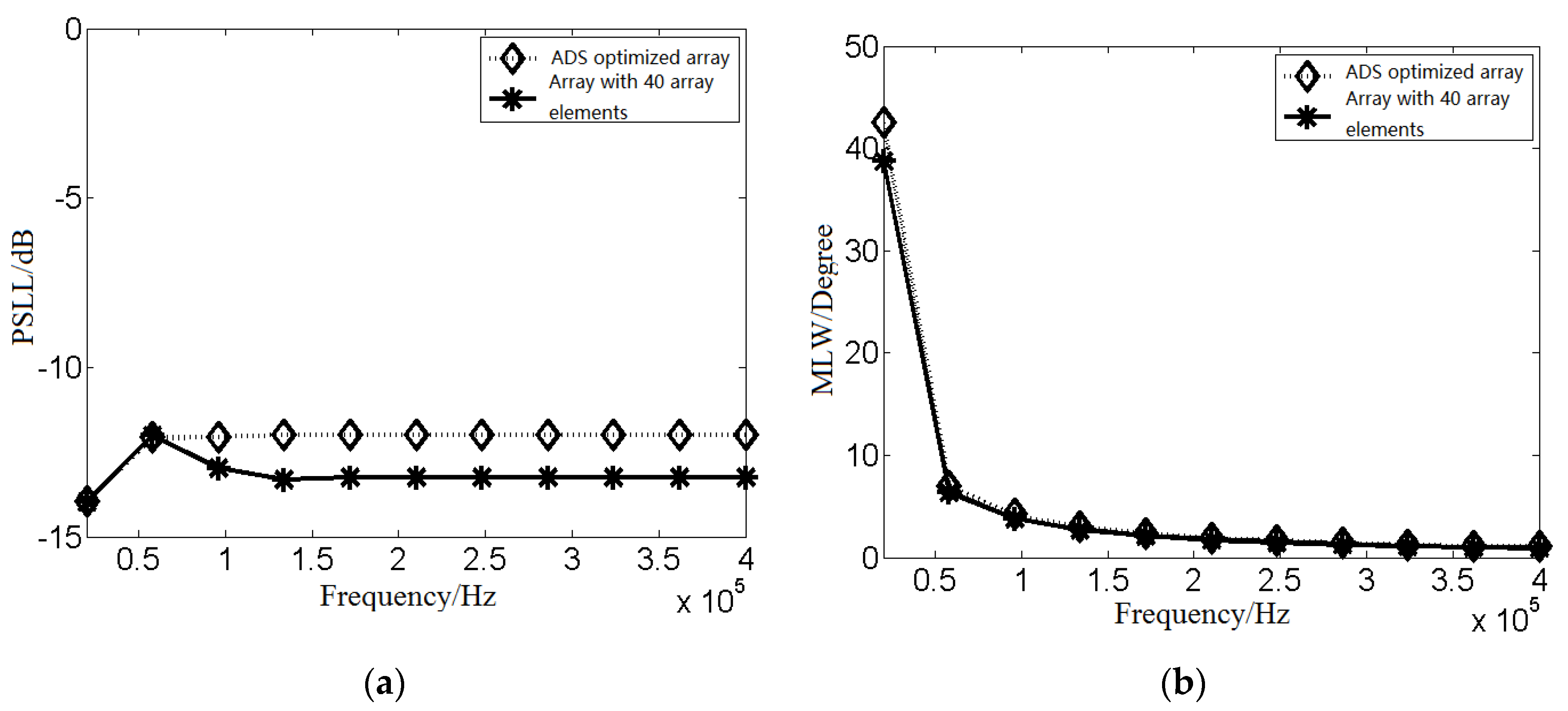
4.4. Frequency Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Silkaitis, J.M.; Douglas, B.L.; Lee, H. Synthetic-aperture sonar imaging: System analysis, image formation, and motion compensation. In Proceedings of the Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 30 October–1 November 1995; pp. 423–427. [Google Scholar]
- Hansen, E.R. Synthetic Aperture Sonar Technology Review. Mar. Technol. Soc. J. 2013, 47, 117–127. [Google Scholar] [CrossRef]
- Repetto, S.; Palmese, M.; Trucco, A. Design and Assessment of a Low-Cost 3-D Sonar Imaging System Based on a Sparse Array. In Proceedings of the 2006 IEEE Instrumentation and Measurement Technology, Sorrento, Sorrento, Italy, 24–27 April 2006; pp. 410–415. [Google Scholar]
- Liu, X.H.; Sun, C.; Yi, F.; Li, M. Underwater three-dimensional imaging using narrowband MIMO array. Sci. China Phys. Mech. Astron. 2013, 56, 1346–1354. [Google Scholar] [CrossRef]
- Ha, B.V.; Zich, R.E.; Mussetta, M.; Pirinoli, P. Improved compact Genetic Algorithm for thinned array design. In Proceedings of the Antennas and Propagation (EuCAP), 2013 7th European Conference on IEEE, Gothenburg, Sweden, 8–12 April 2013; pp. 1807–1808. [Google Scholar]
- Rodríguez, J.A.; Ares, F.; Moreno, E. Linear array pattern synthesis optimizing array element excitations using the simulated annealing technique. Microw. Opt. Technol. Lett. 2015, 23, 224–226. [Google Scholar] [CrossRef]
- D’urso, M.; Prisco, G.; Tumolo, R.M. Maximally Sparse, Steerable, and Nonsuperdirective Array Antennas via Convex Optimizations. IEEE Trans. Antennas Propag. 2016, 64, 3840–3849. [Google Scholar] [CrossRef]
- Yuan, Z.H.; Geng, J.P.; Jin, R.H.; Fan, Y. Pattern Synthesis of 2-D Arrays Based on a Modified Particle Swarm Optimization Algorithm. J. Electron. Inf. Technol. 2007, 29, 1236–1239. [Google Scholar]
- Liu, X.; Zhou, F.; Zhou, H.; Tian, X.; Jiang, R.; Chen, Y. A low-complexity real-time 3-D sonar imaging system with a cross array. Ieee J. Ocean. Eng. 2015, 41, 262–273. [Google Scholar]
- Scenario, I.T. Minimum Redundancy MIMO Array Synthesis by means of Cyclic Difference Sets. Int. J. Antennas Propag. 2013, 2013, 356–360. [Google Scholar]
- Dong, J.; Liu, F.; Guo, Y.; Shi, R. MIMO radar array thinning optimization exploiting almost difference sets, Optik, 2016, 10, 4454-4460. Optik 2016, 10, 4454–4460. [Google Scholar] [CrossRef]
- Luo, Y.Y.; Guo, Q.; Lutsenko, V.I.; Zheng, Y. Nonequidistant Two-Dimensional Antenna Arrays Based on the Structure of Latin Squares Taking Cyclic Difference Sets as Elements. In Proceedings of the 2019 European Microwave Conference in Central Europe (EuMCE), Prague, Czech Republic, 13–15 May 2019; pp. 427–430. [Google Scholar]
- Carlin, M.; Oliveri, G.; Massa, A. On the Robustness to Element Failures of Linear ADS-Thinned Arrays. IEEE Trans. Antennas Propag. 2011, 59, 4849–4853. [Google Scholar]
- Arasu, K.T.; Ding, C.; Helleseth, T.; Kumar, P.V.; Martinsen, H.M. Almost difference sets and their sequences with optimal autocorrelation. IEEE Trans. Inf. Theory 2001, 47, 2934–2943. [Google Scholar] [CrossRef]
- Zhang, Y.; Lei, J.; Zhang, S. A new family of almost difference sets and some necessary conditions. IEEE Trans. Inf. Theory 2006, 52, 2052–2061. [Google Scholar] [CrossRef]
- Oliveri, G.; Donelli, M.; Massa, A. Linear Array Thinning Exploiting Almost Difference Sets. IEEE Trans. Antennas Propag. 2009, 57, 3800–3812. [Google Scholar] [CrossRef] [Green Version]
- Oliveri, G.; Massa, A. ADS-based array design for 2-D and 3-D ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 1568–1582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oliveri, G.; Massa, A. Genetic algorithm (GA)-enhanced almost difference set (ADS)-based approach for array thinning. Microw. Antennas Propag. Iet 2015, 5, 305–315. [Google Scholar] [CrossRef]
- Li, L.; Wang, B.; Xia, C.; Liu, X.; Cao, S. Design of Array with Multiple Interleaved Subarray based on Subarray Excitation Energy-matching. J. Beijing Univ. Aeronaut. Astronaut. 2016, 42, 2395–2402. [Google Scholar]
- Sun, F.; Lan, P.; Gao, B.; Chen, L.A. A low complexity direction of arrival estimation algorithm by reinvestigating the sparse structure of uniform linear arrays. Prog. Electromagn. Res. C 2016, 63, 119–129. [Google Scholar] [CrossRef] [Green Version]
- Skolnik, M. Radar Handbook, 2nd ed.; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]





| K | Sparse Ratio | |||
|---|---|---|---|---|
| 20 | 50% | 2.65 | −13.5 | −7.57 |
| Steering Angle | 0° | 30° | 45° | 60° | 75° | |
|---|---|---|---|---|---|---|
| Array | ||||||
| Original Mills | −13.27 | −13.27 | −13.26 | −13.22 | −13.25 | |
| Thinned by CDS | −12.33 | −12.35 | −12.32 | −12.12 | −12.07 | |
| Thinned by ADS | −11.85 | −11.84 | −11.85 | −11.88 | −11.83 | |
| Items | Transmit Elements | Receive Elements | Aperture Size | Azimuth Average | Azimuth Deviations | |
|---|---|---|---|---|---|---|
| Array | ||||||
| Thinned by ADS | 20 | 20 | 19.5 | 5.25° | 0.31° | |
| Thinned by CDS | 21 | 21 | 18.5 | 5.62° | 0.28° | |
| Mills Cross | 40 | 40 | 19.5 | 5.00° | 0.16° | |
| Mills Cross | 20 | 20 | 9.5 | 10.21° | 0.12° | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Shi, F.; Sun, Y.; Li, P. An ADS-Based Sparse Optimization Method for Sonar Imaging Sensor Arrays. Appl. Sci. 2020, 10, 3176. https://doi.org/10.3390/app10093176
Liu J, Shi F, Sun Y, Li P. An ADS-Based Sparse Optimization Method for Sonar Imaging Sensor Arrays. Applied Sciences. 2020; 10(9):3176. https://doi.org/10.3390/app10093176
Chicago/Turabian StyleLiu, Jiancheng, Feng Shi, Yecheng Sun, and Peng Li. 2020. "An ADS-Based Sparse Optimization Method for Sonar Imaging Sensor Arrays" Applied Sciences 10, no. 9: 3176. https://doi.org/10.3390/app10093176




