Solving Backward Heat Conduction Problems Using a Novel Space–Time Radial Polynomial Basis Function Collocation Method
Abstract
Featured Application
Abstract
1. Introduction
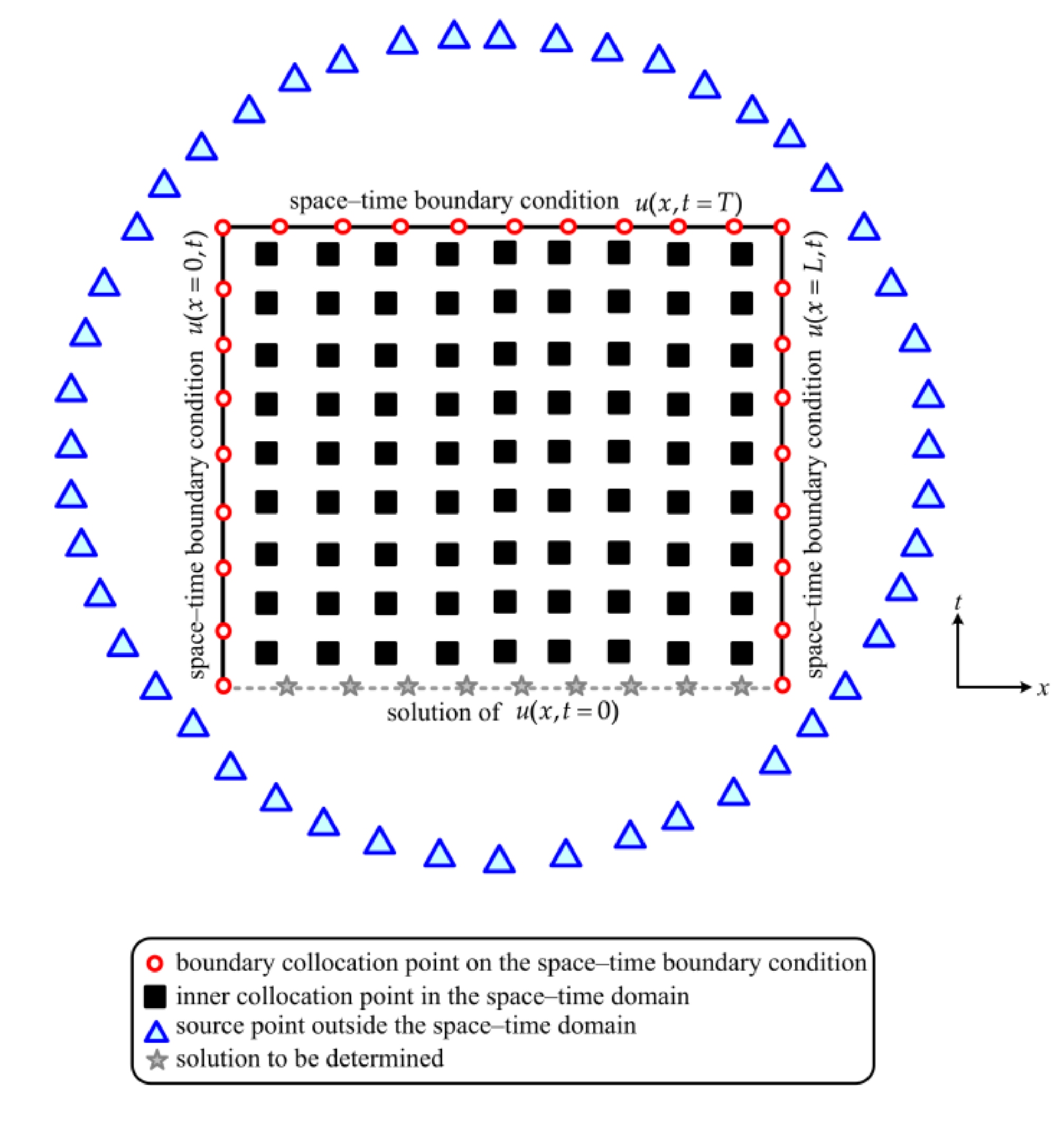
2. The Space–time Radial Polynomial Basis Function Collocation Method
3. Validation of the Proposed Method
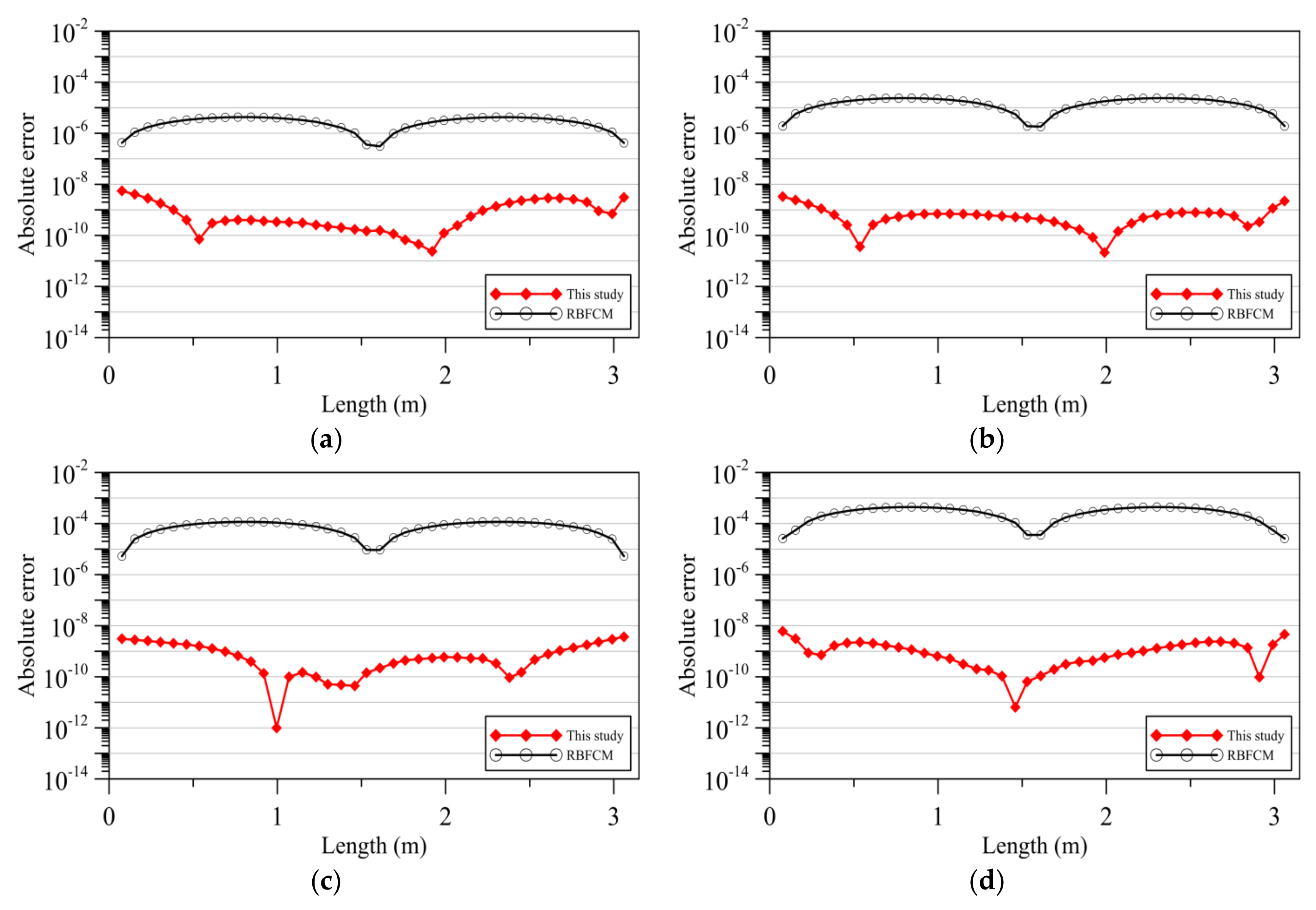
3.1. Accuracy and Convergence Analysis
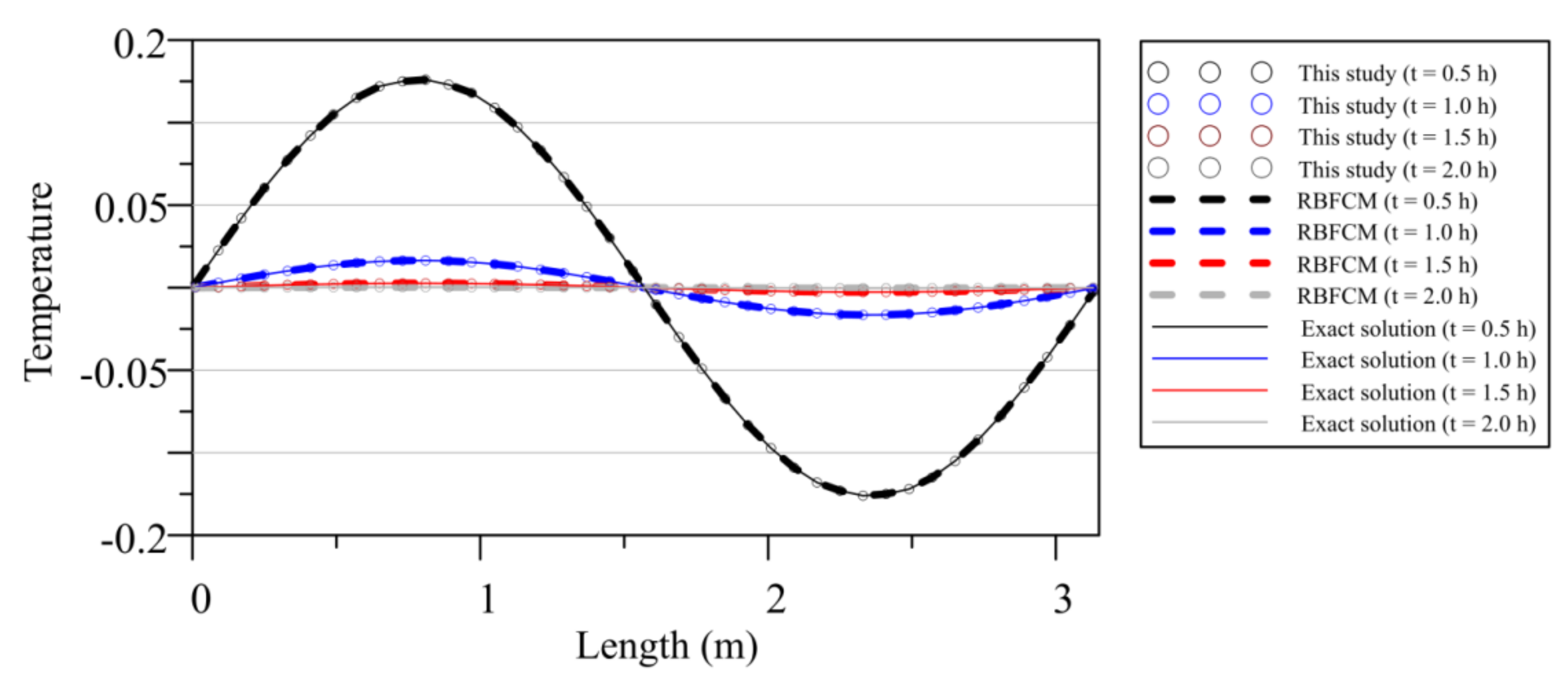
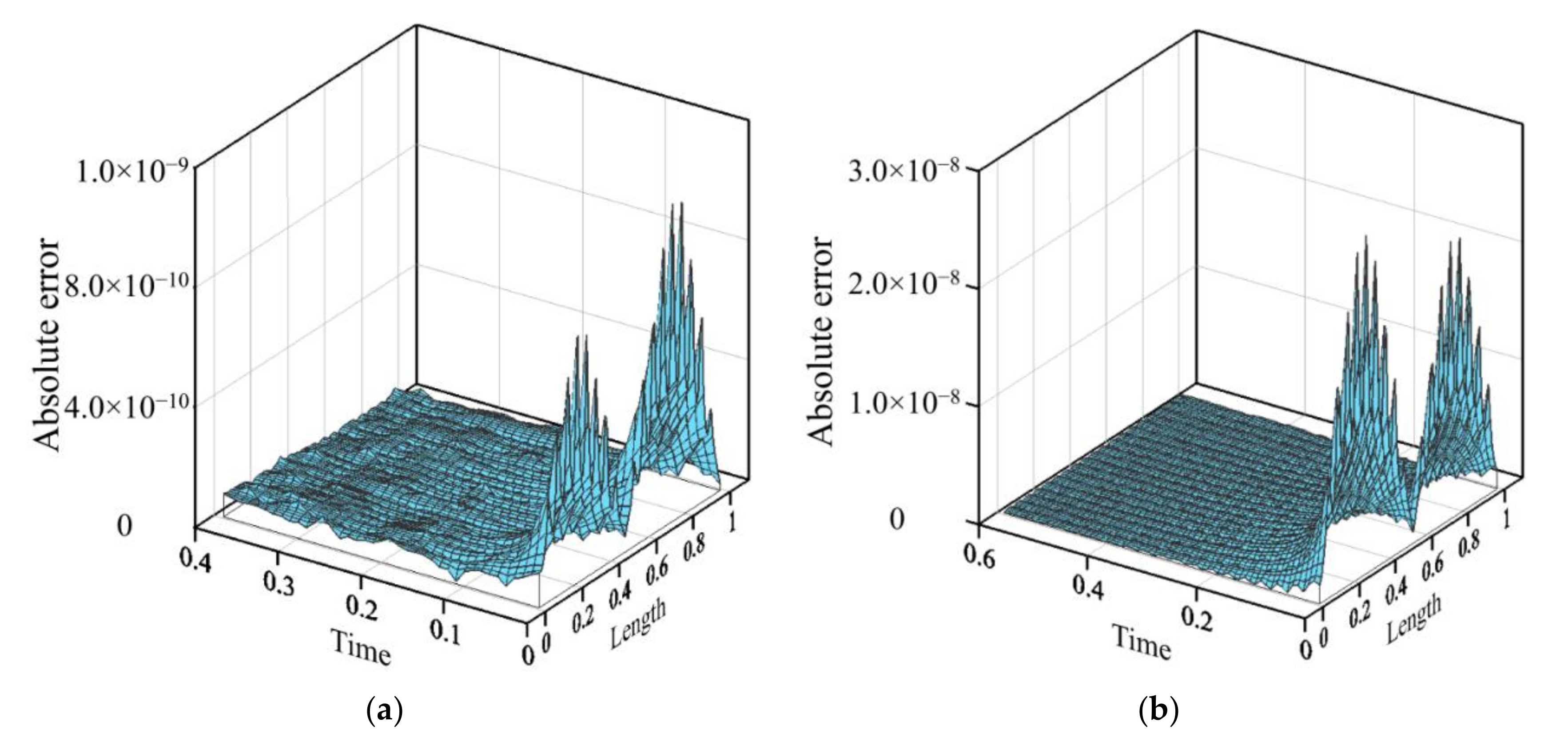
3.2. Comparison with the Radial Basis Function Collocation Method (RBFCM)
4. Numerical Examples
4.1. The Direct Heat Conduction Problem (DHCP)
4.2. The Backward Heat Conduction Problem (BHCP)
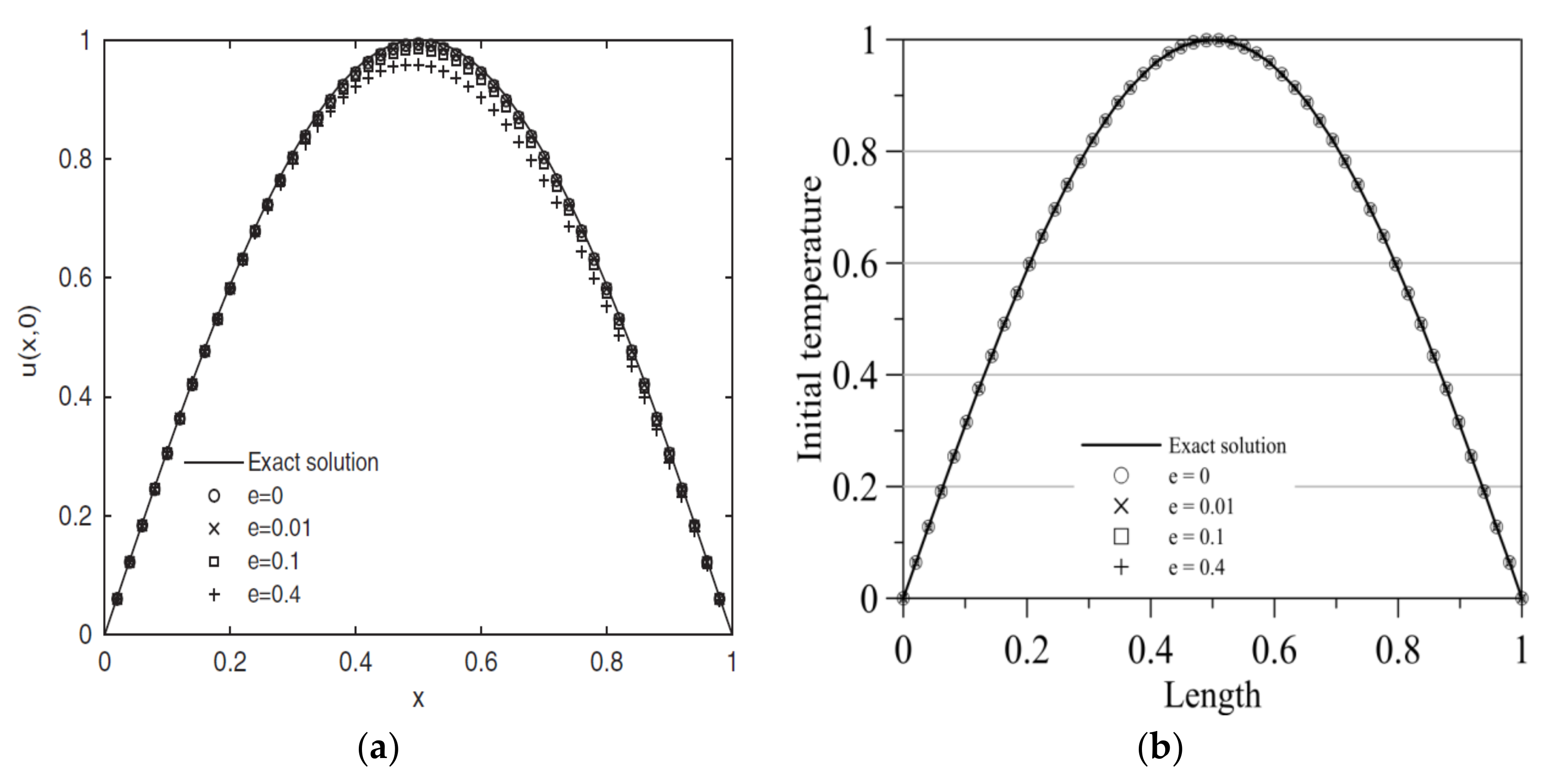
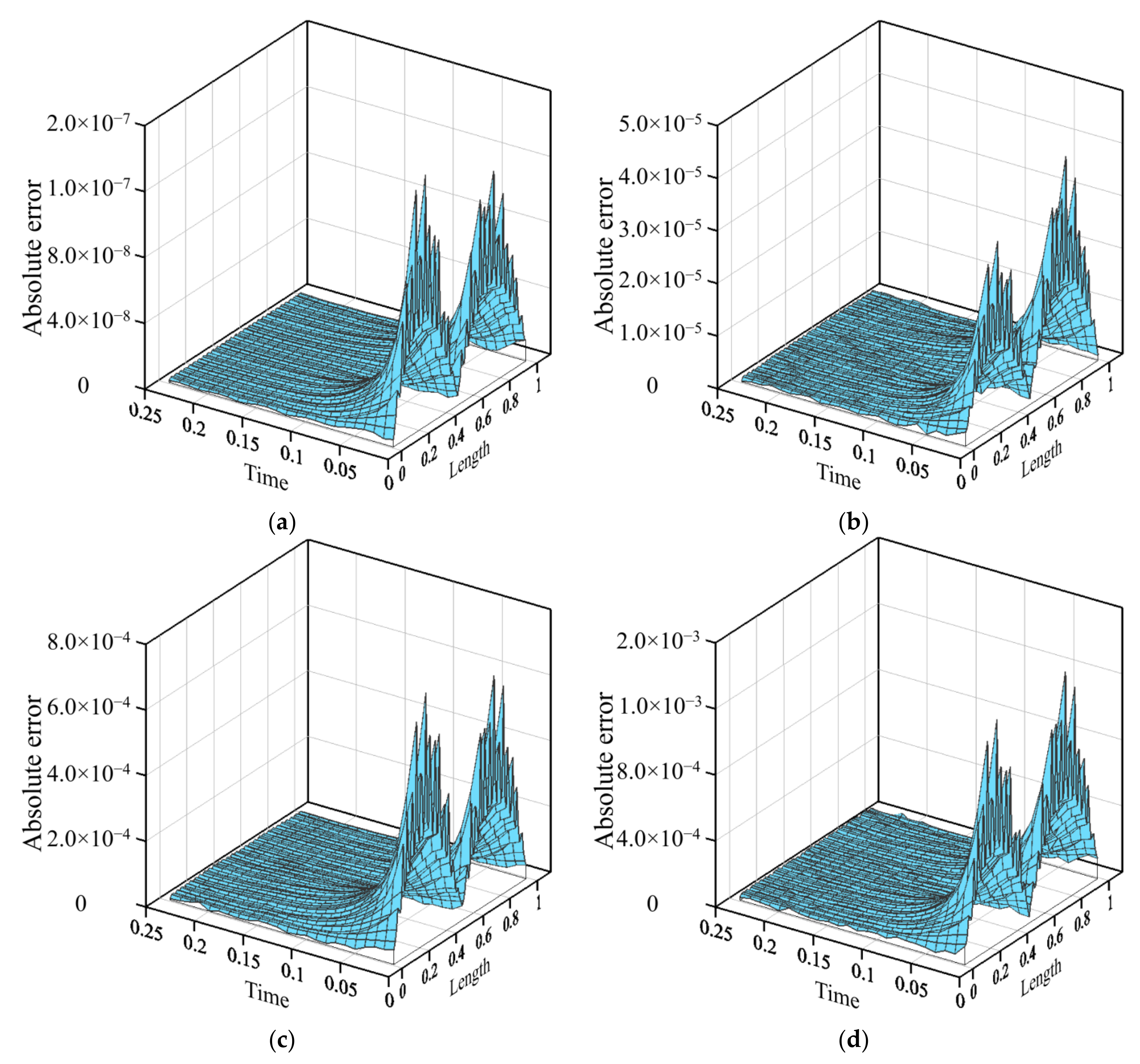
4.3. The Benchmark BHCP
5. Conclusions
- In this article, the novel space–time radial polynomial basis function (SRPBF) is first proposed for the collocation method. Since the SRPBF is infinitely differentiable and the corresponding derivative is a smooth and nonsingular series function, the shape parameter is not required in the proposed method, which may mitigate the main issue in the conventional radial basis function collocation method for determining an optimal shape parameter.
- We propose a new idea for collocating the source points using the inner and outer source collocation schemes. Results demonstrate that the outer source collocation scheme may obtain more accurate results than the regular inner source collocation scheme. Furthermore, results indicate that the location of the source points outside the space–time domain may be not sensitive to the accuracy while the dilation parameter ranges from 2 to 7.
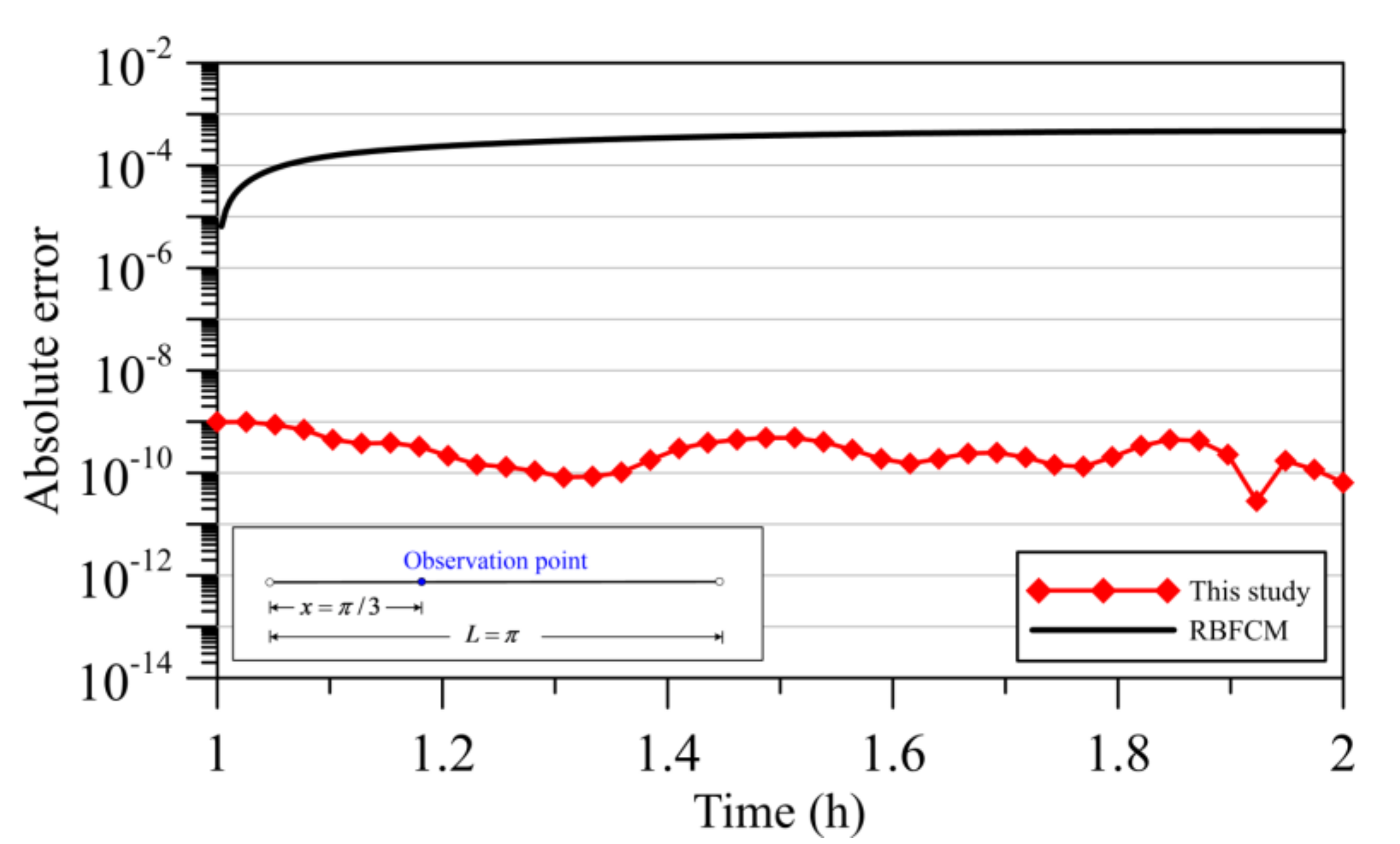
- Results of numerical examples demonstrate that our approach may obtain better solutions than those of the conventional radial basis function collocation method. Since all the collocation points are placed in the space–time domain, the one–dimensional heat conduction initial value problem is turned into the two–dimensional boundary value problem such that the heat conduction problem can be solved without utilizing the conventional time–marching techniques. It is found that the absolute error of our approach does not propagate with the simulation time. Additionally, our approach may yield better solutions than those of the radial basis function collocation method with the time–marching scheme.
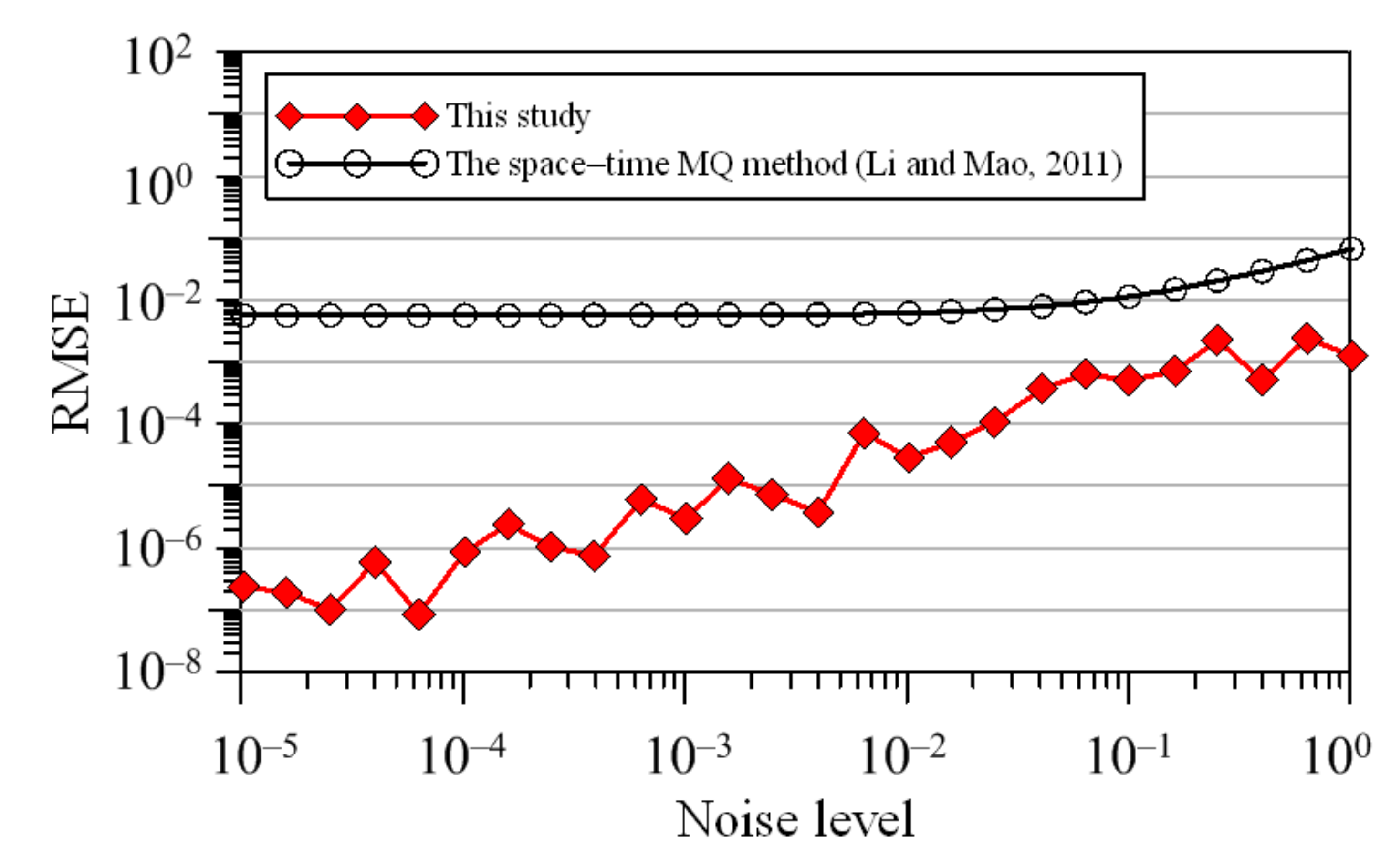
- Numerical results demonstrate that the terms of the SRPBF may not be sensitive to the computed results. Furthermore, the absent heat data on the inaccessible boundary can be recovered with high accuracy even when severely ill–posed inverse backward heat conduction problems under large noises are considered.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, M.; Monjiza, A.; Xu, Y.G.; Wen, P.H. Finite block Petrov–Galerkin method in transient heat conduction. Eng. Anal. Bound. Elem. 2015, 60, 106–114. [Google Scholar] [CrossRef]
- Gu, Y.; He, X.; Chen, W.; Zhang, C. Analysis of three-dimensional anisotropic heat conduction problems on thin domains using an advanced boundary element method. Comput. Math. Appl. 2018, 75, 33–44. [Google Scholar] [CrossRef]
- Grabski, J.K. Numerical solution of non-Newtonian fluid flow and heat transfer problems in ducts with sharp corners by the modified method of fundamental solutions and radial basis function collocation. Eng. Anal. Bound. Elem. 2019, 109, 143–152. [Google Scholar] [CrossRef]
- Li, M.; Jiang, T.; Hon, Y.C. A meshless method based on RBFs method for nonhomogeneous backward heat conduction problem. Eng. Anal. Bound. Elem. 2010, 34, 785–792. [Google Scholar] [CrossRef]
- Shigeta, T.; Young, D.L. Regularized solutions with a singular point for the inverse biharmonic boundary value problem by the method of fundamental solutions. Eng. Anal. Bound. Elem. 2011, 35, 883–894. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, C.; Wang, Y.; Chen, W.; Sladek, J.; Sladek, V. A local RBF collocation method for band structure computations of 2D solid/fluid and fluid/solid phononic crystals. Int. J. Numer. Methods Eng. 2017, 110, 467–500. [Google Scholar] [CrossRef]
- Jankowska, M.A.; Karageorghis, A.; Chen, C.S. Improved Kansa RBF method for the solution of nonlinear boundary value problems. Eng. Anal. Bound. Elem. 2018, 87, 173–183. [Google Scholar] [CrossRef]
- Hong, Y.; Lin, J.; Chen, W. Simulation of thermal field in mass concrete structures with cooling pipes by the localized radial basis function collocation method. Int. J. Heat Mass Transf. 2019, 129, 449–459. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, J.; Hong, J.; Liu, Z.; Wang, Z. A biomimetic generative optimization design for conductive heat transfer based on element-free Galerkin method. Int. Commun. Heat Mass Transf. 2019, 100, 67–72. [Google Scholar] [CrossRef]
- Qiao, Y.; Zhai, S.; Feng, X. RBF-FD method for the high dimensional time fractional convection-diffusion equation. Int. Commun. Heat Mass Transf. 2017, 89, 230–240. [Google Scholar] [CrossRef]
- Li, N.; Su, H.; Gui, D.; Feng, X. Multiquadric RBF-FD method for the convection-dominated diffusion problems base on Shishkin nodes. Int. J. Heat Mass Transf. 2018, 118, 734–745. [Google Scholar] [CrossRef]
- Soleimani, S.; Jalaal, M.; Bararnia, H.; Ghasemi, E.; Ganji, D.D.; Mohammadi, F. Local RBF-DQ method for two-dimensional transient heat conduction problems. Int. Commun. Heat Mass Transf. 2010, 37, 1411–1418. [Google Scholar] [CrossRef]
- Islam, S.; Ismail, S. Meshless collocation procedures for time-dependent inverse heat problems. Int. J. Heat Mass Transf. 2017, 113, 1152–1167. [Google Scholar] [CrossRef]
- Ferreira, A.J.M.; Martins, P.A.L.S.; Roque, C.M.C. Solving time-dependent engineering problems with multiquadrics. J. Sound Vibr. 2005, 280, 595–610. [Google Scholar] [CrossRef]
- Zhu, F.; Yu, Z.; Zhao, L.; Xue, M.; Zhao, S. Adaptive-mesh method using RBF interpolation: A time-marching analysis of steady snow drifting on stepped flat roofs. J. Wind Eng. Ind. Aerodyn. 2017, 171, 1–11. [Google Scholar] [CrossRef]
- Ku, C.-Y.; Liu, C.-Y.; Yeih, W.; Liu, C.-S.; Fan, C.-M. A novel spacetime meshless method for solving backward heat conduction problem. Int. J. Heat Mass Transf. 2019, 130, 109–122. [Google Scholar] [CrossRef]
- Tezduyar, T.E.; Sathe, S.; Keedy, R.; Stein, K. Space–time finite element techniques for computation of fluid–structure interactions. Comput. Meth. Appl. Mech. Eng. 2006, 195, 2002–2027. [Google Scholar] [CrossRef]
- Yue, X.; Wang, F.; Hua, Q.; Qiu, X.Y. A novel space–time meshless method for nonhomogeneous convection–diffusion equations with variable coefficients. Appl. Math. Lett. 2019, 92, 144–150. [Google Scholar] [CrossRef]
- Ku, C.-Y.; Liu, C.-Y.; Xiao, J.-E.; Huang, W.-P.; Su, Y. A spacetime collocation Trefftz method for solving the inverse heat conduction problem. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Ku, C.Y.; Liu, C.Y.; Su, Y.; Yang, L.; Huang, W.P. Modeling tide–induced groundwater response in a coastal confined aquifer using the spacetime collocation approach. Appl. Sci. 2020, 10, 439. [Google Scholar] [CrossRef]
- Klaij, C.M.; van der Vegt, J.J.W.; van der Ven, H. Space–time discontinuous Galerkin method for the compressible Navier–Stokes equations. J. Comput. Phys. 2006, 217, 589–611. [Google Scholar] [CrossRef]
- Sudirham, J.J.; van der Vegt, J.J.W.; van Damme, R.M.J. Space–time discontinuous Galerkin method for advection–diffusion problems on time-dependent domains. Appl. Numer. Math. 2006, 56, 1491–1518. [Google Scholar] [CrossRef]
- Shojaei, A.; Mossaiby, F.; Zaccariotto, M.; Galvanetto, U. A local collocation method to construct Dirichlet-type absorbing boundary conditions for transient scalar wave propagation problems. Comput. Meth. Appl. Mech. Eng. 2019, 356, 629–651. [Google Scholar] [CrossRef]
- Mossaiby, F.; Shojaei, A.; Boroomand, B.; Zaccariotto, M.; Galvanetto, U. Local Dirichlet-type absorbing boundary conditions for transient elastic wave propagation problems. Comput. Meth. Appl. Mech. Eng. 2020, 362, 112856. [Google Scholar] [CrossRef]
- Boroomand, B.; Soghrati, S.; Movahedian, B. Exponential basis functions in solution of static and time harmonic elastic problems in a meshless style. Int. J. Numer. Methods Eng. 2010, 81, 971–1018. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Ku, C.-Y.; Xiao, J.-E.; Yeih, W. A novel spacetime collocation meshless method for solving two-dimensional backward heat conduction problems. CMES 2019, 118, 229–252. [Google Scholar] [CrossRef]
- Li, Z.; Mao, X.Z. Global space–time multiquadric method for inverse heat conduction problem. Int. J. Numer. Methods Eng. 2011, 85, 355–379. [Google Scholar] [CrossRef]
- Hamaidi, M.; Naji, A.; Charafi, A. Space–time localized radial basis function collocation method for solving parabolic and hyperbolic equations. Eng. Anal. Bound. Elem. 2016, 67, 152–163. [Google Scholar] [CrossRef]
- Fasshauer, G.E.; Zhang, J.G. On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Scheuerer, M. An alternative procedure for selecting a good value for the parameter c in RBF-interpolation. Adv. Comput. Math. 2011, 34, 105–126. [Google Scholar] [CrossRef]
- Zhao, R.; Li, C.; Guo, X.; Fan, S.; Wang, Y.; Yang, C. A block iteration with parallelization method for the greedy selection in radial basis functions based mesh deformation. Appl. Sci. 2019, 9, 1141. [Google Scholar] [CrossRef]







| The Size of the Matrix | MAE | |||||
|---|---|---|---|---|---|---|
| The Inner Source Collocation Scheme | The Outer Source Collocation Scheme | |||||
| 500 × 500 | 100 | 400 | 100 | 5 | 1.45 × 10−6 | 2.19 × 10−7 |
| 600 × 600 | 200 | 6 | 9.99 × 10−8 | 6.48 × 10−9 | ||
| 700 × 700 | 300 | 7 | 7.66 × 10−8 | 2.65 × 10−10 | ||
| 800 × 800 | 400 | 8 | 2.21 × 10−9 | 7.81 × 10−11 | ||
| 900 × 900 | 500 | 9 | 1.78 × 10−9 | 6.26 × 10−11 | ||
| 1000 × 1000 | 600 | 10 | 2.80 × 10−7 | 5.17 × 10−11 | ||
| 1100 × 1100 | 700 | 11 | 1.66 × 10−9 | 3.44 × 10−11 | ||
| 1200 × 1200 | 800 | 12 | 4.02 × 10−8 | 9.70 × 10−12 | ||
| 1300 × 1300 | 900 | 13 | 6.16 × 10−10 | 2.05 × 10−11 | ||
| 1400 × 1400 | 1000 | 14 | 2.81 × 10−8 | 1.04 × 10−11 | ||
| 1500 × 1500 | 1100 | 15 | 1.44 × 10−7 | 2.61 × 10−11 | ||
| 1600 × 1600 | 1200 | 16 | 6.96 × 10−9 | 3.17 × 10−11 | ||
| Nx | Nt | MAE | RMSE | ||
|---|---|---|---|---|---|
| Space–time Localized RBFCM [28] | This Study | Space–time Localized RBFCM [28] | This Study | ||
| 40 | 80 | 7.54 × 10−5 | 3.11 × 10−6 | 2.22 × 10−5 | 1.47 × 10−8 |
| 40 | 120 | 3.23 × 10−4 | 7.09 × 10−7 | 6.28 × 10−5 | 3.22 × 10−9 |
| 80 | 40 | 1.16 × 10−4 | 5.57 × 10−6 | 2.35 × 10−5 | 3.15 × 10−8 |
| 80 | 120 | 2.28 × 10−5 | 1.39 × 10−8 | 5.66 × 10−6 | 1.05 × 10−10 |
| 120 | 40 | 1.10 × 10−4 | 5.33 × 10−6 | 2.30 × 10−5 | 3.11 × 10−8 |
| 120 | 80 | 2.98 × 10−5 | 3.52 × 10−8 | 5.73 × 10−6 | 1.75 × 10−10 |
| Final Elapsed Time | Maximum Absolute Error (MAE) | Root Mean Square Error (RMSE) |
|---|---|---|
| 0.2 | 5.46 × 10−9 | 2.61 × 10−11 |
| 0.4 | 1.06 × 10−9 | 3.90 × 10−12 |
| 0.6 | 2.88 × 10−8 | 9.76 × 10−11 |
| 0.8 | 1.24 × 10−7 | 5.28 × 10−10 |
| 1.0 | 9.00 × 10−6 | 3.88 × 10−8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, C.-Y.; Liu, C.-Y.; Xiao, J.-E.; Chen, M.-R. Solving Backward Heat Conduction Problems Using a Novel Space–Time Radial Polynomial Basis Function Collocation Method. Appl. Sci. 2020, 10, 3215. https://doi.org/10.3390/app10093215
Ku C-Y, Liu C-Y, Xiao J-E, Chen M-R. Solving Backward Heat Conduction Problems Using a Novel Space–Time Radial Polynomial Basis Function Collocation Method. Applied Sciences. 2020; 10(9):3215. https://doi.org/10.3390/app10093215
Chicago/Turabian StyleKu, Cheng-Yu, Chih-Yu Liu, Jing-En Xiao, and Ming-Ren Chen. 2020. "Solving Backward Heat Conduction Problems Using a Novel Space–Time Radial Polynomial Basis Function Collocation Method" Applied Sciences 10, no. 9: 3215. https://doi.org/10.3390/app10093215
APA StyleKu, C.-Y., Liu, C.-Y., Xiao, J.-E., & Chen, M.-R. (2020). Solving Backward Heat Conduction Problems Using a Novel Space–Time Radial Polynomial Basis Function Collocation Method. Applied Sciences, 10(9), 3215. https://doi.org/10.3390/app10093215







