High Refractive Index Electromagnetic Devices in Printed Technology Based on Glide-Symmetric Periodic Structures
Abstract
:1. Introduction
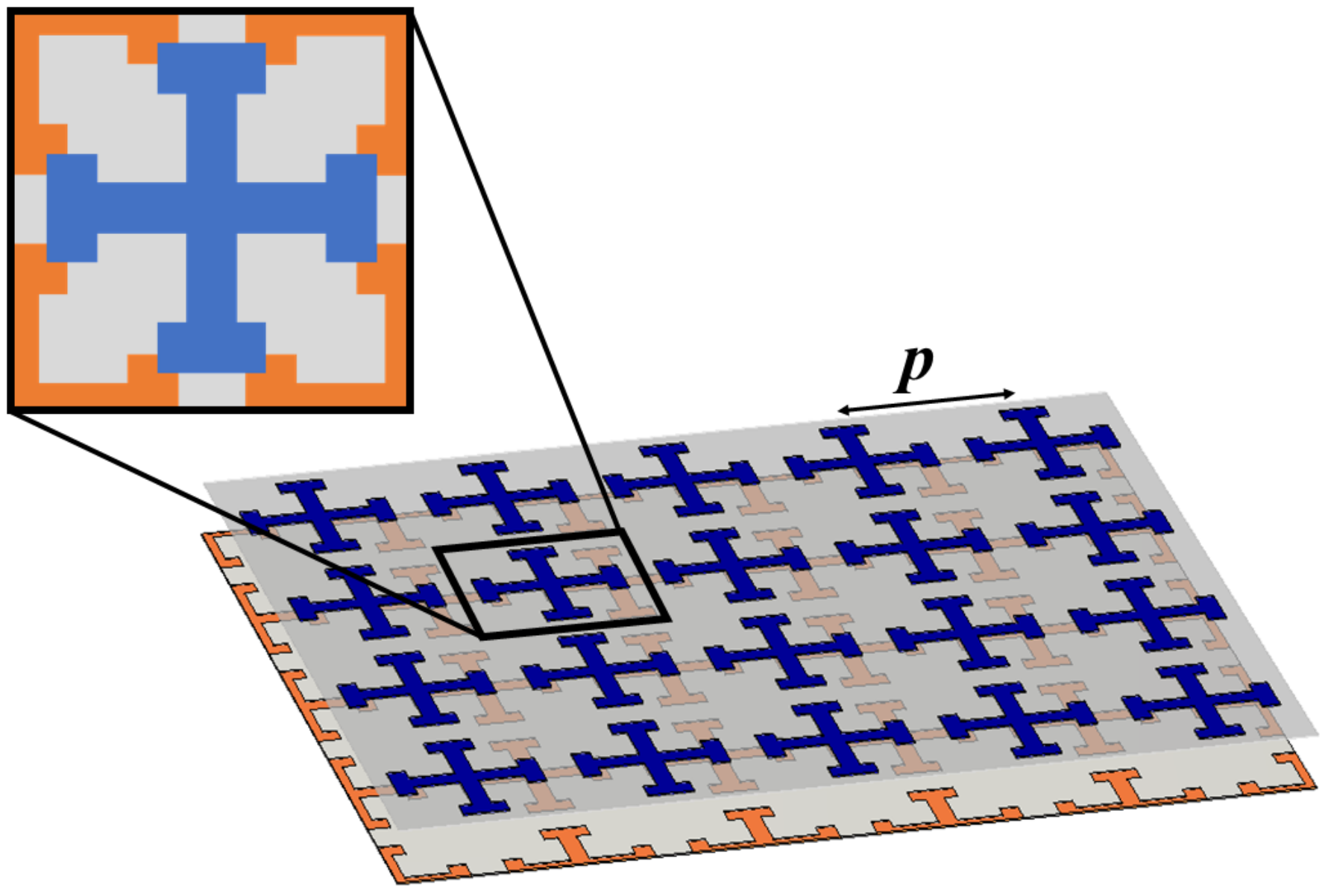
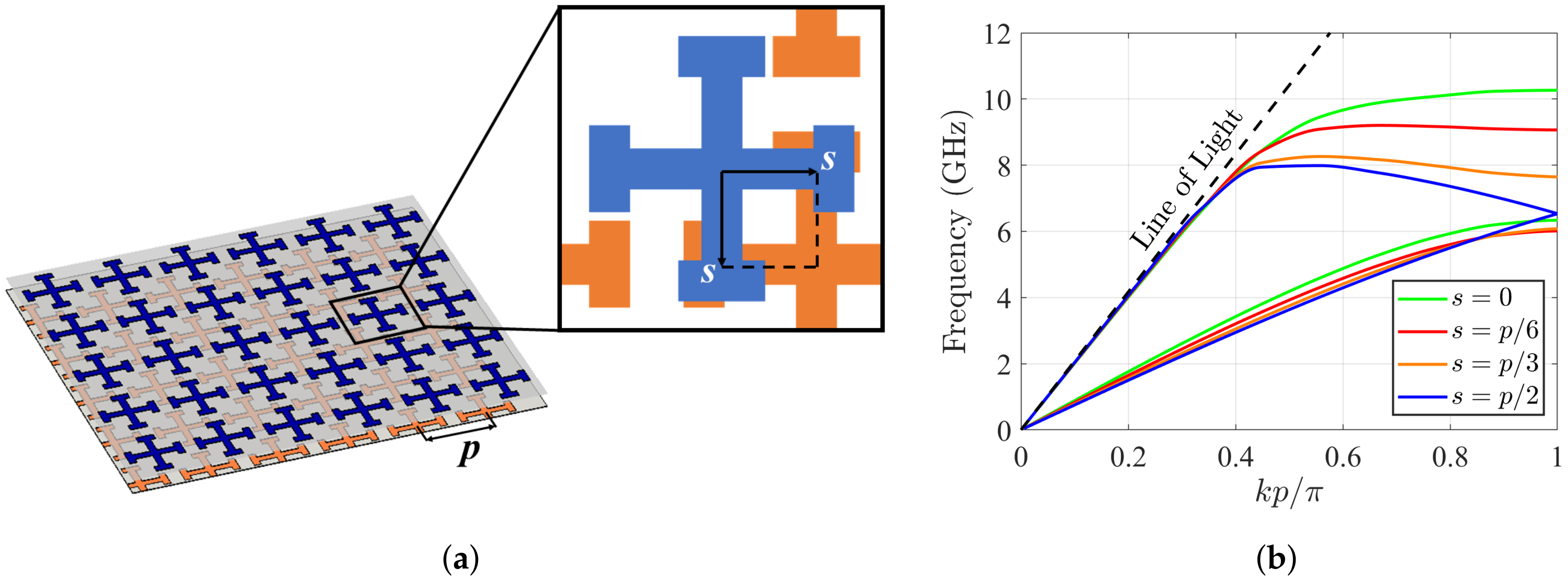
2. Glide Symmetry
3. Lens Design
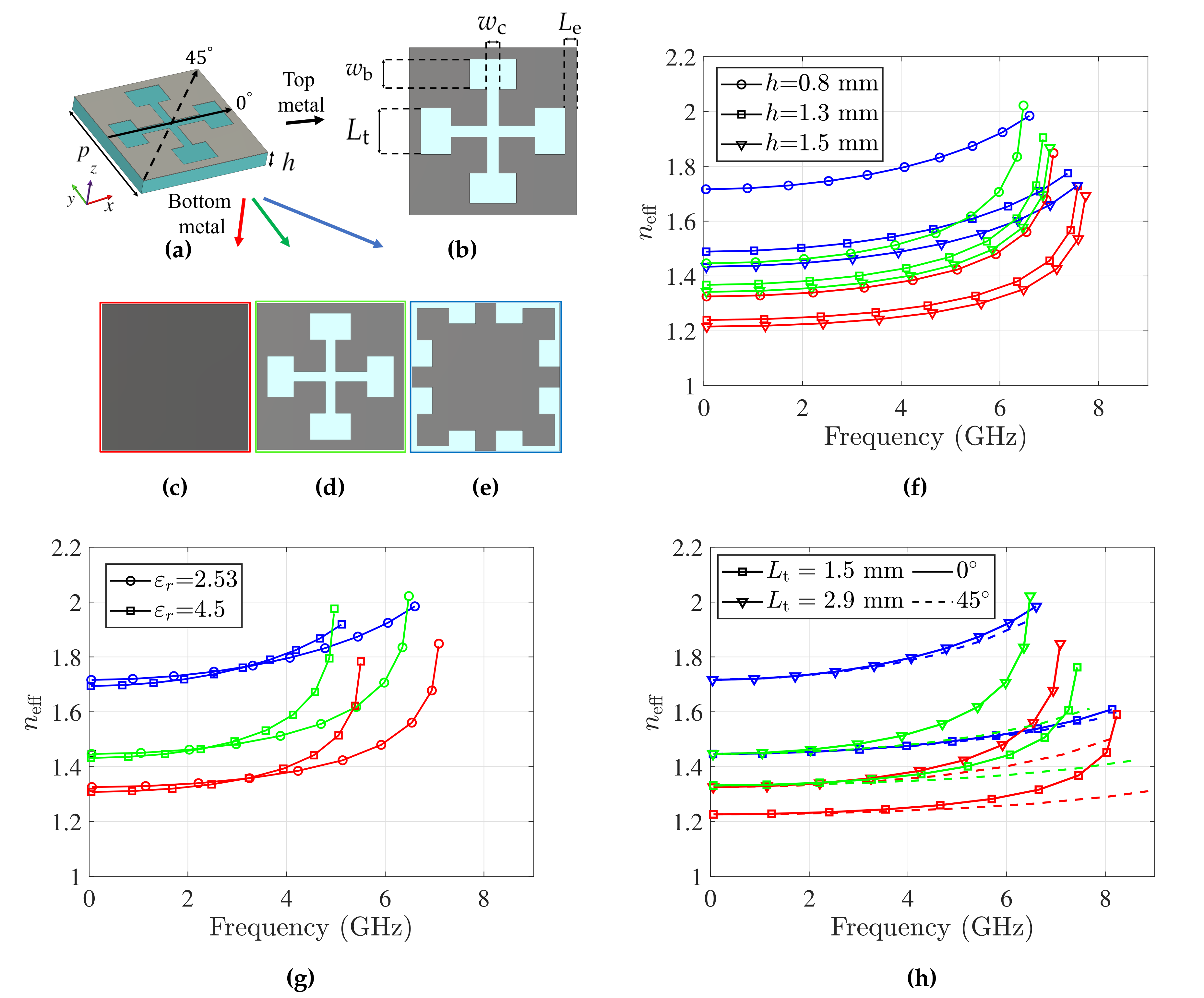
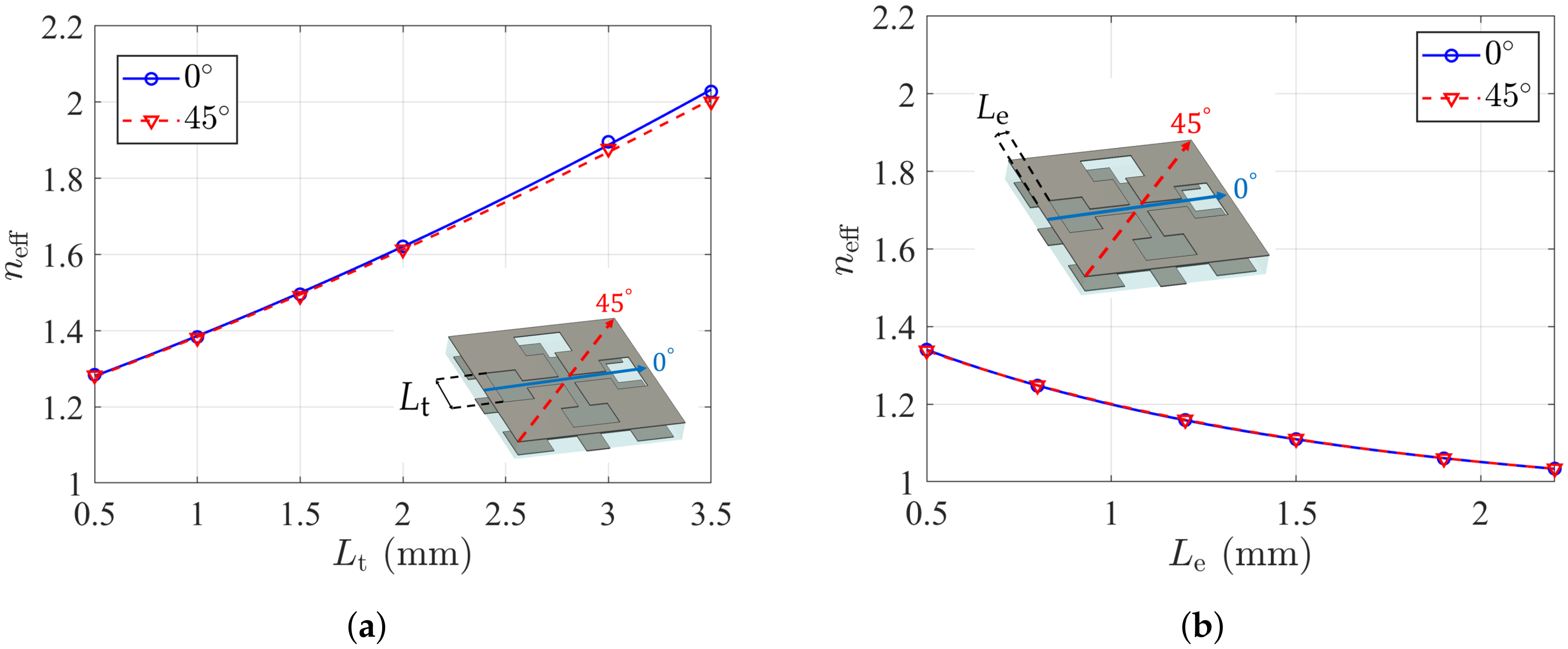
3.1. Unit Cell Design
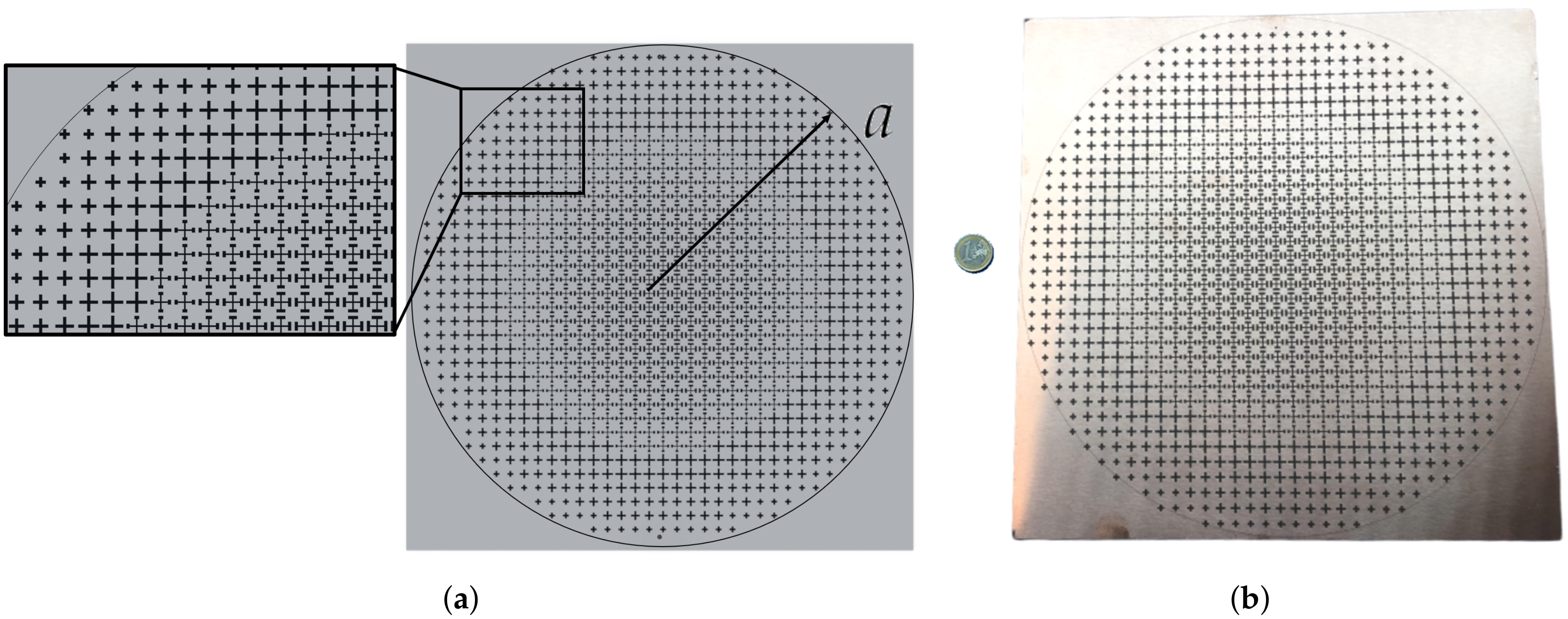
3.2. Maxwell Fish-Eye Lens
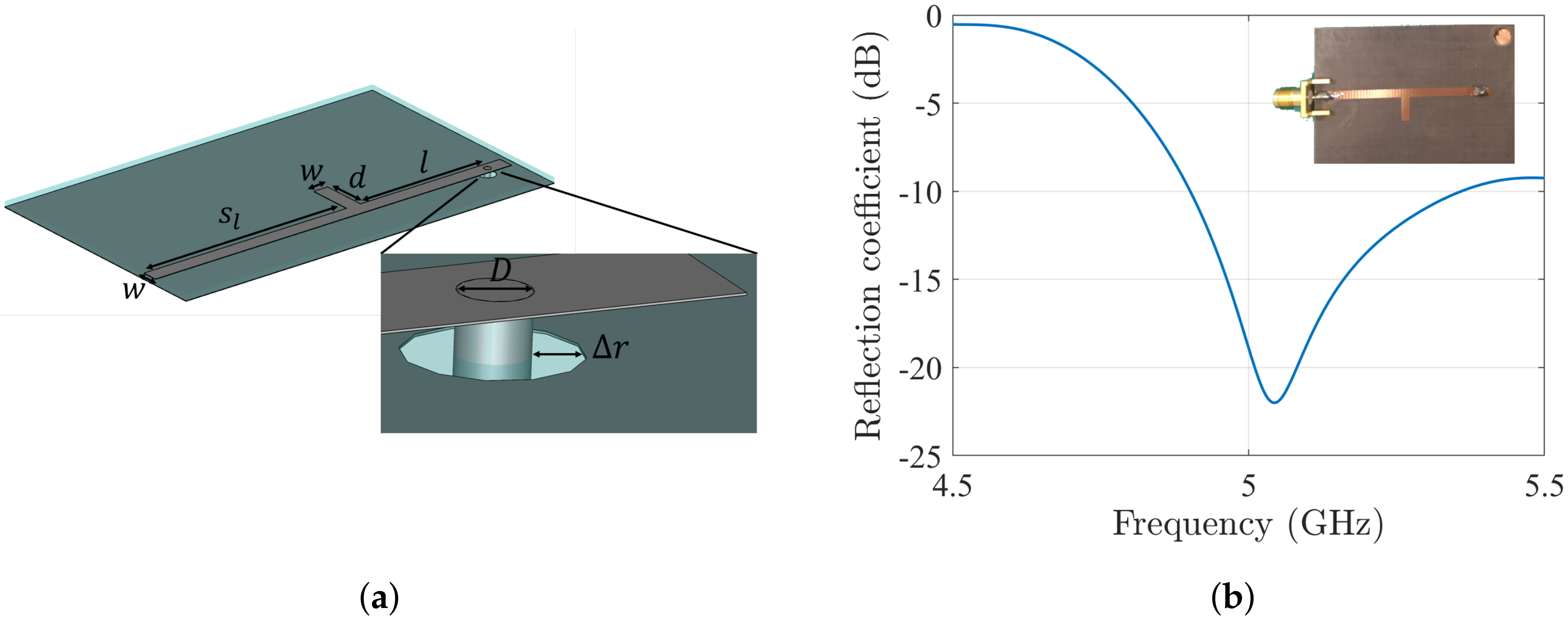
3.3. Feed Design
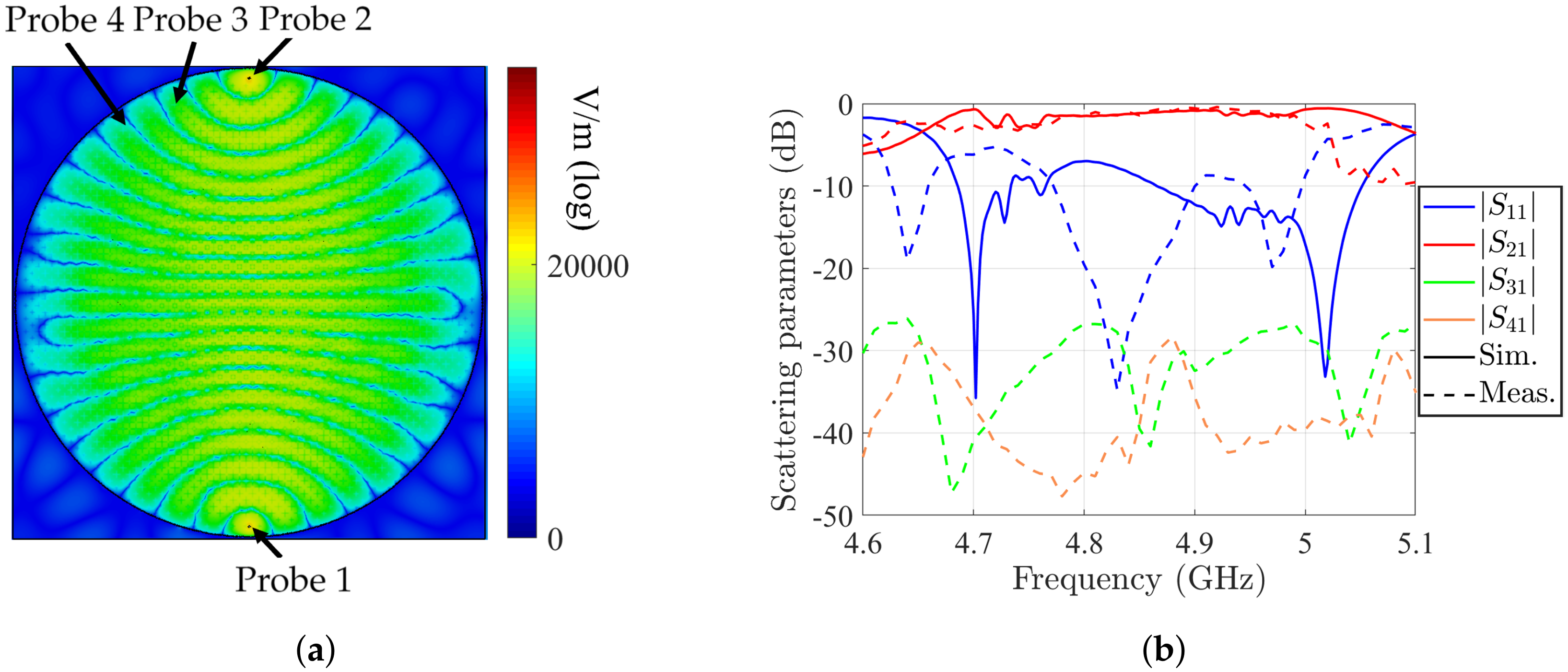
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hessel, A.; Chen, M.H.; Li, R.; Oliner, A. Propagation in periodically loaded waveguides with higher symmetries. Proc. IEEE 1973, 61, 183–195. [Google Scholar] [CrossRef]
- Crepeau, P.; Mcisaac, P. Consequences of symmetry in periodic structures. Proc. IEEE 1964, 52, 33–43. [Google Scholar] [CrossRef] [Green Version]
- Trigg, G.L. Higher Symmetries. Phys. Rev. Lett. 1965, 14, 479. [Google Scholar]
- Mittra, R.; Laxpati, S. Propagation in a wave guide with glide reflection symmetry. Can. J. Phys. 1965, 43, 353–372. [Google Scholar] [CrossRef]
- Kieburtz, R.; Impagliazzo, J. Multimode propagation on radiating traveling-wave structures with glide-symmetric excitation. IEEE Trans. Antennas Propag. 1970, 18, 3–7. [Google Scholar] [CrossRef]
- Pocklington, H.C. Electrical oscillations in wires. Proc. Camb. Philos. Soc. 1897, 9, 324–332. [Google Scholar]
- Sensiper, S. Electromagnetic Wave Propagation on Helical Structures (A Review and Survey of Recent Progress). Proc. IRE 1955, 43, 149–161. [Google Scholar] [CrossRef]
- Chang, T.; Kim, J.U.; Kang, S.K.; Kim, H.; Kim, D.K.; Lee, Y.H.; Shin, J. Broadband giant-refractive-index material based on mesoscopic space-filling curves. Nat. Commun. 2016, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cavallo, D.; Felita, C. Analytical Formulas for Artificial Dielectrics With Nonaligned Layers. IEEE Trans. Antennas Propag. 2017, 65, 5303–5311. [Google Scholar] [CrossRef]
- Cavallo, D. Dissipation Losses in Artificial Dielectric Layers. IEEE Trans. Antennas Propag. 2018, 66, 7460–7465. [Google Scholar] [CrossRef] [Green Version]
- Dahlberg, O.; Ghasemifard, F.; Valerio, G.; Quevedo-Teruel, O. Propagation characteristics of periodic structures possessing twist and polar glide symmetries. EPJ Appl. Metamater. 2019, 6, 14. [Google Scholar] [CrossRef] [Green Version]
- Mitchell-Thomas, R.C.; Sambles, J.R.; Hibbins, A.P. High index metasurfaces for graded lenses using glide symmetry. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 1396–1397. [Google Scholar]
- Camacho, M.; Mitchell-Thomas, R.C.; Hibbins, A.P.; Sambles, J.R.; Quevedo-Teruel, O. Designer surface plasmon dispersion on a one-dimensional periodic slot metasurface with glide symmetry. Opt. Lett. 2017, 42, 3375–3378. [Google Scholar] [CrossRef] [PubMed]
- Camacho, M.; Mitchell-Thomas, R.C.; Hibbins, A.P.; Sambles, J.R.; Quevedo-Teruel, O. Mimicking glide symmetry dispersion with coupled slot metasurfaces. Appl. Phys. Lett. 2017, 111, 121603. [Google Scholar] [CrossRef]
- Dahlberg, O.; Mitchell-Thomas, R.; Quevedo-Teruel, O. Reducing the dispersion of periodic structures with twist and polar glide symmetries. Sci. Rep. 2017, 7, 10136. [Google Scholar] [CrossRef] [PubMed]
- Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O. Dispersion Analysis of 2-D Glide-Symmetric Corrugated Metasurfaces Using Mode-Matching Technique. IEEE Microw. Wirel. Components Lett. 2018, 28, 1–3. [Google Scholar] [CrossRef]
- Ghasemifard, F. Periodic Structures with Higher Symmetries: Analysis and Applications. Ph.D. Thesis, Electrical Engineering School of Electrical Engineering and Computer Science, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- De Pineda, J.D.; Hibbins, A.P.; Sambles, J.R. Microwave edge modes on a metasurface with glide symmetry. Phys. Rev. B 2018, 98, 205426. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimpouri, M.; Quevedo-Teruel, O. Ultrawideband Anisotropic Glide-Symmetric Metasurfaces. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1547–1551. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Herran, L.F.; Quevedo-Teruel, O. Wide-Angle Impedance Matching Using Glide-Symmetric Metasurfaces. IEEE Microw. Wirel. Components Lett. 2020, 30, 8–11. [Google Scholar] [CrossRef]
- Quesada, R.; Martín-Cano, D.; García-Vidal, F.J.; Bravo-Abad, J. Deep-subwavelength negative-index waveguiding enabled by coupled conformal surface plasmons. Opt. Lett. 2014, 39, 2990–2993. [Google Scholar] [CrossRef]
- Padilla, P.; Herrán, L.F.; Tamayo-Domínguez, A.; Valenzuela-Valdés, J.F.; Quevedo-Teruel, O. Glide Symmetry to Prevent the Lowest Stopband of Printed Corrugated Transmission Lines. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 750–752. [Google Scholar] [CrossRef]
- Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O. Twist and Polar Glide Symmetries: An Additional Degree of Freedom to Control the Propagation Characteristics of Periodic Structures. Sci. Rep. 2018, 8, 11266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tamayo-Dominguez, A.; Fernandez-Gonzalez, J.M.; Quevedo-Teruel, O. One-Plane Glide-Symmetric Holey Structures for Stop-Band and Refraction Index Reconfiguration. Symmetry 2019, 11, 495. [Google Scholar] [CrossRef] [Green Version]
- Padilla, P.; Palomares-Caballero, Á.; Alex-Amor, A.; Valenzuela-valdés, J.; Fernández-González, J.M.; Quevedo-Teruel, O. Broken Glide-Symmetric Holey Structures for Bandgap Selection in Gap-Waveguide Technology. IEEE Microw. Wirel. Components Lett. 2019, 29, 327–329. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Ebrahimpouri, M.; Ng Mou Kehn, M. Ultrawideband Metasurface Lenses Based on Off-Shifted Opposite Layers. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 484–487. [Google Scholar] [CrossRef]
- Dahlberg, O.; Valerio, G.; Quevedo-Teruel, O. Fully Metallic Flat Lens Based on Locally Twist-Symmetric Array of Complementary Split-Ring Resonators. Symmetry 2019, 11, 581. [Google Scholar] [CrossRef] [Green Version]
- Shanei, M.M.; Fathi, D.; Ghasemifard, F.; Quevedo-Teruel, O. All-silicon reconfigurable metasurfaces for multifunction and tunable performance at optical frequencies based on glide symmetry. Sci. Rep. 2019, 9, 13641. [Google Scholar] [CrossRef]
- Monje-Real, A.; Fonseca, N.J.G.; Zetterstrom, O.; Pucci, E.; Quevedo-Teruel, O. Holey Glide-Symmetric Filters for 5G at Millimeter-Wave Frequencies. IEEE Microw. Wirel. Components Lett. 2020, 30, 31–34. [Google Scholar] [CrossRef]
- Mouris, B.A.; Fernandez-Prieto, A.; Thobaben, R.; Martel, J.; Mesa, F.; Quevedo-Teruel, O. Increment of the Bandwidth of Mushroom-type EBG Structures with Glide Symmetry. IEEE Trans. Microw. Theory Tech. 2020, 68, 1365–1375. [Google Scholar] [CrossRef]
- Rajo-Iglesias, E.; Ebrahimpouri, M.; Quevedo-Teruel, O. Wideband Phase Shifter in Groove Gap Waveguide Technology Implemented With Glide-Symmetric Holey EBG. IEEE Microw. Wirel. Components Lett. 2018, 28, 476–478. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Dahlberg, O.; Valerio, G. Propagation in Waveguides With Transversal Twist-Symmetric Holey Metallic Plates. IEEE Microw. Wirel. Components Lett. 2018, 28, 858–860. [Google Scholar] [CrossRef]
- Palomares-Caballero, A.; Alex-Amor, A.; Padilla, P.; Luna, F.; Valenzuela-Valdes, J. Compact and Low-Loss V-Band Waveguide Phase Shifter Based on Glide-Symmetric Pin Configuration. IEEE Access 2019, 7, 31297–31304. [Google Scholar] [CrossRef]
- Wei, Z.; Cao, Y.; Fan, Y.; Yu, X.; Li, H. Broadband polarization transformation via enhanced asymmetric transmission through arrays of twisted complementary split-ring resonators. Appl. Phys. Lett. 2011, 99, 221907. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Belkin, M.; Alù, A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nat. Commun. 2012, 3, 870. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Askarpour, A.; Zhao, Y.; Alu, A. Wave propagation in twisted metamaterials. Phys. Rev. Condens. Matter Mater. Phys. 2014, 90, 054305. [Google Scholar] [CrossRef]
- Zhao, Y.; Askarpour, A.N.; Sun, L.; Shi, J.; Li, X.; Alù, A. Chirality detection of enantiomers using twisted optical metamaterials. Nat. Commun. 2017, 8, 14180. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimpouri, M.; Rajo-Iglesias, E.; Sipus, Z.; Quevedo-Teruel, O. Cost-Effective Gap Waveguide Technology Based on Glide-Symmetric Holey EBG Structures. IEEE Trans. Microw. Theory Tech. 2018, 66, 927–934. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimpouri, M.; Quevedo-Teruel, O.; Rajo-Iglesias, E. Design Guidelines for Gap Waveguide Technology Based on Glide-Symmetric Holey Structures. IEEE Microw. Wirel. Components Lett. 2017, 27, 542–544. [Google Scholar] [CrossRef]
- Zetterstrom, O.; Pucci, E.; Padilla, P.; Wang, L.; Quevedo-Teruel, O. Low-Dispersive Leaky Wave Antennas for mmWave Point-to-Point High-Throughput Communications. IEEE Trans. Antennas Propag. 2020, 68, 1322–1331. [Google Scholar] [CrossRef]
- Chen, Q.; Zetterstrom, O.; Pucci, E.; Palomares-Caballero, A.; Padilla, P.; Quevedo-Teruel, O. Glide-Symmetric Holey Leaky-Wave Antenna with Low Dispersion for 60-GHz Point-to-Point Communications. IEEE Trans. Antennas Propag. 2019, 68, 1925–1936. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Algaba Brazalez, A.; Manholm, L.; Quevedo-Teruel, O. Using Glide-Symmetric Holes to Reduce Leakage Between Waveguide Flanges. IEEE Microw. Wirel. Components Lett. 2018, 28, 473–475. [Google Scholar] [CrossRef]
- Valerio, G.; Sipus, Z.; Grbic, A.; Quevedo-Teruel, O. Accurate Equivalent-Circuit Descriptions of Thin Glide-Symmetric Corrugated Metasurfaces. IEEE Trans. Antennas Propag. 2017, 65, 2695–2700. [Google Scholar] [CrossRef] [Green Version]
- Valerio, G.; Ghasemifard, F.; Sipus, Z.; Quevedo-Teruel, O. Glide-Symmetric All-Metal Holey Metasurfaces for Low-Dispersive Artificial Materials: Modeling and Properties. IEEE Trans. Microw. Theory Tech. 2018, 66, 3210–3223. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Ghasemifard, F.; Valerio, G.; Quevedo-Teruel, O. Modeling and Dispersion Analysis of Coaxial Lines With Higher Symmetries. IEEE Trans. Microw. Theory Tech. 2018, 66, 4338–4345. [Google Scholar] [CrossRef]
- Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O.; Valerio, G. Analyzing Glide-Symmetric Holey Metasurfaces Using a Generalized Floquet Theorem. IEEE Access 2018, 6, 71743–71750. [Google Scholar] [CrossRef]
- Bagheriasl, M.; Valerio, G. Bloch Analysis of Electromagnetic Waves in Twist-Symmetric Lines. Symmetry 2019, 11, 620. [Google Scholar] [CrossRef] [Green Version]
- Bagheriasl, M.; Quevedo-Teruel, O.; Valerio, G. Bloch Analysis of Artificial Lines and Surfaces Exhibiting Glide Symmetry. IEEE Trans. Microw. Theory Tech. 2019, 67, 2618–2628. [Google Scholar] [CrossRef] [Green Version]
- Sipus, Z.; Bosiljevac, M. Modeling of Glide-Symmetric Dielectric Structures. Symmetry 2019, 11, 805. [Google Scholar] [CrossRef] [Green Version]
- Mesa, F.; Rodríguez-Berral, R.; Medina, F. On the Computation of the Dispersion Diagram of Symmetric One-Dimensionally Periodic Structures. Symmetry 2018, 10, 307. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, J.; Huang, L.; Jing, Y.; Georgakopoulos, A.; Demestichas, P. 5G Mobile: Spectrum Broadening to Higher-Frequency Bands to Support High Data Rates. IEEE Veh. Technol. Mag. 2014, 9, 39–46. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Ebrahimpouri, M.; Ghasemifard, F. Lens Antennas for 5G Communications Systems. IEEE Commun. Mag. 2018, 56, 36–41. [Google Scholar] [CrossRef]
- Fuchs, B.; Lafond, O.; Rondineau, S.; Himdi, M.; Le Coq, L. Off-Axis Performances of Half Maxwell Fish-Eye Lens Antennas at 77 GHz. IEEE Trans. Antennas Propag. 2007, 55, 479–482. [Google Scholar]
- Fuchs, B.; Lafond, O.; Palud, S.; Le Coq, L.; Himdi, M.; Buck, M.; Rondineau, S. Comparative Design and Analysis of Luneburg and Half Maxwell Fish-Eye Lens Antennas. IEEE Trans. Antennas Propag. 2008, 56, 3058–3062. [Google Scholar]
- Mei, Z.L.; Bai, J.; Niu, T.M.; Cui, T.J. A Half Maxwell Fish-Eye Lens Antenna Based on Gradient-Index Metamaterials. IEEE Trans. Antennas Propag. 2012, 60, 398–401. [Google Scholar]
- Huang, M.; Yang, S.; Gao, F.; Quarfoth, R.; Sievenpiper, D. A 2-D Multibeam Half Maxwell Fish-Eye Lens Antenna Using High Impedance Surfaces. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 365–368. [Google Scholar]
- Xu, H.X.; Wang, G.M.; Tao, Z.; Cai, T. An Octave-Bandwidth Half Maxwell Fish-Eye Lens Antenna Using Three-Dimensional Gradient-Index Fractal Metamaterials. IEEE Trans. Antennas Propag. 2014, 62, 4823–4828. [Google Scholar]
- Shi, Y.; Li, K.; Wang, J.; Li, L.; Liang, C.H. An Etched Planar Metasurface Half Maxwell Fish-Eye Lens Antenna. IEEE Trans. Antennas Propag. 2015, 63, 3742–3747. [Google Scholar]
- Quevedo-Teruel, O.; Miao, J.; Mattsson, M.; Algaba-Brazalez, A.; Johansson, M.; Manholm, L. Glide-Symmetric Fully Metallic Luneburg Lens for 5G Communications at Ka-Band. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1588–1592. [Google Scholar]
- Maxwell, J. Solutions of problems. Camb. Dublin Math. J. 1854, 8, 76. [Google Scholar]
- Leonhardt, U. Reply to comment on perfect imaging without negative refraction. N. J. Phys. 2011, 13, 058001. [Google Scholar]
- Leonhardt, U.; Philbin, T. Reply to “Comment on ‘Perfect imaging with positive refraction in three dimensions”. Phys. Rev. A 2010, 82, 057802. [Google Scholar]
- Miñano, J.C.; Marqués, R.; González, J.C.; Benítez, P.; Delgado, V.; Grabovickic, D.; Freire, M. Super-resolution for a point source better than λ/500 using positive refraction. N. J. Phys. 2011, 13. [Google Scholar] [CrossRef] [Green Version]
- Minano, J.; Sanchez-Dehesa, J.; Gonzalez, J.; Benitez, P.; Grabovickic, D.; Carbonell, J.; Ahmadpanahi, H. Experimental evidence of super-resolution better than [lamada]/105 with positive refraction. N. J. Phys. 2014, 16, 33015. [Google Scholar] [CrossRef] [Green Version]
- Tyc, T.; Zhang, X. Perfect lenses in focus. Nature 2011, 480, 42–43. [Google Scholar] [CrossRef] [PubMed]
- Blaikie, R.J. Comment on perfect imaging without negative refraction. N. J. Phys. 2010, 12, 058001. [Google Scholar] [CrossRef]
- Merlin, R. Comment on “perfect imaging with positive refraction in three dimensions”. Phys. Rev. A At. Mol. Opt. Phys. 2010, 82, 057801. [Google Scholar] [CrossRef] [Green Version]
- Merlin, R. Maxwell’s fish-eye lens and the mirage of perfect imaging. J. Opt. 2011, 13, 024017. [Google Scholar] [CrossRef] [Green Version]
- Blaikie, R.J. Perfect imaging without refraction? N. J. Phys. 2011, 13, 125006. [Google Scholar] [CrossRef]
- Kinsler, P.; Favaro, A. Comment on reply to comment on perfect imaging without negative refraction. N. J. Phys. 2011, 13, 028001. [Google Scholar] [CrossRef]
- Tyc, T.; Danner, A. Resolution of Maxwell’s fisheye with an optimal active drain. N. J. Phys. 2014, 16, 1–11. [Google Scholar] [CrossRef]
- Luneberg, K. Mathematical Theory of Optics; University of California Press: Berkeley, CA, USA, 1944. [Google Scholar]
- CST Microwave Studio, Version 2018. Available online: http://www.cst.com/ (accessed on 21 November 2019).
- Leonhardt, U. Perfect imaging without negative refraction. N. J. Phys. 2009, 11, 093040. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arnberg, P.; Barreira Petersson, O.; Zetterstrom, O.; Ghasemifard, F.; Quevedo-Teruel, O. High Refractive Index Electromagnetic Devices in Printed Technology Based on Glide-Symmetric Periodic Structures. Appl. Sci. 2020, 10, 3216. https://doi.org/10.3390/app10093216
Arnberg P, Barreira Petersson O, Zetterstrom O, Ghasemifard F, Quevedo-Teruel O. High Refractive Index Electromagnetic Devices in Printed Technology Based on Glide-Symmetric Periodic Structures. Applied Sciences. 2020; 10(9):3216. https://doi.org/10.3390/app10093216
Chicago/Turabian StyleArnberg, Philip, Oscar Barreira Petersson, Oskar Zetterstrom, Fatemeh Ghasemifard, and Oscar Quevedo-Teruel. 2020. "High Refractive Index Electromagnetic Devices in Printed Technology Based on Glide-Symmetric Periodic Structures" Applied Sciences 10, no. 9: 3216. https://doi.org/10.3390/app10093216
APA StyleArnberg, P., Barreira Petersson, O., Zetterstrom, O., Ghasemifard, F., & Quevedo-Teruel, O. (2020). High Refractive Index Electromagnetic Devices in Printed Technology Based on Glide-Symmetric Periodic Structures. Applied Sciences, 10(9), 3216. https://doi.org/10.3390/app10093216





