Estimation of Rock Load of Multi-Arch Tunnel with Cracks Using Stress Variable Method
Abstract
:1. Introduction
2. Estimation Methods for Rock Load
2.1. Empirical Methods
2.2. Numerical Analysis Approach
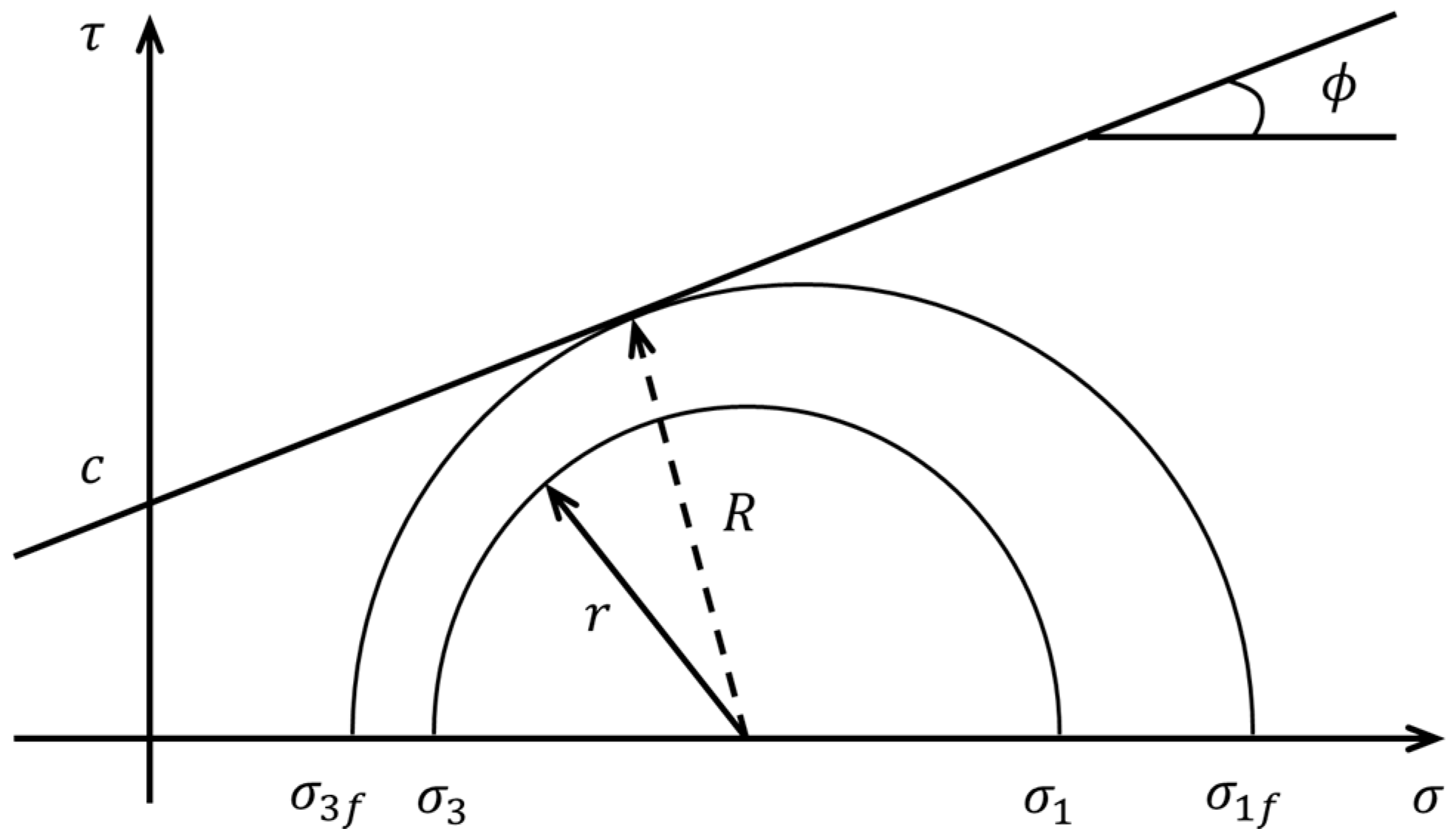
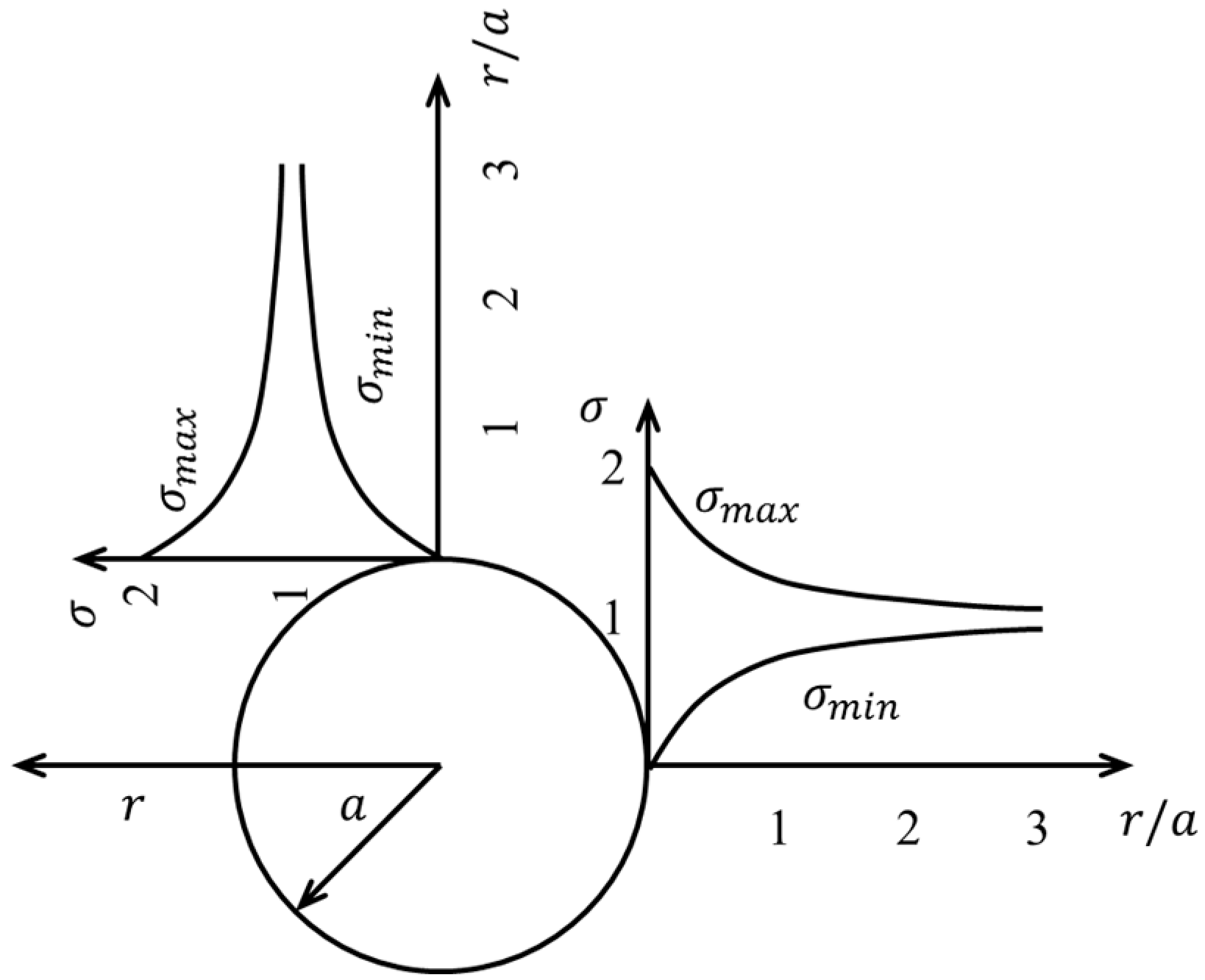
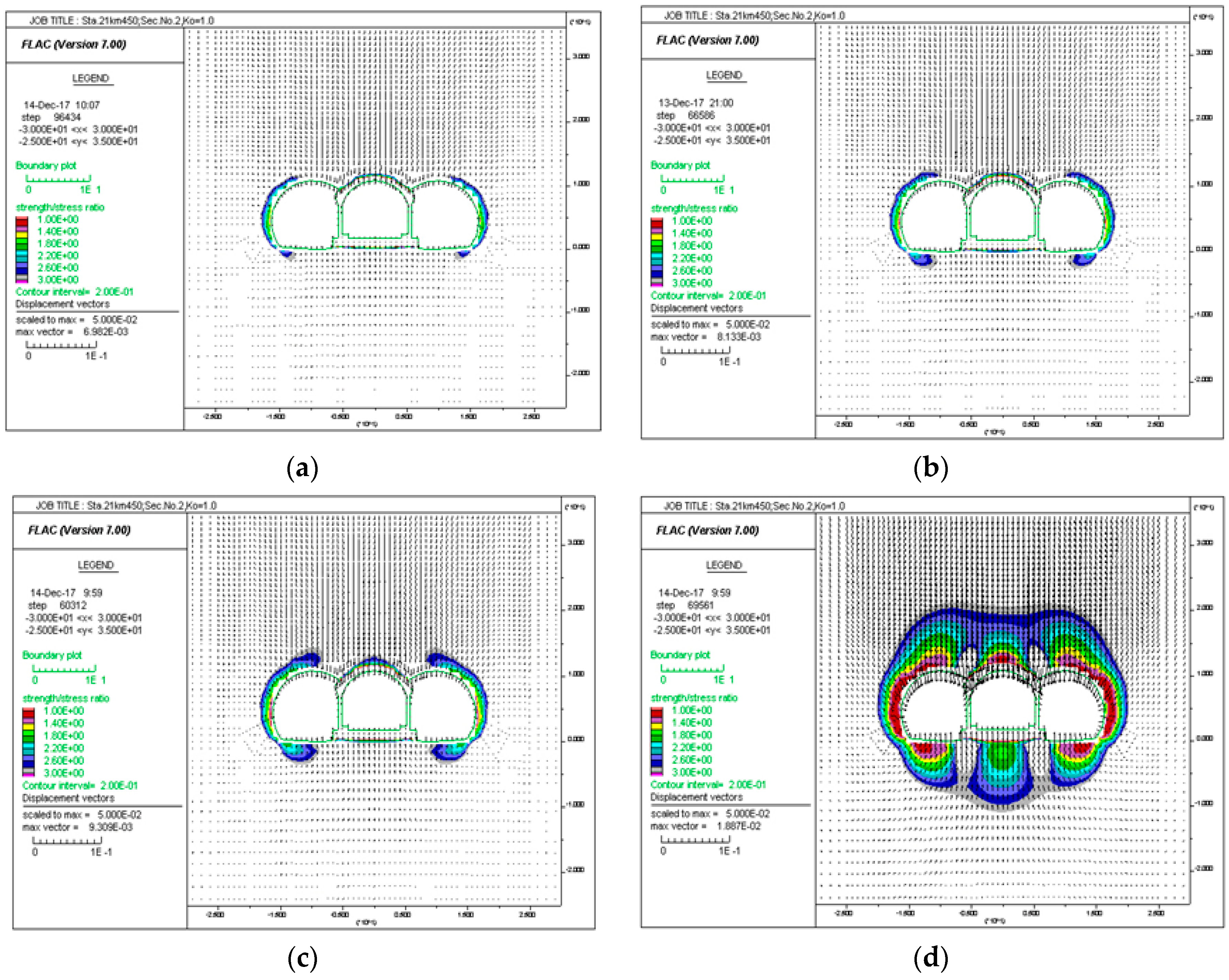
2.2.1. Criterion of Strength/Stress Ratio
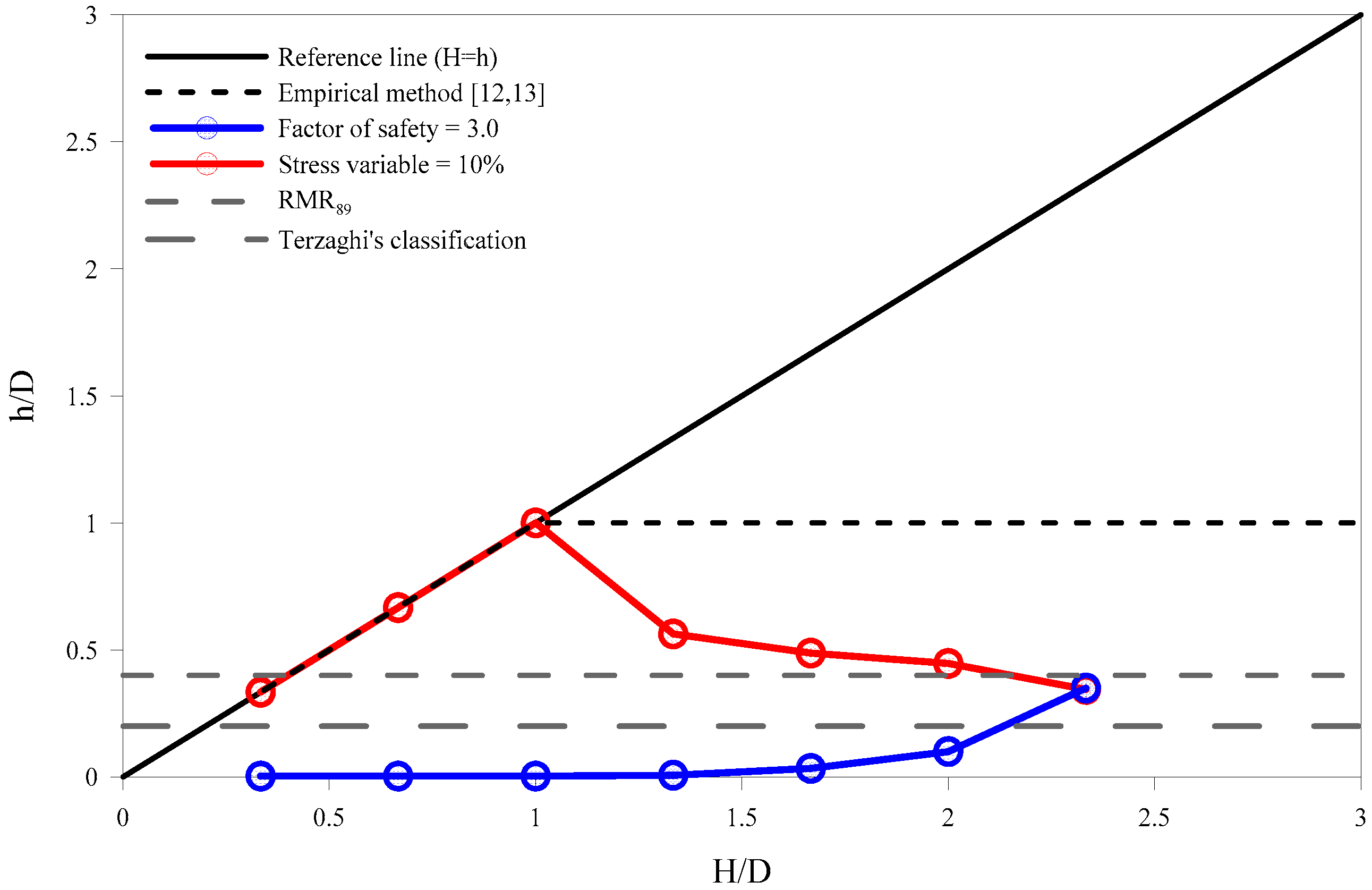
2.2.2. Criterion of Stress Variable
3. Numerical Parametric Study of Three-Arch Tunnel Excavation for Rock Load Estimation
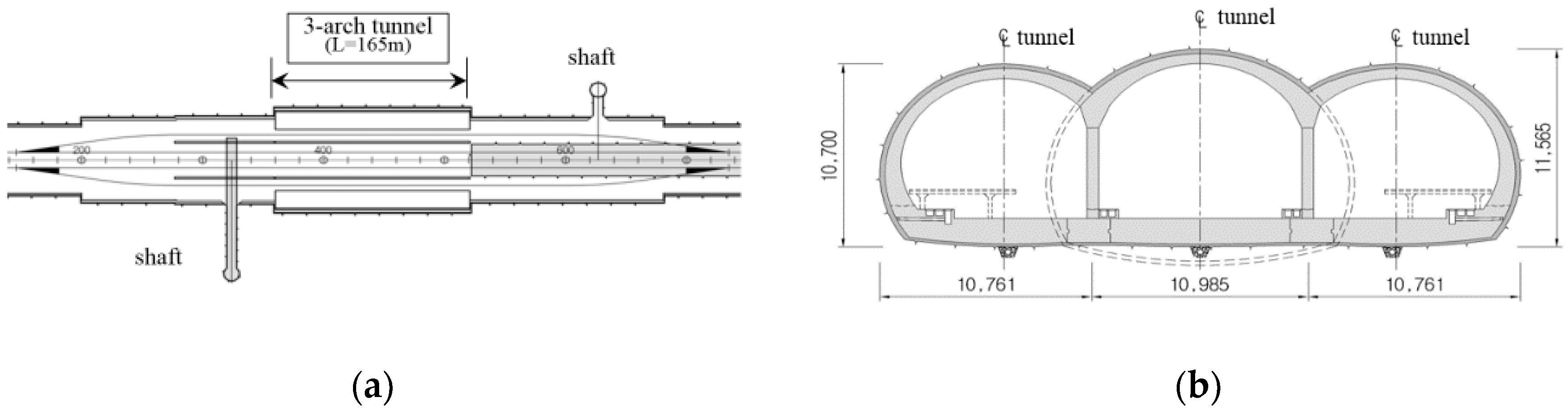
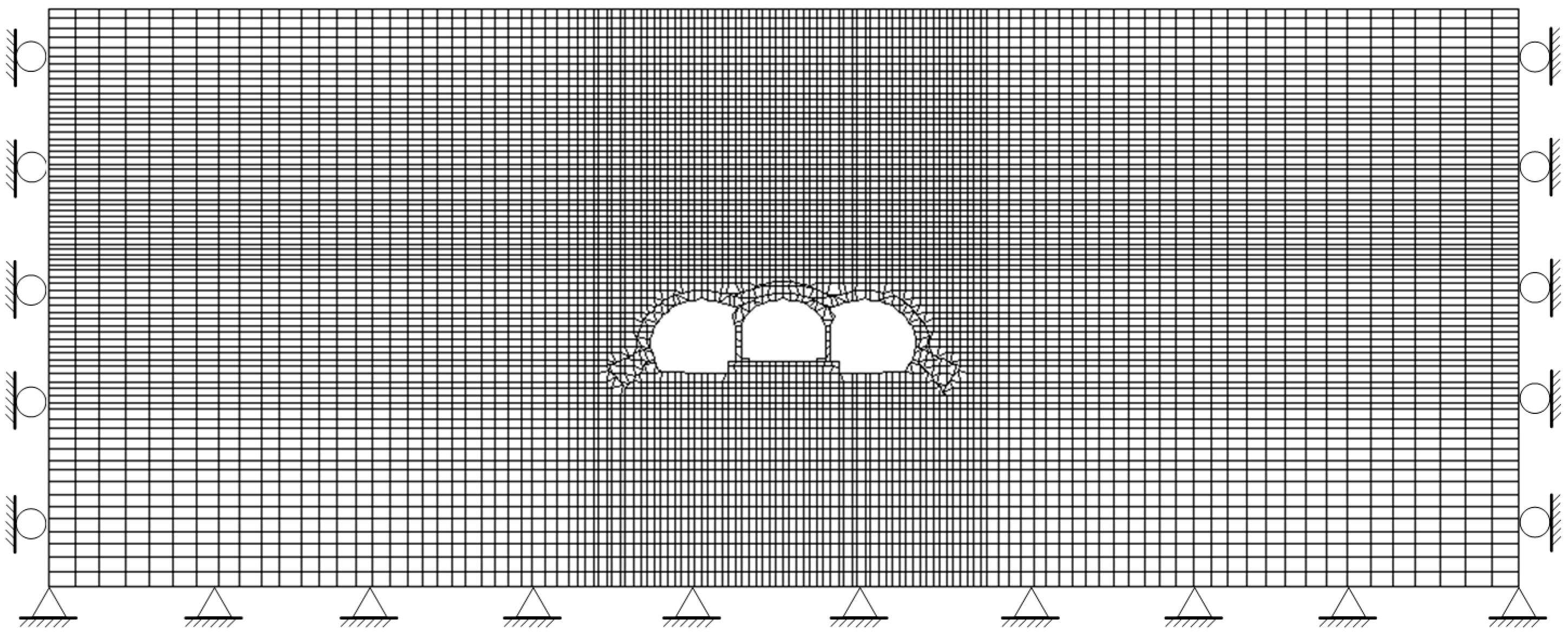
3.1. Three-Arch Tunnel for the Analysis
3.2. Numerical Modeling for Three-Arch Tunnel
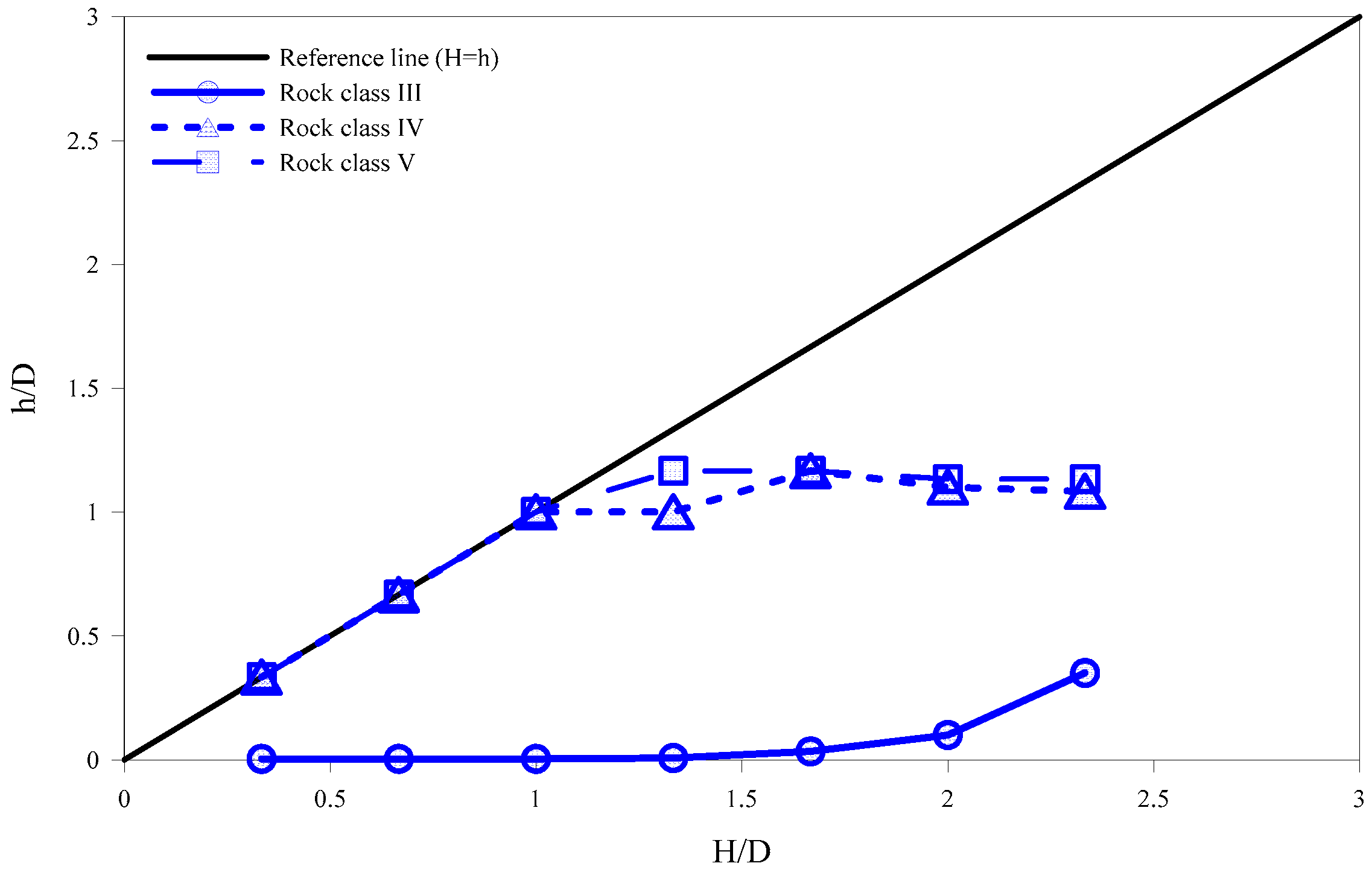
3.3. Estimation of Rock Load According to Overburden in Different Rock Mass Classes
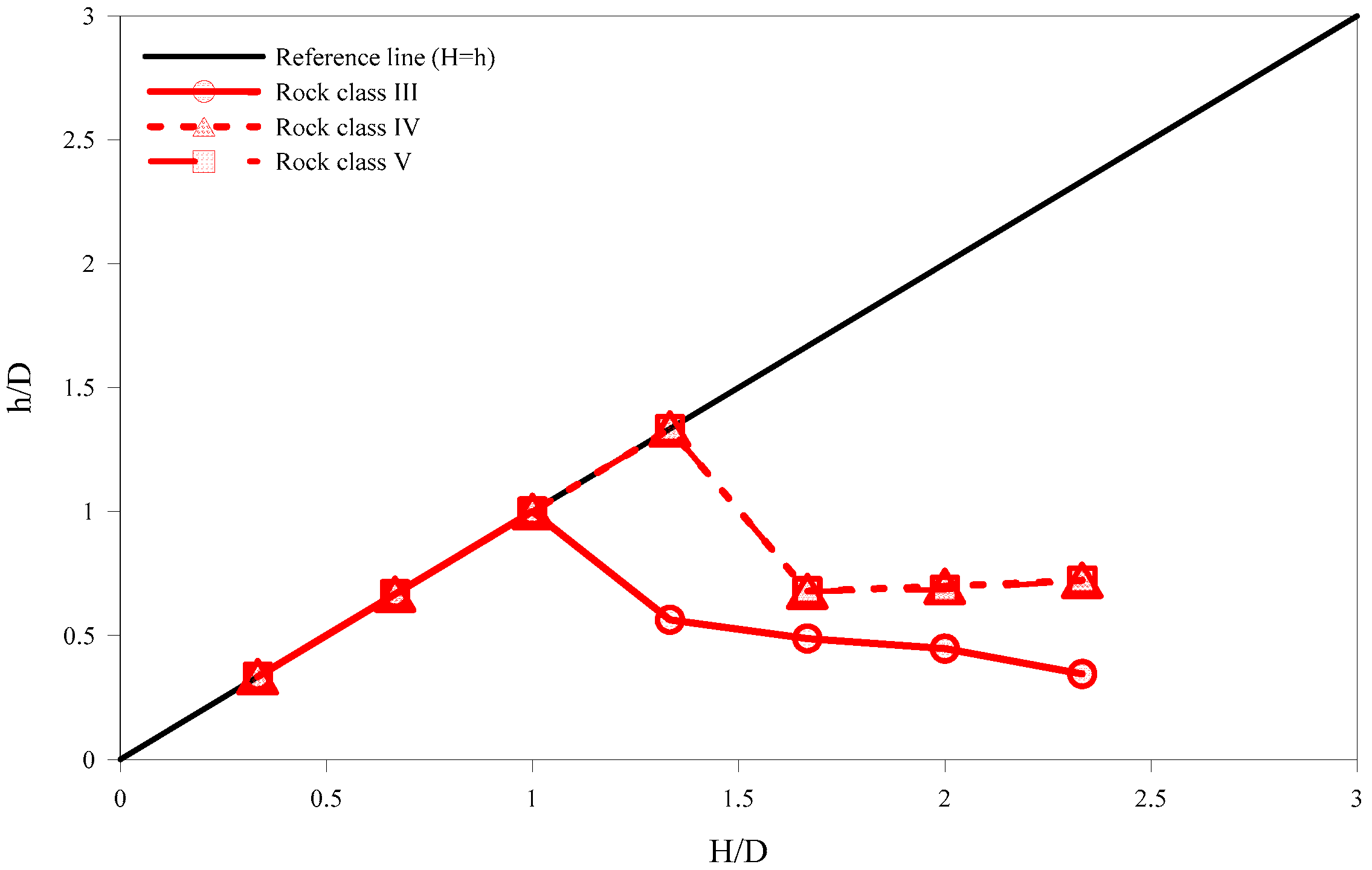
3.4. Analysis of Rock Load Characteristics with Respect to Construction Steps
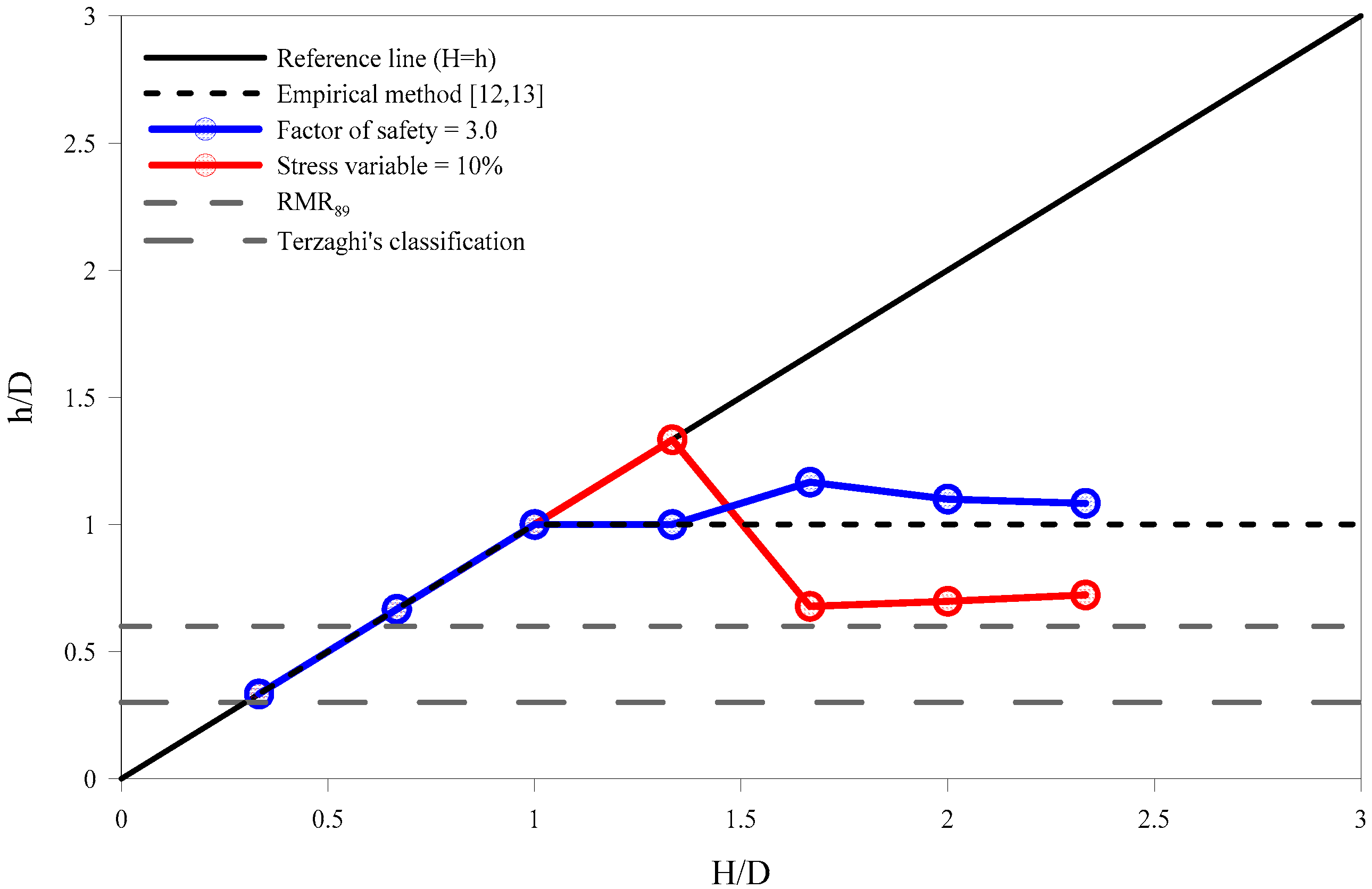
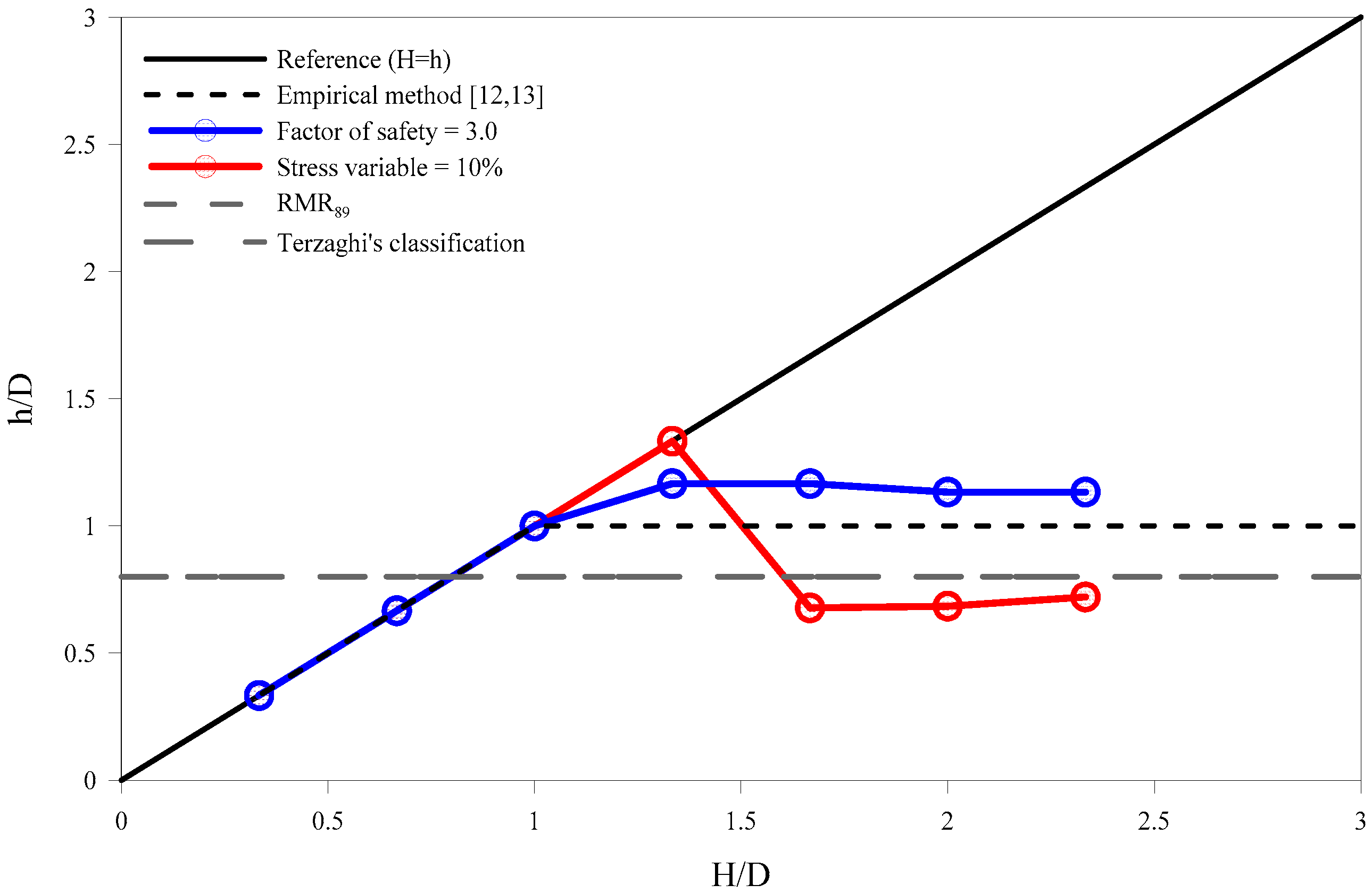
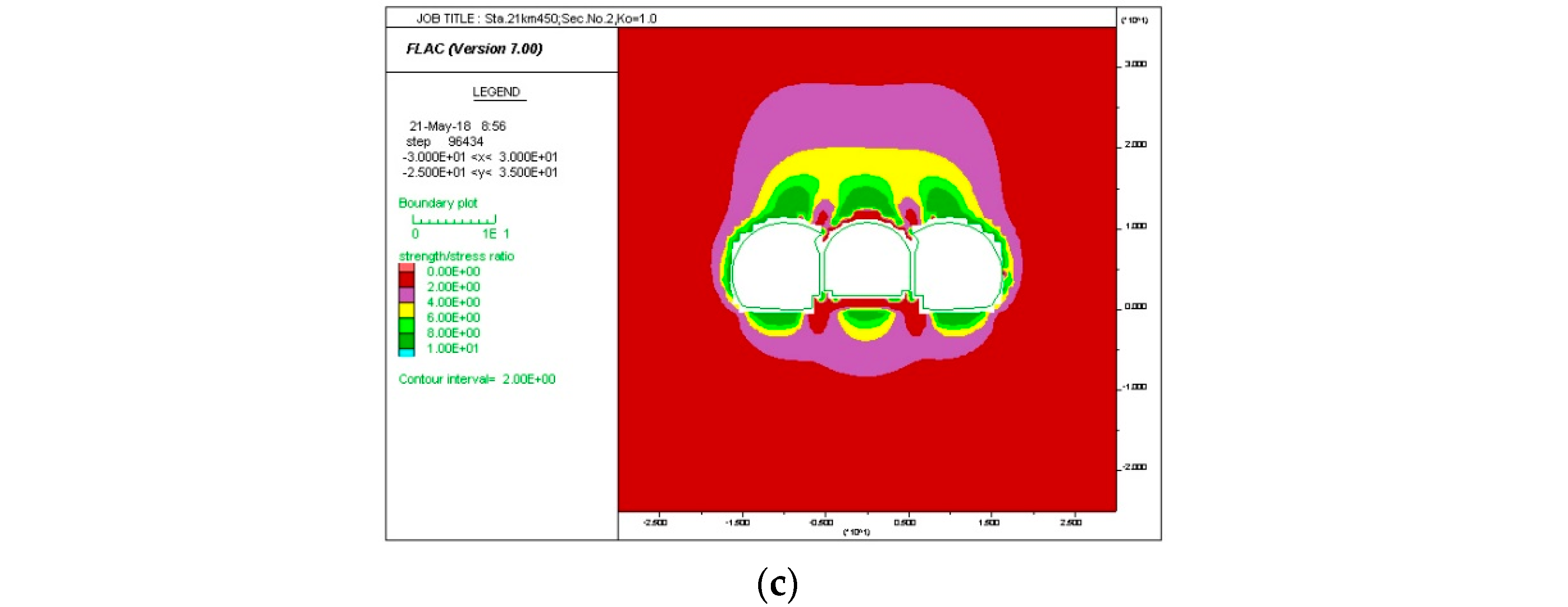
4. Crack Analysis by Stress Transition Effect
5. Conclusions
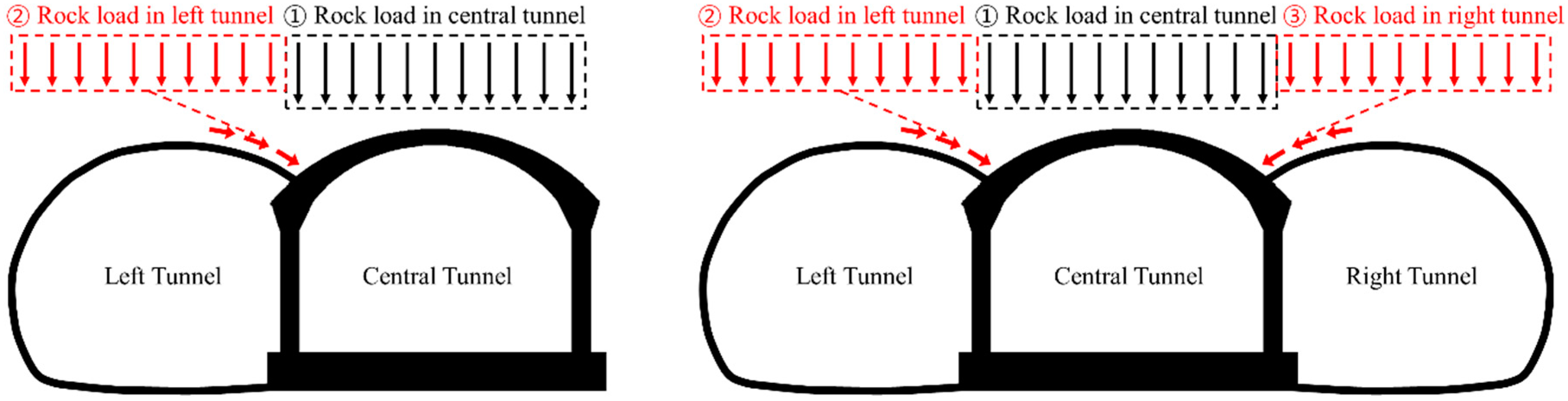
- A multi-arch tunnel consists of multiple tunnels connected parallel to each other, and it has a structurally weak shape because the tunnel width is typically greater than the tunnel height. After the excavation and provision of concrete lining in the initial tunnel, the adjacent tunnels are excavated and connected to the pre-excavated tunnel. The displacement and stress distribution in the periphery of the pre-excavated tunnel are affected by the excavation of the adjacent tunnels until the complete cross-section of the multi-arch tunnel is excavated. Therefore, the rock load developed owing to the excavation of the adjacent tunnels must be considered in designing the concrete lining for the pre-existing tunnel.
- Although many empirical methods have been developed to investigate the rock load for single tunnels, some limitations remain regarding complex construction steps and the consideration of additional rock load for multi-arch tunnels. Therefore, a numerical analysis approach based on the result contours can be more efficient than the empirical method owing to its capability of considering these limitations.
- The excavation of the three-arch tunnel was numerically simulated in this study according to the overburden values of 10–70 m in rock mass classes III, IV, and V. Considering the stress variable as 10% for all the rock mass classes, the rock load was estimated to be equal to the overburden when the overburden value was less than 1.0 D. However, when the overburden value was greater than 1.0 D, the rock load was estimated to be approximately 0.7 D, owing to the development of the arching effect, which was less than the empirical result (rock load calculated to be 1.0 D) obtained in the same conditions without considering the rock classification. Based on the estimation of rock load via numerical simulation, it is possible to develop a relatively economical design of the concrete lining in deep tunnels.
- In the case of poor rock mass conditions, the estimated rock load in multi-arch tunnels varies largely with the construction steps. In rock conditions below rock mass class IV, approximately 60% of the rock load is developed in multi-arch tunnels when the last adjacent tunnel is excavated. Therefore, the design and stability analysis must be performed according to the construction steps while considering the varying rock loads under different rock conditions.
- Cracks can occur at the shoulders of the central tunnel when the excavation of the adjacent tunnels is completed, resulting in an increase in the rock load and stress concentration. Through the back analysis, the crack-induced rock load should be computed with the corresponding deformation moduli of the rock mass. Therefore, the relation between the rock load height and the deformation moduli of the rock mass can provide better insights into the behavior of a three-arch tunnel.
Author Contributions
Funding
Conflicts of Interest
References
- Bieniawski, Z. Engineering classification of jointed rock masses. Civ. Eng. S. Afr. 1973, 15, 333–343. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Kim, J.; Kim, J.; Kim, M.; Yoo, H. Prediction of ground load by performing back analysis using composite support model in concrete lining design. KSCE J. Civ. Eng. 2015, 19, 1697–1706. [Google Scholar] [CrossRef]
- Kim, J.-J.; Lee, J.-K.; Kim, J.-U.; Yoo, H.-K. Evaluation of rock load based on critical shear strain concept on tunnels. J. Korean Tunn. Undergr. Space Assoc. 2013, 15, 637–652. [Google Scholar] [CrossRef] [Green Version]
- Park, K.H.; Shin, Y.W.; Kim, J.J.; Yoo, H.K. A study on the estimation method of rock load applied to concrete lining using back analysis. J. Korean Soc. Civ. Eng. 2013, 33, 1957–1968. [Google Scholar] [CrossRef]
- Lee, J.-K.; Kim, J.-J.; Hafeezur, R.; Yoo, H.-K. Evaluation of rock load based on stress transfer effect due to tunnel excavation. J. Korean Tunn. Undergr. Space Assoc. 2017, 19, 999–1012. [Google Scholar]
- You, K.-H. A study on the estimation of stress relaxed zone around a tunnel periphery for the design of 2-arch tunnel lining. J. Korean Tunn. Undergr. Space Assoc. 2005, 7, 343–352. [Google Scholar]
- Yang, J.; Wang, S.; Wang, Y.; Li, C. Analysis of arching mechanism and evolution characteristics of tunnel pressure arch. Jordan J. Civ. Eng. 2015, 9, 125–132. [Google Scholar]
- Terzaghi, K. Rock Defects and Loads on Tunnel Supports; Harvard University: Cambridge, MA, USA, 1946. [Google Scholar]
- Unal, E. Development of Design Guidelines and Roof-Control Standards for Coal-Mine Roofs. Ph.D. Thesis, Pennsylvania State University, Ann Arbor, MI, USA, 1983. [Google Scholar]
- Rehman, H.; Ali, W.; Naji, A.; Kim, J.-J.; Abdullah, R.; Yoo, H.-K. Review of rock-mass rating and tunneling quality index systems for tunnel design: Development, refinement, application and limitation. Appl. Sci. 2018, 8, 1250. [Google Scholar] [CrossRef] [Green Version]
- Sakai, T.; Miyanomae, S.; Kuroki, S.; Morita, K.; Sakurai, T.; Nashimoto, Y. A design method for reinforced center pillars of twin-bored tunnels. Doboku Gakkai Ronbunshu 2004, 2004, 33–42. [Google Scholar] [CrossRef] [Green Version]
- Matsuda, T.; Toyosato, E.; Igarishi, M.; Nashimoto, Y.; Sugiyama, K. A design method of a center-drift and center-pillar type twin-bore tunnel. Proc. Tunn. Eng. Japan Soc. Civ. Eng. 1997, 7, 1–6. [Google Scholar]
- Wang, S.-R.; Li, C.-L.; Wang, Y.-G.; Zou, Z.-S. Evolution characteristics analysis of pressure-arch in a double-arch tunnel. Teh. Vjesn. 2016, 23, 181–189. [Google Scholar]
- Korean Rail Network Authority. Geotechnical Investigation Report for the Construction of Railway of High Speed Railway in Seoul; Korean Rail Network Authority: Daejeon, Korea, 2011. [Google Scholar]
- Zhu, Z.; Sun, M.; Chen, M. Calculation of surrounding rock pressure on multi-arch tunnel. Int. Conf. Transp. Eng. 2009, 990–996. [Google Scholar]





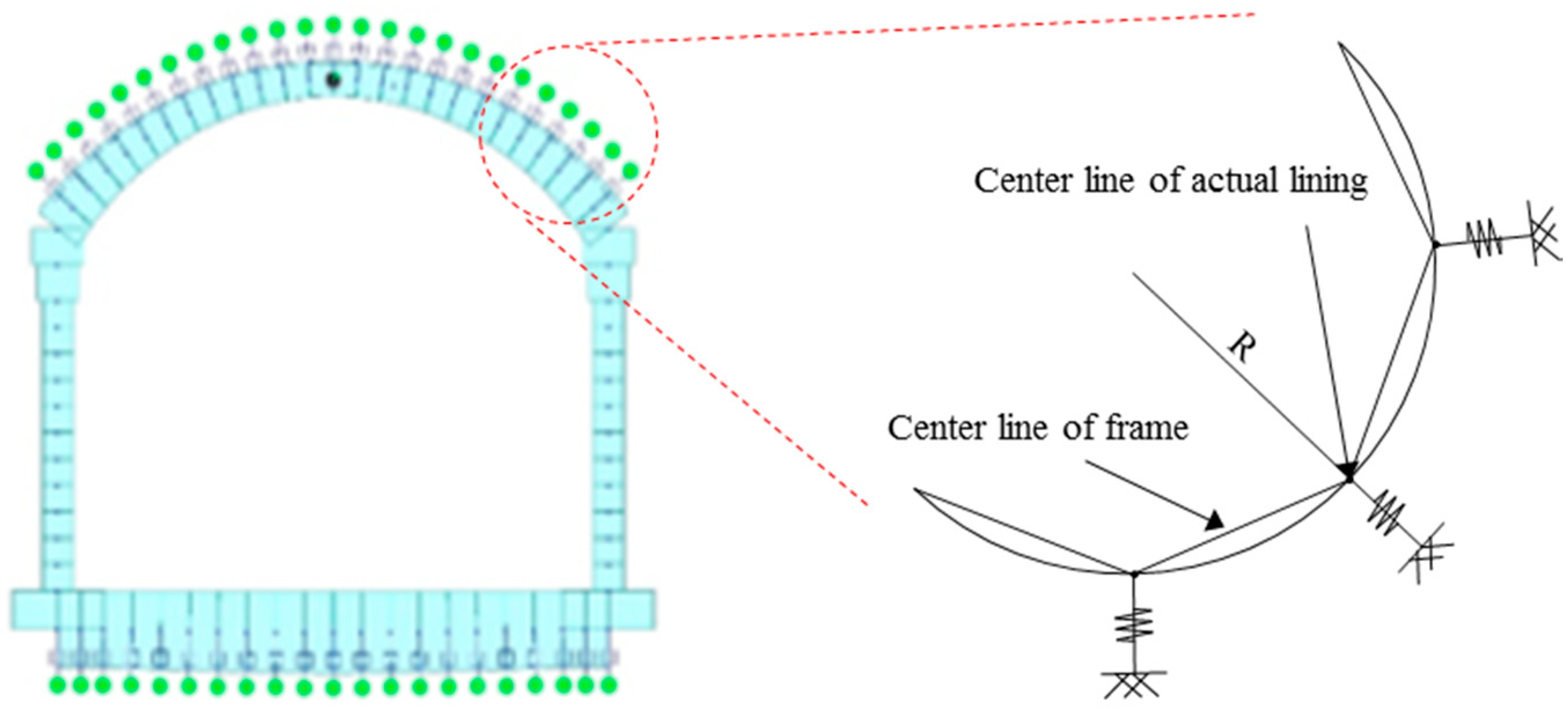
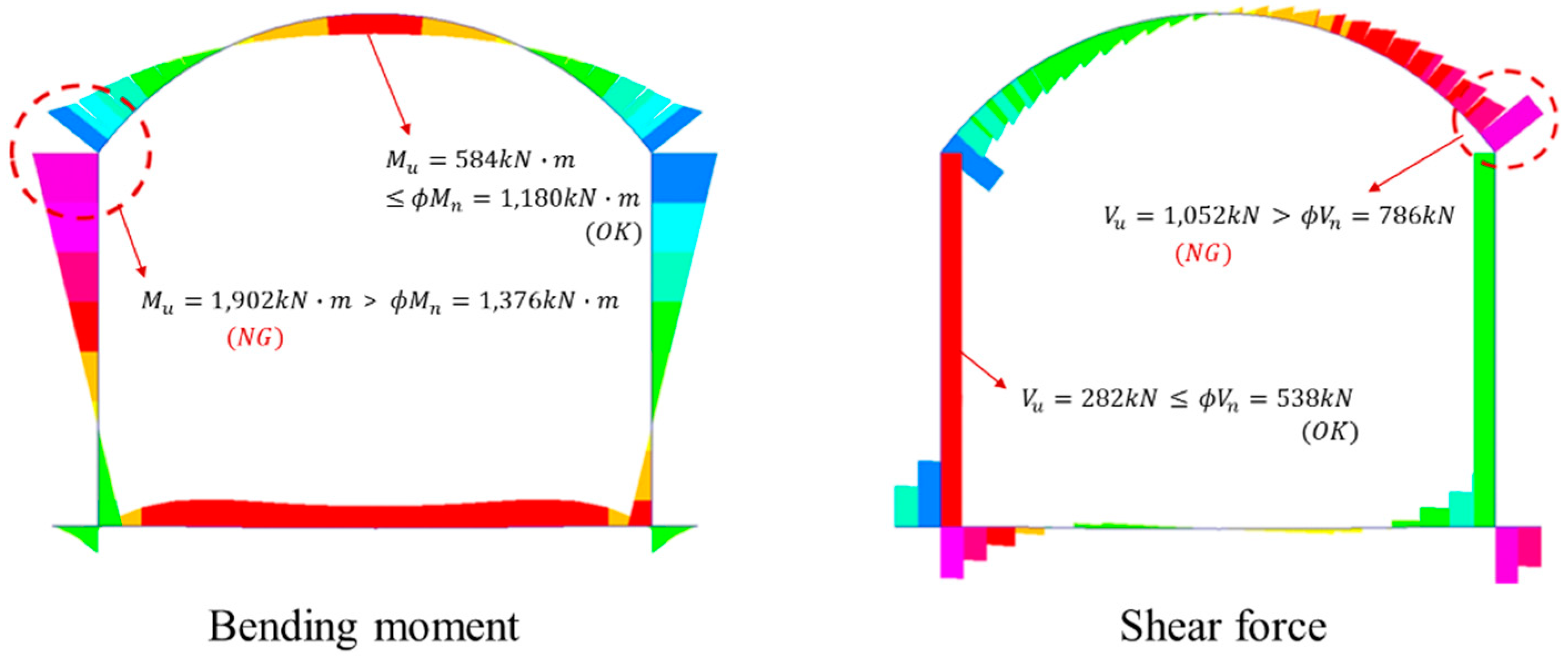

| Rock Mass Class. | Unit Weight (kN/m3) | Cohesion (kPa) | Friction Angle (°) | Deformation Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| III | 25.0 | 1020 | 38.0 | 5000 | 0.25 |
| IV | 23.0 | 500 | 35.0 | 2500 | 0.28 |
| V | 21.0 | 100 | 33.0 | 1000 | 0.30 |
| Construction Steps | Construction Condition | Load Distribution Ratio (%) |
|---|---|---|
| 1 | Excavation of top-heading in central tunnel | 45 |
| 2 | Soft shotcrete at top-heading in central tunnel | 35 |
| 3 | Hard shotcrete at top-heading in central tunnel | 20 |
| 4 | Bench excavation in central tunnel | 45 |
| 5 | Soft shotcrete at bench in central tunnel | 35 |
| 6 | Hard shotcrete at bench in central tunnel | 20 |
| 7 | Concrete lining in central tunnel | - |
| 8 | Excavation of top-heading in left tunnel | 45 |
| 9 | Soft shotcrete at top-heading in left tunnel | 35 |
| 10 | Hard shotcrete at top-heading in left tunnel | 20 |
| 11 | Bench excavation in left tunnel | 45 |
| 12 | Soft shotcrete at bench in left tunnel | 35 |
| 13 | Hard shotcrete at bench in left tunnel | 20 |
| 14 | Excavation of top-heading in right tunnel | 45 |
| 15 | Soft shotcrete at top-heading in right tunnel | 35 |
| 16 | Hard shotcrete at top-heading in right tunnel | 20 |
| 17 | Bench excavation in right tunnel | 45 |
| 18 | Soft shotcrete at bench in right tunnel | 35 |
| 19 | Hard shotcrete at bench in right tunnel | 20 |
| Shotcrete | Unit Weight (kN/m3) | Compressive Strength (MPa) | Deformation Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| Soft shotcrete | 24 | 1.1 | 5000 | 0.20 |
| Hard shotcrete | 24 | 10 | 15,000 | 0.20 |
| Rock Mass Class | Rock Load Height (m) and Extent of Load Distribution 1 (%) | ||
|---|---|---|---|
| Step 6 | Step 13 | Step 19 | |
| III | 3.8 (29.5%) | 8.7 (67.4%) | 12.9 (100%) |
| IV | 9.5 (25.1%) | 15.5 (39.7%) | 39 (100%) |
| V | 9.6 (24.6%) | 15.7 (40.3%) | 39 (100%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.K.; Yoo, H.; Ban, H.; Park, W.-J. Estimation of Rock Load of Multi-Arch Tunnel with Cracks Using Stress Variable Method. Appl. Sci. 2020, 10, 3285. https://doi.org/10.3390/app10093285
Lee JK, Yoo H, Ban H, Park W-J. Estimation of Rock Load of Multi-Arch Tunnel with Cracks Using Stress Variable Method. Applied Sciences. 2020; 10(9):3285. https://doi.org/10.3390/app10093285
Chicago/Turabian StyleLee, Jae Kook, Hankyu Yoo, Hoki Ban, and Won-Jun Park. 2020. "Estimation of Rock Load of Multi-Arch Tunnel with Cracks Using Stress Variable Method" Applied Sciences 10, no. 9: 3285. https://doi.org/10.3390/app10093285
APA StyleLee, J. K., Yoo, H., Ban, H., & Park, W.-J. (2020). Estimation of Rock Load of Multi-Arch Tunnel with Cracks Using Stress Variable Method. Applied Sciences, 10(9), 3285. https://doi.org/10.3390/app10093285





