Simulation Analysis and Experimental Verification of the Locking Torque of the Microgravity Platform of the Chinese Space Station
Abstract
:1. Introduction
2. L/R Mechanism Design
3. Principle
4. Analysis
4.1. Frequency Response Analysis
4.2. Static Analysis
4.3. Locking Force Analysis
5. Experiment
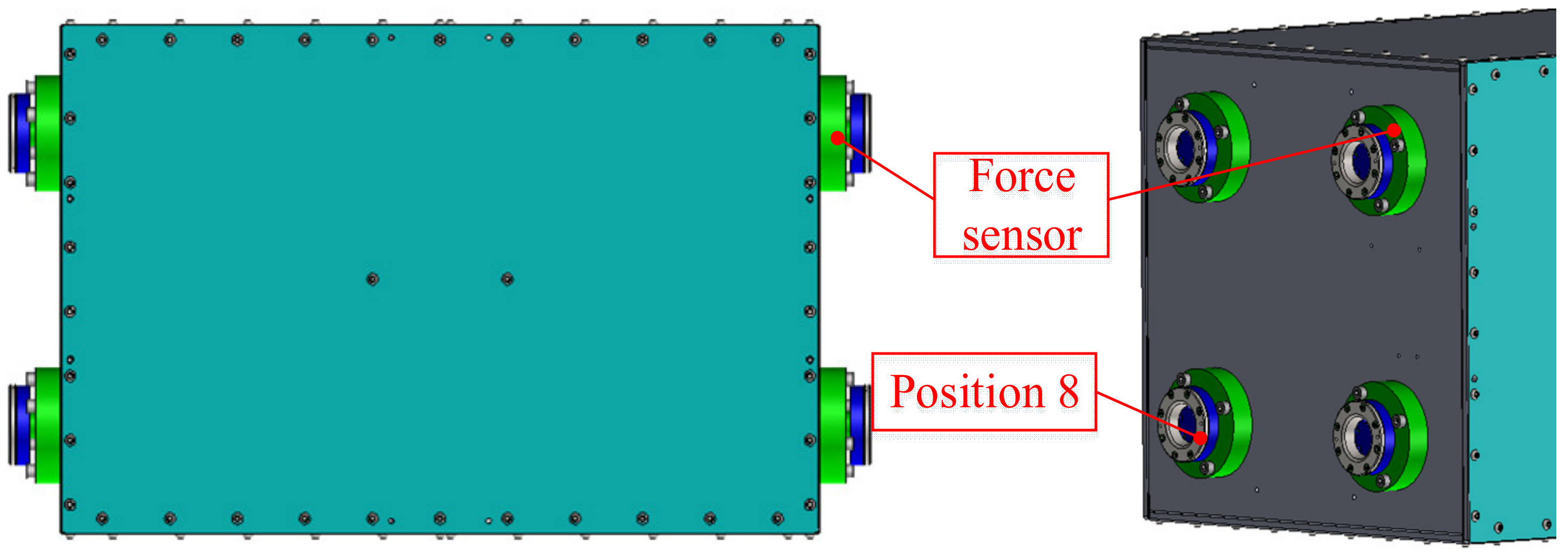
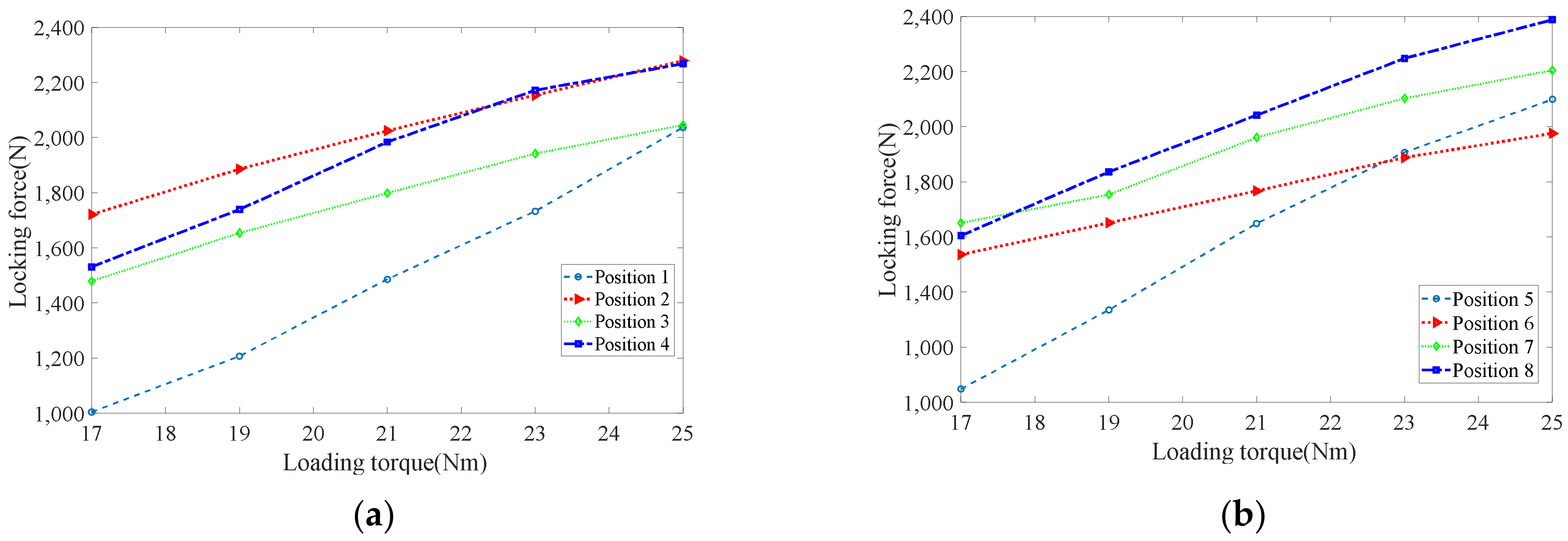
5.1. Locking Force Experiment
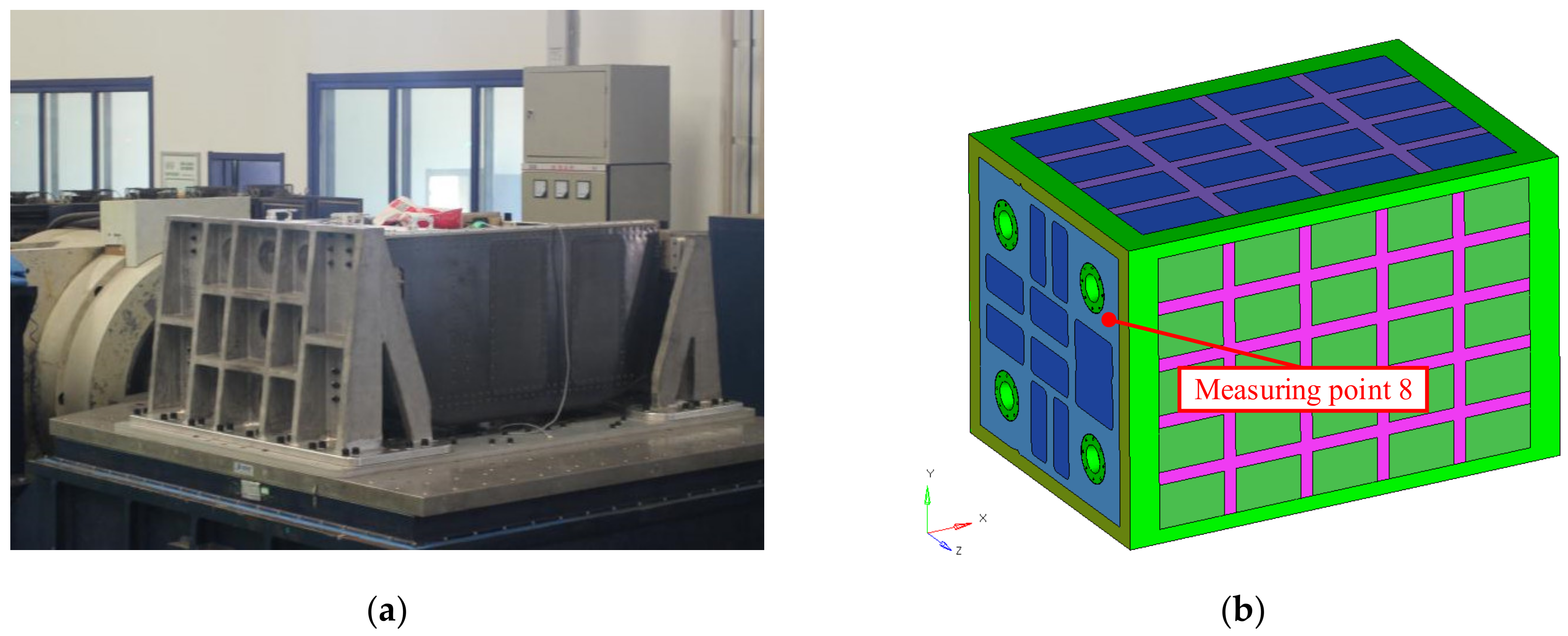
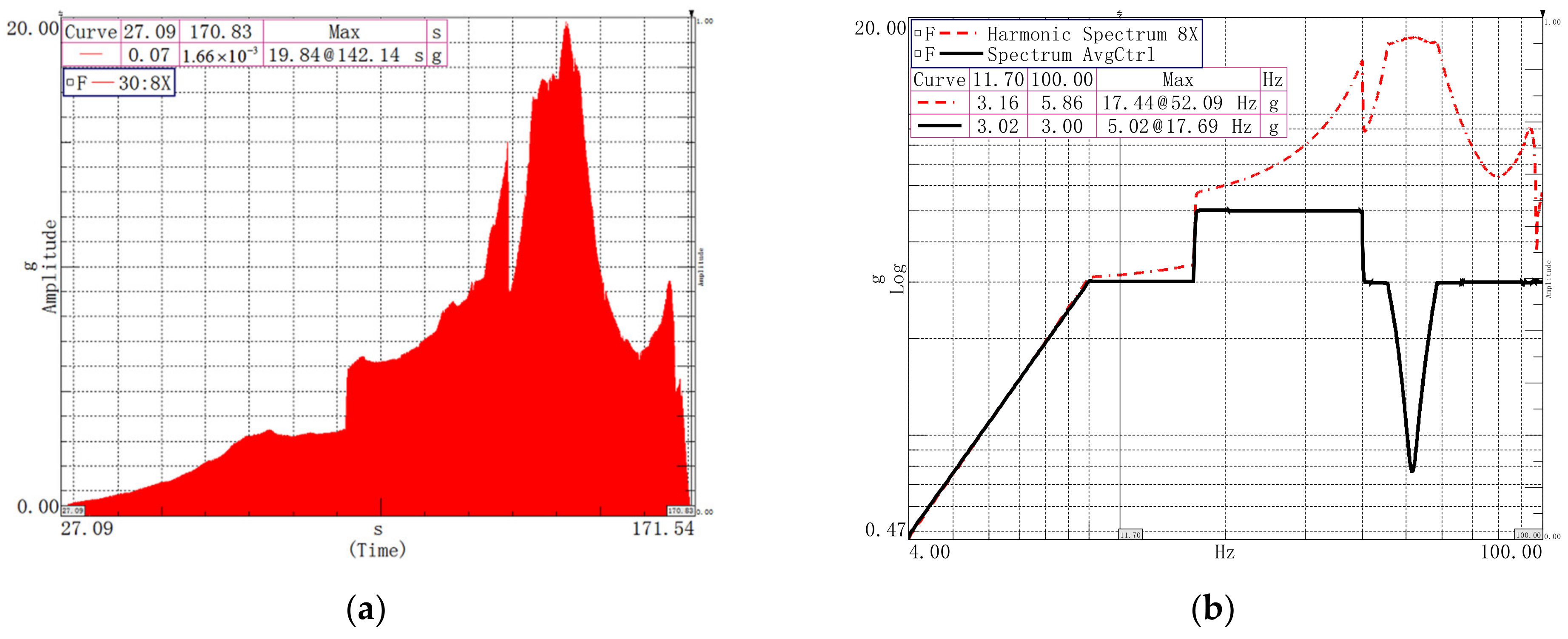
5.2. Vibration Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mora, M.; Wink, L.; Kögler, I.; Mahnert, A.; Rettberg, P.; Schwendner, P.; DeMets, R.; Cockell, C.S.; Alekhova, T.; Klingl, A.; et al. Space Station conditions are selective but do not alter microbial characteristics relevant to human health. Nat. Commun. 2019, 10, 3990. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, W.W.; Han, L.; Wang, H.M. Research and application progress of the International Space Station in 2018. Chin. J. Manned Spacefl. 2019, 25, 271–276. [Google Scholar]
- Kang, S.; Amare, Y.; Anderson, T.; Angelaszek, D.; Anthony, N.; Cheryian, K.; Choi, G.; Copley, M.; Coutu, S.; Derome, L.; et al. On-orbit performance of the top and bottom counting detectors for the ISS-CREAM experiment on the international space station. Adv. Space Res. 2019, 64, 2564–2569. [Google Scholar] [CrossRef]
- Izumi, Y.; Mitsugu, Y.; Momi, I.; Mitsuyasu, K.; Kiyohito, K.; Takuya, I.; Yoshio, W.; Saori, N. Recent Advance in High Quality Protein Crystal Growth Experiment on the International Space Station by JAXA. Int. J. Microgravity Sci. Appl. 2019, 36, 360101. [Google Scholar]
- Zhou, J.P. Chinese space station project overall vision. Manned Spacefl. 2013, 19, 1–10. [Google Scholar]
- Xie, W.J.; Luo, X.H.; Zhang, X.W.; Yu, Y.D. Microgravity material research in China: 2016. Chin. J. Space Sci. 2016, 36, 805–814. [Google Scholar]
- Wang, Y.R.; Dai, G.L.; Wang, J.; Feng, S.; Luo, X.; Zhou, Y.; Chen, L. Microgravity material research in China: 2012–2014. Chin. J. Space Sci. 2014, 34, 757–764. [Google Scholar]
- Liu, Q.S.; Nie, Y.X.; Feng, M.F.; Hu, W.R. Progress on microgravity sciences in China. Chin. J. Space Sci. 2006, 26, 150–159. [Google Scholar]
- Liu, J.G.; Li, Y.M.; Zhang, Y.; Gao, Q.; Zuo, B. Dynamic and control of a parallel mechanism for active vibration isolation in space station. Nonlinear Dynam. 2014, 76, 1737–1751. [Google Scholar] [CrossRef]
- Ding, J.; Liu, J.G.; Zhang, L.; Luo, H.T.; Liu, Y.W. Design of experiment-based tolerance synthesis for a lock-or-release mechanism of the Chinese Space Station Microgravity Platform. Mech. Sci. 2019, 10, 393–412. [Google Scholar] [CrossRef]
- Ding, J.; Liu, J.G.; Zhang, R.P.; Zhang, L.; Hao, G.B. Accuracy modeling and analysis for a lock-or-release mechanism of the Chinese Space Station Microgravity Platform. Mech. Mach. Theory 2018, 30, 552–566. [Google Scholar] [CrossRef]
- Xiang, S.H. Environmental Experimental Technique for Spacecraft Mechanics; China Science and Technology Press: Beijing, China, 2008; pp. 1–17. [Google Scholar]
- Cao, C.; Zhao, X.Y.; Song, Z.H. Dynamic Analysis of Bolted Cantilever Beam with Finite Element Method Considering Thread Relation. Appl. Sci. 2020, 10, 7036. [Google Scholar] [CrossRef]
- Shi, L.J.; Wen, J.; Pan, B.S.; Xiang, Y.Y.; Lin, C.K. Dynamic Characteristics of a Gear System with Double-Teeth Spalling Fault and Its Fault Feature Analysis. Appl. Sci. 2020, 10, 7058. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Chen, W.L.; Chen, L.Q. Mechanics of Vibration; Higher Education Press: Beijing, China, 2011; pp. 31–37. [Google Scholar]
- Li, Z.G. Nastran Quick Start and Practice; National Defence Industry Press: Beijing, China, 2007; pp. 106–111. [Google Scholar]
- Nurprasetio, I.P.; Budiman, B.A.; Afwan, A.A.; Halimah, P.N.; Aziz, M. Nonlinear Piezoresistive Behavior of Plain-Woven Carbon Fiber Reinforced Polymer Composite Subjected to Tensile Loading. Appl. Sci. 2020, 10, 5847. [Google Scholar] [CrossRef] [Green Version]
- Han, K.; Kim, H.; Kim, J.; You, D.; Ko, H. A 24.88 nV/√Hz Wheatstone Bridge Readout Integrated Circuit with Chopper-Stabilized Multipath Operational Amplifier. Appl. Sci. 2020, 10, 399. [Google Scholar] [CrossRef] [Green Version]
- Himelblau, H.; Manning, J.; Kern, D.; Piersol, A.G. Dynamic environmental criteria. In NASA Technical Handbook 7005; NASA: Washington, DC, USA, 2001; p. 249. [Google Scholar]
- Wang, Y.B. Interface Dynamic Model Simplifieation for Satellite and Rocket System in Force Limited Vibration Test. Master’s Thesis, Fudan University, Shanghai, China, 2009. [Google Scholar]
- Ye, H.; Wang, Y.R.; Liu, B.; Jiang, X.H. Experimental Study on the Damping Effect of Multi-Unit Particle Dampers Applied to Bracket Structure. Appl. Sci. 2019, 9, 2912. [Google Scholar] [CrossRef] [Green Version]
- Bao, W.B.; Bai, Q.; Lu, H.Y. Vibration Mechanics Foundation and MATLAB Application; Tsinghua University Press: Beijing, China, 2017; pp. 1–30. [Google Scholar]
- Wang, Y.F.; Liu, B.S.; Zhang, L.X.; Wang, K. Review of Vibration Test Force Limit Control Technology for Aerospace Products. Manned Spacefl. 2015, 21, 163–170. [Google Scholar]
- Zhang, H.T.; Wang, M.Z. Measuring and Testing Technique; Northeastern University Press: Shenyang, China, 2005; pp. 5–30. [Google Scholar]
- Wang, Z.; Chen, H.; Zhang, Z. Environment Test; Electronic Industry Press: Beijing, China, 2015; pp. 201–261. [Google Scholar]












| Material | E1 (MPa) | E2 (MPa) | NU12 | G12 (MPa) | RHO (t/mm3) |
|---|---|---|---|---|---|
| 7075 | 72,000 | - | 0.33 | - | 2.81 × 10−9 |
| T300 | 13,500 | 8500 | 0.35 | 4800 | 1.6 × 10−9 |
| Parameter | The Input Conditions | |||
|---|---|---|---|---|
| Frequency range (Hz) | 4–10 | 10–17 | 17–60 | 60–100 |
| Magnitude | 7.5 mm | 3 g | 5 g | 3 g |
| Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Locking force (N) | 1176.21 | 1210.41 | 1248.44 | 1606.61 | 1167.07 | 1177.53 | 1288.14 | 1614.58 |
| Fs (N) | 1411.45 | 1452.49 | 1498.13 | 1927.93 | 1400.48 | 1413.04 | 1545.77 | 1937.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Luo, H.; Yu, C.; Wang, H.; Meng, L. Simulation Analysis and Experimental Verification of the Locking Torque of the Microgravity Platform of the Chinese Space Station. Appl. Sci. 2021, 11, 102. https://doi.org/10.3390/app11010102
Liu G, Luo H, Yu C, Wang H, Meng L. Simulation Analysis and Experimental Verification of the Locking Torque of the Microgravity Platform of the Chinese Space Station. Applied Sciences. 2021; 11(1):102. https://doi.org/10.3390/app11010102
Chicago/Turabian StyleLiu, Guangming, Haitao Luo, Changshuai Yu, Haochen Wang, and Lilu Meng. 2021. "Simulation Analysis and Experimental Verification of the Locking Torque of the Microgravity Platform of the Chinese Space Station" Applied Sciences 11, no. 1: 102. https://doi.org/10.3390/app11010102






