Experimental and Numerical Investigation of Solar Panels Deployment with Tape Spring Hinges Having Nonlinear Hysteresis with Friction Compensation
Abstract
:1. Introduction
2. Experimental Investigation of Tape Spring Hinges
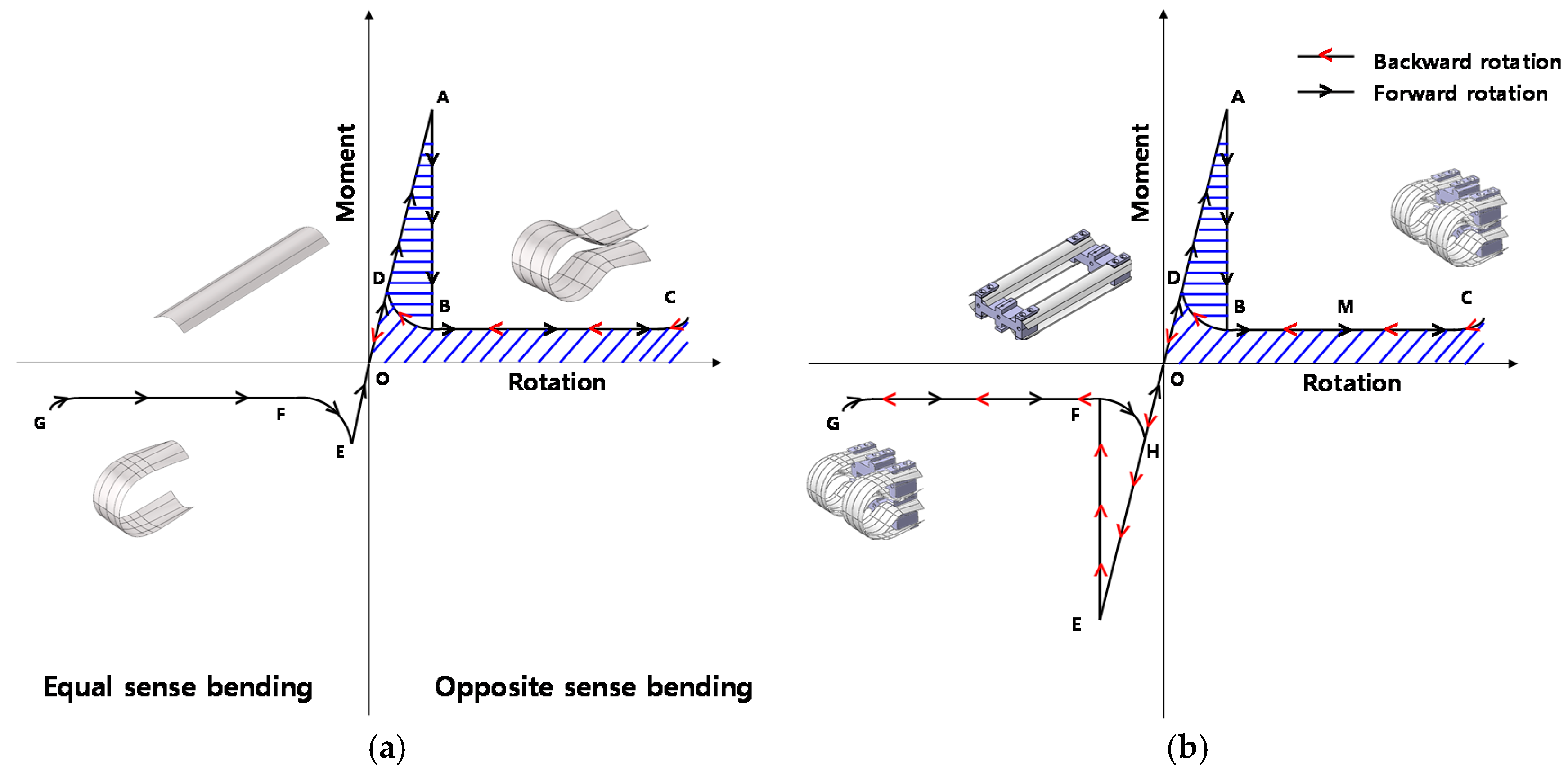
2.1. Moment-Rotation Profile of TS Hinges
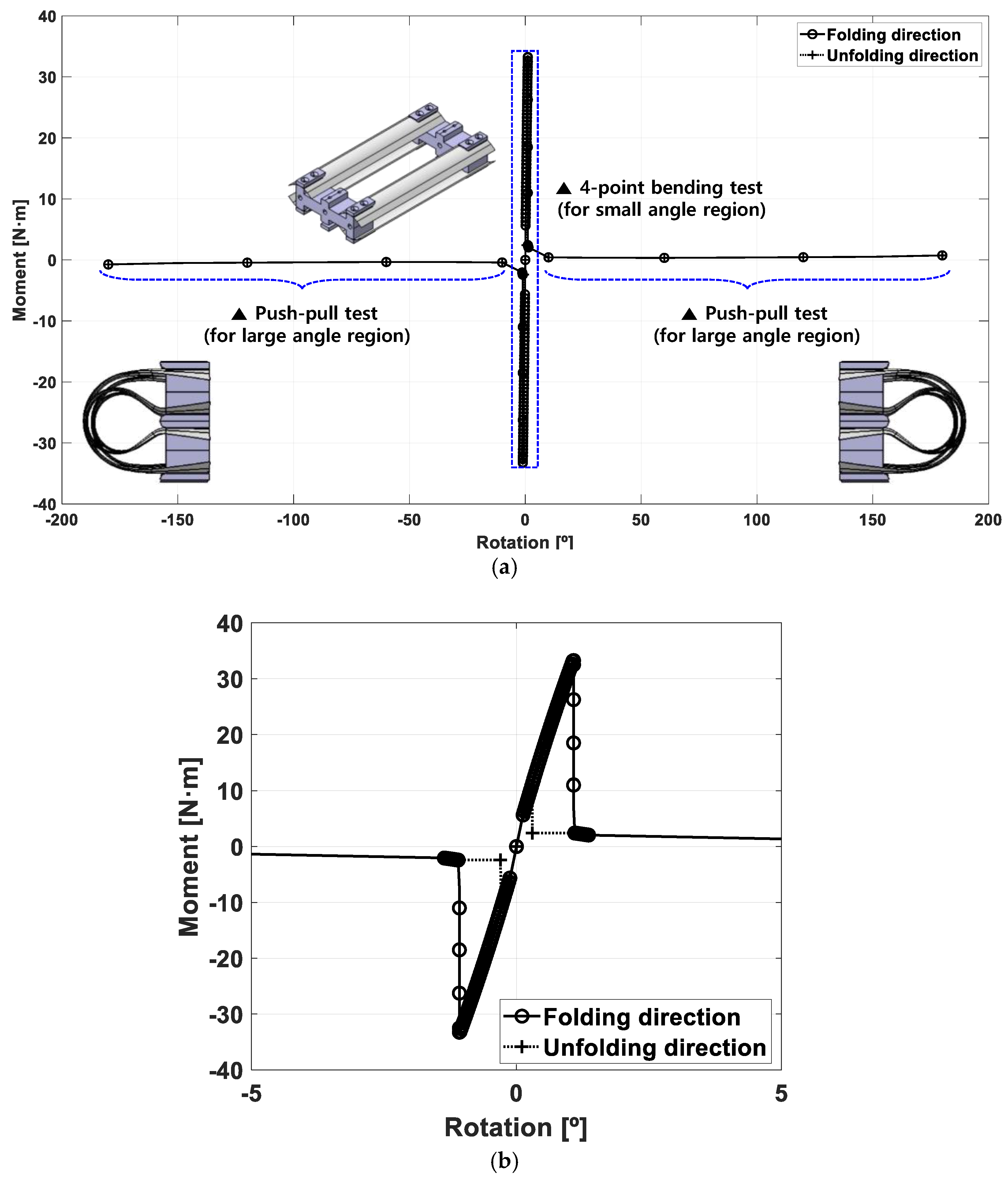
2.2. Measurement of the Moment–Rotation Relationship of TS Hinges
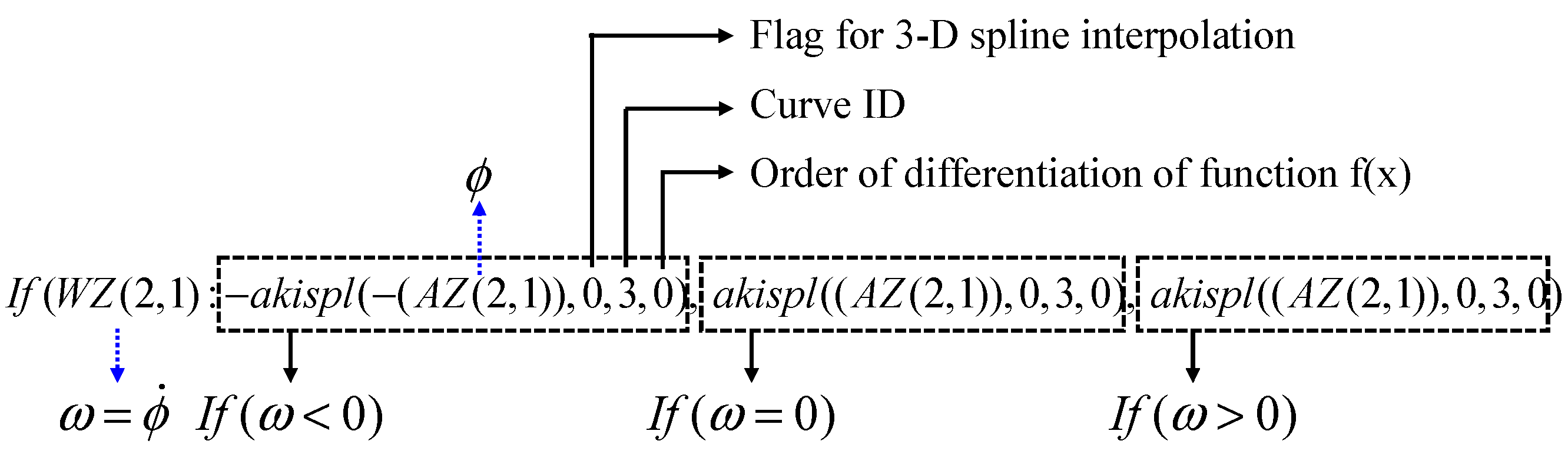
2.3. Implementation of Characteristics of TS Hinges
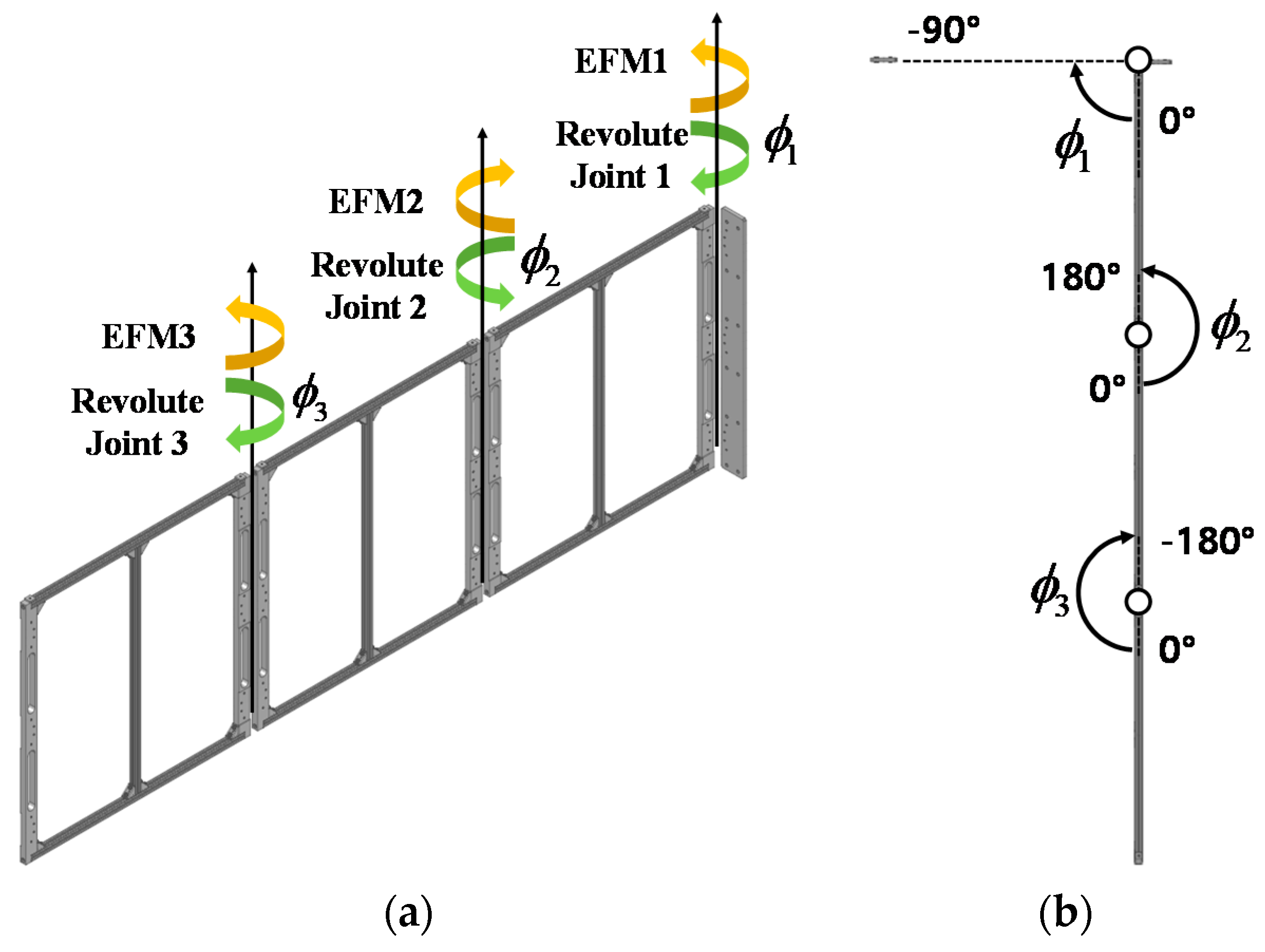
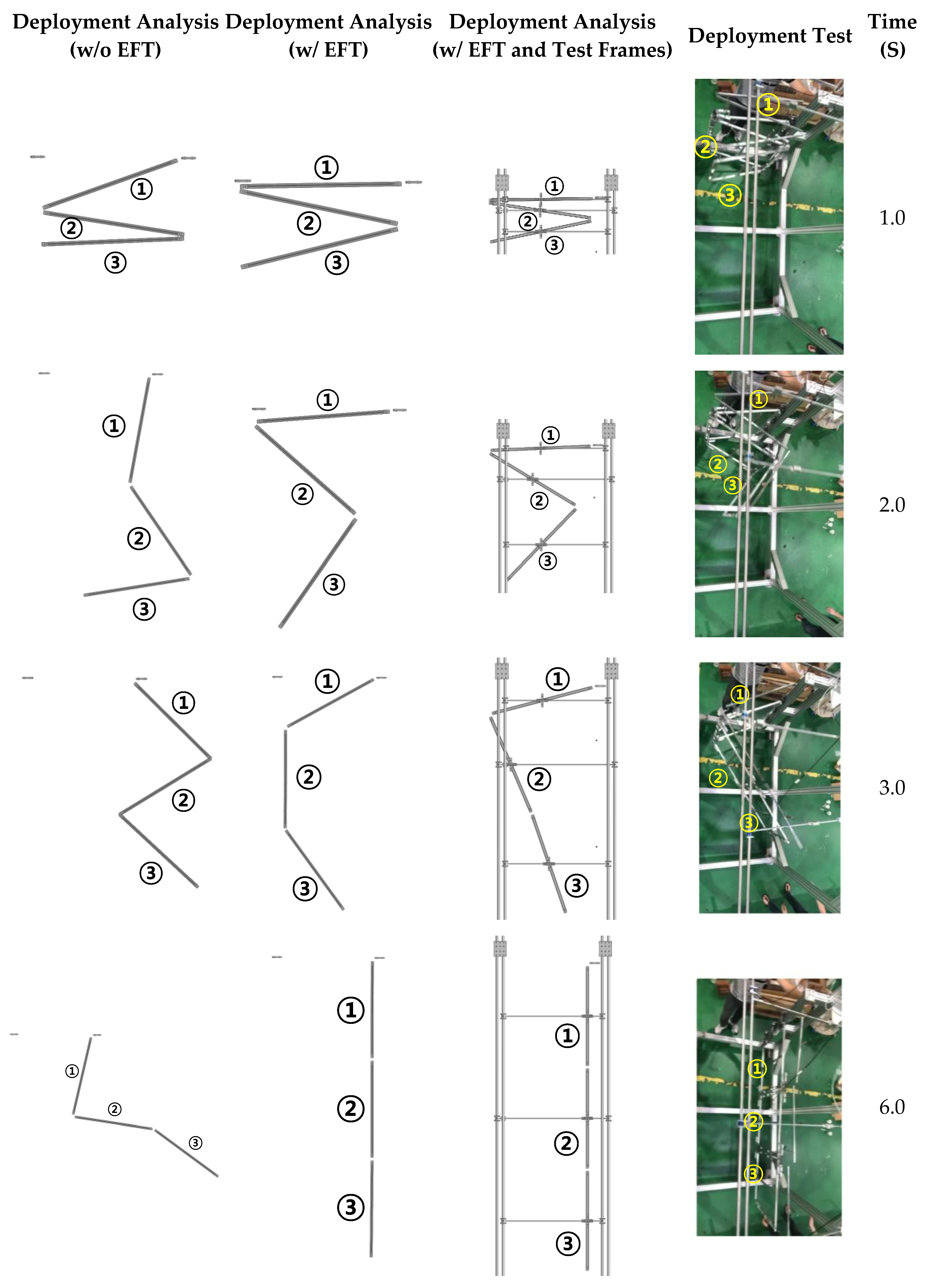
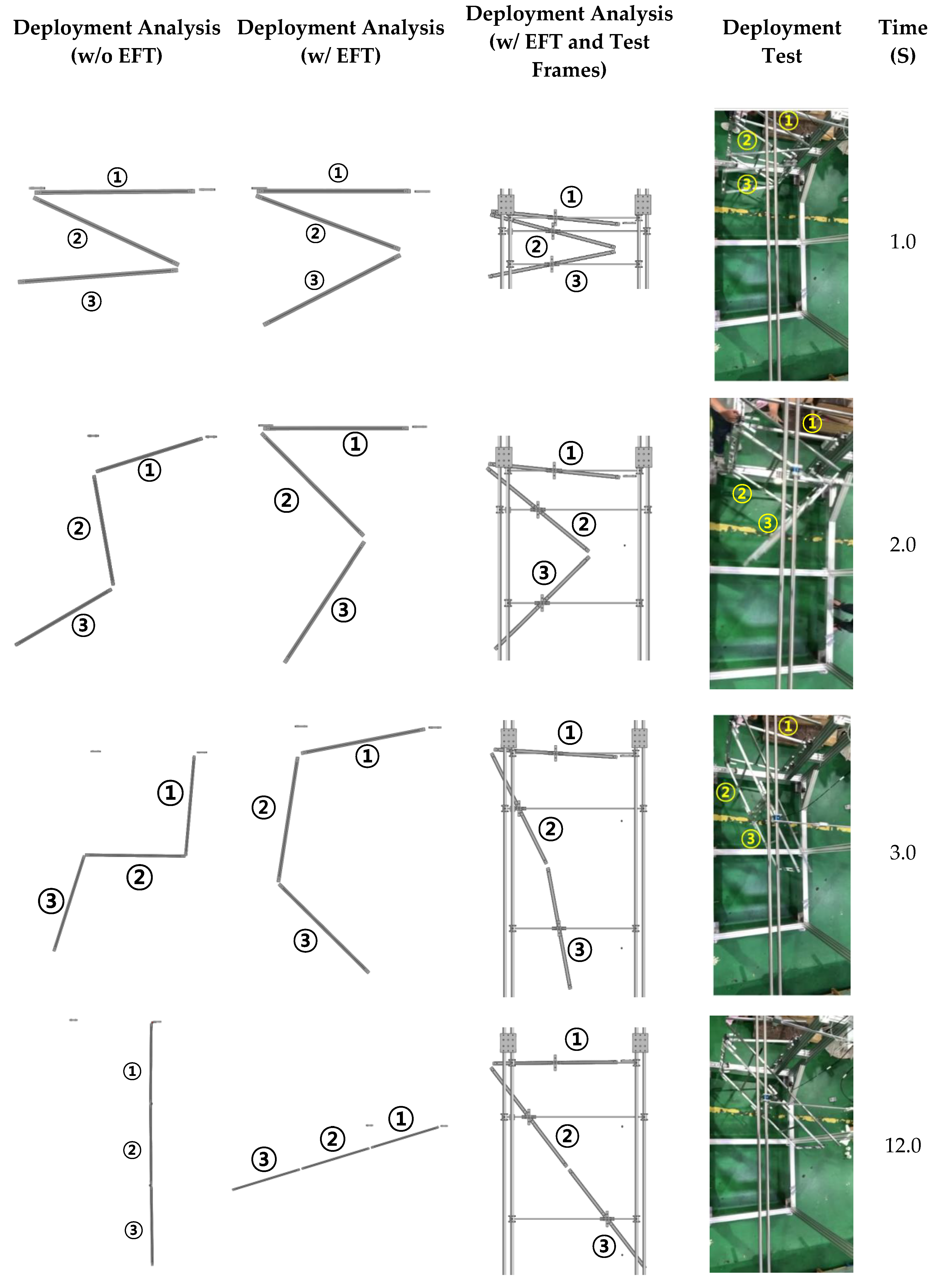
3. Deployment Test of Panels
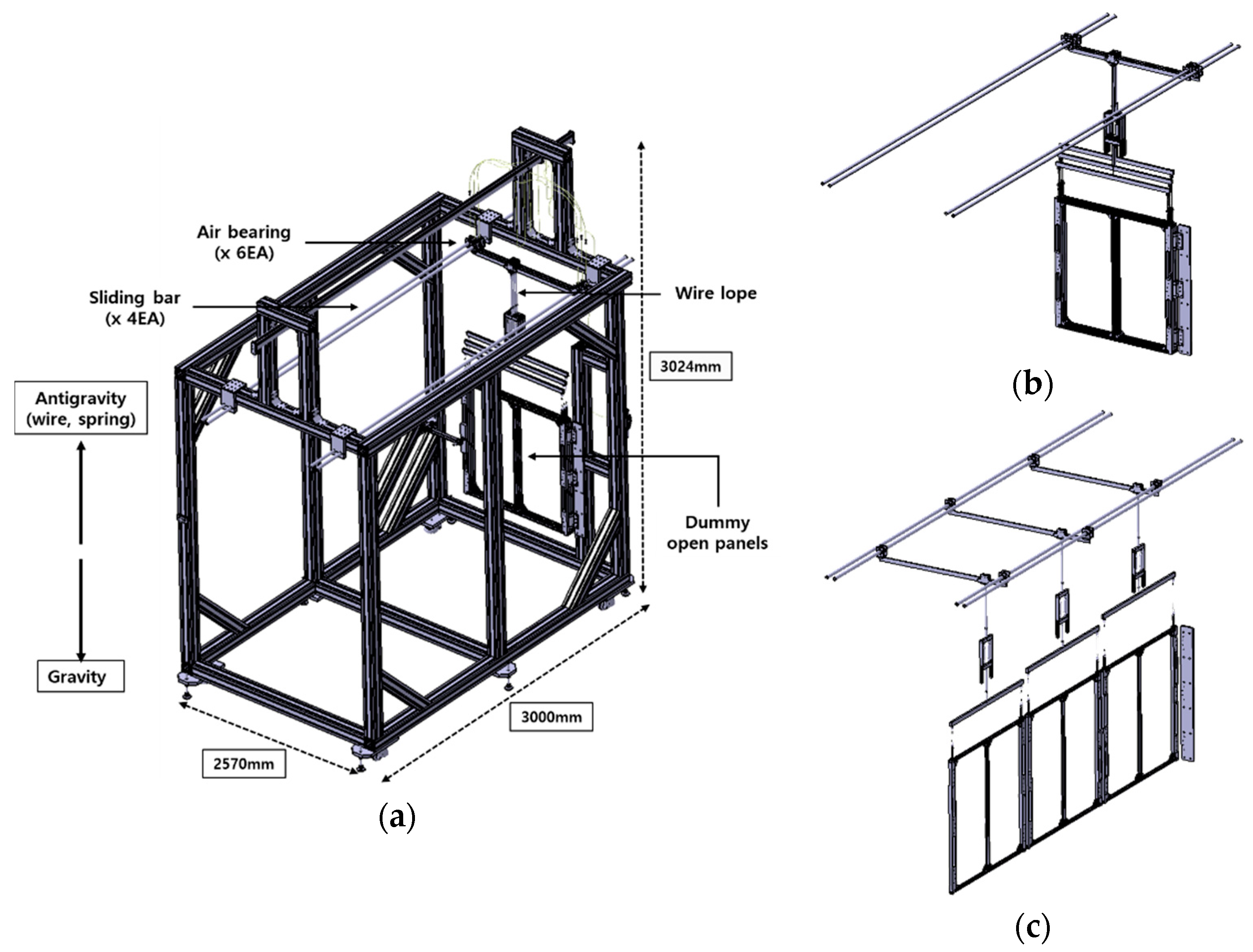
3.1. Test Setup with Zero-G Device
3.2. Test Cases
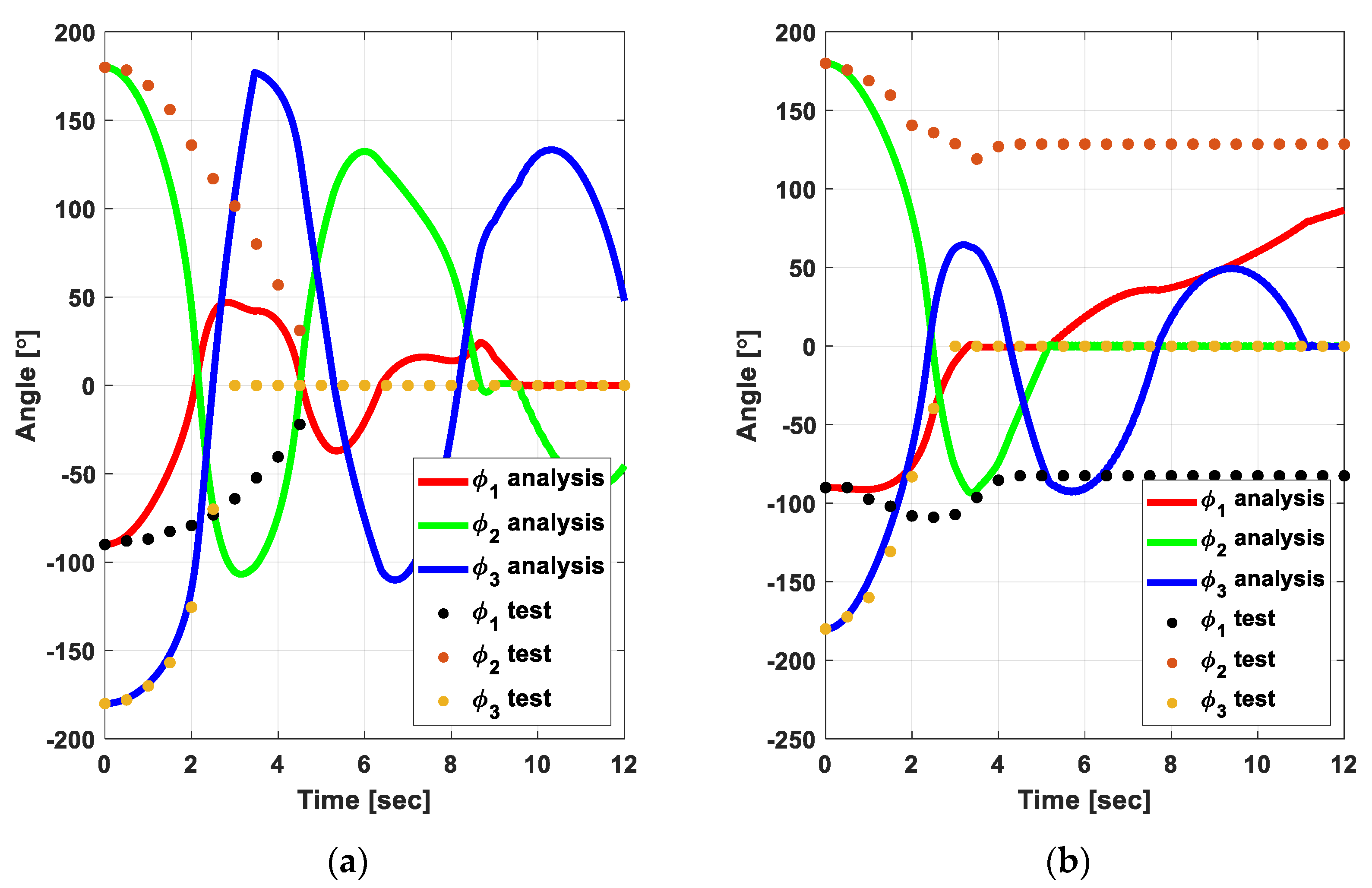
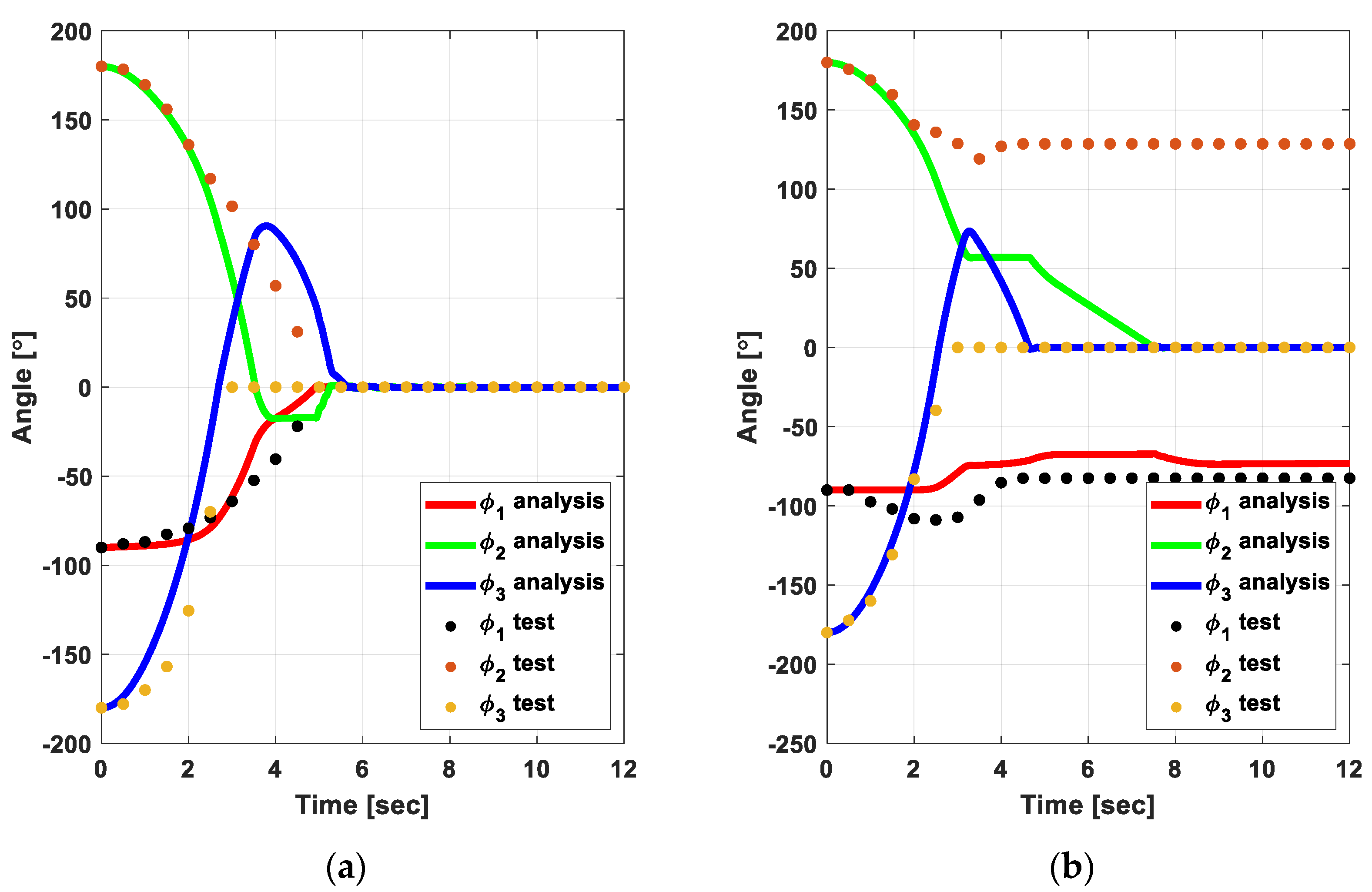
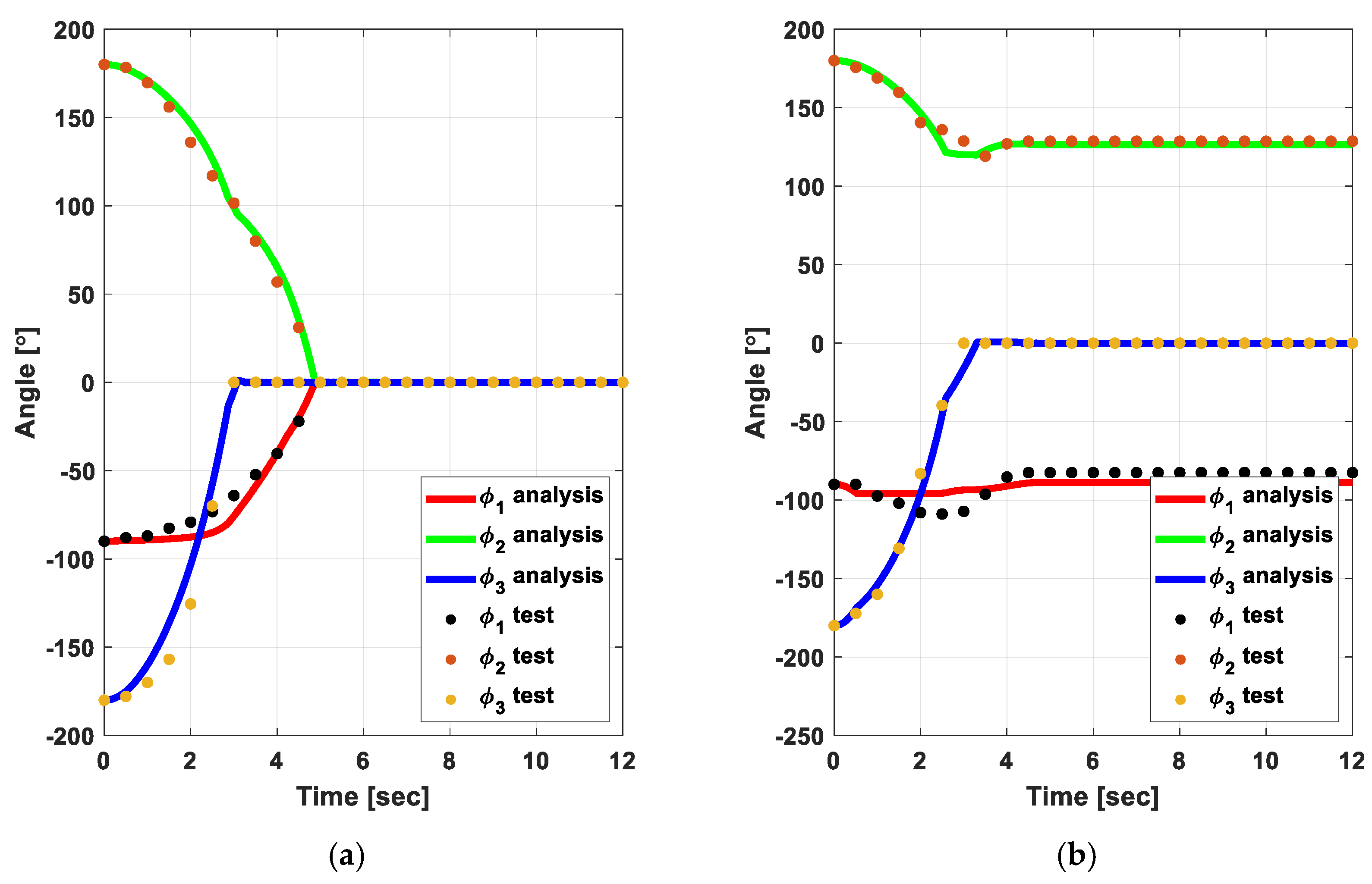
4. Results and Discussion
4.1. Multi-Body Dynamics Modeling of Solar Panels
4.2. Friction Torque Evaluation by Inverse Analysis
4.3. Validation of EFTs by Torque Margin Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fufa, B.; Zhao-Bo, C.; Wensheng, M. Modeling and simulation of satellite solar panel deployment and locking. InfTJ 2010, 9, 600–604. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-Y.; Lim, J.H.; Jang, T.-S.; Cha, W.H.; Lee, S.-J.; Oh, H.-U.; Kim, K.-W. Optimal design of stiffness of torsion spring hinge considering the deployment performance of large scale sar antenna. J. Aerosp. Syst. Eng. 2019, 13, 78–86. [Google Scholar]
- Kim, K.-W.; Park, Y. Solar array deployment analysis considering path-dependent behavior of a tape spring hinge. J. Mech. Sci. Technol. 2015, 29, 1921–1929. [Google Scholar] [CrossRef]
- Hoffait, S.; Brüls, O.; Granville, D.; Cugnon, F.; Kerschen, G. Dynamic analysis of the self-locking phenomenon in tape-spring hinges. Acta Astronaut. 2010, 66, 1125–1132. [Google Scholar] [CrossRef]
- Mobrem, M.; Adams, D.S. Deployment analysis of the lenticular jointed antennas onboard the mars express spacecraft. J. Spacecr. Rocket. 2009, 46, 394–402. [Google Scholar] [CrossRef]
- Mallikarachchi, H. Thin-walled composite deployable booms with tape-spring hinges. Ph.D. Thesis, University of Cambridge, Cambridge, UK, December 2011. [Google Scholar]
- Boesch, C.; Pereira, C.; John, R.; Schmidt, T.; Seifart, K.; Sparr, H.; Lautier, J.; Pyttel, T. Ultra light self-motorized mechanism for deployment of light weight spacecraft appendages. In Proceedings of the 39th Aerospace Mechanisms Symposium, Sunnyvale, CA, USA, 7–9 May 2008; pp. 7–9. [Google Scholar]
- Block, J.; Straubel, M.; Wiedemann, M. Ultralight deployable booms for solar sails and other large gossamer structures in space. Acta Astronaut. 2011, 68, 984–992. [Google Scholar] [CrossRef]
- Sickinger, C.; Herbeck, L.; Ströhlein, T.; Torrez-Torres, J. Lightweight deployable booms: Design, manufacture, verification, and smart materials application. In Proceedings of the 55th International Astronautical Congress of the International Astronautical Federation, the International Academy of Astronautics, and the International Institute of Space Law, Vancouver, BC, Canada, 4–8 October 2004. [Google Scholar]
- Lane, S.A.; Murphey, T.W.; Zatman, M. Overview of the innovative space-based radar antenna technology program. J. Spacecr. Rocket. 2011, 48, 135–145. [Google Scholar] [CrossRef]
- Yang, H.; Liu, R.; Wang, Y.; Deng, Z.; Guo, H. Experiment and multiobjective optimization design of tape-spring hinges. Struct. Multidiscip. Optim. 2015, 51, 1373–1384. [Google Scholar] [CrossRef]
- Seffen, K.; Pellegrino, S. Deployment dynamics of tape springs. Proceedings of the royal society of London. Series A: Mathematical. Phys. Eng. Sci. 1999, 455, 1003–1048. [Google Scholar] [CrossRef] [Green Version]
- Seffen, K.; Pellegrino, S. Deployment of a Rigid Panel by Tape-Springs; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Soykasap, Ö. Analysis of tape spring hinges. Int. J. Mech. Sci. 2007, 49, 853–860. [Google Scholar] [CrossRef]
- Walker, S.J.; Aglietti, G. Study of the dynamics of three dimensional tape spring folds. AIAA J. 2004, 42, 850–856. [Google Scholar] [CrossRef] [Green Version]
- Walker, S.J.; Aglietti, G.S. Experimental investigation of tape springs folded in three dimensions. AIAA J. 2006, 44, 151–159. [Google Scholar] [CrossRef] [Green Version]
- Jeong, J.W.; Yoo, Y.I.; Shin, D.K.; Lim, J.H.; Kim, K.W.; Lee, J.J. A novel tape spring hinge mechanism for quasi-static deployment of a satellite deployable using shape memory alloy. Rev. Sci. Instrum. 2014, 85, 025001. [Google Scholar] [CrossRef]
- Ye, H.; Zhang, Y.; Yang, Q.; Xiao, Y.; Grandhi, R.V.; Fischer, C.C. Optimal design of a three tape-spring hinge deployable space structure using an experimentally validated physics-based model. Struct. Multidiscip. Optim. 2017, 56, 973–989. [Google Scholar] [CrossRef]
- Ye, H.; Zhang, Y.; Yang, Q.; Zhang, B. Quasi-static analysis and multi-objective optimization for tape spring hinge. Struct. Multidiscip. Optim. 2019, 60, 2417–2430. [Google Scholar] [CrossRef]
- Hui, Y.; Ruipeng, Z.; Zhanwen, F.; Yan, W.; Rongqiang, L. Deploying dynamics experiment of tape-spring hinges for deployable mechanism. In Proceedings of the 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2017; pp. 106–110. [Google Scholar]
- Oberst, S.; Tuttle, S. Nonlinear dynamics of thin-walled elastic structures for applications in space. Mech. Syst. Signal Process. 2018, 110, 469–484. [Google Scholar] [CrossRef]
- Dewalque, F.; Schwartz, C.; Denoël, V.; Croisier, J.-L.; Forthomme, B.; Brüls, O. Experimental and numerical investigation of the nonlinear dynamics of compliant mechanisms for deployable structures. Mech. Systems Signal Process. 2018, 101, 1–25. [Google Scholar] [CrossRef]
- Picault, E.; Marone-Hitz, P.; Bourgeois, S.; Cochelin, B.; Guinot, F. A planar rod model with flexible cross-section for the folding and the dynamic deployment of tape springs: Improvements and comparisons with experiments. Int. J. Solids Struct. 2014, 51, 3226–3238. [Google Scholar] [CrossRef]
- Bai, J.-B.; Chen, D.; Xiong, J.-J.; Shenoi, R.A. Folding analysis for thin-walled deployable composite boom. Acta Astronaut. 2019, 159, 622–636. [Google Scholar] [CrossRef] [Green Version]
- Dewalque, F.; Rochus, P.; Brüls, O. Importance of structural damping in the dynamic analysis of compliant deployable structures. Acta Astronaut. 2015, 111, 323–333. [Google Scholar] [CrossRef]
- Kim, K.-W.; Park, Y. Systematic design of tape spring hinges for solar array by optimization method considering deployment performances. Aerosp. Sci. Technol. 2015, 46, 124–136. [Google Scholar] [CrossRef]
- Seo, J.-H.; Chae, J.-S.; Park, T.-W.; Han, S.-W.; Chai, J.-B.; Seo, H.-S. Solar panel deployment analysis of a satellite system. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2003, 46, 508–518. [Google Scholar] [CrossRef] [Green Version]
- Kwak, M.K.; Heo, S.; Kim, H.B. Dynamics of satellite with deployable rigid solar arrays. Multibody Syst. Dyn. 2008, 20, 271–286. [Google Scholar] [CrossRef]
- Moon, H.-Y.; Park, S. Development of deployment test equipment suitable for single large solar panel. J. Korean Soc. Aeronaut. Space Sci. 2018, 46, 583–591. [Google Scholar]
- FunctionBay, Recurdyn/solver Theoretical Manual. Available online: https://functionbay.com/documentation/onlinehelp/default.htm#!Documents/introduction.htm (accessed on 6 November 2020).
- Akima, H. A New Method of Interpolation and Smooth Curve Fitting Based on Local Procedures. J. ACM 1970, 17, 589–602. [Google Scholar] [CrossRef]
- A Two-Axis Digital Leveler. Available online: http://www.dong-do.co.kr (accessed on 6 November 2020).
- A Motion Capture Camera. Available online: http://www.qualisys.com (accessed on 6 November 2020).
- A Tape Measures. Available online: http://www.komelon.co.kr (accessed on 6 November 2020).
- Armstrong, B.; De Wit, C.C. Friction modeling and compensation. Control Handb. 1996, 77, 1369–1382. [Google Scholar]
- Postma, R.W. Force and torque margins for complex mechanical systems. In Proceedings of the 37th Aerospace Mechanisms Symposium, Galveston, TX, USA, 18–21 May 2004; p. 107. [Google Scholar]
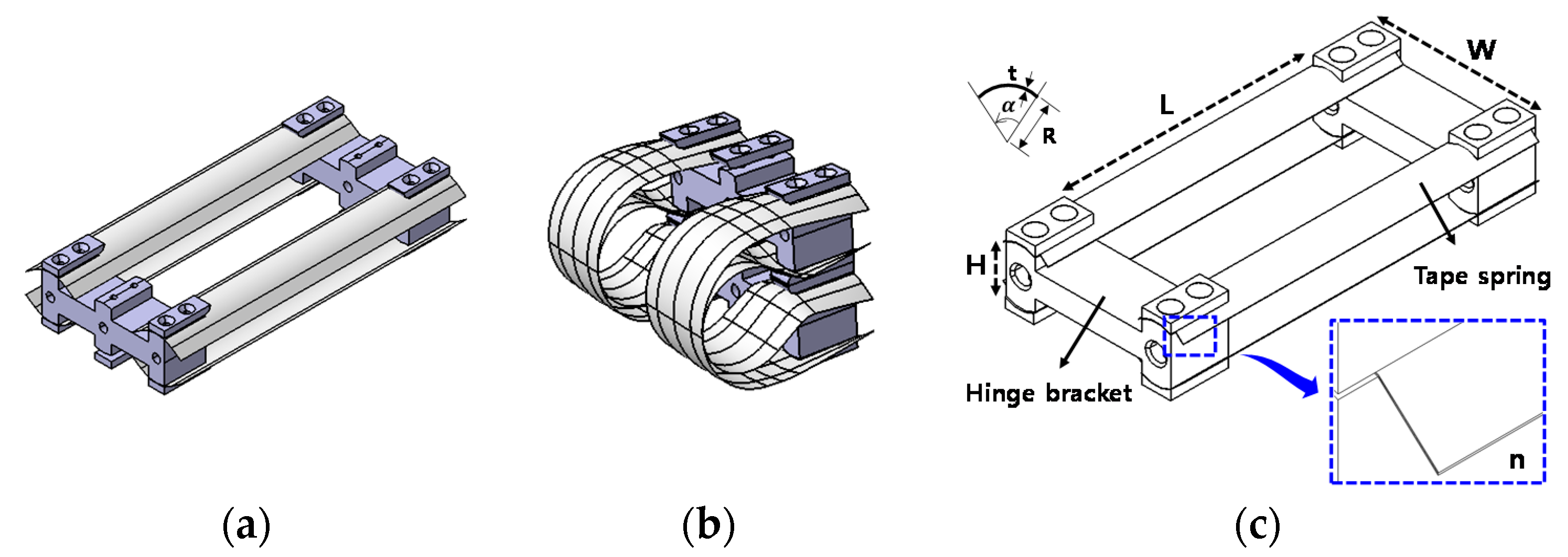


| TS Hinge-1 | TS Hinge-2 | TS Hinge-3 | |
|---|---|---|---|
| Figure |  |  |  |
| No. of tape layers (n) | 2 | 2 | 2 |
| No. of ribs | 3 | 2 | 2 |
| Dimension of TS hinges [mm] (L, W, H) | (98.2, 68.0, 29.0) | (98.2, 68.0, 29.0) | (98.2, 68.0, 29.0) |
| Dimension of TS (R, t, ) | (13 mm, 0.13 mm, 70°) | (13 mm, 0.13 mm, 70°) | (11.5 mm, 0.08 mm, 55°) |
| A | (1.1°, 69.39 N·m) | (1.26°, 58.20 N·m) | (1.08°, 33.43 N·m) |
| B | (1.1°, 1.50 N·m) | (1.28°, 0.86 N·m) | (1.15°, 0.46 N·m) |
| C (180°) | (180°, 2.32 N·m) | (180°, 1.46 N·m) | (180°, 0.74 N·m) |
| D | (0.52°, 37.0 N·m) | (0.65°, 26.0 N·m) | (0.29°, 11.07 N·m) |
| M (90°) | (90°, 1.20 N·m) | (90°, 0.80 N·m) | (90°, 0.385 N·m) |
| Test Case | Hinge-1 (90° Hinge) | Hinge-2 (180° Hinge) | Hinge-3 (180° Hinge) | Remarks | ||
|---|---|---|---|---|---|---|
| T01 |  3.6 Nm (3 × 1.2) | > |  2.92 Nm (2 × 1.46) | > |  1.48 Nm (2 × 0.74) | Normal case |
| T02 |  0.77 Nm (2 × 0.385) | < |  2.92 Nm (2 × 1.46) | > |  1.48 Nm (2 × 0.74) | Worst case |
| Dummy Solar Open Panel | ||
|---|---|---|
| Figure |  | |
| Mass | 3.5 kg | |
| Moment of inertia[kg∙mm2] | ||
| Dimension | 800 mm 800 mm 20 mm | |
| Joint Type | No. of Constraint | No. of Active DOFs |
|---|---|---|
| Fixed | Trans () = 3 Rot () = 3 | 0 |
| Revolute | Trans = 3, Rot = 2 | Rot = 1 |
| Translational | Trans = 2, Rot = 3 | Trans = 1 |
| Spherical | Trans = 3, Rot = 0 | Rot = 3 |
| Test ID | Joint | Driving Torque [N·m] | Friction Torque [N·m] | Torque Margin [%] | Deployment Test Pass/Fail | Deployment Analysis Pass/Fail |
|---|---|---|---|---|---|---|
| T01 | Joint-1 | 3.6 (3 × 1.2) | 2.63 | 38.0 | Pass | Pass |
| Joint-2 | 2.92 (2 × 1.46) | 1.7 | 71.8 | |||
| Joint-3 | 1.48 (2 × 0.74) | 0.001 | 1479 | |||
| T02 | Joint-1 | 0.77 (2 × 0.385) | 2.63 | −70.7 | Fail | Fail |
| Joint-2 | 2.92 (2 × 1.46) | 1.7 | 71.8 | |||
| Joint-3 | 1.48 (2 × 0.74) | 0.001 | 1479 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-Y.; Choi, H.-S.; Lim, J.H.; Kim, K.-W.; Jeong, J. Experimental and Numerical Investigation of Solar Panels Deployment with Tape Spring Hinges Having Nonlinear Hysteresis with Friction Compensation. Appl. Sci. 2020, 10, 7902. https://doi.org/10.3390/app10217902
Kim D-Y, Choi H-S, Lim JH, Kim K-W, Jeong J. Experimental and Numerical Investigation of Solar Panels Deployment with Tape Spring Hinges Having Nonlinear Hysteresis with Friction Compensation. Applied Sciences. 2020; 10(21):7902. https://doi.org/10.3390/app10217902
Chicago/Turabian StyleKim, Dong-Yeon, Han-Sol Choi, Jae Hyuk Lim, Kyung-Won Kim, and Juwon Jeong. 2020. "Experimental and Numerical Investigation of Solar Panels Deployment with Tape Spring Hinges Having Nonlinear Hysteresis with Friction Compensation" Applied Sciences 10, no. 21: 7902. https://doi.org/10.3390/app10217902






