Numerical Simulations of Novel Conning Designs for Future Super-Large Wind Turbines
Abstract
1. Introduction
2. Modeling and Methods
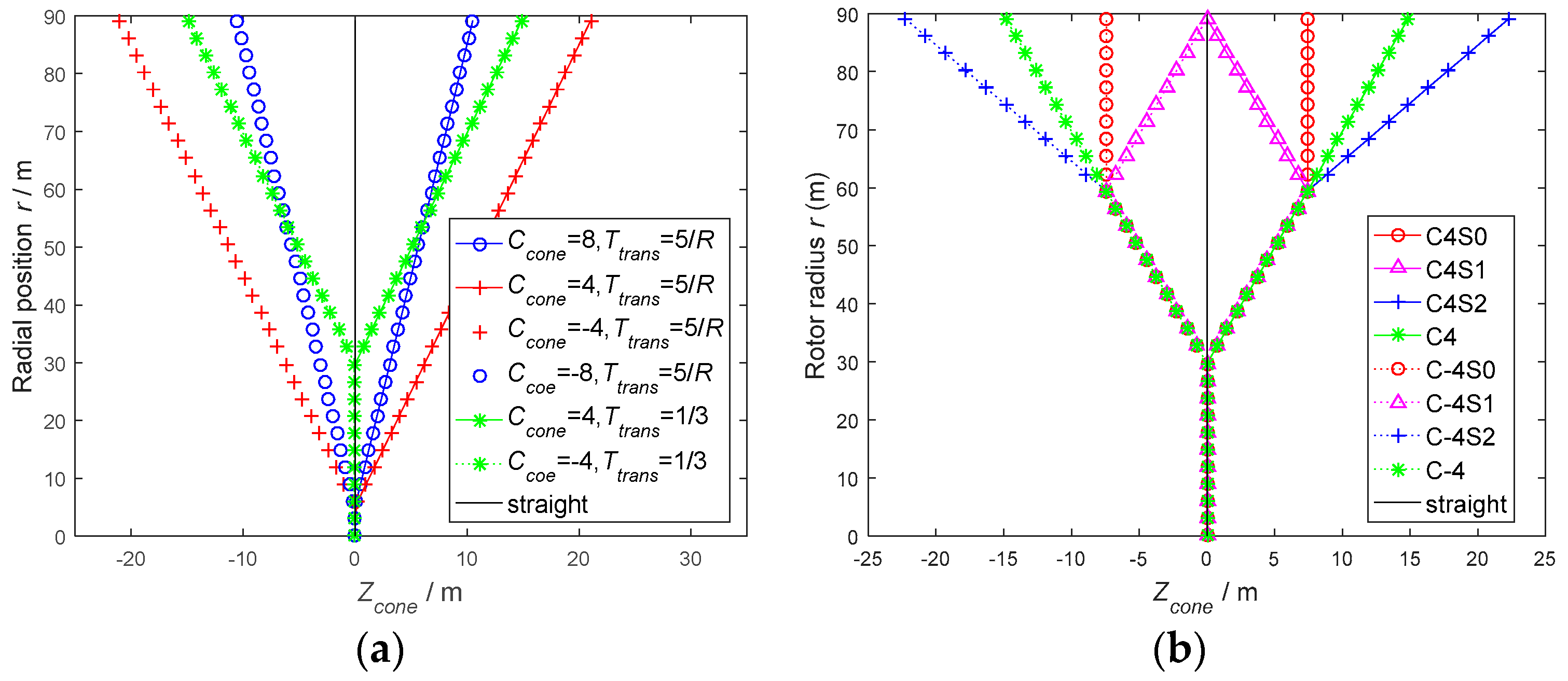
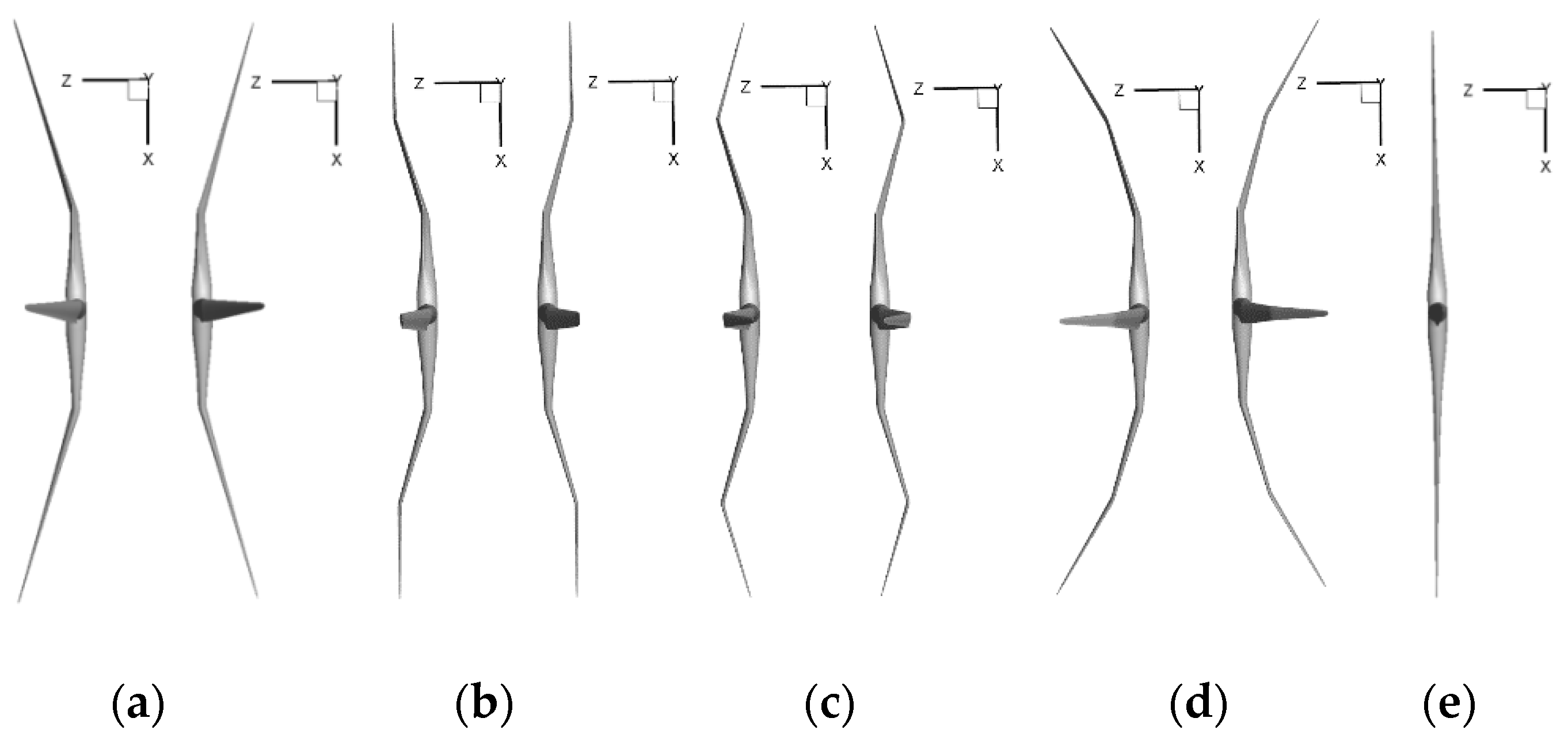
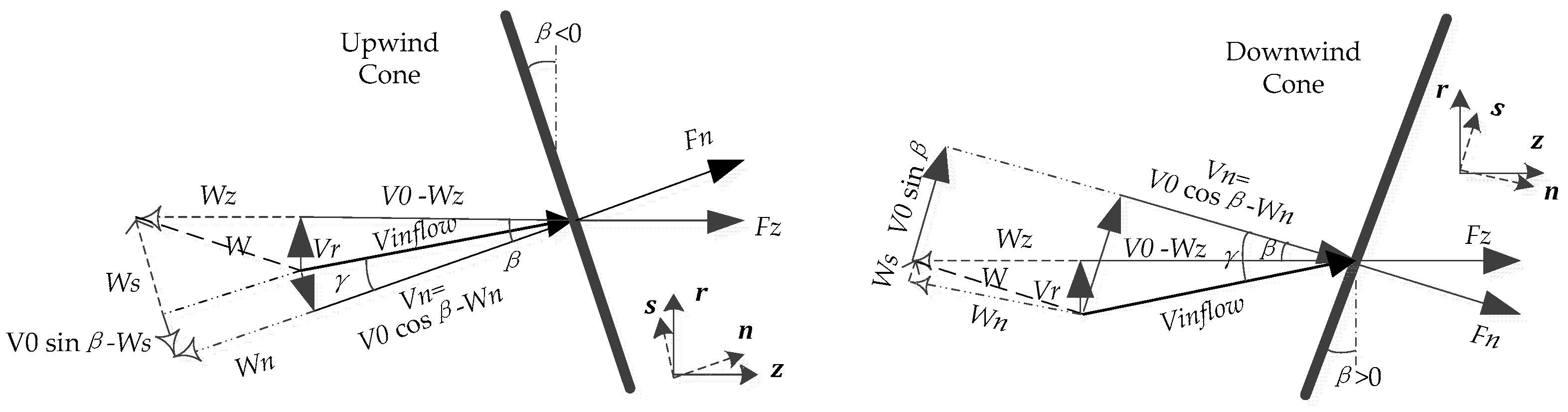
2.1. Modelling of Different Cone Configurations
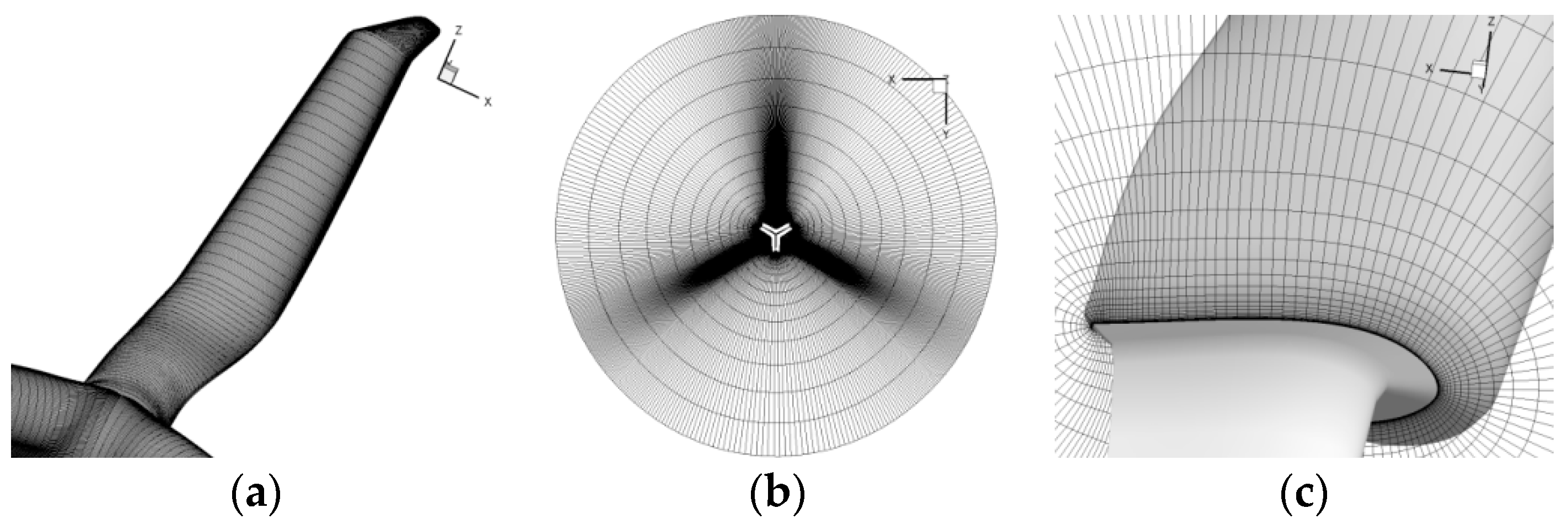
2.2. Mesh Structure and CFD Method
3. Results and Discussions
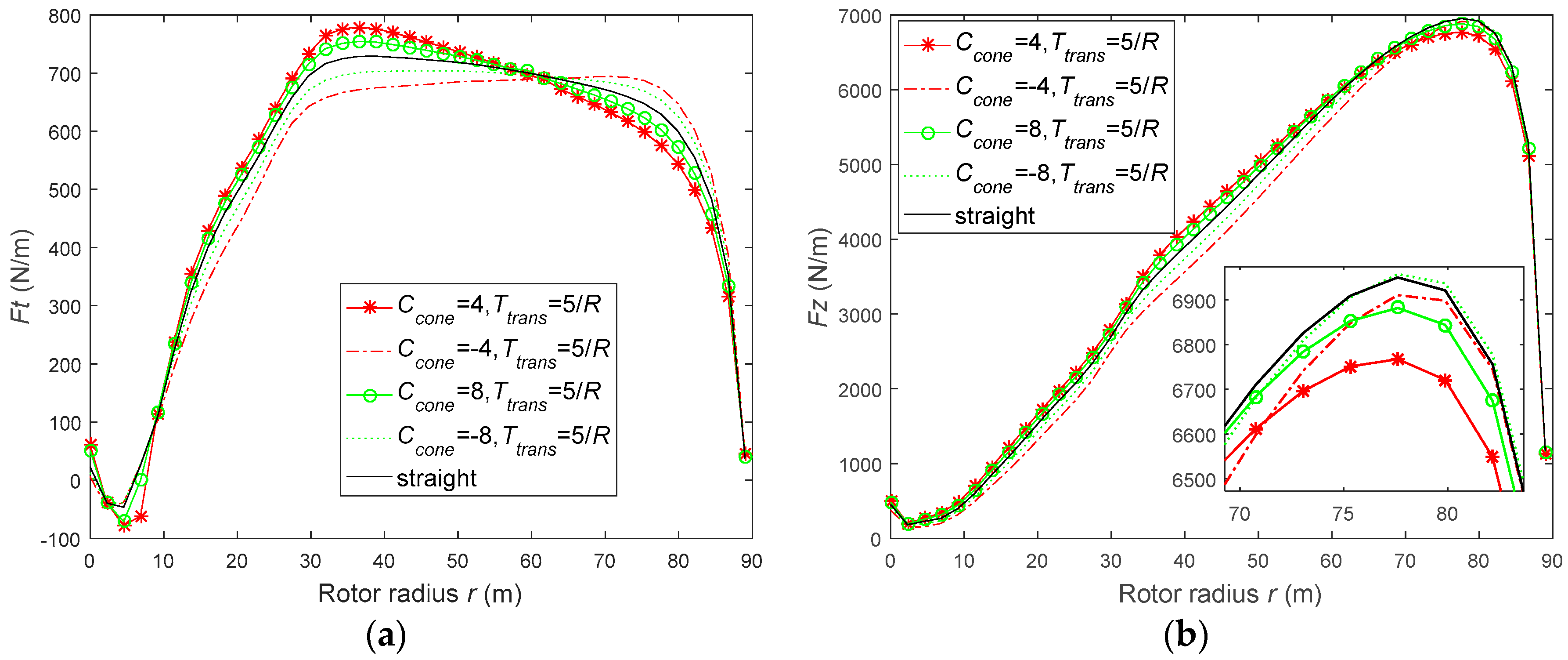
3.1. Four Configurations of Coning Near the Root: Ttrans = 5/R and Ccone = ±4, ±8
3.1.1. Force Performances
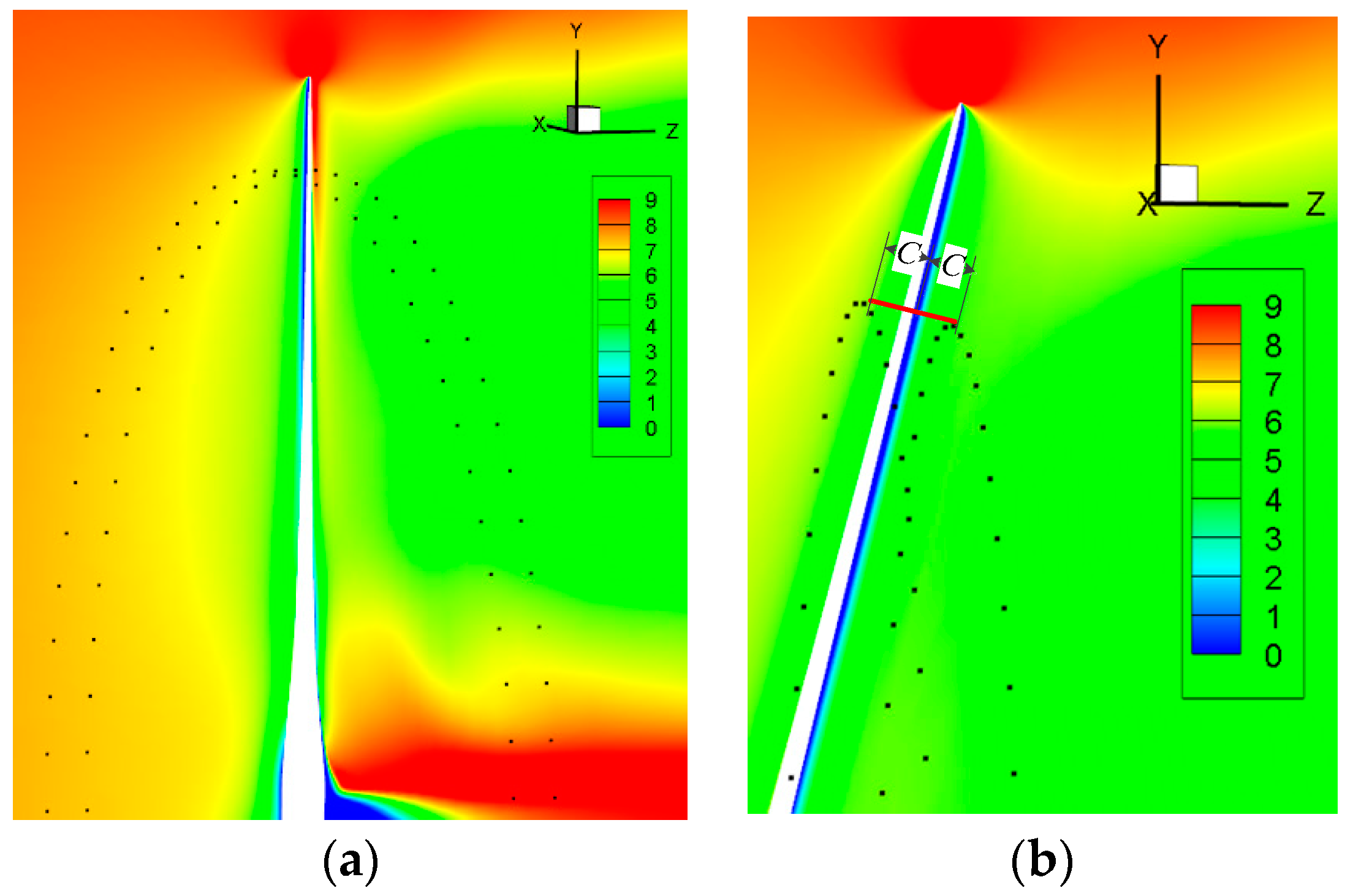
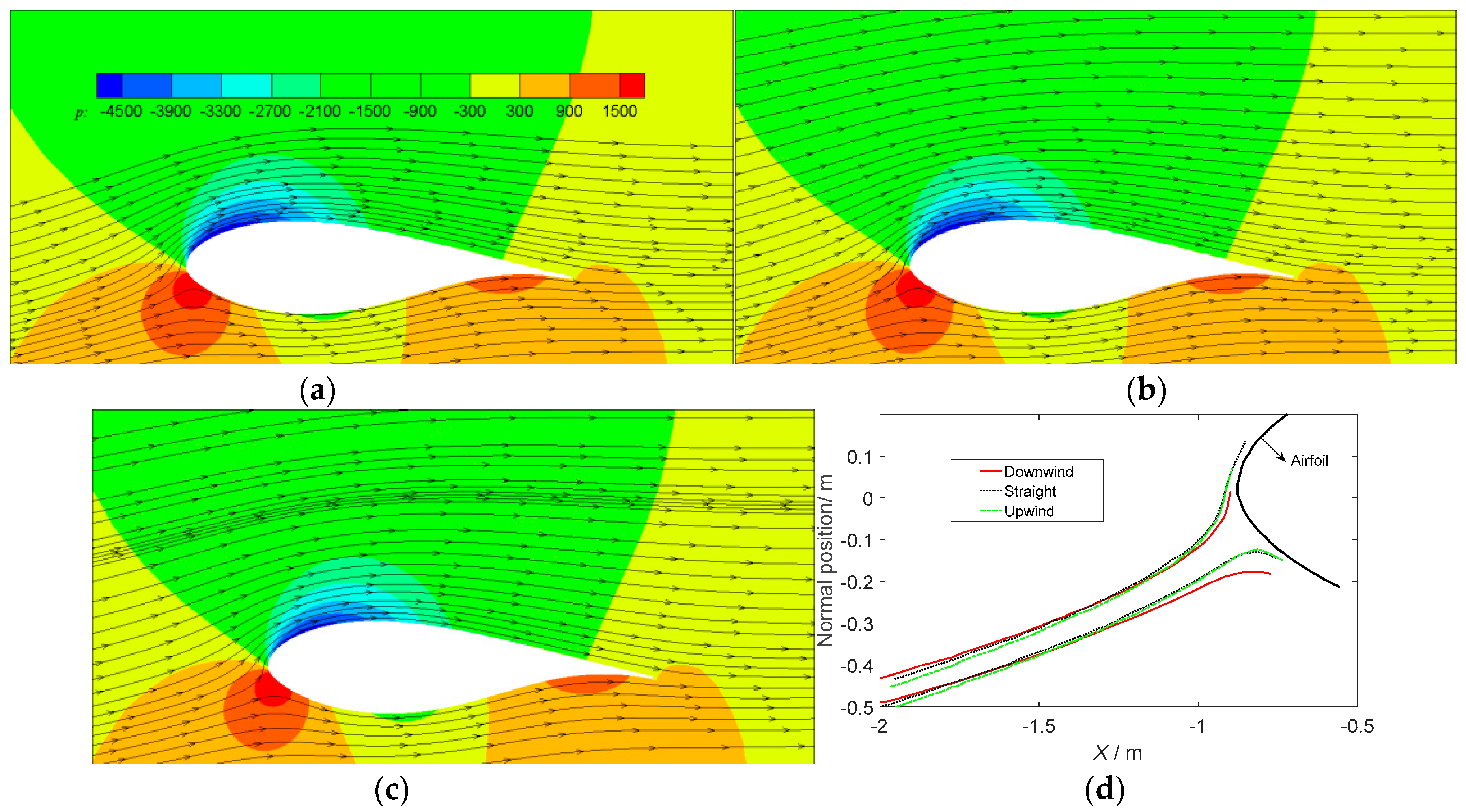
3.1.2. Flow Field Analysis
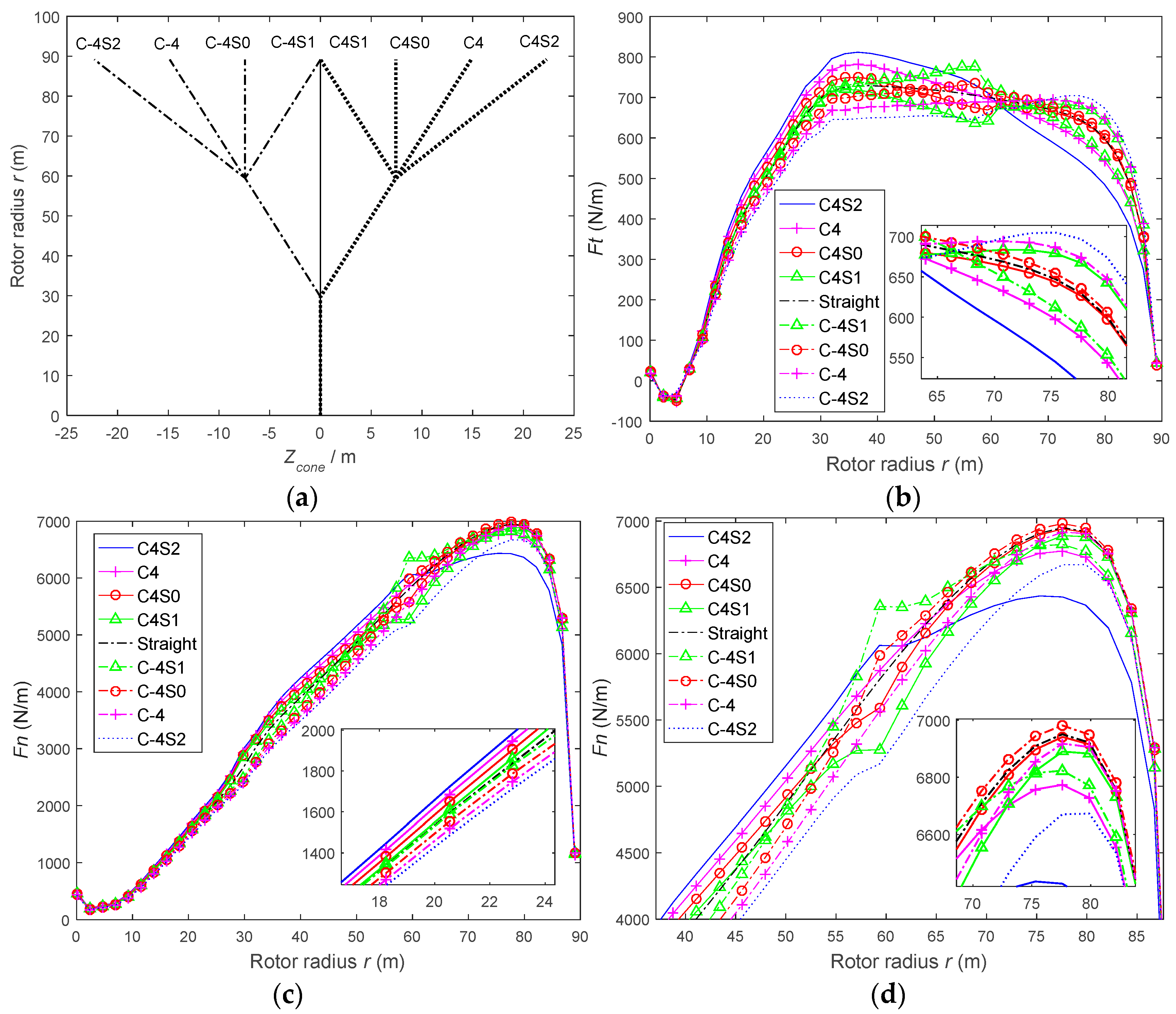
3.2. Special Coned Configurations: C4S0, C4S1, C4S2, C4, C-4S0, C-4S1, C-4 S2 and C-4
3.2.1. Overall Force Performance
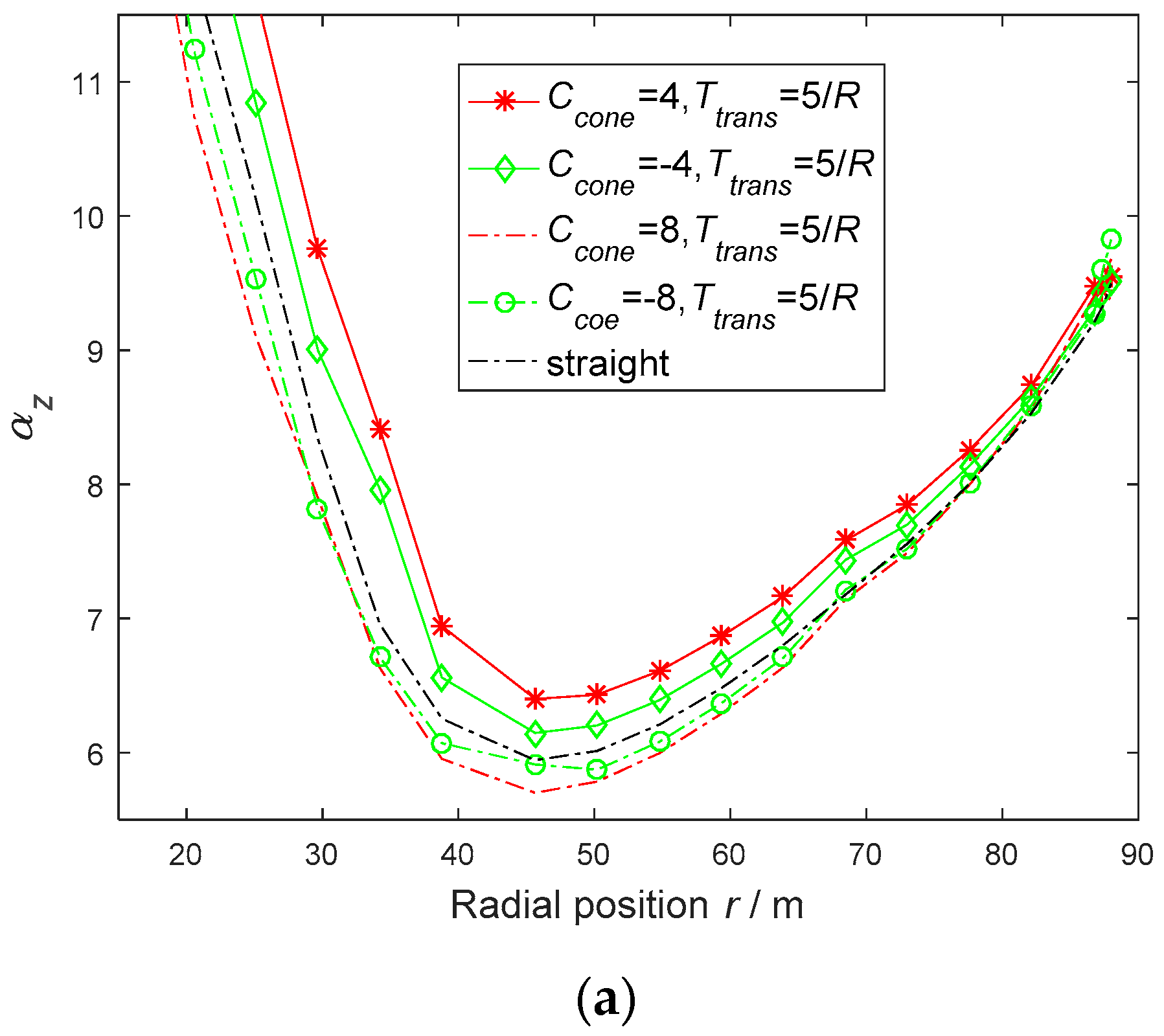
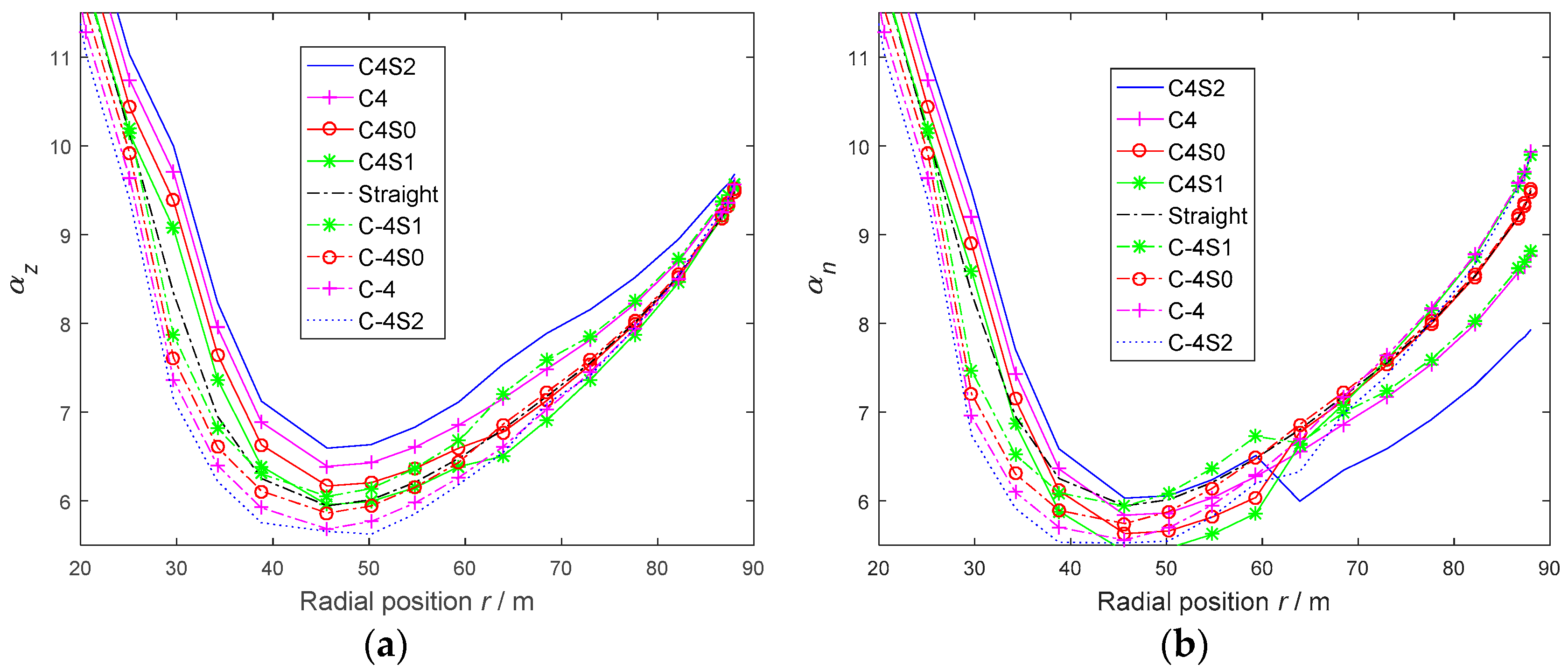
3.2.2. Distributed Force Performances
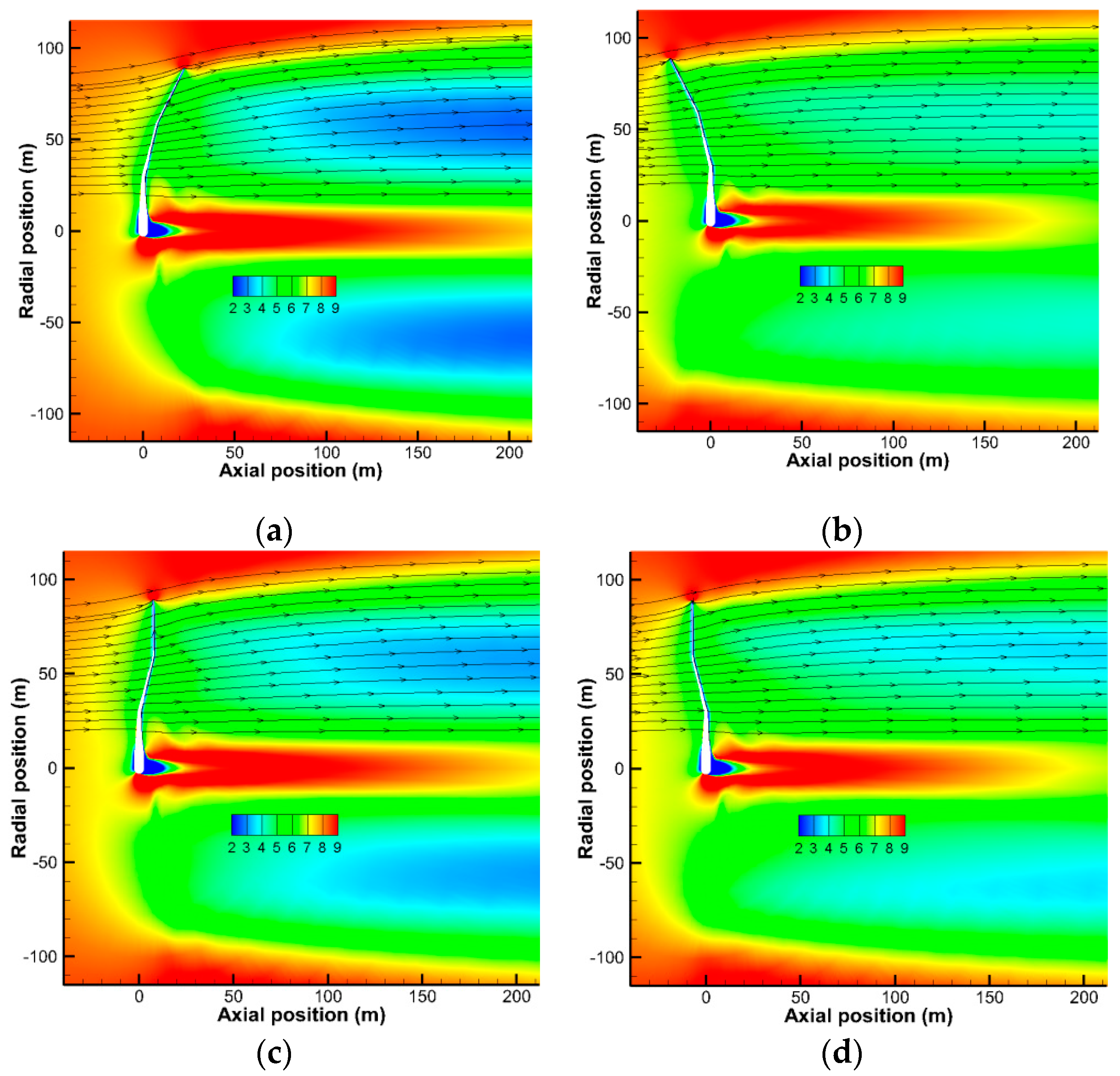
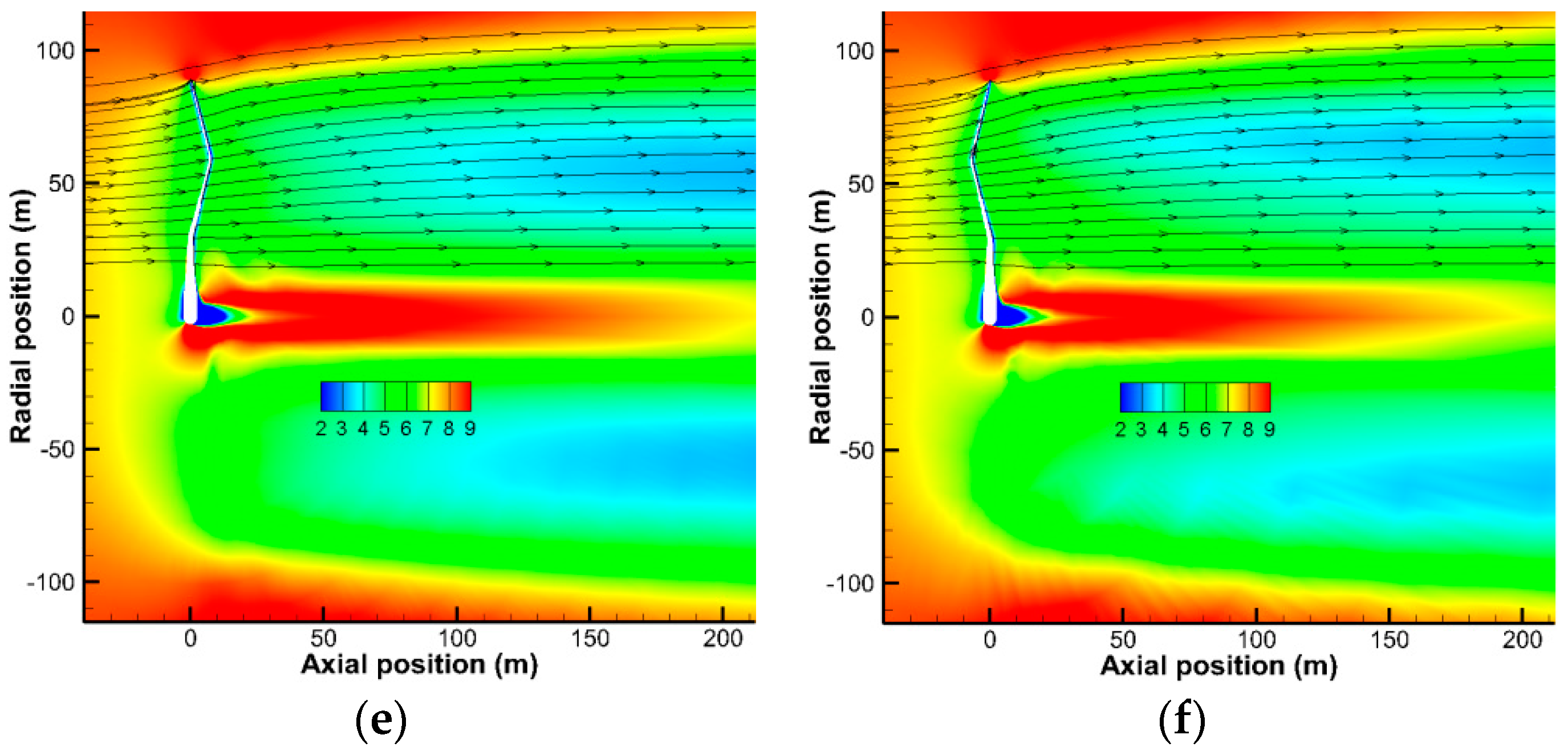
3.2.3. Flow Field Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fingersh, L.; Hand, M.; Laxson, A. Wind Turbine Design Cost and Scaling Model; Office of Scientific and Technical Information (OSTI): Oak Ridge, TN, USA, 2006.
- Loth, E.; Steele, A.; Ichter, B.; Selig, M.; Moriarty, P.J. Segmented Ultralight Pre-Aligned Rotor for Extreme-Scale Wind Turbines. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef][Green Version]
- Barlas, T.K.; Van Kuik, G.A.M. Review of state of the art in smart rotor control research for wind turbines. Prog. Aerosp. Sci. 2010, 46, 1–27. [Google Scholar] [CrossRef]
- Barnes, R.; Morozov, E. Structural optimisation of composite wind turbine blade structures with variations of internal geometry configuration. Compos. Struct. 2016, 152, 158–167. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Q.; Shen, W.; Pang, X.; Li, S.; Guo, X. Structural optimization study of composite wind turbine blade. Mater. Des. 2013, 46, 247–255. [Google Scholar] [CrossRef]
- Sun, Z.; Sessarego, M.; Chen, J.; Shen, W. Design of the OffWindChina 5 MW Wind Turbine Rotor. Energies 2017, 10, 777. [Google Scholar] [CrossRef]
- Crawford, C.; Platts, J. Updating and Optimization of a Coning Rotor Concept. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 9–12 January 2006; pp. 9–12. [Google Scholar] [CrossRef]
- Steele, A.; Ichter, B.; Qin, C.; Loth, E.; Selig, M.; Moriarty, P. Aerodynamics of an Ultra light Load-Aligned Rotor for Extreme-Scale Wind Turbines. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Noyes, C.; Qin, C.; Loth, E. Pre-aligned downwind rotor for a 13.2 MW wind turbine. Renew. Energy 2018, 116, 749–754. [Google Scholar] [CrossRef]
- Noyes, C.; Qin, C.; Loth, E. Analytic analysis of load alignment for coning extreme-scale rotors. Wind. Energy 2020, 23, 357–369. [Google Scholar] [CrossRef]
- Qin, C.; Loth, E.; Zalkind, D.S.; Pao, L.Y.; Yao, S.; Griffith, D.T.; Selig, M.S.; Damiani, R. Downwind coning concept rotor for a 25 MW offshore wind turbine. Renew. Energy 2020, 156, 314–327. [Google Scholar] [CrossRef]
- Wanke, G.; Bergami, L.; Larsen, T.J.; Hansen, M.H. Changes in design driving load cases: Operating an upwind turbine with a downwind rotor configuration. Wind. Energy 2019, 22, 1500–1511. [Google Scholar] [CrossRef]
- Bortolotti, P.; Kapila, A.; Bottasso, C.L. Comparison between upwind and downwind designs of a 10 MW wind turbine rotor. Wind. Energy Sci. 2019, 4, 115–125. [Google Scholar] [CrossRef]
- Ning, A.; Petch, D. Integrated design of downwind land-based wind turbines using analytic gradients. Wind. Energy 2016, 19, 2137–2152. [Google Scholar] [CrossRef]
- Mikkelsen, R.; Sørensen, J.N.; Shen, W.Z. Modelling and analysis of the flow field around a coned rotor. Wind. Energy 2001, 4, 121–135. [Google Scholar] [CrossRef]
- Madsen, H.A.; Bak, C.; Døssing, M.; Mikkelsen, R.F.; Øye, S. Validation and modification of the Blade Element Momentum theory based on comparisons with actuator disc simulations. Wind. Energy 2010, 13, 373–389. [Google Scholar] [CrossRef]
- Crawford, C. Re-examining the precepts of the blade element momentum theory for coning rotors. Wind. Energy 2006, 9, 457–478. [Google Scholar] [CrossRef]
- Madsen, H.A.; Rasmussen, F. The influence on energy conversion and induction from large blade deflections. In Proceedings of the 1999 European Wind Energy Conference and Exhibition, Nice, France, 1–5 March 1999. [Google Scholar]
- Farhan, A.; Hassanpour, A.; Burns, A.; Motlagh, Y.G. Numerical study of effect of winglet planform and airfoil on a horizontal axis wind turbine performance. Renew. Energy 2019, 131, 1255–1273. [Google Scholar] [CrossRef]
- Chattot, J.-J. Effects of blade tip modifications on wind turbine performance using vortex model. Comput. Fluids 2009, 38, 1405–1410. [Google Scholar] [CrossRef]
- Shen, X.; Chen, J.-G.; Zhu, X.-C.; Liu, P.-Y.; Du, Z.-H. Multi-objective optimization of wind turbine blades using lifting surface method. Energy 2015, 90, 1111–1121. [Google Scholar] [CrossRef]
- Xie, W.; Zeng, P.; Lei, L. A novel folding blade of wind turbine rotor for effective power control. Energy Convers. Manag. 2015, 101, 52–65. [Google Scholar] [CrossRef]
- Kress, C.; Chokani, N.; Abhari, R. Downwind wind turbine yaw stability and performance. Renew. Energy 2015, 83, 1157–1165. [Google Scholar] [CrossRef]
- Kress, C.; Chokani, N.; Abhari, R.S. Design Considerations of rotor cone angle for downwind wind turbines. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, W.; Shen, W.; Zhong, W.; Cao, J.; Tao, Q. Aerodynamic Analysis of Coning Effects on the DTU 10 MW Wind Turbine Rotor. Energies 2020, 13, 5753. [Google Scholar] [CrossRef]
- Zahle, F.; Bak, C.; Sørensen, N.N.; Guntur, S.; Troldborg, N. Comprehensive Aerodynamic Analysis of a 10 MW Wind Turbine Rotor Using 3D CFD. In Proceedings of the 32nd ASME Wind Energy Symposium, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- The DTU 10MW Reference Wind Turbine Project Site. Available online: https://rwt.windenergy.dtu.dk/dtu10mw/dtu-10mw-rwt (accessed on 6 November 2018).
- Jost, E.; Lutz, T.; Krämer, E. Steady and Unsteady CFD Power Curve Simulations of Generic 10 MW Turbines. In Proceedings of the 11th EAWE PhD Seminar on Wind Energy in Europe, Stuttgart, Germany, 23–25 September 2015. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Sørensen, N.N. General Purpose Flow Solver Applied to Flow over Hills. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, September 1995. [Google Scholar]
- Jost, E.; Klein, L.; Leipprand, H.; Lutz, T.; Krämer, E. Extracting the angle of attack on rotor blades from CFD simulations. Wind. Energy 2018, 21, 807–822. [Google Scholar] [CrossRef]
- Rahimi, H.; Schepers, J.; Shen, W.; García, N.R.; Schneider, M.; Micallef, D.; Ferreira, C.S.; Jost, E.; Klein, L.; Herráez, I. Evaluation of different methods for determining the angle of attack on wind turbine blades with CFD results under axial inflow conditions. Renew. Energy 2018, 125, 866–876. [Google Scholar] [CrossRef]
- Hansen, M.O.; Sørensen, N.N.; Michelsen, J. Extraction of lift, drag and angle of attack from computed 3-D viscous flow around a rotating blade. In Proceedings of the 1997 European Wind Energy Conference, Dublin, Ireland, 6–9 October 1997. [Google Scholar]



| Wind Speed (m/s) | Pitch (Degree) | Rotational Speed (RPM) |
|---|---|---|
| 9.000 | 0.000 | 7.229 |
| Straight | Ccone = 8 | Ccone = −8 | Ccone = 4 | Ccone = −4 | |
|---|---|---|---|---|---|
| T(KN) δT | 1046.06 | 1057.24 | 1025.85 | 1060.77 | 998.63 |
| 0.00% | 1.07% | −1.93% | 1.41% | −4.53% | |
| Q(KNm) δQ | 7283.11 | 7254.96 | 7268.08 | 7195.15 | 7205.48 |
| 0.00% | −0.39% | −0.21% | −1.21% | −1.07% | |
| QT(m) δQT | 6.96 | 6.86 | 7.08 | 6.78 | 7.22 |
| 0.00% | −1.44% | 1.76% | −2.58% | 3.63% |
| Straight | C4S2 | C4 | C4S0 | C4S1 | C-4S1 | C-4S0 | C-4 | C-4S2 | |
|---|---|---|---|---|---|---|---|---|---|
| T(KN) δT | 1046.06 | 1051.37 | 1061.10 | 1054.99 | 1032.59 | 1040.55 | 1031.22 | 1005.89 | 969.73 |
| 0% | 0.51% | 1.44% | 0.85% | −1.29% | −0.53% | −1.42% | −3.84% | −7.30% | |
| Q(KNm) δQ | 7283.11 | 7055.26 | 7197.34 | 7261.64 | 7254.33 | 7250.16 | 7280.18 | 7242.09 | 7140.14 |
| 0% | −3.13% | −1.18% | −0.29% | −0.40% | −0.45% | −0.04% | −0.56% | −1.96% | |
| QT(m) δQT | 6.96 | 6.71 | 6.78 | 6.88 | 7.03 | 6.97 | 7.06 | 7.20 | 7.36 |
| 0% | −3.62% | −2.58% | −1.14% | 0.90% | 0.07% | 1.40% | 3.41% | 5.75% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Zhu, W.; Shen, W.; Tao, Q.; Cao, J.; Li, X. Numerical Simulations of Novel Conning Designs for Future Super-Large Wind Turbines. Appl. Sci. 2021, 11, 147. https://doi.org/10.3390/app11010147
Sun Z, Zhu W, Shen W, Tao Q, Cao J, Li X. Numerical Simulations of Novel Conning Designs for Future Super-Large Wind Turbines. Applied Sciences. 2021; 11(1):147. https://doi.org/10.3390/app11010147
Chicago/Turabian StyleSun, Zhenye, Weijun Zhu, Wenzhong Shen, Qiuhan Tao, Jiufa Cao, and Xiaochuan Li. 2021. "Numerical Simulations of Novel Conning Designs for Future Super-Large Wind Turbines" Applied Sciences 11, no. 1: 147. https://doi.org/10.3390/app11010147
APA StyleSun, Z., Zhu, W., Shen, W., Tao, Q., Cao, J., & Li, X. (2021). Numerical Simulations of Novel Conning Designs for Future Super-Large Wind Turbines. Applied Sciences, 11(1), 147. https://doi.org/10.3390/app11010147








