A Theoretical Model with Which to Safely Optimize the Configuration of Hydraulic Suspension of Modular Trailers in Special Road Transport

Abstract

The dimensions and weight of machines, structures, and components that need to be transported safely by road are growing constantly. One of the safest and most widely used transport systems on the road today due to their versatility and configuration are modular trailers. These trailers have hydraulic pendulum axles that are that are attached in pairs to the rigid platform above. In turn, these modular trailers are subject to limitations on the load that each axle carries, the tipping angle, and the oil pressure of the suspension system in order to guarantee safe transport by road. Optimizing the configuration of these modular trailers accurately and safely is a complex task. Factors to be considered include the load’s characteristics, the trailer’s mechanical properties, and road route conditions including the road’s slope and camber, precipitation and direction, and force of the wind. This paper presents a theoretical model that can be used for the optimal configuration of hydraulic cylinder suspension of special transport by road using modular trailers. It considers the previously mentioned factors and guarantees the safe stability of road transport. The proposed model was validated experimentally by placing a nacelle wind turbine at different points within a modular trailer. The weight of the wind turbine was 42,500 kg and its dimensions were 5133 × 2650 × 2975 mm. Once the proposed model was validated, an optimization algorithm was employed to find the optimal center of gravity for load, number of trailers, number of axles, oil pressures, and hydraulic configuration. The optimization algorithm was based on the iterative and automatic testing of the proposed model for different positions on the trailer and different hydraulic configurations. The optimization algorithm was tested with a cylindrical tank that weighed 108,500 kg and had dimensions of 19,500 × 3200 × 2500 mm. The results showed that the proposed model and optimization algorithm could safely optimize the configuration of the hydraulic suspension of modular trailers in special road transport, increase the accuracy and reliability of the calculation of the load configuration, save time, simplify the calculation process, and be easily implemented.

1. Introduction

There is a strong relationship between the special transport sector and manufacturers of products that are bulky and heavy. Such products include electricity transformers, metal castings, aircraft components, and wind-generator parts. The manufacturers of these products require the means to transport larger and heavier loads. An item’s weight or maximum dimensions are often determined by the transport’s constraints rather than manufacturing capacity. The infrastructure may determine the maximum loads that vehicles that are allowed to carry. The infrastructure includes the roads, regulations, capacity of roads or canals, or the load bearing capacity of vehicles [1,2]. Some types of loads are transported by water to minimize traffic congestion and disruption on the roads [3]. This occurs particularly when enterprises have convenient access to water. Not all countries have long, internal waterways, such as Europe’s Rhine and Garonne rivers. Therefore, most special loads in such countries are transported by road [4].

The safety of trailers as they travel around curves has been analyzed extensively previously. The effect of axle spacing, the load and the height of the center of gravity height on heavy trucks’ stability and handling properties have been studied [5,6,7,8]. Other works [9,10,11,12] have revealed significant influence of loading and suspension stiffness on tractor-semitrailer yaw stability. That revelation involved theoretical models, simulations by computer, and full-scale tests. The theoretical transversal acceleration of a truck as it enters a horizontal curve is commonly calculated as follows [13]:

$$a_T=\frac{v^2}{g·R}\pm k$$

(1)

With g for the acceleration of gravity, v as the truck’s speed, R as the radius of the curve, and k as the side-slope. However, the equation does not include several other factors that affect the truck in actual operating conditions. These include the force of the wind and the slope of the road. The authors discovered that the lateral acceleration of a 5-axle trailer briefly exceeded the expected values. An earlier study [14] found that the rollover threshold for various articulated vehicles ranges from 0.33 to 0.54 g, according to the dimensions and weight of the load. Other authors [15] determined when the vehicle might roll over and developed a dynamic rollover threshold. The critical lateral accelerations that these authors determined range from 0.28 to 0.42 g according to the height of the center of gravity (CoG). These are in agreement with the values that earlier studies have provided [14,16,17]. In addition, the British Standard [18] describes blocking and lashing procedures for securing loads. It established coefficients of 0.8 for forward direction (braking) and 0.5 for backward (acceleration) and sideways (turning) directions. It does not relate these coefficients to the speed or consider the inclination of the road or force of the wind. This means that the coefficients cover all of these phenomena.

The aerodynamic forces on a truck affect the performance in various ways [19,20,21]. Forces acting on the side increase the roll instability like the lateral acceleration in curve driving does. Furthermore, the longitudinal force affects the speed and acceleration of the truck and, consequently, its fuel consumption [22]. When a standard heavy truck drives at a speed of 70 mph, 65% of its fuel consumption, it has been estimated, is used to overcome the aerodynamic force [23]. Aerodynamic forces usually have a significant effect on the stability of abnormal loads. These forces are caused by the truck’s movement relative to the air. They emanate from the truck’s body, the chassis, the suspension, the axles, the wheels, the trailer, the load, and the space between the truck and trailer or payload. The drag equation below is generally used to calculate the aerodynamic forces:

$$F_D=\frac{1}{2}·\rho ·v_w^2·A·C_d$$

(2)

with F_D as the drag force, ρ as the fluid density, v_w as the velocity of the air relative to the truck, A as the area that is vertical to the relative motion and C_d as the drag coefficient. The drag coefficient depends on the relative position and geometry of the payload. However, the equation is accurate only for isolated objects. It is normally employed for basic load shapes. The actual truck–trailer configuration can increase the aerodynamic forces. The greatest contributor to the longitudinal aerodynamic force acting in commercial tractor-trailer configurations is the space between tractor and semitrailer [22,23]. The space is expressed by $b/\sqrt{A}$, a non-dimensional form, in which b is the width of the space (gap) and A is the area. The drag force that the gap produces is zero for small gaps. It increases suddenly when $b/\sqrt{A}\approx 0.5$, but becomes stable at 0.7 [22,23]. The other parameter that raises the drag force is the yaw angle, especially in trucks that have sharp-edged cabs. Crosswinds on exposed highways and bridges can cause difficulties in driving in tall and long vehicles and the risk of a serious accident. The force of the crosswind on a conventional truck–trailer in North America as it crosses a bridge was examined by using Computational Fluid Dynamics (CFD) [24]. The authors validated the model with experimental data that previous studies had provided [25,26]. The conclusion was that wind pressure can be sufficient to overturn the truck–semitrailer at the wind speeds that were studied.

This paper describes a novel theoretical model that can determine the stability of special transport. The proposed model determines the load on each axle, the tipping angle, and the suspension system’s oil pressure. It was based on modular trailers models that appear in the literature, as well as those in common use within the heavy transport sector [27]. The model was tested experimentally by a full scale test [28] in which oil pressure data and output from the model were compared. To conduct the test, a nacelle wind turbine that weighed 42,500 kg and was 5133 × 2650 × 2975 mm in length, width, and height, respectively, was placed at different points within a modular trailer. With the validated theoretical model, a proposed optimization algorithm is capable of determining the optimal CoG of the load, as well as the number of trailers, number of axles, oil pressures, and hydraulic configuration. The theoretical model and optimization algorithm were tested with a cylindrical tank that weighed 108,500 kg and had dimensions of 19,500 × 3200 × 2500 mm. The results showed that the optimization algorithm could safely optimize the configuration of the hydraulic suspension of modular trailers in special road transport, increase the accuracy and reliability of the calculation of the load configuration, save time, simplify the calculation process, and be easily implemented. The theoretical model and the optimization algorithm proposed are able to (1) optimize safely the configuration of modular trailers’ hydraulic suspension in special road transport, (2) improve the reliability and accuracy of load configuration calculations, (3) saves time, (4) simplify the calculation process, and (5) be easily implemented.

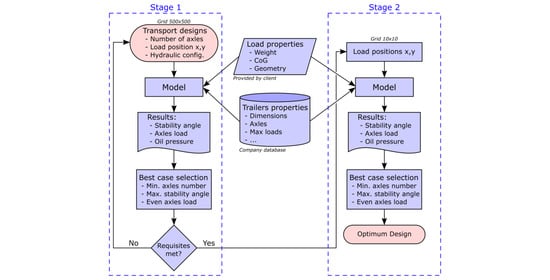
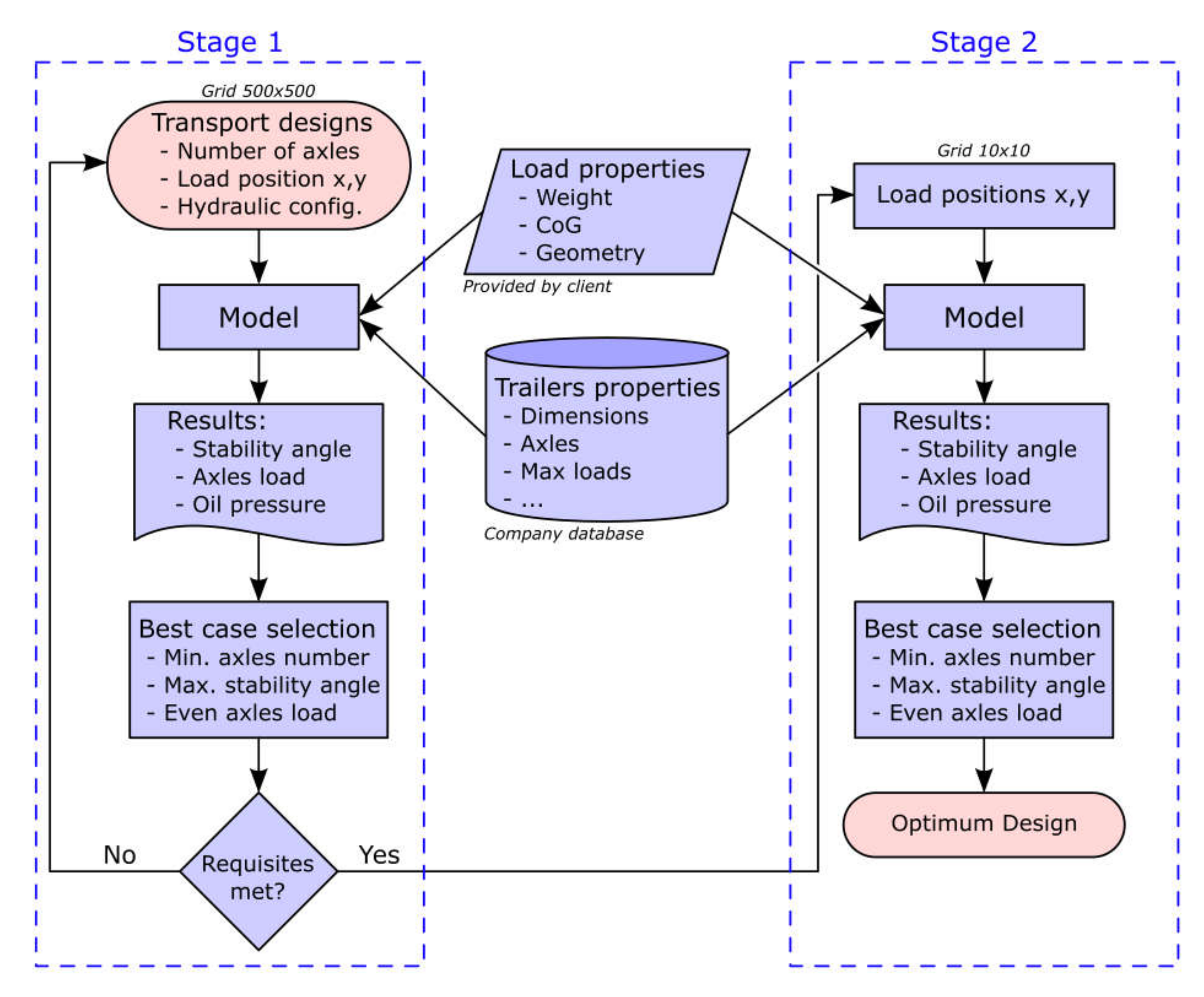
2. Materials and Methods

2.1. Modular Trailers

This work concentrates on the transport of heavy and voluminous payloads by modular trailers. Modular trailer is a term that refers to a multi-axle trailer that has a hydraulic and mechanical steering system, hydraulic suspension, and a steel chassis that provides very good structural rigidity for the transport of oversized and abnormal haulage for long distances by road. Modular trailers provide a cost-effective and flexible means to transport heavy loads. Voluminous payloads can be transported by connecting several modules side by side and/or end to end. Necks, drawbars, turn tables, ballast, and other additional components ensure that the trailers are optimally adapted to the requirements of various loads. The deck of the trailer can be lowered or raised by the hydraulic suspension for loading or removing cargos. The trailer’s hydraulic suspension can be used to level its deck. This is done by increasing the volume of oil on one side. This is possible because each pendulum axle has a hydraulic cylinder that is connected to other cylinders. This ensures uniform loading on pendulum axles. While the trailer is in motion, the hydraulic suspension permits swing axles to have different deflections (See Figure 1).

Mechanically, a modular trailer consists of a rigid platform that is supported by hydraulic pendulum axles that are attached in pairs. Each pendulum axle consists of a hydraulic cylinder, two or four wheels, and a hinged elbow joint. The hydraulic cylinder and the hinged elbow joint provide lifting capability of the trailer and also serve as a suspension system. The hydraulic system also enables the cargo load to be distributed across multiple pendulum axles in uneven surface conditions as illustrated in Figure 2.

2.2. Stability Area

The load’s characteristics (dimension, weight, etc.) and the route determine the number of modules used and their hydraulic configuration. After settling the number of axles and the type of trailer, it is necessary to decide how to group the cylinders for a haulage arrangement that is as stable as possible. Each of the trailer’s modules has a hydraulic system. It consists of various valves, pipes, and cylinders that enable several trailers to connect hydraulically. In practice, the grouping of cylinders is accomplished by a set of valves below the trailer’s platform. Figure 3 shows a configuration of valves that create three groups that are known as 3-point suspension. The minimum number of groups is three, which is actually the most stable configuration.

The transport is deemed to be stable if the total force projection is within the stability area. If this projection is not within the stability area, there is a risk of damage to the trailer and/or of tipping. If the force projection is vertical, inertial forces do not affect the stability of the trailer (deceleration or acceleration, turning, and/or wind force). The corners of the area of stability define a plane that can be defined as ax + by + cz − K_0 = 0 (plane Π). This can be calculated by solving the following determinant:

$$\left|\begin{array}{ccc}x-x_0& y-y_0& z-z_0\\ x_1-x_0& y_1-y_0& z_1-z_0\\ x_2-x_0& y_2-y_0& z_2-z_0\end{array}\right|=0$$

(3)

with (x₀, y₀, z₀), (x₁, y₁, z₁), and (x₂, y₂, z₂) as the coordinates of the centers of the groups 0, 1, and 2, respectively. One can calculate these coordinates’ geometrically by using the location of the junction of the axles and cylinders or analytically is as follows:

$$\begin{array}{c}{x}_i=\frac{1}{n_i}·{\displaystyle \sum _{j=1}^{n_i}}{X}_{ij}\\ y_i=\frac{1}{n_i}·{\displaystyle \sum _{j=1}^{n_i}}{Y}_{ij}\\ z_i=\frac{1}{n_i}·{\displaystyle \sum _{j=1}^{n_i}}{Z}_{ij}\end{array}$$

(4)

with (xi, yi, and zi) as coordinates of group i, n_i as the number of group i pendulum axles, and (X_ij, Y_ij, and Z_ij) are the pendulum axle fulcrum j’s coordinates in group i. Camber and inclination of the road change the spatial position of the cylinders and, therefore, the coordinates of the groups. These inclinations can increase or decrease the safety, depending on the stability area’s definition and the forces that are acting on the transport.

2.3. Forces Acting upon the Transportation Model

The weight of the load itself, as well as that of each if the trailer’s component, must be considered. Thus, the total weight of the load is the sum of the weights of all individual components:

$$W=M·g=\left(m_{load}+{\displaystyle \sum }_{i=1}^n{m}_i\right)·g$$

(5)

with the total mass of the trailer and load in kilogram as M, the load’s mass as m_load, the mass of the trailer’s component i as m_i, the acceleration of gravity as g and the weight as W. This force is exerted on the CoG. The latter is located at a point that corresponds to the weighted average of the CoGs of all items or parts that are being transported:

$$\begin{array}{c}{x}_{CoG}=\frac{1}{M}·\left(m_{load}·x_{load}+{\displaystyle \sum _{i=1}^n}{m}_i·x_i\right)\\ y_{CoG}=\frac{1}{M}·\left(m_{load}·y_{load}+{\displaystyle \sum _{i=1}^n}{m}_i·y_i\right)\\ z_{CoG}=\frac{1}{M}·\left(m_{load}·z_{load}+{\displaystyle \sum _{i=1}^n}{m}_i·z_i\right)\end{array}$$

(6)

with (x_CoG, y_CoG, and z_CoG) as coordinates of the final CoG and (x_i, y_i, and z_i) as the coordinates of the component i’s CoG.

Breaking (acceleration or deceleration) creates an inertial force in the driving direction (axis X). This force is calculated by the following Equation (7):

$$F_A=M·a$$

(7)

with F_A for the acceleration force, M for the total weight, and a for the acceleration. F_A is applied at the CoG.

A turn can be described as a movement by the trailer along a circular path or along a circumference, both of which generate centripetal acceleration. This, together with the weight of the load, creates an inertial force in a direction that is perpendicular to the driving direction (axis Y). This force is calculated by Equation (8):

$$F_T=M·\frac{v^2}{R}$$

(8)

where F_T is the centrifugal force, M is the total weight, R is the turn’s radius, and v is the trailer’s velocity. F_T is applied to the center of gravity. Depending on the turning direction, it can be positive or negative. The radius in Equation (8) is positive when it appears on the left. It is negative if it appears on the right (See Figure 4).

The relative movement between the air and the trailer creates an aerodynamic force against the trailer. This study considers only the forces of drag on the cargo, as they are much greater than those on truck and trailer. The equation to calculate the drag is the same one that is employed to calculate the longitudinal (F_Dx) and transversal (F_Dy) drag forces that movement through a fluid creates:

$$F_{Dx}=\frac{1}{2}·\rho ·{\left(v+v_{wx}\right)}^2·A_x·C_{dx}=\frac{1}{2}·\rho ·{\left(v+cos\left({\alpha }_w\right)·v_w\right)}^2·A_x·C_{dx}$$

(9)

$$F_{Dy}=\frac{1}{2}·\rho ·v_{w·y}^2·A_y·C_{dy}=\frac{1}{2}·\rho ·{\left(sin\left({\alpha }_w\right)·v_w\right)}^2·A_y·C_{dy}$$

(10)

with F_Dy for the longitudinal and transverse drag forces, ρ for the fluid’s density, v_w for the velocity of the air, α_w for the angle between the air velocity and the trailer’s longitudinal axle, and A_x and Ay denote the reference areas. Finally, C_dy and C_dx are drag coefficients, and are dimensionless (they depend on the geometry, surface, and relative position). One should remember that three aerodynamic forces generally act on the trailer. They are a longitudinal force (axis X), a transversal force (axis Y), and a lifting force (axis Z). However, the equations for these forces are valid for certain objects. The drag force on the truck, trailer, and load together cannot be determined easily. Obtaining realistic values for the forces that are acting on the three axles requires CFD and/or wind tunnel experiments. Only transversal and longitudinal forces that act on the load have been considered in order to simplify the calculations, as they are not great and their effect is minor. The model assumes that all of the forces are applied at the CoG. Therefore, the total force on the trailer and its load is the vector total of the dynamic, aerodynamic, and static forces as expressed by:

$$\begin{array}{c}{F}_x=F_A+F_{Dx}\\ F_y=F_T+F_{Dy}\\ F_z=-W\end{array}$$

(11)

A vector and a point determine the line force equation. The point represents the CoG that is calculated by Equation (11), whereas the vector is the combination of forces F_x, F_y and F_z. Thus, the vector of the force can be represented by Equation (12)

$$LineL:\left(x,y,z\right)=\left(x_{CoG},y_{CoG},z_{CoG}\right)+\left(F_x,F_y,F_z\right)·t$$

(12)

2.4. Stability Calculation

A transport’s stability is normally expressed by the “tipping angle”. The tipping angle is the angle between the vertical and the maximum deviation of a trailer with load from the vertical without tipping over [29]. Calculation of that angle requires the coordinates of points O, I, C, and P in Figure 5 to be determined.

Point O is represents center of gravity (CoG), which is calculated by Equation (13). The center of gravity’s vertical projection over the plane Π (1-2-3) is represented by P. The vertical line that intersects CoG can be expressed in parametric form as:

$$\begin{array}{l}x=x_{CoG}+0·t\hfill \\ y=y_{CoG}+0·t\hfill \\ z=z_{CoG}-1·t\hfill \end{array}$$

(13)

By combining Equations (12) and (13), t can be obtained as follows:

$$t=\frac{K_0-\left(a·x_{CoG}+b·y_{CoG}+c·z_{CoG}\right)}{-F_z}$$

(14)

P, the intersection point is calculated replacing t by p in Equation (15). Point C is the point that is closest point I on the stability area at any edge. First, the plane that is perpendicular to edge i through point I is calculated by the following:

$$\left(x_{i+1}-x_i\right)·\left(x-x_I\right)+\left(y_{i+1}-y_i\right)·\left(y-y_I\right)+\left(z_{i+1}-z_i\right)·\left(z-z_I\right)=0$$

(15)

with (x_i, y_i, z_i) and (x_i+1, y _i+1, z_i+1) as coordinates for two consecutive corners. The equation for the plane Ω is obtained by developing this expression:

$$\begin{gathered} Plane\Omega :+\left(x_{i+1}-x_i\right)·x+\left(y_{i+1}-y_i\right)·y+\left(z_{i+1}-z_i\right)·z \\ -\left(x_{i+1}-x_i\right)·x_I+\left(y_{i+1}-y_i\right)·y_I+\left(z_{i+1}-z_i\right)·z_I=0 \end{gathered}$$

(16)

The equation for the edge is the following:

$$\begin{array}{l}x=x_i+\left(x_{i+1}-x_i\right)·t\hfill \\ y=y_i+\left(y_{i+1}-y_i\right)·t\hfill \\ z=z_i+\left(z_{i+1}-z_i\right)·t\hfill \end{array}$$

(17)

Point C marks the intersection of this line with plane Ω:

$$\begin{array}{l}\left(x_{i+1}-x_i\right)·\left(x_i+\left(x_{i+1}-x_i\right)·t\right)-\left(x_{i+1}-x_i\right)·x_I+\hfill \\ \left(y_{i+1}-y_i\right)·\left(y_i+\left(y_{i+1}-y_i\right)·t\right)-\left(y_{i+1}-y_i\right)·y_I+\hfill \\ \left(z_{i+1}-z_i\right)·\left(z_i+\left(z_{i+1}-z_i\right)·t\right)-\left(z_{i+1}-z_i\right)·z_I=0\hfill \end{array}$$

(18)

By developing the preceding further, t can be obtained by:

$$t=\frac{\left(x_{i+1}-x_i\right)·\left(x_i-x_I\right)+\left(y_{i+1}-y_i\right)·\left(y_i-y_I\right)+\left(z_{i+1}-z_i\right)·\left(z_i-z_I\right)}{{\left(x_{i+1}-x_i\right)}^2+{\left(y_{i+1}-y_i\right)}^2+{\left(z_{i+1}-z_i\right)}^2}$$

(19)

Point C’s coordinates can be obtained by replacing t in equation. The tipping angle is determined by points O, I, and C. The tipping angle that is calculated by the following:

$${\alpha }_{tip}=acos\left(\frac{\left|V_{IO}\times V_{CO}\right|}{\left|V_{IO}\right|·\left|V_{CO}\right|}\right)$$

(20)

with v_CD and v_ID as the vectors between points (I,O) and (C,O), v_IO × v_CO as the cross product, and |v_IO| and |v_CO| as the modulus of these vectors.

$${\alpha }_{tip}=\mathit{acos}\left(\frac{\left|\left(\begin{array}{ccc}{x}_I-x_O& y_I-y_O& z_I-z_O\end{array}\right)\times \left(\begin{array}{ccc}{x}_C-x_O& y_C-y_O& z_C-z_O\end{array}\right)\right|}{\left|\left(\begin{array}{ccc}{x}_I-x_O& y_I-y_O& z_I-z_O\end{array}\right)\right|·\left|\left(\begin{array}{ccc}{x}_C-x_O& y_C-y_O& z_C-z_O\end{array}\right)\right|}\right)$$

(21)

2.5. Reactions of the Suspension Groups

A 3-point suspension can be considered as a mechanical system static determinate (or isostatic). The reason is that the unknown reactions and equilibrium equations are equal in number (See Figure 6). The calculation of the reactions assumed the following:

• Load (W) and reactions (F₁, F₂, and F₃) are perpendicular to the stability plane.
• There are no forces in X or Y and/or moment in Z. Thus, the equilibrium equations are three in number.
• The system affects quasi-static loading. That is, it is assumed that the time and mass do not influence the load.
• The ground is assumed to be a completely rigid plane.

$$\sum F_z=0:F_1+F_2+F_3-W=0$$

(22)

$$\sum M_x=0:F_1·y_1+F_2·y_2+F_3·y_3-W·y_w=0$$

(23)

$$\sum M_y=0:F_1·x_1+F_2·x_2+F_3·x_3-W·x_w=0$$

(24)

These equations can also be expressed as matrices:

$$\left[\begin{array}{ccc}1& 1& 1\\ y_1& y_2& y_3\\ x_1& x_2& x_3\end{array}\right]·\left[\begin{array}{c}{F}_1\\ F_2\\ F_2\end{array}\right]=\left[\begin{array}{c}W\\ W·y_w\\ W·x_w\end{array}\right]$$

(25)

To calculate the force in a cylinder (f_cyl,j), divide the force in group i (F_i) by the number of cylinders in the group (n_i):

$$f_{cyl,j}=\frac{F_i}{n_i}$$

(26)

with F_i as the force in group I and n_i as the number of cylinders in the group. Calculate the pressure in each cylinder by the following equation:

$$p_{cylj}=\frac{f_{cylj}}{A_j}$$

(27)

with p_{cyl j} as the cylinder’s oil pressure j and A_j as this cylinder’s area.

3. Results and Discussion

3.1. Experimental Validation of the Proposed Model

For the purpose of validating the proposed theoretical model, several experiments were conducted to measure the oil pressure of the hydraulic cylinders with the load located in various positions on a modular trailer. This validation process is used to determine the reliability of a theoretical model, and is usually applied in the same way in many fields of study [30,31,32,33]. The greater the number and variety of experiments, the more reliable is the validation. However, experiments are generally very expensive. Therefore, it is very important to adopt the correct experimental procedures in order to obtain a successful validation. The number of experiments depends on the number of inputs. The model considers load weight, CoG location, load shape, trailer modules, groups’ definition, road inclinations, speed, acceleration, turning radius, and wind speed. Testing some of these inputs is very difficult. For example, measuring the acceleration and the platform inclination is very complicated, because the trailer is in motion. Dynamic and aerodynamic inputs were not considered in designing a feasible set of experiments in this study. Further, it is assumed that the stability of the trailer depends mainly on the load’s location on the platform. In order to simplify the experiments, only the longitudinal and transverse locations of the load were considered. All of the experiments were carried out under the following conditions:

• Trailer: SPMT 6-axle: weight 23.5 and maximum capacity 216.3 Tn.
• The oil pressure is supplied to the hydraulic cylinders at the axles by a Power Unit (PPU).
• Even surface: camber and slope equal zero.

In addition, the load used in the experiments was a nacelle wind turbine. The cover housing contained the generator and gearbox, drive train, brake assembly, and all other generating components of the wind turbine. The properties of the nacelle wind turbine are:

• Weight: 42,500 kg.
• Dimensions: 5133 × 2650 × 2975 mm.
• CoG position: 97.5 × 0 × −180 mm.

Figure 7 shows the elements used in the experiments to validate the proposed model.

Design of experiments (DoE) is a set of methods to determine relationships between the inputs and outputs of processes [34,35,36]. These techniques establish the order of variables to determine cause and effect relationships with confidence. DoE is used here to define the combination of inputs to determine the accuracy of the model. There are many DoE techniques. However, all involve the construction of a table, in which each row corresponds to a single experiment and each column to a factor. The input variables are called factors, and each of the values are called levels. However, factors can be controllable or uncontrollable, also called noise. The uncontrollable factors are due to environmental changes or small variations in components properties. Their effects can be minimized by randomizing and grouping the experiments. Nevertheless, experiments always have uncontrollable effects, called experimental errors. These can be determined by repeating the same experiment to measure the dispersion of the responses. In this case, there are two inputs with which to create the set of experiments.

Table 1. Design of experiments: inputs, units, and levels.

Inputs	Symbol	Unit	Levels
			−1	0	+1
Longitudinal location of the load	X	mm	0	675	1350
Transversal location of the load	Y	mm	0	175	350

shows the inputs and their symbols, units, and levels (design matrix), whereas Figure 8 clarifies the physical meaning of the inputs.

A full factorial design consists of several factors and levels where the experiments involve all possible combinations of these levels for all factors. In most cases, the levels are quantitative. However, they can be qualitative, as in the cases of gender or logical values. A 2k design is a kind of full factorial design that has only two levels, which are called “low” and “high” or “−1” and “+1.” All possible combinations without repetition of the two levels and the k factors generate 2k experiments. A 3k design is a full factorial design that has three levels, which are coded as “+1”, “0”, and “−1”, that generate 3k experiments without repetition. In this study, 3k DoE with two factors with central points (32 = 9 experiments) were selected for validation of the theoretical model. In addition to nine experiments, four additional repetitions or repeated experiments were proposed to measure the variability of the results of the experiments and equipment in satisfying Equation (28):

$$\sigma =\sqrt{\frac{1}{n}·{\displaystyle \sum }_{i=1}^n{\left(x_i-\mu \right)}^2}$$

(28)

where x_i is a result of the experiment, μ is the mean of this variable, and n is the number of cases (just repeated).

The configuration for all experiments involved a downhill slope of 0.35° and a camber of 0.1°. However, as the values are very low, it was assumed that the ground was perfectly even. In addition, the configuration of the experiments assumes a wind speed of zero, as the latter was very low. The trailer was configured in 3-point suspension, as Figure 6 shows. The platform was set at a height of 1550 mm from the floor. A crane was employed to move the nacelle wind turbine, whereas the location and configuration of the trailer were unchanged. The output was the oil pressure of each group of hydraulic cylinders. The experimental inputs and pressures that were recorded by the manometers are summarized in

Table 2. Experiment inputs (X and Y) and pressures obtained from manometers.

	X	Y	Pressures [bar]
			A	B	C	D
1	0	0	59	61	77	75
2	0	0	55	62	80	79
3	0	0	60	61	75	72
4	0	0	64	56	90	92
5	0	0	58	63	78	74
6	0	335	24	97	80	80
7	0	435	13	108	81	85
8	675	0	66	75	58	58
9	675	335	38	103	58	59
10	675	435	27	117	58	58
11	1350	0	79	85	39	40
12	1350	335	47	120	39	38
13	1350	435	38	127	38	38

.

Additionally, the variabilities of each pressure group were calculated according to Equation (28) and are summarized in

Table 3. Variability of the experiments 1 to 5.

Case	Range	Mean [μ]	SD [s]
Pressure A	9 bar	59.2 bar	2.9 bar
Pressure B	7 bar	60.6 bar	2.4 bar
Pressure C	15 bar	80.0 bar	5.3 bar
Pressure D	20 bar	78.4 bar	7.2 bar
	Average values	69.55 bar	4.45 bar

. The average variability of the pressures in the table of the first four experiments is 4.45 bar. This represents a value of 4.45/69.55 (6.39%) compared to the average pressure. This means that the values registered experimentally in the pressure gauges show a low variability. This can be considered to be very good, in view of the fact that the values were obtained experimentally.

After the 13 experimental values were obtained according to the preset configuration of experimental inputs (X, Y) in Table 3, weight (42,500 kg), dimensions of (5133 × 2650 × 2975 mm), and CoG (97.5 × 0 × −180 mm) of the nacelle wind turbine, the theoretical values of the pressures of the proposed model were obtained (See

Table 4. Predicted values and errors.

Case	Pressures
	A [bar]	B [bar]	C [bar]	D [bar]	MAPE [%]
1–5	59.0	58.0	84.4	84.4	4.4
6	28.0	89.3	84.4	84.4	8.8
7	18.3	98.7	84.4	84.4	13.6
8	69.8	68.9	62.6	62.6	7.4
9	38.6	100.2	62.6	62.6	4.6
10	29.2	109.6	62.6	62.6	7.6
11	80.7	79.8	40.9	40.9	3.8
12	49.4	111.1	40.9	40.9	6.2
13	40.1	120.4	40.9	40.9	6.4
Average:					7.0%

). In addition, the accuracy of the proposed theoretical model is measured by the Mean Absolute Percentage Error (MAPE). This is defined by Equation (29):

$$MAPE=\frac{1}{n}·{\displaystyle \sum }_{i=1}^n\left|\frac{M_i-E_i}{E_i}\right|$$

(29)

where M_i is the model’s result, E_i is the experimental result, and n is the number of cases.

Table 4 indicates that the mean pressure error is 7.0%. This reduced value of the MAPE means that the proposed theoretical model is quite accurate in predicting the values of the hydraulic pressures of each of the cylinders. It should be noted that a large part of this MAPE is due not only to the proposed theoretical model, but also to the variability of the measurements, which is 6.4%.

3.2. Optimization Process Proposed

After the theoretical model had been validated by experimental data, an optimization algorithm was proposed. This was done to ensure that that transport of a load of given weight, dimensions, and CoG by road would be safe, taking into account such route conditions as camber, wind pressure, and slope. The objective of optimization is to minimize the number of axles that are necessary to carry the desired load. The optimization increases the maneuverability of the load and reduces the costs of assembly and transport. The optimization algorithm was developed in R language [37]. Its programming was based on the iterative and automatic testing of the proposed model in different locations on the trailer and with different hydraulic configurations. Accordingly, the load’s weight and CoG, and the trailer’s weight, number of axles, axle distance, and configuration were considered, in addition to highway conditions. The optimization process assumed that the tipping angle would be less than 7° and that the loads per axle would be less than 50% of the limit that the manufacturer had established. This 50% axle load limit is a restriction that is usually imposed by most transport companies as a means to increase the trailer’s useful lifers. The tipping angle restriction ensures the stability of the transport under any road condition.

The optimization was carried out in two stages. The first stage involved determining the minimum number of axles that were necessary and establishing the trailer’s hydraulic configuration and the load’s probable location. In this first stage, the optimization algorithm randomly generated a number of transport designs with different axes, configurations, and location of the transport’s CoG. These were obtained from a grid of 500 × 500 mm nodes. This grid was constructed from the properties of the surfaces of the trailers that were available. They should cover the entire stability triangle. Each transport design was calculated by using the proposed theoretical model for the camber, slope, and wind pressure (route conditions) considered. The model determined the tipping angle and maximum load on the trailer’s axles for each transport design. After these values had been obtained, the design that required the least number of axles and best complied with the tipping angle and load per axle optimization restrictions was selected.

The second stage focused on the search for the load’s optimal location on the trailer, without changing the number of axles and hydraulic configuration that were obtained in stage 1. The best node in stage 1 was assumed to be the CoG of a new 10 × 10 mm node grid. The same iterative process that was used in the first stage was employed in the second stage with the 10 x 10 mm node grid. Thus, the optimal location of the load on all of the modular trailers was located with a precision of 10 mm. Figure 9 provides a flowchart for which the proposed optimization algorithm had been used to find the optimal location of the CoG.

Figure 10 shows the node grids that both stages of the optimization used. Shown on the left is the first 500 × 500 node grid. It covers the entire stability triangle. The first stage of the optimization provided the best node. It can be considered as a first estimation of the optimal CoG location. It is the center of the 10 × 10 node grid and appears at the right of the same figure. This second grid will be used to find the position of the CoG of the load with a precision of 10 × 10 mm.

The optimization process that was used to validate the proposed methodology appears. It is based on the optimal conditions for a load to be carried by a trailer that has two 4- and 6-axle modules. The trailer properties that were considered in this study are those of the Intercombi model of Scheuerle company [38]. In this case, the proposed load was a cylindrical tank of 108.5 tons with five large pipes on its left side (Figure 11). The figure shows the hydraulic configuration of the trailer, which consists of group 1 (red) with six cylinders and groups 2 and 3 (purple and red) with seven cylinders. This configuration traces a stability triangle that also appears in Figure 10.

Table 5. Key values of the optimized transport.

Characteristics	Value
Load	Cylindrical tank
Dimensions	19.5 × 3.2 × 2.5 m
Load weight	108,500 kg
Trailer weight	33,000 kg
Initial CoG coordinates	0.0 × 0.2 × 2.1 m
Optimum CoG coordinates	0.3 × 0.0 × 2.1 m
Number of trailers	2
Number of axles	10 (4 + 6)
Tipping angle (on even road)	7.2°
Maximum axle load	21,600 kg
Oil pressures	8.1 × 8.1 × 5.9 bar
Hydraulic configuration	6, 7, 7

shows the data of the proposed load (weight, dimensions, and position of its CoG). It also shows the optimal number of modular trailers and axles, coordinates to locate the CoG of the load, and oil pressures of the suspension system, as determined by the optimization algorithm.

4. Conclusions

This paper describes a theoretical model that is capable of calculating complex load safety requirements, including the load per cylinder, oil pressures, and tipping angle. It considers the trailers’ mechanical properties, the cargo’s characteristics, road inclinations, and wind pressure. The hydraulic cylinder suspension has been discussed, as well as how the hydraulic groups are defined. The hydraulic cylinders’ spatial position provided a base for calculation of the “stability area” and “plane of stability”. The trailer’s load has been described by use of this data. They include the dead weight, dynamic forces, and aerodynamic forces. The combined force and “stability area” determined the transportation model’s stability and the resulting “tipping angle” or instability. Finally, the load for each cylinder, load on each suspension group, and oil pressures have been calculated. The theoretical model that is proposed has been validated experimentally to measure oil pressures and the platform inclination. The MAPE of the oil pressures that were determined by the model is 7.0% for the data that were obtained experimentally. This error is minimal, which shows the validity of the proposed model. Once the proposed model was validated, an optimization algorithm was proposed in order to find the optimal center of gravity of the load, number of trailers, number of axles, oil pressures, and hydraulic configuration. The algorithm was based on the iterative and automatic testing of the proposed model in different positions on the trailer and different hydraulic configurations. The results showed that the proposed model and optimization algorithm can safely optimize the configuration of the hydraulic suspension of modular trailers in special road transport, increase the accuracy and reliability of the calculation of the load configuration, save time, simplify the calculation process, and be easily implemented. In summary, the novel theoretical model and optimization algorithm that this paper describes improves the reliability and accuracy of heavy transport stability calculations, saves time, minimizes human error, and greatly facilitates the decision-making process.