Behaviour of Steel Tubular Knee Joint in Aluminium Frames with Tension-Tie Element
Abstract
:Featured Application
Abstract
1. Introduction
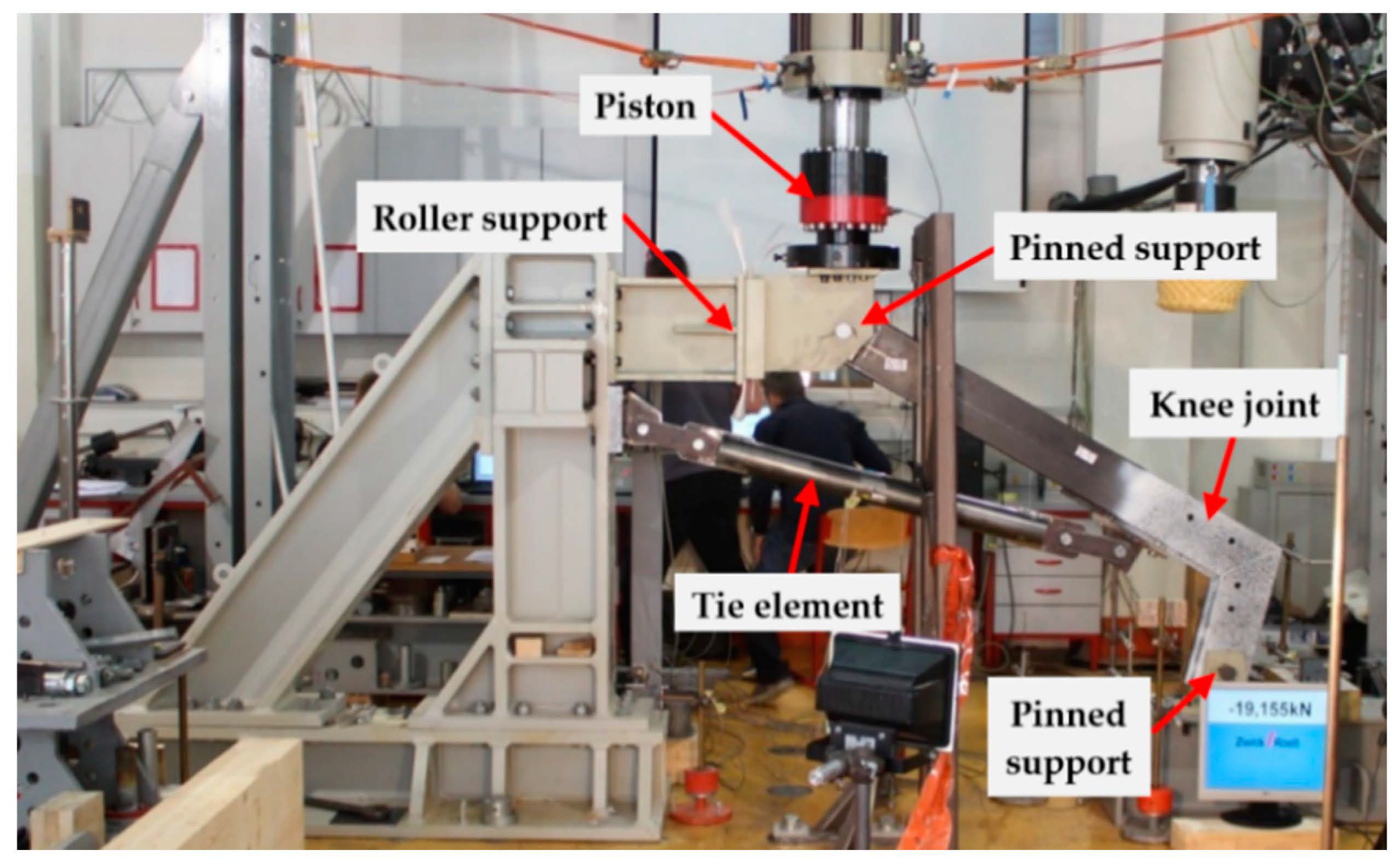
2. Experimental Program
2.1. Scope
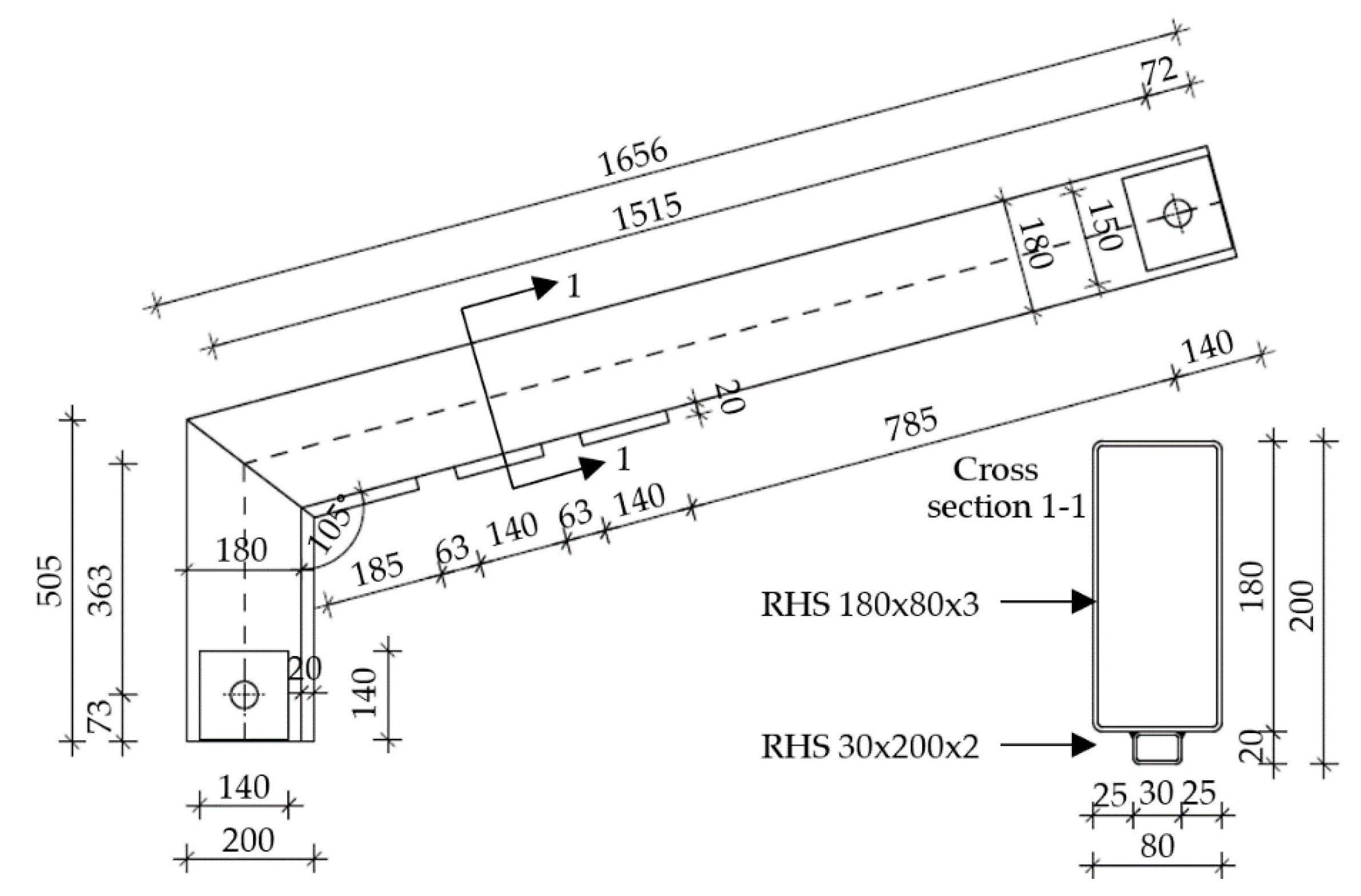
2.2. Geometrical Properties
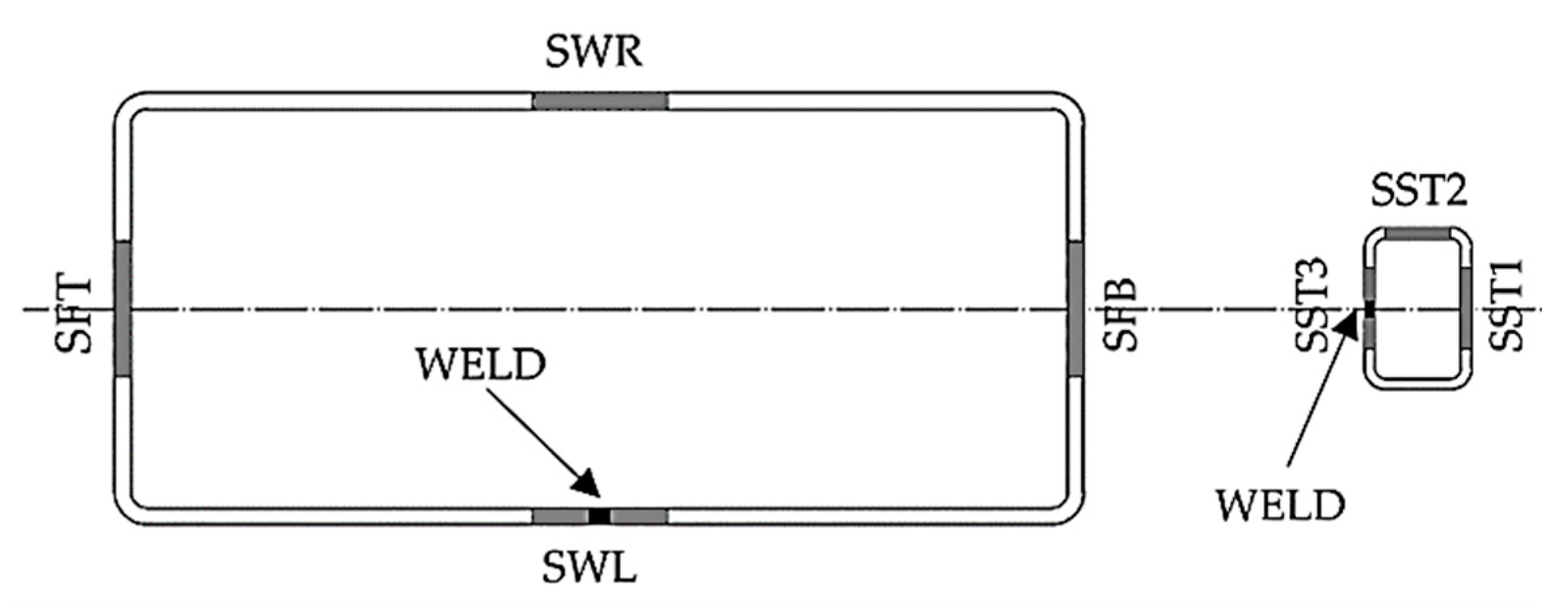
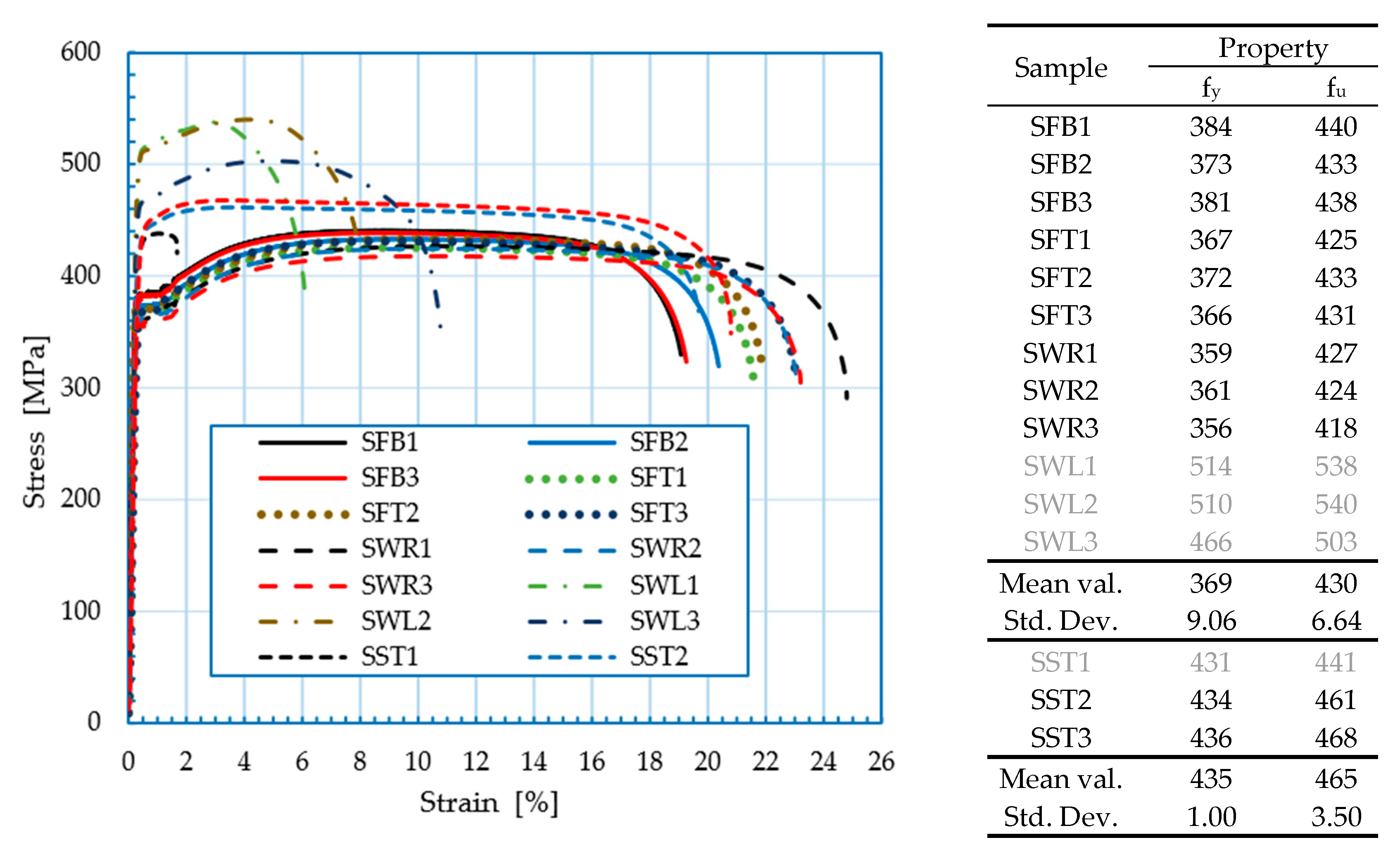
2.3. Mechanical Properties of Base Material and Welds
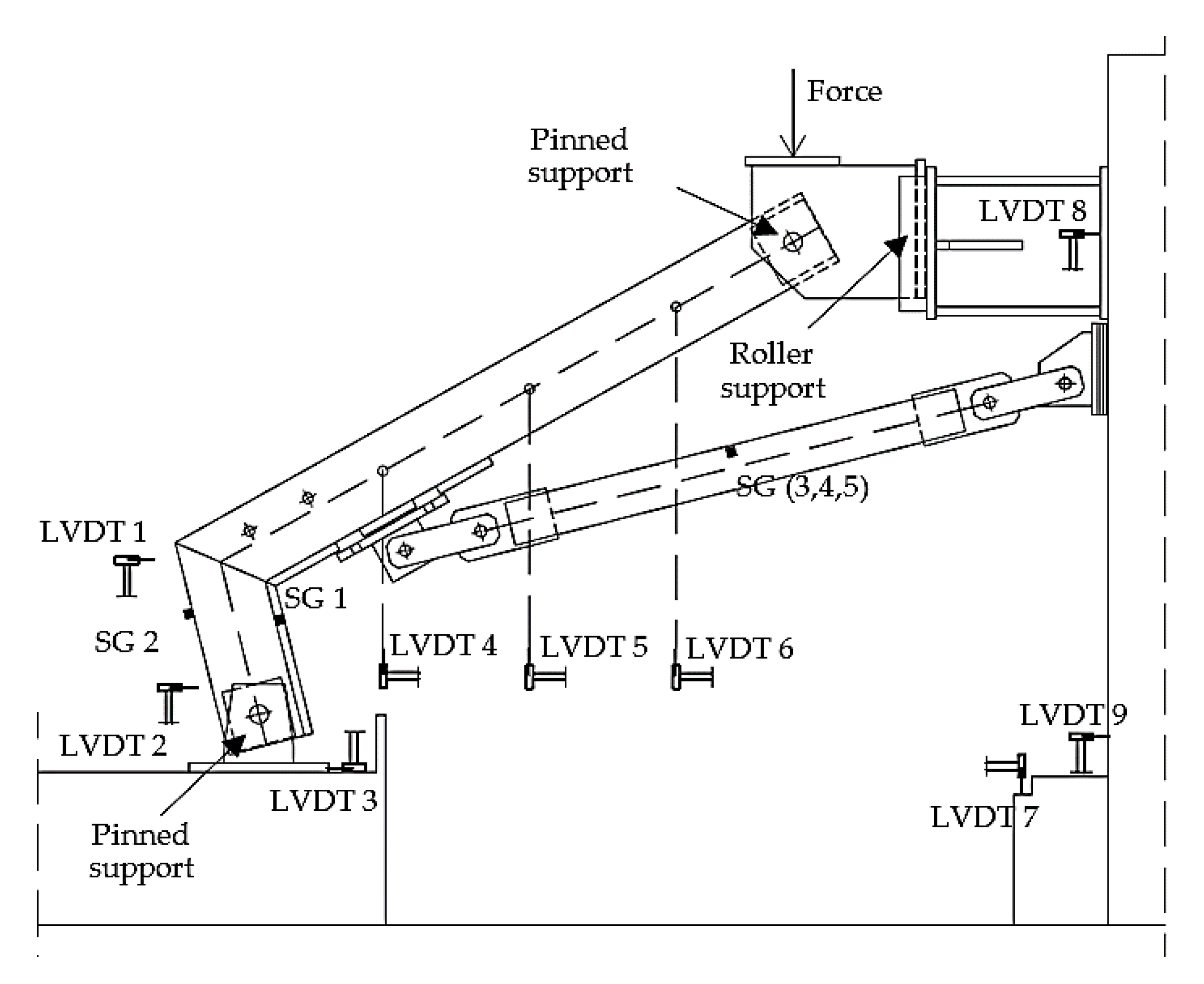
2.4. Loading Protocol and Measurements
2.5. Experimental Results
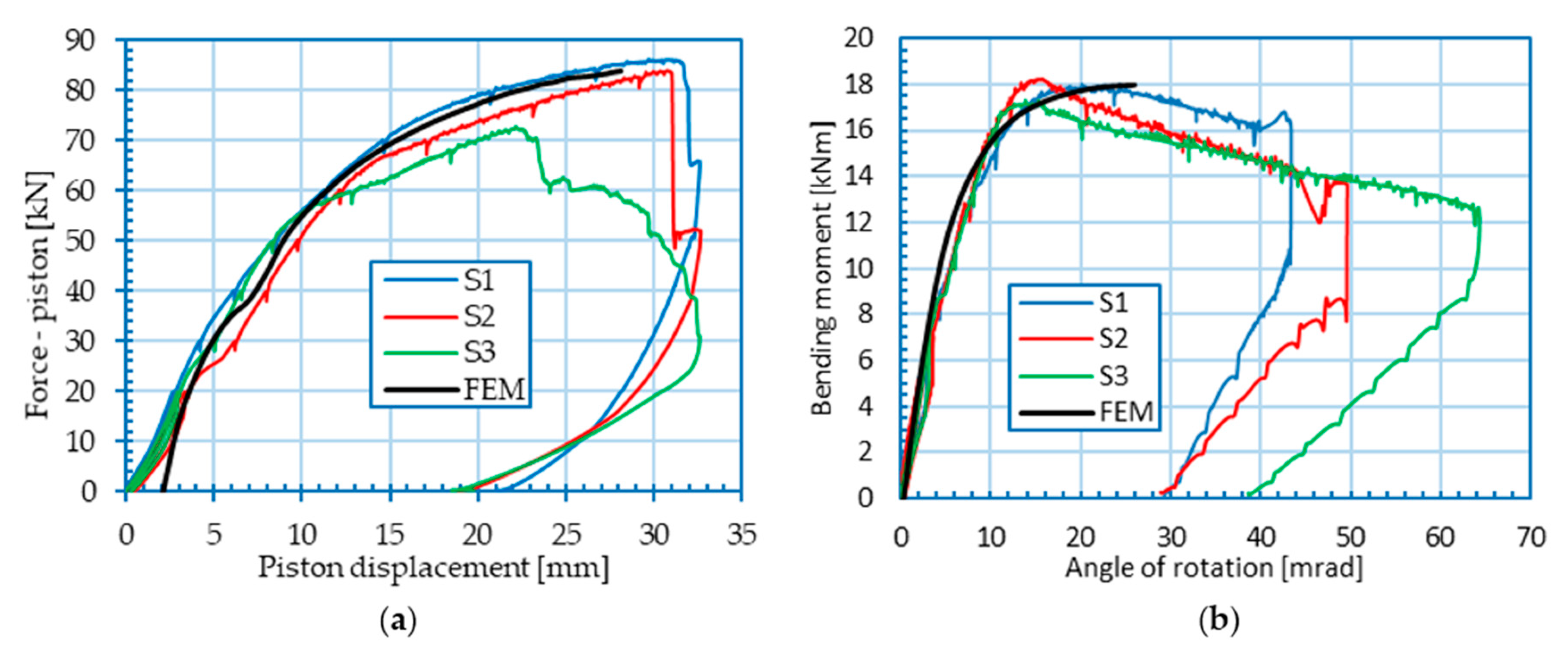
2.5.1. Load–Displacement Relationship
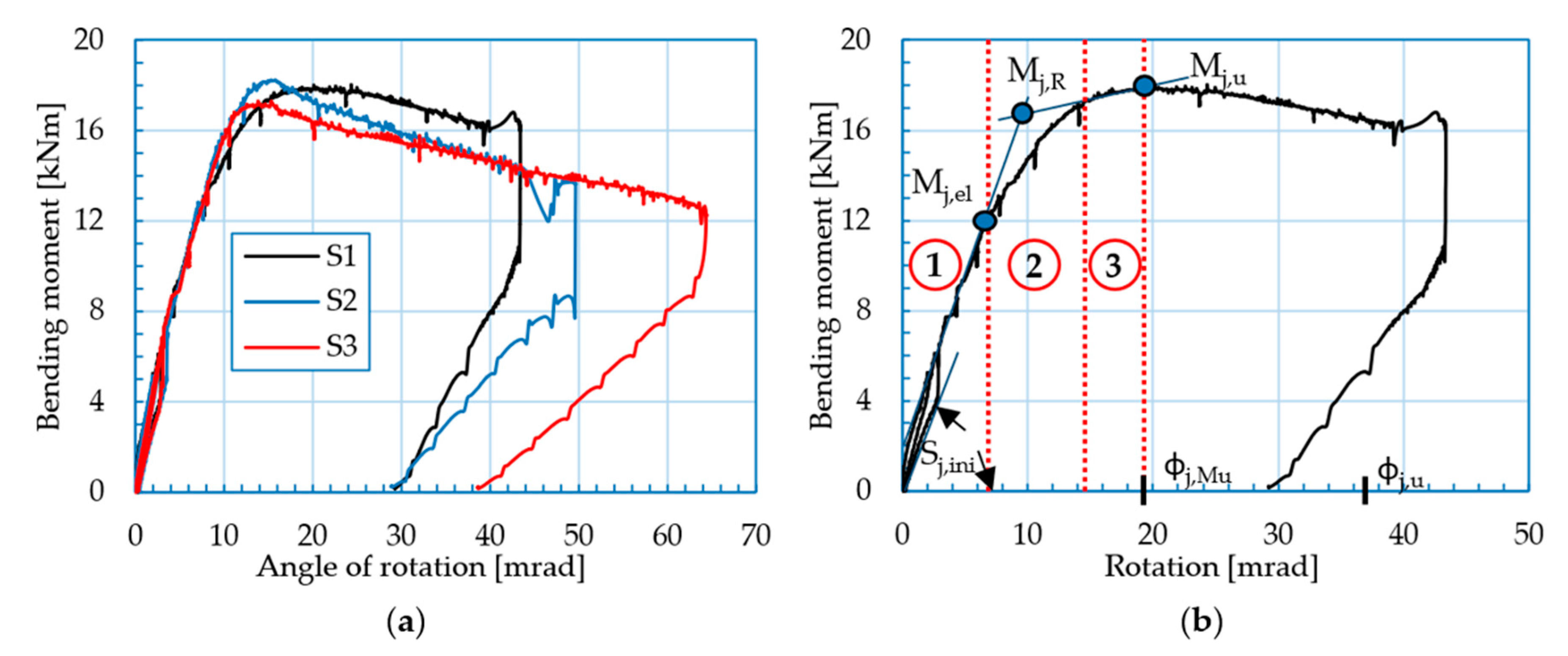
2.5.2. Moment–Rotation Relationship
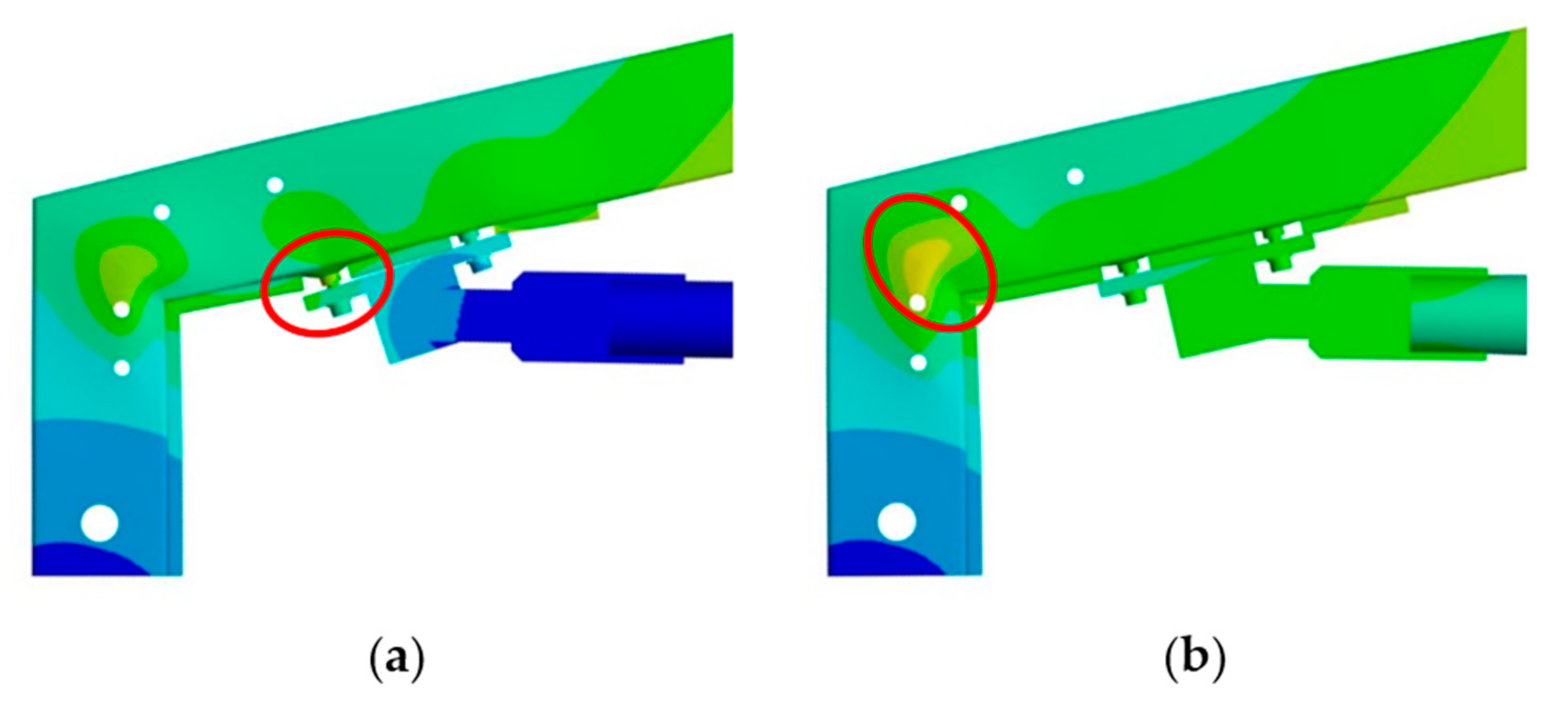
2.5.3. Failure Modes
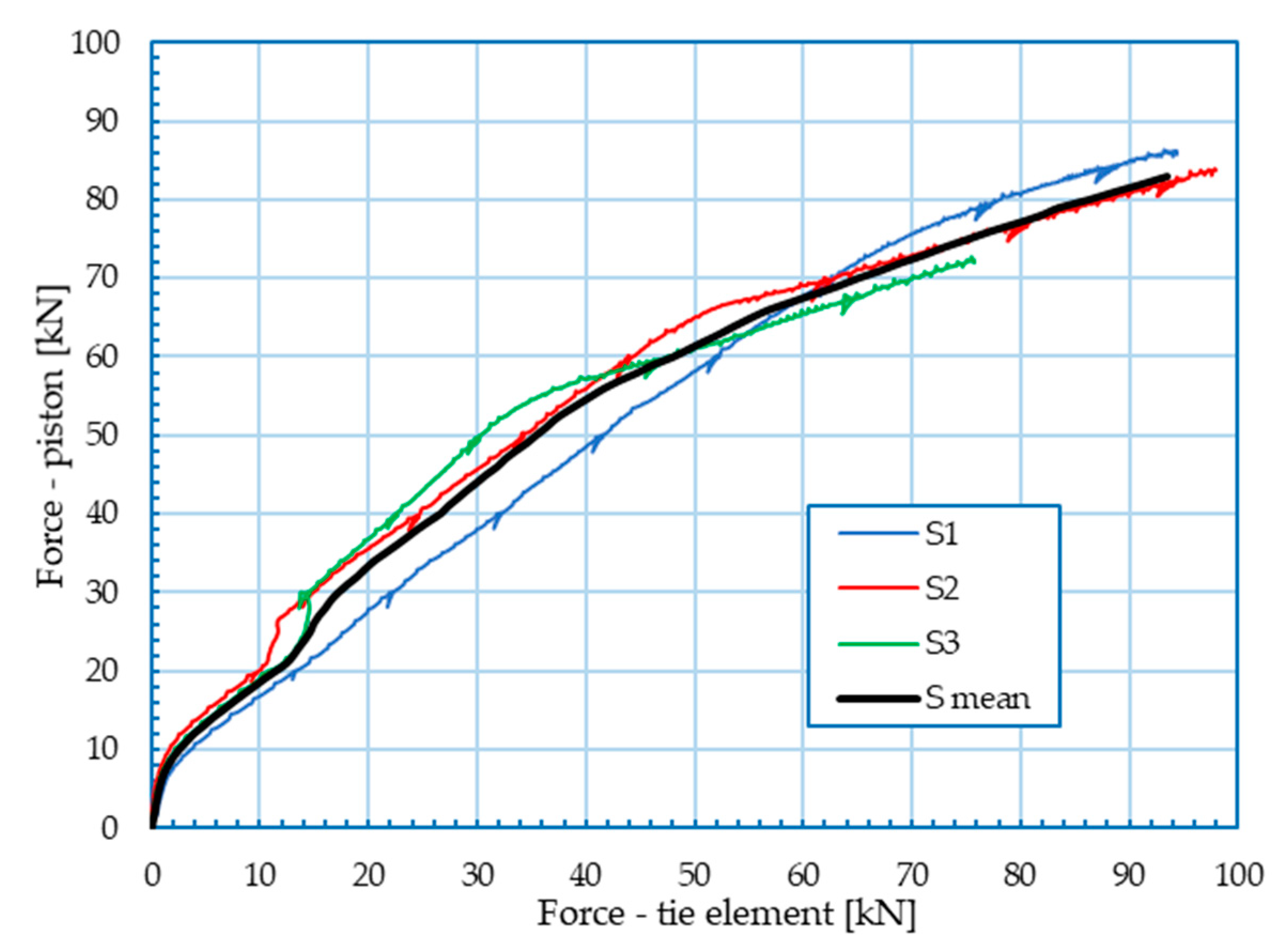
2.5.4. Force in the Piston-Tension in tie Element Relationship
3. Numerical Analysis
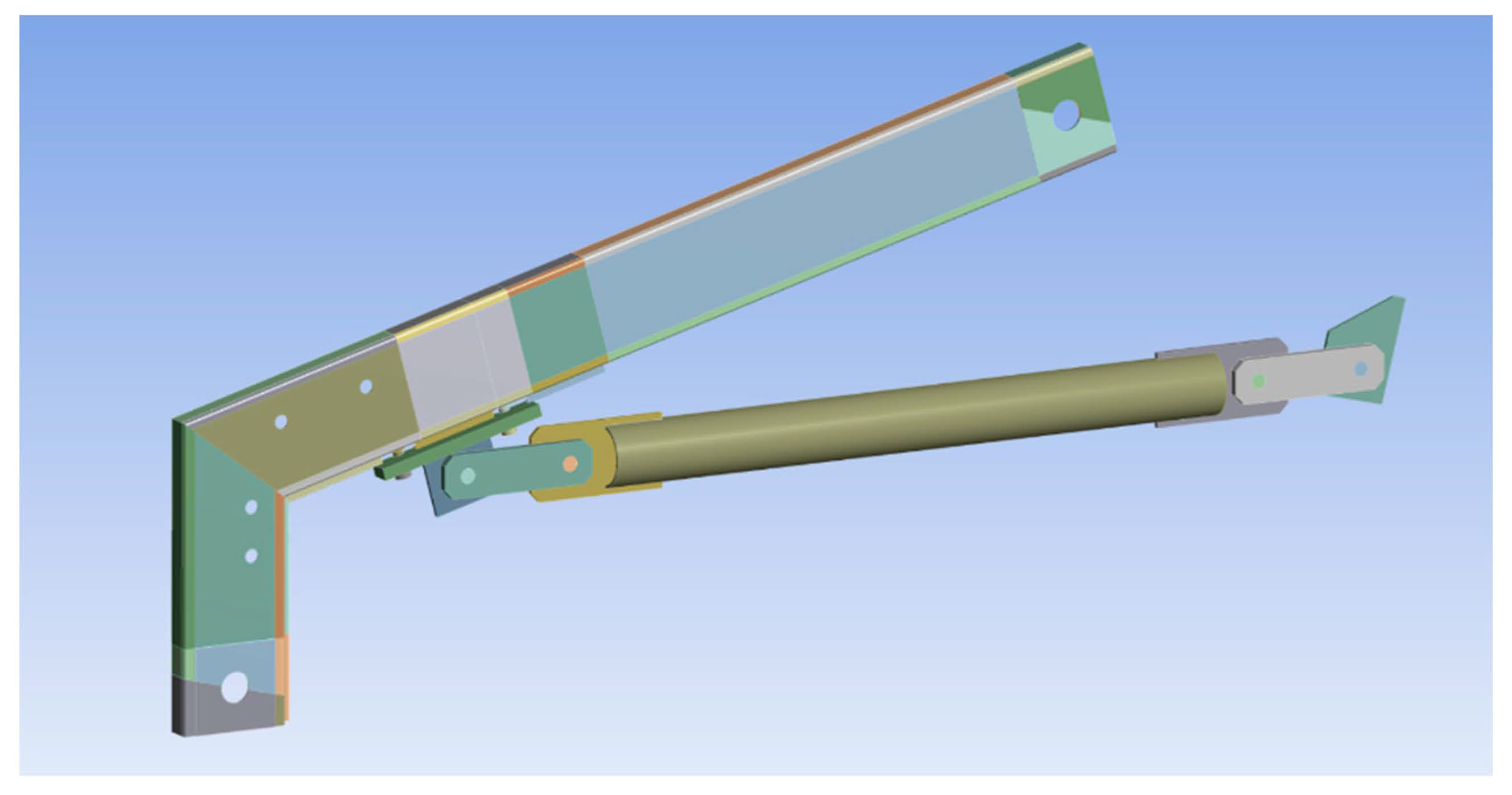
3.1. General Overview of the Numerical Model
3.2. Simulation of Performed Tests
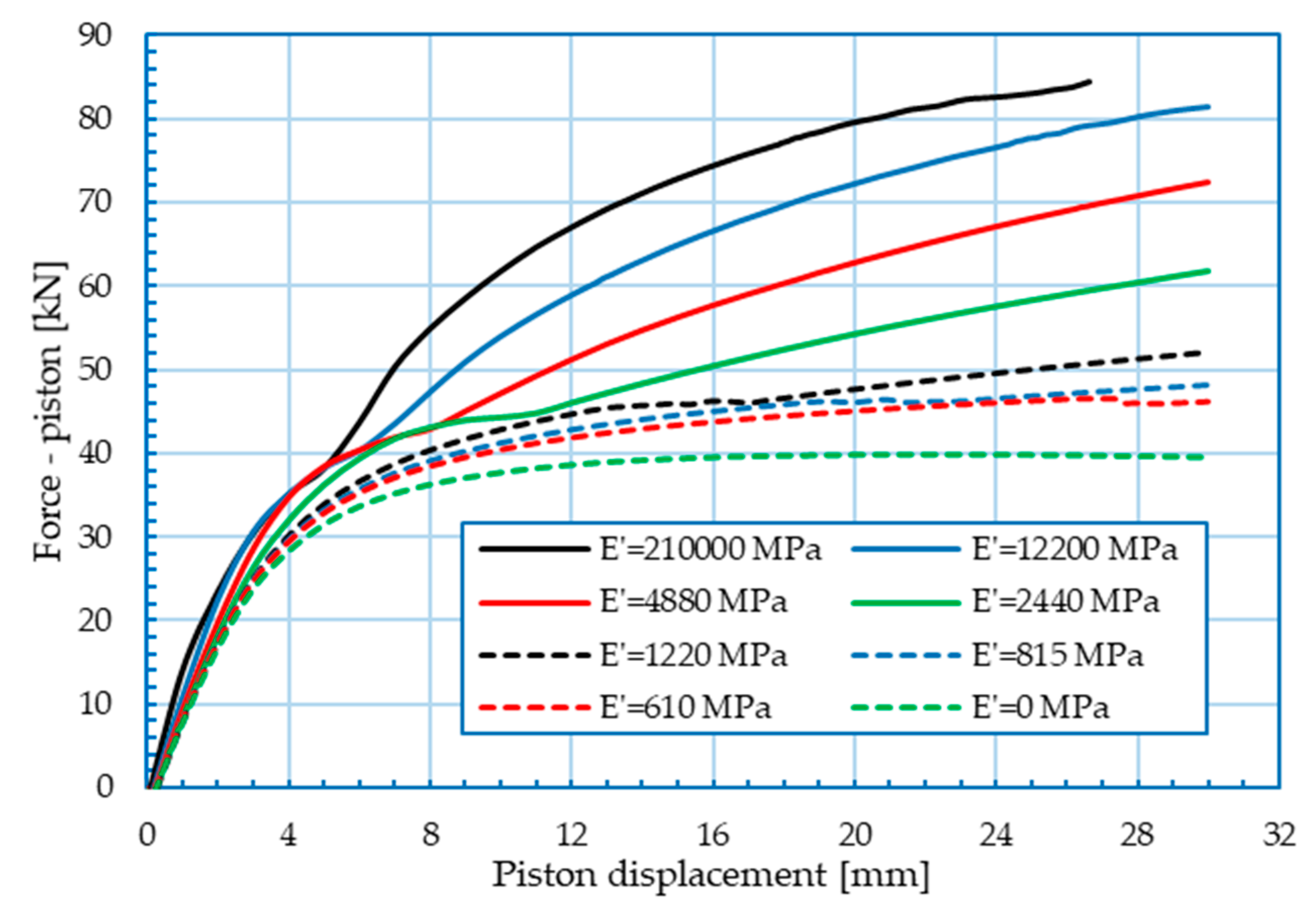
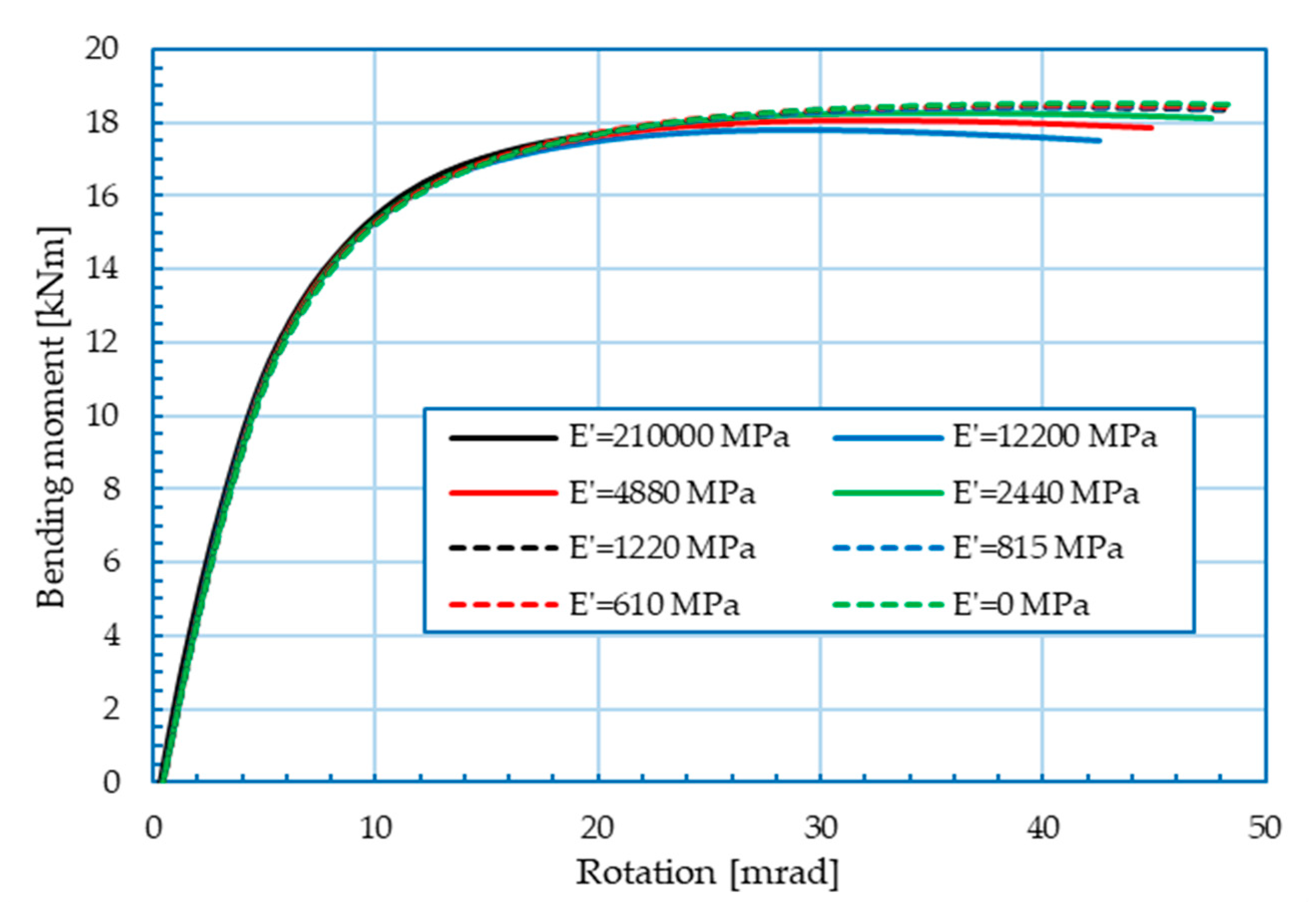
3.3. Numerical Parametric Analysis
- The cross-sectional area of the tie element used in the laboratory testing is 14.2 cm2, which is much higher compared to that of a high-strength steel wire rope that is equal to 1.10 cm2 for commonly used Ø 16, 6 × 37 FC steel wire rope.
- Due to spatial limitations of the laboratory equipment, the length of the tie element was approx. 1 m, which is much shorter compared to real aluminium portal frames with a tie element (usually spanning between 10 and 20 m).
- High strength steel wire ropes in general have a lower modulus of elasticity compared to that of a structural steel. The modulus of elasticity for various types of steel wire ropes with fibre core can vary in the range from 68.7 to 98.1 GPa according to [24]. For this numerical analysis, a modulus of elasticity of 80 GPa was chosen and implemented.
3.4. Discussion of Parametric Numerical Analysis Results
4. Conclusions
- Tested laboratory specimens have similar behaviour, all failing due to weld failure between the beam tube section and the tensile bolt nut.
- In general, the stiffness of the tie element has very little influence on the bending moment–rotation relationship of the knee joint but has high influence on the force–piston displacement relationship.
- The influence of the tie element stiffness on the bending moment–rotation and the force–piston displacement relationship is more pronounced in the knee range and especially in the postcritical region.
- Knee joints with stiffer tie elements are much more prone to tensile bolt (nut) pull-out when reaching failure compared to knee joints with a softer tie element. When a softer tie element is used, web buckling at the beam to column intersection is much more pronounced, giving a more favourable ductile failure mode.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mazzolani, F.M. Structural Applications of Aluminium in Civil Engineering. Struct. Eng. Int. 2006, 16, 280–285. [Google Scholar] [CrossRef]
- Skejić, D.; Boko, I.; Torić, N. Aluminium as a material for modern structures. Gradevinar 2015, 67, 1075–1085. [Google Scholar]
- Skejić, D.; Mazzolani, F.; Ćurković, I.; Damjanović, D. Experimental Testing of Prefabricated Aluminium Knee Joints Reinforced by Steel. In Proceedings of the INALCO2019: 14th International Aluminium Conference, Tokyo, Japan, 13–15 November 2019; pp. 160–161. [Google Scholar]
- Boko, I.; Skejić, D.; Torić, N. Aluminium Structures: Textbook at University of Split and Textbook at University of Zagreb; University of Split, Faculty of Civil Engineering, Architecture and Geodesy: Split, Croatia, 2017. [Google Scholar]
- Wilkinson, T.; Hancock, G.J. Tests of Stiffened and Unstiffened Welded Knee Connections in Cold-Formed RHS. In Proceedings of the Tubular Structures VIII: 8th International Symposium on Tubular Structures, Singapore, 26–28 August 1998; pp. 177–186. [Google Scholar]
- Wilkinson, T.; Hancock, G.J. Tests of Knee Joints in Cold-Formed Rectangular Hollow Sections; Research Report No.: R779; Department of Civil Engineering, University of Sydney: Sydney, Australia, 1998. [Google Scholar]
- Wilkinson, T.; Hancock, G.J. Tests to examine plastic behaviour of knee joints in cold-formed RHS. J. Struct. Eng. 2000, 126, 297–305. [Google Scholar] [CrossRef] [Green Version]
- Standards Australia. AS 1163: Structural Steel Hollow Sections; Standards Australia: Sydney, Australia, 1991. [Google Scholar]
- Packer, J.A.; Wardenier, J.; Kurobane, Y.; Dutta, D.; Yeomans, N. CIDECT Design Guide No. 3: Design Guide for Rectangular Hollow Section (RHS) Joints under Predominantly Static Loading; Verlag TUV Rheinland GmbH: Koln, Germany, 1992. [Google Scholar]
- The, L.H.; Hancock, G. Improving Rotation Capacities of Stiffened Welded Knee Joints between DuraGal C450 RHS; Research Report No.: R832; Department of Civil Engineering, University of Sydney: Sydney, Australia, 2003. [Google Scholar]
- Urbonas, K.; Daniūnas, A. Component method extension to steel beam-to-beam and beam-to-column knee joints under bending and axial forces. J. Civ. Eng. Manag. 2005, 11, 217–224. [Google Scholar] [CrossRef]
- Daniūnas, A.; Urbonas, K. Characteristics of the semi-rigid bolted steel joints under bending and axial forces and its influence on the frame behaviour. In Proceedings of the 9th International Conference “Modern Building Materials, Structures and Techniques”, Vilnius, Lithuania, 16–18 May 2007; Technika: Vilnius, Lithuania, 2007; pp. 512–516. [Google Scholar]
- Mills, J.E. Knee joints in cold-formed channel portal frames: Problems and pitfalls. Aust. J. Struct. Eng. 2012, 13. [Google Scholar] [CrossRef]
- Standards Australia. AS/NZS 4600: Cold-Formed Steel Structures; Standards Australia: Sydney, Australia, 2005. [Google Scholar]
- European Committee for Standardization (CEN). Eurocode 3: Design of Steel Structures—Part 1–8: Design of Joints (EN 1993-1-8:2005+AC:2009); CEN: Brussels, Belgium, 2014. [Google Scholar]
- Packer, J.A.; Wardenier, J.; Zhao, X.-L.; Van der Vegte, G.J.; Kurobane, Y. CIDECT Design Guide No. 3: Design Guide for Rectangular Hollow Section (RHS) Joints under Predominantly Static Loading, 2nd ed.; Verlag TUV Rheinland GmbH: Koln, Germany, 2009. [Google Scholar]
- European Committee for Standardization (CEN). Steel Wire Ropes—Safety—Part 1: General Requirements (EN 12385-1:2002+A1:2008); CEN: Brussels, Belgium, 2008. [Google Scholar]
- International Organization for Standardization (ISO). Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature (ISO 6892-1:2016; EN ISO 6892-1:2016); ISO: Geneva, Switzerland, 2016. [Google Scholar]
- European Committee for Standardization (CEN). Designation Systems for Steels—Part 1: Steel Names (EN 10027-1:2016); CEN: Brussels, Belgium, 2016. [Google Scholar]
- International Organization for Standardization (ISO). Welding—Fusion-Welded Joints in Steel, Nickel, Titanium and Their Alloys (Beam Welding Excluded)—Quality Levels for Imperfections (ISO 5817:2014); ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Josipović, M. Behaviour of Aluminium Prefabricated Beam-to-Column Joint. Graduate Thesis, Faculty of Civil Engineering, University of Zagreb, Zagreb, Croatia, 2018; p. 135. [Google Scholar]
- Harasti, D. Experimental and Numerical Analysis of Aluminium Girder with Steel Infill. Graduate Thesis, Faculty of Civil Engineering, University of Zagreb, Zagreb, Croatia, 2018; p. 71. [Google Scholar]
- ANSYS. Workbench User’s Guide (Release 15.0); ANSYS: Canonsburg, PA, USA, 2013. [Google Scholar]
- Wyss, T. Stahldrahtseile der Transport und Förderseilen, Schweizer Druck—und Verlagshaus; Schweizer Druck und Verlagshaus: Zürich, Switzerland, 2016. [Google Scholar]





| Specimen | Fpl [kN] | Δpl [mm] | Fu [kN] | Δu [mm] |
|---|---|---|---|---|
| S1 | 60.0 | 11.0 | 86.0 | 31.2 |
| S2 | 64.0 | 13.0 | 84.0 | 30.8 |
| S3 | 53.0 | 9.50 | 72.7 | 23.6 |
| Mean value | 59.0 | 11.2 | 80.9 | 28.5 |
| Std. Dev. | 4.55 | 1.43 | 5.86 | 3.49 |
| Joint Property | S1 | S2 | S3 | Avg | Std. Dev. |
|---|---|---|---|---|---|
| Mj,R [kNm] | 17.1 | 17.6 | 16.6 | 17.1 | 0.408 |
| Mj,el [kNm] | 12.4 | 14.9 | 13.7 | 13.7 | 1.02 |
| Mj,u [kNm] | 17.9 | 18.2 | 17.2 | 17.8 | 0.419 |
| φj,Mu [mrad] | 19.9 | 15.4 | 13.9 | 16.2 | 2.55 |
| φj,u [mrad] | 39.2 | 43.9 | 63.3 | 48.8 | 10.4 |
| Sj,ini [kNm/rad] | 1641 | 1663 | 1541 | 1615 | 53.1 |
| Portal Frame Span [m]. | Stiffness Ratio fred [–] | E’=E/fred [MPa] |
|---|---|---|
| 1 | 17 | 12,200 |
| 2.5 | 43 | 4880 |
| 5 | 86 | 2440 |
| 10 | 172 | 1220 |
| 15 | 258 | 815 |
| 20 | 344 | 610 |
| E—modulus of elasticity for steel taken as E = 210 GPa | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skejić, D.; Čudina, I.; Garašić, I.; Mazzolani, F.M. Behaviour of Steel Tubular Knee Joint in Aluminium Frames with Tension-Tie Element. Appl. Sci. 2021, 11, 70. https://doi.org/10.3390/app11010070
Skejić D, Čudina I, Garašić I, Mazzolani FM. Behaviour of Steel Tubular Knee Joint in Aluminium Frames with Tension-Tie Element. Applied Sciences. 2021; 11(1):70. https://doi.org/10.3390/app11010070
Chicago/Turabian StyleSkejić, Davor, Ivan Čudina, Ivica Garašić, and Federico M. Mazzolani. 2021. "Behaviour of Steel Tubular Knee Joint in Aluminium Frames with Tension-Tie Element" Applied Sciences 11, no. 1: 70. https://doi.org/10.3390/app11010070
APA StyleSkejić, D., Čudina, I., Garašić, I., & Mazzolani, F. M. (2021). Behaviour of Steel Tubular Knee Joint in Aluminium Frames with Tension-Tie Element. Applied Sciences, 11(1), 70. https://doi.org/10.3390/app11010070







