Health Monitoring of Stress-Laminated Timber Bridges Assisted by a Hygro-Thermal Model for Wood Material
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Multi-Phase Model
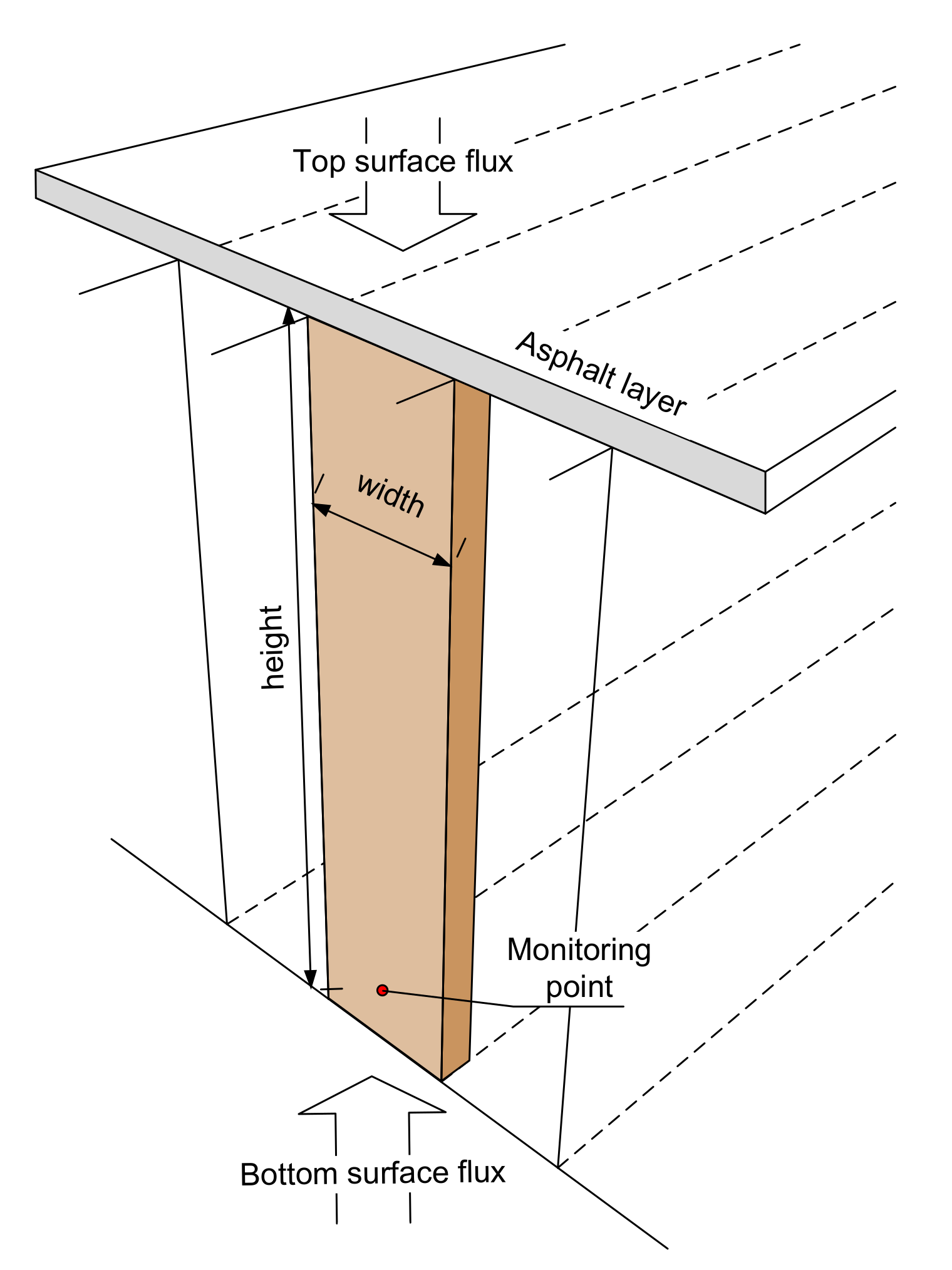
2.2. Implementation of the Hygro-Thermal Model for Stress-Laminated Timber Deck in Abaqus Code
- The model is a 3D slice of the deck far from the ends. The bottom face is exposed to the humidity and temperature of the air. The top surface is exposed only to temperature, because the top of the deck is protected from moisture by the asphalt layer.
- The asphalt layer is not modelled.
- The lateral, back and front faces are internal surfaces and therefore are not exposed to the air temperature or moisture fluxes.
- The bottom surface is sheltered from rain and without water traps.
- The model does not include the effect of solar radiation.
- The height of the model represents the thickness of the timber deck and its width varies depending on the width of the lamella, with the mesh size of the FEM typically between 5 and 10 mm.
- The effect of glue between lamellas is not considered.
- The temperature is chosen equal to the air temperature at the beginning of the analysis.
- The concentration of bound water is calculated as , where is the moisture content in equilibrium with the initial air relative humidity at the beginning of the monitoring. This is obtained from the temperature dependent sorption isotherm listed in Table A2 of Appendix A.
- The concentration of water vapour is calculated by using Equations (7)–(9) and the and .
- The first boundary condition of Equation (6) applies on the top and bottom surfaces.
- The heat flux and thermal flux act on the bottom surface exposed to the air temperature and relative humidity.
- Only the heat flux acts on the top protected by the asphalt.
- There are no fluxes on the lateral (internal) surfaces.
2.3. Case-Study: Sørliveien Bridge
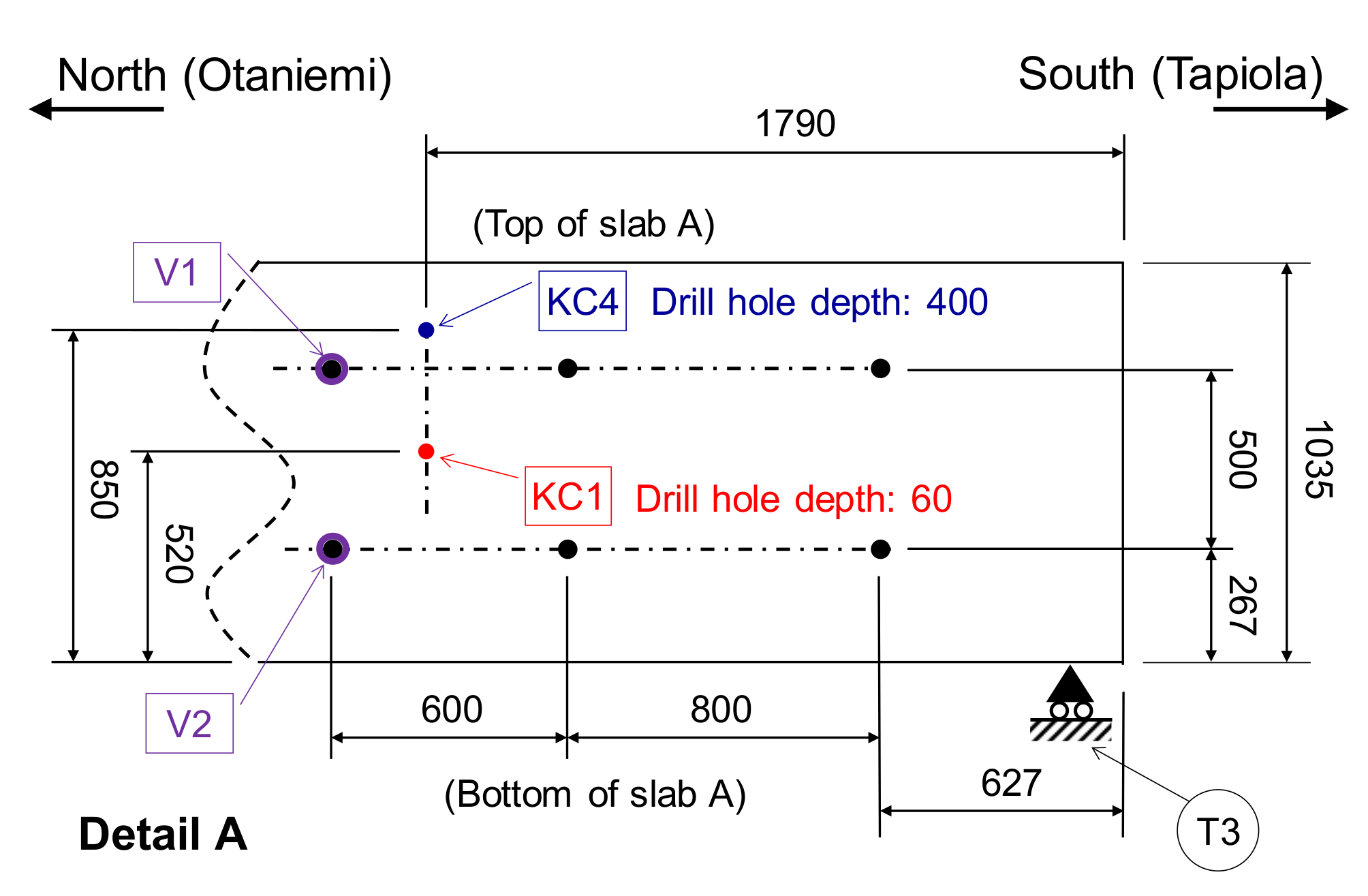
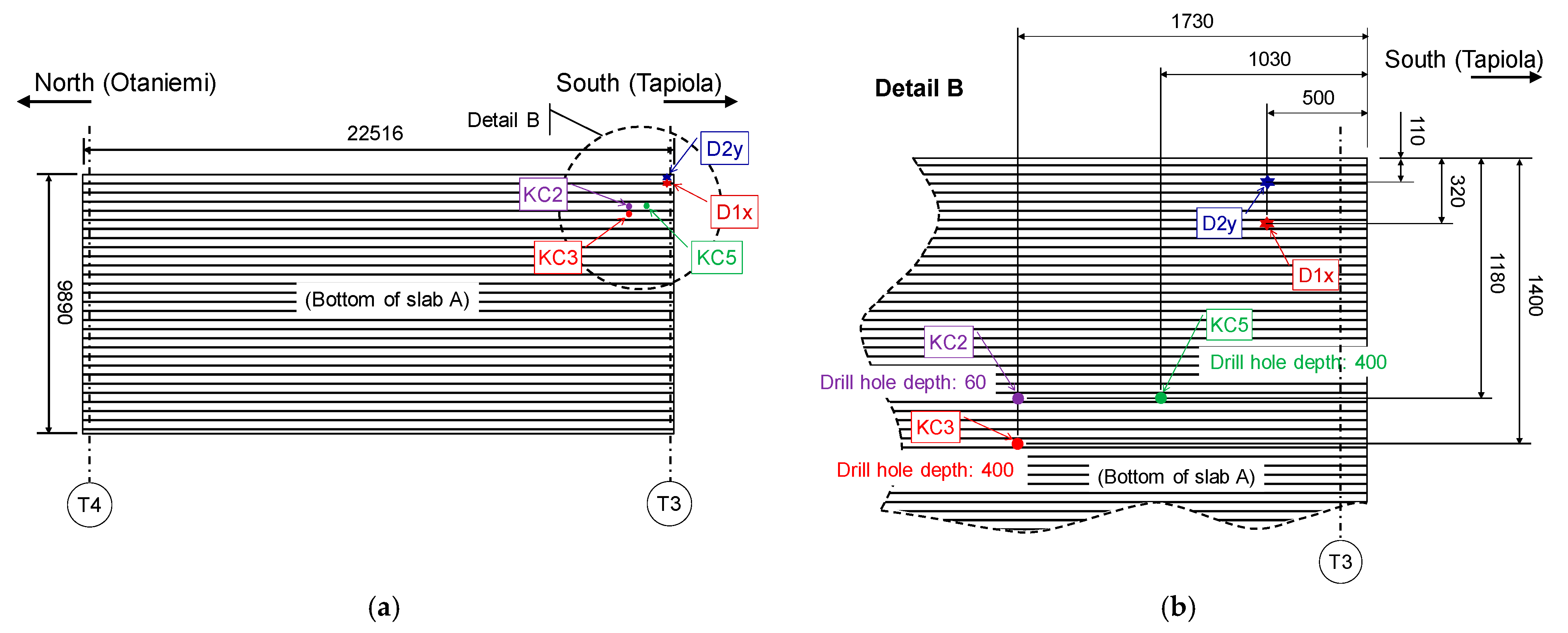
2.4. Case-Study: Tapiola Bridge
3. Results
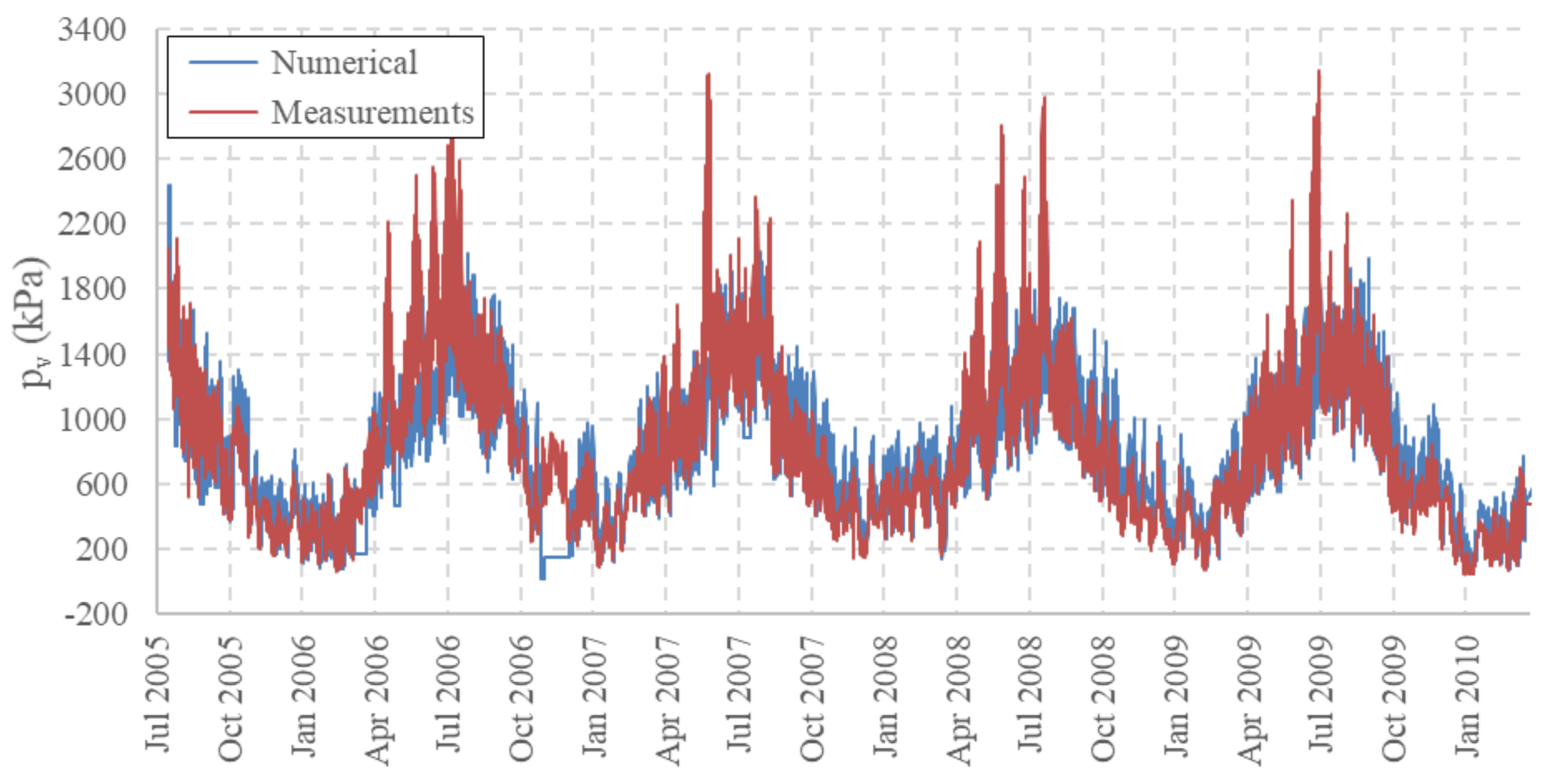
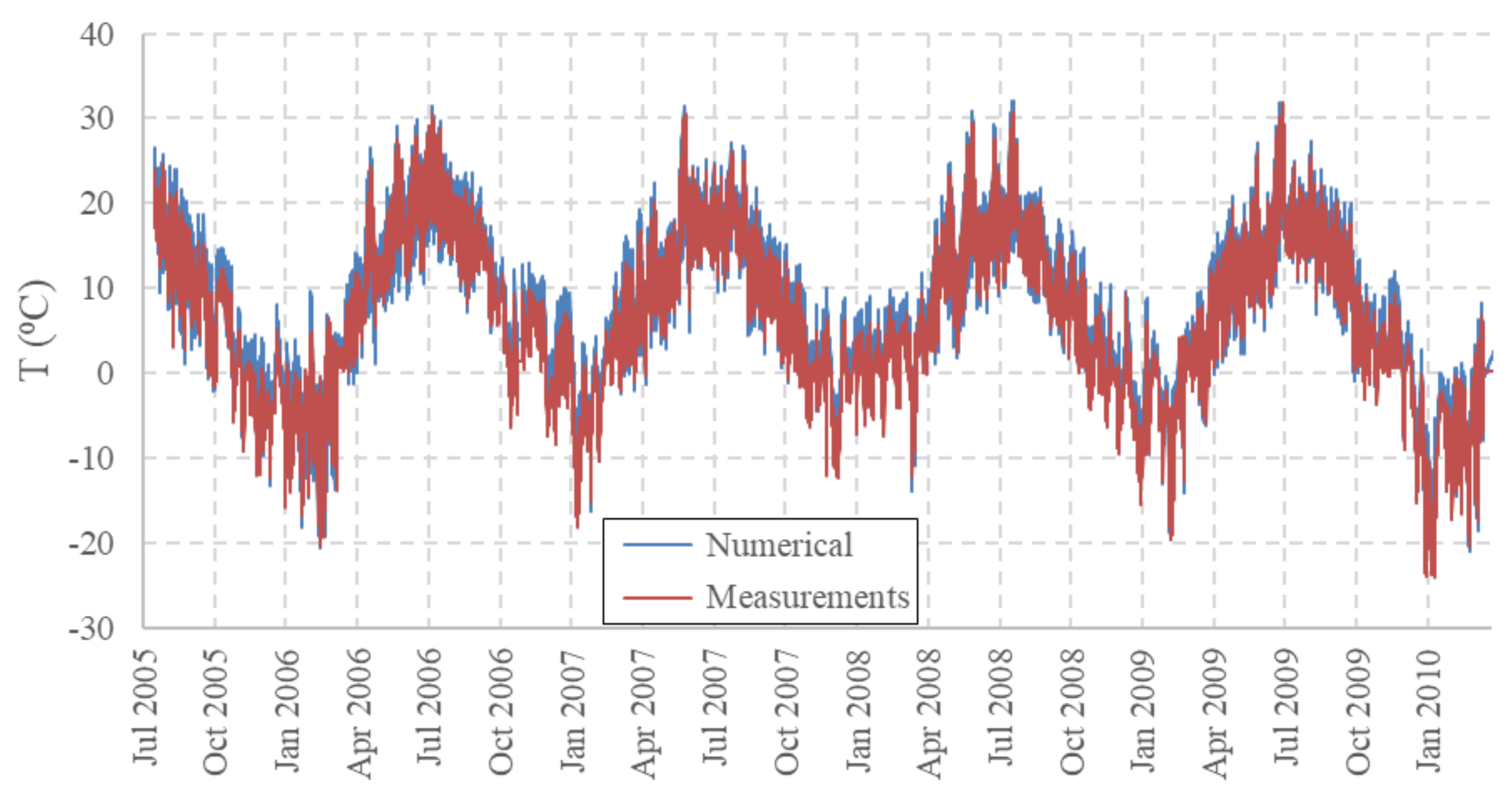
3.1. Hygro-Thermal Response of the Deck of Sørliveien Bridge
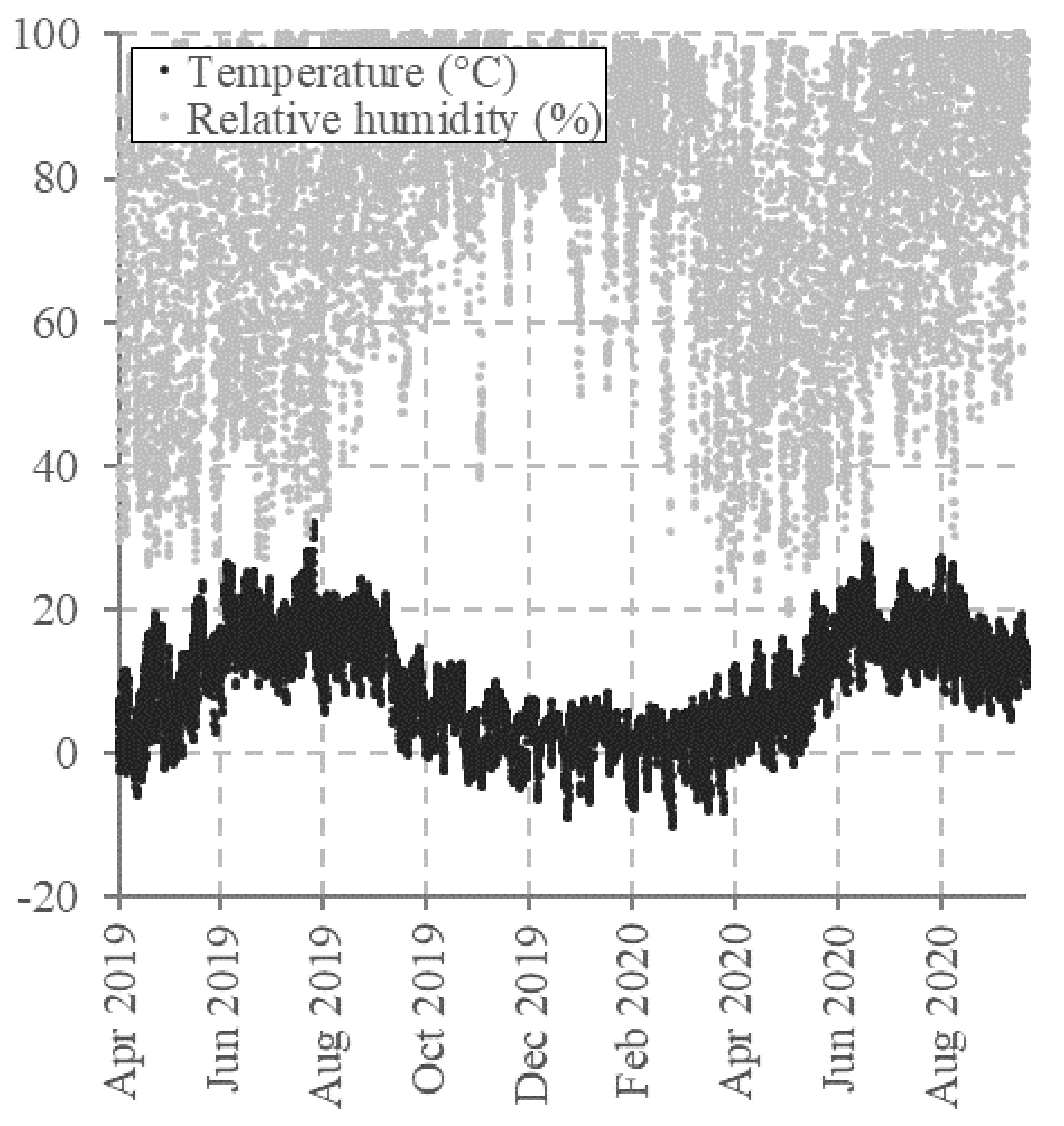
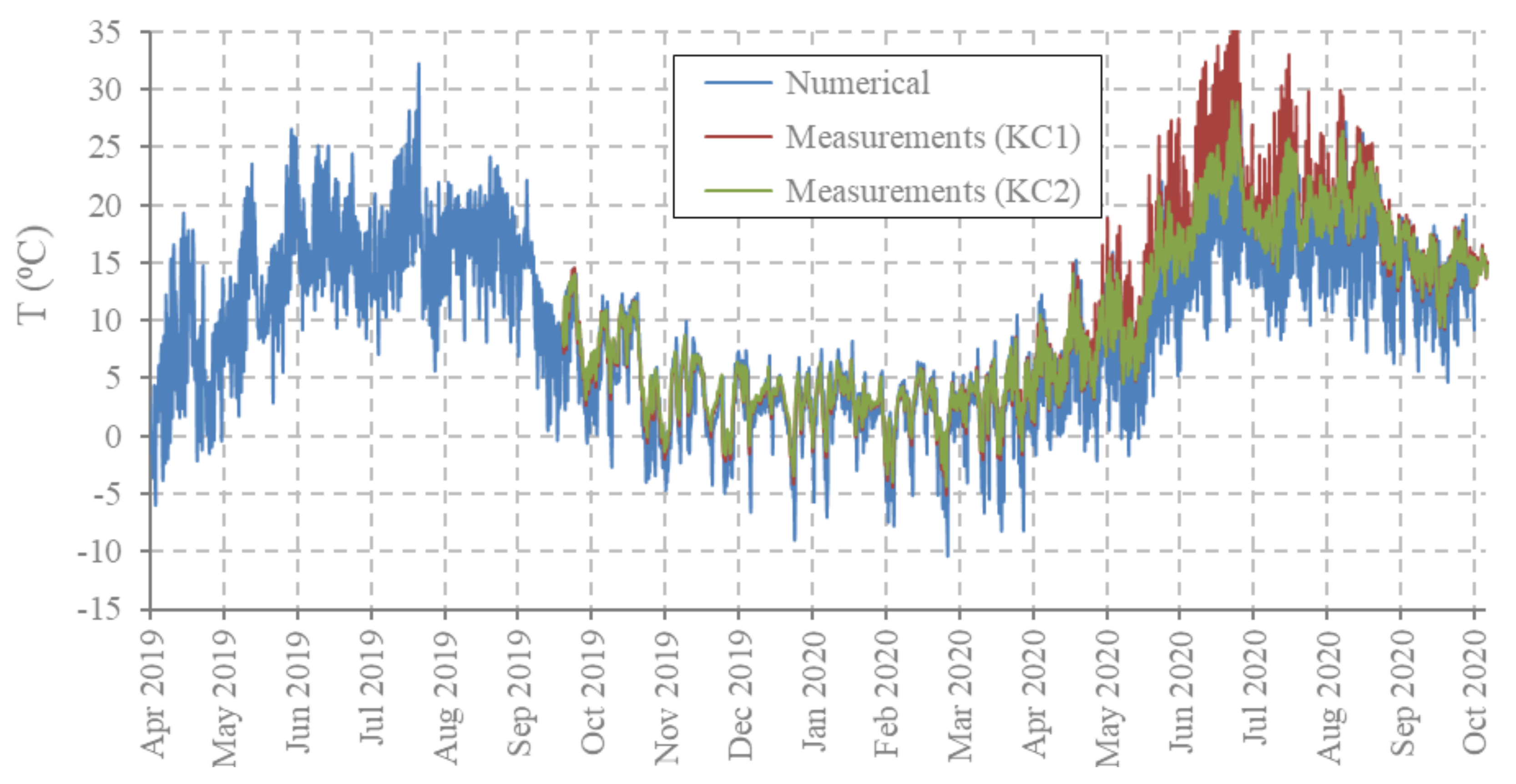
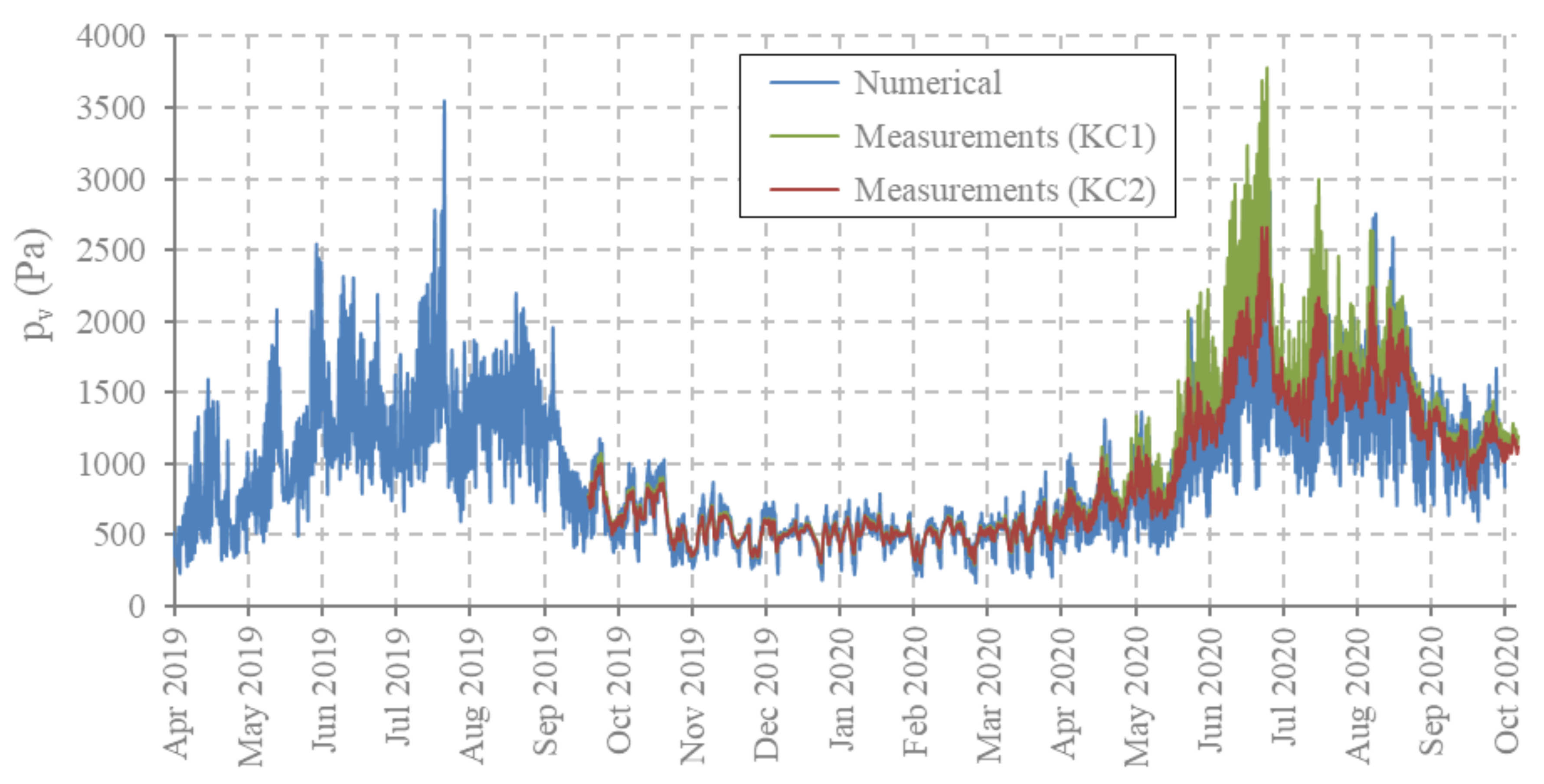
3.2. Hygro-Thermal Response of the Deck of Tapiola Bridge
4. Discussion
- Referring to Table 4, the MC values on the bottom surface span in a range between 4% (reached at the beginning of summer 2006) and 25.8% (autumn 2005), are highest during the first year of the analysis and more stable during the successive years (Figure 12). The minimum and maximum MC values at 20 mm from the bottom surface are 12.5% at the beginning of the summer 2006, and 19% at the end of winter 2010. The results show that no significant changes of the average moisture content would be expected after the first year of the bridge service life, i.e., from June 2006 to January 2010.
- High levels of MC over 20% were found only on the exposed surface at the bottom deck and in locations very close to this surface (Figure 12). These MC levels could be also critical for the wood durability [3], however the decay is a major problem mainly in the presence of liquid water due e.g., to rain and eventual water traps, and these cases were not investigated in the present work.
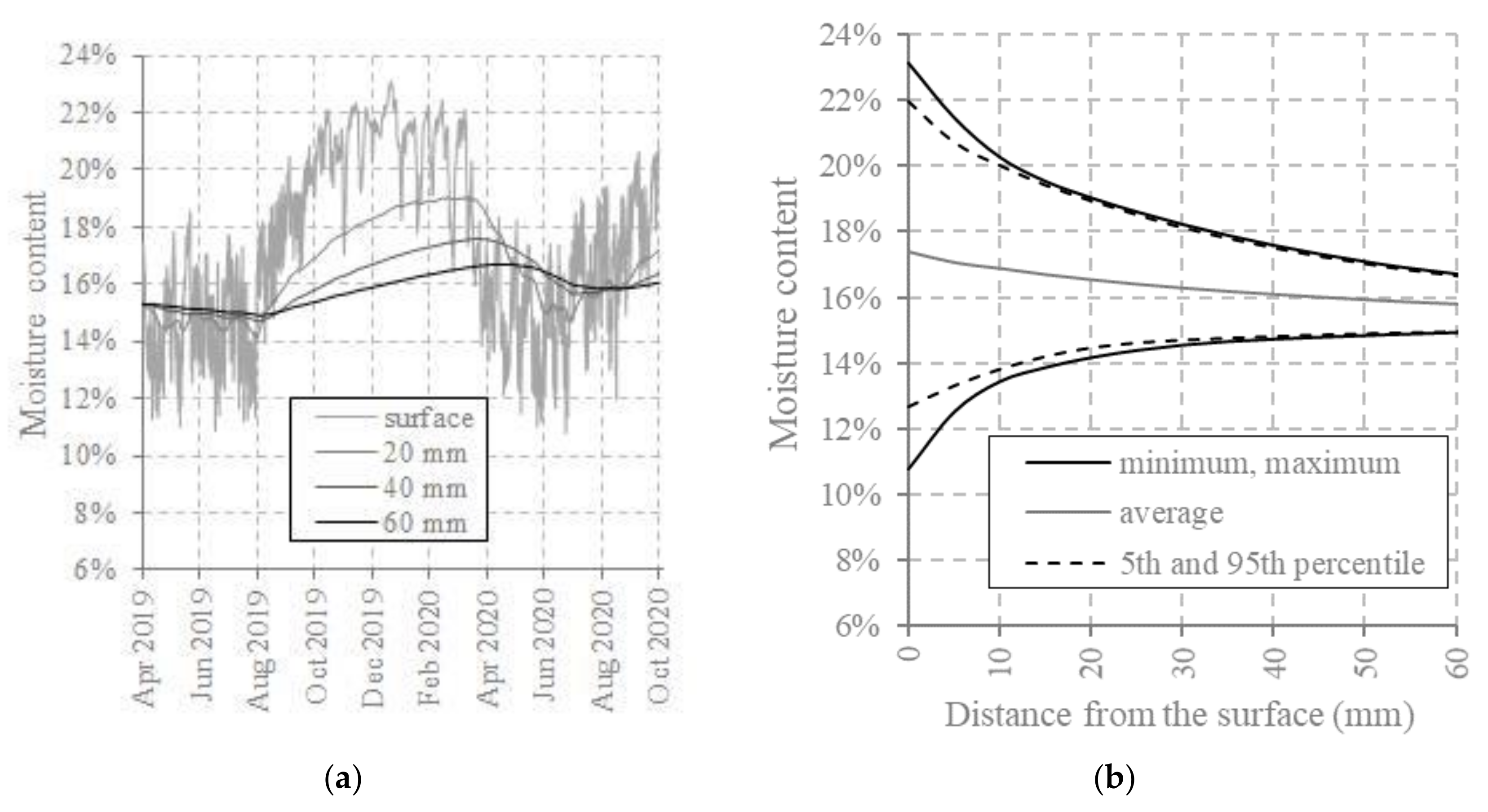
- Referring to Table 5, the moisture contents on the bottom surface varies between 10.8%, reached at the beginning of the summer, and 23% at the beginning of the winter. In the internal locations, the maximum and minimum moisture contents are reached earlier depending on the maximum moisture penetration depth, which is about 200 mm (see Table 5). The maximum and minimum MC values in the location of the humidity-temperature sensor at 60 mm from the bottom surface are 16.7%, at the beginning of spring, and 14.9% at the end of summer.
- High levels of MC (i.e., >20%) were found only on the exposed bottom surface and in locations very close to this surface. Compared to the MCs of Sørliveien Bridge, the peaks remained below 23% (Figure 15). This is because Tapiola Bridge is protected, even if the used paint has low vapour resistance (see Table A3 of Appendix A).
- Considering the MC results of Sørliveien Bridge, it could be estimated that also for Tapiola Bridge the average values of MC will not change significantly during the successive years.
- The envelope curves shown in Figure 15b indicate similar levels of moisture gradients close to the surface as those of the Sørliveien Bridge’s deck (Figure 12b). The average MCs are around 16% up to 20 mm depth, and remain at an almost constant level up until 60 mm depth in Tapiola Bridge’s deck. Previous hygro-thermal models of SLTDs, based on single-phase moisture transport, found cupping deformations of around 16 mm and steel bar force losses of around 33% at these MC levels after 15 months [9].
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Water vapour diffusion tensor
| Components of reduction factor longitudinal transverse (*) |
Bound water diffusion tensor
| Components of diagonal tensor longitudinal transverse |
Thermal conductivity tensor
| Components of reduction factor longitudinal transverse |
| Specific heat Wood density | |
| Enthalpy of bound water | |
| Enthalpy of water vapour | |
| Sorption reaction rate function | Constants |
Anderson–McCarthy model for sorption isotherms
| See Table A2 |
|
Permeances of the painted wood referred to wood temperature and air temperature: Thermal emission: = 20 [W m−2 K−1] | See Table A3 |
| α | n | b10α [-] | b11α [K−1] | b20α [-] | b21α [K−1] |
|---|---|---|---|---|---|
| a | 1 | 7.719 | −0.011 | 5.079 | 0.046 |
| d | 1 | 9.739 | −0.017 | −13.419 | 0.100 |
| Paint | Permeance [kg/m2 s Pa] |
|---|---|
| weak paint | 4.0 × 10−9 |
| uncoated wood | 5.0 × 10−9 |
Appendix B
References
- European Committee for Standardization. EN 1990: Eurocode: Basis of Structural Design; European Committee for Standardization: Brussels, Belgium, 2002. [Google Scholar]
- Obataya, E. Characteristics of aged wood and Japanese traditional coating technology for wood protection. In Proceedings of the Actes de la Journée D’étude Conserver Aujourd’hui: Les “Vieillissements” du Bois, Cité de la Musique, Paris, France, 2 February 2007. [Google Scholar]
- Brischke, C.; Meyer-Veltrup, L. Modelling timber decay caused by brown rot fungi. Mater. Struct. 2016, 49, 3281–3291. [Google Scholar] [CrossRef]
- Wacker, J. Cold Temperature Effect on Stress-Laminated Timber Bridges: A Laboratory Study; Research Paper FPL–RP–605; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2003.
- Scharmacher, F.; Müller, A.; Brunner, M. Asphalt surfacing on timber bridges. In Proceedings of the COST-Timber Bridges, Biel, Switzerland, 25–26 September 2014; Franke, S., Franke, B., Widmann, R., Eds.; Bern University of Applied Sciences: Bern, Switzerland, 2014. [Google Scholar]
- Aasheim, E. Nordic timber bridge program—An overview. In Proceedings of the International Wood Engineering Conference, New Orleans, LA, USA, 21–28 October 1996; Gopu, V.K.A., Ed.; International Wood Engineering Conference: New Orleans, LA, USA, 1996. [Google Scholar]
- Horn, H. Rapport Oppdrag Nr. 310332: Monitoring Five Timber Bridges in Norway—Results 2012; Norsk Treteknisk Institut: Oslo, Norway, 2013. [Google Scholar]
- Ministry of the Environment, Department of the Built Environment. Wood Building Programme. Available online: https://ym.fi/en/wood-building (accessed on 14 November 2020).
- Pousette, A.; Malo, K.; Thelandersson, S.; Fortino, S.; Salokangas, L.; Wacker, J. Durable Timber Bridges—Final Report and Guidelines; SP Report 25; Research Institutes of Sweden RISE: Skellefteå, Sweden, 2017. [Google Scholar]
- Fortino, S.; Genoese, A.; Genoese, A.; Nunes, L.; Palma, P. Numerical modelling of the hygro-thermal response of timber bridges during their service life: A monitoring case-study. Constr. Build. Mater. 2013, 47, 1225–1234. [Google Scholar] [CrossRef]
- Fortino, S.; Hradil, P.; Genoese, A.; Genoese, A.; Pousette, A. Numerical hygro-thermal analysis of coated wooden bridge members exposed to Northern European climates. Constr. Build. Mater. 2019, 208, 492–505. [Google Scholar] [CrossRef]
- Fortino, S.; Hradil, P.; Metelli, G. Moisture-induced stresses in large glulam beams. Case study: Vihantasalmi Bridge. Wood Mater. Sci. Eng. 2019, 14, 366–380. [Google Scholar] [CrossRef]
- Fragiacomo, M.; Fortino, S.; Tononi, D.; Usardi, I.; Toratti, T. Moisture-induced stresses perpendicular to grain in cross-sections of timber members exposed to different climates. Eng. Struct. 2011, 33, 3071–3078. [Google Scholar] [CrossRef]
- Niklewski, J.; Fredriksson, M. The effects of joints on the moisture behaviour of rain exposed wood: A numerical study with experimental validation. Wood Mater. Sci. Eng. 2019, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Florisson, S.; Vessby, J.; Mmari, W.; Ormarsson, S. Three-dimensional orthotropic nonlinear transient moisture simulation for wood: Analysis on the effect of scanning curves and nonlinearity. Wood Sci. Technol. 2020, 54, 1197–1222. [Google Scholar] [CrossRef]
- Krabbenhøft, K. Moisture Transport in Wood: A Study of Physical-Mathematical Models and their Numerical Implementation. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2004. [Google Scholar]
- Frandsen, H.L. Selected Constitutive models for simulating the hygromechanical response of wood. Ph.D. Thesis, Department of Civil Engineering Aalborg University, Aalborg, Denmark, 2007. [Google Scholar]
- Eitelberger, J.; Hofstetter, K.; Dvinskikh, S.V. A multi-scale approach for simulation of transient moisture transport processes in wood below the fiber saturation point. Compos. Sci. Technol. 2011, 71, 1727–1738. [Google Scholar] [CrossRef]
- Konopka, D.; Kaliske, M. Transient multi-Fickian hygro-mechanical analysis of wood. Comput. Struct. 2018, 197, 12–27. [Google Scholar] [CrossRef]
- Huc, S.; Svensson, S.; Hozjan, T. Hygro-mechanical analysis of wood subjected to constant mechanical load and varying relative humidity. Holzforschung 2018, 72, 863–870. [Google Scholar] [CrossRef]
- Autengruber, M.; Lukacevic, M.; Füssl, J. Finite-element-based moisture transport model for wood including free water above the fiber saturation point. Int. J. Heat Mass Transf. 2020, 161, 120228:1–120228:21. [Google Scholar] [CrossRef]
- Svensson, S.; Turk, G.; Hozjan, T. Predicting moisture state of timber members in a continuously varying climate. Eng. Struct. 2011, 33, 3064–3070. [Google Scholar] [CrossRef]
- Thalla, O.; Stiros, S.C. Wind-Induced Fatigue and Asymmetric Damage in a Timber Bridge. Sensors 2018, 18, 3867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kepp, H.; Dyken, T. Thermal cction on timber bridges temperature variation measured in the deck of 3 timber bridges in Norway. In Proceedings of the International Conference Timber Bridges (ICTB2010), Lillehammer, Norway, 12–15 September 2010; Malo, K.A., Kleppe, O., Dyken, T., Eds.; Tapir Academic Press: Trondheim, Norway, 2010. [Google Scholar]
- Dyken, T.; Kepp, H. Monitoring the moisture content of timber bridges. In Proceedings of the International Conference Timber Bridges (ICTB2010), Lillehammer, Norway, 12–15 September 2010; Malo, K.A., Kleppe, O., Dyken, T., Eds.; Tapir Academic Press: Trondheim, Norway, 2010. [Google Scholar]
- Frandsen, H.L. Modelling of Moisture Transport in Wood: State of the Art and Analytic Discussion, 2nd ed.; Aalborg University: Aalborg, Denmark, 2005. [Google Scholar]
- Vaisala Oyj Home Page. Available online: https://www.vaisala.com/ (accessed on 24 November 2020).
- Hottinger Brüel & Kjaer GmbH Home Page. Available online: https://www.hbm.com/ (accessed on 24 November 2020).
- Opkon Optik Elektronik Kontrol San. Tic. Ltd. Şti Home Page. Available online: https://www.opkon.com.tr/ (accessed on 24 November 2020).
- Koski, K. Instrumentation of Tapiolantien Risteyssilta (Bridge); Research Report VTT-R-00837-19; Technical Research Centre of Finland: Espoo, Finland, 2019. [Google Scholar]
- Advantech, Co., Ltd. Home Page. Available online: https://www.advantech.com/ (accessed on 24 November 2020).
- National Instruments. Home Page. Available online: http://www.ni.com/ (accessed on 24 November 2020).
- DWS remote Control. Home Page. Available online: https://www.dwservice.net/ (accessed on 24 November 2020).
- Phoenix Contact. Home Page. Available online: https://www.phoenixcontact.com/ (accessed on 24 November 2020).
- Tikkurila Valtti Color Safety Data Sheet. Available online: https://tikkurila.com/sites/default/files/valtti-color-sds-en.pdf (accessed on 14 November 2020).
- Dietsch, P.; Gamper, A.; Merk, M.; Winter, S. Monitoring building climate and timber moisture gradient in large-span timber structures. J. Civil. Struct. Health Monit. 2015, 5, 153–165. [Google Scholar] [CrossRef]





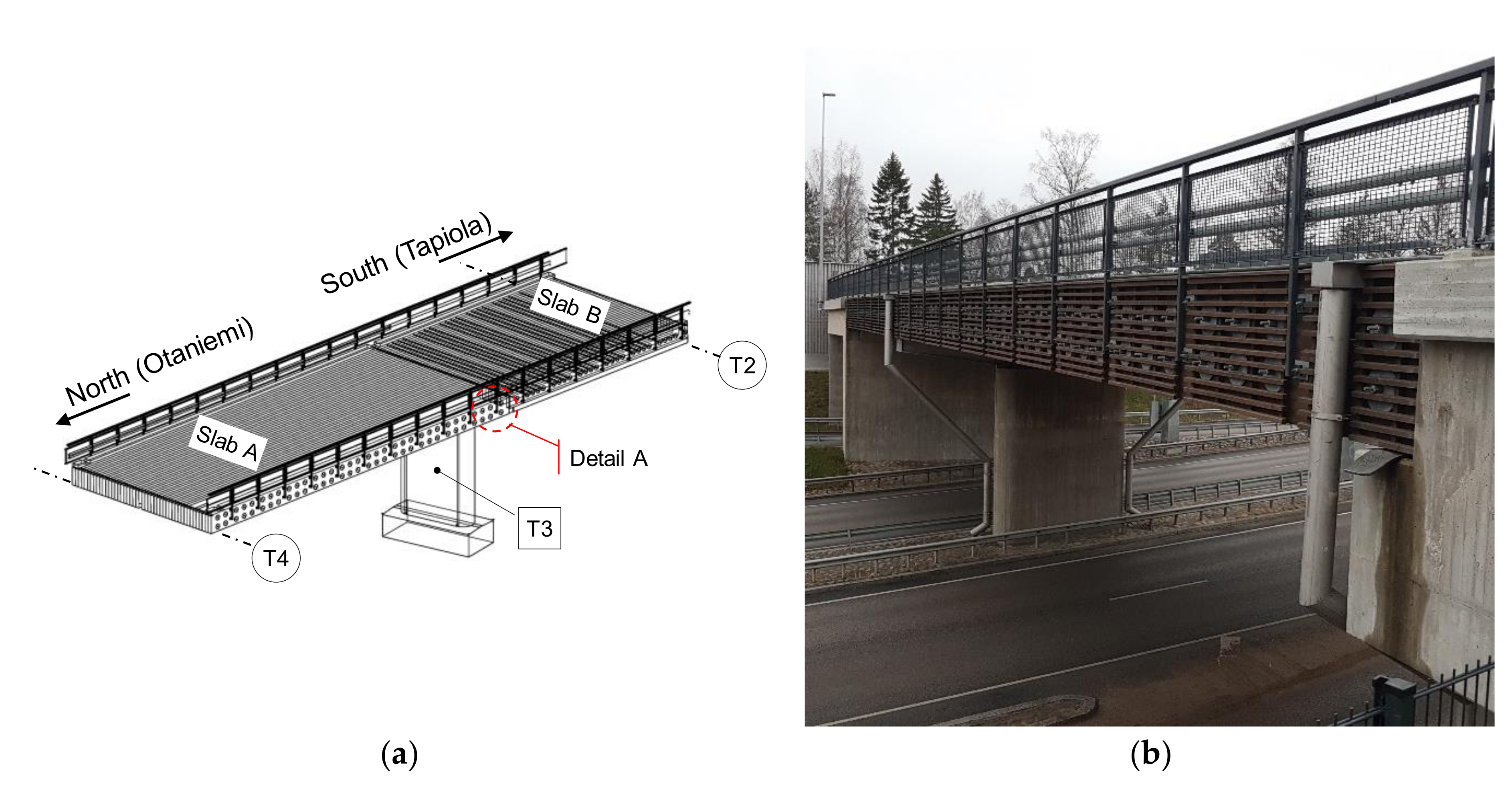
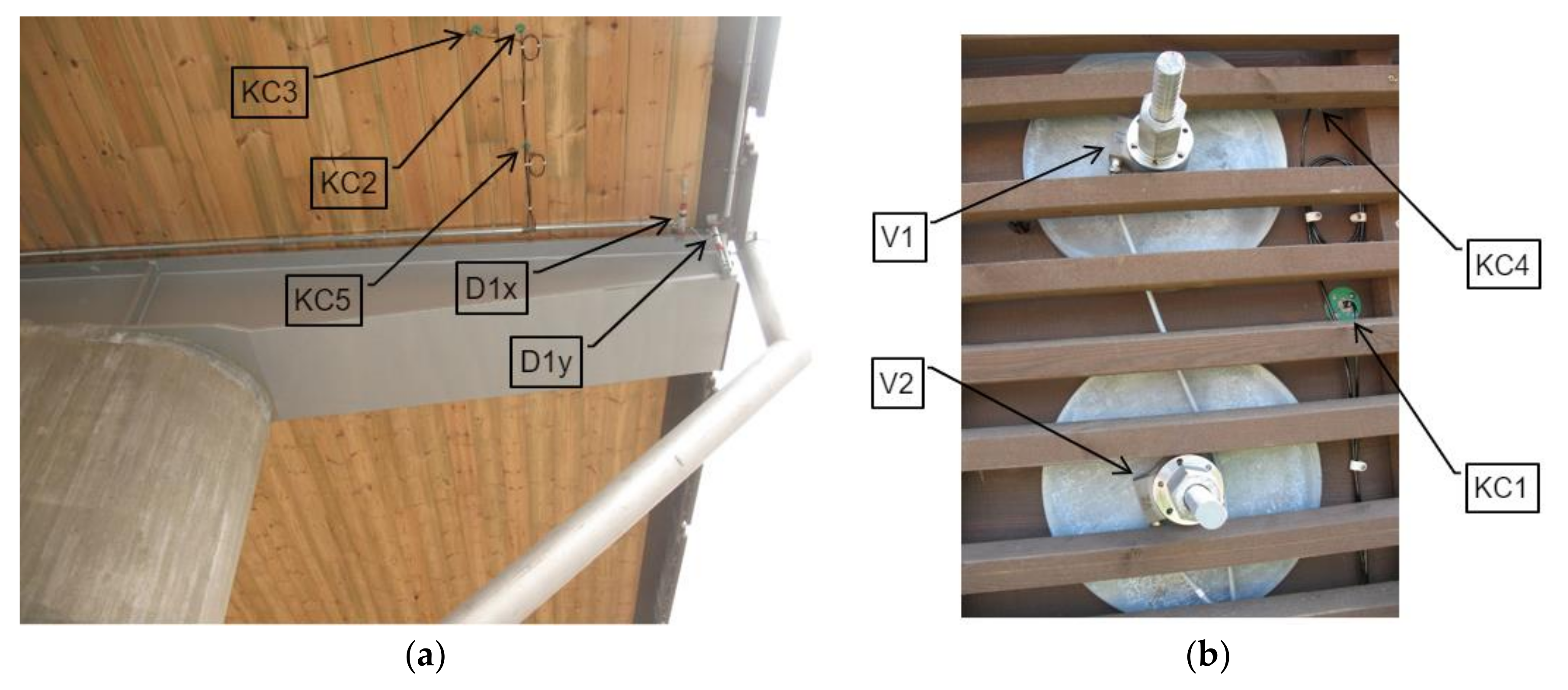

| Span | 13.45 m | 22.13 m | 11.8 m |
| Material | stress-laminated timber | stress-laminated timber | concrete |
| Timber deck thickness | 0.765 m | 1.035 m | n/a |
| Useful deck width | 9.79 m | 9.79 m | 13.13 m |
| No. | ID | Sensor Type | Model |
|---|---|---|---|
| 1 | KC1 | Humidity and temperature | HMP110 [27] |
| 2 | KC2 | Humidity and temperature | HMP110 |
| 3 | KC3 | Humidity and temperature | HMP110 |
| 4 | KC4 | Humidity and temperature | HMP110 |
| 5 | KC5 | Humidity and temperature | HMP110 |
| 6 | V1 | Force | C6A [28] |
| 7 | V2 | Force | C6A |
| 8 | D1x | Slab longitudinal displacement | ELPC100 linear potentiometer of OPKON [29] |
| 9 | D2y | Slab vertical displacement | ELPC 100 linear potentiometer of OPKON |
| Industrial PC: | Advantech [31] |
| Measurement software: | Labview [32] |
| Remote desktop software: | DWAgent [33] |
| Data acquisition chassis: | NI cDAQ-9174 [32] |
| Data acquisition devices: | NI 9211 (thermocouple) [32] |
| NI 9205 (temperature, moisture) [32] | |
| NI 9237 (Force) [33] | |
| Power supply: | Quint Power [34] |
| Enclosure internal thermostat | |
| Enclosure heater | |
| Thermocouples | |
| Distance from Bottom (mm) | Max MC (%) | Date | Min MC (%) | Date |
|---|---|---|---|---|
| 0 | 25.8 | 31 October 2005 | 4 | 26 May 2006 |
| 6 | 23.2 | 12 November 2005 | 8.9 | 27 May 2006 |
| 12 | 21.2 | 19 January 2008 | 11.1 | 28 May 2006 |
| 20 | 19 | 26 February 2010 | 12.5 | 7 June 2006 |
| Distance from Bottom (mm) | Max MC (%) | Date | Min MC (%) | Date |
|---|---|---|---|---|
| 0 | 23.1 | 25 December 2019 | 10.8 | 25 June 2020 |
| 20 | 19 | 15 March 2020 | 14.1 | 8 August 2019 |
| 60 | 16.7 | 19 April 2020 | 14.9 | 10 August 2019 |
| 200 | 15.4 | 30 September 2020 | 15.3 | 18 December 2019 |
| 400 | 15.3 | 12 April 2019 | 15.3 | 25 June 2020 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fortino, S.; Hradil, P.; Koski, K.; Korkealaakso, A.; Fülöp, L.; Burkart, H.; Tirkkonen, T. Health Monitoring of Stress-Laminated Timber Bridges Assisted by a Hygro-Thermal Model for Wood Material. Appl. Sci. 2021, 11, 98. https://doi.org/10.3390/app11010098
Fortino S, Hradil P, Koski K, Korkealaakso A, Fülöp L, Burkart H, Tirkkonen T. Health Monitoring of Stress-Laminated Timber Bridges Assisted by a Hygro-Thermal Model for Wood Material. Applied Sciences. 2021; 11(1):98. https://doi.org/10.3390/app11010098
Chicago/Turabian StyleFortino, Stefania, Petr Hradil, Keijo Koski, Antti Korkealaakso, Ludovic Fülöp, Hauke Burkart, and Timo Tirkkonen. 2021. "Health Monitoring of Stress-Laminated Timber Bridges Assisted by a Hygro-Thermal Model for Wood Material" Applied Sciences 11, no. 1: 98. https://doi.org/10.3390/app11010098
APA StyleFortino, S., Hradil, P., Koski, K., Korkealaakso, A., Fülöp, L., Burkart, H., & Tirkkonen, T. (2021). Health Monitoring of Stress-Laminated Timber Bridges Assisted by a Hygro-Thermal Model for Wood Material. Applied Sciences, 11(1), 98. https://doi.org/10.3390/app11010098






