Reliability-Based Design Optimization of Structures Using Complex-Step Approximation with Sensitivity Analysis
Abstract
:1. Introduction
2. Reliability Analysis and Reliability-Based Design Optimization
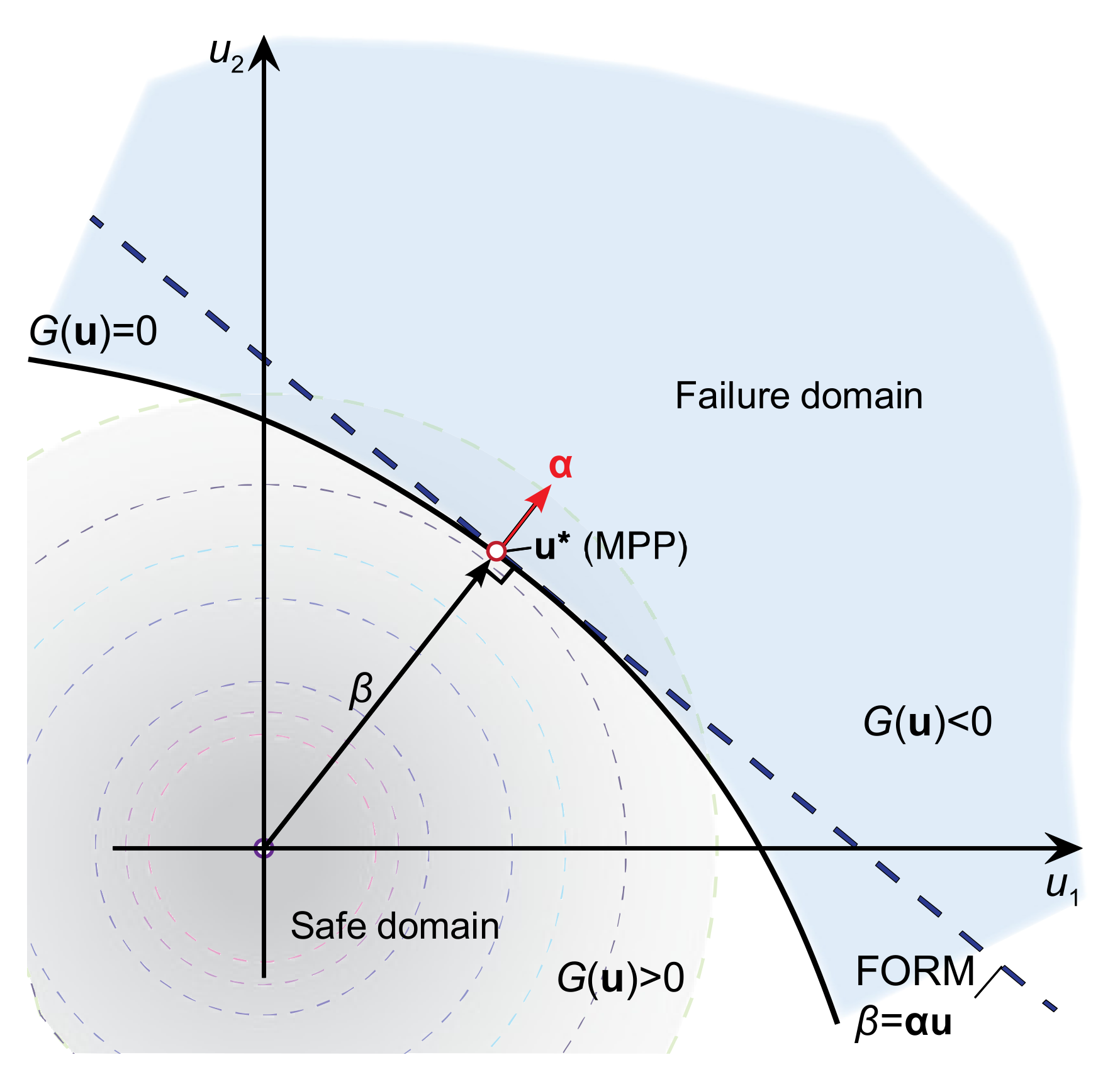
2.1. Reliability Analysis Using the First-Order Reliability Method
2.2. Reliability-Based Design Optimization
2.3. Sensitivity Analysis
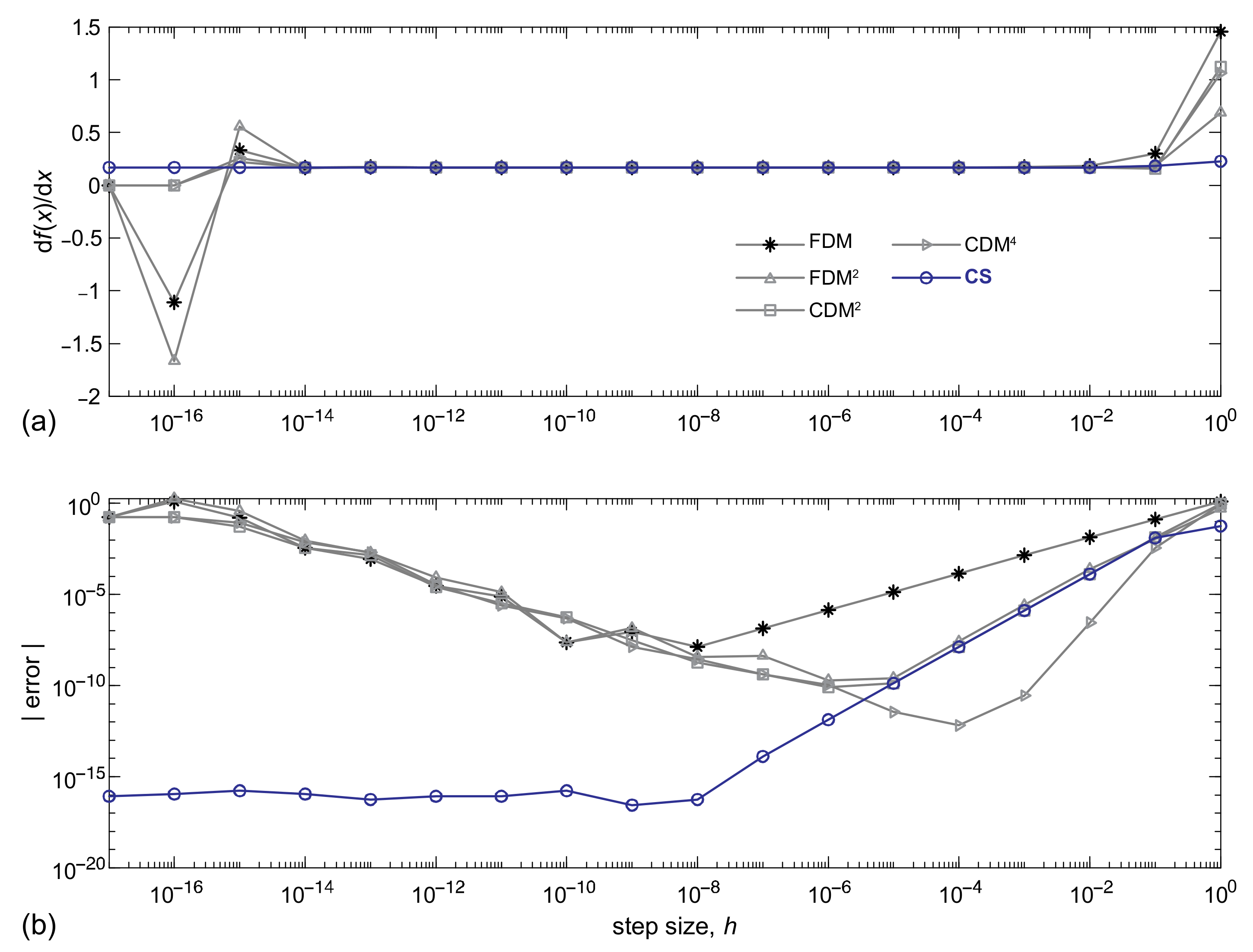
3. Complex-Step Approximation and Finite Difference Method
4. Proposed Method of Sensitivity Analysis
5. Numerical Applications
5.1. Comparative Study of the Accuracy of Complex-Step and Finite Difference Methods
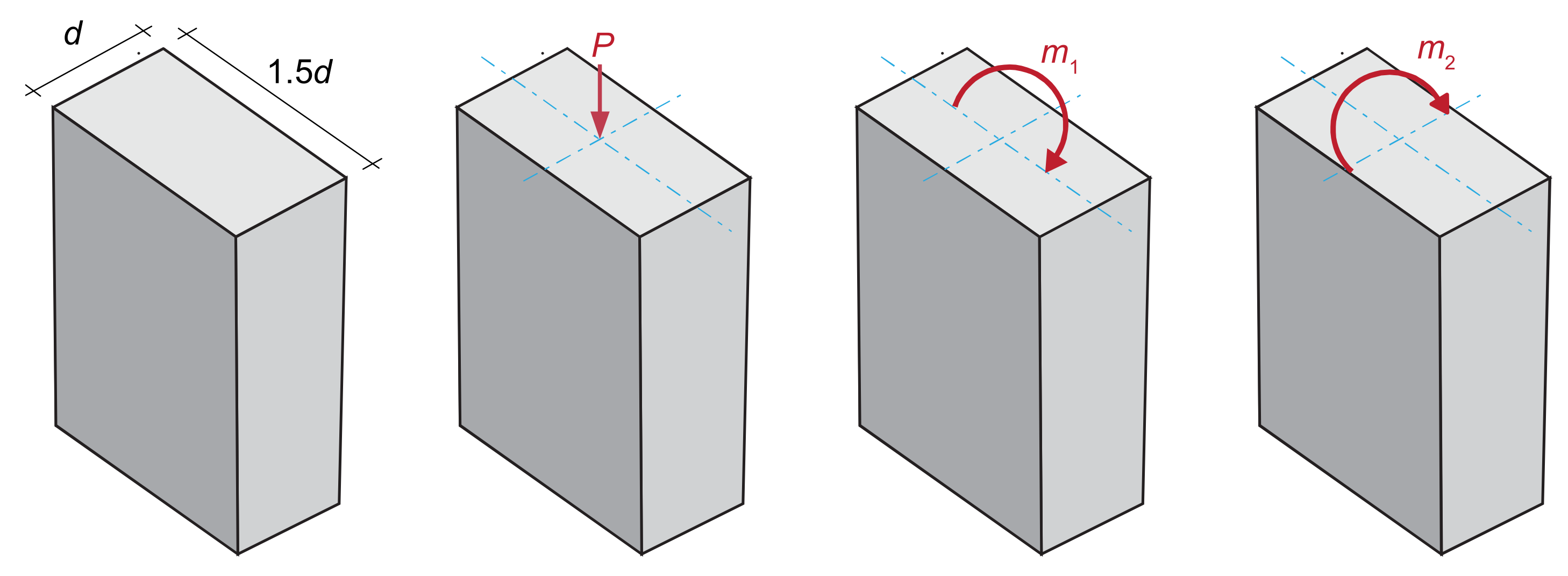
5.2. RBDO of the Short Column under a Probabilistic Strength Constraint
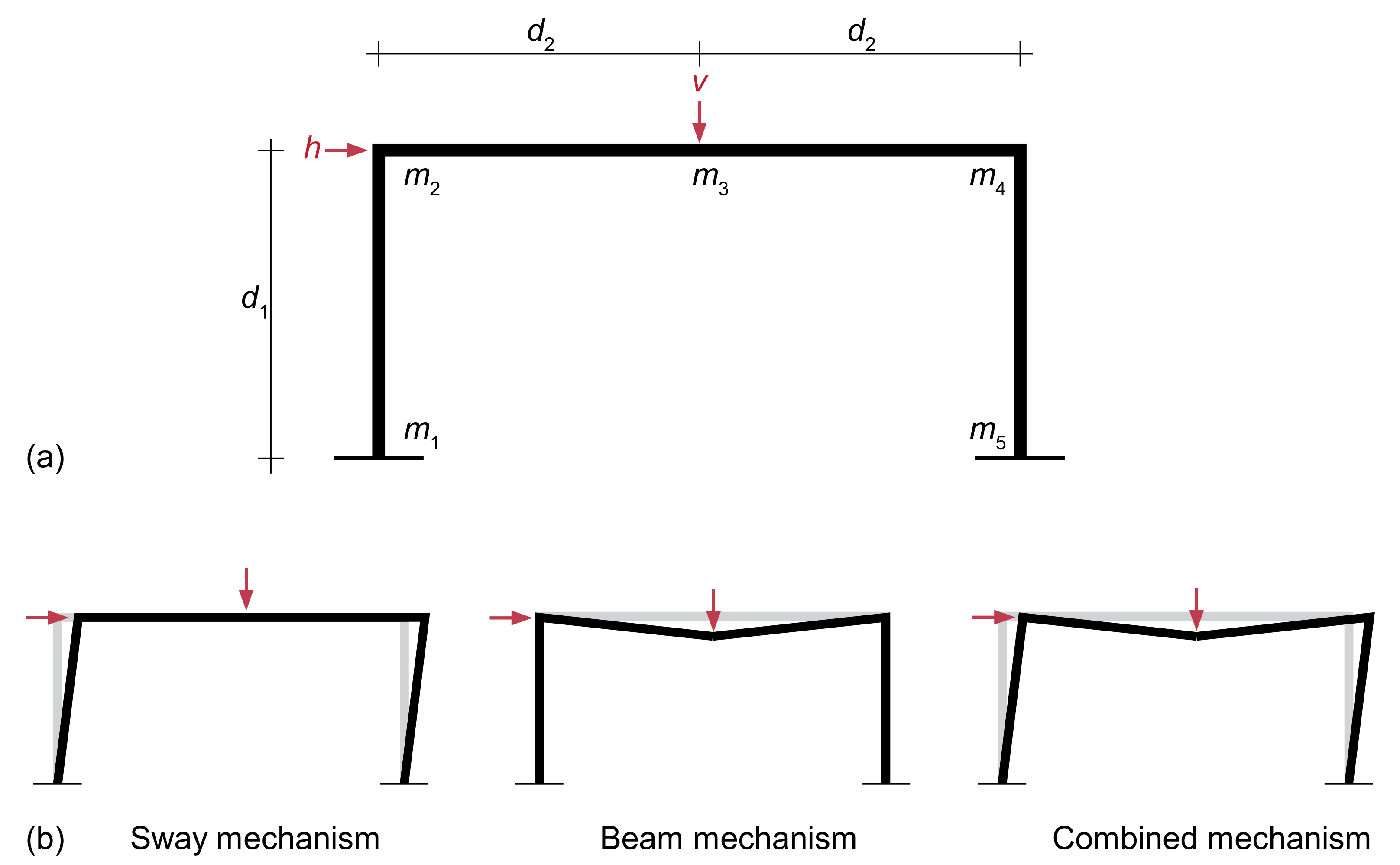
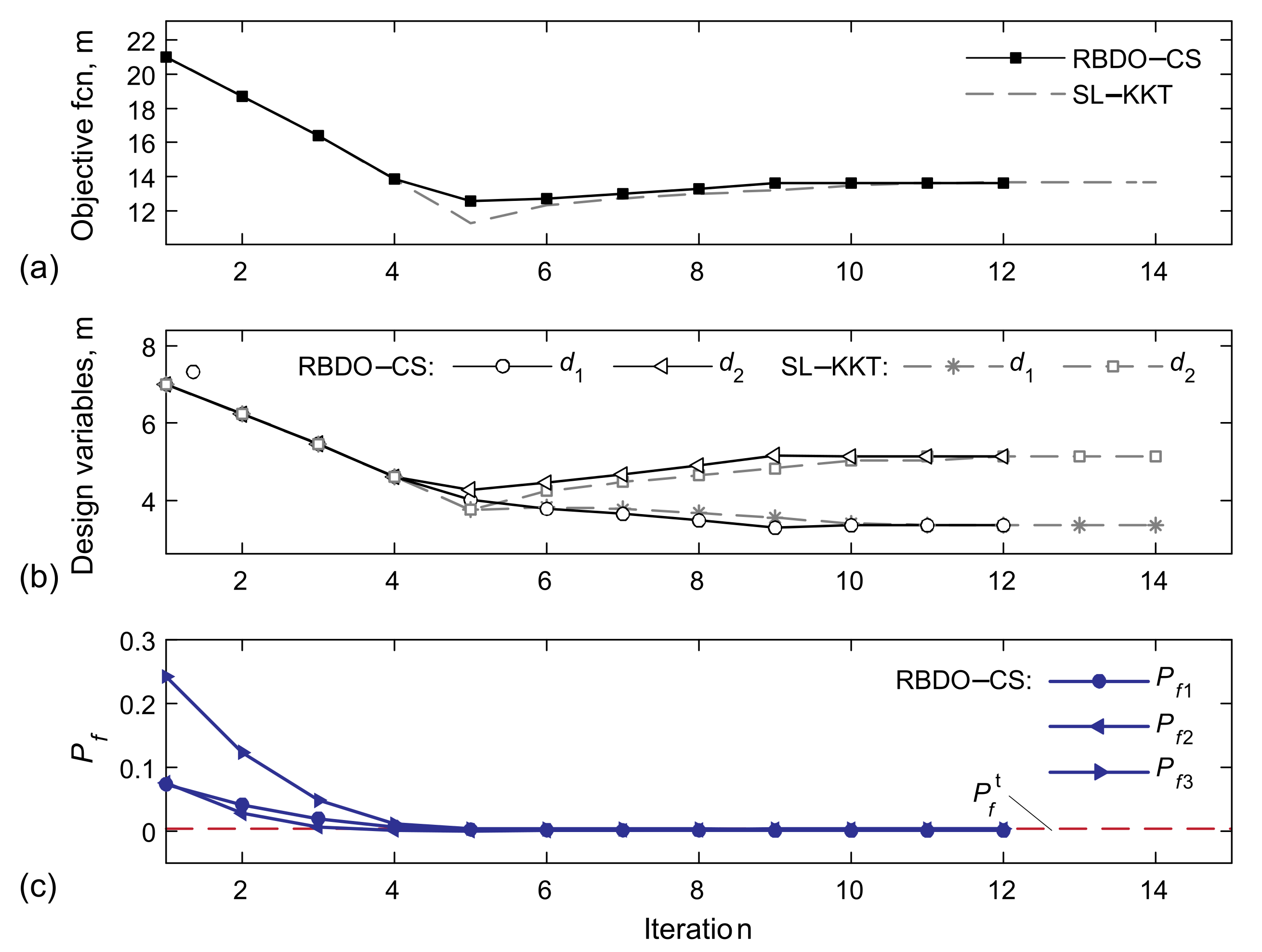
5.3. RBDO of the Ductile Frame Structure Subjected to Probabilistic Moment Strength Constraints
| Limit-State Function | ||
| 1.452 | 0.073 | |
| 1.435 | 0.076 | |
| 0.701 | 0.242 |
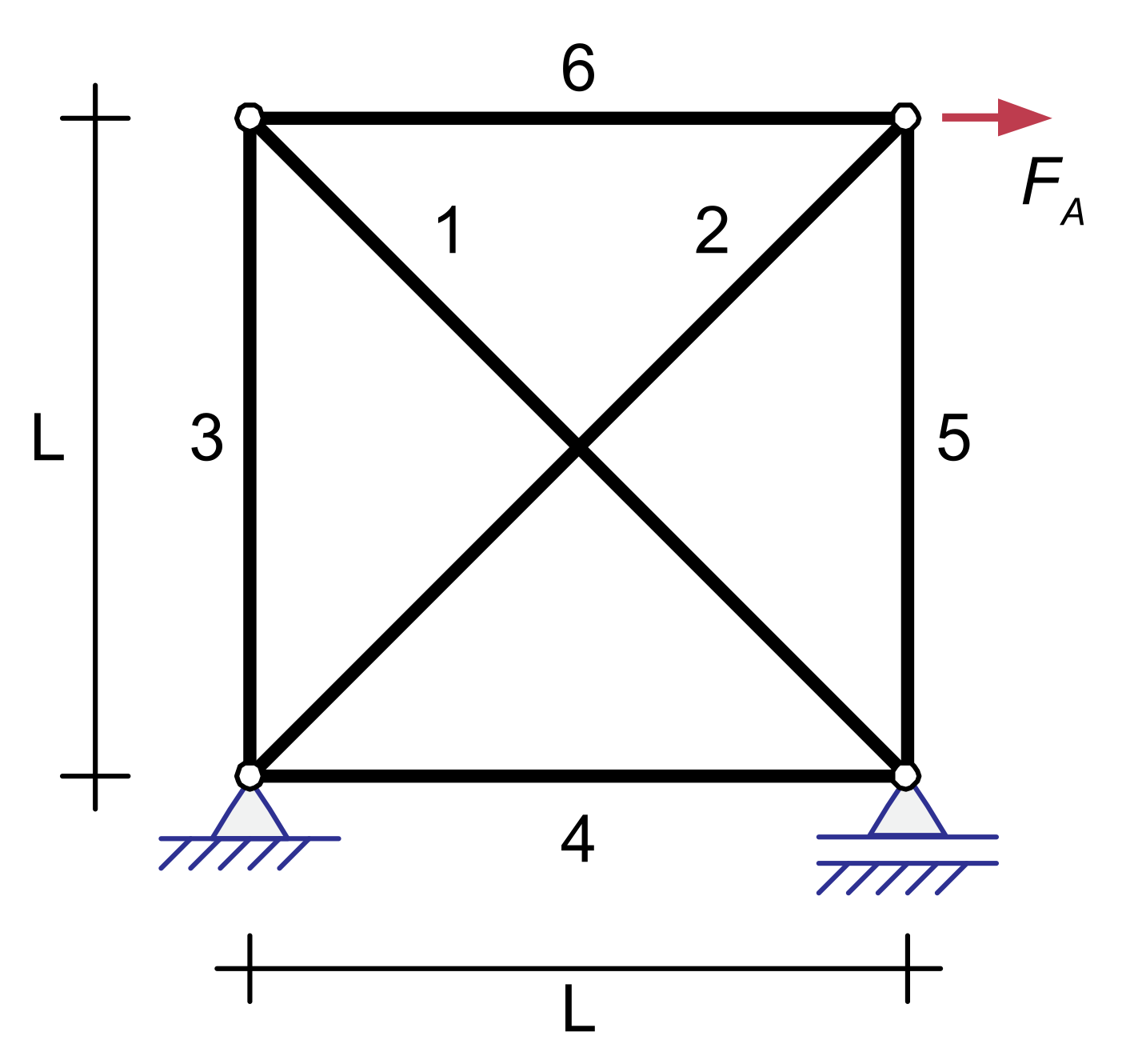
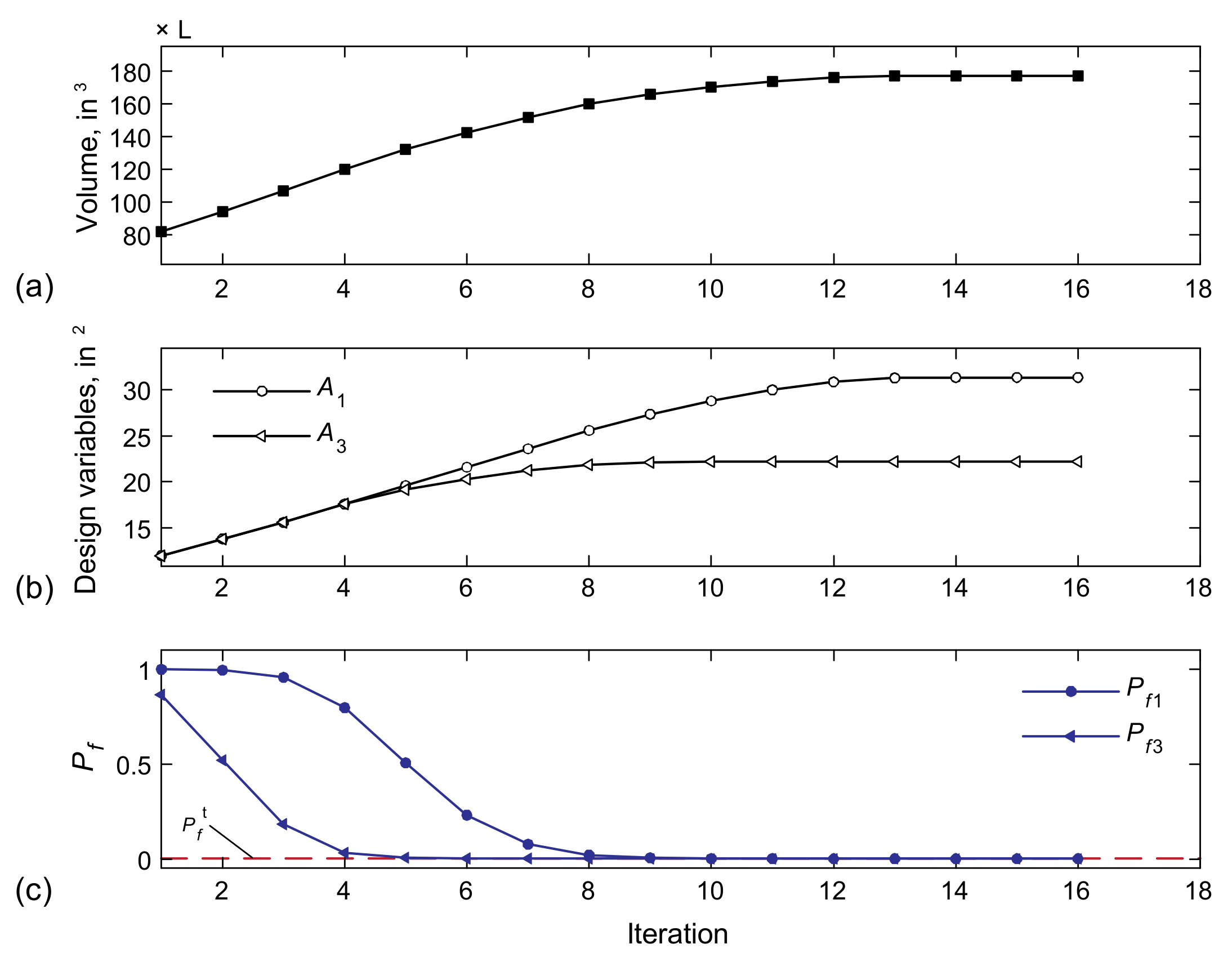
5.4. RBDO of the Truss Structure under Probabilistic Strength Constraints
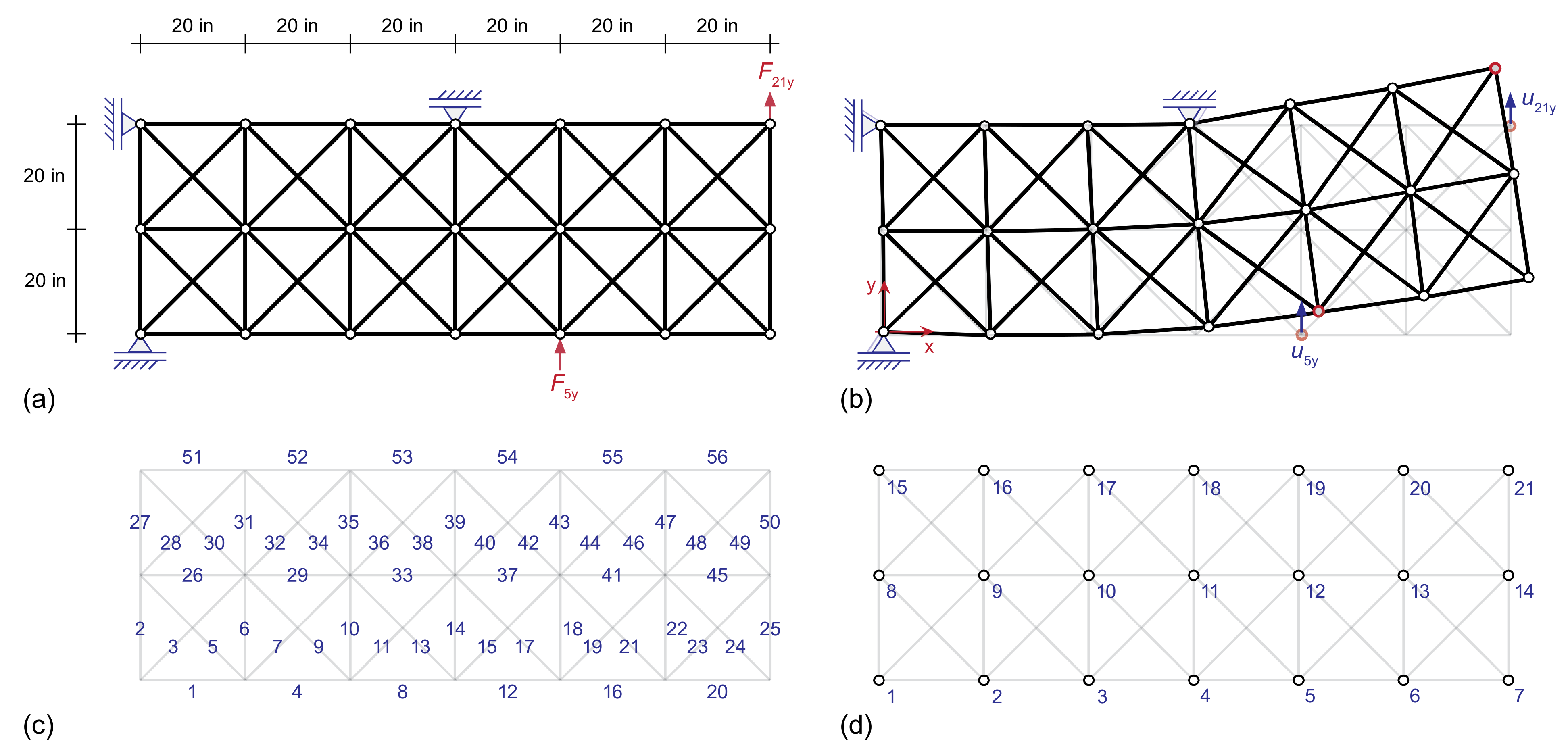
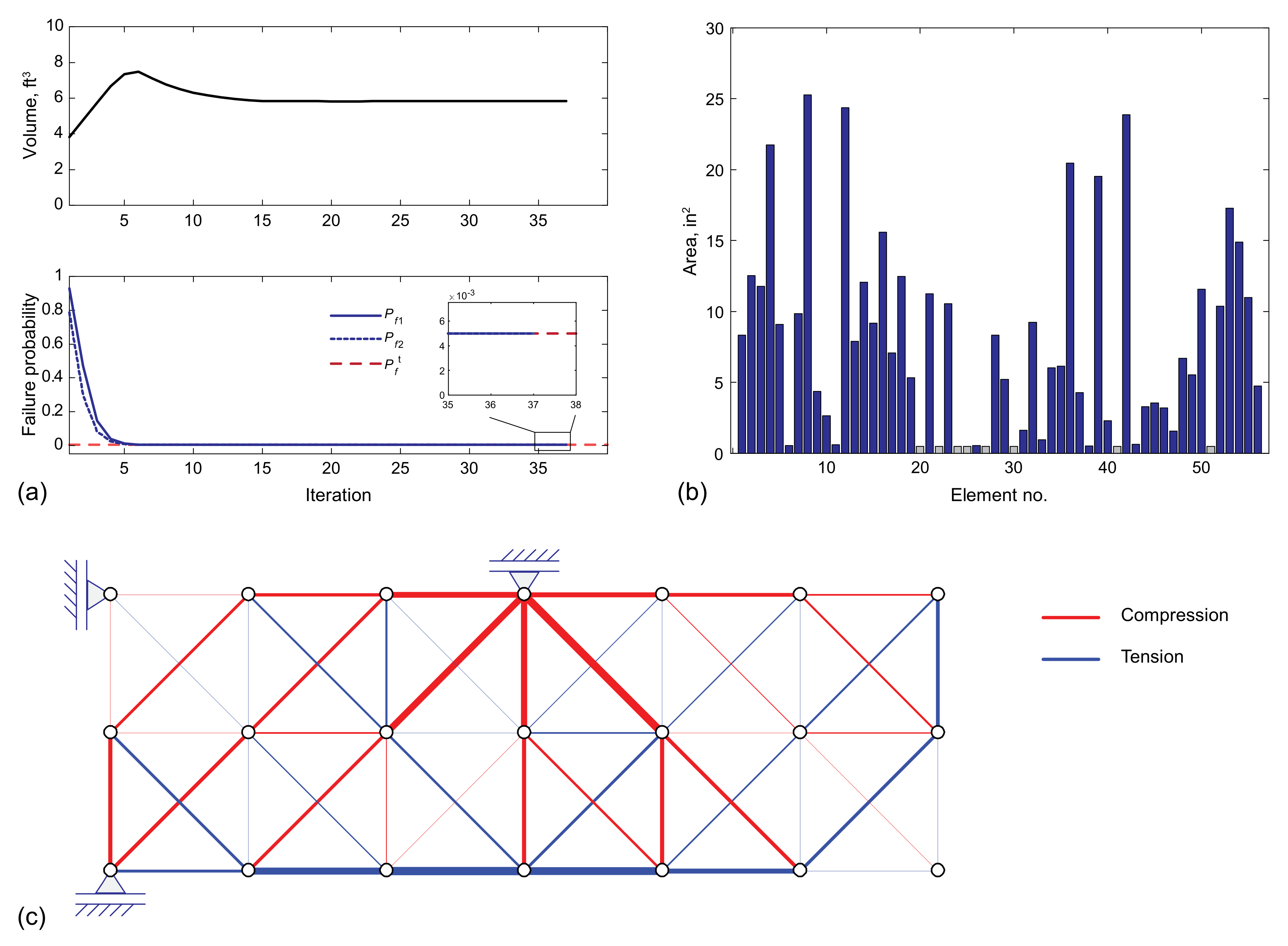
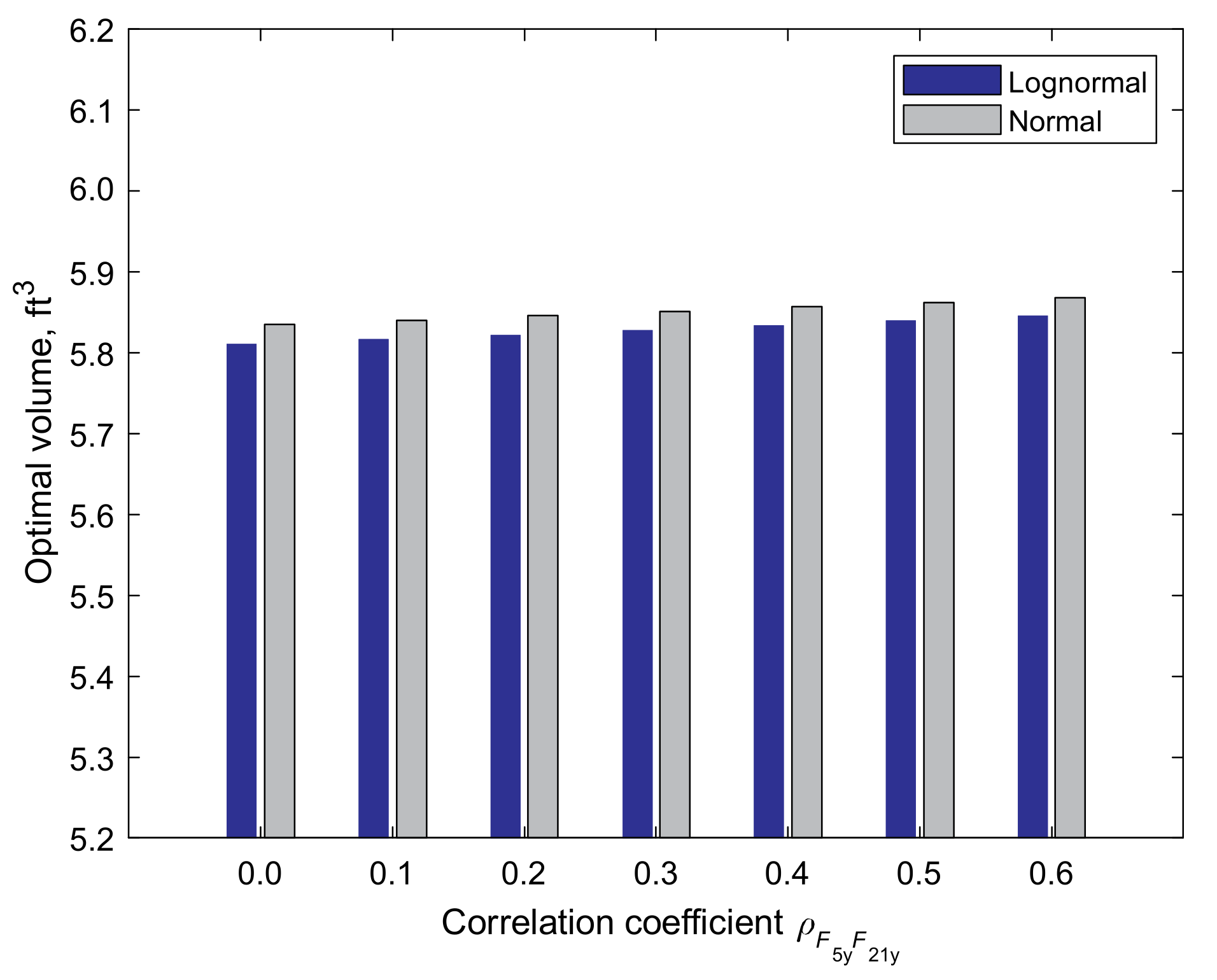
5.5. RBDO of the Truss Cantilever Structure Subjected to Probabilistic Displacement Constraints
6. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Haftka, R.T.; Gürdal, Z. Elements of Structural Optimization; Springer: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Sandgren, E.; Cameron, T. Robust design optimization of structures through consideration of variation. Comput. Struct. 2002, 80, 1605–1613. [Google Scholar] [CrossRef]
- Marano, G.C.; Sgobba, S.; Greco, R.; Mezzina, M. Robust optimum design of tuned mass dampers devices in random vibrations mitigation. J. Sound Vib. 2008, 313, 472–492. [Google Scholar] [CrossRef]
- Zang, C.; Friswell, M.; Mottershead, J. A review of robust optimal design and its application in dynamics. Comput. Struct. 2005, 83, 315–326. [Google Scholar] [CrossRef]
- Parkinson, A.; Sörensen, C.; Pourhassan, N. A General Approach for Robust Optimal Design. J. Mech. Des. 1993, 115, 74–80. [Google Scholar] [CrossRef]
- Chen, W.; Allen, J.K.; Tsui, K.-L.; Mistree, F. A Procedure for Robust Design: Minimizing Variations Caused by Noise Factors and Control Factors. J. Mech. Des. 1996, 118, 478–485. [Google Scholar] [CrossRef] [Green Version]
- Sundaresan, S.; Ishii, K.; Houser, D.R. A robust optimization procedure with variations on design variables and constraints. Eng. Optim. 1995, 24, 101–117. [Google Scholar] [CrossRef]
- Messac, A.; Ismail-Yahaya, A. Multiobjective robust design using physical programming. Struct. Multidiscip. Optim. 2002, 23, 357–371. [Google Scholar] [CrossRef]
- Enevoldsen, I.; Sørensen, J. Reliability-based optimization in structural engineering. Struct. Saf. 1994, 15, 169–196. [Google Scholar] [CrossRef]
- Tu, J.; Choi, K.K.; Park, Y.H. A New Study on Reliability-Based Design Optimization. J. Mech. Des. 1999, 121, 557–564. [Google Scholar] [CrossRef] [Green Version]
- Youn, B.D.; Choi, K.K.; Du, L. Enriched Performance Measure Approach for Reliability-Based Design Optimization. AIAA J. 2005, 43, 874–884. [Google Scholar] [CrossRef]
- Youn, B.D.; Choi, K.K.; Park, Y.H. Hybrid Analysis Method for Reliability-Based Design Optimization. J. Mech. Des. 2003, 125, 221–232. [Google Scholar] [CrossRef]
- Der Kiureghian, A. First- and Second-Order Reliability Methods. In Engineering Design Reliability Handbook; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Du, X.; Chen, W. Sequential Optimization and Reliability Assessment Method for Efficient Probabilistic Design. J. Mech. Des. 2004, 126, 225–233. [Google Scholar] [CrossRef] [Green Version]
- Zou, T.; Mahadevan, S. A direct decoupling approach for efficient reliability-based design optimization. Struct. Multidiscip. Optim. 2006, 31, 190–200. [Google Scholar] [CrossRef]
- Shan, S.; Wang, G.G. Reliable design space and complete single-loop reliability-based design optimization. Reliab. Eng. Syst. Saf. 2008, 93, 1218–1230. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Song, J.; Paulino, G.H. Single-Loop System Reliability-Based Design Optimization Using Matrix-Based System Reliability Method: Theory and Applications. J. Mech. Des. 2009, 132, 011005. [Google Scholar] [CrossRef]
- Liang, J.; Mourelatos, Z.P.; Tu, J. A Single-Loop Method for Reliability-Based Design Optimization. In Proceedings of the 28th Biennial Mechanisms and Robotics Conference, Parts A and B, ASME International. Salt Lake, UT, USA, 28 September–2 October 2004; Volume 1, pp. 419–430. [Google Scholar]
- Liang, J.; Mourelatos, Z.P.; Nikolaidis, E. A Single-Loop Approach for System Reliability-Based Design Optimization. J. Mech. Des. 2007, 129, 1215–1224. [Google Scholar] [CrossRef]
- Chun, J.; Paulino, G.H.; Song, J. Reliability-based topology optimization by ground structure method employing a discrete filtering technique. Struct. Multidiscip. Optim. 2019, 60, 1035–1058. [Google Scholar] [CrossRef]
- Chun, J.; Song, J.; Paulino, G.H. System-reliability-based design and topology optimization of structures under constraints on first-passage probability. Struct. Saf. 2019, 76, 81–94. [Google Scholar] [CrossRef]
- Grujicic, M.; Arakere, G.; Bell, W.C.; Marvi, H.; Yalavarthy, H.V.; Pandurangan, B.; Haque, I.; Fadel, G.M. Reliability-Based Design Optimization for Durability of Ground Vehicle Suspension System Components. J. Mater. Eng. Perform. 2009, 19, 301–313. [Google Scholar] [CrossRef]
- Adams, B.; Eldred, M.; Wittwer, J. Reliability-Based Design Optimization for Shape Design of Compliant Micro-Electro-Mechanical Systems. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006; Volume 2, pp. 1042–1056. [Google Scholar]
- Allen, M.; Maute, K. Reliability-based design optimization of aeroelastic structures. Struct. Multidiscip. Optim. 2004, 27, 228–242. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, C.; Zhu, P.; Chen, W. Reliability-based design optimization of composite battery box based on modified particle swarm optimization algorithm. Compos. Struct. 2018, 204, 239–255. [Google Scholar] [CrossRef]
- Song, J.; Kang, W.-H.; Lee, Y.-J.; Chun, J. Structural System Reliability: Overview of Theories and Applications to Optimization. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part. A Civ. Eng. 2021, 7, 03121001. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Maute, K. Reliability-based optimization of civil and aerospace structural systems. In Engineering Design Reliability Handbook (Chapter 24); Singhal, S., Ghiocel, D., Nikolaidis, E., Eds.; CRC Press: Boca Raton, FL, USA, 2004; pp. 1–32. [Google Scholar]
- Tsompanakis, Y.; Lagaros, N.D.; Papadrakakis, M. Structural Design Optimization Considering Uncertainties; CRC Press: Baca Raton, FL, USA, 2008; Volume 1. [Google Scholar]
- Ambartzumian, R.; Der Kiureghian, A.; Ohaniana, V.; Sukiasiana, H. Multinormal probability by sequential conditioned importance sampling: Theory and application. Probabilistic Eng. Mech. 1998, 13, 299–308. [Google Scholar] [CrossRef]
- Genz, A. Numerical Computation of Multivariate Normal Probabilities. J. Comput. Graph. Stat. 1992, 1, 141–149. [Google Scholar] [CrossRef]
- Wang, Z.; Song, J. Cross-entropy-based adaptive importance sampling using von Mises-Fisher mixture for high dimensional reliability analysis. Struct. Saf. 2016, 59, 42–52. [Google Scholar] [CrossRef]
- Kurtz, N.; Song, J. Cross-entropy-based adaptive importance sampling using Gaussian mixture. Struct. Saf. 2013, 42, 35–44. [Google Scholar] [CrossRef]
- Li, Z. Reliability-Based Design Optimization of Nonlinear Beam-Columns. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 30 April 2018. [Google Scholar]
- Liu, P.L. Der Kiureghian, A. Optimization algorithms for structural reliability. Struct. Saf. 1991, 9, 161–177. [Google Scholar] [CrossRef]
- Bissell, D.; Ang, A.H.S.; Tang, W.H. Probability Concepts in Engineering Planning and Design: Vol. I-Basic Principles. J. R. Stat. Soc. Ser. D Stat. 1979, 28, 226. [Google Scholar] [CrossRef]
- Der Kiureghian, A.; Lin, H.; Hwang, S. Second-Order Reliability Approximations. J. Eng. Mech. 1987, 113, 1208–1225. [Google Scholar] [CrossRef]
- Breitung, K. Asymptotic Approximations for Multinormal Integrals. J. Eng. Mech. 1984, 110, 357–366. [Google Scholar] [CrossRef] [Green Version]
- Der Kiureghian, A.; Dakessian, T. Multiple design points in first and second-order reliability. Struct. Saf. 1998, 20, 37–49. [Google Scholar] [CrossRef]
- Grandhi, R.V.; Wang, L. Reliability-based structural optimization using improved two-point adaptive nonlinear approximations. Finite Elements Anal. Des. 1998, 29, 35–48. [Google Scholar] [CrossRef]
- Au, S.; Papadimitriou, C.; Beck, J. Reliability of uncertain dynamical systems with multiple design points. Struct. Saf. 1999, 21, 113–133. [Google Scholar] [CrossRef]
- Boggs, P.T.; Tolle, J.W. Sequential Quadratic Programming. Acta Numer. 1995, 4, 1–51. [Google Scholar] [CrossRef] [Green Version]
- Fleury, C.; Braibant, V. Structural optimization: A new dual method using mixed variables. Int. J. Numer. Methods Eng. 1986, 23, 409–428. [Google Scholar] [CrossRef]
- Fleury, C. Structural weight optimization by dual methods of convex programming. Int. J. Numer. Methods Eng. 1979, 14, 1761–1783. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Bjerager, P.; Krenk, S. Parametric Sensitivity in First Order Reliability Theory. J. Eng. Mech. 1989, 115, 1577–1582. [Google Scholar] [CrossRef]
- Lyness, J.N.; Moler, C.B. Numerical Differentiation of Analytic Functions. SIAM J. Numer. Anal. 1967, 4, 202–210. [Google Scholar] [CrossRef]
- Squire, W.; Trapp, G. Using Complex Variables to Estimate Derivatives of Real Functions. SIAM Rev. 1998, 40, 110–112. [Google Scholar] [CrossRef] [Green Version]
- Martins, J.R.R.A.; Sturdza, P.; Alonso, J.J. The complex-step derivative approximation. ACM Trans. Math. Softw. 2003, 29, 245–262. [Google Scholar] [CrossRef] [Green Version]
- Rosenblatt, M. Remarks on a Multivariate Transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar] [CrossRef]
- Zhang, Y.; Der Kiureghian, A. Two Improved Algorithms for Reliability Analysis. In Reliability and Optimization of Structural Systems; Springer Science and Business Media LLC: Boston, MA, USA, 1995; pp. 297–304. [Google Scholar]
- McDonald, M.; Mahadevan, S. Design Optimization With System-Level Reliability Constraints. J. Mech. Des. 2008, 130, 021403. [Google Scholar] [CrossRef]

| Random Variables | Marginal Distribution | Mean | c.o.v | Correlation Coefficient | |||
|---|---|---|---|---|---|---|---|
| Normal | 250 | 0.3 | 1.0 | ||||
| Normal | 125 | 0.3 | 0.5 | 1.0 | |||
| Gumbel | 2500 | 0.2 | 0.3 | 0.3 | 1.0 | ||
| Weibull | 40 | 0.1 | 0 | 0 | 0 | 1.0 | |
| Initial Design | Lower Bound | Upper Bound | Convergence Criterion | |
|---|---|---|---|---|
| 0.01 | 0.25 | 0.1 | 2.0 |
| RBDO Method | Averaged Computational Time Carried out to Five Iterations, (Seconds) | Total Number of Iterations | ||||
|---|---|---|---|---|---|---|
| FORM | SORM | |||||
| RBDO−CS | 0.2293 | 0.3909 | 0.0100 | 0.0126 | 0.0130 | 11 |
| SL−KKT | 0.2293 | 0.3908 | 0.0101 | 0.0127 | 0.0108 | 12 |
| Random Variables | Marginal Distribution | Mean | c.o.v | Correlation |
|---|---|---|---|---|
| Joint lognormal | 150 | 0.2 | ||
| Gumbel | 50 | 0.4 | Independent | |
| Gamma | 60 | 0.2 | Independent |
| Initial Design | Lower Bound | Upper Bound | Convergence Criterion | |
|---|---|---|---|---|
| (7.0, 7.0) | (1.0, 1.0) | (10.0, 10.0) |
| RBDO Method | Averaged Computational Time Carried out to Five Iterations, (Seconds) | Total Number of Iterations | |||||
|---|---|---|---|---|---|---|---|
| FORM | SORM | ||||||
| RBDO−CS | 13.658 | (3.362,5.148) | i = 1 | 0.0004 | 0.0004 | 0.105 | 12 |
| i = 2 | 0.0030 | 0.0028 | |||||
| i = 3 | 0.0030 | 0.0032 | |||||
| SL−KKT | 13.667 | (3,364,5.151) | i = 1 | 0.0004 | 0.0012 | 0.031 | 14 |
| i = 2 | 0.0030 | 0.0027 | |||||
| i = 3 | 0.0030 | 0.0033 | |||||
| Random Variables | Marginal Distribution | Mean | Standard Deviation | Correlation |
|---|---|---|---|---|
| Normal | 1000 | 100 | Independent | |
| Normal | 36 | 3 | Independent | |
| Target Failure | Initial Design | Lower Bound | Upper Bound | Convergence Criterion |
|---|---|---|---|---|
| (12, 12) | (5, 5) | (50, 50) |
| RBDO−CS/SL−KKT | Element | RBDO−CS/SL−KKT | FORM | SORM | MCS |
| 177.46 | 1 | 31.37 | |||
| 2 | 31.37 | ||||
| 3 | 22.18 | ||||
| 4 | 22.18 | ||||
| 5 | 22.18 | ||||
| 6 | 22.18 | ||||
| Random Variables | Marginal Distribution | Mean | c.o.v | Correlation |
|---|---|---|---|---|
| Joint lognormal | 120 | 0.1 | ||
| Joint lognormal | 140 | 0.1 | ||
| Normal | 29000 | 0.2 | Independent |
(in) | Lower Bound | Upper Bound | Convergence Criterion | |||
|---|---|---|---|---|---|---|
| 0.005 | 0.1 | 0.3 | 5.0 | 0.5 | 50.0 |
| RBDO Method | Optimal () | Averaged Computational Time Carried out to Five Iterations, (Seconds) | Total Number of Iterations | ||||
|---|---|---|---|---|---|---|---|
| FORM | SORM | MCS | |||||
| RBDO−CS | 5.828 | 1 | 0.0050 | 0.00516 | 0.00516 | 0.0637 | 37 |
| 2 | 0.0050 | 0.00516 | 0.00517 | ||||
| SL−KKT | 5.827 | 1 | 0.0050 | 0.00517 | 0.00518 | 0.0591 | 175 |
| 2 | 0.0050 | 0.00518 | 0.00519 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chun, J. Reliability-Based Design Optimization of Structures Using Complex-Step Approximation with Sensitivity Analysis. Appl. Sci. 2021, 11, 4708. https://doi.org/10.3390/app11104708
Chun J. Reliability-Based Design Optimization of Structures Using Complex-Step Approximation with Sensitivity Analysis. Applied Sciences. 2021; 11(10):4708. https://doi.org/10.3390/app11104708
Chicago/Turabian StyleChun, Junho. 2021. "Reliability-Based Design Optimization of Structures Using Complex-Step Approximation with Sensitivity Analysis" Applied Sciences 11, no. 10: 4708. https://doi.org/10.3390/app11104708
APA StyleChun, J. (2021). Reliability-Based Design Optimization of Structures Using Complex-Step Approximation with Sensitivity Analysis. Applied Sciences, 11(10), 4708. https://doi.org/10.3390/app11104708






