Trace CH4 Gas Detection Based on an Integrated Spherical Photoacoustic Cell
Abstract
1. Introduction
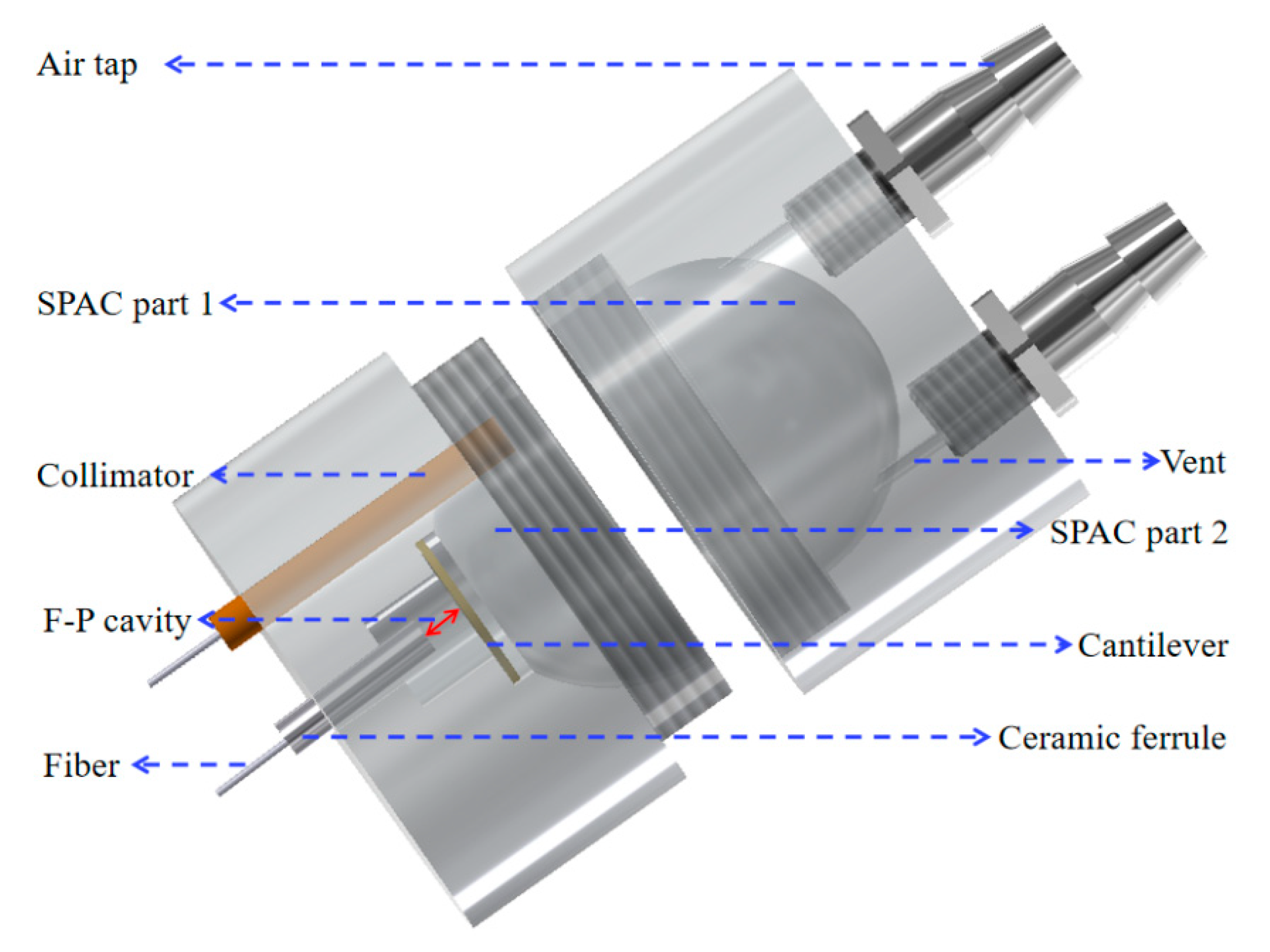
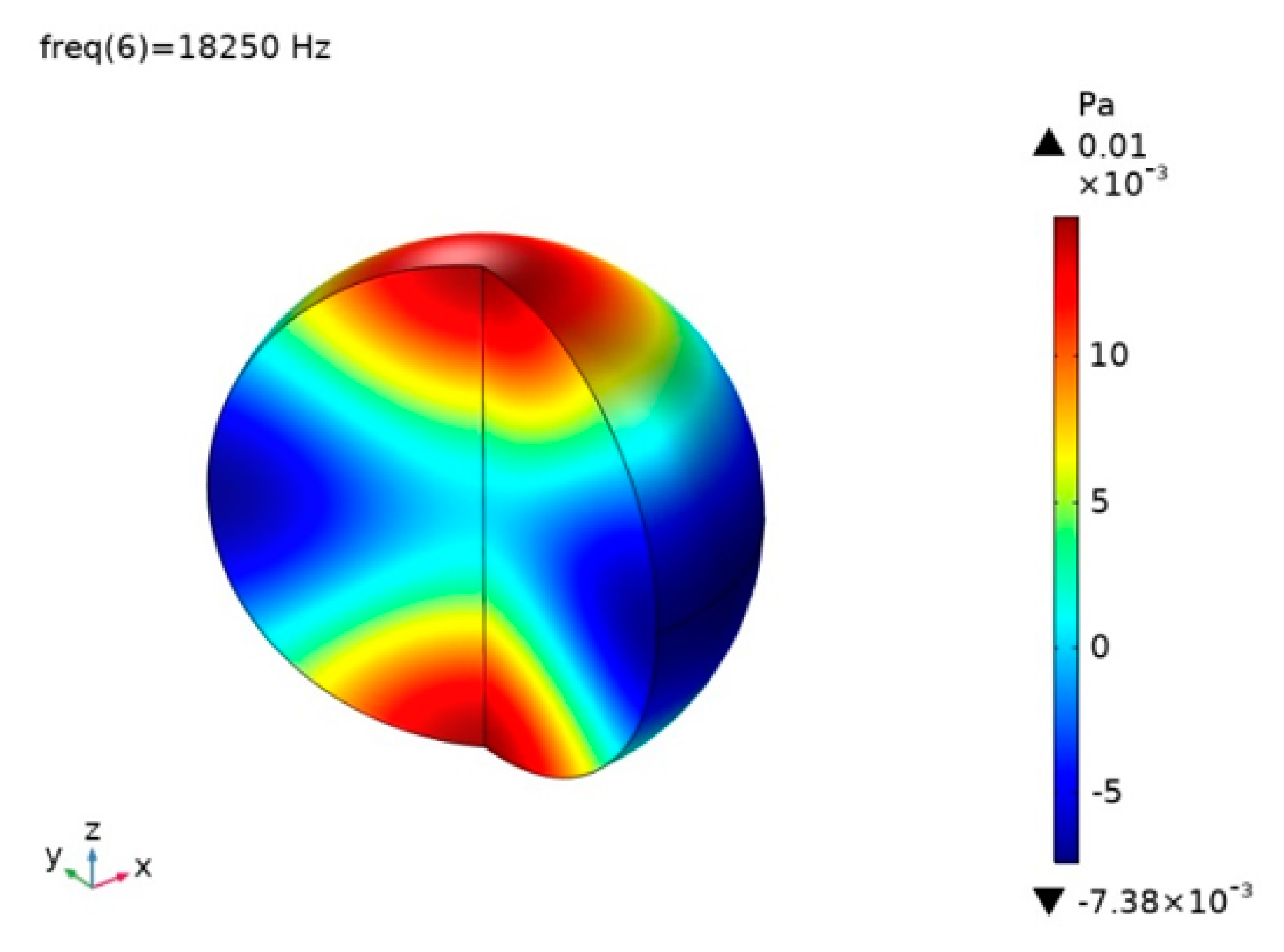
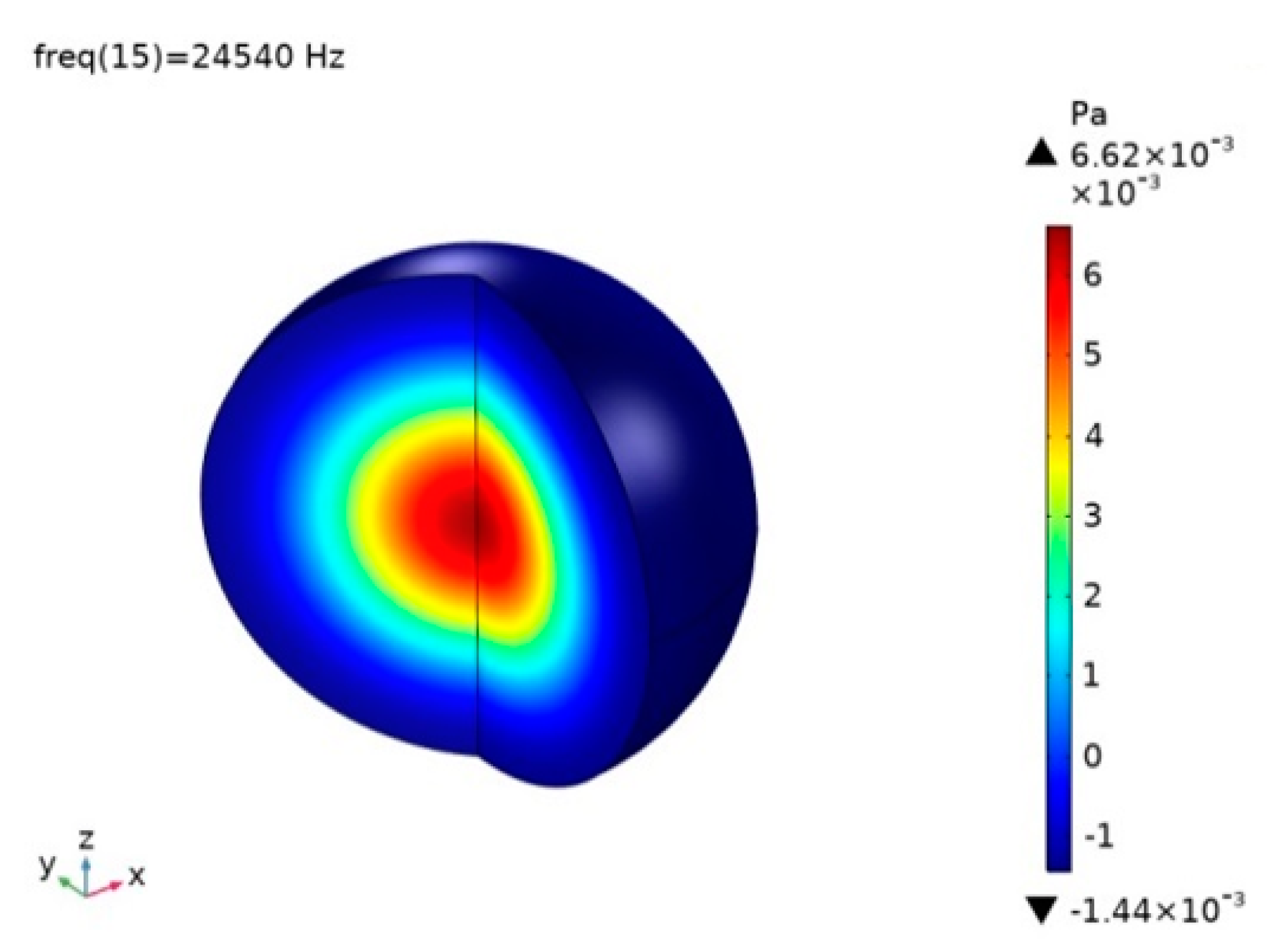
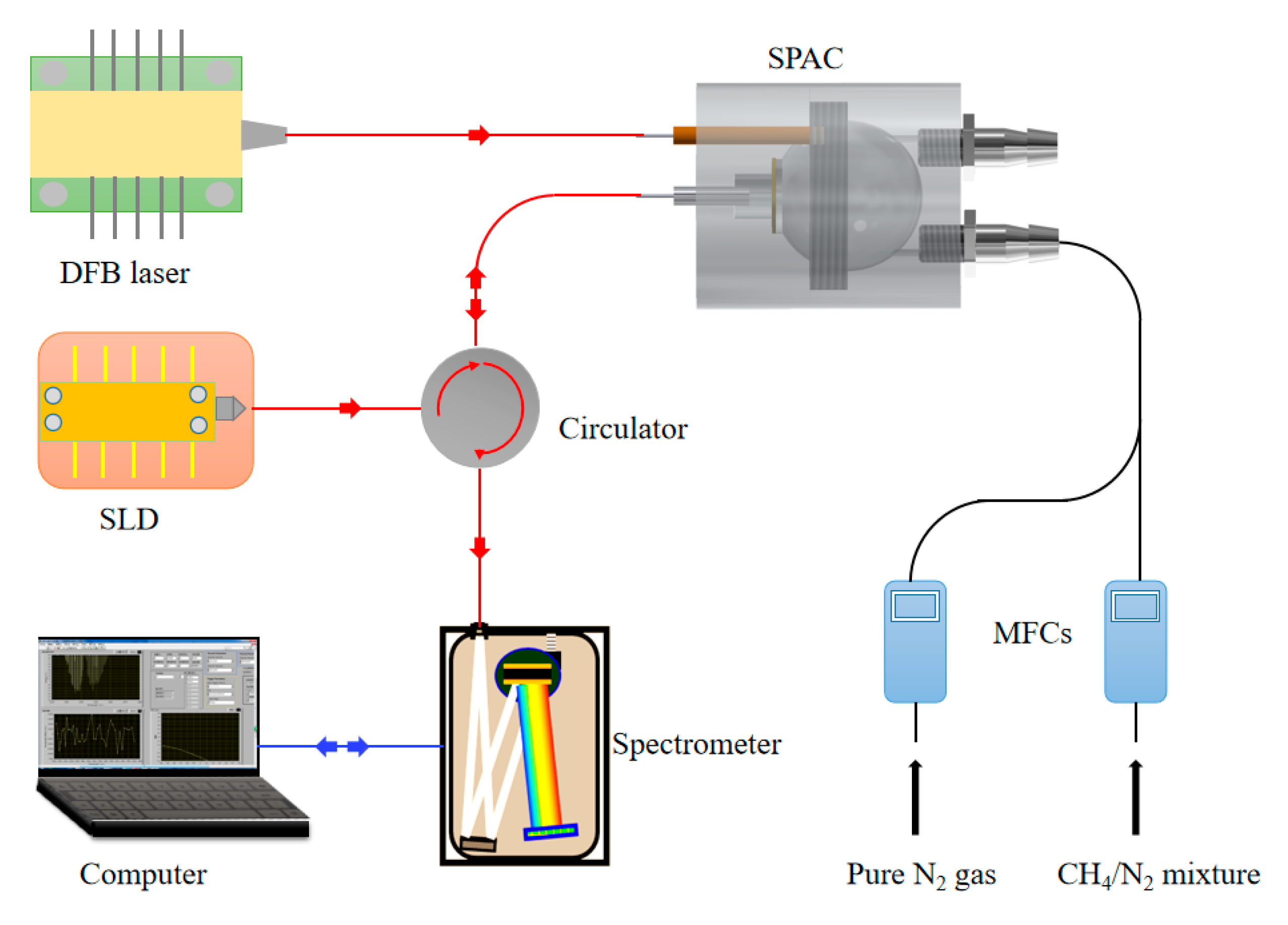
2. SPAC Design and Theoretical Analysis
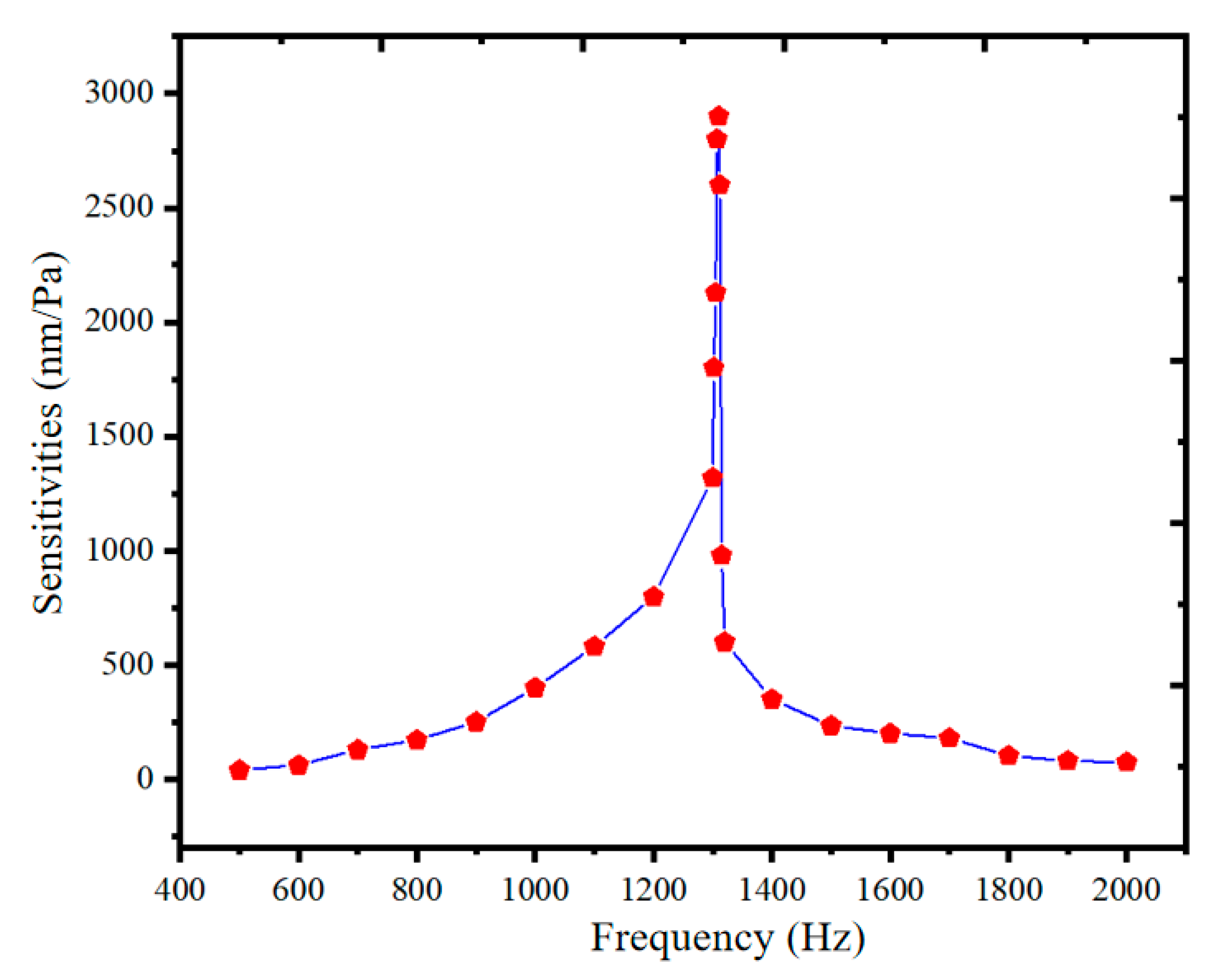
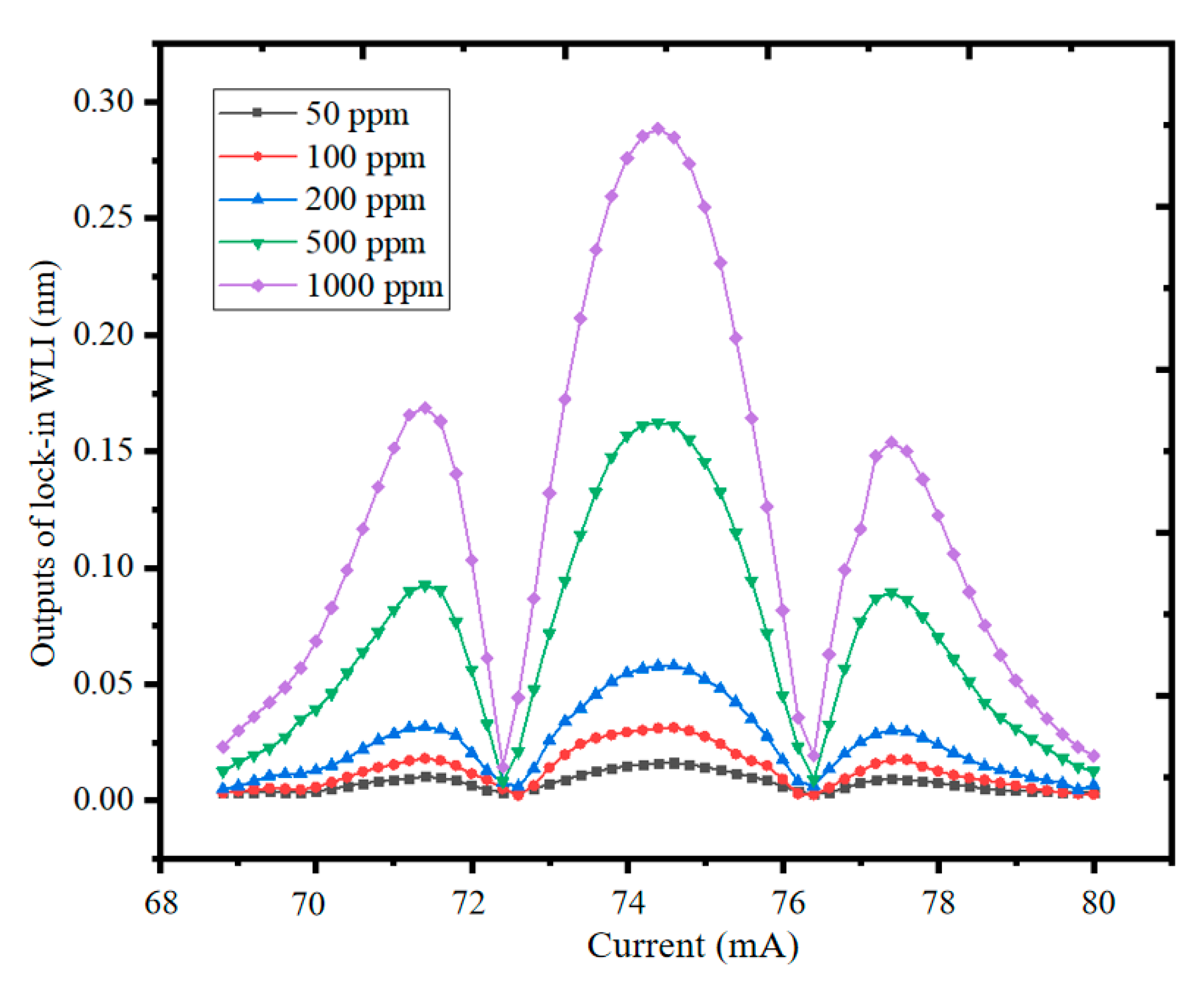
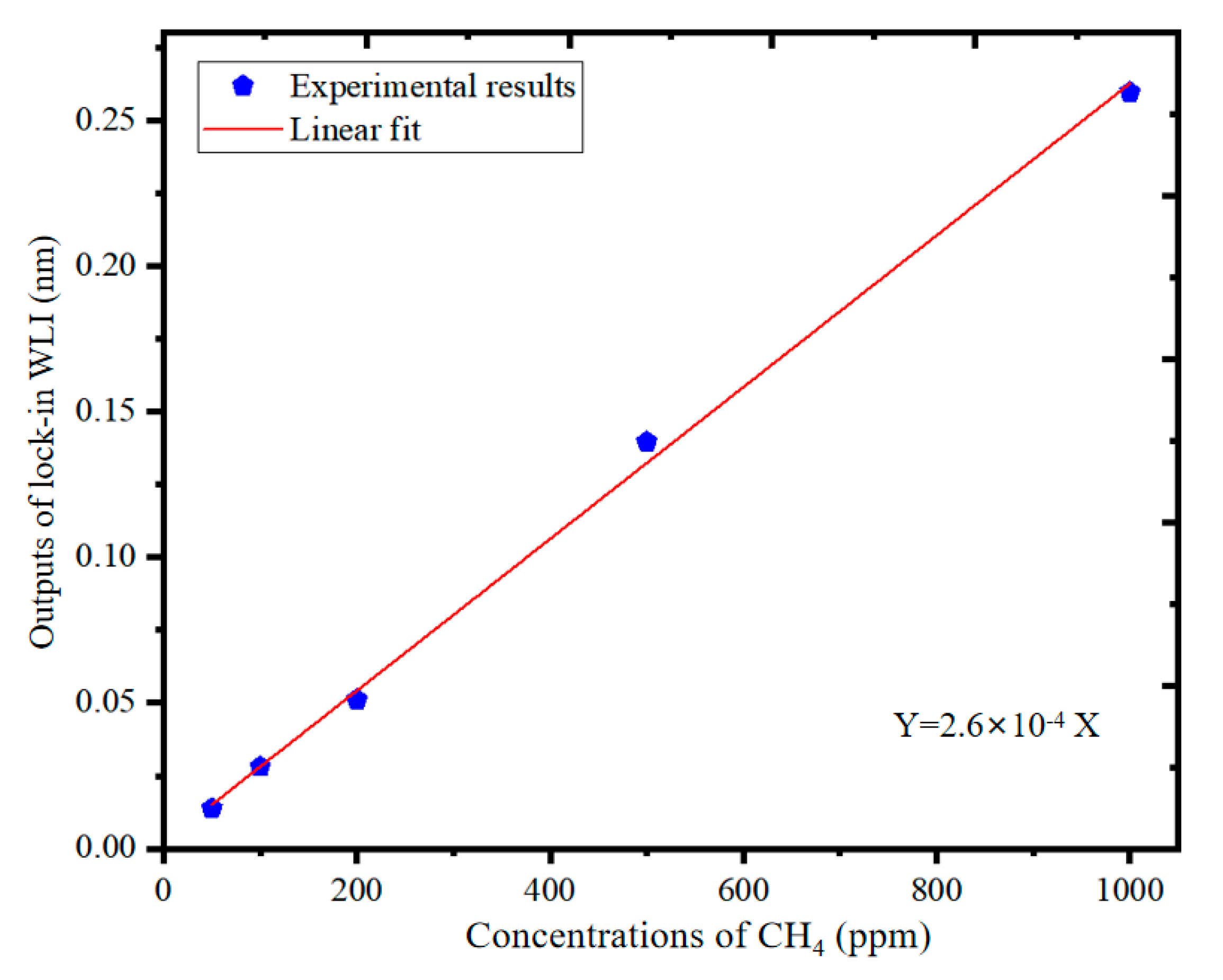
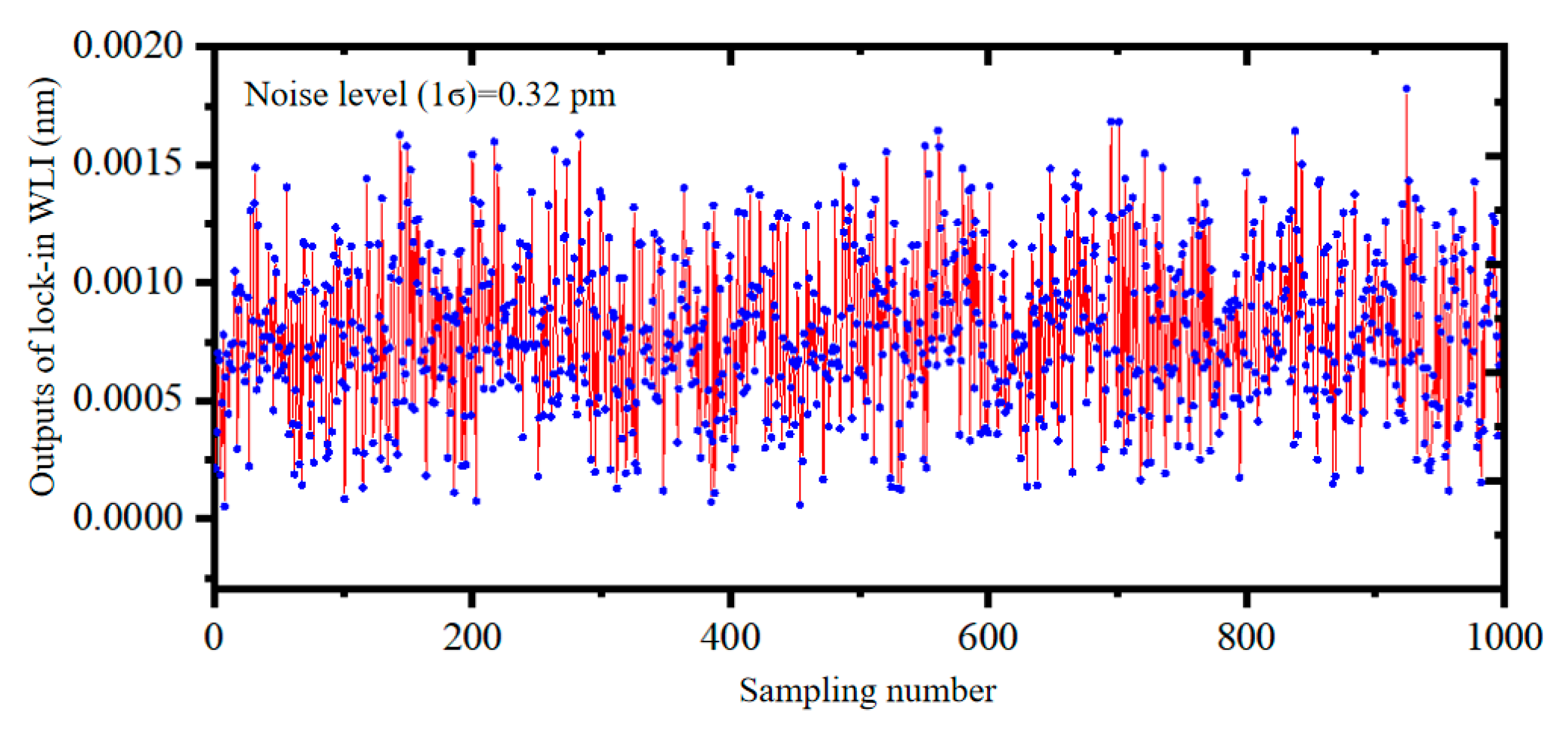
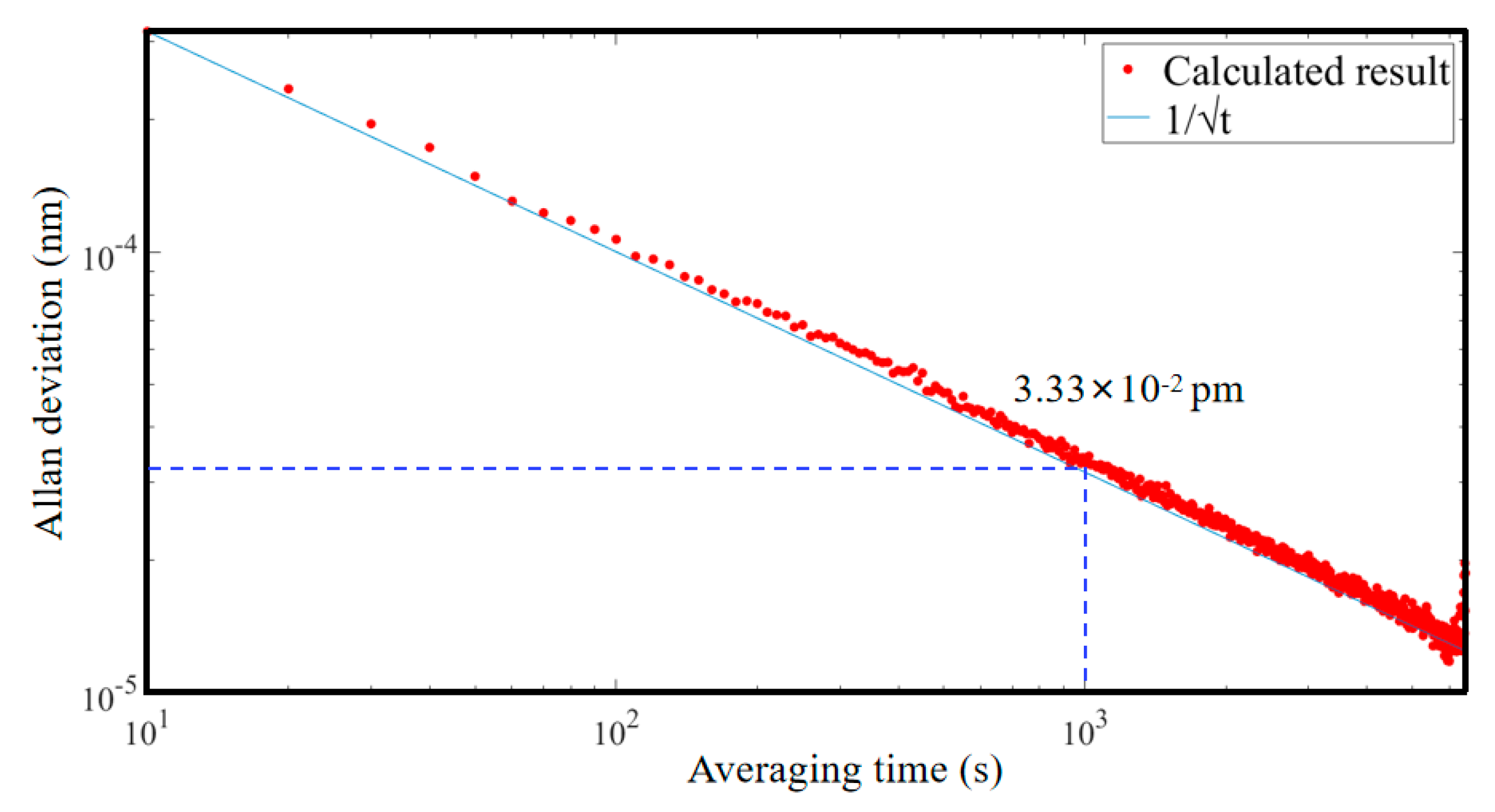
3. Experimental Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pushkarsky, A.M.B.; Dunayevskiy, I.G.; Prasanna, M.; Tsekoun, A.G.; Go, R.; Patel, C.K.N. High-sensitivity detection of TNT. Proc. Natl Acad. Sci. USA 2006, 103, 19630–19634. [Google Scholar] [CrossRef]
- Van Herpen, M.M.J.W.; Ngai, A.K.Y.; Bisson, S.E.; Hackstein, J.H.P.; Woltering, E.J.; Harren, F.J.M. Optical parametric oscillator-based photoacoustic detection of CO2 at 4.23 μm allows real-time monitoring of the respiration of small insects. Appl. Phys. B Laser Opt. 2006, 82, 665–669. [Google Scholar] [CrossRef]
- Zheng, H.; Lou, M.; Dong, L.; Wu, H.; Ye, W.; Yin, X.; Kim, C.S.; Kim, M.; Bewley, W.W.; Merritt, C.D.; et al. Compact photoacoustic module for methane detection incorporating interband cascade light emitting device. Opt. Express 2017, 25, 16761–16770. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Jin, W.; Ho, H.L.; Ma, J. Miniature fiber-tip photoacoustic spectrometer for trace gas detection. Opt. Lett. 2013, 38, 434–436. [Google Scholar] [CrossRef]
- Yun, Y.; Chen, W.; Wang, Y.; Pan, C. Photoacoustic detection of dissolved gases in transformer oil. Euro. Trans. Electr. Power 2008, 18, 562–576. [Google Scholar] [CrossRef]
- Li, J.; Chen, W.; Yu, B. Recent progress on infrared photoacoustic spectroscopy techniques. Appl. Spectrosc. Rev. 2011, 46, 440–471. [Google Scholar] [CrossRef]
- Schilt, S.; Thévenaz, L.; Niklès, M.; Emmenegger, L.; Hüglin, C. Ammonia monitoring at trace level using photoacoustic spectroscopy in industrial and environmental applications. Spectrochim. Acta A 2004, 60, 3259–3268. [Google Scholar] [CrossRef]
- Manohar, S.; Razansky, D. Photoacoustics: A historical review. Adv. Opt. Photonics 2016, 8, 586–617. [Google Scholar] [CrossRef]
- Chen, K.; Yu, Z.; Gong, Z.; Yu, Q. Lock-in white-light-interferometry-based all-optical photoacoustic spectrometer. Opt. Lett. 2018, 43, 5038–5041. [Google Scholar] [CrossRef]
- Jin, W.; Cao, Y.; Yang, F.; Ho, H.L. Ultra-sensitive all-fibre photothermal spectroscopy with large dynamic range. Nat. Commun. 2015, 6, 6767. [Google Scholar] [CrossRef]
- Ma, Y.; Lewicki, R.; Razeghi, M.; Tittel, F.K. QEPAS based ppb-level detection of CO and N2O using a high power CW DFB-QCL. Opt. Express 2013, 21, 1008–1019. [Google Scholar] [CrossRef]
- Kosterev, A.A.; Yu, A.B.; Curl, R.F.; Tittel, F.K. Quartz-enhanced photoacoustic spectroscopy. Opt. Lett. 2002, 27, 1902–1904. [Google Scholar] [CrossRef]
- Gong, Z.; Chen, Y.; Gao, T.; Chen, K.; Jiao, Y.; Guo, M.; Zhang, B.; Liu, S.; Mei, L.; Peng, W.; et al. Parylene-C diaphragm-based low-frequency photoacoustic sensor for space-limited trace gas detection. Opt. Lasers Eng. 2020, 134, 106288. [Google Scholar] [CrossRef]
- Gruca, G.; Heeck, K.; Rector, J.; Lannuzzi, D. Demonstration of a miniature all-optical photoacoustic spectrometer based on ferrule-top technology. Opt. Lett. 2013, 38, 1672–1674. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Slaman, M.; Lannuzzi, D. Demonstration of a highly sensitive photoacoustic spectrometer based on a miniaturized all-optical detecting sensor. Opt. Express 2017, 25, 17541–17548. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; He, Y.; Zhang, L.; Yu, X.; Zhang, J.; Sun, R.; Tittel, F.K. Ultra-high sensitive acetylene detection using quartz-enhanced photoacoustic spectroscopy with a fiber amplified diode laser and a 30.72 kHz quartz tuning fork. Appl. Phys. Lett. 2017, 110, 031107. [Google Scholar] [CrossRef]
- Hu, Y.; Qiao, S.; He, Y.; Lang, Z.; Ma, Y. Quartz-enhanced photoacoustic-photothermal spectroscopy for trace gas sensing. Opt. Express 2021, 29, 5121–5127. [Google Scholar] [CrossRef] [PubMed]
- Qiao, S.; Ma, Y.; Patimisco, P.; Sampaolo, A.; He, Y.; Lang, Z.; Tittel, F.K. Multi-pass quartz-enhanced photoacoustic spectroscopy-based trace gas sensing. Opt. Lett. 2021, 46, 977–980. [Google Scholar] [CrossRef]
- Ma, Y.; Qiao, S.; He, Y.; Li, Y.; Zhang, Z.; Yu, X.; Tittel, F.K. Highly sensitive acetylene detection based on multi-pass retro-reflection-cavity-enhanced photoacoustic spectroscopy and a fiber amplified diode laser. Opt. Express 2019, 27, 14163–14172. [Google Scholar] [CrossRef]
- Wu, H.; Dong, L.; Zheng, H.; Yu, Y.; Ma, W.; Zhang, L.; Yin, W.; Xiao, L.; Jia, S.; Tittel, F.K. Beat frequency quartz-enhanced photoacoustic spectroscopy for fast and calibration-free continuous trace-gas monitoring. Nat. Commun. 2017, 8, 15331. [Google Scholar] [CrossRef]
- Winkowski, M.; Stacewicz, T. Low noise, open-source QEPAS system with instrumentation amplifier. Sci. Rep. 2019, 9, 1838. [Google Scholar] [CrossRef]
- Qiao, S.; He, Y.; Ma, Y. Trace gas sensing based on single-quartz-enhanced photoacoustic-photothermal dual spectroscopy. Opt. Lett. 2021, 46, 2449–2452. [Google Scholar] [CrossRef]
- Lang, Z.; Qiao, S.; He, Y.; Ma, Y. Quartz tuning fork-based demodulation of an acoustic signal induced by photo-thermo-elastic energy conversion. Photoacoustics 2021, 22, 100272. [Google Scholar] [CrossRef]
- Gong, Z.; Chen, K.; Chen, Y.; Mei, L.; Yu, Q. Integration of T-type half-open photoacoustic cell and fiber-optic acoustic sensor for trace gas detection. Opt. Express 2019, 27, 18222–18231. [Google Scholar] [CrossRef] [PubMed]
- Baumann, B.; Wolff, M.; Kost, B.; Groninga, H. Finite element calculation of photoacoustic signals. Appl. Opt. 2007, 46, 1120–1125. [Google Scholar] [CrossRef]
- Parvitte, B.; Risser, C.; Vallon, R.; Zéninari, V. Quantitative simulation of photoacoustic signals using finite element modelling software. Appl. Phys. B 2013, 111, 383–389. [Google Scholar] [CrossRef]
- Germer, M.; Wolff, M. Quantum cascade laser linewidth investigations for high resolution photoacoustic spectroscopy. Appl. Opt. 2009, 48, B80–B86. [Google Scholar] [CrossRef] [PubMed]
- Dong, M.; Zheng, C.; Yao, D.; Zhong, G.; Miao, S.; Ye, W.; Wang, Y.; Tittel, F.K. Double-range near-infrared acetylene detection using a dual spot-ring Herriott cell (DSR-HC). Opt. Express 2018, 26, 12081–12091. [Google Scholar] [CrossRef] [PubMed]
- Krzempek, K.; Hudzikowski, A.; Głuszek, A.; Dudzik, G.; Abramski, K.; Wysocki, G.; Nikodem, M. Multi-pass cell-assisted photoacoustic/photothermal spectroscopy of gases using quantum cascade laser excitation and heterodyne interferometric signal detection. Appl. Phys. B 2018, 124, 74–79. [Google Scholar] [CrossRef]
- Liu, K.; Wang, L.; Tan, T.; Wang, G.; Zhang, W.; Chen, W.; Gao, X. Highly sensitive detection of methane by near-infrared laser absorption spectroscopy using a compact dense-pattern multipass cell. Sens. Actuators B Chem. 2015, 220, 1000–1005. [Google Scholar] [CrossRef]
- Kühnreich, B.; Höh, M.; Wagner, S.; Ebert, V. Direct single-mode fibre-coupled miniature White cell for laser absorption spectroscopy. Rev. Sci. 2016, 87, 023111. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, K.; Chen, Y.; Yang, B.; Guo, M.; Deng, H.; Ma, F.; Zhu, F.; Gong, Z.; Peng, W.; et al. High-sensitivity photoacoustic gas detector by employing multi-pass cell and fiber-optic microphone. Opt. Express 2020, 28, 6618–6630. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Dong, L.; Wu, H.; Zheng, H.; Ma, W.; Zhang, L.; Yin, W.; Jia, S.; Tittel, F.K. Sub-ppb nitrogen dioxide detection with a large linear dynamic range by use of a differential photoacoustic cell and a 3.5 W blue multimode diode laser. Sens. Actuators B Chem. 2017, 247, 329–335. [Google Scholar] [CrossRef]
- Gong, Z.; Gao, T.; Chen, Y.; Zhang, B.; Peng, W.; Yu, Q.; Ma, F.; Mei, L.; Chen, K. Sub-ppb level detection of nitrogen dioxide based on an optimized H-type longitudinal acoustic resonator and a lock-in white-light interferometry demodulation algorithm. J. Quant. Spectrosc. Radiat. Transf. 2020, 253, 107136. [Google Scholar] [CrossRef]
- Gong, Z.; Gao, T.; Mei, L.; Chen, K.; Chen, Y.; Zhang, B.; Peng, W.; Yu, Q. Ppb-level detection of methane based on an optimized T-type photoacoustic cell and a NIR diode laser. Photoacoustics 2021, 21, 100216. [Google Scholar] [CrossRef]
- Ren, W.; Farooq, A.; Davidson, D.F.; Hanson, R.K. CO concentration and temperature sensor for combustion gases using quantum-cascade laser absorption near 4.7 μm. Appl. Phys. B 2012, 107, 849–860. [Google Scholar] [CrossRef]
- Mao, X.; Zheng, P.; Wang, X.; Yuan, S. Breath methane detection based on all-optical photoacoustic spectrometer. Sens. Actuators B Chem. 2017, 239, 1257–1260. [Google Scholar] [CrossRef]
- Wang, Q.; Yin, X.; Yang, L.; Xing, L. Geometrical Optimization of Resonant Ellipsoidal Photoacoustic Cell in Photoacoustic Spectroscopy System. Spectrosc. Spectral Anal. 2020, 40, 1351–1355. [Google Scholar]
- Shi, Q.; Hu, S.; Chen, J.; Hao, L.; Han, J.; Zhu, S. A new type high quality spherical photoacoustic cell for lazer photoacoustic spectroscopy. Chin. J. Chem. Phys. 1998, 11, 20–25. [Google Scholar]
- Zhao, J.; Zhao, Z.; Du, L.; Wu, S.; Xiao, L.; Bai, C. Detection of CO2 in the spherical photoacoustic cell. Chin. J. Sens. Actuator 2012, 25, 289–292. [Google Scholar]
- Hao, L.; Shi, Q.; Ren, Z.; Hu, S.; Cheng, G.; Zhu, Q. Study of collisional relaxation of acetylene with spherical photoacoustic cell. Prog. Nat. Sci. 2001, 11, S242–S247. [Google Scholar]
- Chen, K.; Yu, Z.; Yu, Q.; Guo, M.; Zhao, Z.; Qu, C.; Gong, Z.; Yang, Y. Fast demodulated white-light interferometry–based fiber-optic Fabry–Perot cantilever microphone. Opt. Lett. 2018, 43, 3417–3420. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, Y.; Fan, H.; Gong, Z.; Yang, K.; Shen, F.; Chen, K.; Mei, L.; Peng, W.; Yu, Q. Trace CH4 Gas Detection Based on an Integrated Spherical Photoacoustic Cell. Appl. Sci. 2021, 11, 4997. https://doi.org/10.3390/app11114997
Jiao Y, Fan H, Gong Z, Yang K, Shen F, Chen K, Mei L, Peng W, Yu Q. Trace CH4 Gas Detection Based on an Integrated Spherical Photoacoustic Cell. Applied Sciences. 2021; 11(11):4997. https://doi.org/10.3390/app11114997
Chicago/Turabian StyleJiao, Yexiang, Hongji Fan, Zhenfeng Gong, Kai Yang, Feiyang Shen, Ke Chen, Liang Mei, Wei Peng, and Qingxu Yu. 2021. "Trace CH4 Gas Detection Based on an Integrated Spherical Photoacoustic Cell" Applied Sciences 11, no. 11: 4997. https://doi.org/10.3390/app11114997
APA StyleJiao, Y., Fan, H., Gong, Z., Yang, K., Shen, F., Chen, K., Mei, L., Peng, W., & Yu, Q. (2021). Trace CH4 Gas Detection Based on an Integrated Spherical Photoacoustic Cell. Applied Sciences, 11(11), 4997. https://doi.org/10.3390/app11114997






