Dynamic Performance of Soil–Tunnel System under Transverse Sinusoidal Excitations
Abstract
:1. Introduction
2. Test Design
2.1. Prototype of a Site
2.2. Similitude Ratios
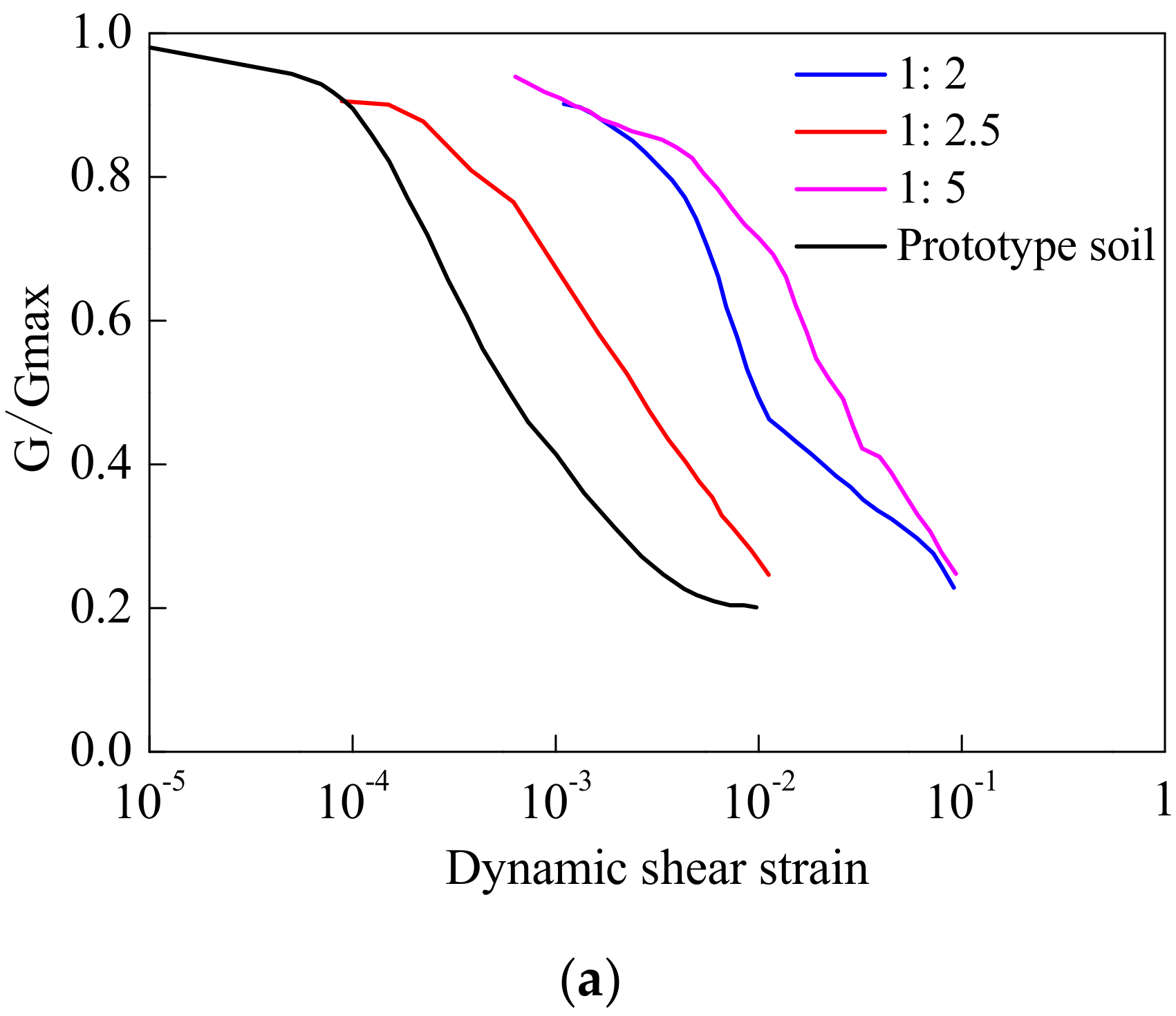
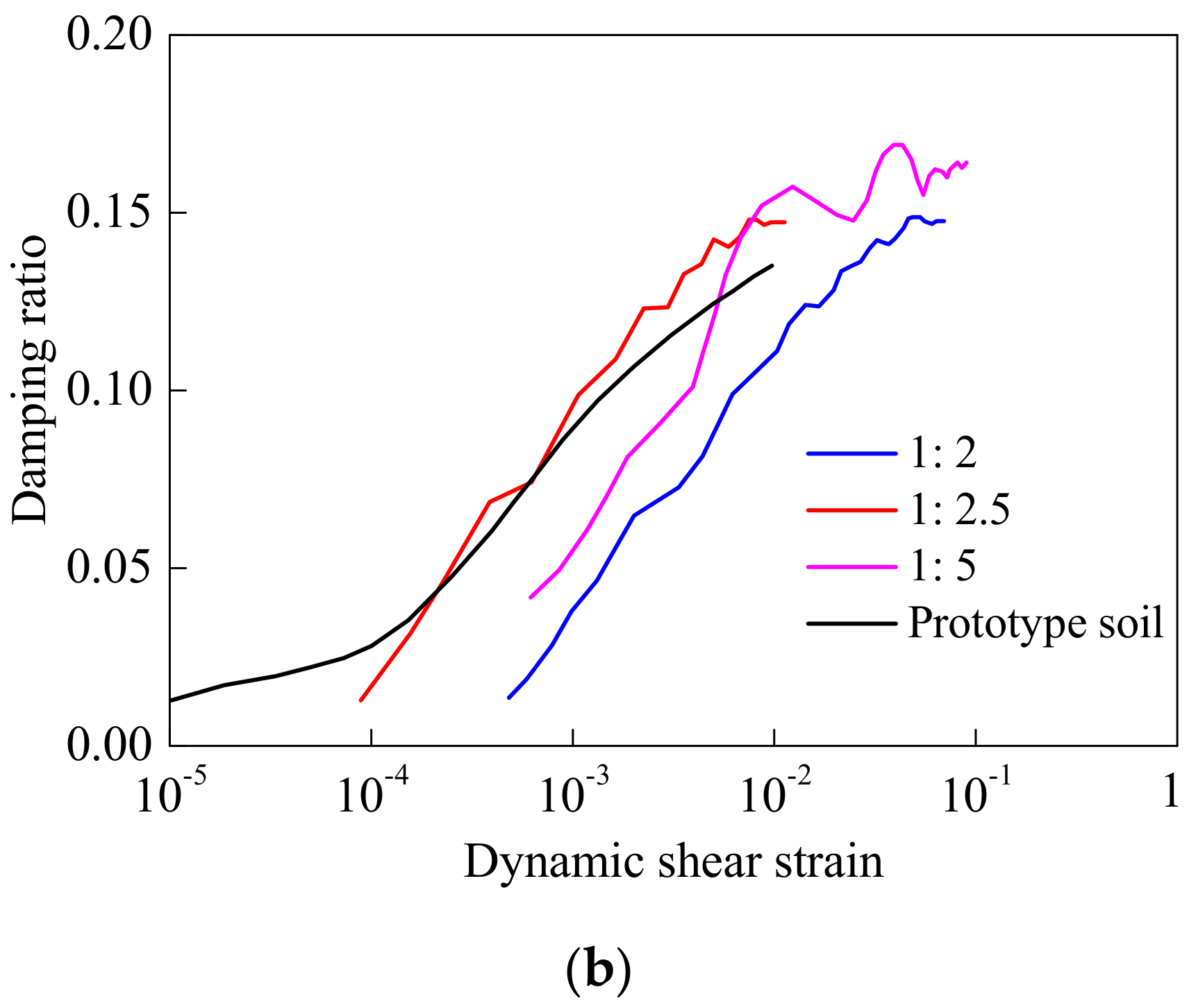
2.3. Model Ground
2.4. Refined Lining Ring of Model Tunnel
2.4.1. Stiffness Ratio of Prototype
2.4.2. Stiffness of Model Tunnel
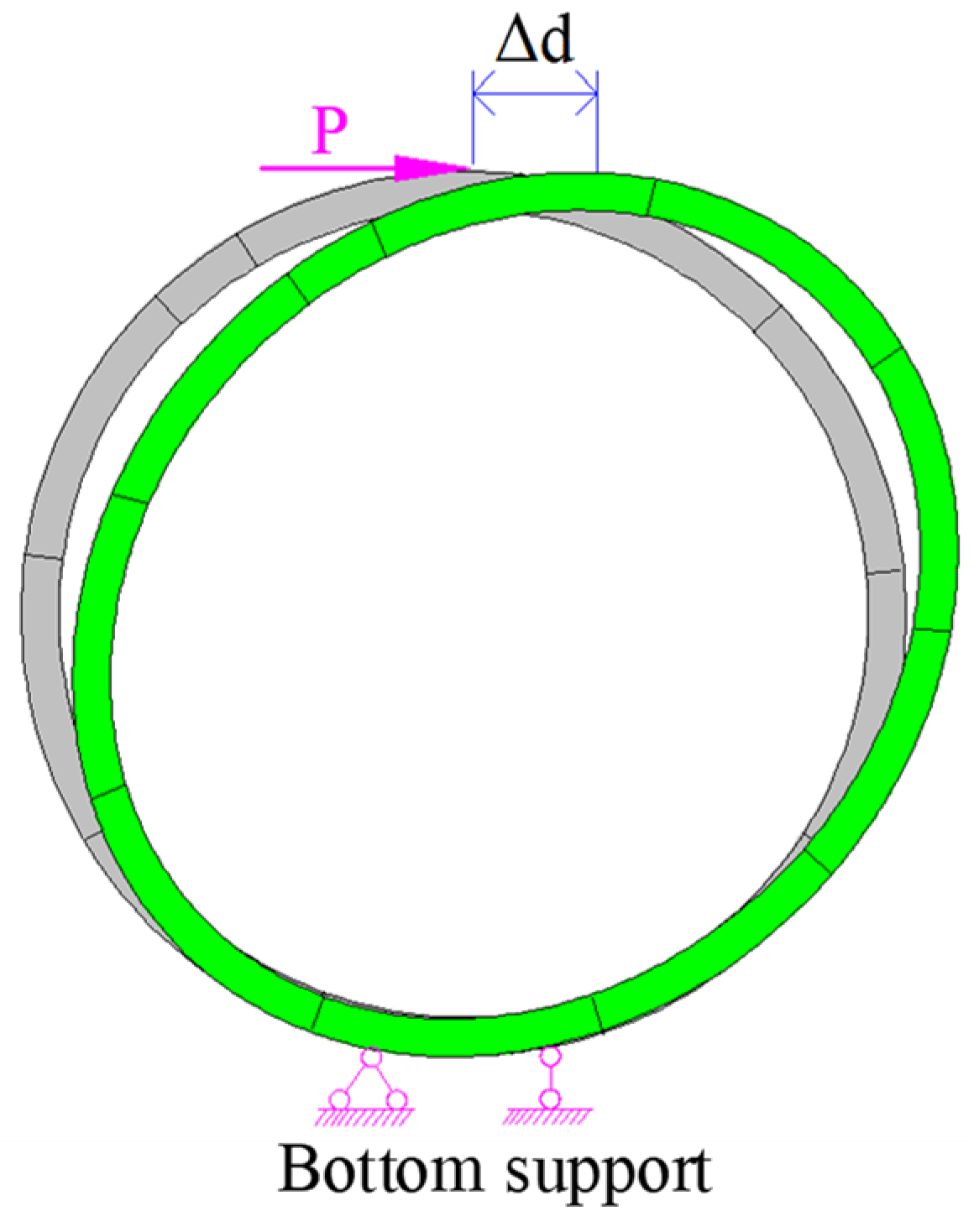
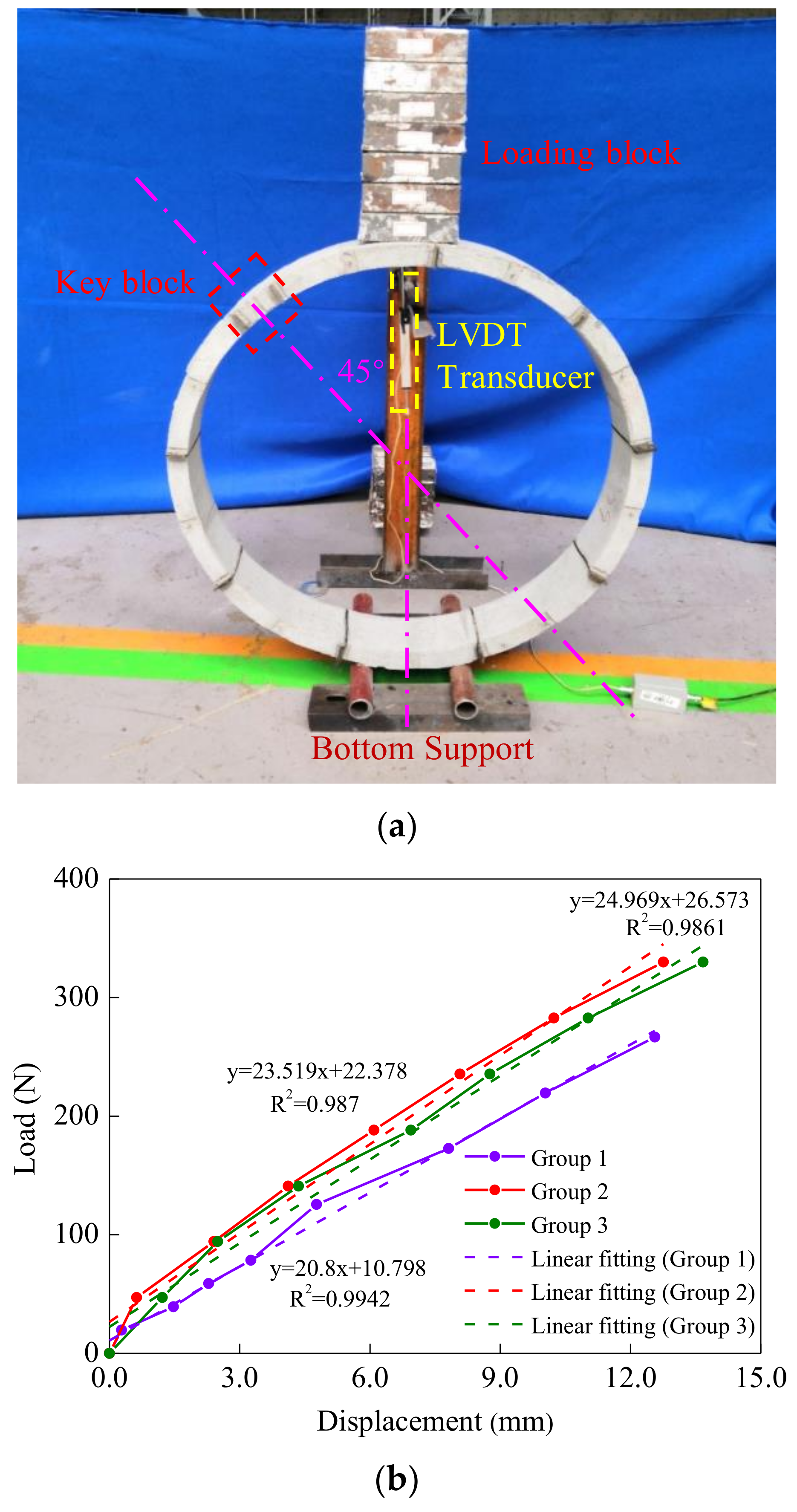
2.4.3. Similarity of Stiffness Ratio and Validation
2.5. Scheme of the Experiment
2.5.1. Preparation of Free-Field Model
2.5.2. Model Tunnel and Its Instrumentation
2.5.3. Input Motions and Testing Cases
3. Fundamental Frequency Responses of Two Model Grounds
4. Response of FF Ground under Sinusoidal Excitation
4.1. Acceleration along Depths
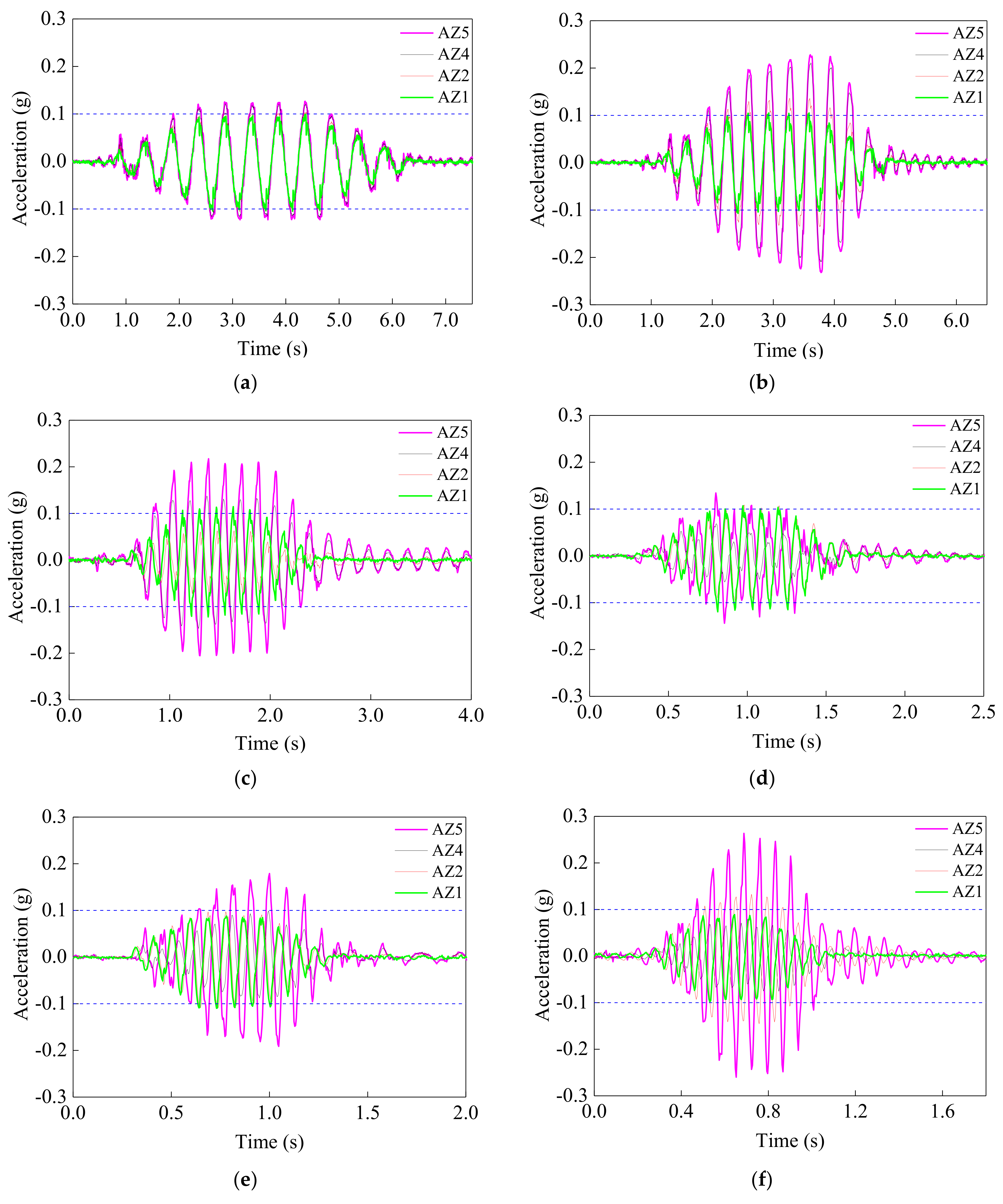
4.1.1. Time Histories
4.1.2. Amplification Coefficients of Acceleration along Depth
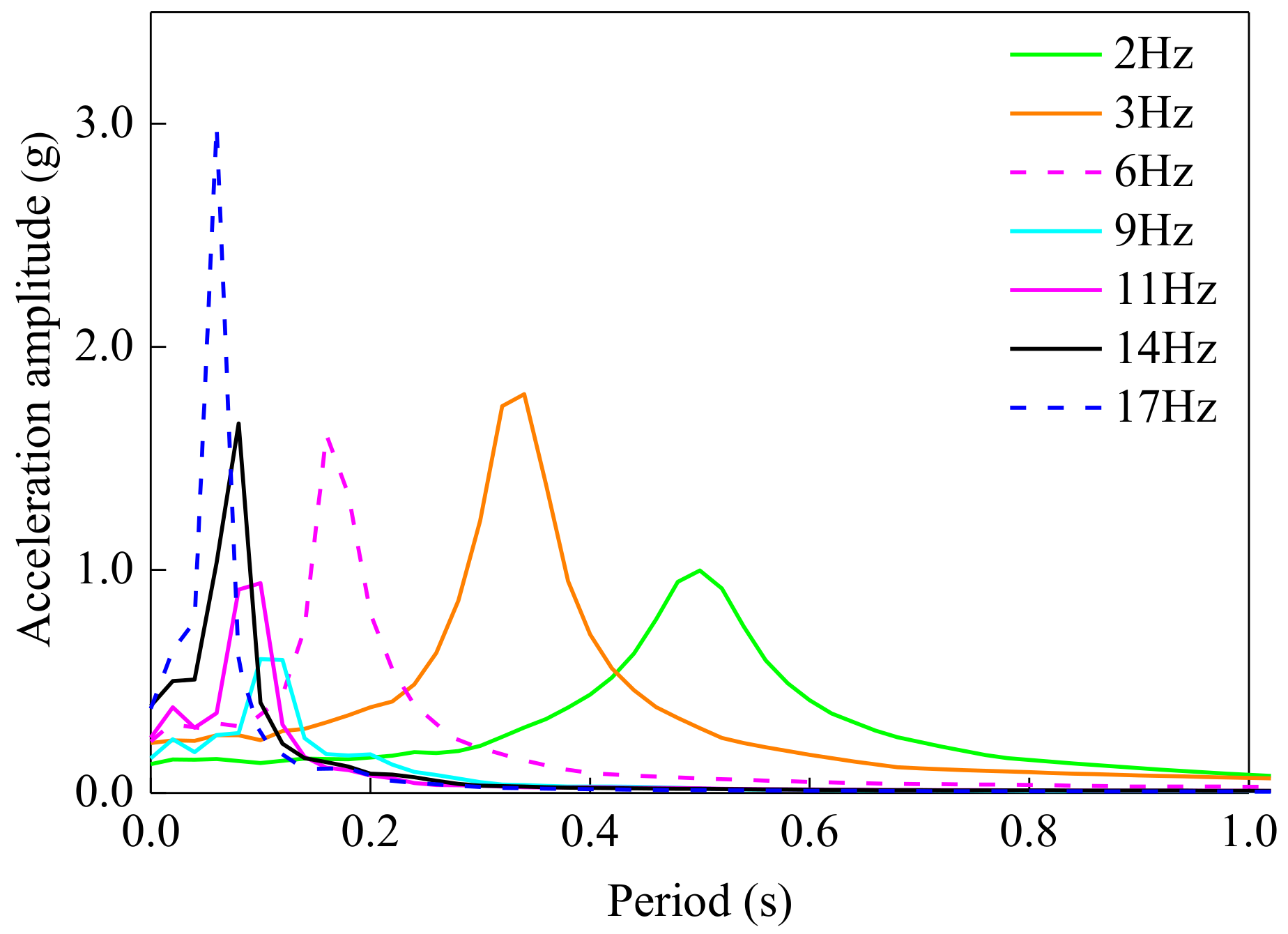
4.1.3. Response Spectrum
4.2. Deformation of the Ground
5. Responses of Segmental Tunnel
5.1. Acceleration Responses of the ST Ground
5.1.1. Time Histories
5.1.2. Differences of Amplification of Acceleration along Depth
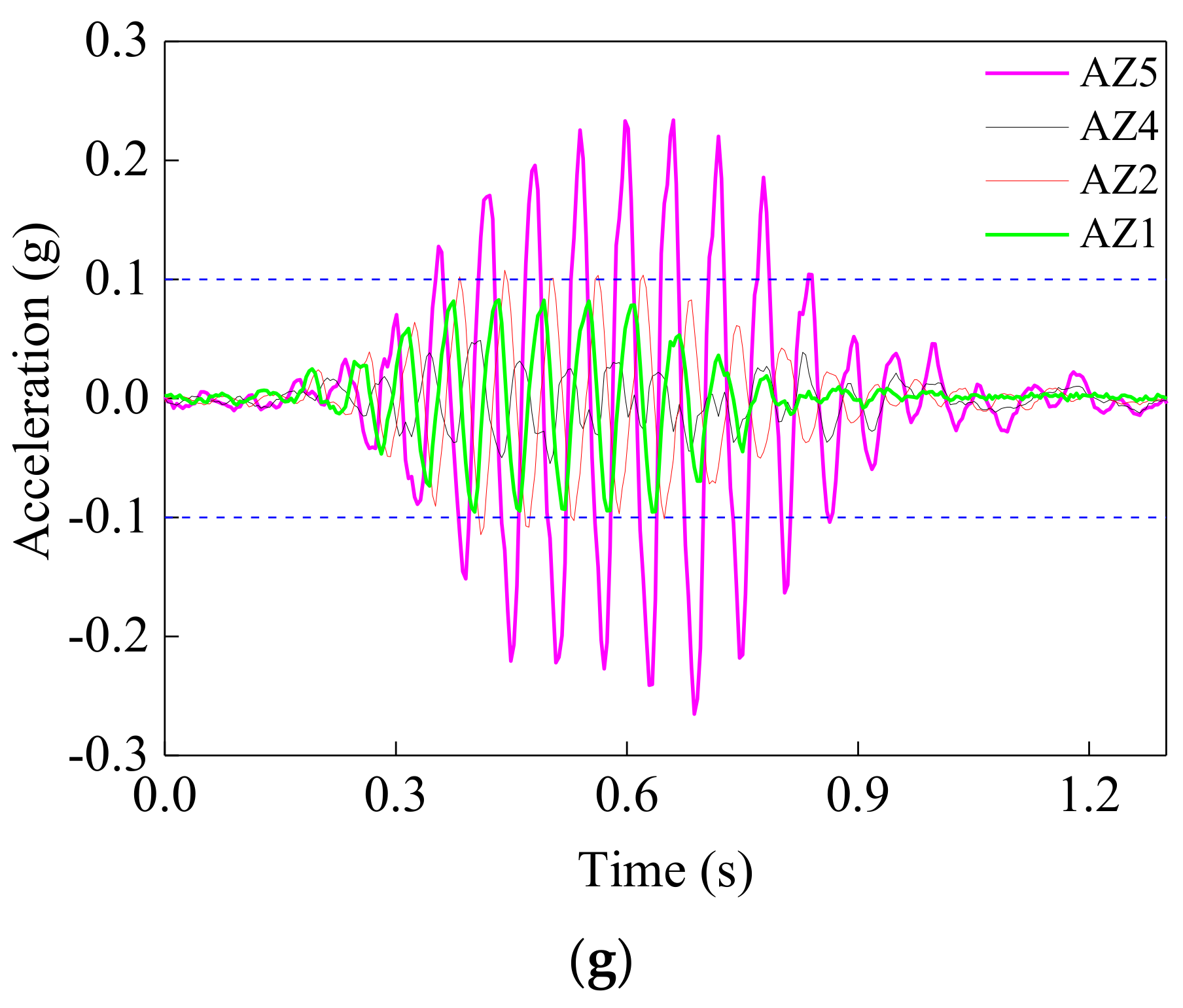
5.2. Acceleration Responses of Model Tunnel
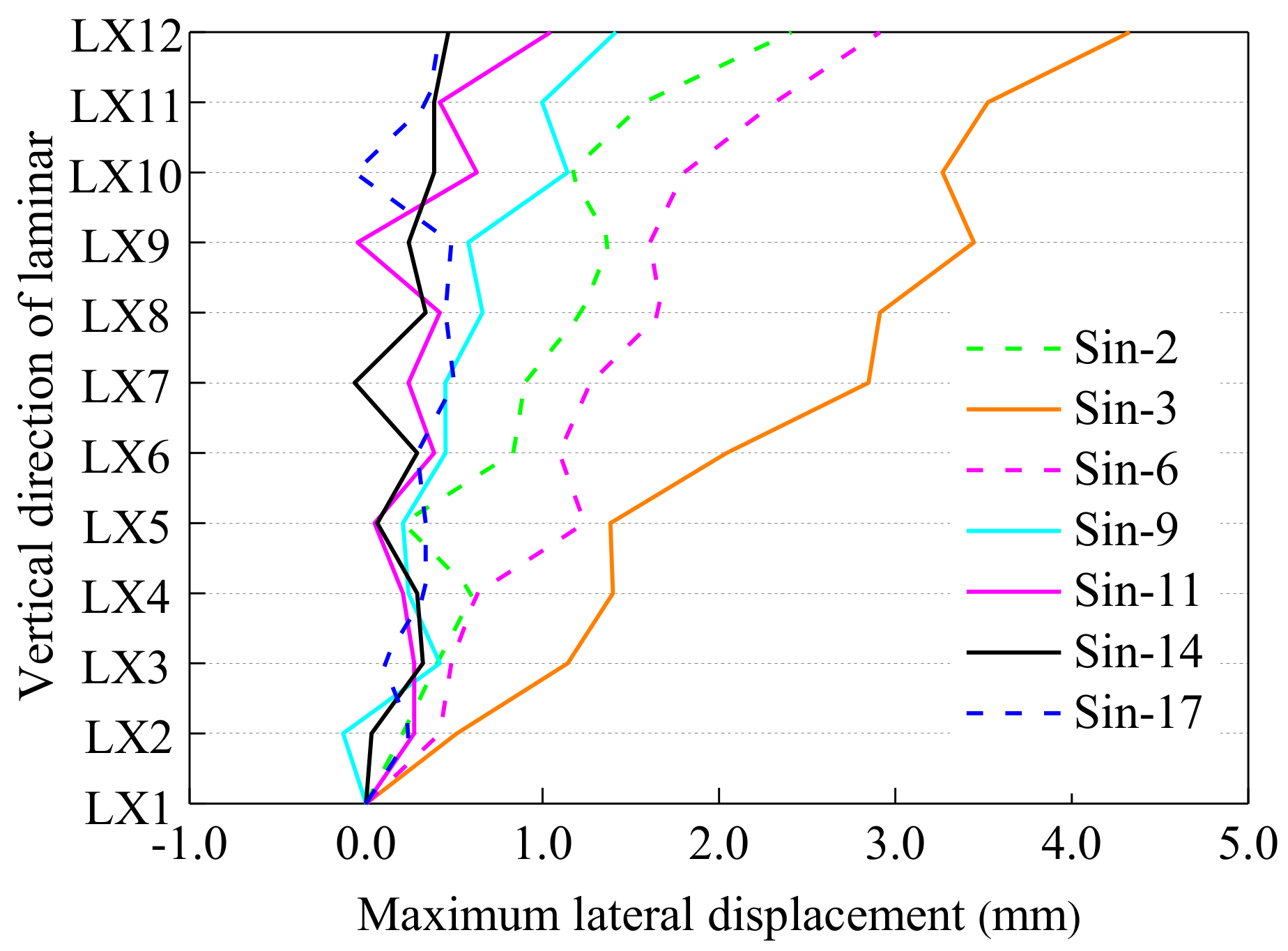
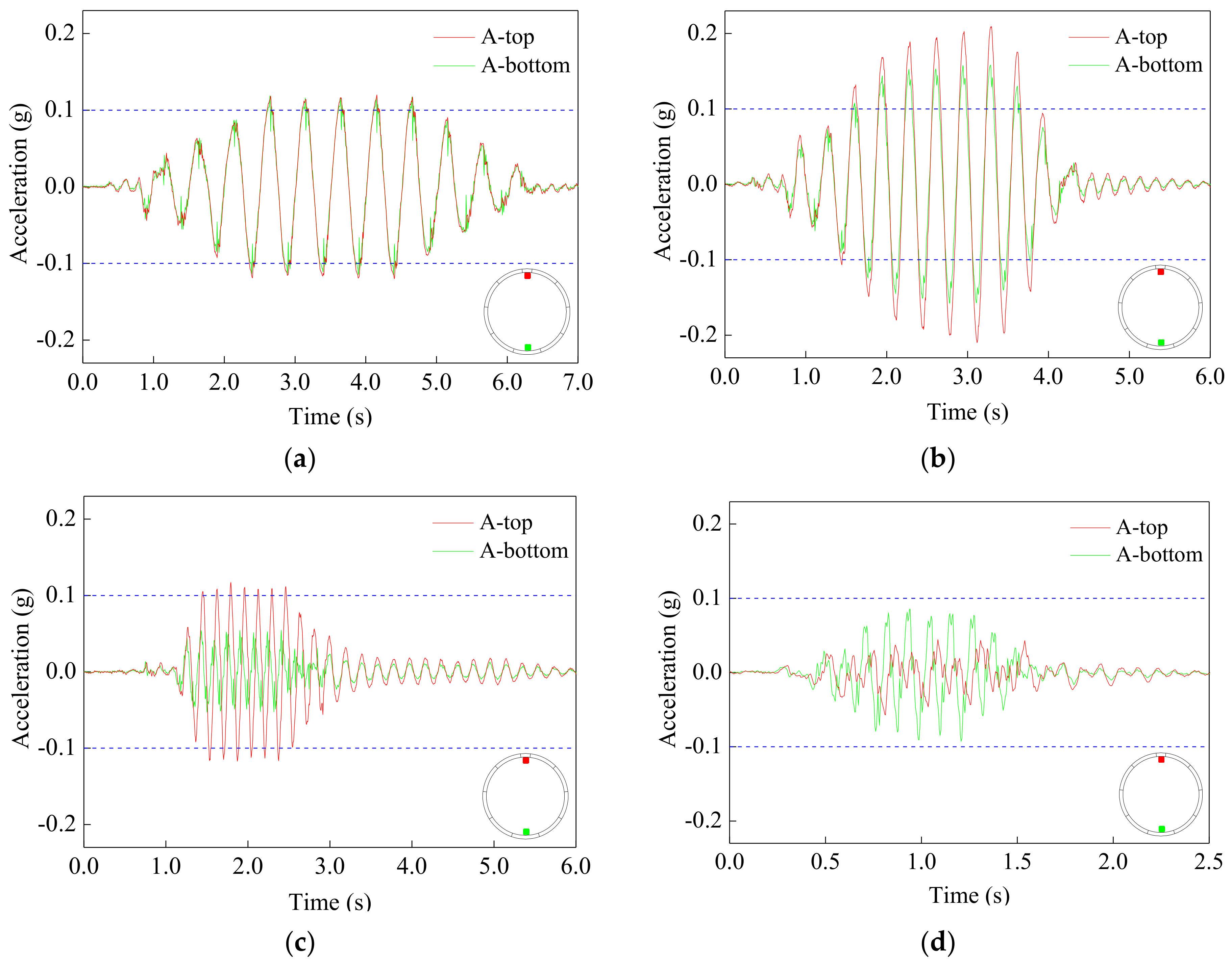
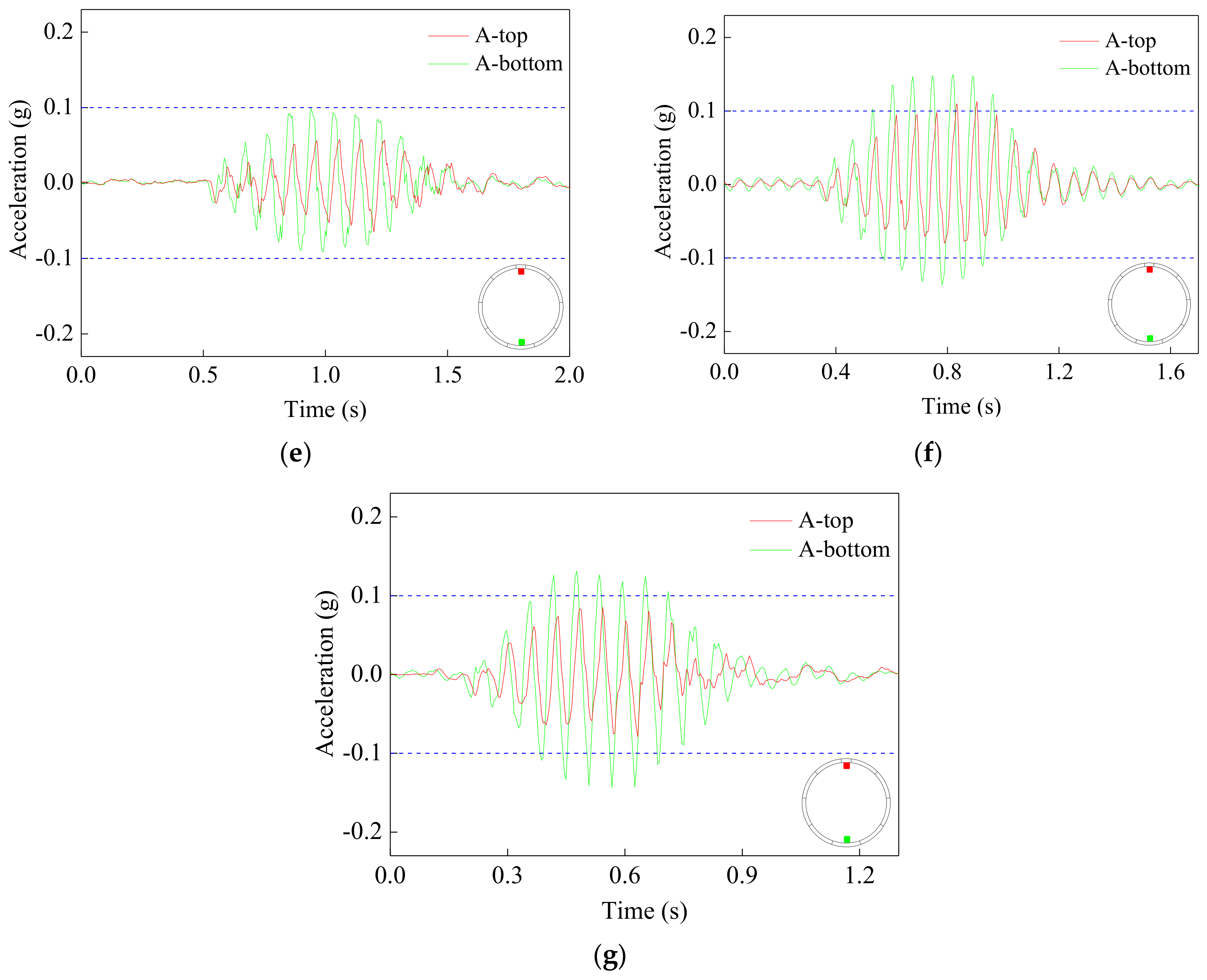
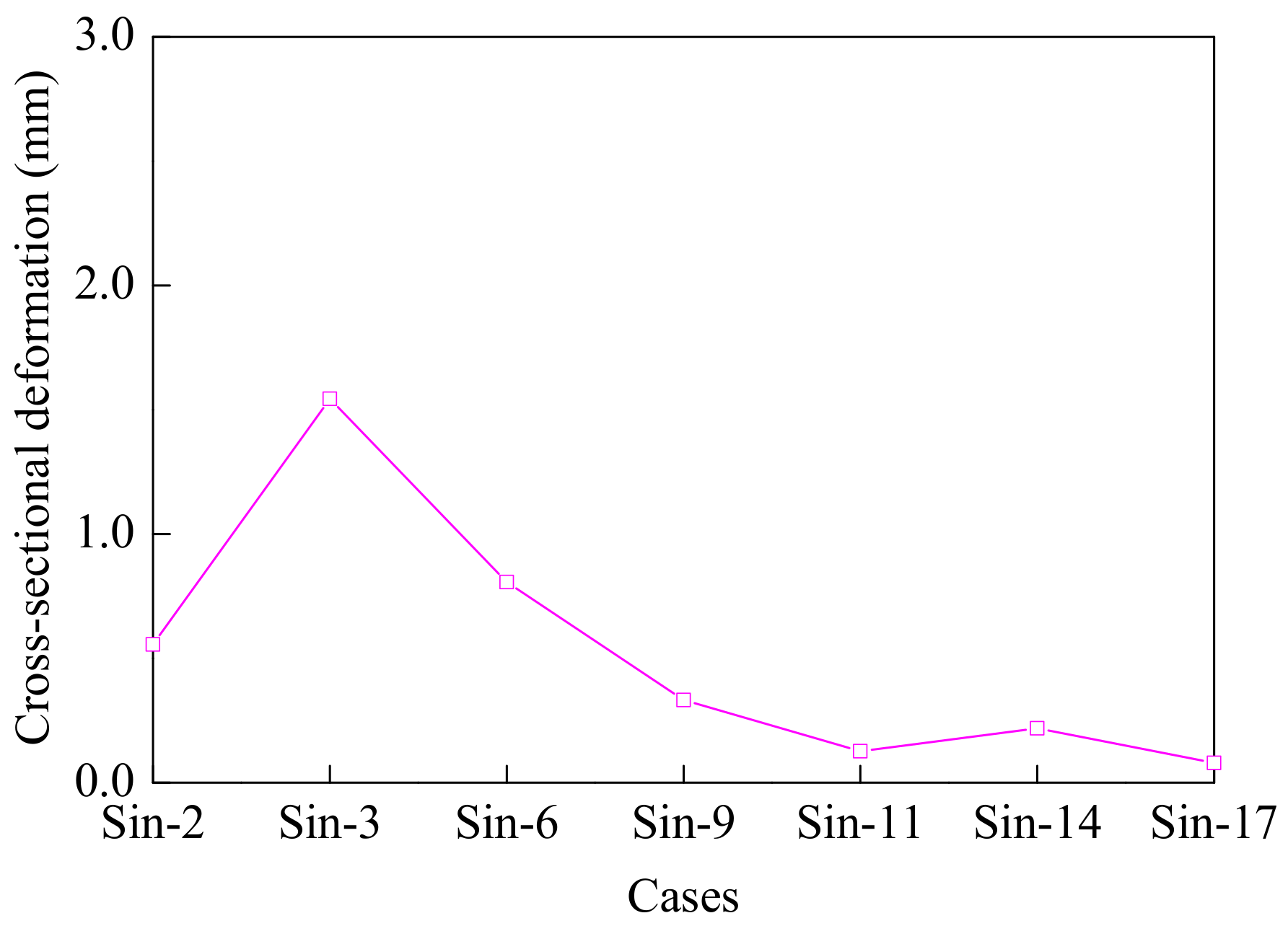
5.3. Cross-Sectional Deformations of Model Tunnel
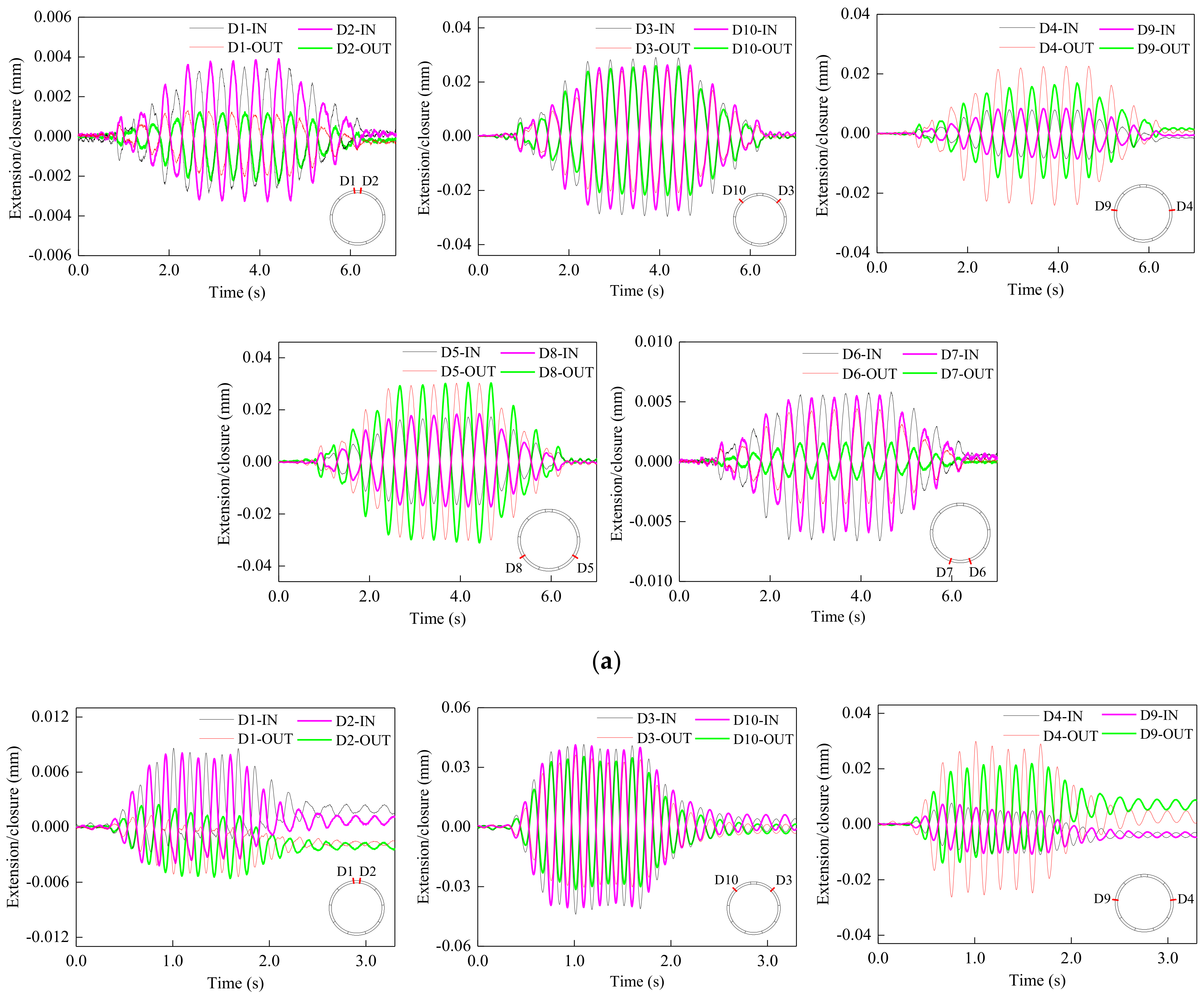
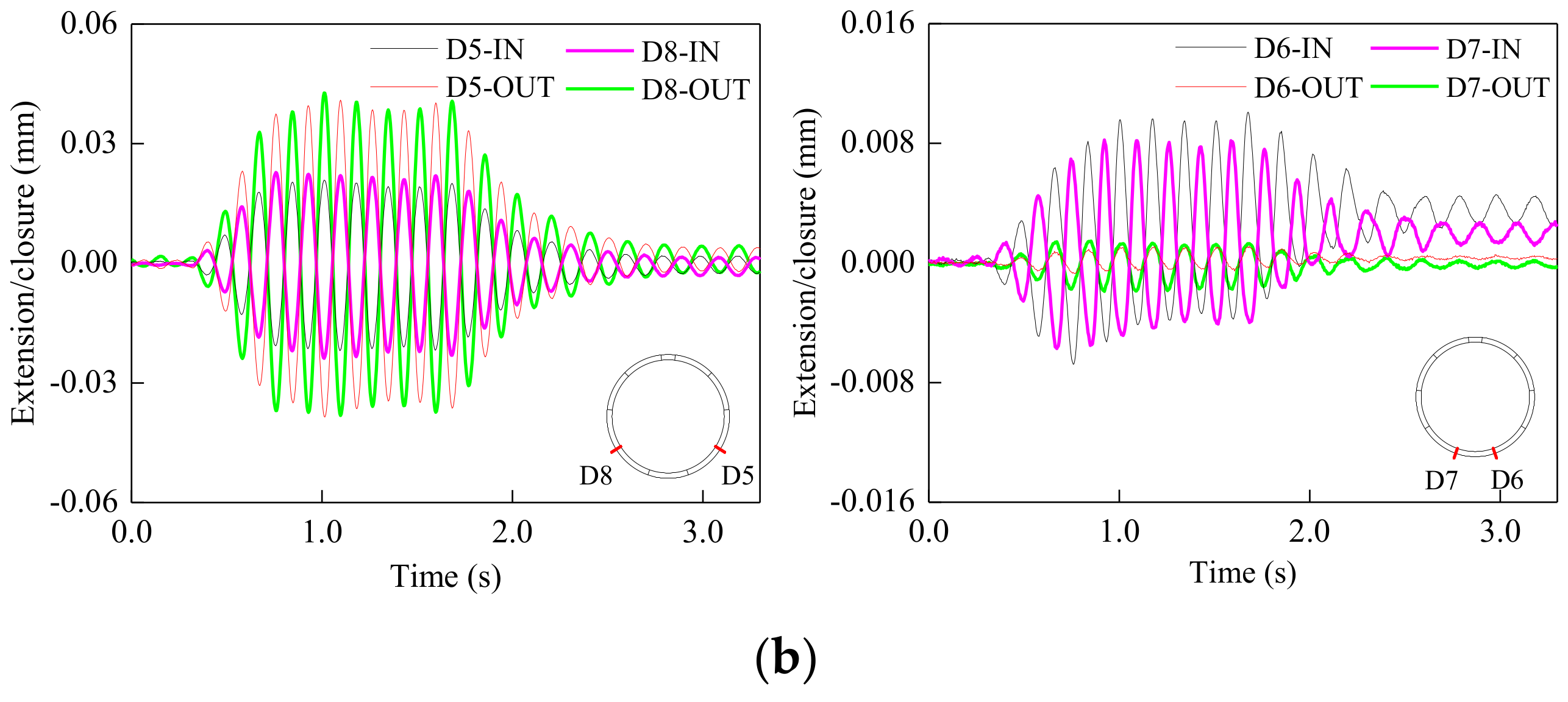
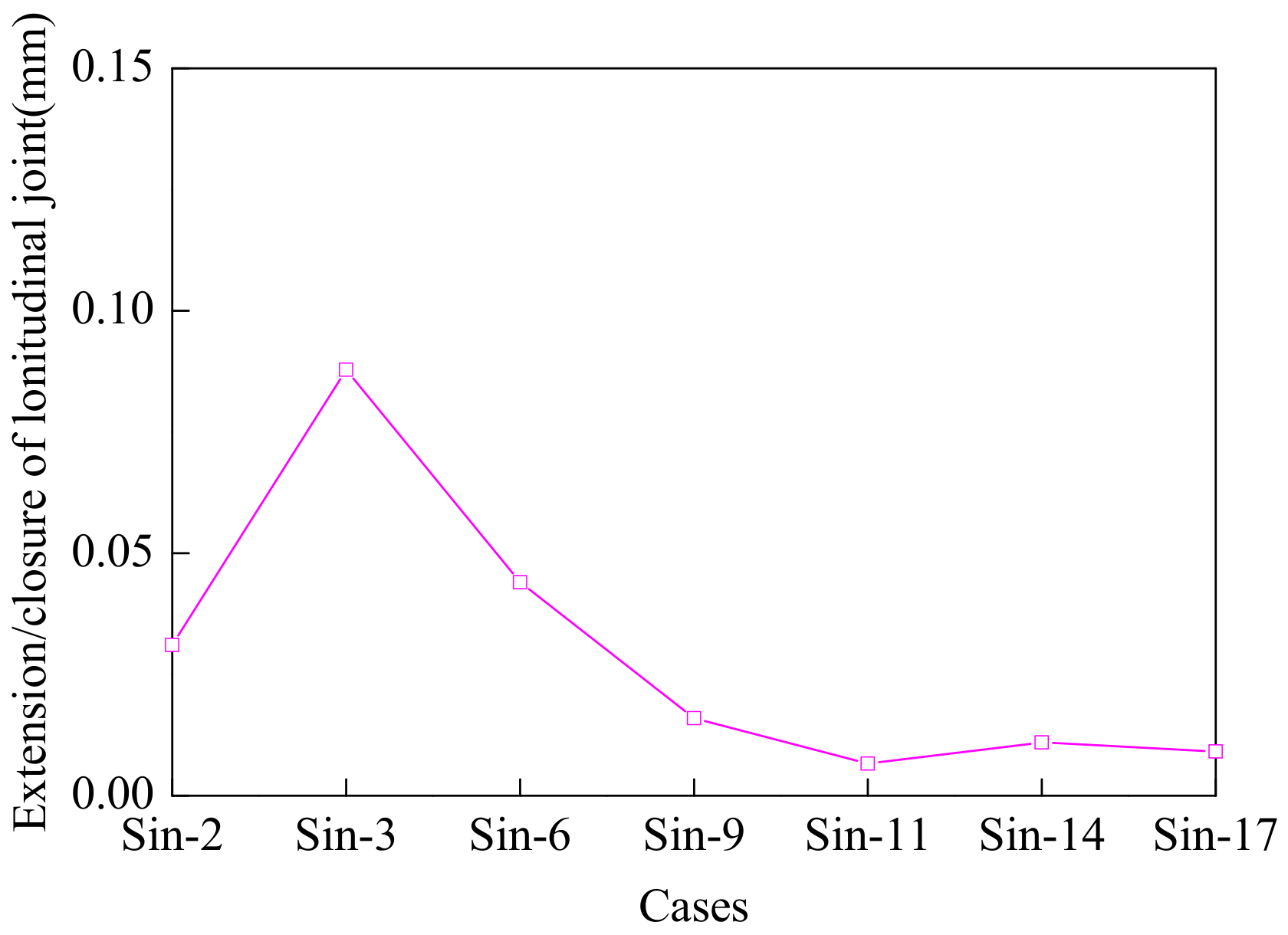
5.4. Extension/Closure of Longitudinal Joints of Model Tunnel
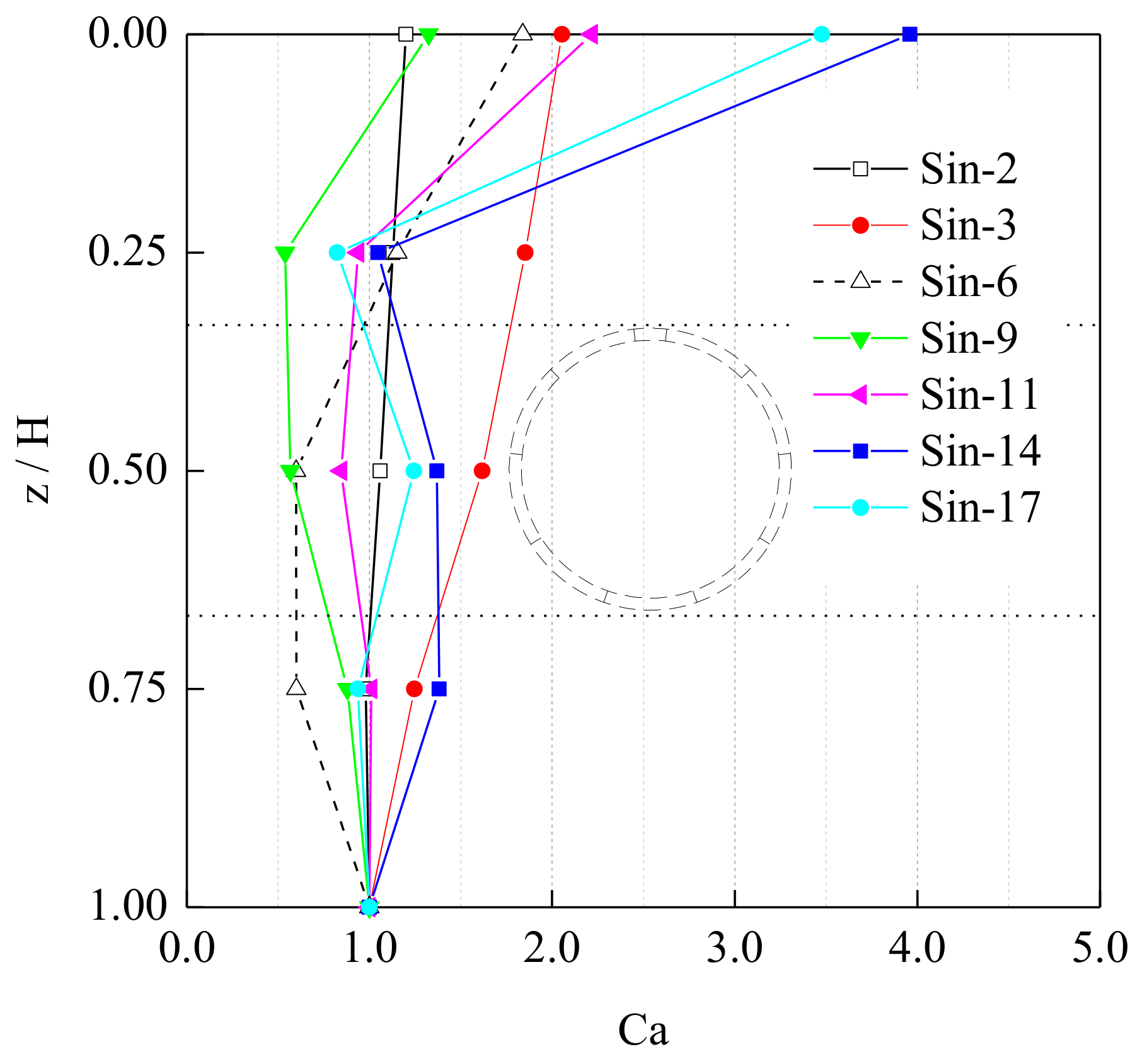
5.5. Dynamic Normal Earth Pressures of Model Tunnel
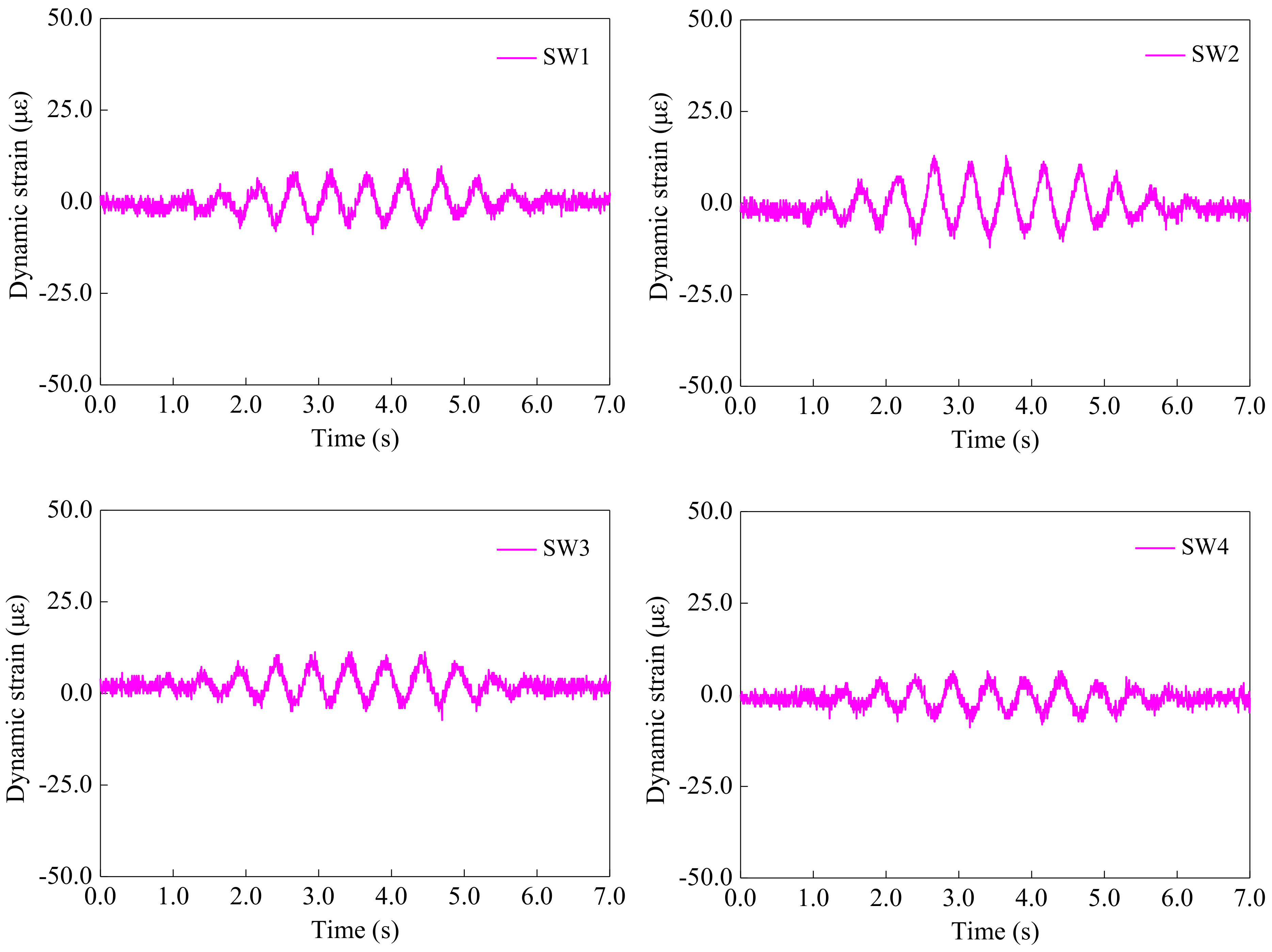
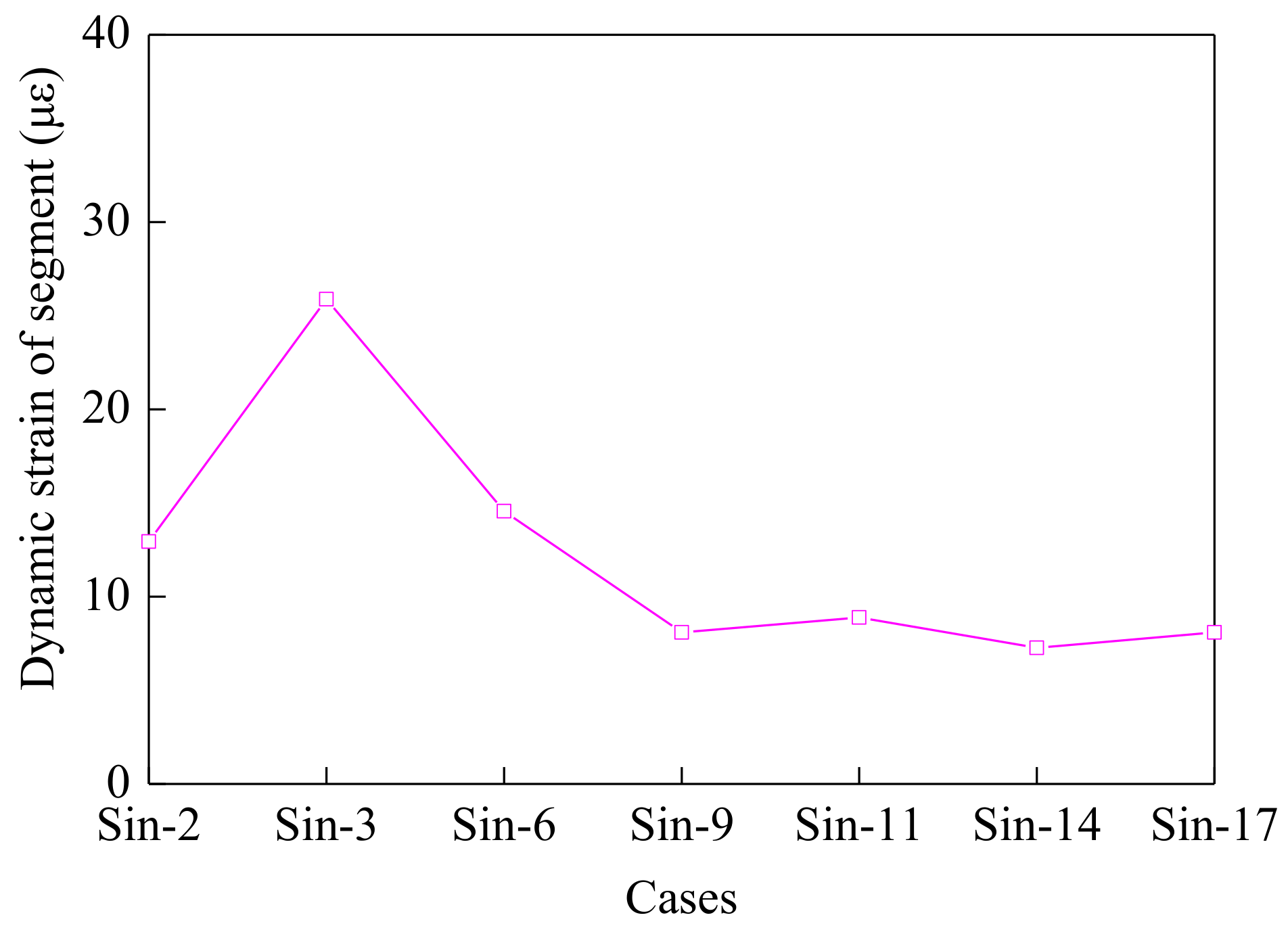
5.6. Dynamic Strain of Segments of Model Tunnel
5.7. Relationship between Sinusoidal Excitations and Maximum Tunnel Responses
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bilotta, E.; Lanzano, G.; Russo, G.; Santucci, F.; Silvestri, F. Methods for the Seismic Analysis of Transverse Section of Circular Tunnels in Soft Ground; Workshop of ERTC12-Evaluation Committee for the Application of EC8 Special Session XIV ECSMGE, Madrid, Patron Editore; University of Naples Federico II: Bologna, Italy, 2007. [Google Scholar]
- Moss, R.E.S.; Crosariol, V.A. Scale Model Shake Table Testing of an Underground Tunnel Cross Section in Soft Clay. Earthq. Spectra 2013, 29, 1413–1440. [Google Scholar] [CrossRef]
- Bao, Z.; Yuan, Y.; Yu, H. Multi-scale physical model of shield tunnels applied in shaking table test. Soil Dyn. Earthq. Eng. 2017, 100, 465–479. [Google Scholar] [CrossRef]
- Cilingir, U.; Madabhushi, S.G. A model study on the effects of input motion on the seismic behaviour of tunnels. Soil Dyn. Earthq. Eng. 2011, 31, 452–462. [Google Scholar] [CrossRef]
- Chen, Z.; Shen, H. Dynamic centrifuge tests on isolation mechanism of tunnels subjected to seismic shaking. Tunn. Undergr. Space Technol. 2014, 42, 67–77. [Google Scholar] [CrossRef]
- Moghadam, M.R.; Baziar, M.H. Seismic ground motion amplification pattern induced by a subway tunnel: Shaking table testing and numerical simulation. Soil Dyn. Earthq. Eng. 2016, 83, 81–97. [Google Scholar] [CrossRef]
- He, C.; Koizumi, A. Dynamic behavior in transverse direction of shield tunnel with considering effect of segment joints. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zeland, 30 January–4 February 2000. [Google Scholar]
- Zhang, J.H.; Yuan, Y.; Yu, H.T. Shaking table tests on discrepant responses of shaft-tunnel junction in soft soil under trans-verse excitations. Soil Dyn. Earthq. Eng. 2019, 120, 345–359. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, X.; He, C.; Huang, C. Seismic Response of a Tunnel Embedded in Compacted Clay through Large-Scale Shake Table Testing. Shock. Vib. 2018, 2018, 1–17. [Google Scholar] [CrossRef]
- Klappers, C.; Grübl, F.; Ostermeier, B. Structural analyses of segmental lining–Coupled beam and spring analyses versus 3D-FEM calculations with shell elements. Tunn. Undergr. Space Technol. 2006, 21, 254–255. [Google Scholar] [CrossRef]
- Ye, F.; Gou, C.-F.; Sun, H.-D.; Liu, Y.-P.; Xia, Y.-X.; Zhou, Z. Model test study on effective ratio of segment transverse bending rigidity of shield tunnel. Tunn. Undergr. Space Technol. 2014, 41, 193–205. [Google Scholar] [CrossRef]
- Yan, X.; Yu, H.T.; Yuan, Y.; Yuan, J.Y. Multi-point shaking table test of the free field under non-uniform earthquake excita-tion. Soils Found. 2015, 55, 985–1000. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Yuan, Y.; Li, C.; Yang, Y.; Yu, H.; Mang, H.A. Effects of interior structure as double deck lanes on seismic performance of segmental linings. Tunn. Undergr. Space Technol. 2020, 103, 103441. [Google Scholar] [CrossRef]
- John, S.; Zahrah, T. Aseismic design of underground structures. Tunn. Undergr. Space Technol. 1985, 2, 165–197. [Google Scholar] [CrossRef]
- Wang, J.N. Seismic Design of Tunnels: A Simple State-of-the-Art Design Approach; Parsons Brinckerhoff: New York, NY, USA, 1993. [Google Scholar]
- Zhang, J.; Meng, Q.; Tu, X.; Zhao, J.; Xiao, M.; Yuan, Y.; Papadrakakis, M.; Fragiadakis, M. Detailed simulation of the shaft ingate of a shield tunnel under seismic impact. In Proceedings of the COMPDYN 2017—6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June 2017; National Technical University of Athens: Athens, Greece, 2017; pp. 1032–1041. [Google Scholar]
- Chopra, A.K.; Kan, C. Effects of stiffness degradation on ductility requirements for multistory buildings. Earthq. Eng. Struct. Dyn. 1973, 2, 35–45. [Google Scholar] [CrossRef]
- Powell, G.; Row, D. Influence of Analysis and Design Assumptions on Computed Inelastic Response of Moderately Tall Frames; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1976. [Google Scholar]
- Peck, R.B.; Hendron, A.J.; Mohraz, B. State of the art of soft-ground tunneling. In Proceedings of the North American Rapid Excavation and Tunneling Conference, Chicago, IL, USA, 5–7 June 1972; Volume 1, pp. 259–286. [Google Scholar]
- Olson, J.V.; Rostoker, G. Longitudinal phase variations of Pc 4-5 micropulsations. J. Geophys. Res. Space Phys. 1978, 83, 2481. [Google Scholar] [CrossRef]
- Zhou, Y.; Tan, X.M.; Chen, J.; Pei, X.J.; Chen, Y.M. Observations and analyses of site amplification effects of deep liquefiable soil deposits by geotechnical downhole array. Chin. J. Geotech. Eng. 2017, 39, 1282–1291. (In Chinese) [Google Scholar]
- Newmark, N.M.; Blume, J.A.; Kapur, K.K. Seismic Design Spectra for Nuclear Power Plants. J. Power Div. 1973, 99, 287–303. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Application to Earthquake Engineering, 3rd ed.; Prentice Hall/Pearson Education: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Wilson, E.L. Three-Dimensional Static and Dynamic Analysis of Structures; Computers & Structures: Berkeley, CA, USA, 2002. [Google Scholar]
- Idriss, I.; Seed, H. Seismic response of horizontal soil layers. Am. Soc. Civil. Engr. J. Soil Mech. 1968, 4, 1003–1031. [Google Scholar]
- Smerzini, C.; Aviles, J.; Paolucci, R.; Sanchez-Sesma, F.J. Effect of underground cavities on surface earthquake ground mo-tion under SH wave propagation. Earthq. Eng. Struct. Dyn. 2009, 38, 1441–1460. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Karina, K.; Koutsoftas, D.; O’Riordan, N. Seismic Design Considerations for Underground Box Structures. Earth Retent. Conf. 3 2010, 3, 620–637. [Google Scholar] [CrossRef]
- Bobet, A.; Fernandez, G.; Huo, H.; Ramirez, J. A practical iterative procedure to estimate seismic-induced deformations of shallow rectangular structures. Can. Geotech. J. 2008, 45, 923–938. [Google Scholar] [CrossRef]
- Takeuti, N.; Ootsuka, M. Seismic behavior of shield tunnel in a sudden change of ground. Tunn. Undergr. 1994, 25, 27–34. (In Japanese) [Google Scholar]




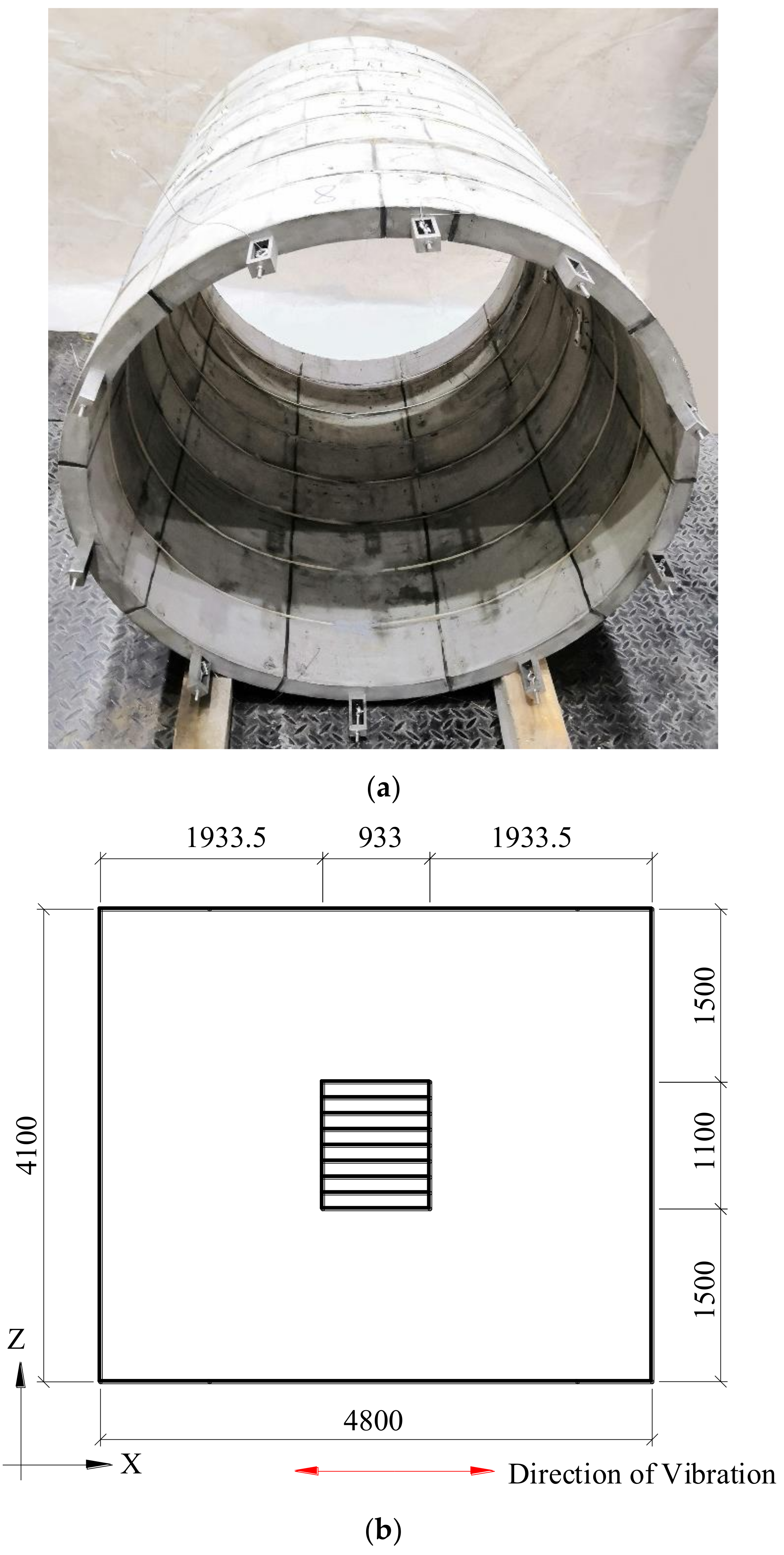


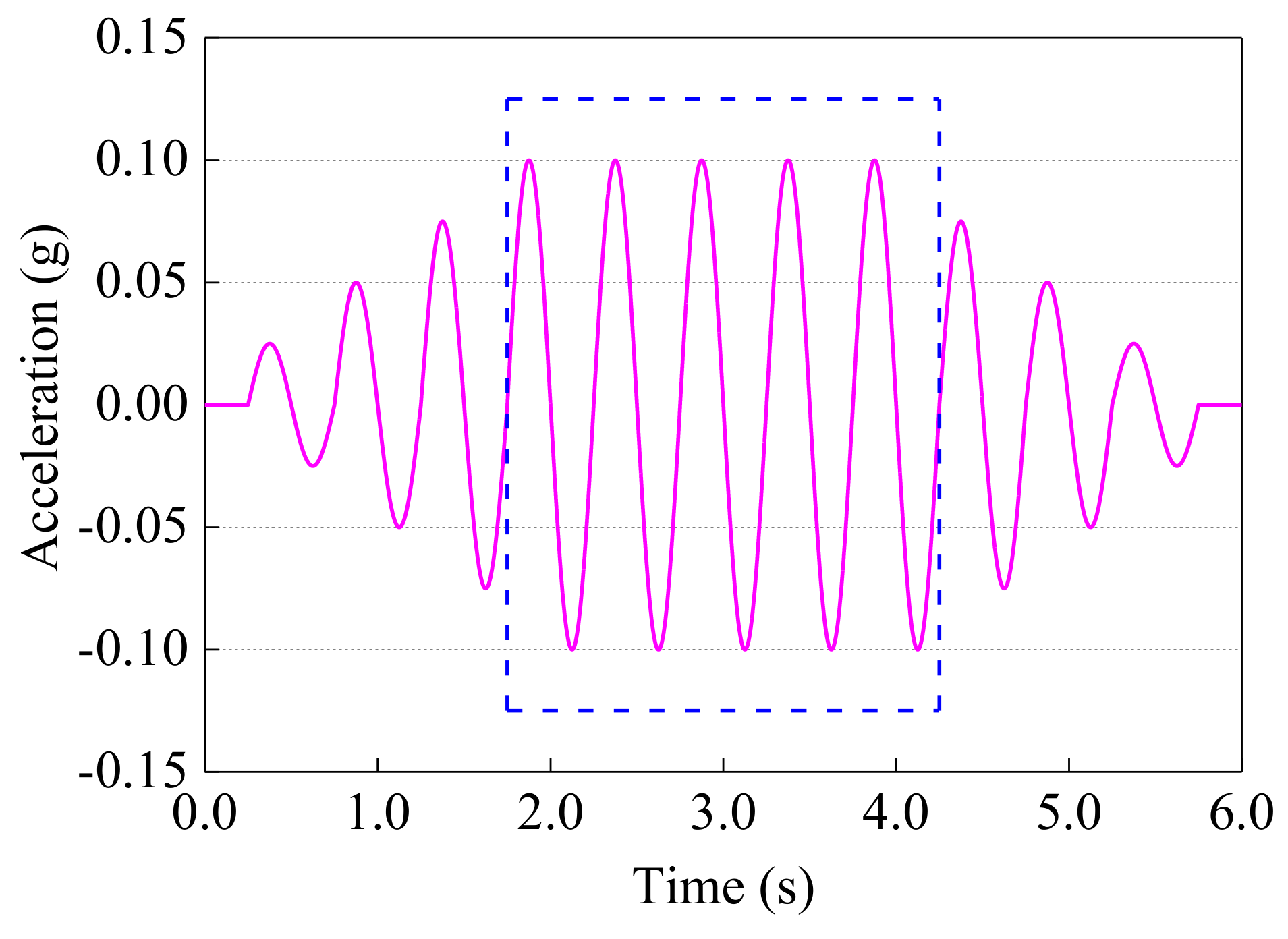
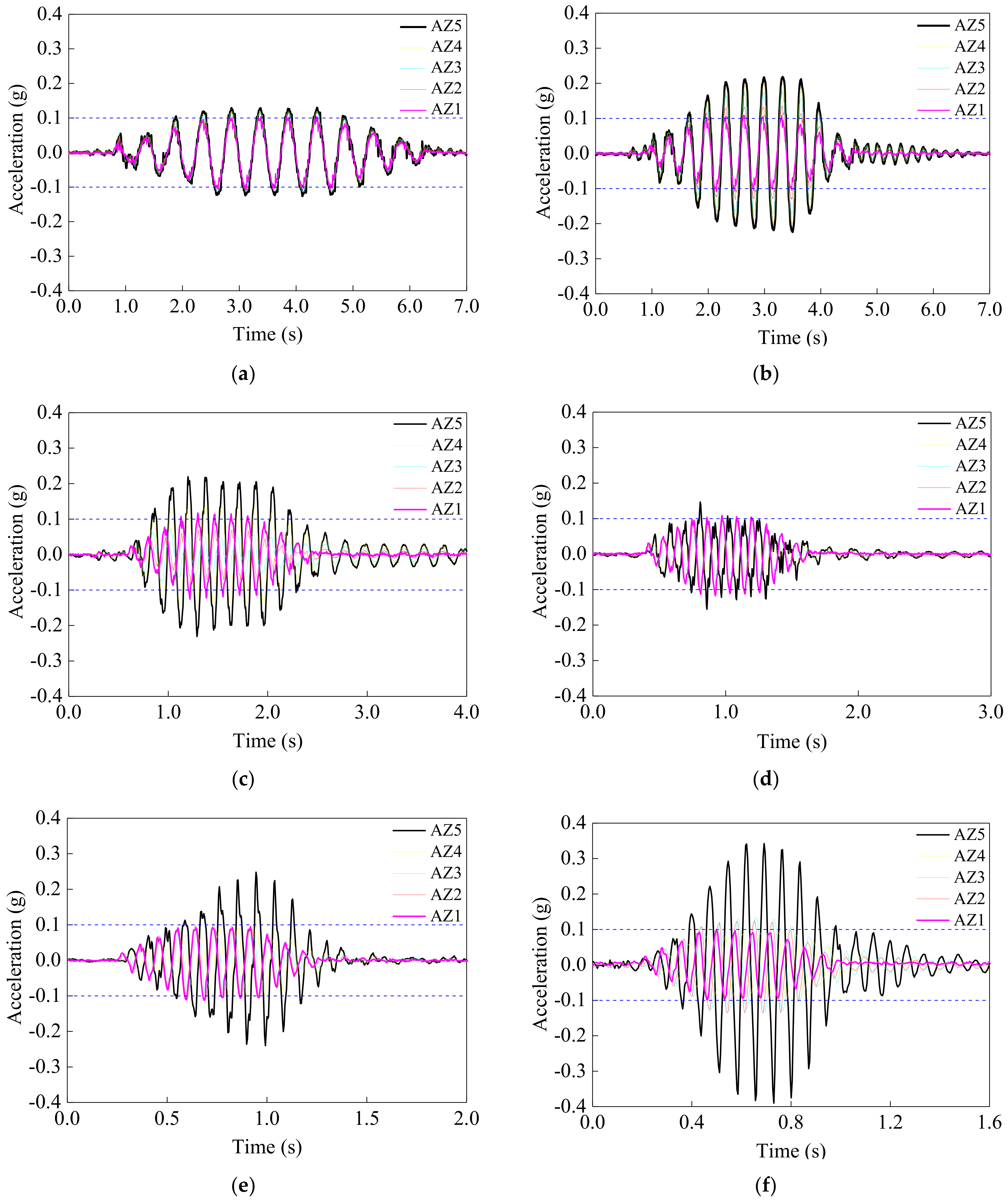
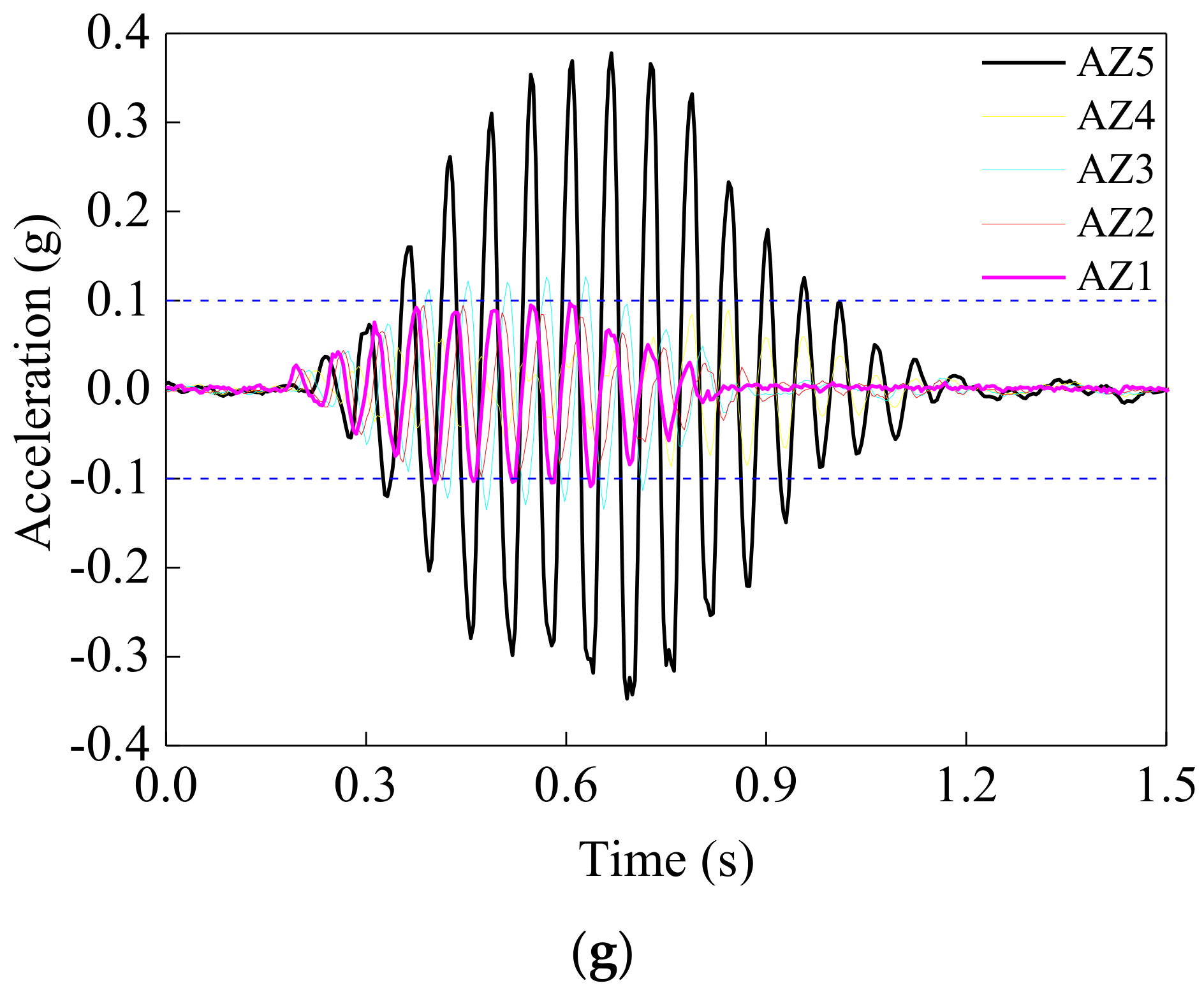







| Number | Type of Soil | Thickness (m) | Depth (m) | Weight (kN/m3) | Density (kg/m3) | Shear Velocity (m/s) |
|---|---|---|---|---|---|---|
| 1 | Backfill | 1.8 | 1.8 | 17.0 | 1730 | 137 |
| 2 | Yellow/gray-yellow silty clay | 7.2 | 9.0 | 18.1 | 1846.94 | 140 |
| 3 | Gray muddy silty clay | 3.3 | 12.3 | 17.6 | 1795.92 | 133 |
| 4 | Gray clay | 4.7 | 17.0 | 17.4 | 1775.51 | 161 |
| 5 | Gray silty clay | 10.0 | 27.0 | 17.8 | 1816.33 | 179 |
| 6 | Dark green silty clay | 2.8 | 29.8 | 19.6 | 2000.00 | 311 |
| 7 | Yellow-gray sandy silt with clay | 9.4 | 39.2 | 19.0 | 1938.78 | 289 |
| 8 | Gray silty fine sand | 2.8 | 42.0 | 18.9 | 1928.57 | 346 |
| Physical Quantities | Symbol | Dimensions | Expression | Similarity Ratio (Model/Prototype) |
|---|---|---|---|---|
| Geometrical dimension | L | 1/15 | ||
| Density | M | 1/2.7 | ||
| Shear modulus | ML−1T−2 | 1/39.2 | ||
| Elastic modulus | ML−1T−2 | 1/39.2 | ||
| Acceleration | LT−2 | 1/1 | ||
| Time | T | 1/3.92 | ||
| Frequency | T−1 | 3.92/1 |
| Parameters | Prototype | Model |
|---|---|---|
| Shear stiffness of grounds (N/mm) | 914,083 | 2926 |
| Radial stiffness of linings (N/mm) | 7022 | 23.10 |
| Transverse stiffness of linings (N/mm) | 994 | 3.15 |
| Stiffness ratio | 920 | 929 |
| Types | Accelerometer (Tunnel) | Accelerometer (Soil) | Displacement Gauge | Inductive Displacement Transducer | Earth Pressure Gauge |
|---|---|---|---|---|---|
| Resolution | 0.1% | <5% | 0.3% | 0.25% | 0.25% |
| Range | ±8 g | ±5 g | 0~0.6 mm | 0~10 mm | 0~30 kPa |
| Maximum sampling frequency | 570 Hz | 1000 Hz | 1000 Hz | 1000 Hz | 5000 Hz |
| Test ID | Input Motions | Frequency (Hz) |
|---|---|---|
| WN-1 | White noise | 0–50 |
| Sin-2 | Sinusoidal Wave | 2 |
| Sin-3 | Sinusoidal Wave | 3 |
| Sin-6 | Sinusoidal Wave | 6 |
| Sin-9 | Sinusoidal Wave | 9 |
| Sin-11 | Sinusoidal Wave | 11 |
| Sin-14 | Sinusoidal Wave | 14 |
| Sin-17 | Sinusoidal Wave | 17 |
| WN-2 | White noise | 0–50 |
| Model | Test ID | Input Motions | Fundamental Frequency (Hz) | Relative Difference (%) |
|---|---|---|---|---|
| FF | WN-1 | White noise | 4.99 | 0.81 |
| WN-2 | 4.95 | |||
| ST | WN-1 | White noise | 5.00 | 1.20 |
| WN-2 | 4.94 |
| Mode Order | Modal Participating Mass Ratios | Total Ratio |
|---|---|---|
| n = 1 | 81.1% | 95.0% |
| n = 2 | 9.0% | |
| n = 3 | 3.2% | |
| n = 4 | 1.7% |
| Modal Amplitude (Absolute Peak Value) | Frequency of Sinusoidal Excitation | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 Hz | 3 Hz | 6 Hz | 9 Hz | 11 Hz | 14 Hz | 17 Hz | ||
| Mode order | 1 | 9.66 | 7.78 | 2.64 | 2.17 | 1.84 | 1.51 | 1.38 |
| 2 | 2.80 | 1.59 | 0.95 | 0.96 | 0.74 | 0.59 | 0.57 | |
| 3 | 1.90 | 1.15 | 0.51 | 0.57 | 0.53 | 0.51 | 0.46 | |
| 4 | 1.45 | 0.83 | 0.50 | 0.44 | 0.40 | 0.39 | 0.31 | |
| Case | A-Top (g) | A-Bottom (g) | Difference (%) | Phase Difference |
|---|---|---|---|---|
| Sin-2 | 0.120 | 0.119 | 0.83 | 1/64π |
| Sin-3 | 0.210 | 0.158 | 24.76 | 3/64π |
| Sin-6 | 0.117 | 0.054 | 53.85 | 3/5π |
| Sin-9 | 0.057 | 0.093 | −63.16 | 1π |
| Sin-11 | 0.065 | 0.099 | −52.31 | 3/7π |
| Sin-14 | 0.113 | 0.150 | −32.74 | 1/3π |
| Sin-17 | 0.085 | 0.144 | −69.41 | 1/4π |
| Cases | Label | Absolute Maximum (με) | Cases | Label | Absolute Maximum (με) |
|---|---|---|---|---|---|
| Sin-2 Hz | SW1 | 9.70 | Sin-3 Hz | SW1 | 22.63 |
| SW2 | 12.94 | SW2 | 25.88 | ||
| SW3 | 11.30 | SW3 | 20.99 | ||
| SW4 | 8.91 | SW4 | 13.76 | ||
| Sin-6 Hz | SW1 | 12.12 | Sin-9 Hz | SW1 | 7.27 |
| SW2 | 12.13 | SW2 | 7.28 | ||
| SW3 | 10.49 | SW3 | 4.85 | ||
| SW4 | 8.90 | SW4 | 8.09 | ||
| Sin-11 Hz | SW1 | 8.89 | Sin-14 Hz | SW1 | 7.27 |
| SW2 | 7.28 | SW2 | 5.66 | ||
| SW3 | 5.65 | SW3 | 6.46 | ||
| SW4 | 6.47 | SW4 | 4.86 | ||
| Sin-17 Hz | SW1 | 6.46 | Sin-17 Hz | SW3 | 5.65 |
| SW2 | 4.85 | SW4 | 8.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Yuan, Y.; Yang, Y.; Li, C.; Mang, H.A. Dynamic Performance of Soil–Tunnel System under Transverse Sinusoidal Excitations. Appl. Sci. 2021, 11, 5097. https://doi.org/10.3390/app11115097
Zhang S, Yuan Y, Yang Y, Li C, Mang HA. Dynamic Performance of Soil–Tunnel System under Transverse Sinusoidal Excitations. Applied Sciences. 2021; 11(11):5097. https://doi.org/10.3390/app11115097
Chicago/Turabian StyleZhang, Shaohua, Yong Yuan, Yusheng Yang, Chong Li, and Herbert A. Mang. 2021. "Dynamic Performance of Soil–Tunnel System under Transverse Sinusoidal Excitations" Applied Sciences 11, no. 11: 5097. https://doi.org/10.3390/app11115097






