Backstepping Control of an Unmanned Helicopter Subjected to External Disturbance and Model Uncertainty
Abstract
:1. Introduction
2. Related Work
3. Model Description of Helicopter and Wind Gust
- The helicopter is treated as a rigid body.
- The off-axis moment of inertia is neglected as they are usually very small.
- The counteractive torque of the tail rotor is ignored because it is too small.
- The drag forces of the fuselage are ignored for simplification.
- The forces and moments of horizontal and vertical fin are ignored for simplification.
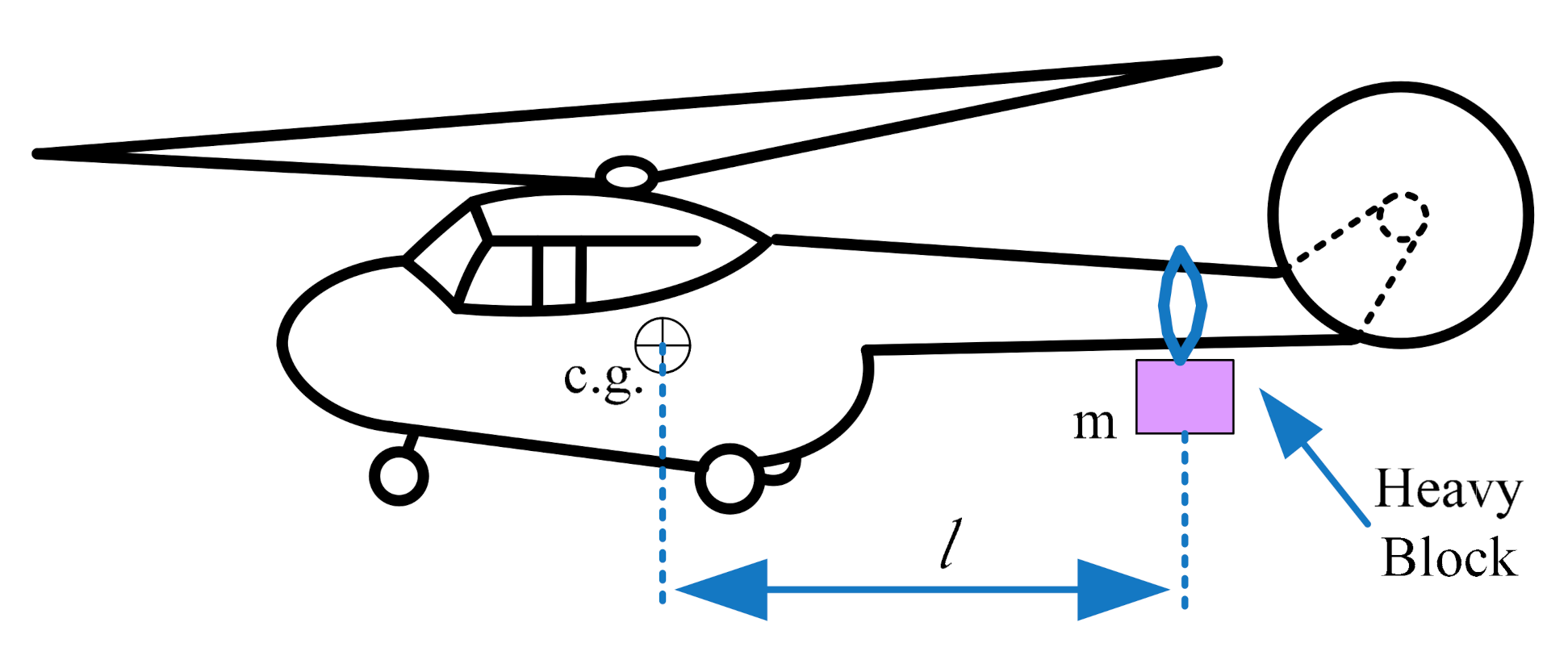
3.1. Helicopter Modeling
3.2. Mathematical Model of Wind Gust
4. Controller Design
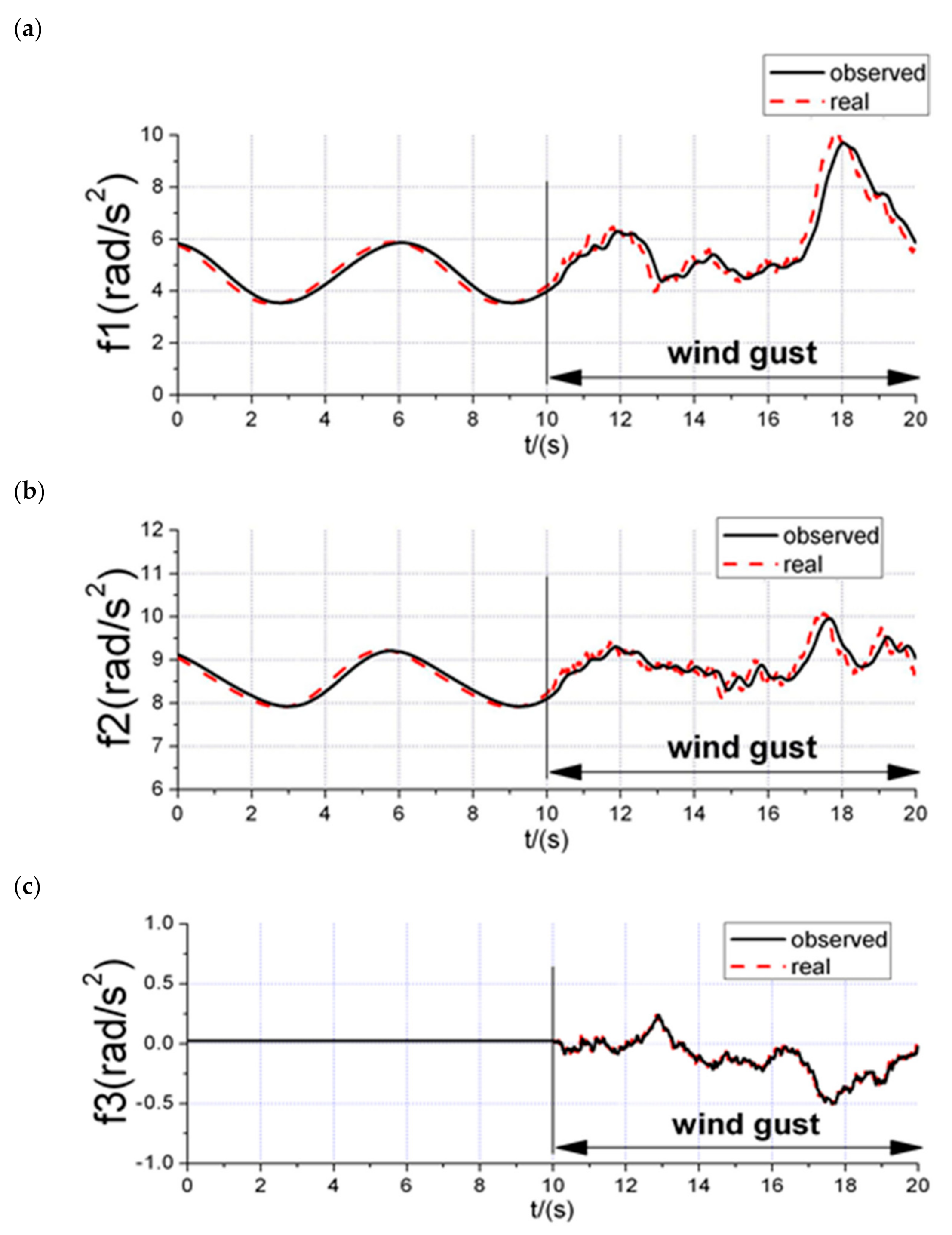
4.1. Design of ESO
4.2. Backstepping Controller
4.3. Analysis of Model Uncertainty
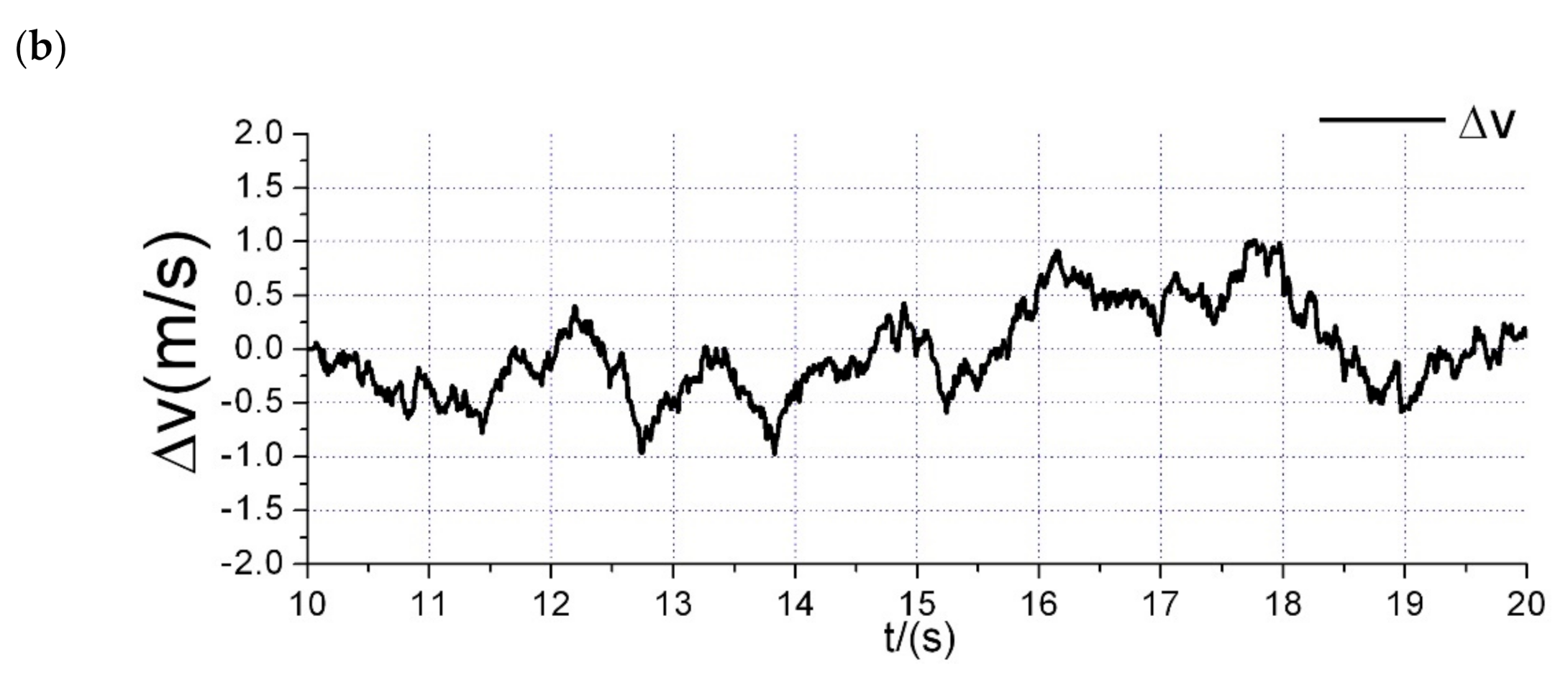
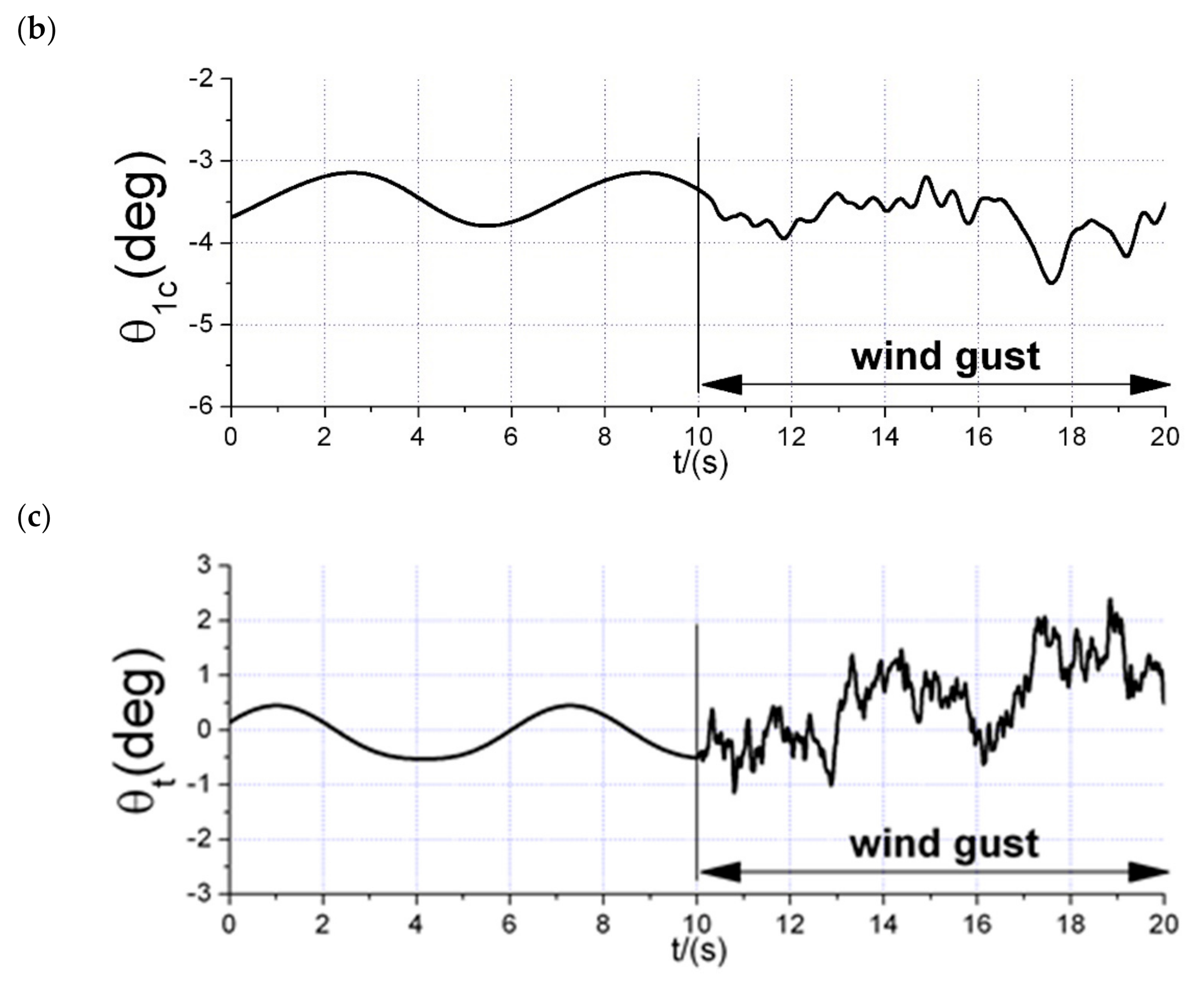
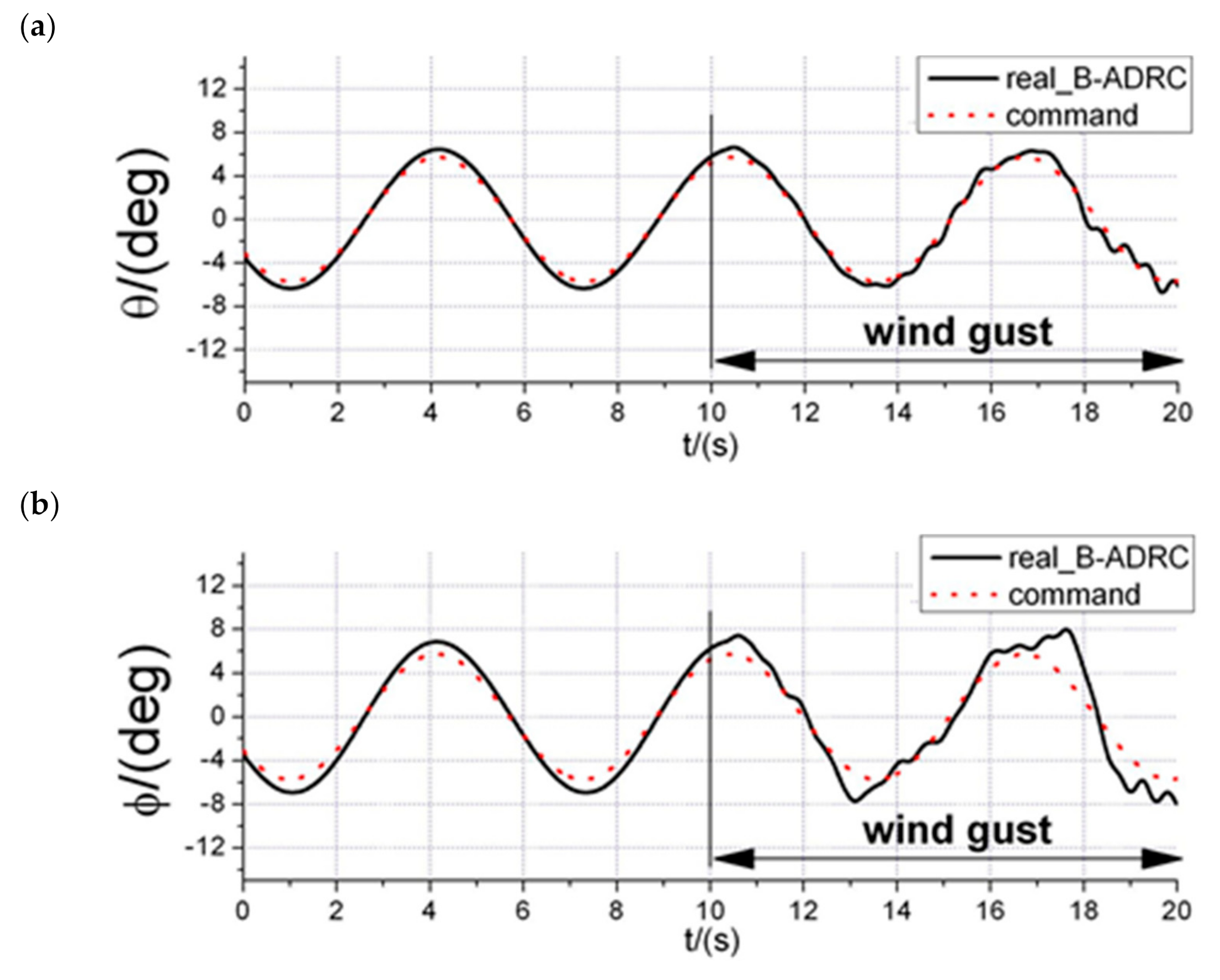
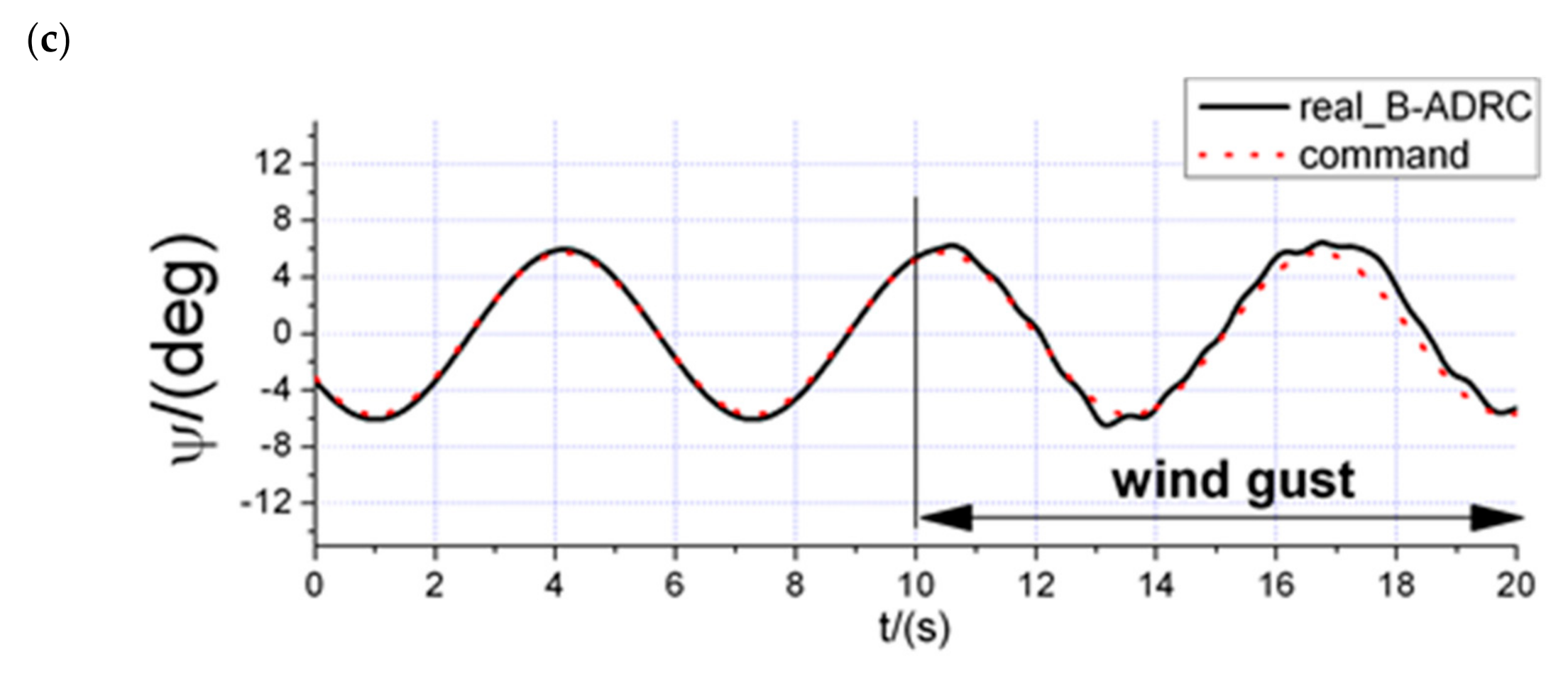
5. Simulation Results
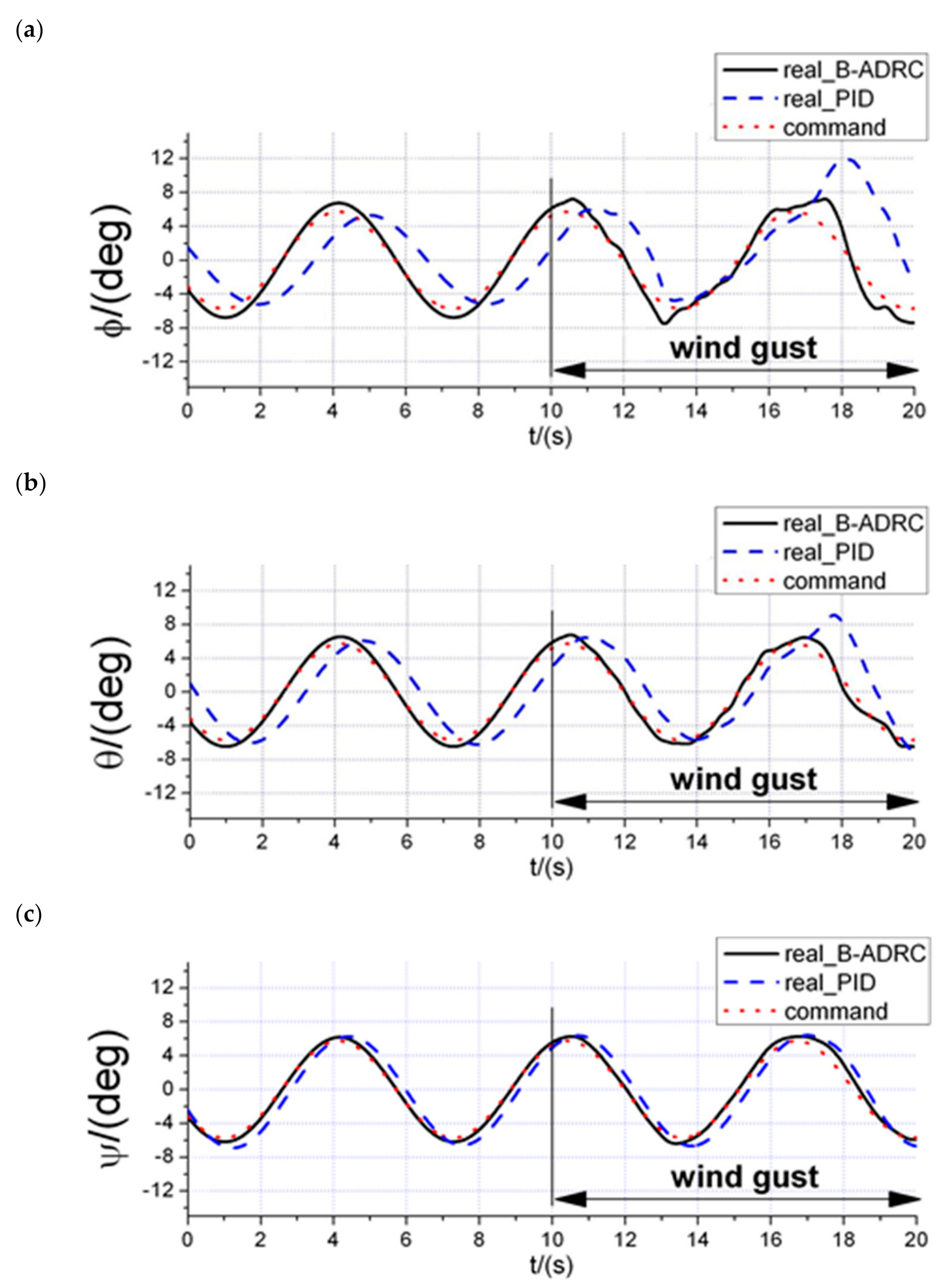
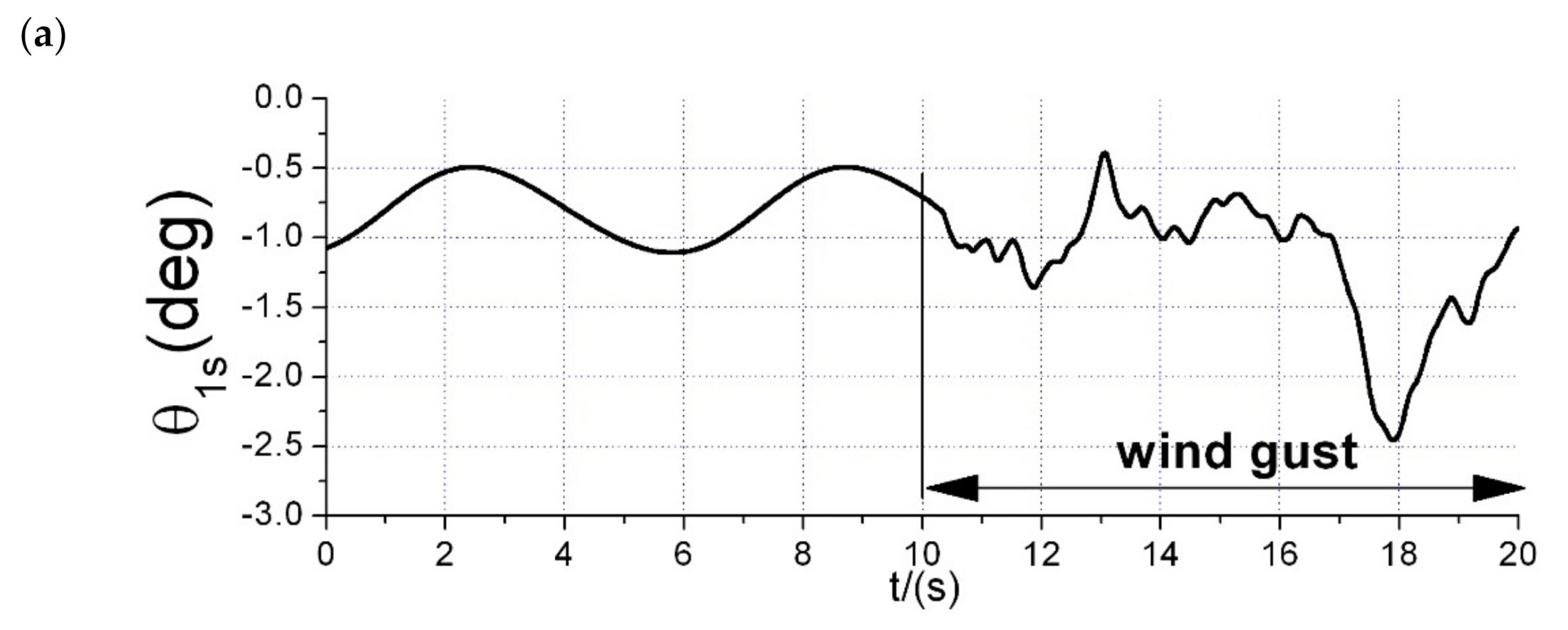
6. Flight Test Experiment
6.1. Testbed Design
6.2. Disturbance Rejection Experiments
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- García, R.; Rubio, F.; Ortega, M. Robust PID Control of the Quadrotor Helicopter. IFAC Proc. Vol. 2012, 45, 229–234. [Google Scholar] [CrossRef] [Green Version]
- Martins, L.; Cardeira, C.; Oliveira, P. Linear Quadratic Regulator for Trajectory Tracking of a Quadrotor. IFAC PapersOnLine 2019, 52, 176–181. [Google Scholar] [CrossRef]
- Xu, J.; Cai, C.; Cai, G.; Zou, Y. Robust H-infinity control for miniature unmanned aerial vehicles at hover by the finite frequency strategy. IET Control Theory Appl. 2016, 10, 190–200. [Google Scholar] [CrossRef]
- Jeong, D.Y.; Kang, T.; Dharmayanda, H.R. H-Infinity Attitude Control System Design for a Small-Scale Autonomous Heli-copter with Nonlinear Dynamics and Uncertainties. J. Aerosp. Eng. 2012, 25, 501–518. [Google Scholar] [CrossRef]
- Tao, L.; Lin, D.; Tao, D. Finite-time control for small-scale unmanned helicopter with disturbances. Nonlinear Dyn. 2019, 96, 1747–1763. [Google Scholar]
- Fang, X.; Wu, A.; Shang, Y.; Dong, N. A novel sliding mode controller for small-scale unmanned helicopters with mismatched disturbance. Nonlinear Dyn. 2015, 83, 1053–1068. [Google Scholar] [CrossRef]
- Wan, M.; Chen, M.; Yan, K. Adaptive Sliding Mode Tracking Control for Unmanned Autonomous Helicopters Based on Neural Networks. Complexity 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Yan, K.; Chen, M.; Wu, Q.; Zhu, R. Robust adaptive compensation control for unmanned autonomous helicopter with input saturation and actuator faults. Chin. J. Aeronaut. 2019, 32, 2299–2310. [Google Scholar] [CrossRef]
- Mallikarjunan, S.; Nesbitt, B.; Kharisov, E.; Xargay, E.; Hovakimyan, N.; Cao, C. L1 Adaptive Controller for Attitude Control of Multirotors. In AIAA Guidance, Navigation, and Control Conference; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; p. 4831. [Google Scholar]
- Ullah, I.; Pei, H.-L. Fixed Time Disturbance Observer Based Sliding Mode Control for a Miniature Unmanned Helicopter Hover Operations in Presence of External Disturbances. IEEE Access 2020, 8, 73173–73181. [Google Scholar] [CrossRef]
- Jiang, T.; Lin, D.; Song, T. Novel integral sliding mode control for small-scale unmanned helicopters. J. Frankl. Inst. 2019, 356, 2668–2689. [Google Scholar] [CrossRef]
- Yu, X.; Yang, J.; Li, S. Disturbance observer-based autonomous landing control of unmanned helicopters on moving shipboard. Nonlinear Dyn. 2020, 102, 131–150. [Google Scholar] [CrossRef]
- Joelianto, E.; Sumarjono, E.M.; Budiyono, A.; Penggalih, D.R. Model predictive control for autonomous unmanned helicopters. Aircr. Eng. Aerosp. Technol. 2011, 83, 375–387. [Google Scholar] [CrossRef]
- Seo, J.; Lee, S.; Lee, J.; Choi, J. Nonaffine Helicopter Control Design and Implementation Based on a Robust Explicit Nonlinear Model Predictive Control. IEEE Trans. Control Syst. Technol. 2021, 1–8. [Google Scholar] [CrossRef]
- Dutta, L.; Das, D.K. Adaptive model predictive control design using multiple model second level adaptation for parameter estimation of two-degree freedom of helicopter model. Int. J. Robust Nonlinear Control 2021, 31, 3248–3278. [Google Scholar] [CrossRef]
- Manzoor, T.; Xia, Y.; Zhai, D.-H.; Ma, D. Trajectory tracking control of a VTOL unmanned aerial vehicle using offset-free tracking MPC. Chin. J. Aeronaut. 2020, 33, 2024–2042. [Google Scholar] [CrossRef]
- Manzoor, T.; Sun, Z.; Xia, Y.; Ma, D. MPC based compound flight control strategy for a ducted fan aircraft. Aerosp. Sci. Technol. 2020, 107, 106264. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, Y.; Li, S.; Zhou, Y. Fuzzy controller design of micro-unmanned helicopter relying on improved genetic optimi-zation algorithm. Aerosp. Sci. Technol. 2020, 98, 105685. [Google Scholar] [CrossRef]
- Jiang, F.; Pourpanah, F.; Hao, Q. Design, Implementation, and Evaluation of a Neural-Network-Based Quadcopter UAV System. IEEE Trans. Ind. Electron. 2020, 67, 2076–2085. [Google Scholar] [CrossRef]
- Pi, C.-H.; Hu, K.-C.; Cheng, S.; Wu, I.-C. Low-level autonomous control and tracking of quadrotor using reinforcement learning. Control Eng. Pr. 2020, 95, 104222. [Google Scholar] [CrossRef]
- Cao, L.; Hu, X.; Zhang, S.; Liu, Y. Robust Flight Control Design Using Sensor-Based Backstepping Control for Unmanned Aerial Vehicles. J. Aerosp. Eng. 2017, 30, 04017068. [Google Scholar] [CrossRef]
- Wang, X.; Yu, X.; Li, S.; Liu, J. Composite block backstepping trajectory tracking control for disturbed unmanned helicopters. Aerosp. Sci. Technol. 2019, 85, 386–398. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive backstepping fast terminal sliding mode controller for uncertain quadrotor UAV. Aerosp. Sci. Technol. 2019, 93, 105306. [Google Scholar] [CrossRef]
- Eliker, K.; Zhang, W. Finite-time Adaptive Integral Backstepping Fast Terminal Sliding Mode Control Application on Quadrotor UAV. Int. J. Control Autom. Syst. 2020, 18, 415–430. [Google Scholar] [CrossRef]
- Pi, C.-H.; Ye, W.-Y.; Cheng, S. Robust Quadrotor Control through Reinforcement Learning with Disturbance Compensation. Appl. Sci. 2021, 11, 3257. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, F.; Guo, Y.; Hua, C. Multivariable sliding mode backstepping controller design for quadrotor UAV based on disturbance observer. Sci. China Inf. Sci. 2018, 61, 112207. [Google Scholar] [CrossRef]
- Chen, F.; Lei, W.; Zhang, K.; Tao, G.; Jiang, B. A novel nonlinear resilient control for a quadrotor UAV via backstepping control and nonlinear disturbance observer. Nonlinear Dyn. 2016, 85, 1281–1295. [Google Scholar] [CrossRef]
- Han, J. A class of extended state observers for uncertain systems. Control Decis. 1995, 10, 85–88. [Google Scholar]
- Alexis, K.; Papachristos, C.; Siegwart, R.; Tzes, A. Robust Model Predictive Flight Control of Unmanned Rotorcrafts. J. Intell. Robot. Syst. 2015, 81, 443–469. [Google Scholar] [CrossRef]
- Xian, B.; Guo, J.; Zhang, Y.; Zhao, B. Sliding mode tracking control for miniature unmanned helicopters. Chin. J. Aeronaut. 2015, 28, 277–284. [Google Scholar] [CrossRef] [Green Version]
- Sheng, S.; Sun, C. An adaptive attitude tracking control approach for an unmanned helicopter with parametric uncertainties and measurement noises. Int. J. Control Autom. Syst. 2016, 14, 217–228. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M. Adaptive Neural Discrete-Time Fractional-Order Control for a UAV System with Prescribed Performance Using Disturbance Observer. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 742–754. [Google Scholar] [CrossRef]
- Maqsood, H.; Qu, Y. Nonlinear Disturbance Observer Based Sliding Mode Control of Quadrotor Helicopter. J. Electr. Eng. Technol. 2020, 15, 1453–1461. [Google Scholar] [CrossRef]
- Fang, X.; Wu, A.; Shang, Y.; Dong, N. Robust control of small-scale unmanned helicopter with matched and mismatched dis-turbances. J. Franklin Inst. 2016, 353, 4803–4820. [Google Scholar] [CrossRef]
- Chen, R.T.N. Effects of Primary Rotor Parameters on Flapping Dynamics. NASA TP-1431; NASA: Washington, DC, USA, 1980. [Google Scholar]
- Cai, G.; Chen, B.M.; Lee, T.H. Unmanned Rotorcraft Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 107–110. [Google Scholar]
- Johnson, W. Helicopter Theory; Courier Dover Publications: New York, NY, USA, 2012; pp. 45–72. [Google Scholar]
- Beal, T.R. Digital simulation of atmospheric turbulence for Dryden and von Karman models. J. Guid. Control Dyn. 1993, 16, 132–138. [Google Scholar] [CrossRef]
- Avanzini, G.; Matteis, G.D. Two-timescale inverse simulation of a helicopter model. J. Guid. Control Dyn. 2001, 24, 330–339. [Google Scholar] [CrossRef]
- Han, J. Active Disturbance Rejection Control Technique—The Technique for Estimating and Compensating the Uncertain-Ties; National Defense Industry Press: Beijing, China, 2008; pp. 183–242. [Google Scholar]




| Parameter | Description | Value |
|---|---|---|
| Moments of inertia | ) | |
| M | Gross weight | 2.8(kg) |
| Rm | Radius of main rotor | 0.485(m) |
| (,) | Turbulence scale length | 23.6, 23.6 |
| (, ) | The turbulence intensities | 0.99, 0.99 |
| U | Reference air speed | 5(m/s) |
| Control input coefficients |
| Parameter | Description | Value |
|---|---|---|
| Control parameter matrix 1 | diag(6,6,6) | |
| Control parameter matrix 2 | diag(4,4,4) | |
| Feedback parameter matrix 1 for ESO | diag(200,200,200) | |
| Feedback parameter matrix 2 for ESO | diag(1400,1400,1400) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Meng, Z.; Wang, K.; Zhang, H. Backstepping Control of an Unmanned Helicopter Subjected to External Disturbance and Model Uncertainty. Appl. Sci. 2021, 11, 5331. https://doi.org/10.3390/app11125331
Zhao W, Meng Z, Wang K, Zhang H. Backstepping Control of an Unmanned Helicopter Subjected to External Disturbance and Model Uncertainty. Applied Sciences. 2021; 11(12):5331. https://doi.org/10.3390/app11125331
Chicago/Turabian StyleZhao, Wenlong, Zhijun Meng, Kaipeng Wang, and Haoyu Zhang. 2021. "Backstepping Control of an Unmanned Helicopter Subjected to External Disturbance and Model Uncertainty" Applied Sciences 11, no. 12: 5331. https://doi.org/10.3390/app11125331
APA StyleZhao, W., Meng, Z., Wang, K., & Zhang, H. (2021). Backstepping Control of an Unmanned Helicopter Subjected to External Disturbance and Model Uncertainty. Applied Sciences, 11(12), 5331. https://doi.org/10.3390/app11125331






