A Hybrid Control Approach for the Swing Free Transportation of a Double Pendulum with a Quadrotor
Abstract
:1. Introduction
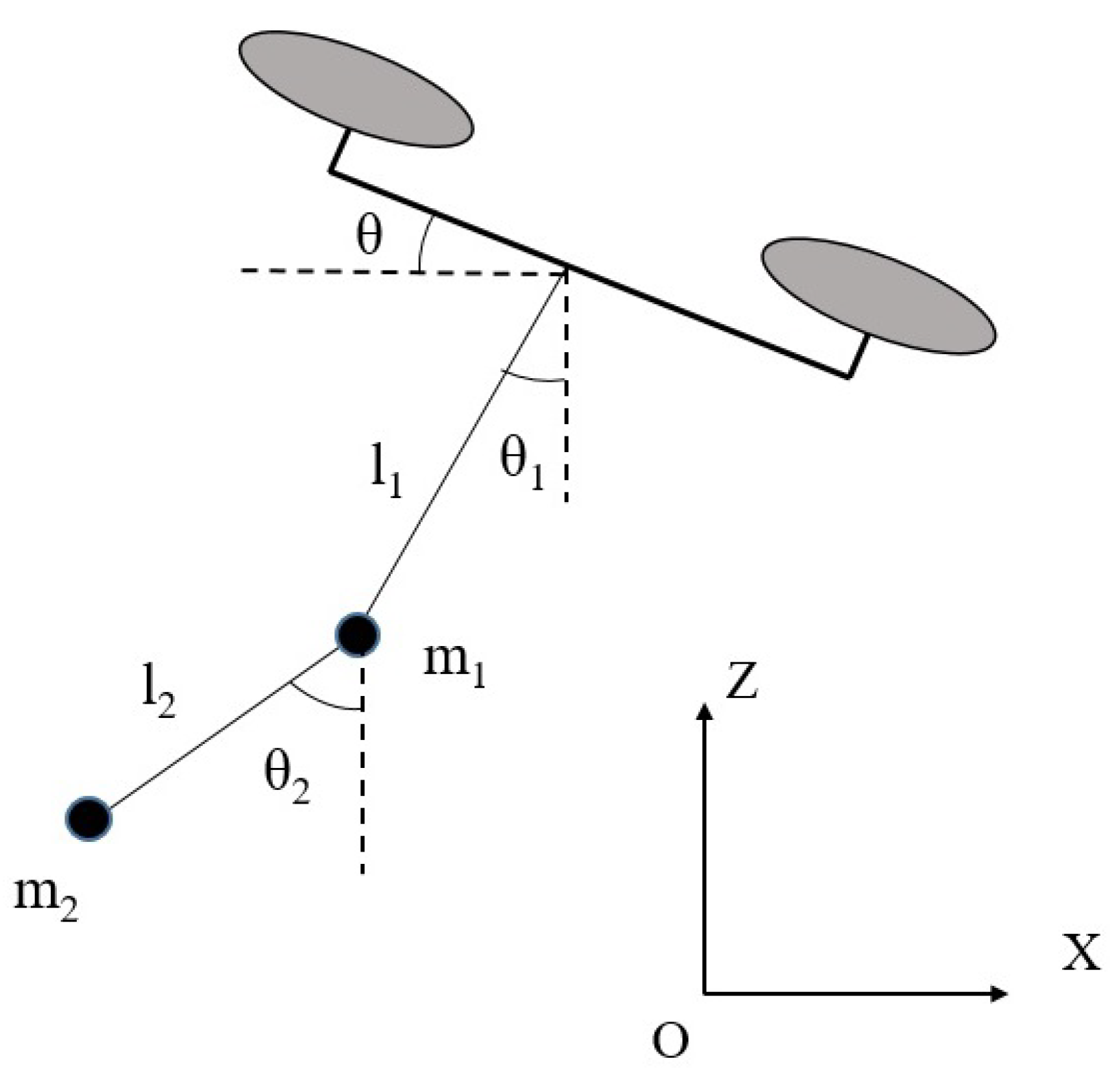
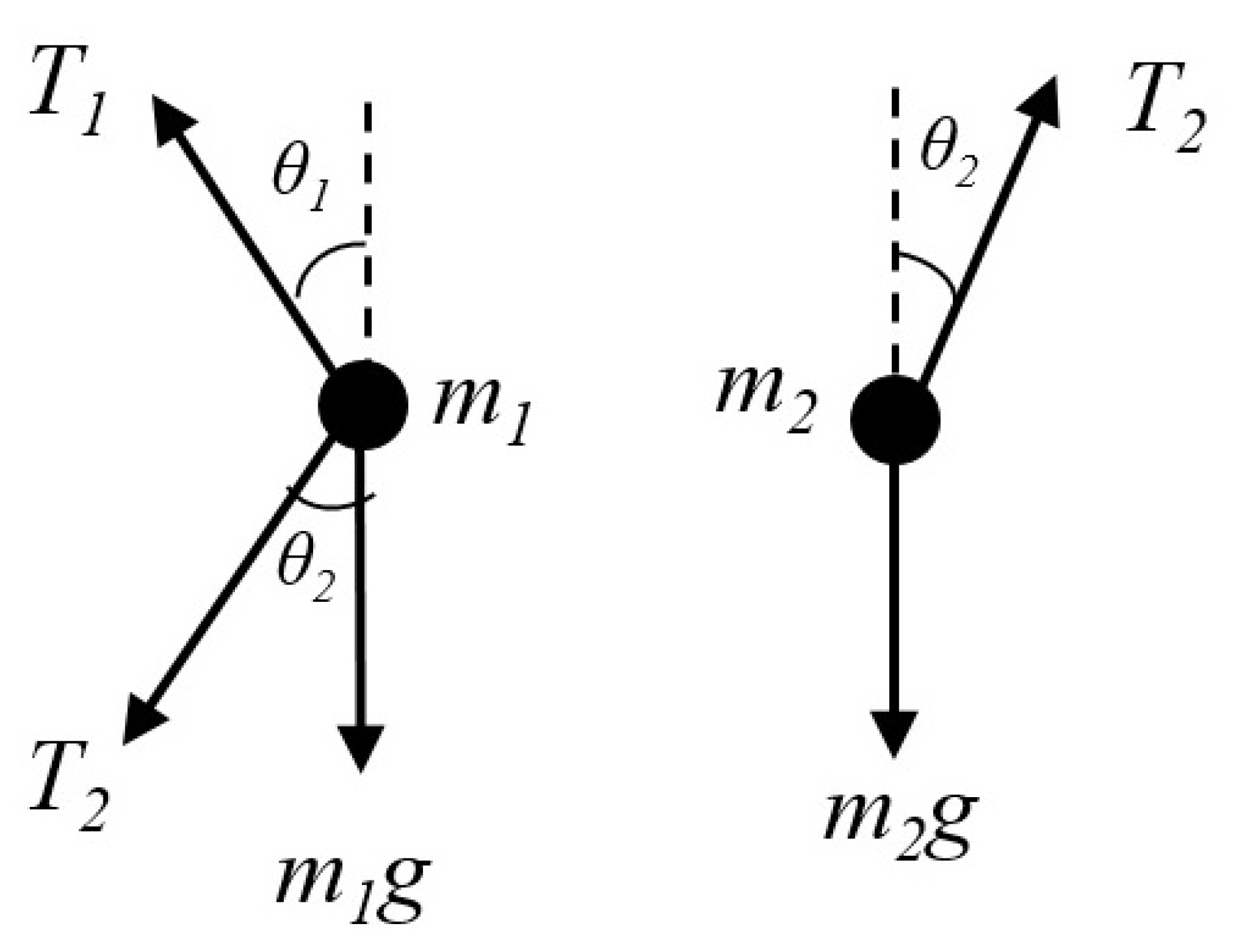
2. Dynamic Modeling of the System
2.1. Double Pendulum System
2.2. Quadrotor Dynamics
2.3. Linearization and Discretization of the Model
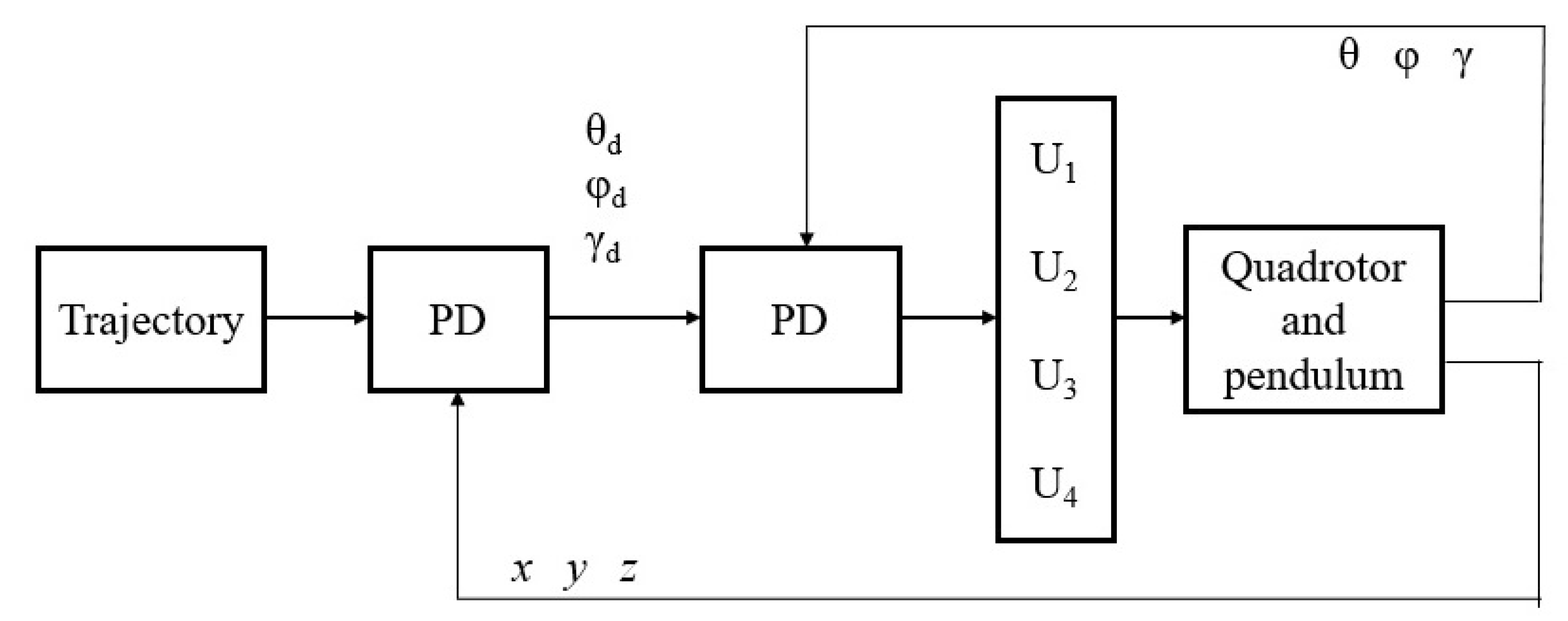
3. Control System
3.1. MPC-PD Control Configuration
- The PD controller computes the quadrotor torques and lift in Equation (4). It consists of four decoupled Single Input Single Output (SISO) PD circuits, each in charge of one of the four degrees of freedom (z, , and ). The PD equation is a discrete time controller, where the error derivative is obtained with the division of two consequent error in time and the chosen time increment. The main equation of the PD control is shown next:where is the difference between the desired value of each degree of freedom (denoted by subindex d) and the actual value in each discrete moment. and are the gain of the proportional and derivative terms, respectively.
- The MPC block is in charge of computing the desired attitude angles minimizing the payload swing (, , and ). MPC is a class of advanced process control methods [46] which computes the optimal control parameters of the system in finite window of time, denoted the control horizon, and then applies the first step in this control horizon. The process goes on moving the control horizon one step ahead. The algorithm minimizes a cost function, consisting of the error between the output and desired tracking state, subjected to some constraints. Our MPC controller is designed over a discrete-time state space linear time-invariant (LTI) system, the linearization of the double pendulum dynamic system described in Section 2.3. We apply a Kalmann filter for the prediction of the states in the control horizon, thus we have a Robust MPC, that has shown promising results in highly nonlinear quadrotor related applications [47,48].
Robust MPC Using Kalmann Filter for State Prediction
3.2. PD-PD Configuration
4. Experimental Results
4.1. Experimental Setting
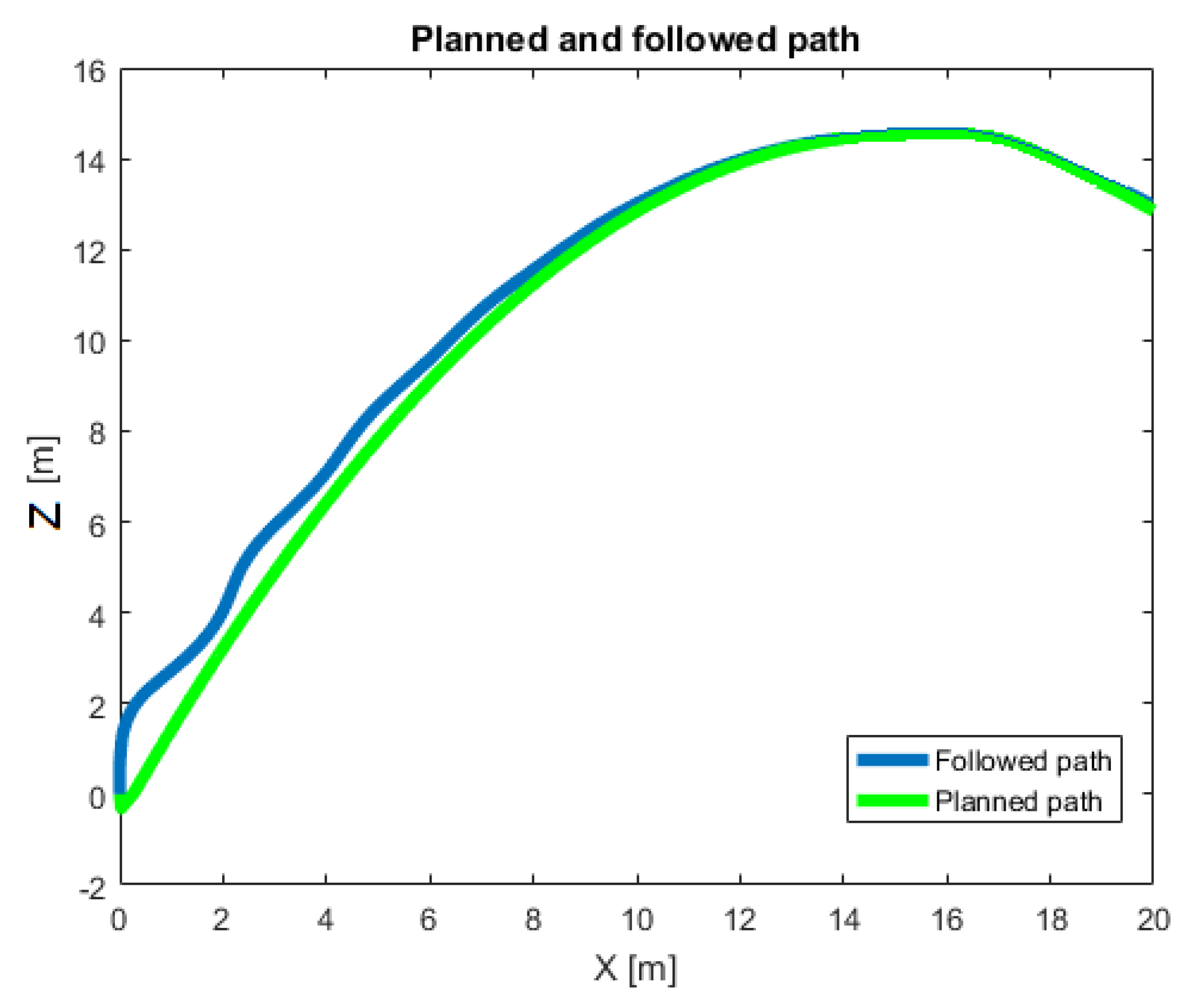
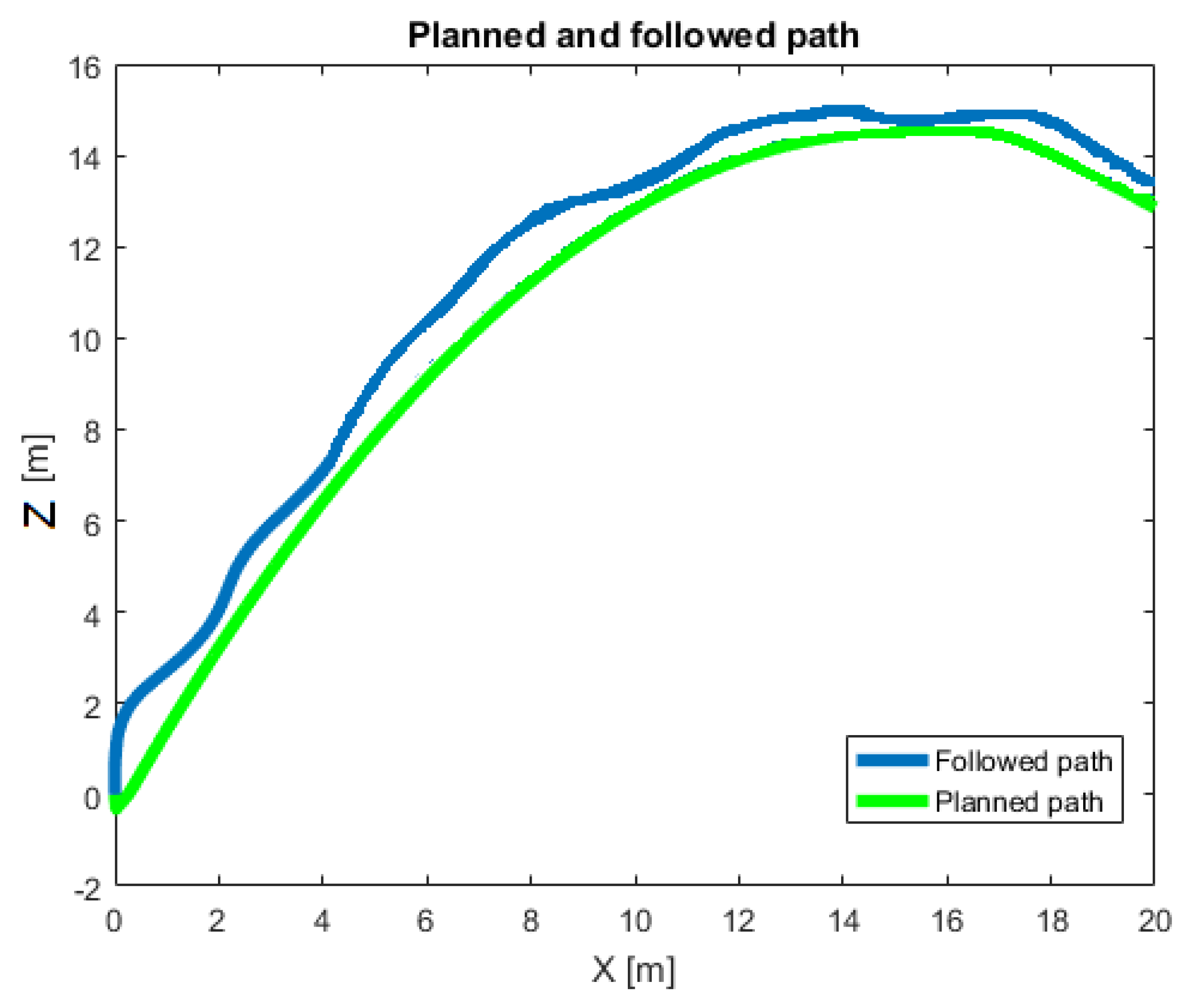
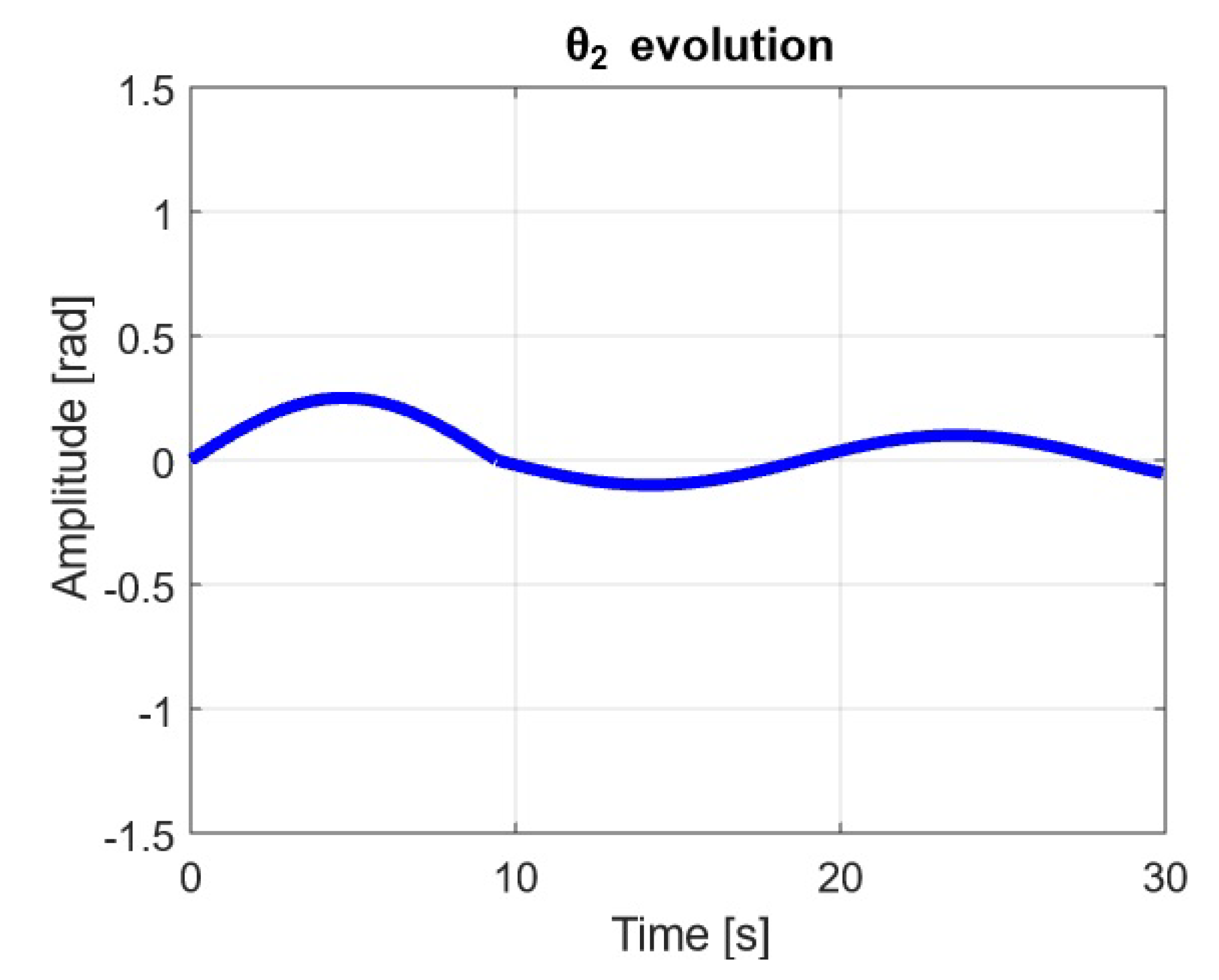
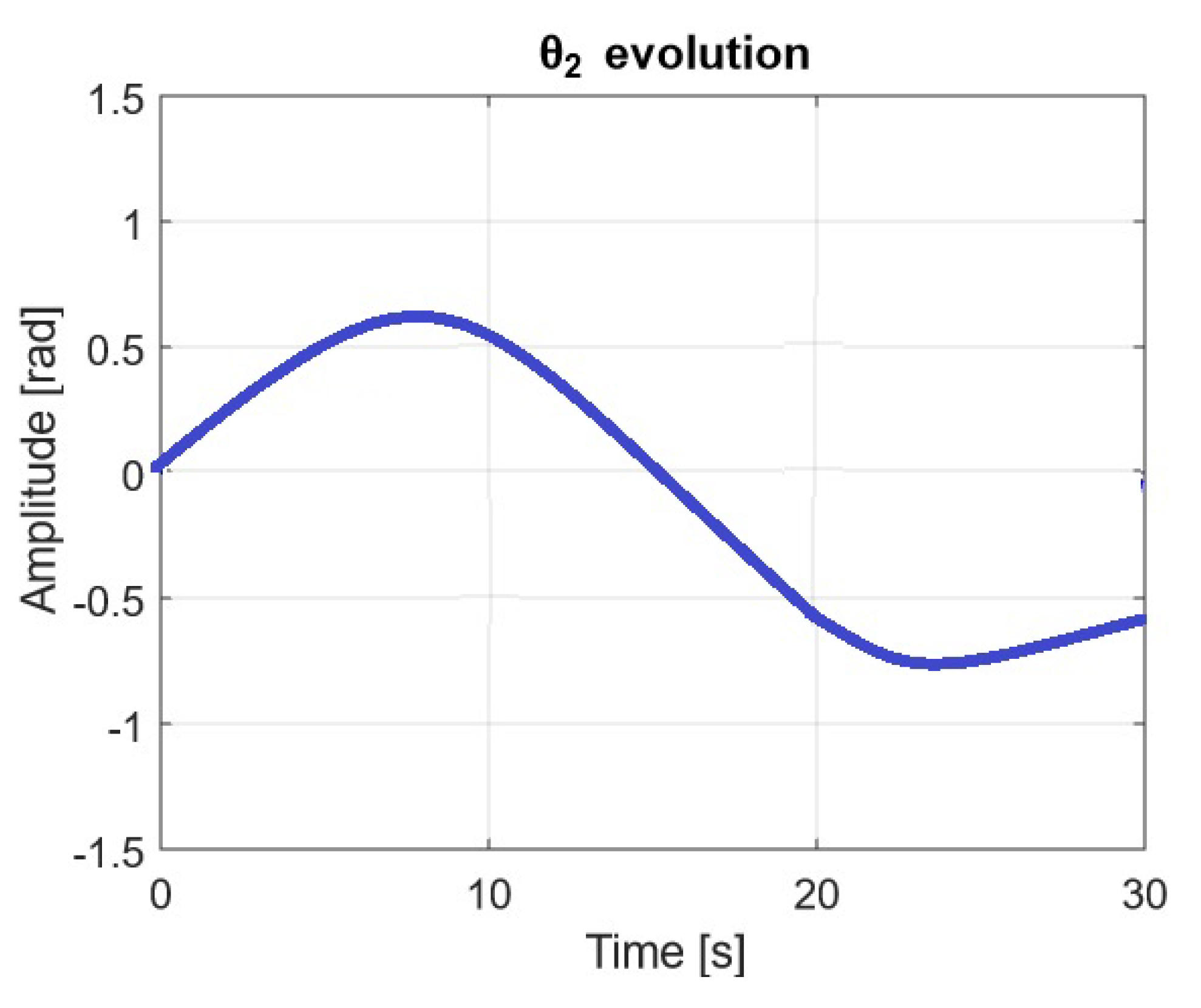
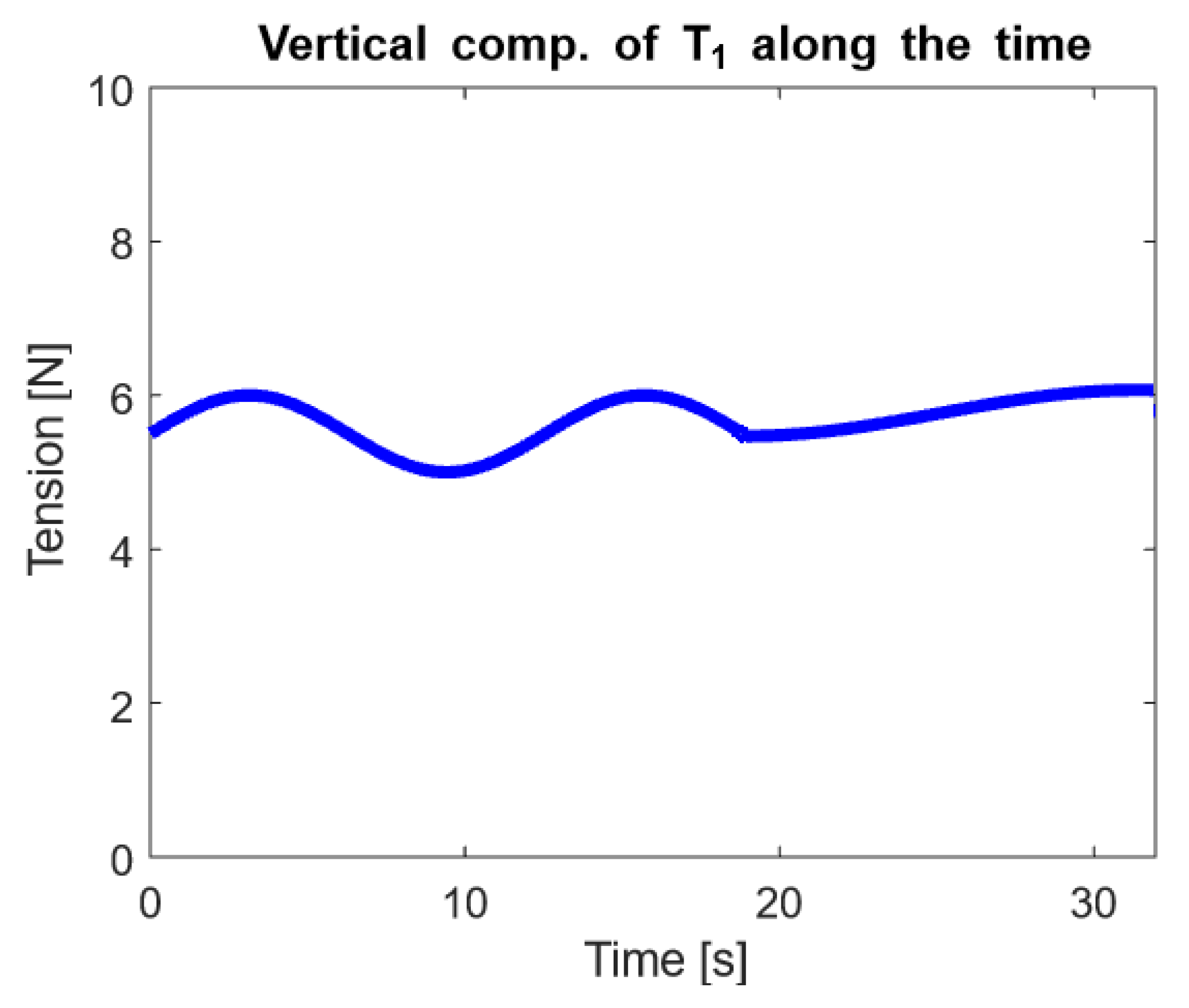
4.2. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Michael, N.; Fink, J.; Kumar, V. Cooperative manipulation and transportation with aerial robots. Auton. Robot. 2011, 30, 73–86. [Google Scholar] [CrossRef] [Green Version]
- Tang, S.; Wüest, V.; Kumar, V. Aggressive flight with suspended payloads using vision-based control. IEEE Robot. Autom. Lett. 2018, 3, 1152–1159. [Google Scholar] [CrossRef]
- Villa, D.K.; Brandao, A.S.; Sarcinelli-Filho, M. A survey on load transportation using multirotor uavs. J. Intell. Robot. Syst. 2020, 98, 267–296. [Google Scholar] [CrossRef]
- Foehn, P.; Falanga, D.; Kuppuswamy, N.; Tedrake, R.; Scaramuzza, D. Fast Trajectory Optimization for Agile Quadrotor Maneuvers with a Cable-Suspended Payload; Robotics Science and System: Cambridge, MA, USA, 2017. [Google Scholar]
- Qian, L.; Liu, H.H. Path-Following Control of A Quadrotor UAV With A Cable-Suspended Payload Under Wind Disturbances. IEEE Trans. Ind. Electron. 2019, 67, 2021–2029. [Google Scholar] [CrossRef]
- Estevez, J.; Lopez-Guede, J.M.; Graña, M. Quasi-stationary state transportation of a hose with quadrotors. Robot. Auton. Syst. 2015, 63 Pt 2, 187–194. [Google Scholar] [CrossRef]
- Bernard, M.; Kondak, K.; Maza, I.; Ollero, A. Autonomous transportation and deployment with aerial robots for search and rescue missions. J. Field Robot. 2011, 28, 914–931. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Ma, X.; Chai, H.; Rong, X.; Tian, X.; Li, Y. A novel online motion planning method for double-pendulum overhead cranes. Nonlinear Dyn. 2016, 85, 1079–1090. [Google Scholar] [CrossRef]
- Starr, G. Swing-free transport of suspended objects with a robot manipulator. In Proceedings of the 22nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 14–16 December 1983; pp. 1484–1487. [Google Scholar] [CrossRef]
- Starr, G. Swing-free transport of suspended objects with a path-controlled robot manipulator. J. Dyn. Syst. Meas. Control 1985, 107, 97–100. [Google Scholar] [CrossRef]
- Xian, B.; Wang, S.; Yang, S. An online trajectory planning approach for a quadrotor UAV with a slung payload. IEEE Trans. Ind. Electron. 2019, 67, 6669–6678. [Google Scholar] [CrossRef]
- Oshman, Y.; Isakow, M. Mini-UAV altitude estimation using an inertially stabilized payload. Aerosp. Electron. Syst. IEEE Trans. 1999, 35, 1191–1203. [Google Scholar] [CrossRef]
- Borky, J.M. Payload technologies and applications for uninhabited air vehicles (UAVs). In Proceedings of the 1997 IEEE Aerospace Conference, Snowmass, CO, USA, 13 February 1997; Volume 3, pp. 267–283. [Google Scholar] [CrossRef]
- Trachte, J.; Gonzalez, F.; McFadyen, A. Nonlinear Model Predictive Control for a multi-rotor with heavy slung load. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 1105–1110. [Google Scholar] [CrossRef]
- Lee, B.Y.; Lee, H.I.; Yoo, D.W.; Moon, G.H.; Lee, D.Y.; Young Kim, Y.; Tahk, M.J. Study on payload stabilization method with the slung-load transportation system using a quad-rotor. In Proceedings of the Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 2097–2102. [Google Scholar]
- Tang, S.; Kumar, V. Mixed integer quadratic program trajectory generation for a quadrotor with a cable-suspended payload. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2216–2222. [Google Scholar]
- Guerrero, M.; Mercado, D.; Lozano, R.; García, C. Passivity based control for a quadrotor UAV transporting a cable-suspended payload with minimum swing. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 6718–6723. [Google Scholar]
- Goodarzi, F.A.; Lee, D.; Lee, T. Geometric stabilization of a quadrotor UAV with a payload connected by flexible cable. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 4925–4930. [Google Scholar]
- Dai, S.; Lee, T.; Bernstein, D.S. Adaptive Control of a Quadrotor UAV Transporting a Cable-Suspended Load with Unknown Mass. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014. [Google Scholar]
- Carrio, A.; Sampedro, C.; Rodriguez-Ramos, A.; Campoy, P. A review of deep learning methods and applications for unmanned aerial vehicles. J. Sens. 2017, 2017. [Google Scholar] [CrossRef]
- Al-Kaff, A.; Armingol, J.M.; de La Escalera, A. A vision-based navigation system for Unmanned Aerial Vehicles (UAVs). Integr. Comput. Aided Eng. 2019, 26, 297–310. [Google Scholar] [CrossRef]
- Sadeghzadeh, I.; Abdolhosseini, M.; Zhang, Y.M. Payload drop application of unmanned quadrotor helicopter using gain-scheduled PID and model predictive control techniques. In Proceedings of the International Conference on Intelligent Robotics and Applications, Montreal, QC, Canada, 3–5 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 386–395. [Google Scholar]
- Faust, A.; Palunko, I.; Cruz, P.; Fierro, R.; Tapia, L. Automated aerial suspended cargo delivery through reinforcement learning. Artif. Intell. 2017, 247, 381–398. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.; Sreenath, K.; Kumar, V. Geometric control of cooperating multiple quadrotor UAVs with a suspended payload. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 5510–5515. [Google Scholar]
- Estevez, J.; Graña, M.; Lopez-Guede, G.J. Online fuzzy modulated adaptive PD control for cooperative aerial transportation of deformable linear objects. Integr. Comput. Aided Eng. 2016, 24, 41–55. [Google Scholar] [CrossRef]
- Mellinger, D.; Shomin, M.; Michael, N.; Kumar, V. Cooperative grasping and transport using multiple quadrotors. In Distributed Autonomous Robotic Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 545–558. [Google Scholar]
- Slegers, N.; Costello, M. Model predictive control of a parafoil and payload system. J. Guid. Control Dyn. 2005, 28, 816–821. [Google Scholar] [CrossRef]
- Kang, Y.; Hedrick, J.K. Linear tracking for a fixed-wing UAV using nonlinear model predictive control. IEEE Trans. Control Syst. Technol. 2009, 17, 1202–1210. [Google Scholar] [CrossRef]
- Tartaglione, G.; DAmato, E.; Ariola, M.; Rossi, P.S.; Johansen, T.A. Model predictive control for a multi-body slung-load system. Robot. Auton. Syst. 2017, 92, 1–11. [Google Scholar] [CrossRef]
- Faust, A.; Palunko, I.; Cruz, P.; Fierro, R.; Tapia, L. Learning swing-free trajectories for UAVs with a suspended load. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4902–4909. [Google Scholar]
- De Crousaz, C.; Farshidian, F.; Neunert, M.; Buchli, J. Unified motion control for dynamic quadrotor maneuvers demonstrated on slung load and rotor failure tasks. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2223–2229. [Google Scholar]
- Palunko, I.; Fierro, R.; Cruz, P. Trajectory generation for swing-free maneuvers of a quadrotor with suspended payload: A dynamic programming approach. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 2691–2697. [Google Scholar] [CrossRef]
- Zameroski, D.; Starr, G.; Wood, J.; Lumia, R. Rapid swing-free transport of nonlinear payloads using dynamic programming. J. Dyn. Syst. Meas. Control 2008, 130, 041001. [Google Scholar] [CrossRef]
- Nicotra, M.M.; Garone, E.; Naldi, R.; Marconi, L. Nested saturation control of an UAV carrying a suspended load. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3585–3590. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, M.E.; Mercado-Ravell, D.A.; Lozano, R.; García-Beltrán, C.D. Swing-attenuation for a quadrotor transporting a cable-suspended payload. ISA Trans. 2017, 68, 433–449. [Google Scholar] [CrossRef]
- Sadr, S.; Moosavian, S.A.A.; Zarafshan, P. Dynamics modeling and control of a quadrotor with swing load. J. Robot. 2014, 2014. [Google Scholar] [CrossRef]
- Choo, Y.i.; Casarella, M.J. A Survey of Analytical Methods for Dynamic Simulation of Cable-Body Systems. J. Hydronautics 1973, 7, 137–144. [Google Scholar] [CrossRef]
- Yang, S.; Xian, B. Energy-based nonlinear adaptive control design for the quadrotor UAV system with a suspended payload. IEEE Trans. Ind. Electron. 2019, 67, 2054–2064. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, P.; Fang, Y.; Lin, H.; Li, C.; Zhao, X. A Novel Nonlinear Control Scheme for Double-Pendulum Quadrotor Transportation Systems. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 714–719. [Google Scholar]
- Liang, X.; Zhang, P.; Fang, Y.; Lin, H.; He, W. Nonlinear Control for Aerial Transportation Systems with Double-Pendulum Swing Effects. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Supeł, B.; Lamarque, C.H.; Kudra, G.; Wasilewski, G.; Olejnik, P. Numerical and experimental study of regular and chaotic motion of triple physical pendulum. Int. J. Bifurc. Chaos 2008, 18, 2883–2915. [Google Scholar] [CrossRef]
- Butusov, D.; Karimov, A.; Tutueva, A.; Kaplun, D.; Nepomuceno, E.G. The effects of Padé numerical integration in simulation of conservative chaotic systems. Entropy 2019, 21, 362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Potdar, N.D.; de Croon, G.C.; Alonso-Mora, J. Online trajectory planning and control of a MAV payload system in dynamic environments. Auton. Robot. 2020, 44, 1065–1089. [Google Scholar] [CrossRef]
- de Alcantara Andrade, F.A.; Reinier Hovenburg, A.; Netto de Lima, L.; Dahlin Rodin, C.; Johansen, T.A.; Storvold, R.; Moraes Correia, C.A.; Barreto Haddad, D. Autonomous unmanned aerial vehicles in search and rescue missions using real-time cooperative model predictive control. Sensors 2019, 19, 4067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jain, R.P.K. Transportation of Cable Suspended Load Using Unmanned Aerial Vehicles: A Real-Time Model Predictive Control Approach. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- Garriga, J.L.; Soroush, M. Model predictive control tuning methods: A review. Ind. Eng. Chem. Res. 2010, 49, 3505–3515. [Google Scholar] [CrossRef]
- Baca, T.; Hert, D.; Loianno, G.; Saska, M.; Kumar, V. Model predictive trajectory tracking and collision avoidance for reliable outdoor deployment of unmanned aerial vehicles. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 6753–6760. [Google Scholar]
- Bemporad, A.; Rocchi, C. Decentralized linear time-varying model predictive control of a formation of unmanned aerial vehicles. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 7488–7493. [Google Scholar]
- Huang, R.; Patwardhan, S.C.; Biegler, L.T. Robust stability of nonlinear model predictive control based on extended Kalman filter. J. Process Control 2012, 22, 82–89. [Google Scholar] [CrossRef]
- Zenere, A.; Zorzi, M. On the coupling of model predictive control and robust Kalman filtering. IET Control Theory Appl. 2018, 12, 1873–1881. [Google Scholar] [CrossRef] [Green Version]
- Alexis, K.; Papachristos, C.; Siegwart, R.; Tzes, A. Robust model predictive flight control of unmanned rotorcrafts. J. Intell. Robot. Syst. 2016, 81, 443–469. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, C.; Baek, S.; Rawashdeh, S.; Mohammadi, A. Autonomous landing of a UAV on a moving platform using model predictive control. Drones 2018, 2, 34. [Google Scholar] [CrossRef] [Green Version]
- Estevez, J.; Graña, M. Robust control tuning by PSO of aerial robots hose transportation. In Proceedings of the International Work-Conference on the Interplay Between Natural and Artificial Computation, Elche, Spain, 1–5 June 2015; Springer: Cham, Switzerland, 2015; pp. 291–300. [Google Scholar]


| Parameter | Value |
|---|---|
| mass, m | 1 kg |
| arm length, l | m |
| inertia moments, | |
| inertia moment, | |
| propeller thrust coefficient, b | |
| drag, d |
| Parameter | Value |
|---|---|
| 0.3 kg | |
| 0.5 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estevez, J.; Lopez-Guede, J.M.; Garate, G.; Graña, M. A Hybrid Control Approach for the Swing Free Transportation of a Double Pendulum with a Quadrotor. Appl. Sci. 2021, 11, 5487. https://doi.org/10.3390/app11125487
Estevez J, Lopez-Guede JM, Garate G, Graña M. A Hybrid Control Approach for the Swing Free Transportation of a Double Pendulum with a Quadrotor. Applied Sciences. 2021; 11(12):5487. https://doi.org/10.3390/app11125487
Chicago/Turabian StyleEstevez, Julian, Jose Manuel Lopez-Guede, Gorka Garate, and Manuel Graña. 2021. "A Hybrid Control Approach for the Swing Free Transportation of a Double Pendulum with a Quadrotor" Applied Sciences 11, no. 12: 5487. https://doi.org/10.3390/app11125487
APA StyleEstevez, J., Lopez-Guede, J. M., Garate, G., & Graña, M. (2021). A Hybrid Control Approach for the Swing Free Transportation of a Double Pendulum with a Quadrotor. Applied Sciences, 11(12), 5487. https://doi.org/10.3390/app11125487







