New Affordable Method for Measuring Angular Variations Caused by High Heels on the Sagittal Plane of Feet Joints during Gait

Featured Application

This paper presents a procedure to measure angular variations to the sagittal plane by metatarsophalangeal and tibiotalar joints with increasing heel heights, using a geometrical model and free video analysis software.

Abstract

Gait is influenced by many factors, but one of the most prominent ones is shoe heel height. Optical motion tracking technology is widely used to analyze high-heeled gait, but it normally involves several high-quality cameras and licensed software, so clinics and researchers with low budgets cannot afford them. This article presents a simple, effective technique to measure the rotation angles on the sagittal plane of the ankle (tibiotalar) and toe (metatarsophalangeal) joints when no shoes (0 cm heel) and high-heeled shoes (2, 6 and 10 cm heels) are worn. The foot’s position was determined by a set of equations based on its geometry and video analysis techniques with free software (Tracker). An evaluation of the spatio-temporal variables confirmed observations from previous studies: increasing heel heights reduces gait cycle length and speed but does not change cadence. The range of movement at the tibiotalar joint progressively narrowed from 28° when no heel height was worn to 9° when a 10 cm heel was used, and these reductions ranged from 30° to 5° for metatarsophalangeal joints, respectively. This aligns with other authors’ previous studies, and confirms that the proposed method accurately measures kinematic ankle–foot set changes when wearing high heels.

1. Introduction

Typical human locomotion, also known as gait, is described as a series of rhythmical, alternative movements of the limbs and the trunk with a harmonic cadence that makes the body, and therefore the center of mass (CoM), move forward [1]. Although gait presents subtle differences in each individual, mainly caused by gender and age [2,3], from an anatomical point of view, these differences usually fall within a narrow margin in healthy individuals when they walk barefoot; hence, several models and expressions that characterize gait have been proposed [4,5,6].

The gait cycle starts when one foot contacts the ground, and ends with the same foot’s next contact with the ground [7]. The gait cycle can be divided into two phases, the stance phase and the swing phase, where the stance phase comprises approximately 60% of the cycle. Both of these phases can be subdivided into several stages, and those of the stance phase are as follows: initial contact; plantar flexion or loading response; dorsal flexion or mid-stance; and plantar flexion or terminal stance [7]. The swing phase can also be divided into several stages: initial swing; mid-swing; and terminal swing. However, these are not considered in the initial statical study in which the geometrical model used here is proposed because it focuses only on the stance phase.

1.1. General Foot Movement on the Sagittal Plane

An average healthy adult’s foot comprises 28 bones, sesamoids included, that can be divided into three anatomical groups: tarsals, metatarsals and phalanges. Foot movement is a complex process that takes place on three axes and on the body’s three planes to allow dorsiflexion/plantar flexion movements on the sagittal plane, eversion/inversion on the transversal plane and abduction/adduction on the frontal plane [8]. These movements determine general foot movement during gait [9].

1.1.1. Movement of the Tibiotalar Foot Joint

The term “ankle” describes the tibiotalar joint, which is the joint of the tibia, fibula and astragalus. It has one degree of freedom and its movements on the sagittal plane are dorsiflexion and plantar flexion. Movement is produced around a rotation axis that passes through the astragalus body and the ends of both malleoli. Dorsiflexor muscles are known as the tibialis anterior, extensor hallucis longus and extensor digitorum longus, which come into contract to lift the foot from the ground [10]. Plantar flexion muscles or extensors are the gastrocnemius, the soleus and the flexors of toes, which generate the plantar flexion moment at the ankle [11].

During a complete gait cycle, ankles alternately perform two plantar flexion and two other dorsiflexion trajectories [9]. In the stance phase, plantar flexion is followed by dorsiflexion, and then plantar flexion reoccurs. In the swing phase, only dorsiflexion occurs [7].

1.1.2. Metatarsophalangeal Foot Joint Movement

The metatarsophalangeal joint is constituted by the binding of metatarsal heads with their respective phalanges. This joint makes dorsiflexion and plantar flexion movements by means of a transversal axis.

First the metatarsophalangeal joint plays a very important role during gait. It is characterized by its wide mobility range from plantar flexion to dorsiflexion that takes a ground surface as a reference to allow feet to perform many tasks [9]. The first toe is responsible for conferring the internal foot side stability. As the body surpasses the foot in the toe take-off, the proximal phalange surpasses the metatarsal head and depresses it. Thus, pressure under the first metatarsal head increases at the end of the stance phase.

Other toes are characterized as having three phalanges in which their metatarsophalangeal joints possess regular extension and flexion movement. The supporting mechanism of toes is provided by intrinsic and extrinsic muscles, which are those that control the movement of metatarsophalangeal and interphalangeal joints [8].

1.2. High-Heeled Gait

Wearing high-heeled shoes is one of the factors that most affects general gait and posture characteristics [12]. The influence of high heels on gait has been studied in the scientific literature from many viewpoints, such as clinical [13], biomechanical [14,15], energetic [16], kinetic [2,17,18] and kinematic [2,19,20].

The use of high heels induces prejudicial effects on the musculoskeletal system [21], such as foot pain [22], lower back pain [23], ankle sprains [24], and increases the probability of suffering degenerative osteoarthritis in the knee [25]. High heels also perturbate the synchronic interaction between the joints of the pelvis–leg system during gait, having a noticeable effect on spatio-temporal parameters [26], joint kinematics [23,26], muscle activity [27], energy consumption [16] and plantar foot pressures [28].

From a kinematic point of view, many experimental techniques can be followed to analyze human joints [29], such as radiographic measurements [30], inertial sensors [31] or traditional goniometry [32,33], but one of the most widely used in clinical, biomechanical and sports fields is optical motion tracking [34]. Such tracking techniques use markers stuck to the body to facilitate the identification of the anatomical points required by the system by their contrast so that movement can be later reproduced in a computer [35]. However, optical motion tracking systems normally involve several high-quality cameras (from 2 to 8) and licensed software is necessary to process footage. Clinics with low budgets might not be able to afford such systems, for example, those in underdeveloped countries. Therefore, finding low-cost systems that seek research sustainability and, therefore, pursue attaining one of the sustainable development goals (number 10—“Reduce Inequalities”) [36] is of paramount interest.

Kinematics can also be used to evaluate the function of healthy, pathological and operated joints [37] and, although the scientific literature about hip, knee and ankle joints when using high heels is ample, very few articles have studied metatarsophalangeal joints [18,38,39]. Otter et al. [38] focused on this joint, but just studied the validity of a smartphone goniometer when compared with a traditional one, so all measures were statically taken. Samson et al. [39] validated a portable system for kinematic and dynamic analysis of the foot during gait against a gold standard, but this system only covered the stance phase. McBride et al. [18] are the only authors that seem to have studied the metatarsophalangeal joint when high heels are used, but they focused on a kinetic approach, centering in ground reaction forces; although they obtained data of angular variation in the joint, they did so just for 6.8 ± 0.8 cm high heels. Therefore, as far as the authors know, no studies have investigated variations in the sagittal plane from a kinematic point of view while wearing different heights in the heel.

This article presents a low-cost system capable of measuring angular variations in the sagittal plane in metatarsophalangeal and tibiotalar joints by means of a geometrical model and free video analysis software. A pilot study of healthy participants walking with high heels tested the effectiveness of the method, which has the potential to make gait analysis more affordable.

2. Materials and Methods

2.1. Geometrical Model

The anatomical complexity of the set foot–ankle means that the first approach to study the angular variations of the joints caused by the heel height in this set’s kinematics involves performing an analysis on the sagittal plane. This is the plane on which the widest variations in movement-related variables are observed.

The initial geometrical study is circumscribed only to the stance phase because this is the phase in which the heel height influence is evidenced. Increasing it implies reducing monopodal support, caused by the tendency to accomplish greater stability during gait, which becomes more insecure as the heel height increases [3]. In Figure 1, points A and B represent the tibiotalar and metatarsophalangeal joints, respectively, where one is located at the ankle level and the other on the metatarsal heads. θA and θB represent these joints’ angles of rotation.

In this case, angle $\alpha$ depends on the projection of L3 on both the horizontal plane (P) and the new height that the ankle reaches after increasing the heel height (h). Then, the calculation of $\alpha$ can be determined by Equation (1):

$$\alpha =arctan\left(\frac{(ht-\mathrm{L}2·sin\left(\rho \right))+\mathrm{L}1}{{\left({\mathrm{L}3}^2-{\left(ht-\mathrm{L}2·sin\left(\rho \right)\right)}^2\right)}^{\frac{1}{2}}}\right)$$

(1)

and the length of R can be obtained by Equation (2):

$$\mathrm{R}={\left(\left(ht-\mathrm{L}2·sin\left(\rho \right)\right)+\mathrm{L}1{)}^2+\left({\mathrm{L}3}^2-\left(ht-\mathrm{L}2·sin\left(\rho \right)\right)\right)\right)}^{\frac{1}{2}}$$

(2)

where:

$ht$ is the heel height.

$\rho$ is the tilt angle of the seating heel.

Equations (1) and (2) can also be applied under typical conditions (without high heels), as ht = 0 and $\rho =0$, then $ha=0$ and, therefore, $\mathrm{P}=\mathrm{L}3$ and $\mathrm{h}=\mathrm{L}1$.

Having calculated angle α, rotations of the tibiotalar and metatarsophalangeal joints can also be found because, in the proposed model, they initially depend on angle α, and later depend on the action angles that come into play during the gait. Consequently, values $\mathsf{\theta }\mathrm{A}$ and $\mathsf{\theta }\mathrm{B}$ can be calculated by Equation (3) and Equation (4), respectively.

Therefore,

$$\mathsf{\theta }\mathrm{A}=\left(\pi /2+arctan\left(\frac{(ht-\mathrm{L}2·\sin \left(\rho \right))+\mathrm{L}1}{{\left({\mathrm{L}3}^2-{\left(ht-\mathrm{L}2·\sin \left(\rho \right)\right)}^2\right)}^{\frac{1}{2}}}\right)\right)\pm \phi$$

(3)

$$\mathsf{\theta }\mathrm{B}=\left(\pi -arctan\left(\frac{(ht-\mathrm{L}2·\sin \left(\rho \right))+\mathrm{L}1}{{\left({\mathrm{L}3}^2-{\left(ht-\mathrm{L}2·\sin \left(\rho \right)\right)}^2\right)}^{\frac{1}{2}}}\right)\right)\pm \phi$$

(4)

$\phi$ represents the angles of action during the gait cycle, and it is be taken as a negative ($\phi$(−)) during plantar flexion (PF) and as a positive ($\phi$(+)) during dorsiflexion (DF). It is also used below to determine positions.

2.2. Subjects

Three healthy women (26 + 2.5 years, 1.60 + 0.2 m, 75 + 1.3 kg) with the same shoe size (6 US size, 38 EU size) were recruited from the Universidad Tecnológica de La Habana-José Antonio Echeverría (CUJAE). They all were tested before the experiment started to ensure that they presented no gait anomalies, previous lower extremity damage, foot diseases or deformities. The subjects in this study were all inexperienced high heel wearers. Before the study started, all the subjects were adequately informed about it, and voluntarily agreed to participate. The study complied with the ethical guidelines of the Declaration of Helsinki (7th revision, October 2013, Fortaleza, Brazil).

2.3. Equipment and Procedure

The hardware used for measuring purposes consisted of two digital cameras (model GE A1050) of 10.1 megapixels, two extensible tripods capable of reaching a height of 20 cm, a USB 2.0 cable of 1 m length, and a laptop ACER Intel Core i3-370M (2.40 Ghz) with 4 GB of RAM. Cameras recorded the walks of the participants in Quick Time Motion JPEG format, which was later exported to the laptop, using the USB 2.0 cable.

Software required for the procedure was ArcSoft (provided with the cameras), which allowed the PC to recognize the camera as an external storage drive; the free software Tracker, which is built on the Java Open-Source Physics (OSP) platform [40], was used to import the JPEG videos and analyze the motion.

First, the spatio-temporal variables were measured. Considering that the mean height of the three women who participated in our experiment was 1.60 m, a 6 m track length (T_L) was set (Figure 2). Each participant did three walks and maintained a pace of approximately 1 m/s with each heel height along the track. The values obtained for the gait cycle length (L_C), time spent to do a full cycle (T_C) and speed (S_C), were recorded.

The experimental design to measure the kinematic variables was based on recording each individual’s full gait cycle under barefoot conditions and wearing high heels of 2, 6 and 10 cm. The procedure followed to collect data from this study was divided into several steps:

• Step 1. Filming location selection and conditioning: A sports center with daylight was selected to avoid any shadow projections that could affect the quality of recordings.
• Step 2. Mounting recording cameras: Cameras were mounted on the horizontal plane at a height of 12 cm and were placed 32 cm away from where the track began. They were oriented toward the sagittal plane. One was placed in front of the other and they were separated by 4 m. The objective was to record both the medial and lateral foot sides at the same time as the participants moved along the line between them.
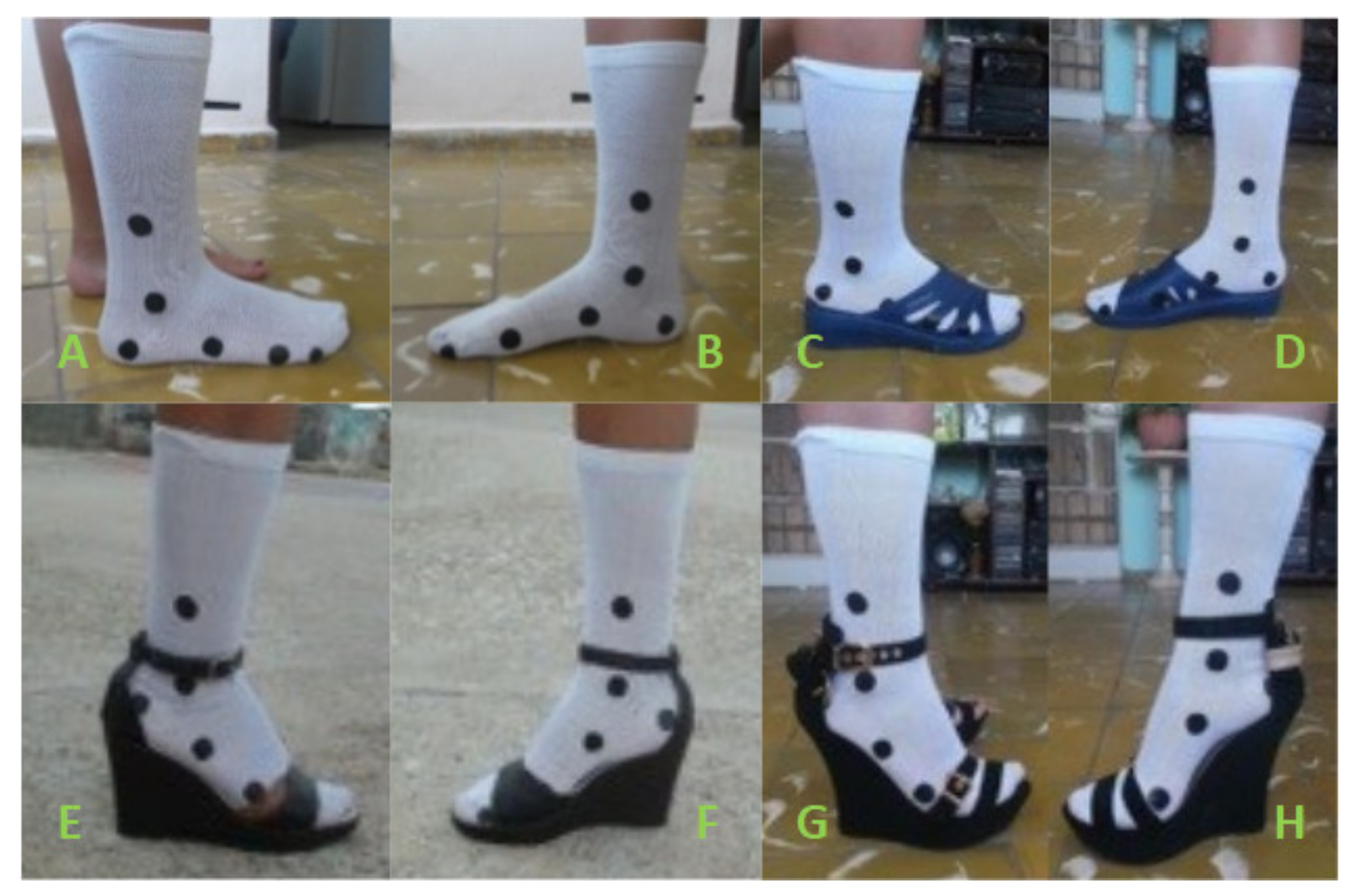
• Step 3. Fixing markers on the participants: Markers were made of adhesive cloth. Two sizes were used. Those with a 2 cm diameter were placed on tarsals and metatarsals, while those with a 1 cm diameter signaled phalanges. They were all stuck onto a thin, white sock that tightly fitted to the feet (Figure 3). Markers stuck onto a sock instead of directly on the skin may induce one to think of losses of accuracy. However, the use of markers stuck onto pieces of cloth, such as suits or gloves, are common in motion capture works, and in some cases, they are even stuck onto the shoes, as Chien et al. [21] did. In our case, an elastic rubber was placed on top of the sock (Figure 3) to ensure its tight fit to the legs, and after each walk, checks were made to see if the sock was in exactly the same position as it was at the beginning. The proposed method would also work with markers stuck onto the skin, so any possible bias, if they exist, can be easily avoided. On the lateral foot side, markers were placed on the lateral malleolus, 5 cm over the lateral malleolus, the calcaneus lower part, the head and base of the fifth metatarsal and the distal phalange of the fifth toe. On the medial foot side, markers were placed on the medial malleolus, 5 cm over the medial malleolus, the calcaneus lower part, the head and base of the first metatarsal and the distal phalange of the hallux. As shown, the 2 cm high heeled shoe was a slipper with wide open spaces around the metatarsal that tightly fitted around the instep, while the shoes selected for 6 and 10 cm high heels were ankle-strap wedges.
• Step 4. Video recording and exporting to a PC: Video recording was done as 30 frames per second (fps) at a resolution of 640 × 480 p. The synchronization between both cameras was achieved by using a reference event: the moment the heel contacted the ground. Videos were exported to the PC via the camera’s USB connection.
• Step 5. Digital image processing: The data were manually acquired from recordings, using the Tracker software.
• Step 6. Calculating angles and angular velocity.

3. Results

Table 1. The average results for the spatio-temporal variables. NC: number of cycles; T_NC: time to complete NC cycles; L_NC: distance covered in NC cycles; L_C: gait cycle length; T_C: time spent doing a full cycle; S_C: speed.

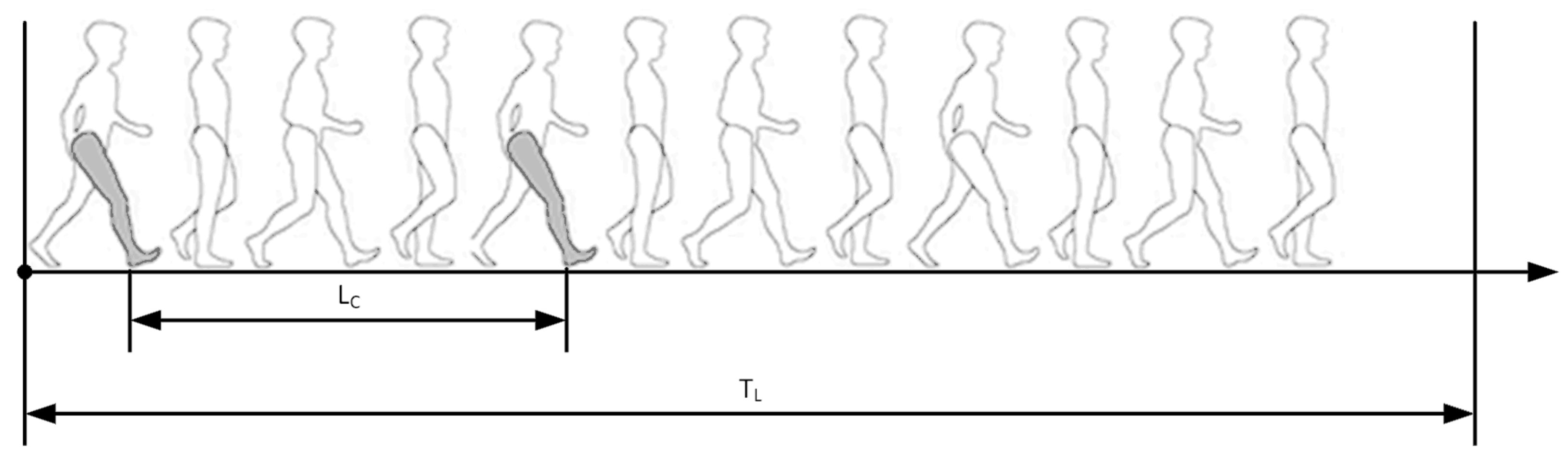
Variable	Unit	Heel Height (cm)
		0	2	6	10
NC	cycles	5	5	5	5
TNC	seconds	5.8 ± 0.02	5.8 ± 0.02 (0%)	5.5 ± 0.02 (−5.2%)	5.5 ± 0.02 (−5.2%)
LNC	meters	5.85 ± 0.02	5.8 ± 0.01 (−0.9%)	5.45 ± 0.01 (−6.8%)	5.15 ± 0.01 (−12%)
LC	meters	1.17 ± 0.01	1.16 ± 0.01 (−0.9%)	1.09 ± 0.01(−6.8%)	1.03 ± 0.01 (−12%)
TC	seconds	1.16 ± 0.01	1.16 ± 0.01 (0%)	1.1 ± 0.01 (−5.2%)	1.1 ± 0.01 (−5.2%)
SC	m/s	1.01 ± 0.01	1 ± 0.01 (−1%)	0.99 ± 0.01 (−2%)	0.94 ± 0.01 (−6.9%)

shows the averaged results obtained after all three participants completed three walks wearing each heel type: barefoot and 2, 6, and 10 cm heels.

Figure 4 shows the variation of the angle at the tibiotalar joint ($\mathsf{\theta }\mathrm{A}$) during the gait cycle for each heel height considered in this study.

For ht = 0, the tibiotalar joint movement indicates a total range of movement (RoM) of 28°. For ht = 2 cm, the total RoM slightly decreased and reached 20° in this case. For ht = 6 cm, the reduction in the total RoM was more evident, with a value of only 11°. For ht = 10 cm, it further lowered and obtained a value of only 9°.

The metatarsophalangeal joint behavior ($\mathsf{\theta }\mathrm{B}$) was monitored. The results are displayed in Figure 5, which shows the four curves obtained with the Tracker software from the metatarsophalangeal joint movement for one full gait cycle with each heel height.

For ht = 0, a total RoM of approximately 30° was seen at the joint. When the heel height was ht = 2 cm, the total RoM slightly decreased and obtained a value of approximately 22°. For ht = 6 cm, the magnitude of the total RoM at the joint in the stance phase reduced and its value was 7°. For ht = 10 cm, RoM considerably decreased and its value was slightly above 5°.

4. Discussion

According to the spatio-temporal analysis results shown in Table 1, and by taking the barefoot case as a reference, we affirm that as the heel height increased, the steps shortened and, consequently, so did the gait cycle length; however, cadence was not apparently affected. These results align with the findings provided by several other authors [42,43,44,45], and confirm the validity of our measuring method for spatio-temporal parameters.

The angles of action at the tibiotalar and metatarsophalangeal joints can be described as curves that are a function of the gait cycle over time. These can be represented by wavy lines with variable amplitudes and irregular periods. However, generalized shapes can be found in a statistically averaged scenario (Figure 4 and Figure 5) and can, therefore, be used to find their angles, among other parameters [5,7,19,42].

Focusing on tibiotalar joints (Figure 4) under the barefoot conditions, the obtained results agree with several authors’ findings [11,19]. Whittle analyzed gait from a kinematic, kinetic and electromyographic point of view, and observed how dorsiflexion reached a maximum angle of 8°, which occurred in the stance phase, and plantar flexion had a minimum angle of only −20° immediately after take-off, with a total RoM of 28° [11]. Mika et al. [3] evaluated changes in electromyographic (EMG) activity of the lower limb muscles, and hip, knee and ankle kinematics during gait while wearing low-(4-cm) and high-heeled (10 cm) shoes in young and middle-aged adult women, and found that the mean RoM values at ankle joints for barefoot participants were around 25° for middle-aged women and 29° for young women, which falls in line with our findings.

Wang et al. [19] did not monitor ankle joints, but worked with hallux dorsi/plantar flexion angles, and reported that they ranged from −8.68 ± 1.13 (plantar-flexion) to 22.55 ± 1.62 (dorsiflexion) during the full cycle. Once again, this finding falls in line with our results. These findings support the validity of the measuring procedure and suggest that it can be used for other heel heights.

The present study revealed that as heel height increased, the RoM at ankles considerably narrowed, and this finding also agrees with other authors’ previous findings [3]. Stefanyshyn et al. [46] investigated whether a graded response in gait kinematics, kinetics, and EMG occurs as shoe heel height increases, and found that ankle plantar flexion increased while wearing high heels, which was also observed herein. This falls in line with the findings of Mika et al. [3], who observed that the angles at ankles increased when heels contacted the ground, with a significant effect when the heel height increased. Regarding the ankle angle, it appears that wearing high heels forces the foot into a more plantar flexed position. Therefore, the ankle angle is noticeably different in the initial stance phase and after toe off [6].

When centering on metatarsophalangeal joint kinematics (Figure 5), RoM notably narrowed with increasing heel height, which was also previously reported [18]. On the values obtained for joint dorsiflexion angles, the scientific literature is, as far as the authors know, inexistent for the 2 cm and 10 cm high heels, but the values presented here for barefoot and 6 cm high heels fall in line with other authors’ findings [18].

5. Conclusions

This article introduces a low-cost system based on a geometrical model and free video analysis software that is capable of measuring angular variations at the sagittal plane in metatarsophalangeal and tibiotalar joints when high heels are used.

The information collected in this study for ankle joints is not novel, but allowed the authors to confirm the validity of the followed measuring method and to, thus, support the validity of the angular variations measured at the metatarsophalangeal joints when high heels were used. As far as the authors are aware, these metatarsophalangeal joint angular variations on the sagittal plane when wearing high heels have not been previously published by anyone.

The method herein exposed may be especially useful for those new researchers with a limited budget who are looking for a simple gait analysis technique. It also opens new analysis possibilities for walk race trainers that want to improve the technique of newcomers to the discipline, without having to spend a lot of money on expensive gadgets, and even for therapists that want to follow their patient’s progression.

This study also has several limitations. First, our participants wore shoes that were provided for the experiments, and not their own. This may have influenced their gait characteristics. However, the subjects were allowed enough time to become familiar with the shoes before measures were taken so as to minimize any possible bias. Second, the participants were inexperienced high heel users. According to some authors, such as Ebbeling et al. [16], experience has no effect on heart rate, oxygen consumption or lower limb mechanics. Simonsen et al. [47] also found that lower limb joint moments or EMG activity remain the same. Others, such as Opilia-Correia [23], indicated a strong influence on the upper trunk, but a lesser one on knees, and evidence was almost unnoticeable on ankles. Chien et al. [21] studied several variables of the joint angles in the sagittal plane for experienced and non-experienced women, finding that there were no significant differences in any variables of the joint angles in the sagittal plane between the two groups, except that experienced wearers showed a decreased range of motion (ROM) during knee flexion–extension and greater mean ankle plantar flexion during the stance phase. Consequently, although it may initially seem that experience may have an effect on gait, precursory studies indicate no obvious differences in gait kinematics and kinetics on the sagittal plane between experienced and inexperienced high heel users when just the ankle and metatarsophalangeal joints are considered [3,21].

The use of a low number of subjects in pilot studies, as we have done here, is not ideal, but it is neither unusual. For example, Loredo et al. [48] used just one participant, and Panero et al. [2] used three participants to validate their proposals. However, this may potentially introduce undesired biases, and although the results obtained align with those published in previous studies, suggesting that its precision suffices for the intended purpose of studying the angular variations in the joints of the feet, it would be convenient to compare the precision of the methodology with other methods to validate its applicability in fields that usually require more precise approaches, such as the clinical and pathological fields. Future studies of the author’s research group intend to follow this line and compare this system with a gold standard one.