Effect of Parameters on Lumbar Compressive Force during Patient Transfer
Abstract
:1. Introduction
2. Method
2.1. Experiment
2.1.1. Subjects
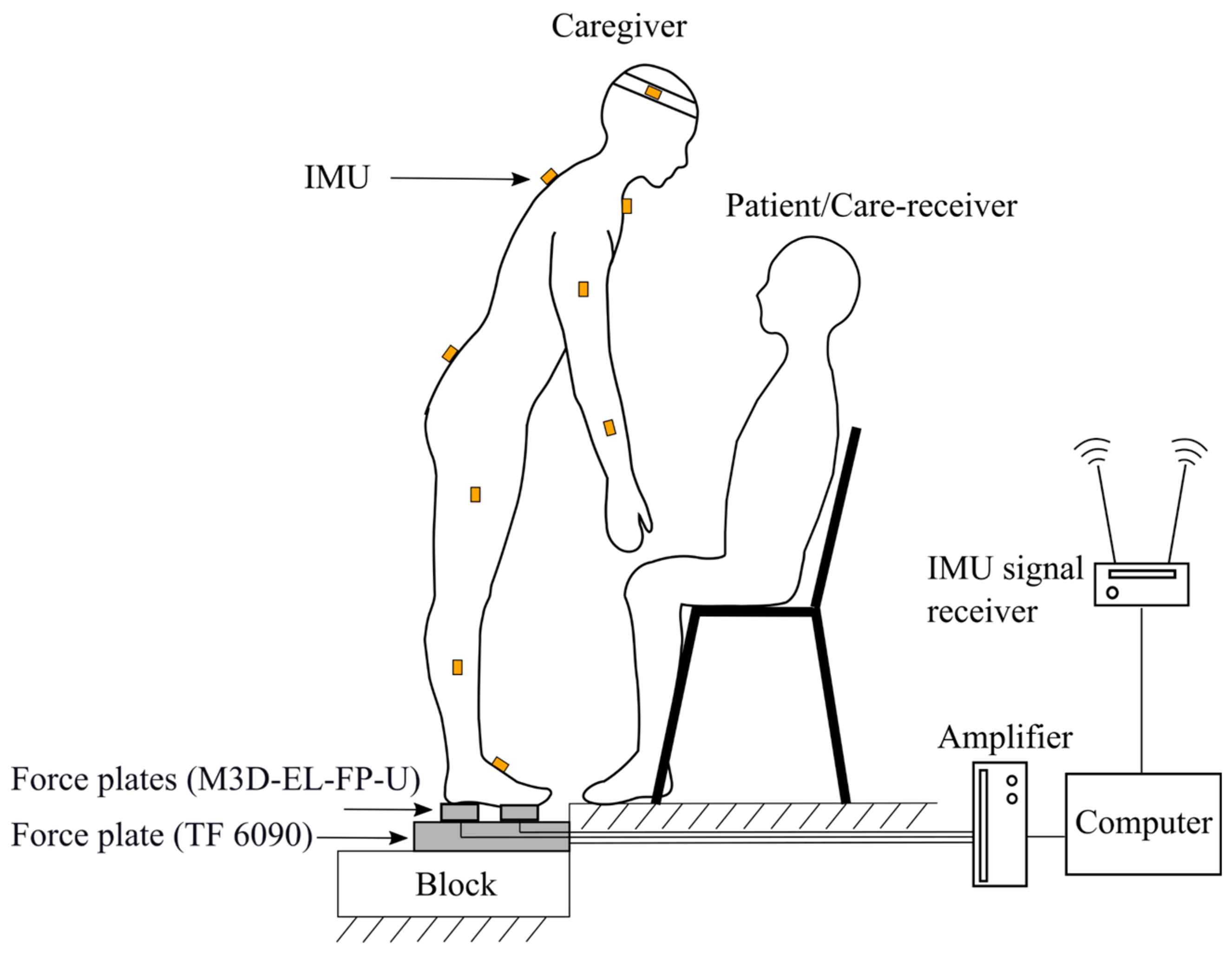
2.1.2. Instrumentation
2.1.3. Tasks for Transfer Motion
2.2. CF Estimation
2.2.1. Inverse Dynamic Computation
2.2.2. McGill’s Compressive Force Model (McGM)
2.3. Dominant Factors of Peak CF
2.4. Statistical Analysis
2.5. Model Implementation and Comparison with State of the Art
3. Result
3.1. Patient Transferring Task
3.1.1. Peak CF Timing and Peak CF in the Patient Transferring Tasks
3.1.2. Multiple Linear Regression Equation for Peak CF
3.1.3. Comparison between the 3D Regression and Merryweather Models
3.2. Dumbbell Lifting Task
4. Discussion
4.1. Lag of Peak CF with Respect to the Initiation
4.2. Effect of Primitive Motion on Peak CF
4.3. Incipience of Patient Transfer and Sagittal Lifting
4.4. Merryweather’s Model vs. 3D Regression Model
4.5. Benefits of This Study
4.6. Application of the Regression Model in Other Scenarios
4.7. Limitations
- This experiment did not include a considerable weight and age group or a large number of subjects because of the massive number of tasks and large analysis, which is a reason the R-square value was not high in the regression analysis. In addition, it is unclear to what extent the small sample can explain the peak CF timing when considering the individual differences requires validation in the real transfer tasks.
- The subjects were college students who could not perform the tasks as professional caregivers or patients with physical constraints. Usually, well-trained caregivers will start at a lower speed than those without experience in transfer. It will take away the peak timing of all the factors, thereby causing a reduction of the peak CF. If we use well-trained caregivers, we can observe the difference among the peak CF timing, peak angular velocity timing, and peak H timing. We can probably use peak angular velocity or peak H to estimate the timing of peak CF instead of using peak trunk angle or angular acceleration.
- The peak trunk flexion angle in the PT task was 48.5°, which is greater than 31° as reported by Marras et al. [32], but smaller than 84.1° as demonstrated by Hodder et al. [33]. Different trunk angles result in errors in the CF estimation. There are three possible reasons for the difference between trunk angles in our study and other studies. The first reason is the knee angle. In lifting, an increase of knee angle leads to a decrease of trunk angle and a decrease of peak CF. A lifting sample is provided in ISO 11228-1, which states that the caregivers need to perform a larger trunk flexion when they keep their legs straight compared to when they bend their knee, and the peak CF in the latter is much smaller than the former. The second reason is the location where the caregiver holds the patient. As the caregivers support the patients at their hip, waist, and underarm, the peak trunk angles of the caregivers vary. Third, the experimental setup also affects the peak trunk angle. For example, using a taller chair leads to a smaller peak trunk angle.
- For the safety of the lumbar, this study referred to the description of the acceptable external load in the international standard for manual lifting ISO 11228-1, which states, “In order to lower the risk for people at work, particularly those with less physical capability, the recommended limit for mass should not exceed 15 kg” [34]. Therefore, the maximum change in the on the caregivers was limited to 150 N in the experiment. When the external force exceeds 15 kgf, assisting devices should be used to facilitate the transfer.
- Not controlling the knee angle is a limitation of this study because the knee angle could affect the upper trunk angle, resulting in a variation in the estimation of the CF. In our study, the Kruskal-Wallis test showed that both the left and right knee angles varied among subjects (p < 0.001), while the trunk angle did not (p = 0.1754). One possible explanation is that the posture of each subject was well coordinated to maintain the trunk angle. This posture may have been similar among all subjects, with each subject adjusting their hip and knee angles at the same time. Therefore, a change in knee angle did not lead to a large variance of trunk angle in this study.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davis, K.G.; Kotowski, S.E. Prevalence of musculoskeletal disorders for nurses in hospitals, long-term care facilities, and home health care: A comprehensive review. Hum. Factors 2015, 57, 754–792. [Google Scholar] [CrossRef] [PubMed]
- Knibbe, J.J.; Friele, R.D. Prevalence of back pain and characteristics of the physical workload of community nurses. Ergonomics 1996, 39, 186–198. [Google Scholar] [CrossRef]
- Waters, T.R.; Rockefeller, K. Safe patient handling for rehabilitation professionals. Rehabil. Nurs. 2010, 35, 216–222. [Google Scholar] [CrossRef] [PubMed]
- Yassi, A.; Lockhart, K. Work-relatedness of low back pain in nursing personnel: A systematic review. Int. J. Occup. Environ. Health 2013, 19, 223–244. [Google Scholar] [CrossRef]
- Waters, T.R.; Putz-Anderson, V.; Garg, A.; Fine, L.J. Revised NIOSH equation for the design and evaluation of manual lifting tasks. Ergonomics 1993, 36, 749–776. [Google Scholar] [CrossRef] [PubMed]
- Adams, M.A.; McNally, D.S.; Chinn, H.; Dolan, P. The clinical biomechanics award paper 1993 posture and the compressive strength of the lumbar spine. Clin. Biomech. 1994, 9, 5–14. [Google Scholar] [CrossRef]
- Genaidy, A.M.; Waly, S.M.; Khalil, T.M.; Hidalgo, J. Spinal compression tolerance limits for the design of manual material handling operations in the workplace. Ergonomics 1993, 36, 415–434. [Google Scholar] [CrossRef]
- Potvin, J.R. Use of NIOSH equation inputs to calculate lumbosacral compression forces. Ergonomics 1997, 40, 691–707. [Google Scholar] [CrossRef]
- Merryweather, A.S. Model Development for the Estimation of Back Compressive Force and Subsequent Low Back Disorder Risk. Doctoral Dissertation, Department of Mechanical Engineering, University of Utah, Salt Lake City, UT, USA, 2007. [Google Scholar]
- van Dieën, J.H.; Faber, G.S.; Loos, R.C.; Kuijer, P.P.F.; Kingma, I.; van der Molen, H.F.; Frings-Dresen, M.H. Validity of estimates of spinal compression forces obtained from worksite measurements. Ergonomics 2010, 53, 792–800. [Google Scholar] [CrossRef] [PubMed]
- Xiang, X.; Yamada, Y.; Akiyama, Y.; Tao, Z.; Kudo, N. Validation of lumbar compressive force simulation in forward flexion condition. Appl. Sci. 2021, 11, 726. [Google Scholar] [CrossRef]
- Nachemson, A.L.F.; Morris, J.M. In vivo measurements of intradiscal pressure: Discometry, a method for the determination of pressure in the lower lumbar discs. J. Bone Jt. Surg. 1964, 46, 1077–1092. [Google Scholar] [CrossRef]
- Wilke, H.J.; Neef, P.; Caimi, M.; Hoogland, T.; Claes, L.E. New in vivo measurements of pressures in the intervertebral disc in daily life. Spine 1999, 24, 755–762. [Google Scholar] [CrossRef] [PubMed]
- Sato, K.; Kikuchi, S.; Yonezawa, T. In vivo intradiscal pressure measurement in healthy individuals and in patients with ongoing back problems. Spine 1999, 24, 2468. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, I.; Kikuchi, S.I.; Sato, K.; Sato, N. Mechanical load of the lumbar spine during forward bending motion of the trunk—A biomechanical study. Spine 2006, 31, 18–23. [Google Scholar] [CrossRef] [PubMed]
- Marras, W.S.; Davis, K.G. Spine loading during asymmetric lifting using one versus two hands. Ergonomics 1998, 41, 817–834. [Google Scholar] [CrossRef] [PubMed]
- Chaffin, D.B.; Andersson, G.B.; Martin, B.J. Occupational Biomechanics; John Wiley & Sons: Chicago, IL, USA, 2006; pp. 133–134. [Google Scholar]
- Nussbaum, M.A.; Chaffin, D.B.; Rechtien, C.J. Muscle lines-of-action affect predicted forces in optimization-based spine muscle modeling. J. Biomech. 1995, 28, 401–409. [Google Scholar] [CrossRef]
- Keir, P.J.; MacDonell, C.W. Muscle activity during patient transfers: A preliminary study on the influence of lift assists and experience. Ergonomics 2004, 47, 296–306. [Google Scholar] [CrossRef] [PubMed]
- Skotte, J.H.; Essendrop, M.; Hansen, A.F.; Schibye, B. A dynamic 3D biomechanical evaluation of the load on the low back during different patient-handling tasks. J. Biomech. 2002, 35, 1357–1366. [Google Scholar] [CrossRef]
- Jäger, M.; Jordan, C.; Theilmeier, A.; Wortmann, N.; Kuhn, S.; Nienhaus, A.; Luttmann, A. Lumbar-load analysis of manual patient-handling activities for biomechanical overload prevention among healthcare workers. Ann. Occup. Hyg. 2013, 57, 528–544. [Google Scholar] [PubMed] [Green Version]
- Marras, W.S.; Davis, K.G.; Kirking, B.C.; Bertsche, P.K. A comprehensive analysis of low-back disorder risk and spinal loading during the transferring and repositioning of patients using different techniques. Ergonomics 1999, 42, 904–926. [Google Scholar] [CrossRef] [PubMed]
- McGill, S.M.; Norman, R.W.; Cholewicki, J. A simple polynomial that predicts low-back compression during complex 3-D tasks. Ergonomics 1996, 39, 1107–1118. [Google Scholar] [CrossRef] [PubMed]
- Schibye, B.; Hansen, A.F.; Hye-Knudsen, C.T.; Essendrop, M.; Böcher, M.; Skotte, J. Biomechanical analysis of the effect of changing patient-handling technique. Appl. Ergonom. 2003, 34, 115–123. [Google Scholar] [CrossRef]
- Theilmeier, A.; Jordan, C.; Luttmann, A.; JäGer, M. Measurement of action forces and posture to determine the lumbar load of healthcare workers during care activities with patient transfers. Ann. Occup. Hyg. 2010, 54, 923–933. [Google Scholar]
- Damsgaard, M.; Rasmussen, J.; Christensen, S.T.; Surma, E.; De Zee, M. Analysis of musculoskeletal systems in the AnyBody Modeling System. Simul. Model. Pract. Theory 2006, 14, 1100–1111. [Google Scholar] [CrossRef]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Thelen, D.G. OpenSim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roetenberg, D.; Luinge, H.; Slycke, P. Xsens MVN: Full 6DOF human motion tracking using miniature inertial sensors. Xsens Motion Technol. BV Tech. Rep. 2009, 1–9. [Google Scholar]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Keller, T.S.; Colloca, C.J.; Harrison, D.E.; Harrison, D.D.; Janik, T.J. Influence of spine morphology on intervertebral disc loads and stresses in asymptomatic adults: Implications for the ideal spine. Spine J. 2005, 5, 297–309. [Google Scholar] [CrossRef] [PubMed]
- Plamondon, A.; Gagnon, M.; Gravel, D. Moments at the L5/S1 joint during asymmetrical lifting: Effects of different load trajectories and initial load positions. Clin. Biomech. 1995, 10, 128–136. [Google Scholar] [CrossRef]
- Marras, W.S.; Lavender, S.A.; Leurgans, S.E.; Rajulu, S.L.; Allread, S.W.G.; Fathallah, F.A.; Ferguson, S.A. The role of dynamic three-dimensional trunk motion in occupationally-related. Spine 1993, 18, 617–628. [Google Scholar] [CrossRef] [PubMed]
- Hodder, J.N.; Holmes, M.W.; Keir, P.J. Continuous assessment of work activities and posture in long-term care nurses. Ergonomics 2010, 53, 1097–1107. [Google Scholar] [CrossRef] [PubMed]
- ISO. 11228-1:2003 Ergonomics. Anthropometry and Biomechanics. Ergonomics—Manual Handling—Part 1: Lifting and Carrying; International Organization for Standardization: Geneva, Switzerland, 2003; p. 33. [Google Scholar]



| Conditions | Beginning of Lifting | End of Lowering |
|---|---|---|
| 2141 | 1968 |
| Variables | ||||||
|---|---|---|---|---|---|---|
| Mean | ||||||
| s) | 0.25 | |||||
| % | % | % | 5.9% | % | % | |
| 0 | −8.4% | +7.6% | −10.5% | +14.2% | −2.4% |
| 0.02 | 0.257 | 0.001 | 0.001 | 1 | ||
| 0.001 | 1 | 0.001 | 0.006 | |||
| 0.001 | 0.322 | 0.634 | ||||
| 0.001 | 0.001 | |||||
| 0.001 | ||||||
| Factor | VIF |
|---|---|
| 1.17 | |
| 1.34 | |
| 1.52 | |
| 1.10 | |
| 1.03 |
| Conditions | Com | t-e | e-t | Mean |
|---|---|---|---|---|
| lag (s) | 0.21 ± 0.17 | 0.31 ± 0.32 | 0.34 ± 0.38 | 0.29 |
| (N) | 2387 ± 389 | 2451 ± 154 | 2324 ± 246 | 2387 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, X.; Yamada, Y.; Akiyama, Y.; Nakamura, H.; Kudo, N. Effect of Parameters on Lumbar Compressive Force during Patient Transfer. Appl. Sci. 2021, 11, 11622. https://doi.org/10.3390/app112411622
Xiang X, Yamada Y, Akiyama Y, Nakamura H, Kudo N. Effect of Parameters on Lumbar Compressive Force during Patient Transfer. Applied Sciences. 2021; 11(24):11622. https://doi.org/10.3390/app112411622
Chicago/Turabian StyleXiang, Xiaohan, Yoji Yamada, Yasuhiro Akiyama, Hibiki Nakamura, and Naoki Kudo. 2021. "Effect of Parameters on Lumbar Compressive Force during Patient Transfer" Applied Sciences 11, no. 24: 11622. https://doi.org/10.3390/app112411622
APA StyleXiang, X., Yamada, Y., Akiyama, Y., Nakamura, H., & Kudo, N. (2021). Effect of Parameters on Lumbar Compressive Force during Patient Transfer. Applied Sciences, 11(24), 11622. https://doi.org/10.3390/app112411622






