The Influence of Floor Layering on Airborne Sound Insulation and Impact Noise Reduction: A Study on Cross Laminated Timber (CLT) Structures
Abstract
:1. Introduction
2. Materials and Methods
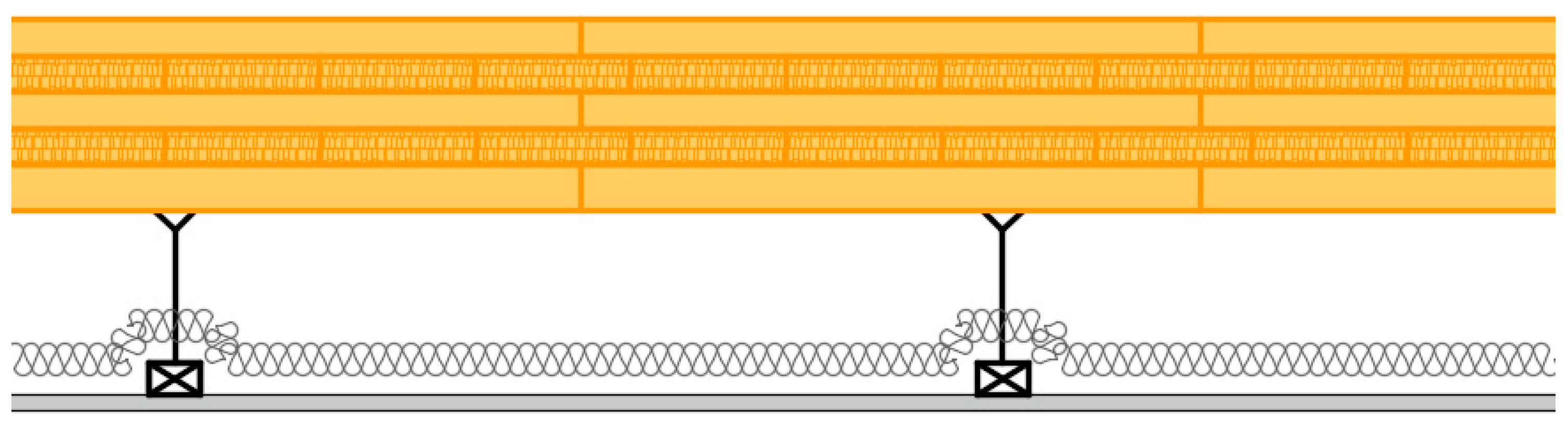
2.1. Investigated Structures
- Bare floor;
- Bare floor coupled with suspended ceiling;
- Bare floor coupled with a floating floor;
- Bare floor coupled both with suspended ceiling (rigid connections) and floating floor.
2.2. Experimental Structures Characterization
- five hammers placed in a line. The distance between centerlines of hammers is (100 ± 3) mm;
- the distance between the center of the supports of the tapping machine and the centerlines of neighboring hammers is at least 100 mm;
- height of fall of the hammers is 40 ± 2 mm;
- the mass of each hammer is 500 ± 12 g from which it follows that the velocity at impact should be 0.886 ± 0.022 m/s. The tolerance limits of the velocity may be increased to a maximum of ±0.033 m/s if it is ensured that the hammer mass lies within accordingly reduced limits of 500 ± 6 g;
- the falling direction of the hammers is perpendicular to the test surface to within ±0.5°.
- the part of the hammer carrying the impact surface is cylindrical with a diameter of 30 ± 0.2 mm;
- the impact surface shall be of hardened steel and is spherical with a curvature radius of 500 ± 100 mm;
- the mean time between impacts is 100 ± 5 ms. The time between successive impacts is 100 ± 20 ms;
- the time between impact and lift of the hammer is less than 80 ms;
- the weight of the tapping machine is less than 25 kg.
2.3. Acoustic Parameters
2.4. Acoustic Models
3. Results and Discussion
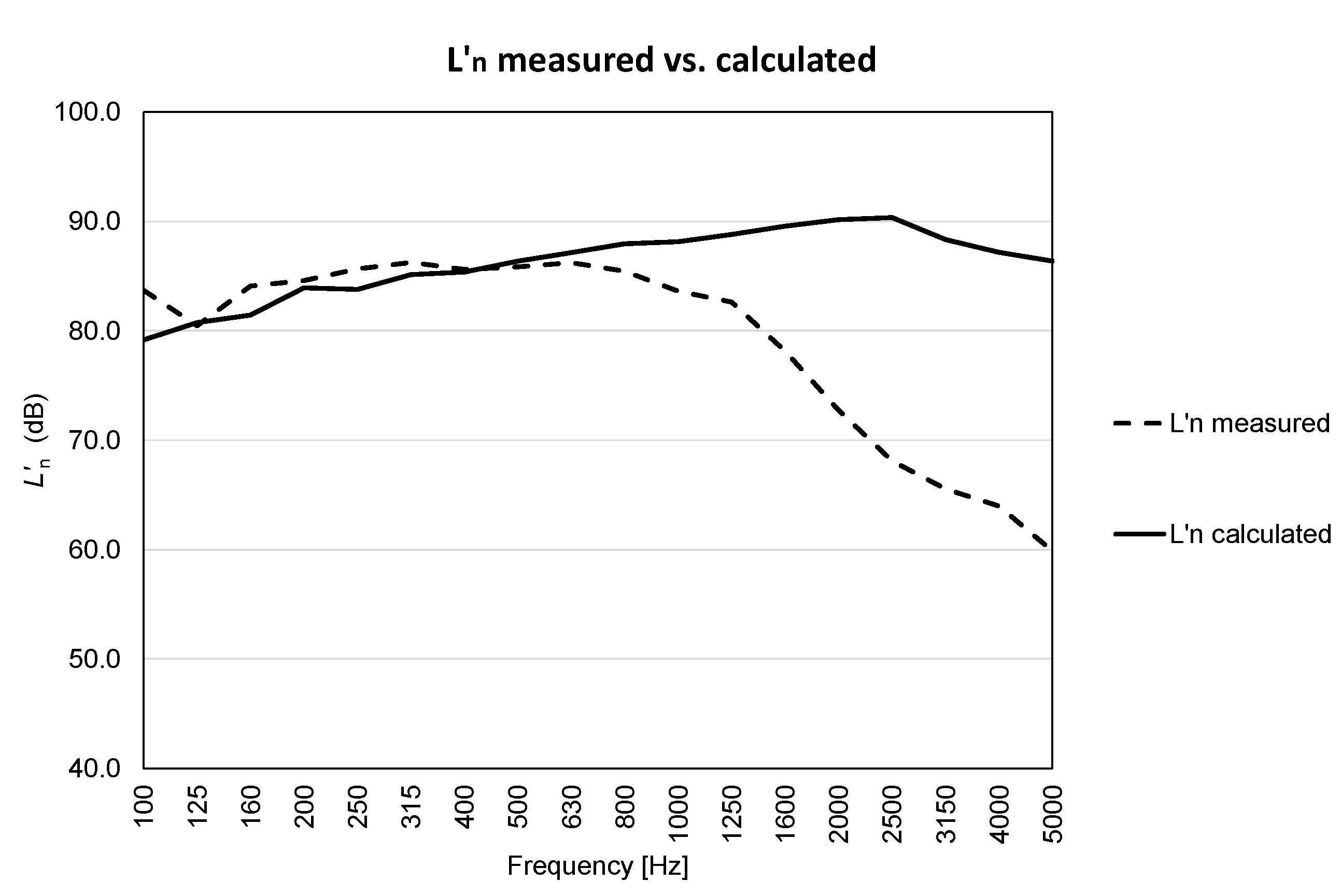
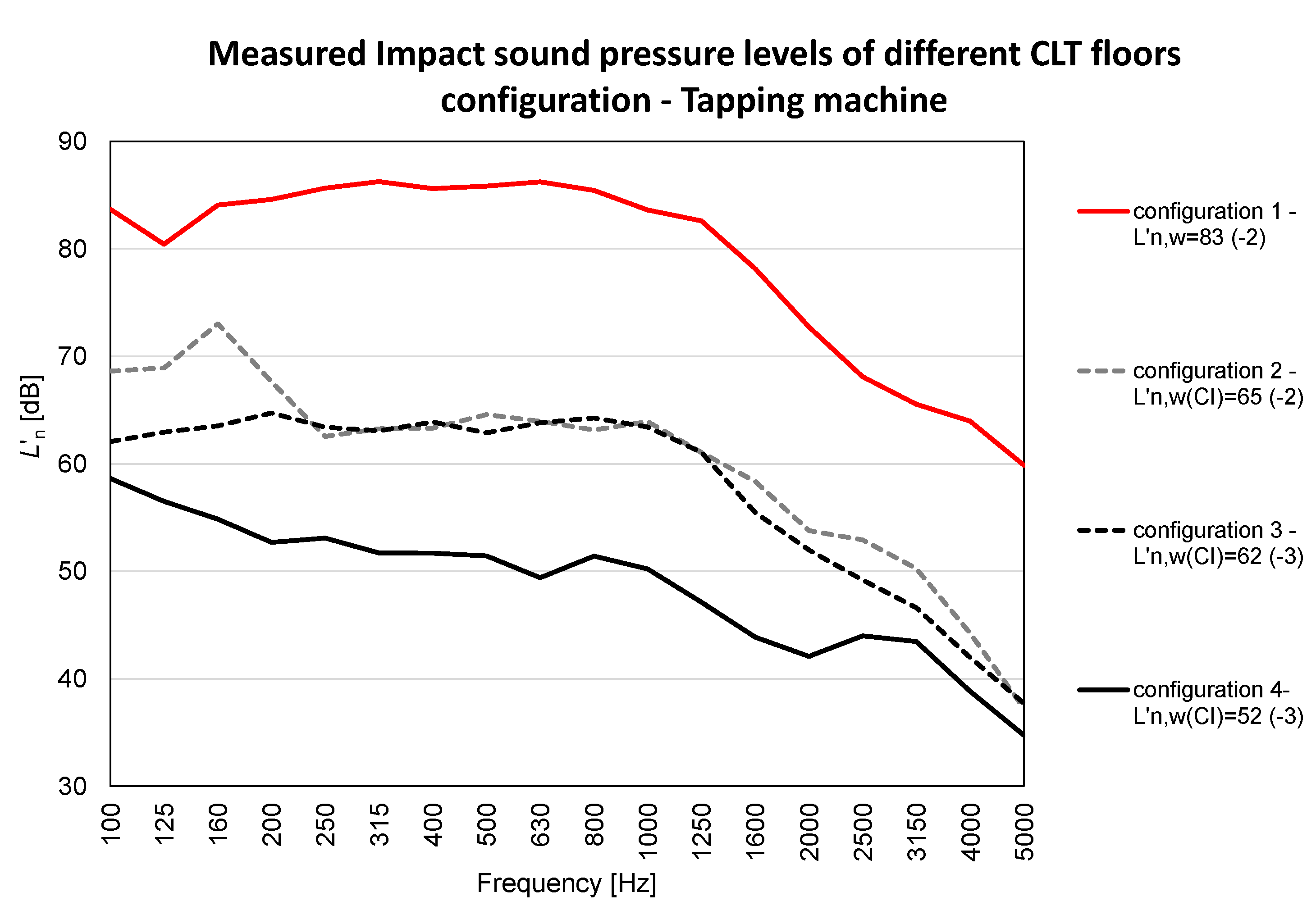
3.1. Impact Noise–Tapping Machine
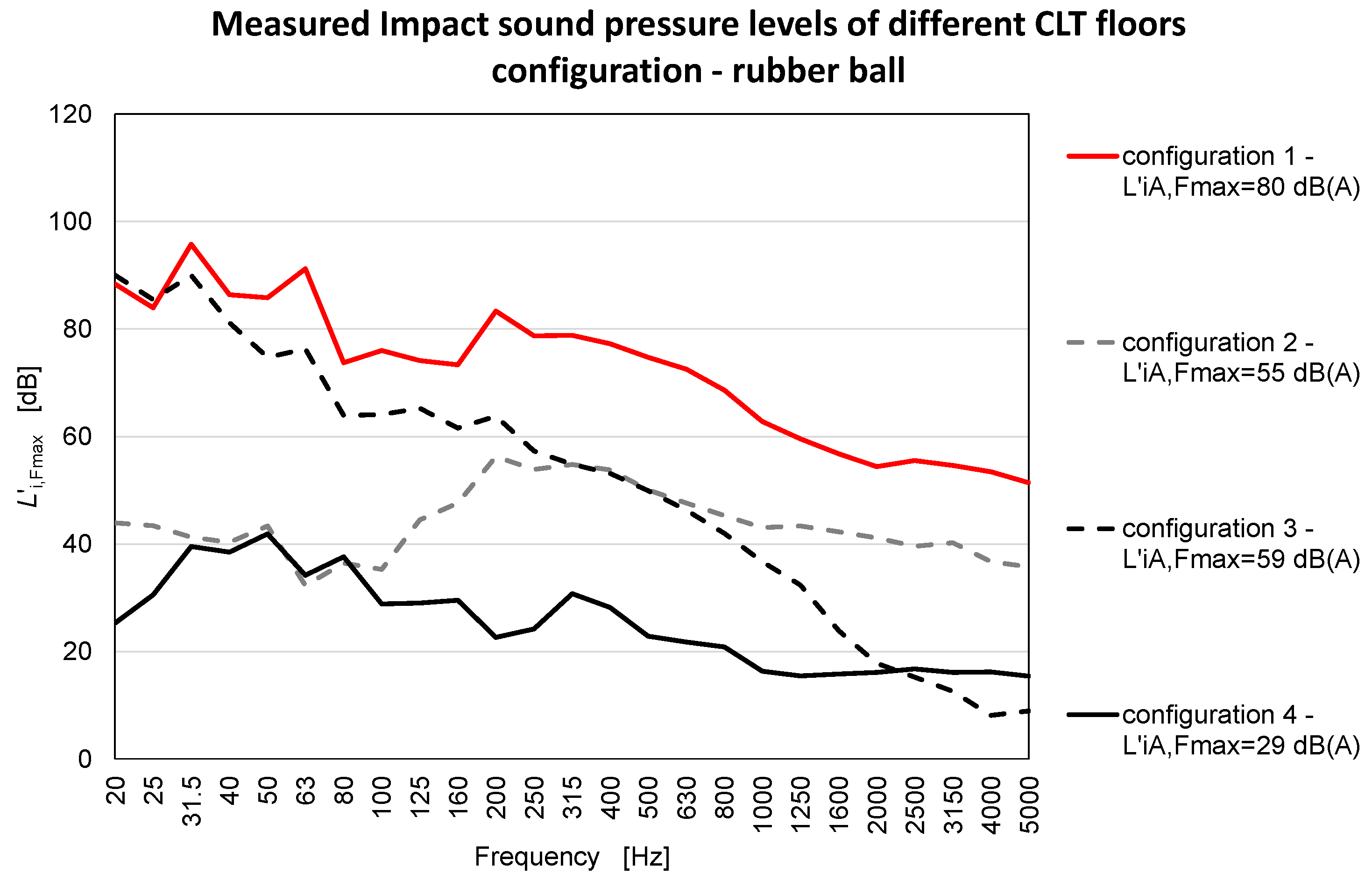
3.2. Impact Noise–Rubber Ball
3.3. Airborne Sound Insulation
3.4. Weighted Indexes Results
4. Conclusions
- -
- the bare Cross Laminated Timber floors present similar acoustic performances, thus an average trend can be considered;
- -
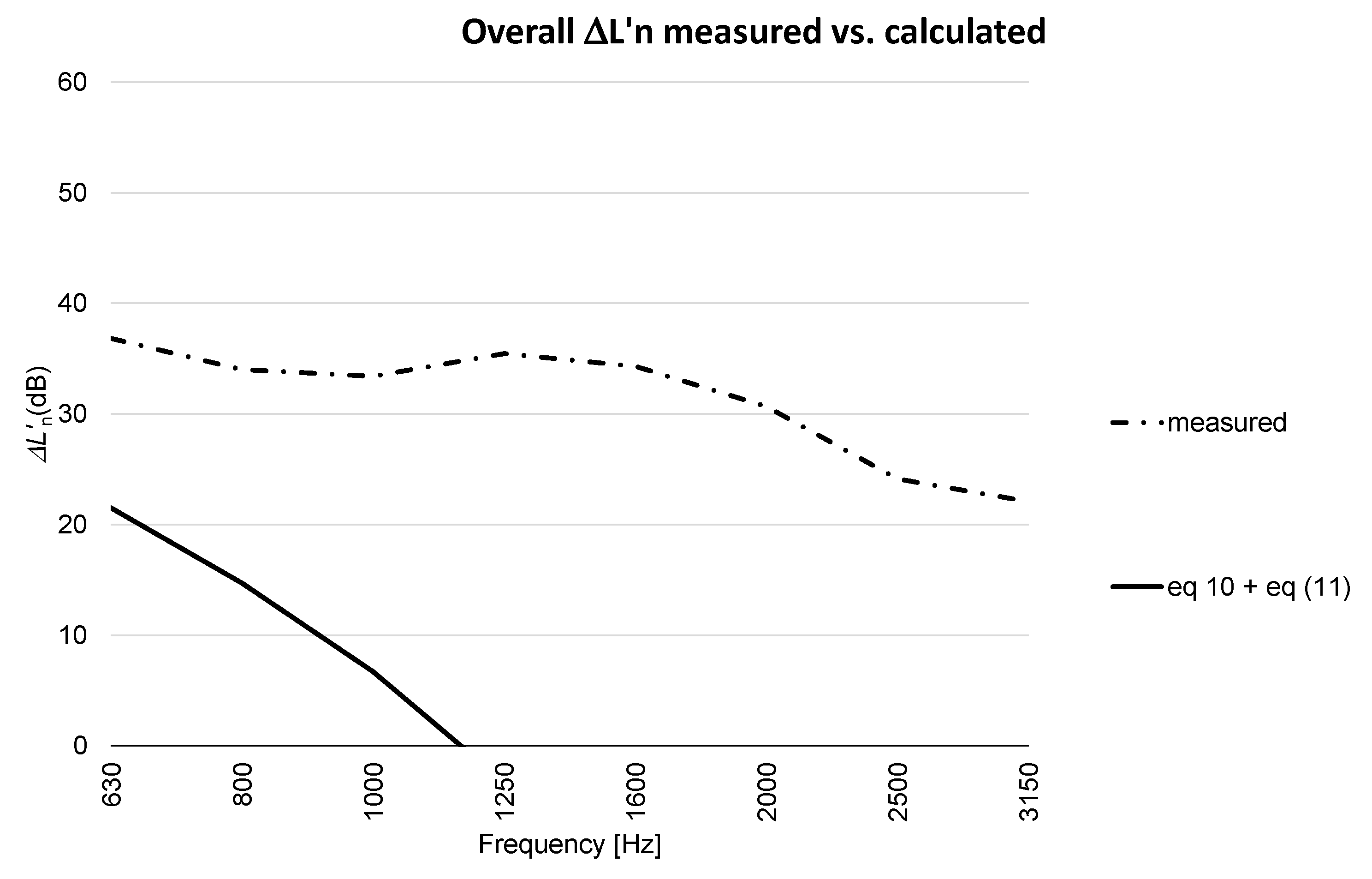
- the impact noise reduction offered by suspended ceiling or floating floor excited by a tapping machine is very similar. Regression equations demonstrate that frequencies do not play a significant role; the same consideration is possible even when considering both these techniques at the same time.
- -
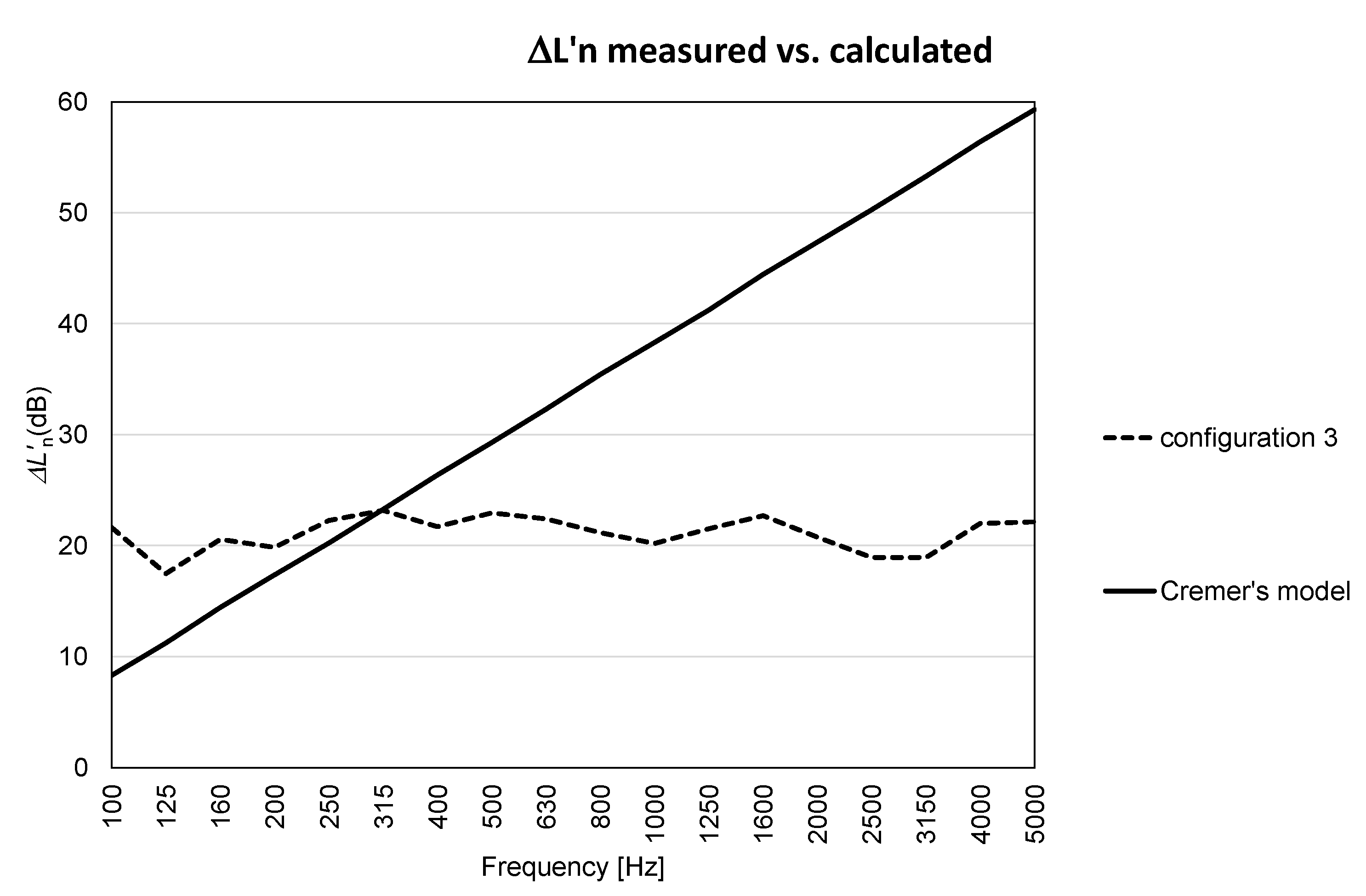
- the Cremer’s equation does not work with this structure. In particular, for middle-low frequency, Cremer’s law fails by a large amount.
- -
- when excited by a rubber ball, a suspended ceiling acts better than the floating floor, especially at low frequencies. The floating floor presents a linear-decreasing trend, which anyway is not able to reduce efficiently the impulse injected by the rubber ball;
- -
- in the case of airborne sound insulation, both floating floor and suspended ceiling offer similar improvements. When merging the two technologies, no significant performance increasing is assessed. In this case, no analytical model was found to correctly predict the final results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ramage, M.H.; Burridge, H.; Busse-Wicher, M.; Fereday, G.; Reynolds, T.; Shah, D.U.; Wu, G.; Yu, L.; Fleming, P.; Densley-Tingley, D.; et al. The Wood from the Trees: The Use of Timber in Construction. Renew. Sustain. Energy Rev. 2017, 68, 333–359. [Google Scholar] [CrossRef]
- Frangi, A.; Fontana, M.; Knobloch, M. Fire Design Concepts for Tall Timber Buildings. Struct. Eng. Int. 2008, 18, 148–155. [Google Scholar] [CrossRef]
- Kuzman, M.K.; Sandberg, D. A New Era for Multi-Storey Timber Buildings in Europe; Forest Products Society: Portlan, OR, USA, 2016. [Google Scholar]
- Smith, I.; Frangi, A. Overview of Design Issues for Tall Timber Buildings. Struct. Eng. Int. 2008, 18, 141–147. [Google Scholar] [CrossRef]
- Kaiser, A.; Larsson, M.; Girhammar, U.A. From File to Factory: Innovative Design Solutions for Multi-Storey Timber Buildings Applied to Project Zembla in Kalmar, Sweden. Front. Archit. Res. 2019, 8, 1–16. [Google Scholar] [CrossRef]
- Kuzmanovska, I.; Gasparri, E.; Monné, D.T.; Aitchison, M. Tall Timber Buildings: Emerging Trends and Typologies. In Proceedings of the WTCE 2018, Seoul, Korea, 20–23 August 2018. [Google Scholar]
- Mayo, J. Solid Wood: Case Studies in Mass Timber Architecture, Technology and Design; Routledge: England, UK, 2015; ISBN 978-1-317-58749-1. [Google Scholar]
- Asiz, A.; Smith, I. Connection System of Massive Timber Elements Used in Horizontal Slabs of Hybrid Tall Buildings. J. Struct. Eng. 2011, 137, 1390–1393. [Google Scholar] [CrossRef]
- Bolvardi, V.; Pei, S.; van de Lindt, J.W.; Dolan, J.D. Direct Displacement Design of Tall Cross Laminated Timber Platform Buildings with Inter-Story Isolation. Eng. Struct. 2018, 167, 740–749. [Google Scholar] [CrossRef]
- Di Bella, A.; Mitrovic, M. Acoustic Characteristics of Cross-Laminated Timber Systems. Sustainability 2020, 12, 5612. [Google Scholar] [CrossRef]
- Pérez, M.; Fuente, M. Acoustic Design through Predictive Methods in Cross Laminated Timber (CLT) Panel Structures for Buildings. In Proceedings of the Internoise, Innsbruck, Austria, 15–18 September 2013. [Google Scholar]
- Pagnoncelli, L.; Fuente, M. Cross-Laminated Timber System (CLT): Laboratory and in Situ Measurements of Airborne and Impact Sound Insulation. In Proceedings of the EuroRegio Conference, Porto, Portugal, 13–15 June 2016. [Google Scholar]
- Öqvist, R.; Ljunggren, F.; Ågren, A. On the Uncertainty of Building Acoustic Measurements—Case Study of a Cross-Laminated Timber Construction. Appl. Acoust. 2012, 73, 904–912. [Google Scholar] [CrossRef]
- Ljunggren, F.; Simmons, C.; Hagberg, K. Findings from the AkuLite Project: Correlation between Measured Vibro-Acoustic Parameters and Subjective Perception in Lightweight Buildings. In Proceedings of the Internoise, Innsbruck, Austria, 15–18 September 2013. [Google Scholar]
- Zhang, X.; Hu, X.; Gong, H.; Zhang, J.; Lv, Z.; Hong, W. Experimental Study on the Impact Sound Insulation of Cross Laminated Timber and Timber-Concrete Composite Floors. Appl. Acoust. 2020, 161, 107173. [Google Scholar] [CrossRef]
- Kim, K.-W.; Jeong, G.-C.; Yang, K.-S.; Sohn, J. Correlation between Dynamic Stiffness of Resilient Materials and Heavyweight Impact Sound Reduction Level. Build. Environ. 2009, 44, 1589–1600. [Google Scholar] [CrossRef]
- Fortini, M.; Granzotto, N.; Piana, E.A. Vibro-Acoustic Characterization of a Composite Structure Featuring an Innovative Phenolic Foam Core. Appl. Sci. 2019, 9, 1276. [Google Scholar] [CrossRef] [Green Version]
- Vardaxis, N.-G.; Bard, D.; Persson Waye, K. Review of Acoustic Comfort Evaluation in Dwellings—Part I: Associations of Acoustic Field Data to Subjective Responses from Building Surveys. Build. Acoust. 2018, 25, 151–170. [Google Scholar] [CrossRef] [Green Version]
- Vardaxis, N.-G.; Bard, D. Review of Acoustic Comfort Evaluation in Dwellings: Part II—Impact Sound Data Associated with Subjective Responses in Laboratory Tests. Build. Acoust. 2018, 25, 171–192. [Google Scholar] [CrossRef]
- Späh, M.; Hagberg, K.; Bartlomé, O.; Weber, L.; Leistner, P.; Liebl, A. Subjective and Objective Evaluation of Impact Noise Sources in Wooden Buildings. Build. Acoust. 2013, 20, 193–213. [Google Scholar] [CrossRef]
- Ågren, A.; Ljunggren, F.; Jarnerö, K.; Bolmsvik, Å. Flanking Transmission in Light Weight Timber Houses with Elastic Flanking Isolators. In Proceedings of the Internoise, New York, NY, USA, 19–22 September 2012. [Google Scholar]
- Mahn, J.; Müller-Trapet, M. Characterization of Laminated Timber Building Elements to Estimate Flanking Transmission. INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Inst. Noise Control Eng. 2019, 259, 4170–4178. [Google Scholar]
- Ågren, A.; Ljunggren, F. In Situ Measured Flanking Transmission in Light Weight Timber Houses with Elastic Flanking Isolators: Part II. In Proceedings of the Internoise, Innsbruck, Austria, 15–18 September 2013. [Google Scholar]
- Rabold, A.; Hessinger, J. Flanking Transmission at Impact Sound Excitation—Calculation According to DIN 4109 and PrEN ISO 12354-2—INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Inst. Noise Control Eng. 2016, 253, 4308–4317. [Google Scholar]
- Tronchin, L. Variability of Room Acoustic Parameters with Thermo-Hygrometric Conditions. Appl. Acoust. 2021, 177, 107933. [Google Scholar] [CrossRef]
- Herzog, T.; Natterer, J.; Schweitzer, R.; Volz, M.; Winter, W. Timber Construction Manual; Birkhäuser: Basel, Switzerland, 2012; ISBN 978-3-0346-1463-4. [Google Scholar]
- Östman, B.; Brandon, D.; Frantzich, H. Fire Safety Engineering in Timber Buildings. Fire Saf. J. 2017, 91, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Cho, T. Vibro-Acoustic Characteristics of Floating Floor System: The Influence of Frequency-Matched Resonance on Low Frequency Impact Sound. J. Sound Vib. 2013, 332, 33–42. [Google Scholar] [CrossRef]
- Schiavi, A. Improvement of Impact Sound Insulation: A Constitutive Model for Floating Floors. Appl. Acoust. 2018, 129, 64–71. [Google Scholar] [CrossRef]
- ISO 16283-1:2014. Acoustics—Field Measurement of Sound Insulation in Buildings and of Building Elements—Part 1: Airborne Sound Insulation; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- ISO 16283-2:2020. Acoustics—Field Measurement of Sound Insulation in Buildings and of Building Elements—Part 2: Impact Sound Insulation; ISO: Geneva, Switzerland, 2020. [Google Scholar]
- ISO 12354-2. Building Acoustics—Estimation of Acoustic Performance of Buildings from the Performance of Elements—Part 2: Impact Sound Insulation between Rooms; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- Carl, H. Sound Insulation; Butterworth-Heinemann: Oxford, UK, 2007; 648p, ISBN 978-0-7506-6526-1. £55.99, [PDF Document]; Available online: https://fdocuments.in/document/sound-insulation-carl-hopkins-butterworth-heinemann-oxford-uk-2007-648.html (accessed on 18 May 2021).
- Cremer, L. Theorie Der Schalldämmung Dünner Wände Bei Schrägem Einfall. Akust Z 1942, 7, 81–104. [Google Scholar]
- Bies, D.A.; Hansen, C.H. Engineering Noise Control: Theory and Practice; Spon: London, UK, 1995; p. 745. [Google Scholar]
- Woo, S.-H.A. The Measurement of Transmission Loss and Absorption Coefficient of the Rat and Porcine Skin: Synthesizing Artificial Material for an Implantable Microphone Test. Appl. Acoust. 2013, 74, 1388–1393. [Google Scholar] [CrossRef]
- Hagberg, K.G. Evaluating Field Measurements of Impact Sound. Build. Acoust. 2010, 17, 105–128. [Google Scholar] [CrossRef]
- Hui, C.K.; Ng, C.F. New Floating Floor Design with Optimum Isolator Location. J. Sound Vib. 2007, 303, 221–238. [Google Scholar] [CrossRef]
- Rasmussen, B. Sound Insulation between Dwellings. Comparison of National Requirements in Europe and Interaction with Acoustic Classification Schemes. In Proc 23rd International Congress on Acoustics; Deutsche Gesellschaft für Akustik: Aachen, Germany, 2019. [Google Scholar]



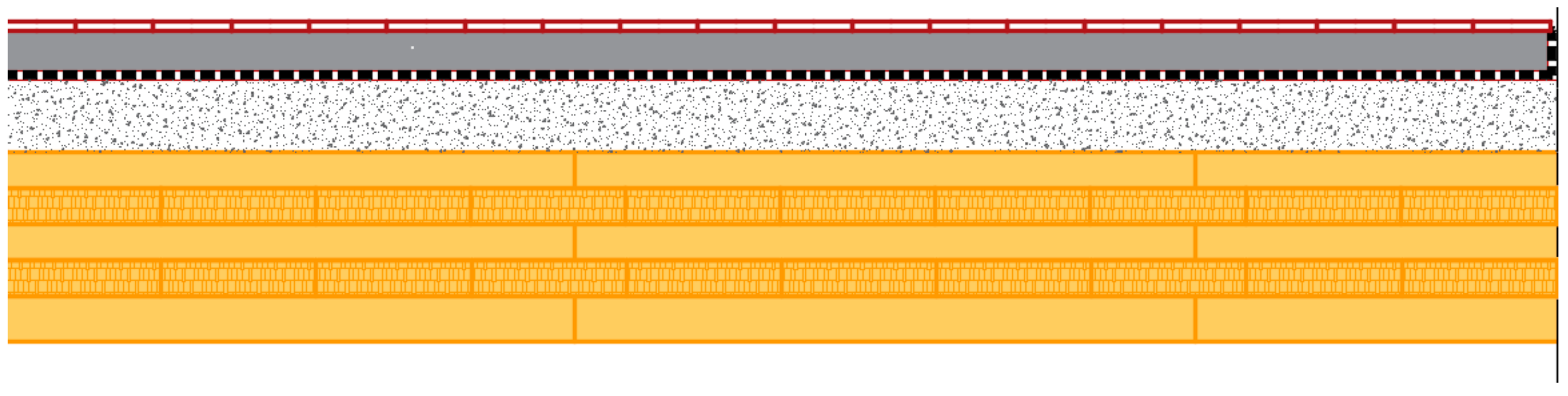
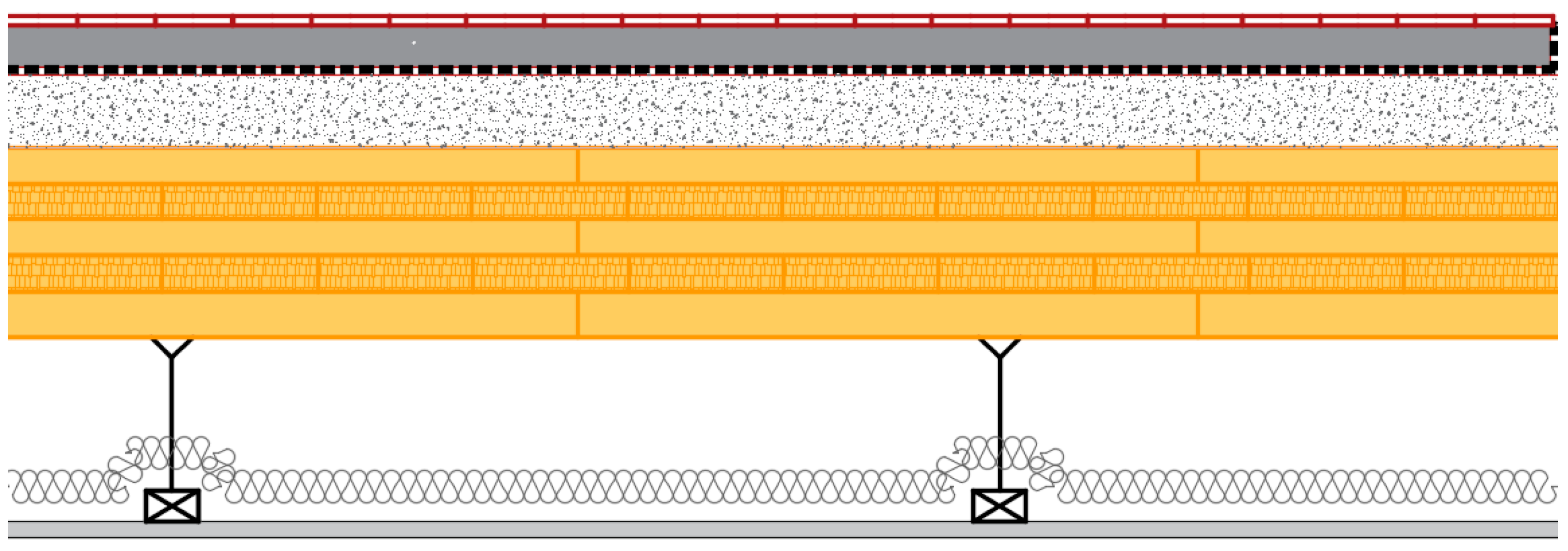



| Element | Thickness d [mm] | Density ρ [kg/m3] | Dynamic Stiffness s′ [Mn/m3] |
|---|---|---|---|
| Screed | 40 | 1150 | - |
| Resilient layer | 9 | 700 | 11 |
| Screed | 100 | 400 | - |
| Waterproof membrane | 0.2 | 33 | - |
| CLT floor panel. | 180 | 470 | - |
| Air layer | 62 | 1 | - |
| Rock wool panel | 60 | 70 | - |
| Gypsum board | 1.25 | 730 | - |
| Octave Band Centre Frequency [Hz] | Impact Force Exposure Level, LFE (dB re 1 N) |
|---|---|
| 31.5 | 39.0 ± 1.0 |
| 63 | 31.0 ± 1.5 |
| 125 | 23.0 ± 1.5 |
| 250 | 17.0 ± 2.0 |
| 500 | 12.5 ± 2.0 |
| Frequency [Hz] | IMPACT Noise Average (dB) | Standard Deviation (dB) |
|---|---|---|
| 100 | 83.7 | 3.2 |
| 125 | 80.4 | 3.7 |
| 160 | 84.1 | 3.0 |
| 200 | 84.6 | 2.9 |
| 250 | 85.7 | 2.6 |
| 315 | 86.2 | 2.5 |
| 400 | 85.6 | 2.5 |
| 500 | 85.8 | 2.3 |
| 630 | 86.2 | 2.1 |
| 800 | 85.4 | 1.8 |
| 1000 | 83.6 | 1.7 |
| 1250 | 82.6 | 1.7 |
| 1600 | 78.2 | 1.6 |
| 2000 | 72.7 | 1.7 |
| 2500 | 68.1 | 1.9 |
| 3150 | 65.5 | 3.3 |
| 4000 | 64.0 | 4.2 |
| 5000 | 59.9 | 4.4 |
| Frequency [Hz] | Impact Noise Average (dB) | Δ (dB) |
|---|---|---|
| 100 | 83.7 | 4.6 |
| 125 | 80.4 | −0.3 |
| 160 | 84.1 | 2.7 |
| 200 | 84.6 | 0.7 |
| 250 | 85.7 | 1.9 |
| 315 | 86.2 | 1.1 |
| 400 | 85.6 | 0.2 |
| 500 | 85.8 | −0.5 |
| 630 | 86.2 | −0.9 |
| 800 | 85.4 | −2.5 |
| 1000 | 83.6 | −4.5 |
| 1250 | 82.6 | −6.2 |
| 1600 | 78.2 | −11.4 |
| 2000 | 72.7 | −17.4 |
| 2500 | 68.1 | −22.2 |
| 3150 | 65.5 | −22.8 |
| 4000 | 64.0 | −23.2 |
| 5000 | 59.9 | −26.5 |
| Configuration and Difference (dB) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Frequency [Hz] | 1 | Δ1 | 2 | Δ2 | 3 | Δ3 | 4 | Δ4 |
| 100 | 31.9 | −4.3 | 33.2 | −1.2 | 38.4 | −7.2 | 38.8 | −3.0 |
| 125 | 33.8 | −6.6 | 35.2 | 1.2 | 40.3 | −2.2 | 40.8 | 4.1 |
| 160 | 36.0 | −6.8 | 37.3 | −1.1 | 42.5 | 2.3 | 42.9 | 3.2 |
| 200 | 37.9 | −11.4 | 39.2 | 0.5 | 44.4 | −4.3 | 44.8 | 2.8 |
| 250 | 39.8 | −13.0 | 41.2 | 2.8 | 46.3 | −2.2 | 46.8 | 2.5 |
| 315 | 41.9 | −14.6 | 43.2 | 3.7 | 48.3 | −1.6 | 48.8 | 0.6 |
| 400 | 43.9 | −16.5 | 45.3 | 3.5 | 50.4 | −2.3 | 50.9 | −0.5 |
| 500 | 45.9 | −15.3 | 47.2 | 1.7 | 52.4 | −4.6 | 52.8 | −2.4 |
| 630 | 47.9 | −14.7 | 49.2 | 0.0 | 54.4 | −5.8 | 54.8 | −4.8 |
| 800 | 49.9 | −16.4 | 51.3 | 2.2 | 56.4 | −6.9 | 56.9 | −5.8 |
| 1000 | 51.9 | −16.5 | 53.2 | −2.1 | 58.4 | −8.2 | 58.8 | −6.8 |
| 1250 | 53.8 | −14.3 | 55.2 | 0.0 | 60.3 | −9.2 | 60.8 | −8.0 |
| 1600 | 56.0 | −14.0 | 57.3 | −3.8 | 62.5 | −8.8 | 62.9 | −9.5 |
| 2000 | 57.9 | −13.7 | 59.2 | −3.0 | 64.4 | −8.2 | 64.8 | −9.6 |
| 2500 | 59.8 | −15.2 | 61.2 | −6.5 | 66.3 | −10.3 | 66.8 | −11.1 |
| 3150 | 61.9 | −17.9 | 63.2 | −8.1 | 68.3 | −10.3 | 68.8 | −12.5 |
| 4000 | 63.9 | −18.9 | 65.3 | −8.4 | 70.4 | −11.4 | 70.9 | −13.8 |
| 5000 | 65.9 | −19.8 | 67.2 | −9.8 | 72.4 | −12.4 | 72.8 | −15.0 |
| Configuration | L′n,w (dB) | L′iA,Fmax,50–630 (dB) | L′iA,Fmax,20–2500 (dB) | R′ (dB) |
|---|---|---|---|---|
| 1 | 83 | 80 | 80 | 35 |
| 2 | 65 | 55 | 56 | 52 |
| Δ2 | 18 | 25 | 24 | 17 |
| 3 | 62 | 59 | 60 | 51 |
| Δ3 | 21 | 21 | 20 | 16 |
| 4 | 52 | 29 | 31 | 53 |
| Δ4 | 31 | 51 | 49 | 18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bettarello, F.; Gasparella, A.; Caniato, M. The Influence of Floor Layering on Airborne Sound Insulation and Impact Noise Reduction: A Study on Cross Laminated Timber (CLT) Structures. Appl. Sci. 2021, 11, 5938. https://doi.org/10.3390/app11135938
Bettarello F, Gasparella A, Caniato M. The Influence of Floor Layering on Airborne Sound Insulation and Impact Noise Reduction: A Study on Cross Laminated Timber (CLT) Structures. Applied Sciences. 2021; 11(13):5938. https://doi.org/10.3390/app11135938
Chicago/Turabian StyleBettarello, Federica, Andrea Gasparella, and Marco Caniato. 2021. "The Influence of Floor Layering on Airborne Sound Insulation and Impact Noise Reduction: A Study on Cross Laminated Timber (CLT) Structures" Applied Sciences 11, no. 13: 5938. https://doi.org/10.3390/app11135938
APA StyleBettarello, F., Gasparella, A., & Caniato, M. (2021). The Influence of Floor Layering on Airborne Sound Insulation and Impact Noise Reduction: A Study on Cross Laminated Timber (CLT) Structures. Applied Sciences, 11(13), 5938. https://doi.org/10.3390/app11135938








