Diamond-Shaped Extended Fins for Heat Transfer Enhancement in a Double-Pipe Heat Exchanger: An Innovative Design
Abstract
:1. Introduction
2. Materials and Methods
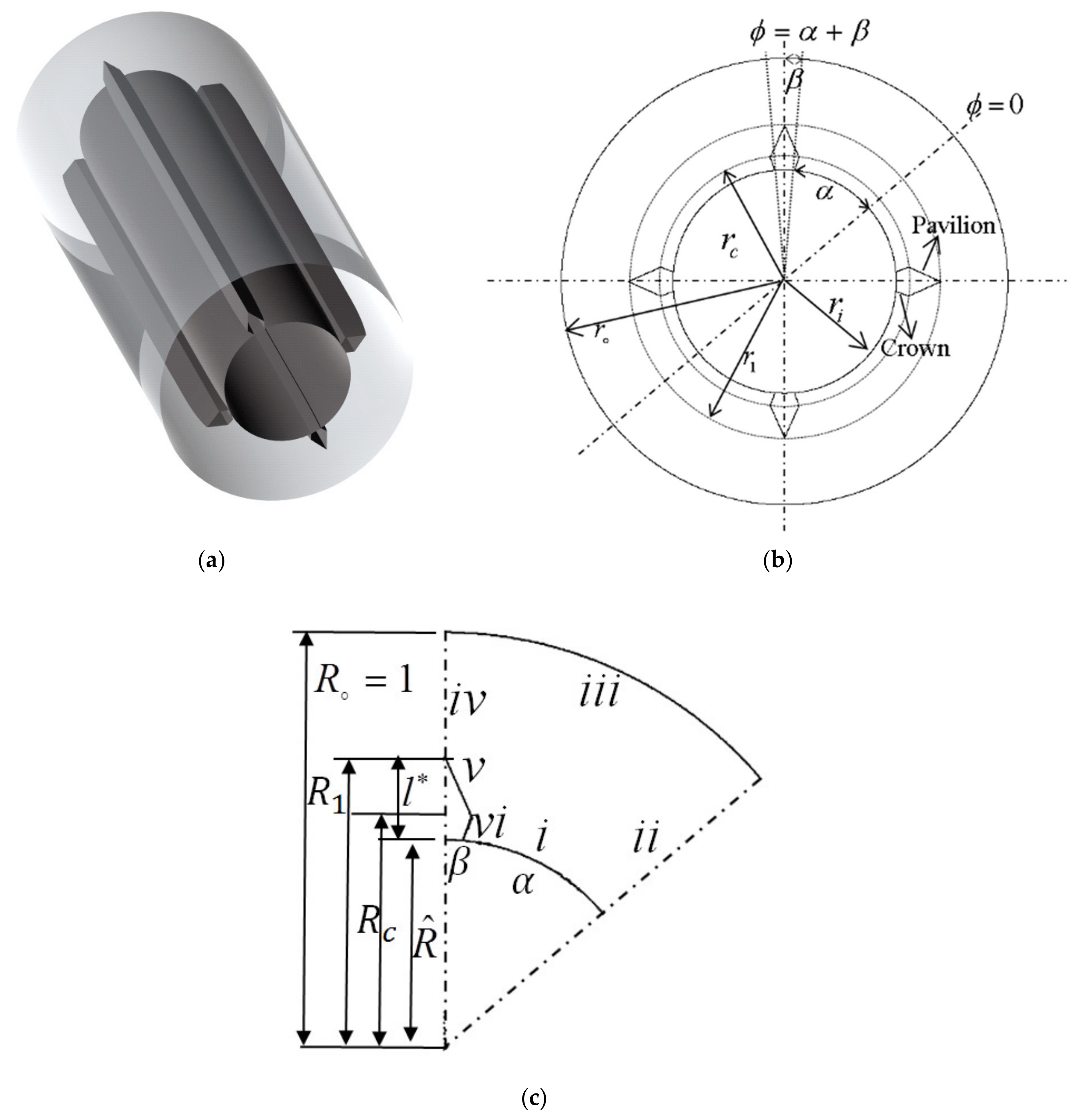
2.1. Problem Description
2.2. Finite Element Formulation
2.3. h-Adaptation and Grid Independence Test
2.4. Validation of Computed Results
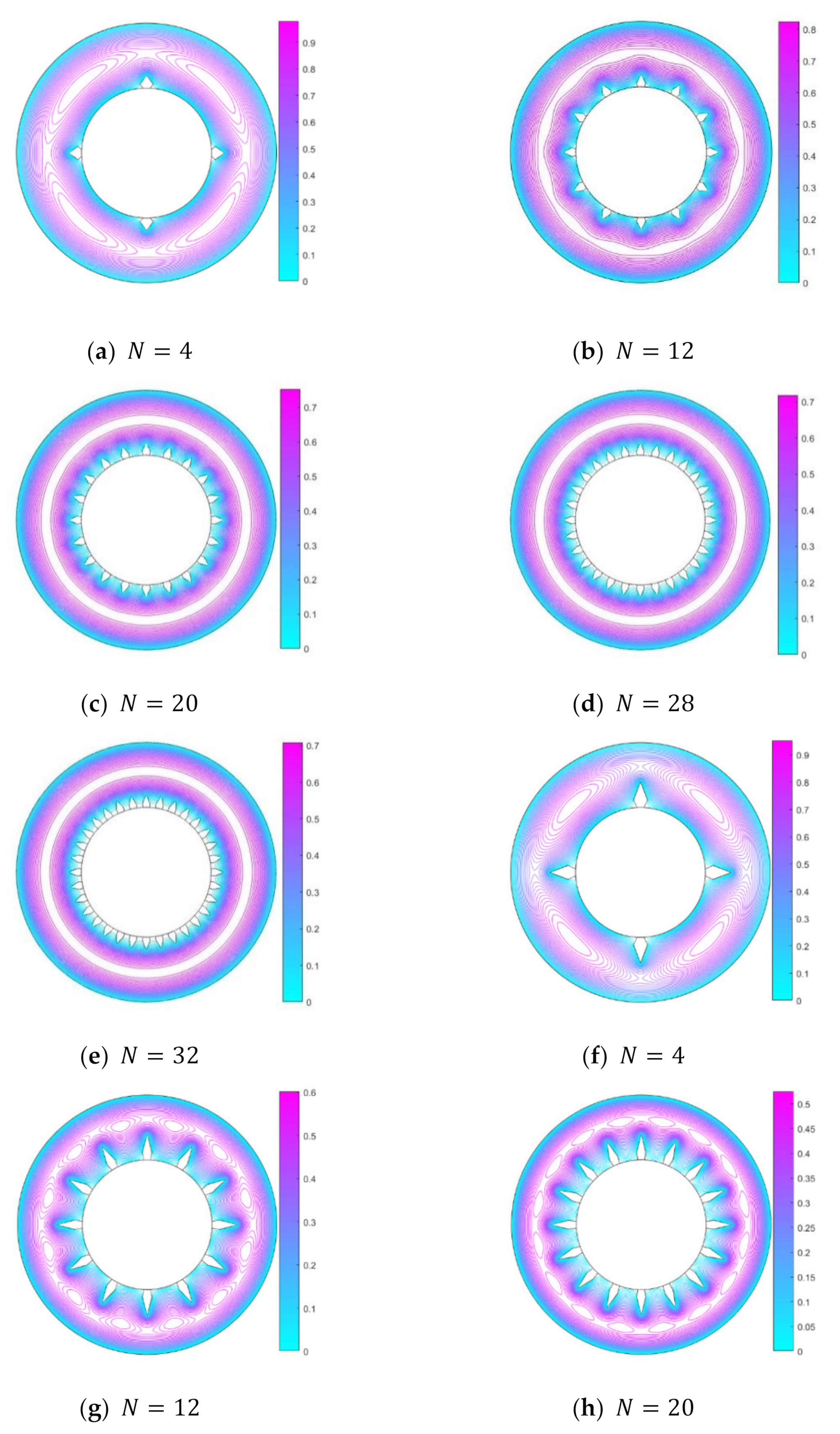
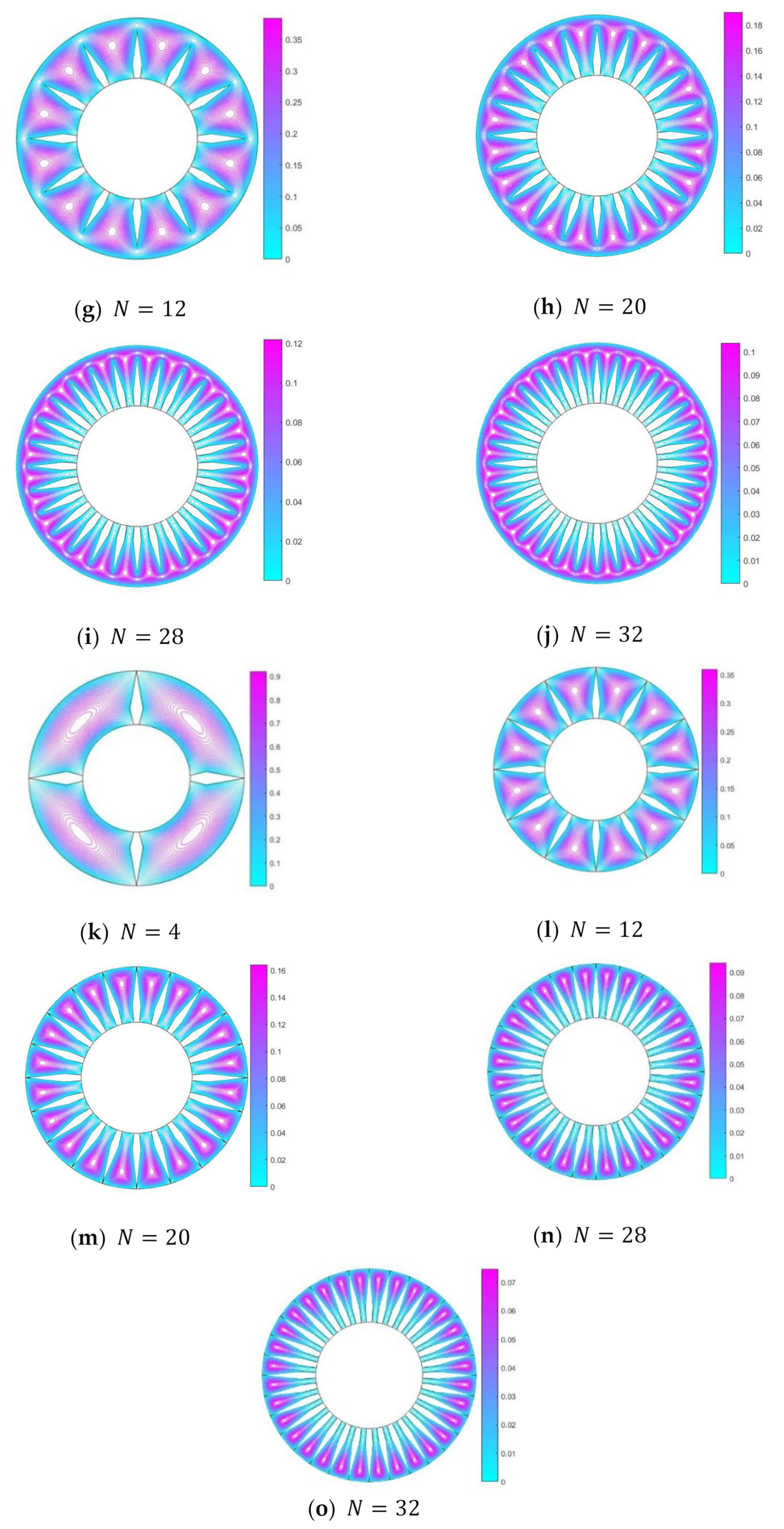
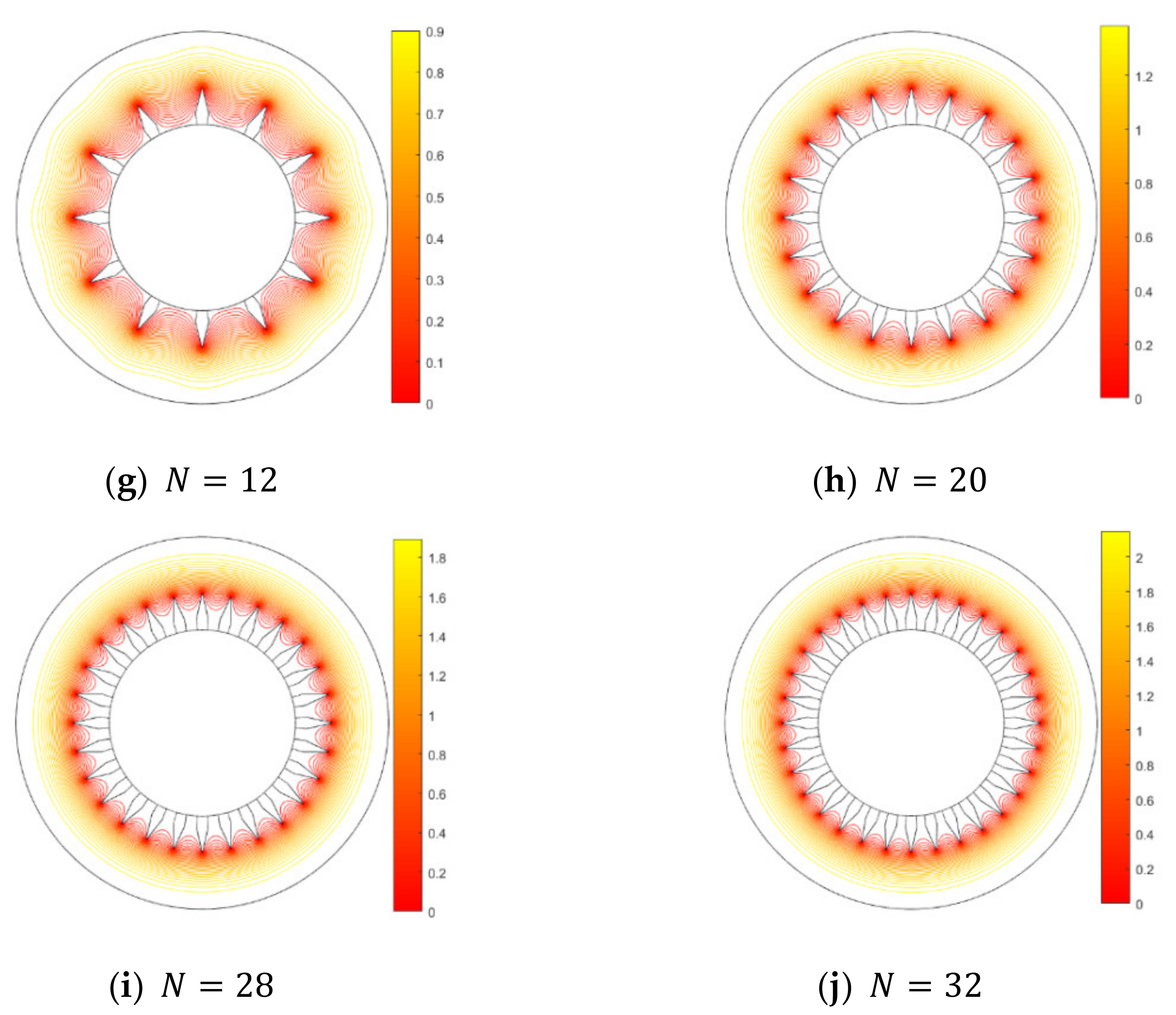
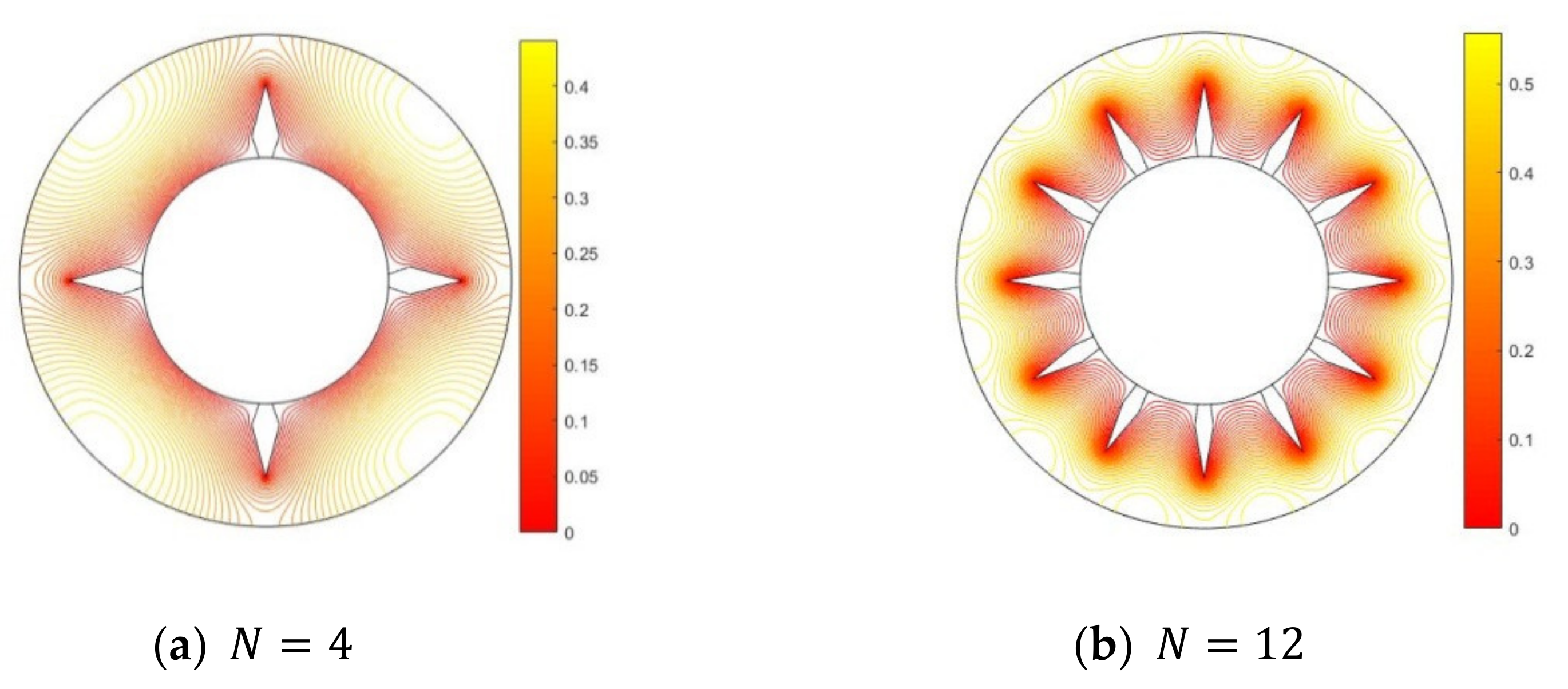
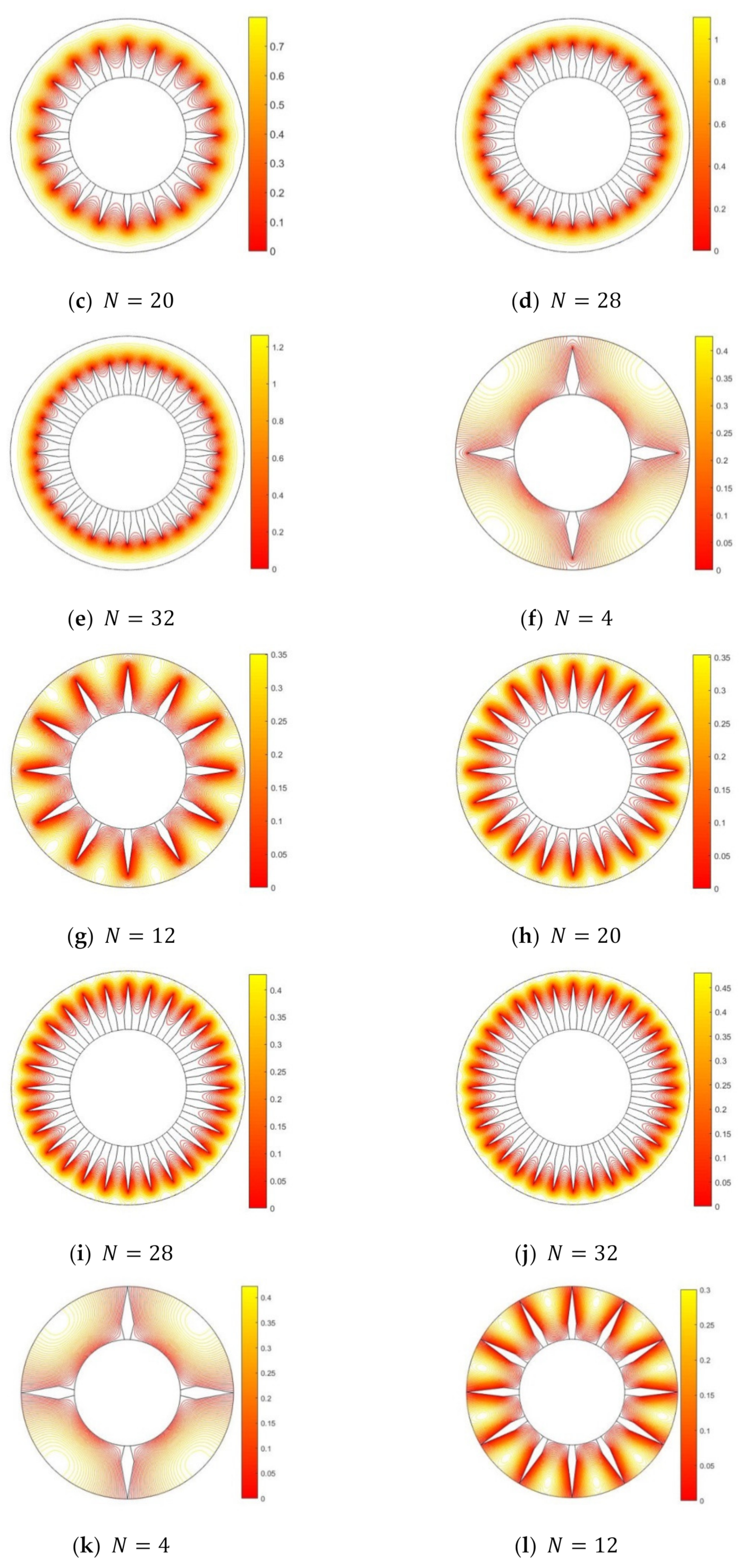
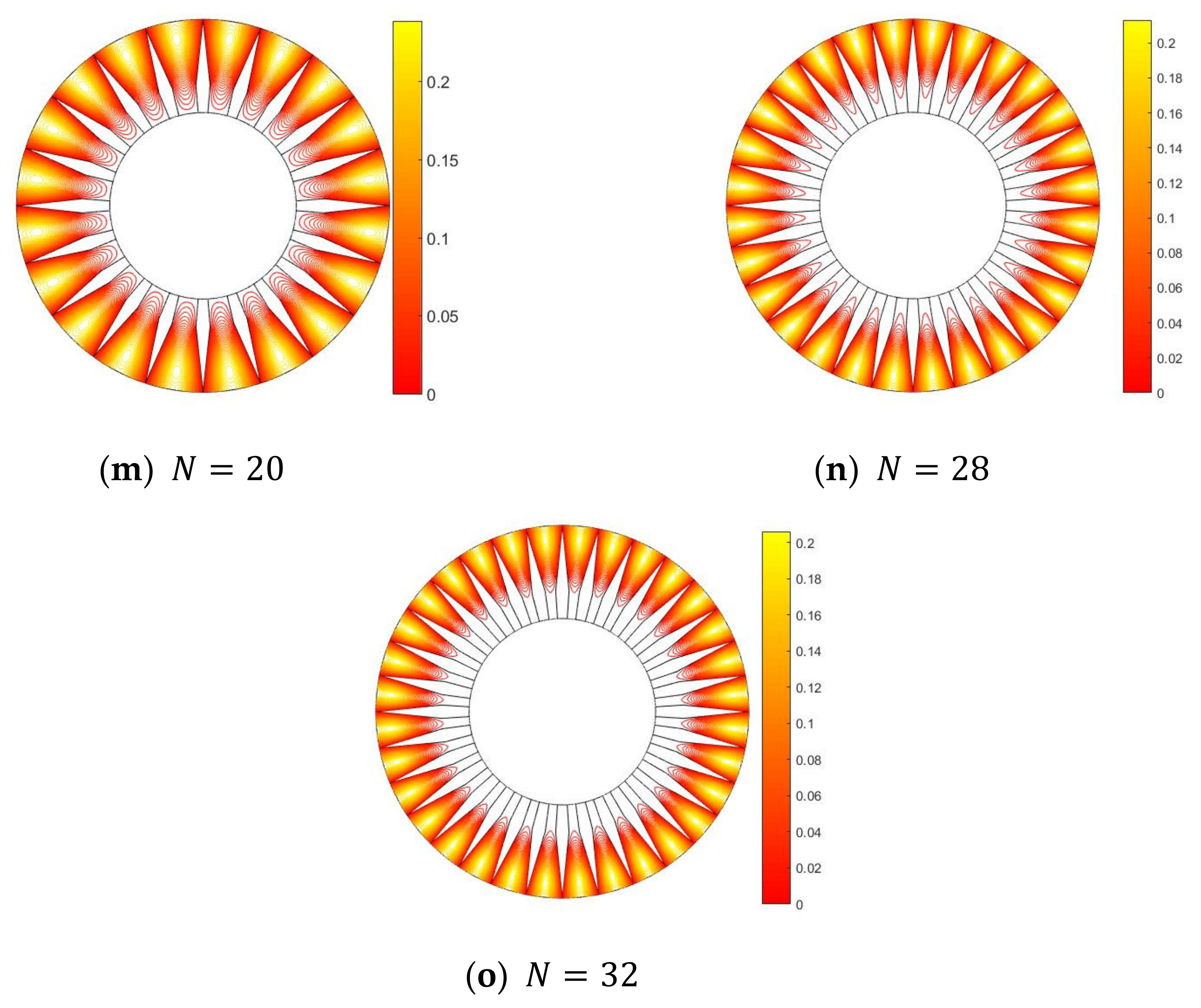
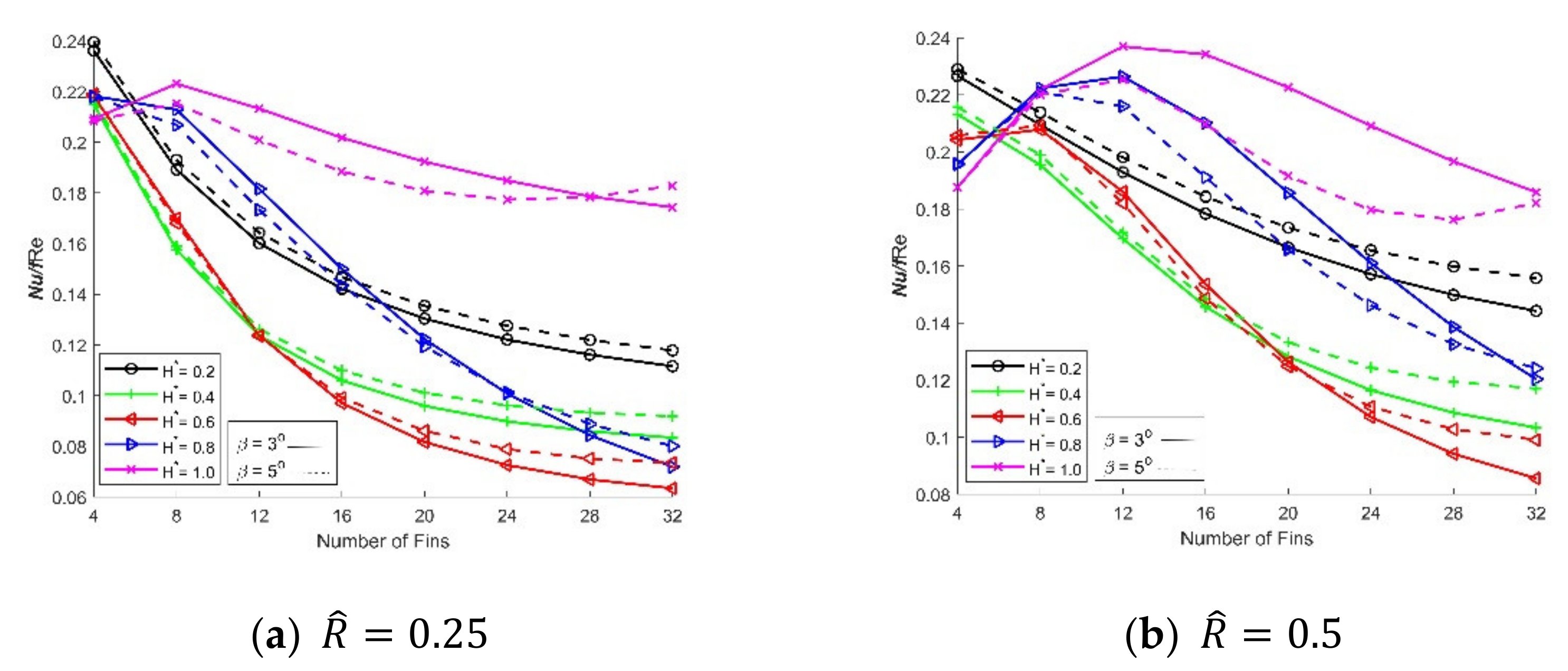
3. Results and Discussion
4. Conclusions
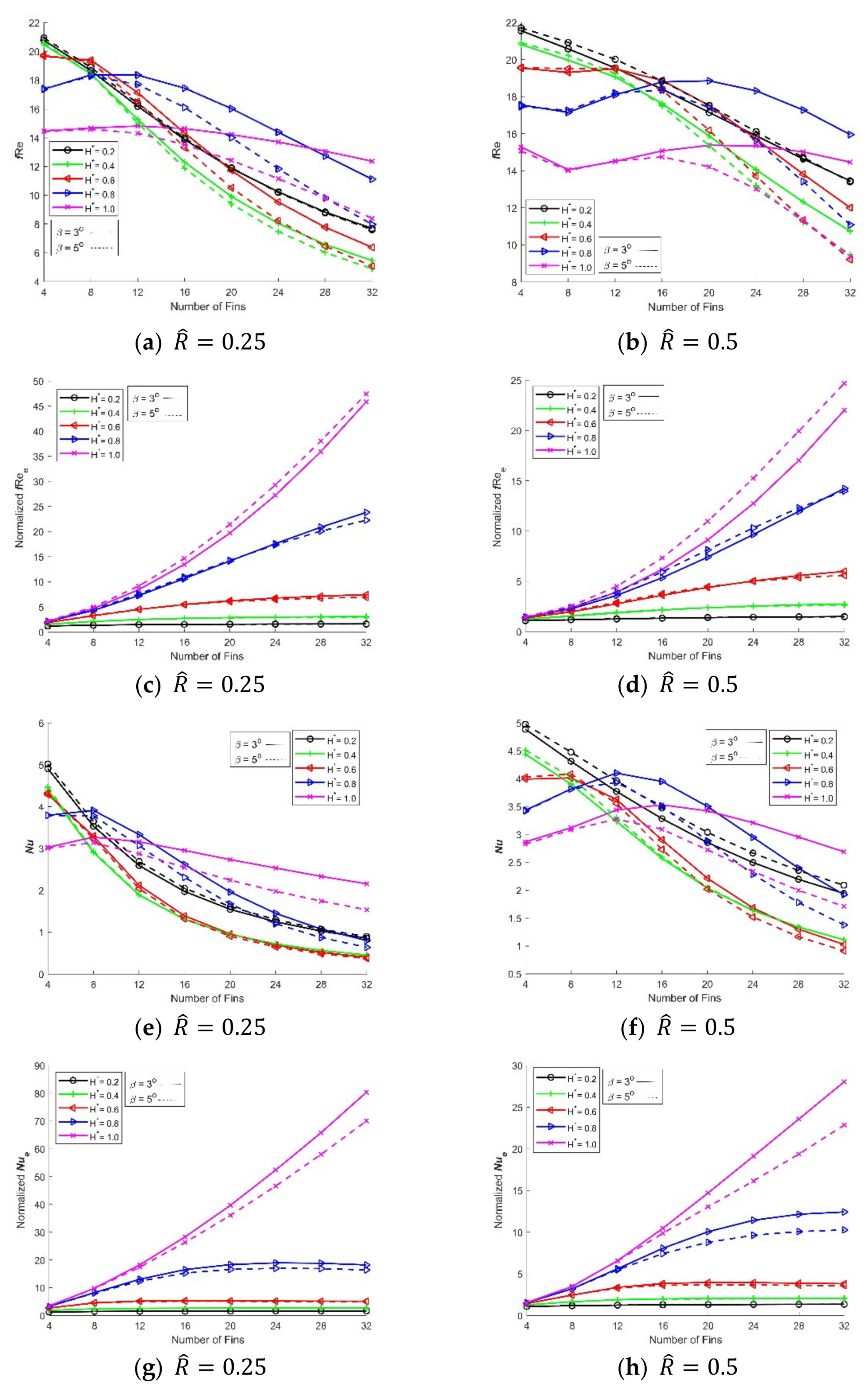
- Flow analysis suggests that the height and the number of diamond fins play a significant role in the velocity profile.
- The reduction of the pressure drop in the proposed DPHE design depends on the choice of fin thickness, fin-height, radii ratio, and the number of diamond fins.
- Enhanced heat transfer is observed in a DPHE with proposed diamond-shaped fins, at a radii ratio of , for the following cases: (i) 4 fins for a fin-height of 20% to 80% of the annulus, (ii) 8–12 fins for a fin-height of 80% of the annulus, and (iii) 16–32 fins for a fin-height of 100% of the annulus.
- The normalized heat transfer coefficient is greater than unity, showing that the augmentation of the fins increases the coefficient of heat transfer as compared to finless DPHE.
- The thermal performance of a DPHE with proposed diamond-shaped fins is significantly better in terms of the corresponding rise in the friction factor compared to the finless double pipe. A fin-height of of the annulus of DPHE gives the maximum performance for any of the tested choices of the number of diamond fins and radii ratio.
- Enhanced heat transfer is noted in the DPHE with proposed diamond-shaped fins for the following cases: considering frictional loss, four fins for fin-height varying from 20% to 80% of the annulus, and eight fins for fin-height 100% of the annulus, at a radii ratio of .
- With a change in the radii ratio, the configurations of the diamond-shaped fins in a DPHE may need to be altered to avoid performance decrease.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Patents
Nomenclature
| Ac | flow cross-sectional area, m2 |
| DH | hydraulic diameter of finned geometry, m |
| f | Fanning friction factor, dimensionless |
| j | Colburn j-factor, dimensionless |
| N | number of fins |
| Nu | average Nusselt number, dimensionless |
| pressure gradient in finned geometry, pa/m | |
| Pr | Prandtl number, dimensionless |
| ph | heated perimeter, m |
| R | dimensionless radial coordinate, dimensionless |
| Re | Reynolds number, dimensionless |
| r, z | cylindrical coordinates |
| ri | radius of inner pipe, m |
| ro | radius of outer pipe, m |
| T | temperature, oC |
| Tb | bulk mean fluid temperature, oC |
| Tw | fluid temperature at the solid–fluid interface, oC |
| U* | dimensionless axial velocity component, dimensionless |
| Umax | maximum axial fluid speed at a cross-section, m/s |
| crown angle (6% of the angle ,rad | |
| half-angle between successive fins, rad | |
| fin half angle, rad | |
| thermal diffusivity, m2/s | |
| thermal conductivity of the fluid, W/m K | |
| dimensionless temperature | |
| average heat transfer coefficient, Wm−2K−1 | |
| heat transfer per unit length, W/m |
Subscripts
| b | bulk |
| e | equivalent diameter |
| h | heated parameter |
| H | hydraulic diameter |
| w | solid wall |
Superscripts
| * | dimensionless quantity |
| overbar () | average value |
References
- Ozisik, M.N. Heat Transfer: A Basic Approach; McGraw-Hill: Singapore, 1985. [Google Scholar]
- Nandakumar, K.; Masliyah, J.H. Fully developed viscous flow in internally finned tubes. Chem. Eng. J. 1975, 10, 113–120. [Google Scholar]
- Masliyah, J.H.; Nandakumar, K. Heat transfer in internally finned tubes. J. Heat Transf. 1976, 98, 257–261. [Google Scholar]
- Shah, R.K.; London, A.L. Laminar Flow Forced Convection in Ducts; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Soliman, H.M.; Chau, T.S.; Trupp, A.C. Analysis of laminar heat transfer in internally finned tubes with uniform outside wall temperature. J. Heat Transf. 1980, 102, 598–604. [Google Scholar]
- Sparrow, E.M.; Charmchi, M. Laminar heat transfer in the externally finned circular tubes. J. Heat Transf. 1980, 102, 605–611. [Google Scholar]
- Parakash, C.; Liu, Y.D. Analysis of laminar flow and heat transfer in the entrance region of an internally finned circular duct. J. Heat Transf. 1985, 107, 84–91. [Google Scholar]
- Tao, W.Q. Conjugated laminar forced convective heat transfer from internally finned tubes. J. Heat Transf. 1987, 109, 791–795. [Google Scholar]
- Agrawal, A.K.; Sengupta, S. Laminar flow and heat transfer in a finned tube annulus. Int. J. Heat Fluid Flow 1990, 11, 54–59. [Google Scholar]
- Suryanarayana, N.V.; Apparao, T.V.V.R. Heat transfer augmentation and pumping power in double-pipe heat exchangers. Exp. Therm. Fluid Sci. 1994, 9, 436–444. [Google Scholar]
- Syed, K.S. Simulation of Fluid Flow Through a Double-Pipe Heat Exchanger. Ph.D. Thesis, University of Bradford, Bradford, UK, 1997. [Google Scholar]
- Yu, B.; Nie, J.H.; Wang, Q.W.; Tao, W.Q. Experimental study on the pressure drop and heat transfer characteristics of tubes with internal wave-like longitudinal fins. Heat Mass Transf. 1999, 35, 65–73. [Google Scholar]
- Nasiruddin, M.H.; Siddiqui, K. Heat transfer augmentation in a heat exchanger tube using a baffle. Int. J. Heat Fluid Flow 2007, 28, 318–328. [Google Scholar]
- Syed, K.S.; Iqbal, M.; Mir, N.A. Convective heat transfer in the thermal entrance region of finned double-pipe. Heat Mass Transf. 2007, 43, 449–457. [Google Scholar]
- Syed, K.S.; Ishaq, M.; Bakhsh, M. Laminar convection in the annulus of a double-pipe with triangular fins. Comput. Fluids 2011, 44, 43–55. [Google Scholar]
- Ishaq, M.; Syed, K.S.; Iqbal, Z.; Hassan, A.; Ali, A. DG-FEM based simulation of laminar convection in an annulus with triangular fins of different heights. Int. J. Therm. Sci. 2013, 72, 125–146. [Google Scholar]
- Iqbal, Z.; Syed, K.S.; Ishaq, M. Optimal configuration of finned annulus in a double pipe with fully developed laminar flow. Appl. Therm. Eng. 2011, 31, 435–1446. [Google Scholar]
- Ishaq, M.; Syed, K.S.; Zafar, I.; Hassan, A. A Conjugate Heat Transfer Analysis of a Triangular Finned Annulus Based on DG-FEM. Math. Probl. Eng. 2018, 2018, 6947565. [Google Scholar]
- Arjmandi, H.; Amiri, P.; Pour, M.S. Geometric optimization of a double pipe heat exchanger with combined vortex generator and twisted tape: A CFD and response surface methodology (RSM) study. Therm. Sci. Eng. Prog. 2020, 18, 100514. [Google Scholar]
- Maakoul, A.E.; Feddi, K.; Saadeddine, S.; Abdellah, A.B.; Metoui, M.E. Performance enhancement of finned annulus using surface interruptions in double-pipe heat exchangers. Energy Convers. Manag. 2020, 210, 112710. [Google Scholar]
- Karoueia, S.S.H.; Ajarostaghi, S.S.M. Influence of a curved conical turbulator on heat transfer augmentation in a helical double-pipe heat exchanger. Heat Transf. 2021, 50, 1872–1894. [Google Scholar]
- Dalkılıç, A.S.; Mercan, H.; Özçelik, G.; Wongwises, S. Optimization of the finned double-pipe heat exchanger using nanofluids as working fluids. J. Therm. Anal. Calorim. 2021, 143, 859–878. [Google Scholar]
- Luo, C.; Song, K. Thermal performance enhancement of a double-tube heat exchanger with novel twisted annulus formed by counter-twisted oval tubes. Int. J. Therm. Sci. 2021, 164, 106892. [Google Scholar]
- Poongavanam, G.; Kim, S.C. Effect of shot peening on augmenting the thermo-fluid characteristic of a concentric tube water-to-air counter flow heat exchanger. Case Stud. Therm. Eng. 2021, 25, 100887. [Google Scholar]
- Ali, A.; Khalid, S.S. An outlook of high performance computing infrastructures for scientific computing. Adv. Comput. 2013, 91, 87–118. [Google Scholar]





| Triangles | ||||||
|---|---|---|---|---|---|---|
| 4 | 0.2 | 1.3000 | 20.7725 | 4.9051 | 0.2685 | 4315 |
| 0.4 | 1.1389 | 20.4763 | 4.3981 | 0.2443 | 4189 | |
| 0.6 | 1.0087 | 19.6619 | 4.2889 | 0.2481 | 3922 | |
| 0.8 | 0.9015 | 17.3747 | 3.7919 | 0.2482 | 3783 | |
| 1.0 | 0.8113 | 14.4670 | 3.0280 | 0.2380 | 3294 | |
| 8 | 0.2 | 1.1547 | 18.6648 | 3.5309 | 0.2151 | 2367 |
| 0.4 | 0.9216 | 18.4451 | 2.9066 | 0.1792 | 2319 | |
| 0.6 | 0.7607 | 19.3996 | 3.2968 | 0.1933 | 2123 | |
| 0.8 | 0.6426 | 18.3673 | 3.9105 | 0.2421 | 1894 | |
| 1.0 | 0.5516 | 14.6700 | 3.2728 | 0.2537 | 1783 | |
| 12 | 0.2 | 1.0371 | 16.1870 | 2.5926 | 0.1821 | 1662 |
| 0.4 | 0.7714 | 15.2731 | 1.8899 | 0.1407 | 1573 | |
| 0.6 | 0.6069 | 17.1333 | 2.1223 | 0.1409 | 1461 | |
| 0.8 | 0.4942 | 18.3535 | 3.3330 | 0.2065 | 1294 | |
| 1.0 | 0.4116 | 14.8160 | 3.1601 | 0.2426 | 1174 | |
| 16 | 0.2 | 0.9404 | 13.8735 | 1.9727 | 0.1617 | 1323 |
| 0.4 | 0.6617 | 12.3026 | 1.3041 | 0.1205 | 1256 | |
| 0.6 | 0.5022 | 14.3244 | 1.3904 | 0.1104 | 1147 | |
| 0.8 | 0.3981 | 17.4476 | 2.6178 | 0.1706 | 951 | |
| 1.0 | 0.3240 | 14.6330 | 2.9529 | 0.2295 | 866 | |
| 20 | 0.2 | 0.8596 | 11.8639 | 1.5470 | 0.1483 | 1026 |
| 0.4 | 0.5780 | 9.9060 | 0.9504 | 0.1091 | 1000 | |
| 0.6 | 0.4264 | 11.7185 | 0.9574 | 0.0929 | 884 | |
| 0.8 | 0.3308 | 16.0240 | 1.9603 | 0.1391 | 764 | |
| 1.0 | 0.2641 | 14.2170 | 2.7342 | 0.2187 | 644 | |
| 24 | 0.2 | 0.7911 | 10.2341 | 1.2498 | 0.1389 | 802 |
| 0.4 | 0.5120 | 8.0371 | 0.7221 | 0.1022 | 780 | |
| 0.6 | 0.3690 | 9.5238 | 0.6912 | 0.0825 | 739 | |
| 0.8 | 0.2810 | 14.3850 | 1.4505 | 0.1147 | 611 | |
| 1.0 | 0.2205 | 13.7050 | 2.5339 | 0.2103 | 509 | |
| 28 | 0.2 | 0.7323 | 8.8284 | 1.0255 | 0.1321 | 753 |
| 0.4 | 0.4588 | 6.5799 | 0.5655 | 0.0977 | 723 | |
| 0.6 | 0.3240 | 7.7713 | 0.5203 | 0.0761 | 624 | |
| 0.8 | 0.2427 | 12.7328 | 1.0745 | 0.0960 | 535 | |
| 1.0 | 0.1874 | 13.0630 | 2.3334 | 0.2031 | 426 | |
| 32 | 0.2 | 0.6812 | 7.6880 | 0.8581 | 0.1269 | 707 |
| 0.4 | 0.4148 | 5.4547 | 0.4549 | 0.0948 | 647 | |
| 0.6 | 0.2878 | 6.3751 | 0.4042 | 0.0721 | 572 | |
| 0.8 | 0.2123 | 11.1190 | 0.7998 | 0.0818 | 476 | |
| 1.0 | 0.1614 | 12.3670 | 2.1563 | 0.1983 | 358 |
| Triangular Fin Case | Rectangular Fin Case | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Present Results | Literature [15] Results | Present Results | Literature [11] Results | ||||||
| 0.2 | 12 | 20.071 | 3.9125 | 20.0691 | 3.9118 | 19.153 | 3.4864 | 19.125 | 3.4833 |
| 24 | 16.563 | 2.6075 | 16.5504 | 2.606 | 14.319 | 2.0474 | 14.302 | 2.0466 | |
| 0.4 | 12 | 19.608 | 3.3675 | 19.5545 | 3.3543 | 19.391 | 3.1677 | 19.358 | 3.1644 |
| 24 | 15.067 | 1.7428 | 15.0379 | 1.7399 | 13.032 | 1.358 | 12.998 | 1.3572 | |
| 0.6 | 12 | 19.937 | 3.8454 | 19.9076 | 3.8319 | 20.083 | 3.9379 | 20.027 | 3.9256 |
| 24 | 17.251 | 1.9279 | 17.1831 | 1.9172 | 15.874 | 1.4214 | 15.815 | 1.4213 | |
| 0.8 | 12 | 18.282 | 4.3454 | 18.251 | 4.3235 | 17.197 | 4.2436 | 17.145 | 4.2311 |
| 24 | 19.59 | 3.6711 | 19.4964 | 3.6305 | 21.024 | 3.7524 | 20.818 | 3.7216 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishaq, M.; Ali, A.; Amjad, M.; Syed, K.S.; Iqbal, Z. Diamond-Shaped Extended Fins for Heat Transfer Enhancement in a Double-Pipe Heat Exchanger: An Innovative Design. Appl. Sci. 2021, 11, 5954. https://doi.org/10.3390/app11135954
Ishaq M, Ali A, Amjad M, Syed KS, Iqbal Z. Diamond-Shaped Extended Fins for Heat Transfer Enhancement in a Double-Pipe Heat Exchanger: An Innovative Design. Applied Sciences. 2021; 11(13):5954. https://doi.org/10.3390/app11135954
Chicago/Turabian StyleIshaq, Muhammad, Amjad Ali, Muhammad Amjad, Khalid Saifullah Syed, and Zafar Iqbal. 2021. "Diamond-Shaped Extended Fins for Heat Transfer Enhancement in a Double-Pipe Heat Exchanger: An Innovative Design" Applied Sciences 11, no. 13: 5954. https://doi.org/10.3390/app11135954
APA StyleIshaq, M., Ali, A., Amjad, M., Syed, K. S., & Iqbal, Z. (2021). Diamond-Shaped Extended Fins for Heat Transfer Enhancement in a Double-Pipe Heat Exchanger: An Innovative Design. Applied Sciences, 11(13), 5954. https://doi.org/10.3390/app11135954






